Оглавление:

| Здравствуйте! Я Людмила Анатольевна Фирмаль, занимаюсь помощью студентам более 17 лет. У меня своя команда грамотных, сильных преподавателей. Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И неважно – она по объёму на две формулы или огромная, сложно структурированная, на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте. |
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
Как получить помощь в выполнении заданий по математике
Вы можете написать сообщение в WhatsApp. После этого я оценю ваш заказ и укажу стоимость и срок выполнения вашей работы. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за вашу работу, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл готовой работы в личные сообщения.
Сколько стоит помощь
Стоимость помощи зависит от задания и требований Вашего учебного заведения. На цену влияют: сложность, количество заданий и срок выполнения. Поэтому для оценки стоимости заказа максимально качественно сфотографируйте или пришлите файл задания, при необходимости, загружайте поясняющие фотографии лекций, файлы методичек, указывайте свой вариант.
Какой срок выполнения
Минимальный срок выполнения составляет 2-4 дня, но помните, срочные задания оцениваются дороже.
Как оплатить
Сначала пришлите задание, я оценю, после вышлю вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.
Гарантии и исправление ошибок
В течение 1 года с момента получения Вами готового решения действует гарантия. В течении 1 года я и моя команда исправим любые ошибки.
Чуть ниже я предоставила примеры оформления работ по математике, так я буду оформлять ваши работы если закажите у меня.
Кроме примеров, я разместила и полный курс теории в виде лекций, если вдруг вы захотите попробовать сами решить.
Элементы линейной алгебры
- Матрица
- Операции над матрицами
- Определитель матрицы
- Обратная матрица
- Системы линейных уравнений n*n
- Ранг матрицы
- Системы линейных уравнений m*n
Пример оформления заказа №1.4.
Задана система линейных алгебраических уравнений:
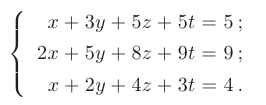
Требуется, используя метод Гаусса, найти общее и соответствующее ему базисное решение заданной системы уравнений.
► Совместность системы. Выпишем расширенную матрицу системы 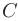 , найдем ее ранг и одновременно ранг матрицы коэффициентов
, найдем ее ранг и одновременно ранг матрицы коэффициентов 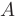 заданной системы уравнений:
заданной системы уравнений:
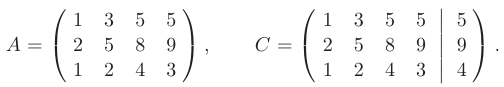
Для этого с помощью серии элементарных преобразований приведем расширенную матрицу системы к трапециевидной форме.
Вначале исключим переменную 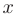 из всех уравнений, кроме первого. Для этого умножим первую строку матрицы
из всех уравнений, кроме первого. Для этого умножим первую строку матрицы 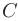 на коэффициент —2/1 = —2 и почленно сложим полученную строку со второй строкой расширенной матрицы. Затем умножим первую строку матрицы
на коэффициент —2/1 = —2 и почленно сложим полученную строку со второй строкой расширенной матрицы. Затем умножим первую строку матрицы 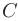 на—1/1 = — 1 и почленно сложим полученную строку с третьей строкой расширенной матрицы:
на—1/1 = — 1 и почленно сложим полученную строку с третьей строкой расширенной матрицы:
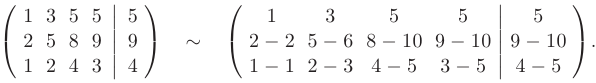
Заметим, что в полученной матрице вторая и третья строки содержат только отрицательные ненулевые элементы. Для большего удобства запишем эти строки в эквивалентную матрицу с обратными знаками. Затем исключим переменную у из третьего уравнения. Для этого умножим вторую строку матрицы 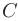 на коэффициент — 1/1 = —1 и почленно сложим полученную строку с третьей строкой расширенной матрицы:
на коэффициент — 1/1 = —1 и почленно сложим полученную строку с третьей строкой расширенной матрицы:
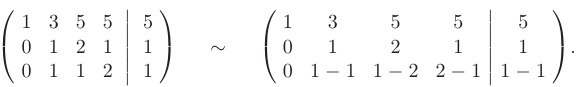
В результате получим эквивалентную запись расширенной матрицы 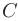 и матрицы коэффициентов системы
и матрицы коэффициентов системы 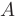 в трапециевидной форме:
в трапециевидной форме:
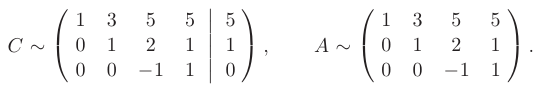
Как видно, ранг матрицы коэффициентов системы равен 3 и добавлением столбца не может быть увеличен. Из этого следует, что исходная система уравнений совместна.
Решение системы. Найдем общее решение полученной системы, воспользовавшись ее трапециевидной структурой
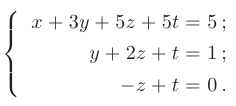
Так как число неизвестных системы 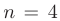 больше числа уравнений
больше числа уравнений 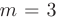 , то переменные необходимо разделить на свободные и базисные. Число базисных переменных будет равно рангу матрицы коэффициентов системы
, то переменные необходимо разделить на свободные и базисные. Число базисных переменных будет равно рангу матрицы коэффициентов системы 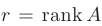 . Выберем в качестве базисных три произвольные переменные такие, что определитель, составленный из их коэффициентов, будет отличен от нуля. Пусть это будут переменные
. Выберем в качестве базисных три произвольные переменные такие, что определитель, составленный из их коэффициентов, будет отличен от нуля. Пусть это будут переменные 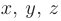 :
:
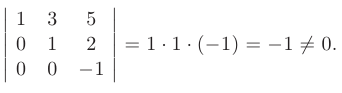
Тогда переменная 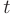 остается свободной. Выразим через
остается свободной. Выразим через 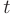 базисные переменные
базисные переменные 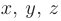 , перенося
, перенося 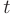 в правую часть равенства, начиная с последнего.
в правую часть равенства, начиная с последнего.
Из третьего уравнения найдем выражение для 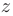 :
:

Из второго уравнения найдем выражение для 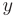 :
:
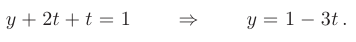
Наконец, из первого уравнения найдем выражение для 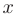 :
:
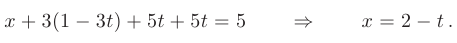
Общее решение заданной системы уравнений найдено:
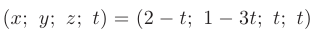
Соответствующее ему базисное решение найдем приравняв к нулю свободную переменную, т.е. при 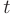 = 0:
= 0:
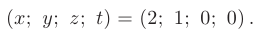
Матрицы и квадратичные формы
Элементы векторной алгебры и аналитической геометрии
- Декартовы координаты
- Векторы и операции над ними
- Линейная зависимость и координаты векторов
- Линейные операции над векторами в координатной форме
- Уравнение прямой на плоскости
- Уравнения прямой и плоскости в пространстве
- Уравнения линий второго порядка на плоскости
- Эллипс
- Гипербола
- Парабола
Пример оформления заказа №2.4.
Дано уравнение окружности
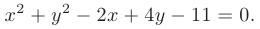
Требуется найти координаты центра и радиус окружности.
► Выделяя полные квадраты для членов, содержащих 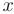 , и членов, содержащих
, и членов, содержащих 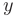 , приведем это уравнение к виду
, приведем это уравнение к виду
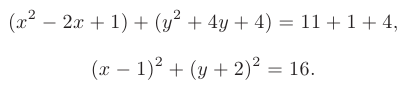
Таким образом, центр данной окружности находится в точке 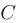 (1; —2), а радиус окружности
(1; —2), а радиус окружности 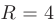 .
.
Пример оформления заказа №2.5.
Дано уравнение гиперболы
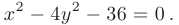
Требуется найти параметры 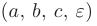 гиперболы.
гиперболы.
► Приведем данное уравнение к каноническому виду
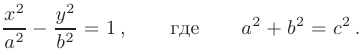
Для этого разделим заданное уравнение на 36:
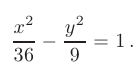
Отсюда следует, что действительная полуось гиперболы 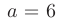 , а мнимая полуось
, а мнимая полуось 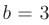 . По формуле
. По формуле 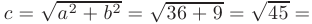
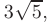 т.е. координаты фокусов
т.е. координаты фокусов 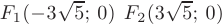 . Эксцентриситет гиперболы равен
. Эксцентриситет гиперболы равен 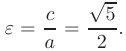
Введение в анализ функций одной переменной
- Предел последовательности
- Функция одной переменной
- Предел функции
- Бесконечно малые и бесконечно большие функции
- Раскрытие неопределённостей
- Непрерывность функции
- Асимптоты графика функции
Пример оформления заказа №3.7.
Найти асимптоты графика функции
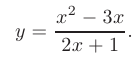
► Так как функция непрерывна на всей оси, кроме точки 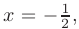 то вертикальная асимптота может существовать лишь в этой точке:
то вертикальная асимптота может существовать лишь в этой точке:
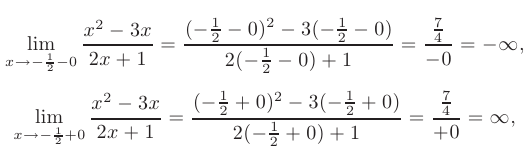
и, следовательно, прямая  вертикальная асимптота.
вертикальная асимптота.
Найдем наклонные асимптоты. Так как
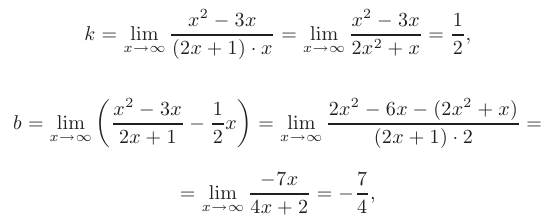
то прямая
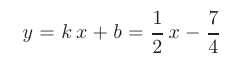
является наклонной асимптотой.
Дифференциальное исчисление функций одной переменной
- Определение производной функции
- Производные основных элементарных функций
- Дифференциал функции
- Производные и дифференциалы высших порядков
- Теоремы о дифференцируемых функциях
- Правило Лопиталя
Пример оформления заказа №4.1.
Вычислить предел из примера 3.3 (п.3.5) с применением правила Лопиталя.
► В данном пределе при 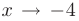 числитель и знаменатель дроби неограниченно убывают, т.е. мы сталкиваемся с неопределенностью вида
числитель и знаменатель дроби неограниченно убывают, т.е. мы сталкиваемся с неопределенностью вида
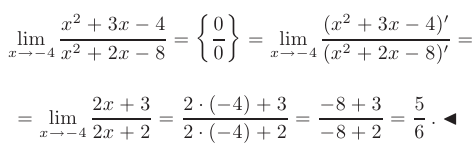
Сравнивая два приема раскрытия неопределенностей делаем вывод, что применение правила Лопиталя существенно снижает трудоемкость процесса.
Исследование функций
Одним из важнейших приложений производной является ее применение к исследованию функций и построению графиков.
- Возрастание и убывание функции
- Максимум и минимум функции
- Наибольшее и наименьшее значение функции на отрезке
- Выпуклость графика функции. Точки перегиба
Схема исследования функции и построения ее графика
- Найти область определения функции;
- Исследовать функцию на непрерывность и найти асимптоты графика функции;
- Найти критические точки первого рода, интервалы возрастания, убывания функции и точки ее экстремума;
- Найти критические точки второго рода, интервалы выпуклости, вогнутости графика функции и точки перегиба;
- Найти точки пересечения графика функции с осями координат и при необходимости составить таблицу дополнительных точек;
- Построить график функции
 в системе координат
в системе координат 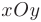 на основании полученных данных.
на основании полученных данных.
Пример оформления заказа №4.2.
Требуется, используя методы дифференциального исчисления, провести исследование заданных функций и на основании полученных данных построить их графики:
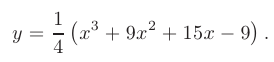
► 1. Областью определения данной функции являются все действительные значения аргумента 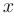 :
:
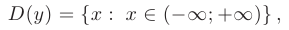
следовательно, функция непрерывна на всей числовой прямой и ее график не имеет вертикальных асимптот.
- Выясним наличие у графика заданной функции наклонных асимптот. Для определения коэффициентов уравнения асимптоты
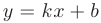 воспользуемся формулами:
воспользуемся формулами:
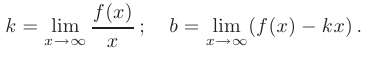
В нашем случае имеем:
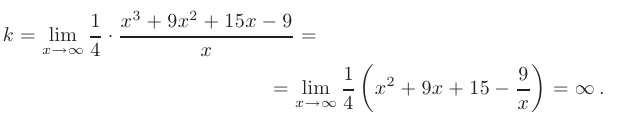
Следовательно, график функции не имеет наклонных асимптот.
- Исследуем функцию на экстремумы и определим интервалы монотонности. С этой целью найдем и приравняем к нулю ее производную:
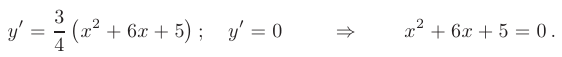
Решая полученное квадратное уравнение, находим координаты двух критических точек первого рода:
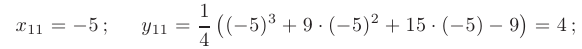
Разбиваем область определения функции этими точками на части и по знаку ее первой производной выявляем интервалы монотонности и наличие экстремумов.

- Определим точки перегиба графика функции и интервалы его выпуклости и вогнутости. Для этого найдем вторую производную заданной функции и приравняем ее к нулю:
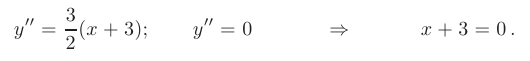
Решая полученное уравнение, находим координаты критической точки второго рода:
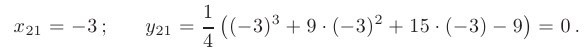
Разбиваем область определения функции полученной точкой на части и по знаку ее второй производной выявляем интервалы выпуклости и наличие точки перегиба.

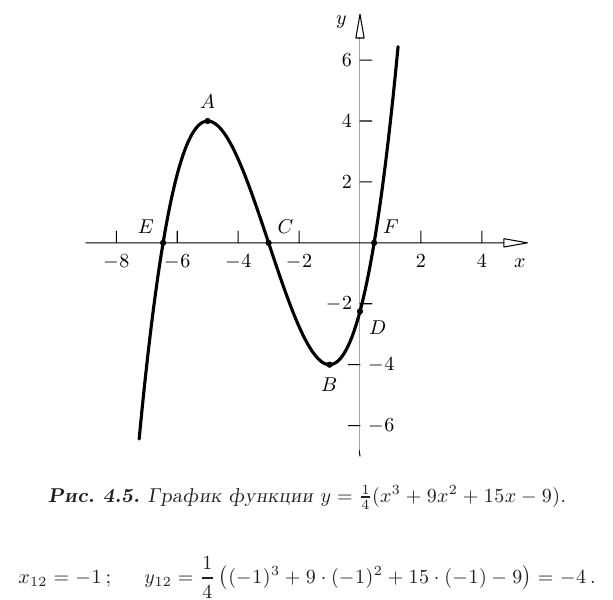
- Для построения графика в выбранной системе координат изобразим: точку максимума
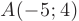 , минимума
, минимума 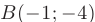 , перегиба
, перегиба 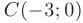 и точку пересечения графика функции с осью
и точку пересечения графика функции с осью  — точку
— точку 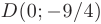 . В качестве дополнительных точек можно использовать точки пересечения графика функции с осью
. В качестве дополнительных точек можно использовать точки пересечения графика функции с осью 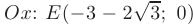 и
и 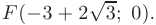
- С учетом результатов проведенных исследований построим график функции и все характерные точки в системе координат
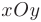 (см. рис. 4.5).
(см. рис. 4.5).
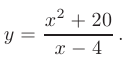
► 1. Областью определения данной функции являются все действительные значения аргумента 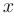 , за исключением точки в которой знаменатель дроби становится равен нулю. Это значит, что функция непрерывна на всей числовой прямой, кроме точки
, за исключением точки в которой знаменатель дроби становится равен нулю. Это значит, что функция непрерывна на всей числовой прямой, кроме точки 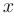 = 4 в которой она претерпевает разрыв:
= 4 в которой она претерпевает разрыв:
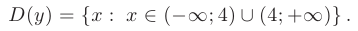
- Для классификации точки разрыва вычислим односторонние пределы функции в этой точке:
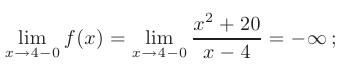
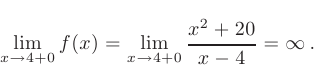
Таким образом, данная точка является точкой разрыва второго рода, а прямая 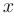 = 4 — вертикальной асимптотой графика.
= 4 — вертикальной асимптотой графика.
Выясним наличие у графика заданной функции наклонных асимптот. Для определения коэффициентов уравнения асимптоты 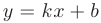 воспользуемся формулами:
воспользуемся формулами:
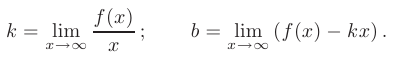
В нашем случае имеем:
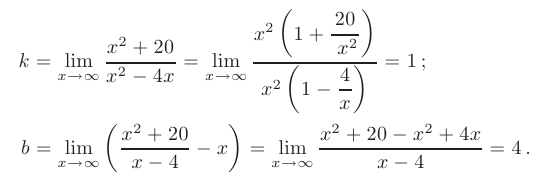
Из этого следует, что прямая 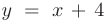 является наклонной асимптотой графика исследуемой функции.
является наклонной асимптотой графика исследуемой функции.
- Исследуем функцию на экстремумы и определим интервалы монотонности. С этой целью найдем ее критические точки первого рода для чего приравняем к нулю первую производную функции:
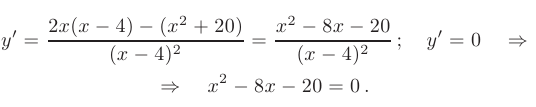
Решая полученное квадратное уравнение, находим координаты двух критических точек первого рода:
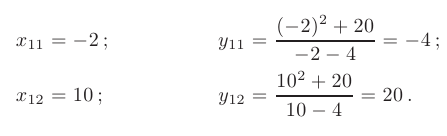
Разбиваем область определения функции найденными точками на части и на основании знака ее первой производной выявляем интервалы монотонности и наличие экстремумов.

- Для определения точек перегиба и интервалов выпуклости и вогнутости графика необходимо отыскать критические точки второго рода для заданной функции. С этой целью найдем вторую производную функции и приравняем ее числитель к нулю:
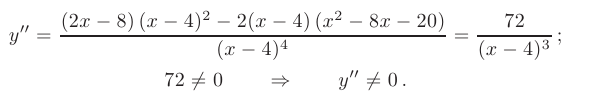
Отсюда следует, что исследуемая функция не имеет ни одной точки перегиба.
В таком случае, разобьем область определения функции точкой разрыва  = 4 на две части, в каждой из которых установим знак второй производной.
= 4 на две части, в каждой из которых установим знак второй производной.

- Для построения графика в выбранной системе координат изобразим: точку максимума
 , минимума
, минимума 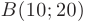 . точку пересечения вертикальной асимптоты с наклонной — точку
. точку пересечения вертикальной асимптоты с наклонной — точку 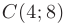 и точку пересечения графика функции с осью
и точку пересечения графика функции с осью 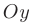 — точку
— точку 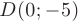 .
. - С учетом результатов проведенных исследований построим график функции, его асимптоты и все характерные точки в системе координат
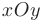 (см. рис. 4.6).
(см. рис. 4.6).
Дифференциальное исчисление функций многих переменных
- Функция многих переменных
- Непрерывность и частные производные
- Полное приращение и дифференциал
- Достаточное условие дифференцируемости
- Производная по направлению и градиент
- Экстремум функции двух переменных
- Необходимое условие экстремума двух переменных
- Достаточное условие экстремума
- Наибольшее и наименьшее значения функции
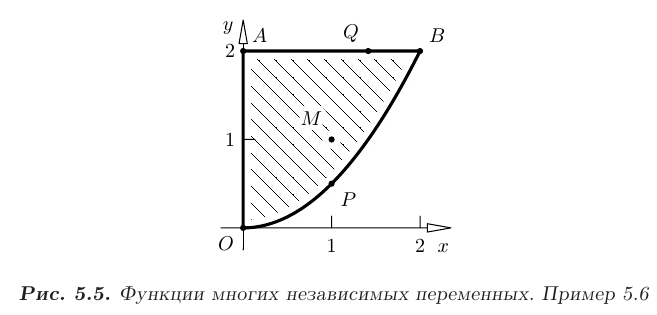
Пример оформления заказа №5.6.
Требуется найти наибольшее и наименьшее значения функции
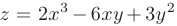
в замкнутой ограниченной области 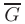 , заданной системой неравенств:
, заданной системой неравенств:
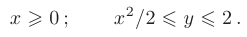
Все полученные линии и характерные точки изобразить в системе координат  .
.
► 1. Для решения поставленной задачи изобразим заданную область  в системе координат
в системе координат  .
.
Первому неравенству 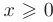 соответствует полуплоскость, лежащая справа от оси
соответствует полуплоскость, лежащая справа от оси 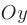 . Второе неравенство
. Второе неравенство 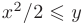 отсекает от этой полуплоскости часть, лежащую ниже параболы
отсекает от этой полуплоскости часть, лежащую ниже параболы 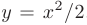 , а третье неравенство
, а третье неравенство 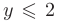 отсекает часть, лежащую выше горизонтальной линии
отсекает часть, лежащую выше горизонтальной линии 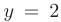 . В результате получим область G, изображенную на рис. 5.5.
. В результате получим область G, изображенную на рис. 5.5.
Точки, соответствующие пересечению линий, которые ограничивают область 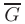 , обозначим буквами
, обозначим буквами
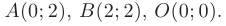
- Для исследования функции
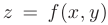 на экстремум вначале найдем ее частные производные первого порядка
на экстремум вначале найдем ее частные производные первого порядка 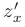 и
и 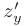 и, используя необходимое условие экстремума, найдем координаты критических точек:
и, используя необходимое условие экстремума, найдем координаты критических точек:

Решив систему уравнений:
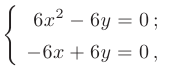
найдем две точки 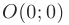 и
и 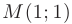 , удовлетворяющие необходимому условию экстремума.
, удовлетворяющие необходимому условию экстремума.
Первая из них принадлежит границе области (см. рис. 5.5). Следовательно, единственной внутренней точкой, в которой функция 2 может иметь экстремум, является точка 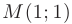 .
.
Отыскав частные производные второго порядка
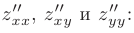
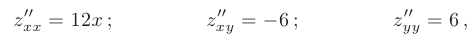
найдем значение выражения  в точке
в точке 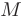 :
:
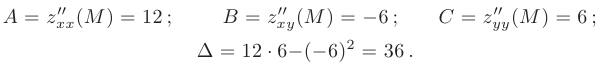
Так как 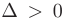 и
и 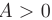 , то функция
, то функция 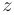 в точке
в точке 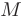 имеет минимум:
имеет минимум:
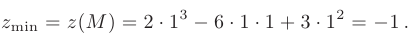
- Точки, в которых функция
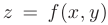 принимает наибольшее и наименьшее значения могут находиться как внутри области, так и на ее границе.
принимает наибольшее и наименьшее значения могут находиться как внутри области, так и на ее границе.
Если функция принимает наибольшее (или наименьшее) значение во внутренней точке области, то она имеет в этой точке экстремум. Единственной точкой экстремума, лежащей внутри исследуемой области является точка 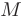 .
.
Исследуем функцию на границе, которая состоит из отрезков 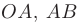 и дуги параболы
и дуги параболы 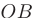 .
.
Линия 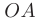 . На отрезке
. На отрезке 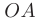 выполняется равенство
выполняется равенство  , поэтому на этом отрезке функция
, поэтому на этом отрезке функция 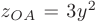 . При
. При 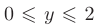 это возрастающая функция одной переменной
это возрастающая функция одной переменной 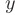 . Наибольшее и наименьшее значения она принимает на концах отрезка
. Наибольшее и наименьшее значения она принимает на концах отрезка  .
.
Линия  . На отрезке
. На отрезке 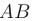 выполняется равенство
выполняется равенство 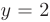 , следовательно, на этом отрезке функция
, следовательно, на этом отрезке функция
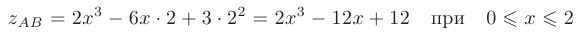
представляет собой функцию одной переменной 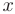 . Наибольшее и наименьшее значения этой функции находятся среди ее значений в критических точках и на концах отрезка
. Наибольшее и наименьшее значения этой функции находятся среди ее значений в критических точках и на концах отрезка 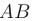 .
.
Исследуем полученную функцию на экстремум. Для этого найдем производную функции 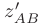 и приравняем ее к нулю:
и приравняем ее к нулю:
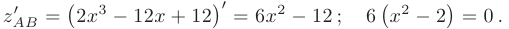
Решив уравнение 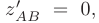 , находим координаты критических точек
, находим координаты критических точек 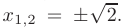 . Заданном}’ условию
. Заданном}’ условию 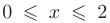 удовлетворяет лишь одно значение
удовлетворяет лишь одно значение  . На отрезке
. На отрезке 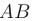 ему соответствует точка
ему соответствует точка 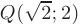 .
.
Итак, наибольшее и наименьшее значения функции 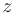 на отрезке
на отрезке 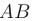 находятся среди ее значений в точках
находятся среди ее значений в точках 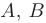 и
и 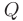 (см. рис. 5.5).
(см. рис. 5.5).
Линия 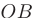 . На линии
. На линии 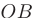 выполняется равенство
выполняется равенство
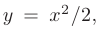
в результате исследуемая функция имеет вид
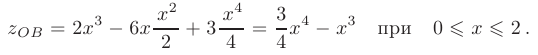
Исследуем полученную функцию на экстремум. Для этого найдем производную функции 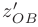 и приравняем ее к нулю:
и приравняем ее к нулю:
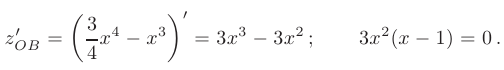
Решив уравнение 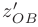 = 0, находим координаты критических точек
= 0, находим координаты критических точек
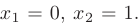
Координаты обеих найденных точек удовлетворяют заданному неравенству 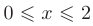 . На дуге
. На дуге  этим значениям соответствуют точки
этим значениям соответствуют точки
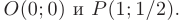
Таким образом, наибольшее и наименьшее значения функции  на дуге
на дуге 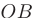 находятся среди ее значений в точках
находятся среди ее значений в точках 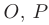 и
и 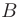 .
.
На основании выше изложенного можно сделать вывод о том, что наибольшее и наименьшее значения функции
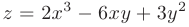
в замкнутой ограниченной области 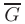 , заданной системой неравенств
, заданной системой неравенств
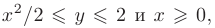
находятся среди ее значений в точках 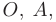
 и
и 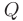 .
.
Координаты указанных точек  и значения функции
и значения функции  в них приведены в таблице:
в них приведены в таблице:
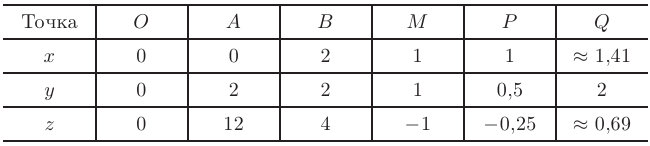
Наибольшее и наименьшее значения функции 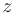 в замкнутой ограниченной области
в замкнутой ограниченной области 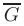 соответственно равны
соответственно равны 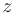 = 12 (точка А) и
= 12 (точка А) и 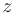 = — 1
= — 1
(точка 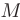 ). Все полученные линии и характерные точки в системе координат
). Все полученные линии и характерные точки в системе координат 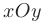 показаны на рис. 5.5.
показаны на рис. 5.5.
Интегральное исчисление функций одной переменной
- Первообразная и интеграл
- Основные методы интегрирования
- Интегрирование некоторых классов функций
- Интегрирование рациональных дробей
- Интегрирование иррациональных функций
Пример оформления заказа №6.1.
Требуется найти неопределенные интегралы от указанных тригонометрических функций:
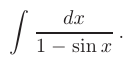
► Для вычисления этого интеграла воспользуемся универсальной тригонометрической подстановкой 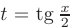 :
:
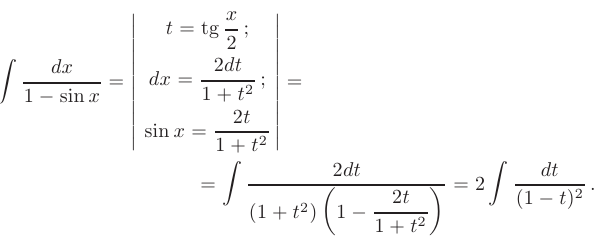
Используя замену переменной 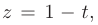 проинтегрируем полученную функцию, а затем, возвращаясь к первоначальным переменным
проинтегрируем полученную функцию, а затем, возвращаясь к первоначальным переменным 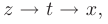 окончательно запишем:
окончательно запишем:
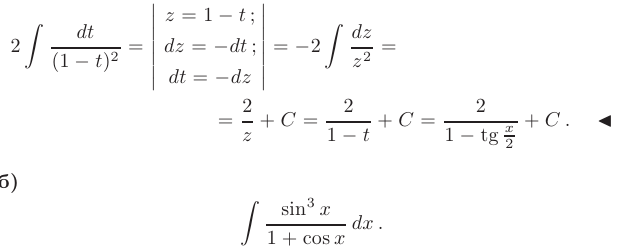
Заметим, что подынтегральная функция
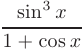
является нечетной:
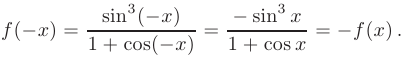
Поэтому воспользуемся заменой 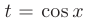 и, учитывая, что
и, учитывая, что 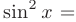
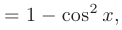 , получим:
, получим:
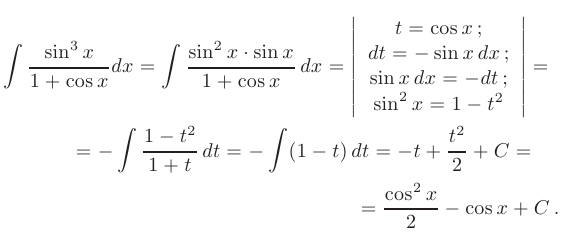
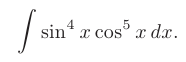
► Так как подынтегральная функция имеет вид 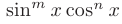 и показатель степени
и показатель степени 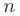 — нечетный, то для ее интегрирования выполним подстановку
— нечетный, то для ее интегрирования выполним подстановку 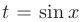 . С учетом того, что
. С учетом того, что 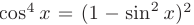 получим:
получим:
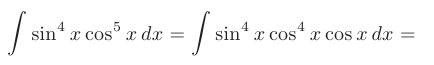
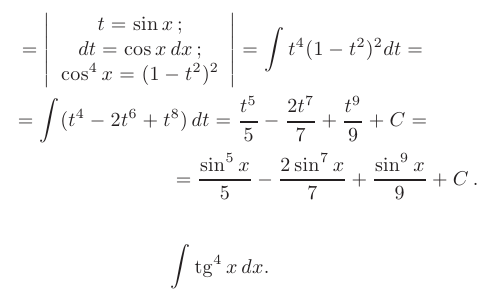
Так как подынтегральная функция имеет вид 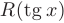 , то для ее интегрирования воспользуемся заменой
, то для ее интегрирования воспользуемся заменой 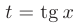 :
:
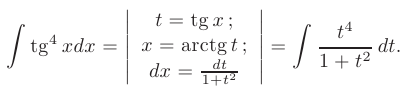
Полученная подынтегральная функция является неправильной рациональной дробью, следовательно, произведя деление многочленов, получим легко интегрируемую сумму многочлена и правильной рациональной дроби:
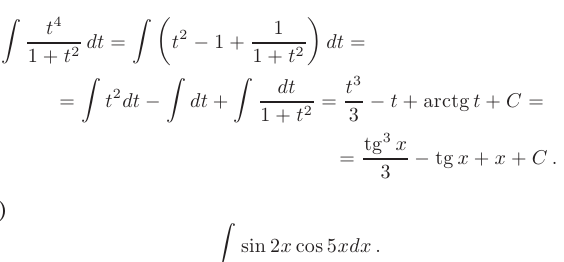
► Для нахождения этого интеграла воспользуемся формулой, преобразующей произведение двух тригонометрических функций в их сумму, которая интегрируется с помощью простейшей замены переменных:
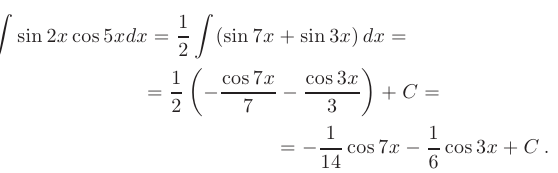
Завершая обзор методов интегрирования, заметим, что хотя для всякой непрерывной функции существует первообразная, но не для всякой элементарной функции эта первообразная сама является элементарной функцией. Например, первообразная для функции 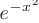 не может быть выражена в элементарных функциях. Неопределенные интегралы от подобных функций принято называть «неберущимися».
не может быть выражена в элементарных функциях. Неопределенные интегралы от подобных функций принято называть «неберущимися».
Понятие определенного интеграла
Пример оформления заказа №6.4.
Вычислить определенный интеграл методом интегрирования по частям
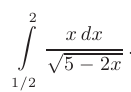
► В соответствии с формулой интегрирования по частям принимаем:
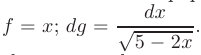
Дифференцируя функцию 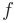 и интегрируя дифференциал функции
и интегрируя дифференциал функции 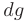 получим:
получим:
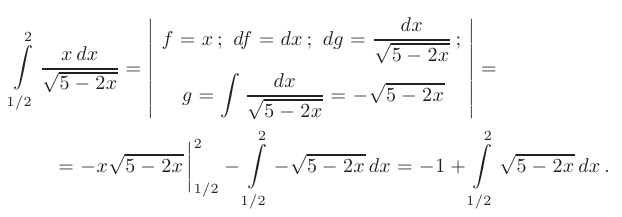
При нахождении последнего интеграла воспользуемся методом замены переменной. Пусть
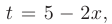
тогда
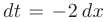
и искомый интеграл может быть приведен к табличному виду:
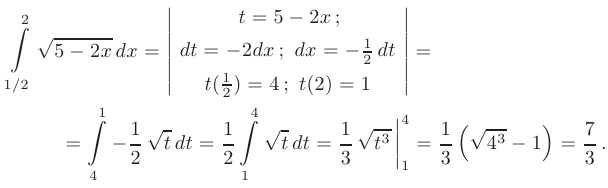
Таким образом,
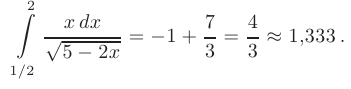
Понятие о несобственных интегралах
Обыкновенные дифференциальные уравнения
- Обыкновенные дифференциальные уравнения
- Дифференциальные уравнения с разделяющимися переменными
- Линейные дифференциальные уравнения первого порядка
- Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- Линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами
- Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами
Пример оформления заказа №7.2.
В демографии известно, что число новорожденных и число умерших за единицу времени пропорциональны численности населения с коэффициентами пропорциональности 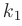 и
и 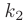 соответственно, значения которых специфичны для каждого региона. Описать протекание демографического процесса (т. е. установить закон изменения численности населения с течением времени).
соответственно, значения которых специфичны для каждого региона. Описать протекание демографического процесса (т. е. установить закон изменения численности населения с течением времени).
► Обозначим число жителей в момент 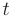 через
через 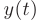 . Прирост населения
. Прирост населения 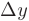 за время
за время 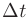 равен разности между числом родившихся
равен разности между числом родившихся 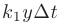 и числом умерших
и числом умерших 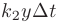 за это время, т. е.
за это время, т. е.
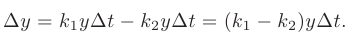
Поделим обе части равенства на 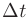 :
:
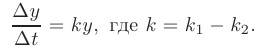
Переходя к пределу при 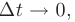 приходим к уравнению:
приходим к уравнению:
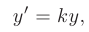
решая которое (см. пример 7.1), получаем математическую модель демографического процесса
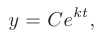
где 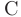 — постоянная, определяемая начальными условиями. В данном случае численностью населения в начальный момент времени.
— постоянная, определяемая начальными условиями. В данном случае численностью населения в начальный момент времени.
Пример оформления заказа №7.7.
Найти общее решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами
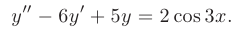
► Составим характеристическое уравнение:
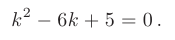
Дискриминант уравнения больше нуля: 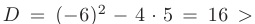 0. В таком случае:
0. В таком случае: 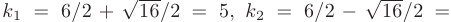 1.
1.
Следовательно, общее решение однородного дифференциального уравнения, соответствующего исходному, имеет вид
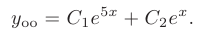
Правая часть неоднородного дифференциального уравнения: 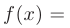
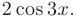 . Имеем II случай. Число
. Имеем II случай. Число
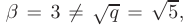
следовательно 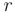 = 0. Запишем частное решение в виде
= 0. Запишем частное решение в виде
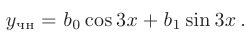
Для определения неизвестных коэффициентов 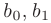 дважды продифференцируем полученную форму частного решения:
дважды продифференцируем полученную форму частного решения:
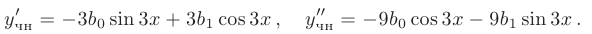
Подставим выражения для 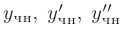 в исходное дифференциальное уравнение. После группировки по одноименным тригонометрическим функциям аргумента
в исходное дифференциальное уравнение. После группировки по одноименным тригонометрическим функциям аргумента 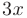 получим следующее уравнение:
получим следующее уравнение:
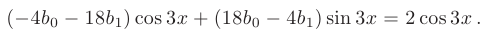
Приравняв коэффициенты при одноименных тригонометрических функциях, перейдем к эквивалентной системе уравнений:
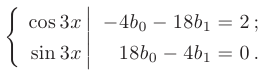
Находим значения неизвестных коэффициентов, решая последнюю систему:
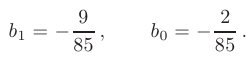
Подстановляя значения коэффициентов, получим
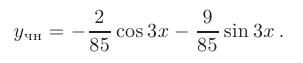
Тогда, искомое общее решение можно записать в виде
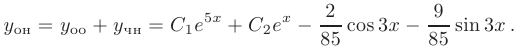
3 случай. Пусть правая часть линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами является суммой нескольких функций.
Тогда частное решение 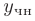 такого уравнения будет равно сумме частных решений:
такого уравнения будет равно сумме частных решений:
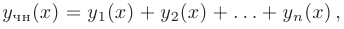
где каждое из частных решений 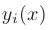 соответствует дифференциальному уравнению:
соответствует дифференциальному уравнению:
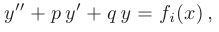
при
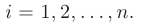
Числовые ряды. Степенные ряды
Функциональные и степенные ряды
Ряды Тейлора и Маклорена
Приложения степенных рядов
- Вычисление определенных интегралов при помощи степенных рядов
- Решение дифференциальных уравнений при помощи степенных рядов
Возможно эти страницы вам будут полезны:

