Предел последовательности
Если каждому натуральному числу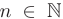 
поставлено в соответствие некоторое вещественное число 
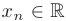, то говорят, что задана числовая последовательность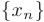 
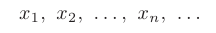
Проще говоря, числовая последовательность есть функция натурального аргумента
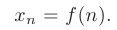
Число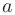 
называется пределом последовательности 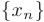, если для любого 
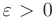существует такой номер 
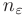, что для всех 
выполняется неравенство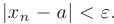 
Формально этот факт записывается в виде
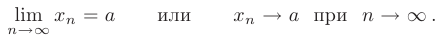
Т.е., начиная с некоторого номера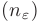 
члены последовательности 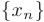как угодно мало отличаются от числа .
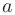Последовательность, для которой существует конечный предел 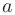, называют сходящейся. В противном случае говорят, что последовательность расходится. Пример сходящейся последовательности 
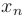показан на рис. 3.1.
Последовательность называется ограниченной, если существует константа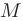 
такая, что 
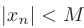для всех .
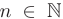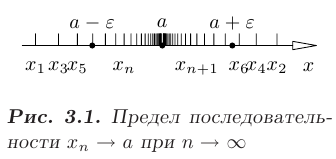
Если число а является пределом последовательности, то для всех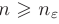 
члены последовательности 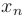будут принадлежать интервалу 
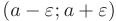называемому 
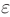-окрестностью точки 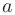(см. рис. 3.1). Другими словами в 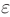-окрестности предела последовательности 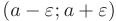содержится бесконечное множество членов этой последовательности, а вне 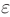-окрестности содержится лишь конечное их число.
Одной из наиболее известных числовых последовательностей является последовательность
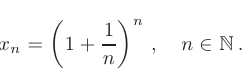
Предел этой последовательности представляет собой иррациональное число, принятое за основание натуральных логарифмов и обозначаемое как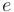 
— число Эйлера:
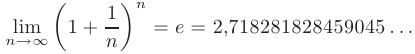
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
| Гипербола в математике |
| Парабола в математике |
| Функция одной переменной в математике |
| Предел функции в математике |
