Контрольные работы по высшей математике с решением и примерами

Оглавление:

Готовые контрольные работы с теорией и примерами решения по всем разделам высшей математики для студентов и школьников!

Высшая математика

Высшая математика — курс обучения в средних и высших учебных заведениях, включающий высшую алгебру и математический анализ.

Высшая математика включает обычно аналитическую геометрию, элементы высшей и линейной алгебры, дифференциальное и интегральное исчисления, дифференциальные уравнения, теорию множеств, теорию вероятностей и элементы математической статистики. Часто используется в экономике и технике. Является обязательным предметом в российских высших учебных заведениях, за исключением специальностей, в которых различные разделы математики разнесены по разным дисциплинам.

Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!

Раздел №1. Элементы линейной алгебры

Контрольная работа на тему: операции над матрицами

1. Транспонирование матриц

Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется транспонированной к данной и обозначается .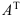

Пример №1.

Транспонируйте матрицу .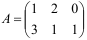

Решение:

Операция транспонирования матрицы 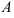осуществляется следующим образом: первая строка матрицы 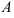становится первым столбцом матрицы 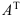, вторая строка 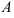— вторым столбцом 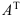, т.е.

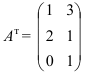
2. Сложение (вычитание) матриц

Складывать (вычитать) можно только такие матрицы, которые имеют одинаковую размерность.

Суммой (разностью) матриц 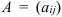и 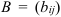называется матрица 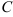, элементы которой равны суммам (разностям) соответствующих элементов матриц 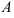и 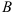, т.е. .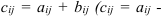

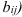Пример №2.

Найдите сумму и разность матриц 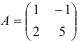и .

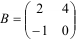Решение:

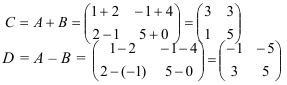
Произведением матрицы 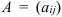на число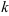 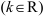называется матрица 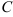той же размерности, элементы которой равны произведению числа к на соответствующие элементы матрицы 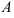, т.е. .

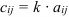Пример №3.

Найдите произведение матрицы 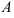на число 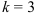, если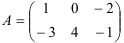

Решение:

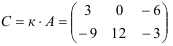
4. Умножение матриц

Матрицу 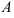можно умножать на матрицу 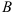тогда и только тогда, когда число столбцов матрицы 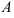равно числу строк матрицы .

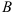Произведением матрицы 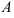размера 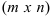на матрицу 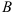размера 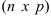называется матрица 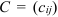размера 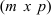, элементы которой равны сумме произведений элементов 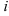-ой строки матрицы 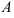на соответствующие элементы 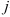-го столбца матрицы .

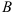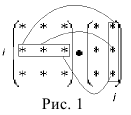
Получение элемента 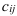можно представить в виде схемы (рис. 1):

Пример №4.

Найдите произведение матриц 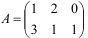и .

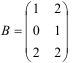Решение:

Размер матрицы 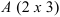, размер .

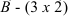Число столбцов матрицы 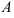равно числу строк матрицы 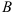, следовательно, умножение возможно. При этом матрица 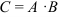будет иметь размерность (2 х 2).

Найдем элементы 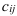матрицы :

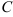Для нахождения элемента 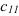находим сумму произведений элементов первой строки матрицы 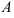и первого столбца матрицы :

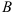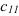= (1 строка 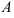и 1 столбец ) ;

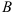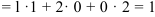Аналогично 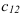= (1 строка 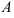и 2 столбец ) ;

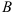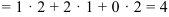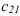= (2 строка 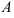и 1 столбец ) ;

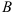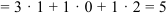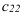= (2 строка 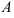и 2 столбец ) .

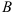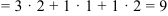Получили,что 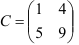. Ответ: .

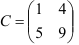Дополнительные контрольные работы:

Раздел №2. Элементы аналитической геометрии

Контрольная работа на тему: векторы, операции над векторами

Задание: Операции над векторами в координатах

Цель: формирование умения выполнять основные операции над векторами в координатах.

Задание для самостоятельной внеаудиторной работы:

Выучите определение свободного вектора, координат вектора на плоскости. Пользуясь обобщающей таблицей, проанализируйте, какие операции над векторами в координатах выполнимы, в чем заключаются признаки коллинеарности и перпендикулярности векторов.

В треугольнике 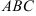вершины имеют координаты . Найдите:

1) координаты вектора ;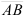

2) длину стороны ;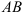

3) координату точки 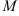— середины отрезка ;

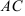4) длину медианы ;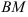

5) координаты вектора ;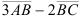

6) косинус угла между векторам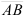и и ;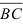

7) треугольник 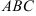достроили до параллелограмма 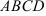; найдите координату вершины .

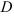Решив задания 1 — 6 и заменив получившиеся ответы буквами из таблицы, вы узнаете, какой профессии были отданы три года жизни создателя аналитической геометрии Рене Декарта (1596-1650).

Профессия:

Карта ответов:

При каком значении 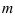векторы 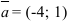и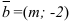

а) взаимно перпендикулярны; б) коллинеарны.

Докажите, что 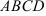, где 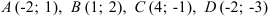— трапеция с основаниям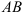и и 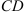. Определите, является ли трапеция равнобокой. На оси 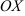найдите координаты точки, равноудаленной от точек 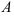и .

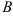Методические указания по выполнению работы:

Вектор — это направленный отрезок. Все равные между собой направленные отрезки называют свободным вектором.

Коэффициенты 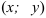разложения вектора 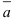по векторам 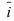и 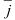(единичным взаимно перпендикулярным векторам) 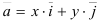называют координатами вектора на плоскости.

При решении задач по теме «Векторы» используйте следующие рекомендации:

Выпишите исходные данные — дано. Если в условии задачи сказано о коллинеарности, перпендикулярности, равенстве длин векторов, то это также необходимо выписать.
Определите, что нужно найти или что доказать в соответствии с условием задачи.
Опираясь на то, что нужно найти, попытайтесь поискать ключ к решению: выбрать в таблице нужные операции или использовать признаки коллинеарности и перпендикулярности векторов, сформулированные в теоремах 1 и 2.

Операции над векторами в координатах

Теорема 1. Если векторы 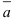и 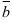коллинеарны, то их соответствующие координаты пропорциональны:

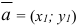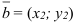если и коллинеарны, то .

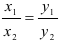Теорема 2. Если ненулевые векторы 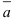и 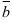взаимно перпендикулярны, то их скалярное произведение равно нулю, и наоборот, если скалярное произведение векторов равно нулю, то векторы перпендикулярны: .

Пример №5.

Даны точки .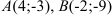

Найти: 1) координаты вектора ;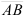

2) длину вектора ;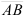

3) координаты точки 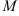— середины .

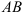Решение:

1) Воспользуемся формулой нахождения координат вектора: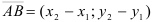

Тогда .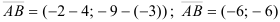

2) Зная координаты вектора 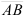, найдем его длину по формуле: .

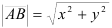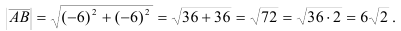
3) Пусть точка 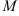— середина отрезка 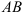. Тогда ее координаты находятся по формуле:

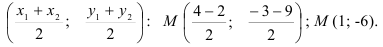
Ответ: .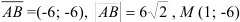

Пример №6.

Даны .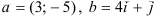

Найдите: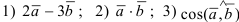

Решение:

1) Вектор 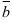задан в виде разложения по базисным векторам 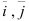. Его координаты находятся как коэффициенты разложения вектора по базису: .

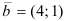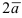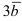Найдем координаты векторов и по формуле: 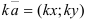. Тогда

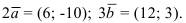
Воспользуемся формулой нахождения суммы и разности векторов: .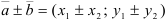

Получим, что .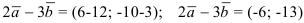

2) Воспользуемся формулой нахождения скалярного произведения векторов: .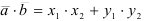

Получим:

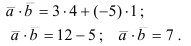
3) Найдем косинус угла между векторами по формуле .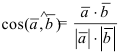

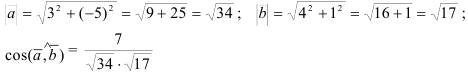
Ответ: .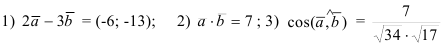

Пример №7.

При каком значении 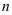векторы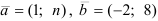

1) коллинеарны; 2) перпендикулярны?

Решение:

1) Воспользуемся теоремой 1: если векторы коллинеарны, то их соответствующие координаты пропорциональны. Получим, что

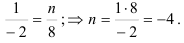
Следовательно, при 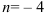векторы 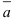и 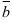коллинеарны.

2) Воспользуемся теоремой 2: если .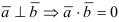

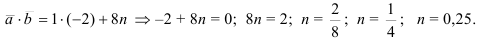
Следовательно, при 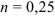векторы 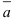и 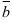перпендикулярны.

Ответ: .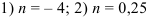

Дополнительные контрольные работы:

Раздел №3. Основы математического анализа

Контрольная работа на тему: теория пределов, непрерывность

Задание: Виды числовых последовательностей. Определение пределов последовательностей.

Цель: формирование умения классифицировать числовые последовательности и вычислять их пределы.

Задание для самостоятельной внеаудиторной работы:

Выучите определение числовой последовательности, видов числовой последовательности (возрастающей, убывающей, ограниченной), предела числовой последовательности.

Выпишите первые пять членов числовой последовательности, классифицируйте данную последовательность по критериям монотонности и ограниченности, найдите её предел:

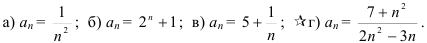
Используя материал учебника, составьте опорный конспект но теме «Бесконечно малые и бесконечно большие числовые последовательности, число 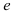» по следующему плану:

определение бесконечно малой числовой последовательности, пример такой последовательности;
определение бесконечно большой числовой последовательности, пример такой последовательности;
теорема, устанавливающая связь между бесконечно малыми и бесконечно большими числовыми последовательностями;
теорема Вейерштрасса (признак существования предела последовательности);
числовая последовательность, приводящая к числу .

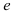Найдите предел числовой последовательности:

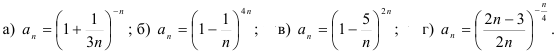
Используя дополнительную литературу, найдите апории философа Зенона Эллинского (490-430 г. до н.э.) — задачи, содержащие в себе противоречия. Попробуйте объяснить причину возникающих противоречий с точки зрения математики. Возможно ли решение этих задач на основании понятия предела последовательности?

Методические указания по выполнению работы:

Знание следующего теоретического материала будет Вам полезно при классификации и нахождении предела числовой последовательности.

Бесконечной числовой последовательностью называется функция 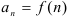, заданная на множестве натуральных чисел (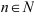). Для обозначения числовой последовательности принята следующая запись: .

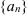Последовательность 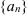называется убывающей, если каждый последующий член последовательности меньше или равен предыдущему, т.е. если 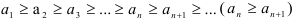для всех .

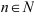Последовательность 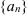называется возрастающей, если каждый последующий член последовательности больше или равен предыдущему .

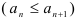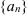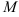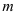Последовательность называется ограниченной, если существуют числа и такие, что для любого номера 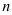имеет место неравенство: .

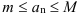Геометрически ограниченность последовательности 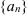означает существование отрезка 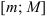, на котором помещены все члены этой последовательности. Для неограниченной последовательности 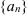отрезка 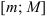, которому принадлежат все члены 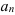, не существуют.

Число 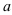называется пределом последовательности 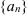, если для любого наперед заданного положительного числа 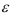найдется такое натуральное число 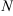, что для любого номера элемента 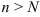выполняется неравенство: 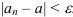. В этом случае пишут .

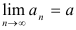Последовательность, имеющая конечный предел, называется сходящейся, а не имеющая предела — расходящейся.

Для практического нахождения пределов числовых последовательностей используют следующие свойства пределов.

Пусть 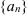и 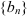— сходящиеся последовательности, т.е. 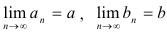. Тогда справедливы следующие утверждения:

Всякая сходящаяся последовательность имеет только один предел.
Для любого числа 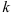последовательность 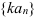также сходится, причем .
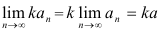Сумма (разность) 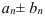также сходится, причем .
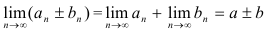Произведение 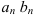также сходится, причем .
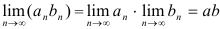При дополнительном условии 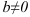частное 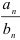также сходится, причем .

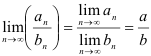Проиллюстрируем использование теоретического материала при исследовании числовых последовательностей.

Пример №8.

Исследуйте числовую последовательность .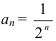

Решение:

Выпишем элементы числовой последовательности, поочерёдно подставляя вместо 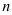значения 1, 2, 3, 4, 5 и т.д. Получим бесконечное числовое множество: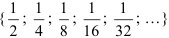

Последовательности 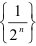соответствует следующее геометрическое изображение:

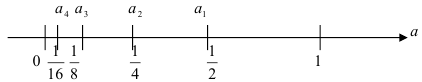
Последовательность 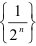убывающая, т.к.

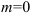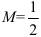Она ограничена, т.к. существует и , такие, что 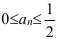. Геометрически все элементы последовательности 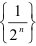принадлежат промежутку .

Покажем, что 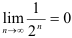. Выберем любую точность 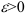(например, 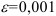). Тогда найдется натуральное число 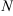(в нашем случае 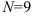), такое что для всех 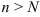выполняется неравенство: 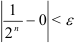(уже для 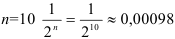будет меньше ).

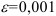Пример №9.

Исследуйте числовую последовательность .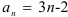

Решение:

Подставляя вместо 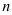значения 1, 2, 3 и т.д., найдем следующие элементы последовательности: {1; 4; 7; 10; 13; 16…}.

Последовательности 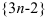соответствует следующее изображение:

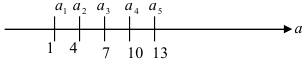
Последовательность 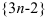является возрастающей, т.к. каждый следующий член последовательности больше предыдущего: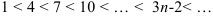

Она не ограничена, т.к. не существует числа 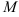, которое бы ограничивало последовательность сверху.

Последовательность 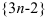не имеет предела, т.к. ее элементы неограниченно возрастают, следовательно, эта последовательность является расходящейся ().

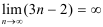Пример №10.

Найдите предел последовательности .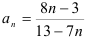

Решение:

Числитель и знаменатель представляют собой расходящиеся последовательности (так как они не ограничены), поэтому непосредственно применять теорему о пределе частного нельзя. В этом случае поступим так: числитель и знаменатель разделим на 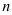(от этого дробь не изменится), а затем применим теоремы о пределах последовательностей. Приведем подробную запись вычисления предела:

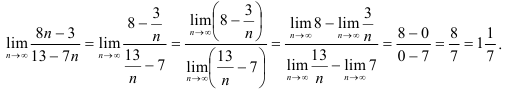
Ответ: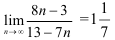

Дополнительные контрольные работы:

Раздел №4. Основы теории комплексных чисел

Возможно эти страницы вам будут полезны: