Оглавление:
Задание: Решение дифференциальных уравнений с разделёнными и разделяющимися переменными.
Цель: формирование умений решать дифференциальные уравнения первого порядка: простейшие, с разделёнными и разделяющимися переменными.
Задание для самостоятельной внеаудиторной работы:
45.1. Какие дифференциальные уравнения называют простейшими первого порядка? Какова техника их решения?
45.2. Решите простейшее дифференциальное уравнение первого порядка:
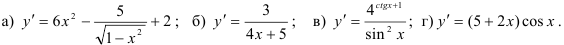
45.3. Найдите частное решение простейшего дифференциального уравнения первого порядка:
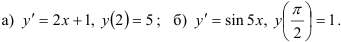
45.4. Какие дифференциальные уравнения первого порядка называют уравнениями с разделёнными и разделяющимися переменными? Какова техника их решения?
45.5. Решите дифференциальное уравнение с разделёнными и разделяющимися переменными:
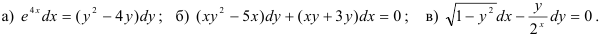
45.6. Найдите решение задачи Коши:
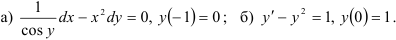
45.7. Определите численность населения России через 5 лет, считая, что скорость прироста населения пропорциональна его количеству (коэффициент пропорциональности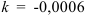 
), и зная, что в население России в начале 2010 года составляло 141,9 млн. человек, а прирост населения за 2010 год был равен (-0,06)%.
Методические указания по выполнению работы:
Выделяют следующие виды дифференциальных уравнений первого порядка:
1. Простейшие дифференциальные уравнения — уравнения вида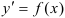 
.
Метод решения: взять интеграл от правой и левой части по переменной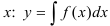 
.
Пример 1.
Найдите решение дифференциального уравнения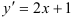 
.
Решение:
Поскольку перед нами простейшее дифференциальное уравнение первого порядка, найдем его решение по формуле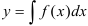 
:
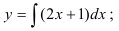
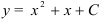— общее решение дифференциального уравнения .
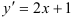Ответ: .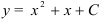
Пример 2.
Найдите частное решение уравнения 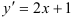, если 
.
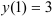Решение:
Общее решение заданного дифференциального уравнения имеет вид:
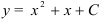(см. пример 1). Воспользуемся начальными условиями: 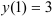, следовательно, при 
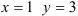. Подставим эти числа в общее решение:
. Выразим из данного уравнения 
.
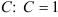Подставив найденное значение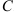 
в общее решение 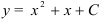, получим следующее частное решение дифференциального уравнения: 
.
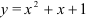Ответ: .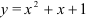
2. Дифференциальные уравнения с разделёнными переменными — уравнения вида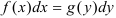 
.
Если дифференциальное уравнение путем преобразований можно привести к виду 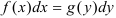, то оно называется дифференциальным уравнением с разделяющимися
переменными.
Метод решения: проинтегрировать обе части уравнения: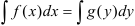 
.
Пример 3.
Найдите решение дифференциального уравнения: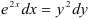 
.
Решение:
Данное дифференциальное уравнение представляет собой уравнение с разделенными переменными. Проинтегрируем обе части уравнения:
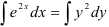. Тогда
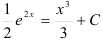— общее решение дифференциального уравнения .
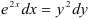Ответ: .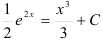
Для решения уравнений с разделяющимися переменными целесообразно использовать следующий алгоритм:
- Если в уравнении встречается
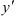, то представьте его как 
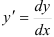. - Произведите разделение переменных (в одной части при
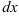соберите выражения, содержащие только переменную 
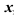; в другой части при 
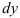соберите выражения, содержащие только переменную 
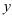). - Почленно проинтегрируйте обе части уравнения с разделёнными переменными.
- Выпишите в ответе получившееся общее решение дифференциального уравнения.
Пример 4.
Найдите решение дифференциального уравнения: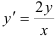 
.
Найдите решение дифференциального уравнения: .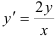
Решение:
1. Данное уравнение — дифференциальное уравнение с разделяющимися переменными. Представим 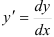, тогда 
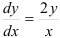или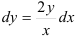 
.
2. Будем собирать множители с 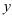в левой части, с 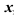— в правой: 
.
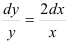3. Интегрируя обе части, получим: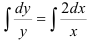 
или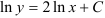 
— общее решение.
Ответ: .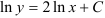
На этой странице вы сможете посмотреть все остальные темы готовых контрольных работ по высшей математике:
Готовые контрольные работы по высшей математике
Обратите внимание на похожие контрольные работы возможно они вам будут полезны:
