Оглавление:
Число — это важнейшее математическое понятие. В математике некоторые понятия являются первичными, неопределяемыми. К ним относятся понятия натурального числа, точки, прямой и т.д. Натуральные числа — это числа, используемые для счета предметов: 1, 2, 3, …, п, …
Другим фундаментальным понятием математики является понятие множества. Принято говорить, что множество объединяет элементы по какому-либо признаку. Множества можно составлять из самых разнообразных объектов на основе различных признаков. Элементами множества могут быть как материальные объекты, так и абстрактные понятия, такие как числа, геометрические фигуры, символы и т. п. Если в роли элементов множества выступают числа, то оно называется числовым множеством. Множества чаще всего обозначаются большими латинскими буквами А, В, С, …, а их элементы — малыми латинскими буквами а, Ь, с, … Если множество А состоит из k элементов 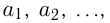
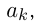 то пишут
то пишут 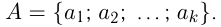
Если элемент а принадлежит множеству А, то пишут 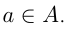
Множество, которое не содержит элементов, называется пустым и обозначается 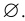
Пересечением множеств А и В называется множество С, которое состоит из элементов, входящих и в множество А, и в множество В, обозначается 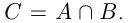 Объединением множеств А и В называется множество С, состоящее из всех элементов множеств А и В и только из них, обозначается
Объединением множеств А и В называется множество С, состоящее из всех элементов множеств А и В и только из них, обозначается 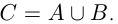
Множество натуральных чисел обозначают буквой N. Если какое-либо число n принадлежит множеству натуральных чисел, пишут 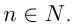
На множестве натуральных чисел определены операции сложения и умножения. Сумма и произведение натуральных чисел — также натуральные числа.
Вычитание натуральных чисел приводит не только к натуральным числам, но и к числам вида 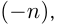 , где
, где 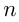 — натуральное число. Множество чисел, состоящее из натуральных чисел, нуля и чисел вида
— натуральное число. Множество чисел, состоящее из натуральных чисел, нуля и чисел вида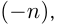 называется множеством целых чисел и обозначается Z. На множестве целых чисел определены операции сложения, вычитания и умножения. Деление целых чисел выводит нас за рамки этого множества, т. к. при делении результат не всегда оказывается целым числом, и возникает необходимость записи чисел, более «мелких», чем целые. Одна или несколько равных частей единицы называется обыкновенной дробью.
называется множеством целых чисел и обозначается Z. На множестве целых чисел определены операции сложения, вычитания и умножения. Деление целых чисел выводит нас за рамки этого множества, т. к. при делении результат не всегда оказывается целым числом, и возникает необходимость записи чисел, более «мелких», чем целые. Одна или несколько равных частей единицы называется обыкновенной дробью.
Обыкновенная дробь состоит из числителя и знаменателя, разделенных чертой, например 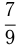 . Знаменатель 9 обозначает, что нечто целое разделено на 9 частей, а числитель 7, что взято 7 таких частей.
. Знаменатель 9 обозначает, что нечто целое разделено на 9 частей, а числитель 7, что взято 7 таких частей.
Важнейшим свойством дроби является то, что числитель и знаменатель дроби можно разделить на одно и то же число,т.е. дрооь можно сократить. Например, 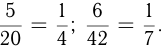 Дробь, у которой числитель меньше знаменателя, называется правильной.
Дробь, у которой числитель меньше знаменателя, называется правильной.
Если числитель дроби больше знаменателя, дробь — неправильная. 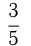 — правильная дробь,
— правильная дробь, 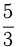 — неправильная дробь. Из неправильной дроби можно выделить целую часть, разделив числитель на знаменатель с остатком. Частное от деления будет целой частью числа, остаток — числителем дробной части, в знаменателе будет знаменатель неправильной дроби. Например,
— неправильная дробь. Из неправильной дроби можно выделить целую часть, разделив числитель на знаменатель с остатком. Частное от деления будет целой частью числа, остаток — числителем дробной части, в знаменателе будет знаменатель неправильной дроби. Например, 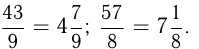
Число, состоящее из целой и дробной частей, — дробное число. Такое число можно превратить в неправильную дробь. Для этого нужно умножить целую часть на знаменатель дроби и добавить это произведение к числителю, а знаменатель оставить прежним. Например, 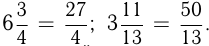 Над дробями можно совершать арифметические действия по следующим правилам:
Над дробями можно совершать арифметические действия по следующим правилам:
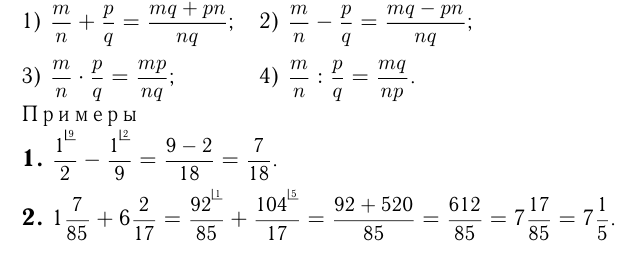
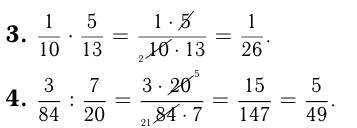
Дроби со знаменателями 10, 100, 1000 и т.д. называются десятичными дробями и записываются 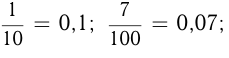
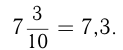
При сложении и вычитании десятичных дробей числа записывают так, чтобы одинаковые разряды были записаны один под другим, а запятая — под запятой. Например,
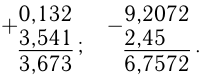
При умножении десятичных дробей надо выполнить это действие, не обращая внимания на запятые, а затем в полученном произведении отделить справа запятой столько цифр, сколько их стоит после запятой в обоих множителях вместе.
При делении десятичных дробей на натуральное число делим сначала целую часть числа на это натуральное число, затем десятые, сотые и т.д. доли. Если целая часть меньше делителя, то в целой части частного получим 0. Например, 4,52 : 2 = 2,26; 1,28 : 4 = 0,32.
При делении на десятичную дробь надо в делимом и делителе перенести запятую вправо на столько цифр, сколько их после запятой в делителе, и затем делить на натуральное число.
Можно преобразовать десятичную дробь в обыкновенную и, обратно, обыкновенную дробь в десятичную. Для первого преобразования достаточно в числителе дроби записать число, стоящее после запятой, а в знаменателе — единицу с нулями, причем нулей должно быть столько, сколько цифр справа от запятой. Например,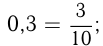
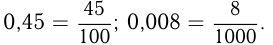 Чтобы совершить обратное преобразование, следует разделить числитель на знаменатель по правилу деления десятичной дроби на целое число. Например,
Чтобы совершить обратное преобразование, следует разделить числитель на знаменатель по правилу деления десятичной дроби на целое число. Например, 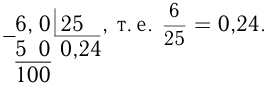
Отметим, что при этом может получиться бесконечная десятичная дробь. Например,

Бесконечная десятичная дробь, в которой, начиная с некоторого разряда, цифры повторяются, называется периодической. Записываются периодические дроби следующим образом: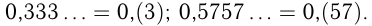
Важно уметь переводить периодические дроби в обыкновенные. Для того чтобы обратить бесконечную периодическую десятичную дробь в обыкновенную, надо из числа, стоящего до 2-го периода, вычесть число, стоящее до 1-го периода, и сделать эту разность числителем, а в знаменателе написать цифру 9 столько раз, сколько цифр в периоде, и после девяток дописать столько нулей, сколько цифр между запятой и 1-м периодом.
Например, 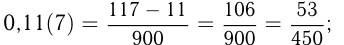
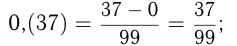
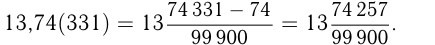
Рациональными называются числа, которые могут быть представлены в виде 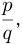 , где
, где 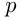 — целое, a
— целое, a 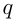 — натуральное число. Множество рациональных чисел обозначается
— натуральное число. Множество рациональных чисел обозначается 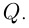 Любое рациональное число может быть представлено в виде конечной либо бесконечной периодической десятичной дроби.
Любое рациональное число может быть представлено в виде конечной либо бесконечной периодической десятичной дроби.
На множестве рациональных чисел определены операции сложения, вычитания, умножения, деления, возведения в натуральную степень, т. к. последняя операция сводится к умножению: 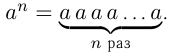
Возведение в отрицательную целую степень возможно для любого рационального числа, кроме 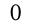 , т.к.
, т.к. 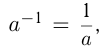 , а на
, а на 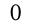 делить нельзя.
делить нельзя.
Прямую линию с выбранными на ней началом отсчета, еиничным отрезком и направлением называют числовой прямой, или числовой осью.
Два числа, отличающиеся друг от друга только знаком, называются противоположными. Например, 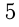 и
и 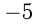 ;
; 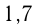 и
и 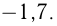
Каждому рациональному числу соответствует единственная точка на числовой прямой. Противоположные числа на числовой прямой расположены симметрично относительно нуля.

Модулем (абсолютной величиной) числа 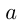 называется само это число, если
называется само это число, если 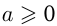 , и противоположное число
, и противоположное число 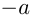 , если
, если 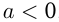 .
.
На числовой прямой 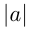 означает расстояние от точки, соответствующей числу
означает расстояние от точки, соответствующей числу 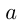 , до точки, обозначающей
, до точки, обозначающей 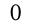 .
.
|0|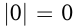 ; если
; если 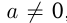 , то на числовой прямой находятся две точки, равноудаленные от нуля, соответствующие
, то на числовой прямой находятся две точки, равноудаленные от нуля, соответствующие 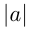 , это
, это 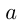 и
и 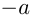 .
.
На числовой прямой правее расположено то из двух чисел, которое больше. Поэтому любое положительное число больше нуля и больше отрицательного числа; любое отрицательное число меньше нуля; из двух отрицательных чисел больше то, модуль которого меньше. Например,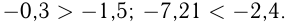
Сумма двух рациональных чисел с одинаковыми знаками равна числу того же знака, модуль которого равен сумме модулей слагаемых. Сумма двух чисел с разными знаками равна числу, модуль которого равен разности большего и меньшего модулей этих чисел, а знак суммы совпадает со знаком того слагаемого, модуль которого больше. Например, 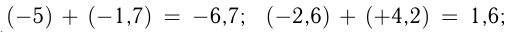
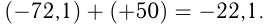
Разности двух рациональных чисел соответствует сложение уменьшаемого с числом, противоположным вычитаемому.
Например, 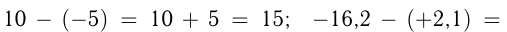
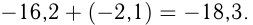
Произведение и частное двух рациональных чисел одного знака является положительным числом, произведение и частное двух чисел с разными знаками — число отрицательное.
Итак, множество 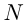 натуральных чисел было расширено при введении нуля и чисел
натуральных чисел было расширено при введении нуля и чисел 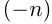 до множества
до множества 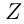 целых чисел, и затем при введении дробных чисел до множества
целых чисел, и затем при введении дробных чисел до множества 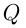 рациональных чисел. Однако существуют алгебраические и геометрические задачи, которые не имеют решения на множестве рациональных чисел. Например, нельзя выразить рациональным числом длину диагонали квадрата со стороной 1 см; нельзя найти отношение длины окружности к диаметру.
рациональных чисел. Однако существуют алгебраические и геометрические задачи, которые не имеют решения на множестве рациональных чисел. Например, нельзя выразить рациональным числом длину диагонали квадрата со стороной 1 см; нельзя найти отношение длины окружности к диаметру.
Числа, которые нельзя представить в виде 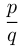 и которые поэтому не являются рациональными, называются иррациональными. Т.к. любое рациональное число представляется либо в виде конечной, либо бесконечной периодической десятичной дроби, то иррациональное число может быть представлено в виде бесконечной непериодической десятичной дроби.
и которые поэтому не являются рациональными, называются иррациональными. Т.к. любое рациональное число представляется либо в виде конечной, либо бесконечной периодической десятичной дроби, то иррациональное число может быть представлено в виде бесконечной непериодической десятичной дроби.
Рациональные и иррациональные числа вместе составляют множество действительных чисел, которое обозначается буквой 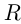 .
.
Итак, вся числовая прямая представляет собой множество действительных чисел, состоящее из рациональных и иррациональных чисел. Множество рациональных чисел включает в себя множество целых чисел и множество дробных чисел, множество целых чисел включает в себя множество натуральных чисел и множество противоположных им чисел.
На числовой прямой вводятся обозначения для числовых промежутков:
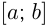 — отрезок (замкнутый промежуток) с началом
— отрезок (замкнутый промежуток) с началом 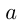 и концом
и концом 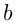 ;
;
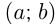 — интервал (незамкнутый промежуток);
— интервал (незамкнутый промежуток);
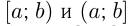 — полуинтервалы (полузамкнутые промежутки);
— полуинтервалы (полузамкнутые промежутки);
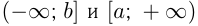 —лучи, где
—лучи, где 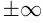 — обозначение бесконечности; часто вместо
— обозначение бесконечности; часто вместо 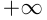 пишут просто
пишут просто 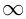 ;
;
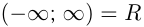 — вся числовая прямая.
— вся числовая прямая.
Если число 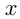 входит в какой-либо числовой промежуток, то пишут
входит в какой-либо числовой промежуток, то пишут 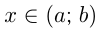 или
или 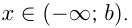
Эта теория с решениями взята со страницы решения задач по математике:
Возможно вам будут полезны эти страницы:
| Законы сложения и умножения чисел в математике |
| Преобразование числовых выражении с примерами решения |
| Решение задач на прогрессии по математике |
| Решение задач на функции по математике |
Употребление букв для обозначения чисел (буквенная символика)
1. Буква — это письменный знак для обозначения каждого отдельного звука речи. Однако это не значит, что буквы нельзя употреблять и для других целей. -Например, в учреждении, расположенном в нескольких корпусах, иногда буквы употребляют для обозначения этих корпусов. Одни корпус называют корпусом А, другой — корпусом Б и т. д.
Буквы употребляются и для обозначения чисел. Поясним на примерах, когда обозначать число буквой полезно и даже необходимо и когда это делать нет пользы.
Пример:
Когда дежурный по классу докладывает классному руководителю устно или письменно о числе учеников, не явившихся в этот день на занятия, то он произносит наименование этого числа или записывает его цифрами. Например, говорит «четыре» или записывает «4». В данном случае нет смысла число 4 обозначать буквой.
Пример:
Если же мы хотим сказать о числе учеников, которые в конце текущего учебного года окончат данную школу с золотой медалью, то мы можем это число обозначить какой-нибудь буквой, например буквой а, так как мы еще не знаем сколько таких учеников окажется. Если таких учеников окажется 3, то мы скажем, что а = 3, если их окажется 10, то а = 10, если же не окажется ни одного, то а = 0 и т. д.
Пример:
Пусть произведение двух чисел равно 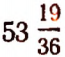 и при этом второе число на единицу больше первого. Если теперь мы захотим назвать первое число, то придется его обозначить какой-нибудь буквой, например буквой х, так как оно нам неизвестно. Если бы нам удалось найти это число, то оказалось бы, что
и при этом второе число на единицу больше первого. Если теперь мы захотим назвать первое число, то придется его обозначить какой-нибудь буквой, например буквой х, так как оно нам неизвестно. Если бы нам удалось найти это число, то оказалось бы, что
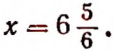
Пример:
Пусть паровоз движется без остановок со скоростью 80 км в час по Октябрьской железной дороге по направлению от Ленинграда к Москве и пусть в нуль часов (т. е. в полночь) проходит ст. Бологое. Расстояние от ст. Бологое в сторону Москвы будем считать положительным, а в сторону Ленинграда отрицательным (рис. 35)
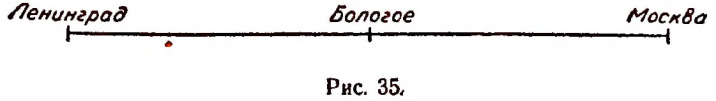
При этих условиях расстояние от ст. Бологое до локомотива будет все время изменяться, а потому не может быть выражено каким-нибудь одним числом. Целесообразно величину этого расстояния обозначить какой-нибудь буквой, например буквой S. Тогда через час после полуночи S = 80; через 1 час 30 мин. S = 120 и т. д. За один час до полуночи S = — 80, за 1 час 30 мин. до полуночи S = —120 и т. д.
В алгебре любая буква, например а, может в одном случае обозначать собой число — 5, в другом, скажем, 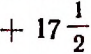 и т. д., т. е. под буквой а мы можем подразумевать, вообще говоря, любое известное или неизвестное отвлеченное число.
и т. д., т. е. под буквой а мы можем подразумевать, вообще говоря, любое известное или неизвестное отвлеченное число.
Если буквой а обозначено, скажем, число жильцов в доме, то в этом случае под буквой а нельзя подразумевать ни дробного, ни отрицательного числа.
Если буквой а обозначена длина веревки, то под буквой а нельзя подразумевать отрицательного числа.
Если число учеников, получивших золотую медаль, мы обозначили буквой а, то число учеников, получивших серебряную медаль, следует обозначить какой-либо другой буквой, например буквой b. Если мы захотим выразить число всех медалистов (и тех, и других), то напишем а + b.
Если при рассмотрении какого-либо вопроса одна и «га же буква, например буква x, употребляется несколько раз, то под значением этой буквы во всех случаях мы должны мыслить одно и то же. Например, если имеется частное (х + 2) : (х + 1). и если букве х, стоящей в делимом, мы припишем значение + 7, то букве х, стоящей в делителе, мы обязаны будем приписать то же самое значение + 7. Для обозначения чисел общепринято употреблять буквы преимущественно латинского и греческого алфавита. (Эти алфавиты помещены в конце вступительной статьи «Учащимся о математике»),
2. Возникает естественный вопрос: какие же обстоятельства, кроме указанных выше, побуждают нас к тому, чтобы употребление букв для обозначения чисел сделать систематическим и какая от этого получается польза? На этот вопрос очень трудно дать ответ, который, с одной стороны, был бы полным и конкретным, а с другой — оказался бы доступным пониманию лица, только что приступившего к изучению элементарной алгебры. Однако некоторые пояснения все же уместно сейчас сделать.
Пусть требуется решить, например, такую задачу. Смешали кофе двух сортов: 12 кг ценой по 4 руб. за 1 кг с 8 кг ценой по 4,5 руб. за 1 кг. Определить цену 1 кг смеси.
Решение этой задачи можно получить с помощью следующей последовательности действий:

На этом примере дана иллюстрация того, что решение всякой более или менее сложной арифметической задачи сводится к выполнению некоторой определенной последовательности действий над числами, данными в условии задачи. В итоге всех этих действий получается числовой ответ задачи. Если же мы эти действия не станем выполнять, а будем их только указывать, то в итоге получим некоторое арифметическое выражение, значение которого и будет ответом задачи.
Для сформулированной выше задачи получится следующее арифметическое выражение:
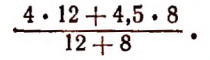
Значение этого выражения равно 4,2. Следовательно, цена смеси 4,2 руб. за 1 кг.
Решение задачи, записанное в виде арифметического выражения, имеет то преимущество, что позволяет видеть в собранной форме ту последовательность действий, которая решает данную задачу.
Если мы изменим числа, данные в условии задачи, то полученная в написанном выше арифметическом выражении последовательность действий не изменится. Так, например, если смешать 85 кг кофе ценой по 3,5 руб. за 1 кг с 15 кг ценой по 4,5 руб. за 1 /кг, то цена 1 кг смеси в рублях за 1 кг изобразится выражением:
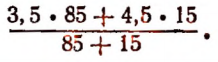
Решим эту же задачу в общем виде, т. е. в предположении, что количества и цены двух сортов кофе какие угодно.
Пусть смешали р кг кофе ценой в а руб. за 1 кг с q кг ценой в b руб. за 1 кг. Тогда цена смеси в рублях за 1 кг изобразится выражением:
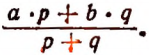
Конечно, числовое значение последнего выражения не будет определенным; оно будет зависеть от того, какие отдельные числовые значения мы станем давать буквам a, b, р и q. Однако наряду с этим выражение
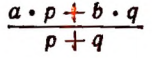
имеет то преимущество перед простым числовым ответом, что оно, во-первых, является общим решением задачи, т. е. решением при любых данных, и, во-вторых, позволяет видеть в собранной форме план или правило решения поставленной задачи.
При изменении значений букв a, b, р и q или даже при изменении значения одной из этих букв будет изменяться, вообще говоря, и значение выражения
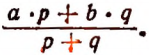
При а = 42; b = 50; р = 8 и q = 2 получим
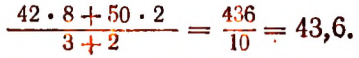
При а = 42; b = 50; р = 3 и q = 2 получим
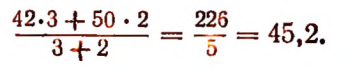
3. Рассмотрим несколько других примеров.
1. Пусть длина комнаты равна а м, а ширина — b м; тогда площадь комнаты в кв. м выразится произведением
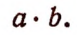
2. Пусть магазин принял со склада m м сукна ценой по а руб. за 1 м и n м драпа ценой по b руб за 1 м. Тогда стоимость принятого товара в рублях изобразится следующей суммой двух произведений:
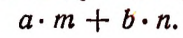
3. Пусть требуется найти р% от числа А.
Один процент числа А будет 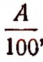 а р процентов от числа А изобразится выражением
а р процентов от числа А изобразится выражением
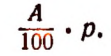
4. Площадь поперечного сечения цилиндрической колонны равна S кв. см, а высота — h м. Пусть 1 куб. см материала колонны весит d г. Тогда вес колонны в тоннах представится выражением
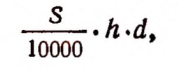
так как S кв. см составляют 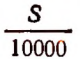 кв. м и 1 куб. м материала колоны весит d т.
кв. м и 1 куб. м материала колоны весит d т.
Таким образом, буквенное обозначение чисел позволяет получать решение задач в общем виде и тем самым выражать в краткой форме весь ход решения задачи.
4. Кроме того, буквенная символика позволяет кратко выражать законы, которым подчиняются числа. Например, вместо того, чтобы сказать, что сумма двух любых чисел не меняется от перемены мест слагаемых, достаточно написать:
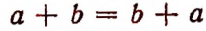 (переместительный закон сложения).
(переместительный закон сложения).
Рекомендуется сформулировать словами следующие законы:
 (сочетательный закон сложения);
(сочетательный закон сложения);
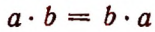 (переместительный закон умножения);
(переместительный закон умножения);
 (сочетательный закон умножения);
(сочетательный закон умножения);
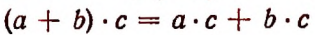 (распределительный закон умножения);
(распределительный закон умножения);
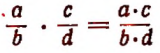 (правило умножения дробей);
(правило умножения дробей);
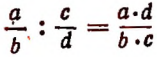 (правило деления дробей).
(правило деления дробей).
5. В дальнейшем мы увидим, что буквенная символика позволяет легко обнаруживать новые свойства чисел, имеющие общий характер. Например, в главе III будет показана справедливость равенства
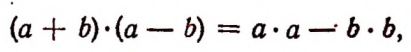
в котором буквы а и b обозначают собой любые числа, а в главе VI мы встретимся уже и с применениями новых свойств чисел к решению практических задач.
Геометрия, физика, механика и другие науки выдвигают многочисленные задачи, решение которых нельзя осуществить без буквенной символики.
Алгебраическое выражение
1. В дальнейшем нам постоянно придется иметь дело с алгебраическими выражениями. Что же такое алгебраическое выражение?
Алгебраическим выражением называется совокупность чисел, соединенных между собой с помощью знаков действий. Эти числа могут быть изображенными с помощью цифр и с помощью букв.
Алгебраическое выражение может содержать и скобки, служащие для указания порядка действий.
Примеры алгебраических выражений:
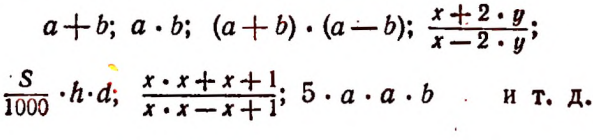
Примечание:
Любое число или любую букву, обозначающую число, мы также будем считать алгебраическим выражением. Например: 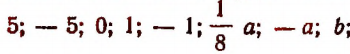 суть алгебраические выражения.
суть алгебраические выражения.
2. Приведем примеры нахождения числового значения алгебраического выражения.
Пусть под буквой а подразумевается число — 5, тогда
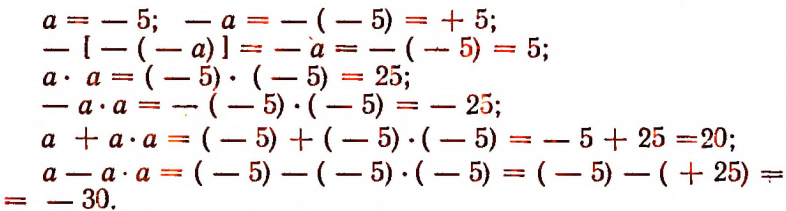
Пусть а = — 5 и b = — 3. Тогда
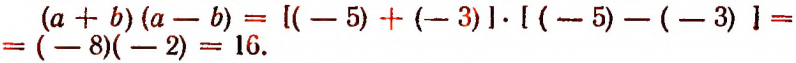
Пусть а= — 5 и b = — 3. Тогда
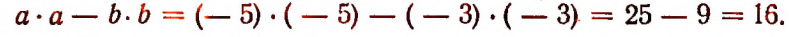
Замечание:
Выражение +а или просто а может иметь положительное, отрицательное и нулевое значения. Например, при
а = — 5 выражение +а имеет отрицательное значение — 5.
Выражение — а также может иметь положительное, отрицательное и нулевое значения. Например, при а = —5 выражение — а имеет положительное значение + 5.
3. Написанные ниже равенства
( _ а) • ( — Ь) = + аЬ\ — ( — с) = + а
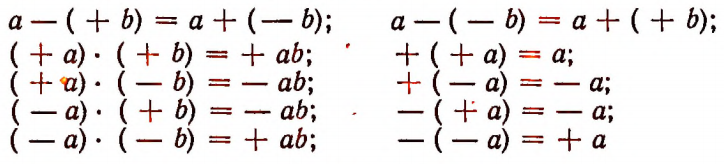
справедливы при любых значениях букв а и b .
Справедливость каждого из этих равенств легко доказать путем рассмотрения в отдельности каждого из следующих возможных случаев:
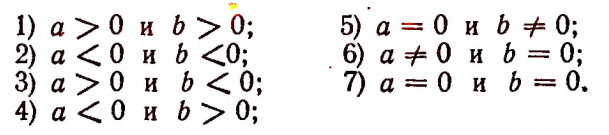
Равенство а = — а справедливо тогда и только тогда, когда а = 0. (Два противоположных числа равны друг другу лишь тогда, когда каждое из них равно нулю.)
Зависимости между величинами
1. При помощи алгебраических выражений можно представлять во многих случаях зависимости между величинами.
Примеры:
1. Проезд в такси стоит 0,1 руб. за включение счетчика и 0, 1 руб. за каждый километр пути. Если х есть число километров пути, а у стоимость проезда, выраженная в рублях, то зависимость величины у от величины х можно выразить равенством:
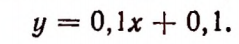
Составим таблицу значений у для нескольких отдельных значений х.
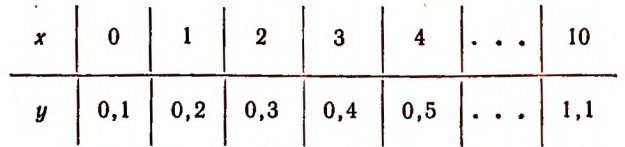
На рисунке 36 эта таблица изображена графически.
На числовой оси Х1Х от начальной точки О отложены отрезки , 2, 3 и т. д., изображающие расстояние в масштабе 5 мм 1 км. (Знак  здесь обозначает соответствие.)
здесь обозначает соответствие.)
Вертикальными отрезками изображена стоимость в масштабе 5 мм 0,1 руб., соответствующая отмеченным на оси Х1Х расстояниям.
0,1 руб., соответствующая отмеченным на оси Х1Х расстояниям.
По расположению точек А, B,C,D,E,F и т. д. являющихся концами вертикальных отрезков, можно составить наглядное представление о зависимости стоимости проезда от расстояния.
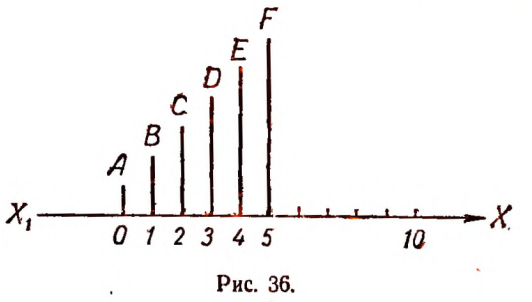
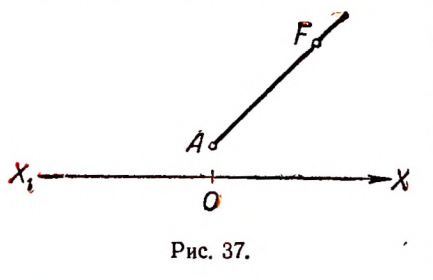
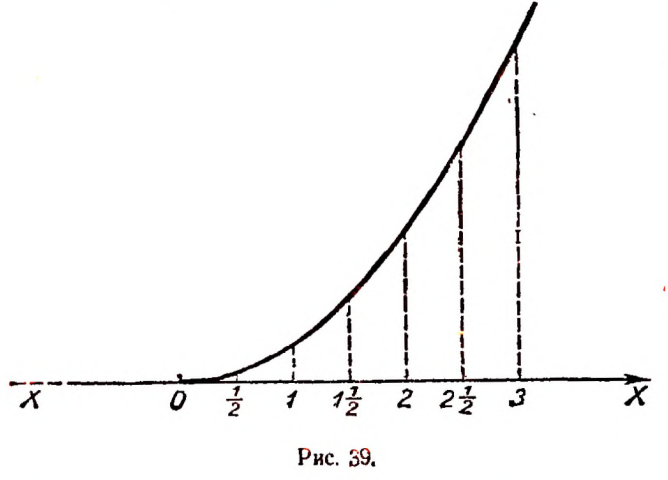
Если вообразить, что вертикальные отрезки построены не только для целых, но и для всевозможных дробных значений буквы х, то тогда концы вертикальных отрезков расположатся на луче AF (рис. 37). Луч AF называется графиком зависимости у = 0,1 х + 0,1 построенным для положительных значений х .
Если длину стороны квадрата в метрах обозначить буквой х , а площадь в квадратных метрах — буквой у, то зависимость величины у от величины х выразится равенством
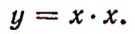
Эта зависимость (формула) точная; она известна из арифметики.
Составим таблицу значений величины у для нескольких отдельных значений величины х .
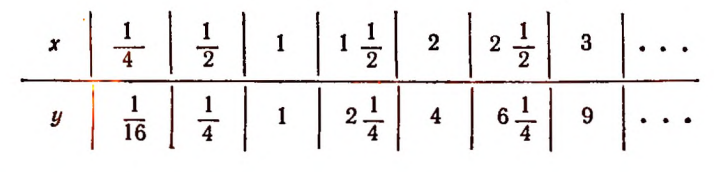
Графическое изображение этой таблицы дано на рисунке 38.
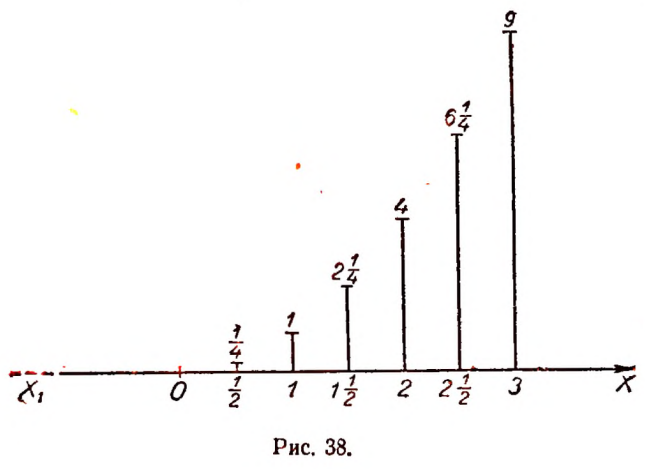
Масштаб по оси Х1Х: 1,5см  1 м. Вертикальные отрезки изображают площадь в масштабе 0,5 см
1 м. Вертикальные отрезки изображают площадь в масштабе 0,5 см  1 кв. м.
1 кв. м.
Если опять вообразить, что вертикальные отрезки построены не только для целых но, и для всевозможных дробных значений буквы х, то тогда концы вертикальных отрезков расположатся на кривой линии, изображенной на рисунке 39. Эта кривая является графиком зависимости 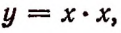 построенным для положительных значений .
построенным для положительных значений .
Масштаб по оси Х1Х: 1,5см  1 м. Вертикальные отрезки построены в масштабе 1 см
1 м. Вертикальные отрезки построены в масштабе 1 см  1 кв. м.
1 кв. м.
3. Условимся выражать расстояние от точки О по прямой А В (рис. 40) вправо- положительным числом, а влево отрицательным.
Условимся скорость точки, движущейся по прямой А В слева направо, выражать положительным числом, а при движении справа налево— отрицательным. Пусть точка движется по прямой А В равномерно со скоростью 2 м в сек. и в нуль часов находится от точки О на расстоянии 3 м. Расстояние от точки О до движущейся точки, выраженное в метрах, обозначим буквой S, а время в секундах — буквой t.
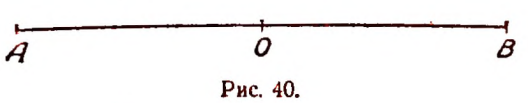
При этих условиях зависимость величины S от величины t выразится равенством
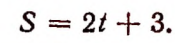
Составим таблицу значений величины S для нескольких отдельных значений величины t.
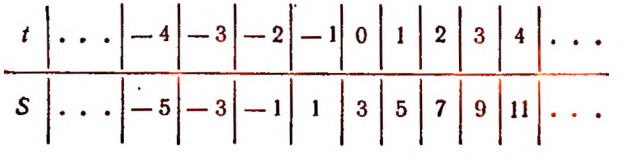
Графическим изображением зависимости
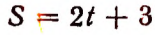
служит прямая MN на рисунке 41.
Масштаб по оси t1t : 0,5 см  1 сек. Вертикальные отрезки изображены в масштабе 0,5 см
1 сек. Вертикальные отрезки изображены в масштабе 0,5 см  1 м.
1 м.
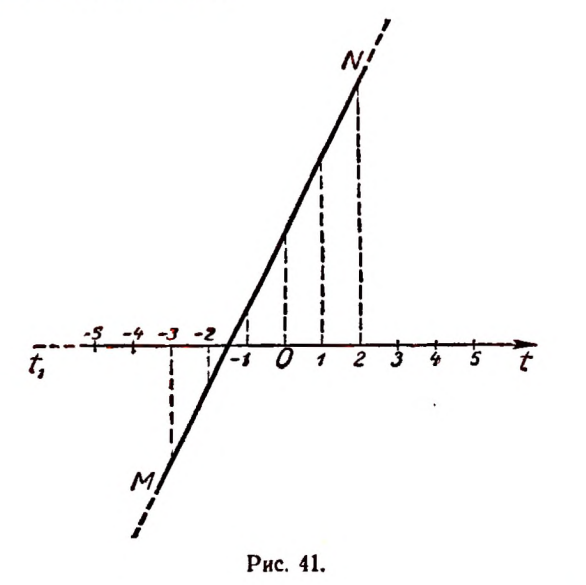
4. Если возраст человека в годах обозначить буквой t, а нормальное число часов ежедневного сна — буквой Н, то для возраста до 18 лет зависимость величины Н от величины t выразится приближенно следующим равенством:
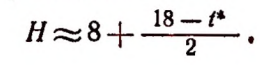
Эта приближенная зависимость (формула) получена не теоретически, а на основе наблюдений и опытов врачей.
Составим таблицу значений величины Н для нескольких отдельных значений величины t.
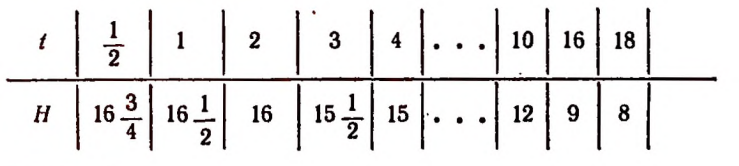
Графическим изображением зависимости
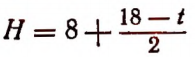
для значений t, больших или равных  и меньших или равных 18, будет отрезок прямой MN на рисунке 42.
и меньших или равных 18, будет отрезок прямой MN на рисунке 42.
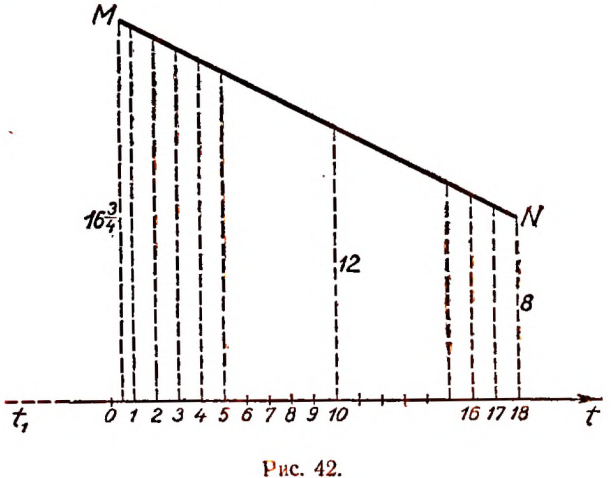
Масштаб по оси t1t : 2,5 мм  1 год. Вертикальные отрезки изображены в масштабе 2,5 мм
1 год. Вертикальные отрезки изображены в масштабе 2,5 мм  1 час.
1 час.
5. Измеряя температуру воздуха в Москве через каждые два часа (с 11 час. 26 марта до 11 час. 27 марта 1957 года), получили следующую таблицу:

В первой строке указано время t в часах, а во второй — температура Т в градусах по Цельсию. За начало счета времени здесь принят момент нуль часов 27 марта. Время после этого момента выражено положительным числом, а до этого момента — отрицательным.
Например:
—13 обозначает момент времени 11 час. 26 марта;
—11 обозначает момент времени 13 час. 26 марта;
+ 11 обозначает момент времени 11 час. 27 марта.
Числом 9 обозначаем момент времени 9 час. 27 марта и т. д. Графическое изображение этой таблицы дано на рисунке 43.
Масштаб по оси t1t: 0,5 см  2 часам. Вертикальные отрезки изображены в масштабе 0,5 см
2 часам. Вертикальные отрезки изображены в масштабе 0,5 см  1 °C.
1 °C.
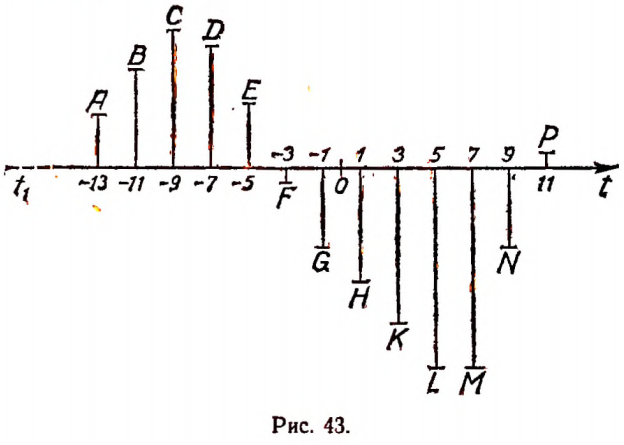
Соединяя на рисунке 43 точки А, В, С, D, Е, F, G, Н, К, L, М, N, Р плавной линией, получим график суточного изменения температуры (рис. 44).
В рассмотренном примере зависимость температуры Т от времени t получена путем непосредственного измерения температуры воздуха через равные промежутки времени.
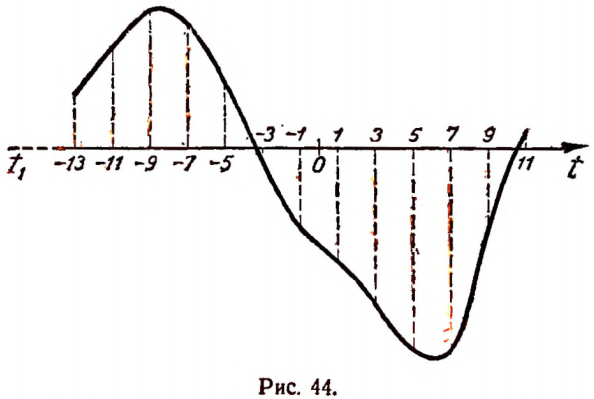
Всякая зависимость, полученная путем наблюдений и опытов, называется эмпирической*.
* Прилагательное «эмпирический» происходит от греческого слова «ejmipiа», что означает «опыт»
Зависимости, приведенные в примерах 4 и 5, эмпирические.
дополнительная
Алгебраические выражения и действия над ними
Степень
1. Степенью называется произведение, составленное из одинаковых множителей.
Повторяющийся множитель называется основанием степени, а число всех одинаковых множителей называется показателем степени.
Например, произведение 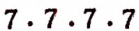 есть степень; основание этой степени равно 7, а показатель равен 4.
есть степень; основание этой степени равно 7, а показатель равен 4.
Произведение 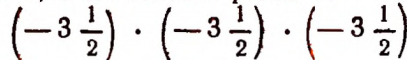 есть степень; основание этой степени равно
есть степень; основание этой степени равно  , а показатель равен 3.
, а показатель равен 3.
Произведение 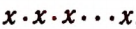 , в котором множитель х повторяется n раз, есть степень с основанием х и показателем n .
, в котором множитель х повторяется n раз, есть степень с основанием х и показателем n .
Эту степень принято обозначать символом 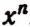 .
.
Степень 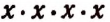 изобразится символом
изобразится символом 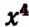 , а степень
, а степень 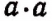 символом
символом 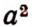 .
.
Выражение 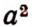 принято называть квадратом числа а, выражение а3 кубом числа а. Выражение
принято называть квадратом числа а, выражение а3 кубом числа а. Выражение 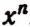 будем называть n -й (читается: «энной») степенью числа х.
будем называть n -й (читается: «энной») степенью числа х.
Выражение 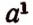 называется первой степенью а и оно представляет собой просто число а.
называется первой степенью а и оно представляет собой просто число а.
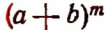 есть m-я (читается: «эмная») степень суммы чисел а и b;
есть m-я (читается: «эмная») степень суммы чисел а и b; 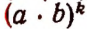 есть k-я (читается: «катая») степень произведения чисел а и b .
есть k-я (читается: «катая») степень произведения чисел а и b .
Очевидно, что
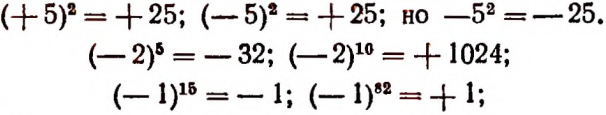
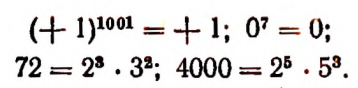
Действие, с помощью которого вычисляется значение степени, называется возведением в степень.
Замечание:
Обратим внимание на то, что символ 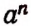 в принятом нами определении имеет пока смысл лишь в том случае, когда n есть целое положительное число. В дальнейшем мы будем пользоваться выражением
в принятом нами определении имеет пока смысл лишь в том случае, когда n есть целое положительное число. В дальнейшем мы будем пользоваться выражением 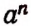 и при других значениях буквы п, т. е. рассматривать его более расширенно.
и при других значениях буквы п, т. е. рассматривать его более расширенно.
Умножение степеней с одинаковыми основаниями
Очевидно, что
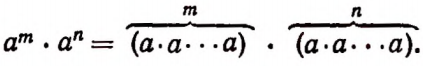
По сочетательному закону умножения
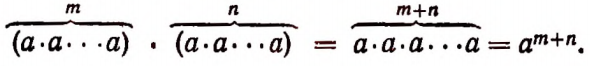
Следовательно,
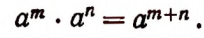
Итак, при умножении степеней с одинаковыми основаниями их показатели складываются. Например:
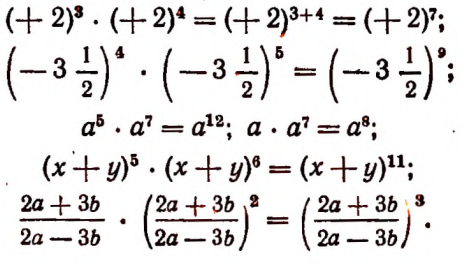
Коэффициент
Сумму, составленную из одинаковых слагаемых, можно записать в виде произведения. Например:
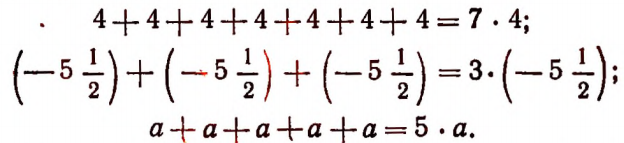
Произведение 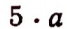 принято записывать в форме 5а. Если один или оба множителя обозначены буквами или заключены в скобки, то знак умножения принято опускать.
принято записывать в форме 5а. Если один или оба множителя обозначены буквами или заключены в скобки, то знак умножения принято опускать.
Например, вместо выражений
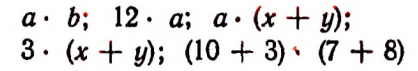
пишут
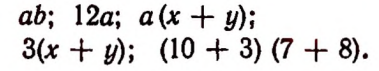
Определение:
Числовой множитель, выраженный цифрами, называется числовым коэффициентом.
Его принято ставить впереди буквенных множителей. Например, вместо выражений
принято писать
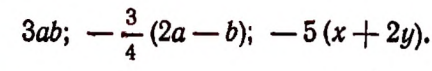
В выражениях
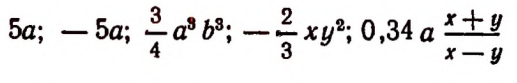
числовыми коэффициентами будут соответственно
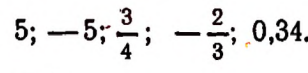
В каждом из выражений
числовой коэффициент равен 1, так как
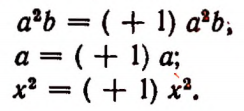
В каждом из выражений
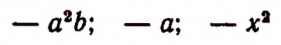
числовой коэффициент равен — 1, так как
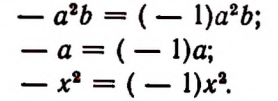
Коэффициент, равный 1 и — 1, принято не писать. Вместо 1 • а пишут а. Вместо — 1 • а пишут — а.
Возведение в степень произведения частного и степени
Возведение произведения в степень
Чтобы возвысить произведение в степень, можно возвысить в эту степень каждый множитель в отдельности и полученные степени перемножить.
Иначе говоря, степень произведения равна произведению тех же степеней множителей. Действительно,
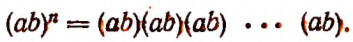
По сочетательному закону умножения
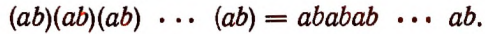
По переместительному закону
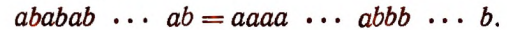
По сочетательному закону
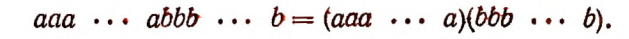
Поэтому
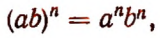
что и требовалось доказать.
Примеры:
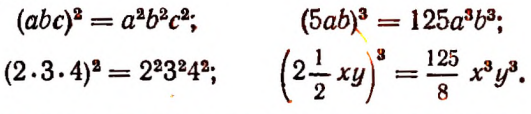
Поменяв местами левую и правую части равенства
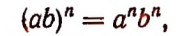
получим
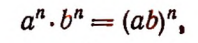
т. е. произведение степеней с одинаковыми показателями равно степени, основанием которой служит произведение оснований данных степеней.
Примеры:
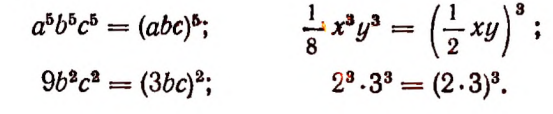
Возведение частного в степень
Чтобы возвысить частное в степень, достаточно возвысить в эту степень делимое и делитель и первый результат разделить на второй.
Короче говоря, степень частного равна частному степеней. Действительно,
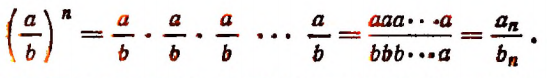
Поменяв местами левую и правую части равенства
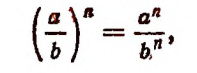
получим, что
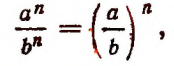
т. е. частное степеней с одинаковым показателем равно степени с тем же показателем и основанием, равным частному оснований данных степеней.
Возведение степени в степень
Чтобы возвести степень числа в новую степень, достаточно возвести это число в степень, показатель который равен произведению показателей степеней.
Действительно,
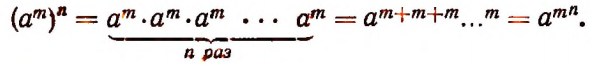
Примеры:
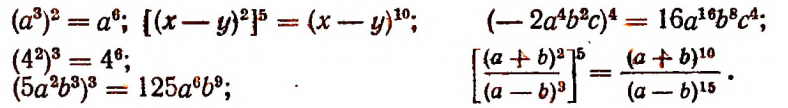
Классификация алгебраических выражений и порядок действий
Порядок действий в алгебраических выражениях сохраняется таким же, что и в арифметических выражениях.
Например, в выражении x+pq сначала p умножается на q , а затем полученное произведение прибавляется к х; в выражении (x+ p )q сначала х складывается с p , а затем полученная сумма умножается на q ; в выражении 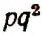 сперва q возводится во вторую степень, а затем p умножается на получаемый результат; в выражении
сперва q возводится во вторую степень, а затем p умножается на получаемый результат; в выражении 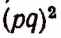 сначала p умножается на q, а затем полученный результат возводится во вторую степень; в выражении
сначала p умножается на q, а затем полученный результат возводится во вторую степень; в выражении 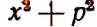 сперва х возводится во вторую степень, затем р возводится во вторую степень и, наконец, полученные степени складываются.
сперва х возводится во вторую степень, затем р возводится во вторую степень и, наконец, полученные степени складываются.
Рациональное алгебраическое выражение
Определение:
Всякое алгебраическое выражение, в котором нет никаких других действий, кроме сложения, вычитания, умножения, деления и возведения в целую степень*, называется рациональным.
* Кроме этих пяти действий, в алгебре изучаются еще и другие математические действия.
Примеры рациональных выражений:
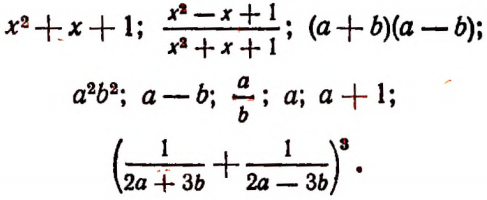
Целое выражение
Определение:
Если в рациональном выражении не содержится деление на буквенное выражение, то это рациональное выражение называется целым.
Примеры целых выражений:
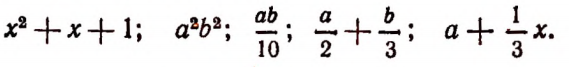
Дробное выражение
Определение:
Выражение, содержащее деление на буквенное выражение, называется дробным.
Примеры дробных выражений
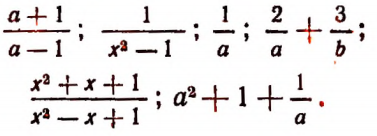
Одночлен
Определение:
Всякое выражение, в котором последнее действие не есть сложение или вычитание, называется одночленом.
Например, выражения
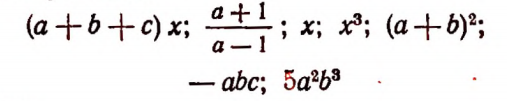
суть одночлены.
Многочлен
Определение:
Выражение, в котором последнее действие есть сложение или вычитание, называется многочленом.
Например, выражения
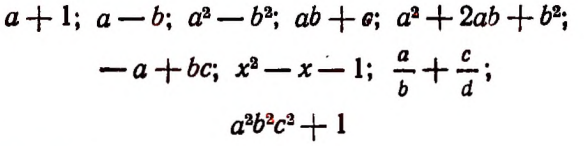
суть многочлены.
Определение типа любого выражения по последнему действию
1. Если в выражении последнее по порядку действие есть сложение, то это выражение называется суммой. Например, выражения
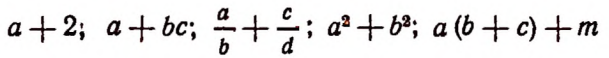
суть суммы.
2. Если в выражении последнее действие есть вычитание, то это выражение называется разностью. Например, выражения
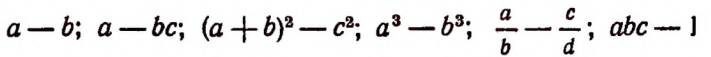
суть разности.
3. Если в выражении последнее действие есть умножение, то это выражение называется произведением. Например, выражения
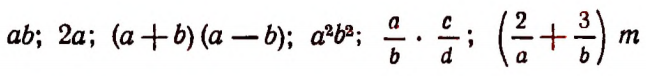
суть произведения.
Произведение, составленное из нескольких букв, принято записывать с соблюдением алфавитного порядка. Например, вместо 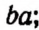
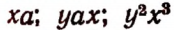 пишут
пишут 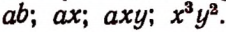
4. Если в выражении последнее действие есть деление, то это выражение называется частным. Например, выражения
суть частные.
5. Если в выражении последнее действие есть возведение в степень, то это выражение называется степенью.
Например, выражения
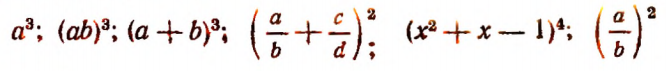
суть степени.
Примечaние:
Если последнее действие есть возведение во вторую степень, то выражение называется квадратом, а если в третью, то кубом.
Например, выражение 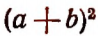 есть квадрат,
есть квадрат,  и
и 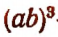 — кубы.
— кубы.
Полное название выражения
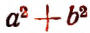 — есть сумма квадратов чисел а и b ;
— есть сумма квадратов чисел а и b ;  — квадрат суммы чисел а и b;
— квадрат суммы чисел а и b; 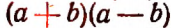 — произведение суммы чисел а и b на их разность;
— произведение суммы чисел а и b на их разность;  — разность кубов чисел а и b;
— разность кубов чисел а и b;  — куб разности чисел а и b;
— куб разности чисел а и b;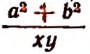 — частное от деления суммы квадратов чисел а и b на произведение чисел х и у;
— частное от деления суммы квадратов чисел а и b на произведение чисел х и у; 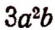 — утроенное произведение квадрата числа а на число b.
— утроенное произведение квадрата числа а на число b.
Обратим внимание на то, что полное название выражения 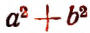 мы начали со слова «сумма», потому что в этом выражении последнее действие есть сложение, а полное название выражения
мы начали со слова «сумма», потому что в этом выражении последнее действие есть сложение, а полное название выражения  мы начали со слова «квадрат», потому что в этом выражении последнее действие есть возведение в квадрат. Полное название выражения
мы начали со слова «квадрат», потому что в этом выражении последнее действие есть возведение в квадрат. Полное название выражения  мы должны начинать со слова «разность», а выражения
мы должны начинать со слова «разность», а выражения 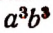 — со слова «произведение».
— со слова «произведение».
Если бы последнее действие было деление, то мы должны были бы начинать формулировку со слова «частное».
Числовое значение алгебраического выражения
Определение:
Числовым значением алгебраического выражения пои заданных значениях букв называется тот результат, который получится после замены букв их значениями и выполнения всех действий.
Примеры:
1. Числовым значением выражения а + b при а = + 12 и b = — 8 будет
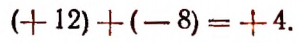
2. Числовым значением 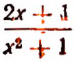 при х = 5 будет число
при х = 5 будет число 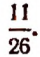
Действительно,
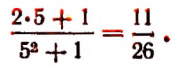
3. Числовое значение выражения 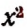 при х = 5 будет 25; при x = — 5 оно также будет 25.
при х = 5 будет 25; при x = — 5 оно также будет 25.
Очевидно, что значения выражения 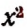 будут положительными как при положительных, так и при отрицательных значениях буквы х.
будут положительными как при положительных, так и при отрицательных значениях буквы х.
Очевидно, что значения выражения —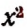 будут отрицательны как при положительных, так и при отрицательных значениях буквы х.
будут отрицательны как при положительных, так и при отрицательных значениях буквы х.
4. Значение выражения 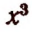 при х = 5 будет 125, а при х =—5 будет —125.
при х = 5 будет 125, а при х =—5 будет —125.
Значение выражения — 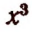 при х = 2 будет — 8, а при х = — 2 будет 8.
при х = 2 будет — 8, а при х = — 2 будет 8.
5. Значение выражения 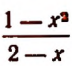 при х = — 5 будет
при х = — 5 будет
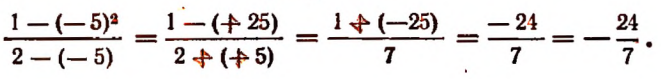
Таблица значений алгебраических выражений
Составим следующую таблицу значений выражения 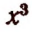 при нескольких различных значениях буквы х:
при нескольких различных значениях буквы х:
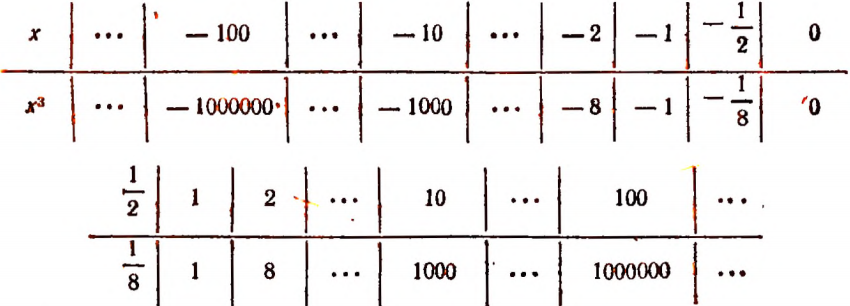
Очевидно, что при всех значениях буквы х, больших единицы, значения выражения 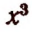 будут также большими единицы.
будут также большими единицы.
Если значение буквы л: заключается между 0 и -}» 1, то и значение выражения х3 также будет заключаться между 0 и 1.
Если значение буквы х заключается между —1 и 0, то значение выражения 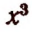 также будет заключаться между — 1 и 0.
также будет заключаться между — 1 и 0.
Если значение буквы х меньше — 1, то значение выражения 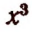 также будет меньше —1.
также будет меньше —1.
Составим таблицу значений выражения 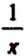 .
.
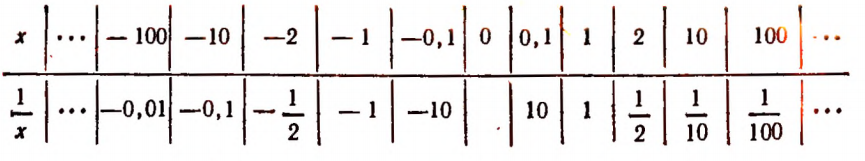
Выражение 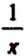 при х = 0 лишено смысла.
при х = 0 лишено смысла.
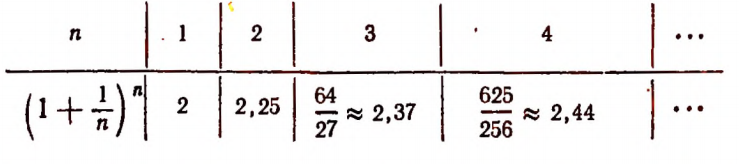
Составим таблицу значений выражения 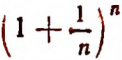 , давая букве n только целые положительные значения.
, давая букве n только целые положительные значения.
Примеры алгебраических выражений, теряющих смысл при некоторых значениях букв
Встречаются такие алгебраические выражения, которые теряют смысл при некоторых значениях входящих в них букв. Например, выражение 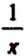 теряет смысл при х = 0; выражение
теряет смысл при х = 0; выражение 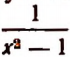 теряет смысл при х = 1 и при х = — 1; выражение
теряет смысл при х = 1 и при х = — 1; выражение 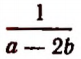 теряет смысл при а = 2 и b = 1 или при а = 6 и b = 3 при многих других парах значений букв а и b, обращающих выражение а — 2 b в нуль. Выражение
теряет смысл при а = 2 и b = 1 или при а = 6 и b = 3 при многих других парах значений букв а и b, обращающих выражение а — 2 b в нуль. Выражение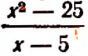 теряет смысл при x = 5, так как оно при х = 5 принимает вид
теряет смысл при x = 5, так как оно при х = 5 принимает вид 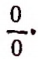
Все такие значения букв, при которых данное выражение не теряет смысла, называются допустимыми для данного выражения.
Для выражений 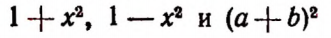 допустимы любые значения входящих в них букв. Допустимыми значениями будут
допустимы любые значения входящих в них букв. Допустимыми значениями будут
а) для 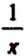 все значения х, кроме x = 0;
все значения х, кроме x = 0;
б) для 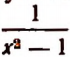 все значения х, кроме х = 1 и х = — 1;
все значения х, кроме х = 1 и х = — 1;
в) для 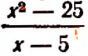 все значения х , кроме х = 5.
все значения х , кроме х = 5.
Примечание:
Значения буквы илb букв, обращающие знаменатель дроби в нуль, заслуживают особого внимания. В этих случаях дробь теряет смысл.
Алгебраическая сумма
Выражение 8—5 понимается в арифметике в единственном смысле, а именно кдк разность между числами 8 и 5.
В алгебре же это выражение можно понимать двояко:
либо как разность

либо же как сумму
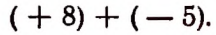
Поэтому выражение 8 — 5 можно считать сокращенной записью суммы (+ 8) + (— 5) или, что то же самое, суммы 8 + (— 5). Аналогично выражение
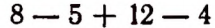
можно считать сокращенной записью суммы
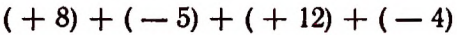
или, что то же самое, суммы ,
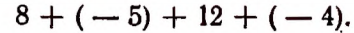
Ввиду того что в алгебре разность можно рассматривать как сумму, выражения 8 — 5, 8 — 5+12 — 4 и им подобные называются алгебраическими суммами.
Выражение
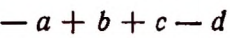
обозначает сумму следующих слагаемых: 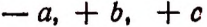 и
и 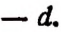
Точно так же выражение
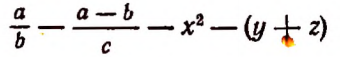
обозначает сумму следующих выражений:
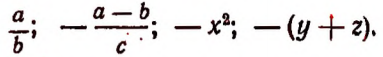
Изложенное можно сформулировать следующим образом. Несколько алгебраических выражений, соединенных знаками + или —, можно рассматривать как сумму. Имея это в виду, совокупность алгебраических выражений, соединенных между собой знаками + или —, называют алгебраической суммой.
Например, выражения
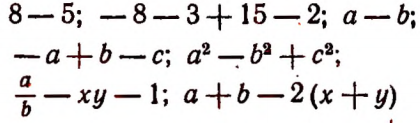
суть алгебраические суммы.
Слагаемыми алгебраической суммы а — b будут а и — b ; слагаемыми алгебраической суммы 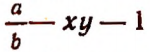 будут
будут 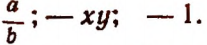
Слагаемые алгебраической суммы называются ее членами.
Каждая алгебраическая сумма является в то же время и многочленным выражением. Члены алгебраической суммы называются одновременно и членами многочлена.
Обратно, каждый многочлен является в то же время и алгебраической суммой.
Пример:
Выражение
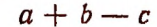
есть алгебраическая сумма. Слагаемыми этой суммы будут a, b и — с. В то же время 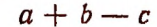 есть многочлен. Членами этого многочлена будут опять же a, b и — с .
есть многочлен. Членами этого многочлена будут опять же a, b и — с .
Алгебраическая сумма обладает всеми свойствами суммы, перечисленными в § 4 главы I.
На основании изложенного выше мы можем вместо выражения
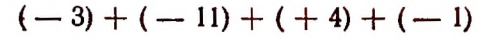
писать
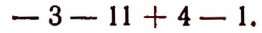
Так же можно вместо выражения
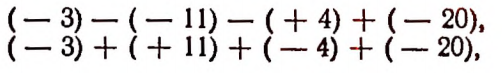
писать
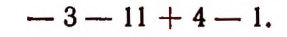
Вместо
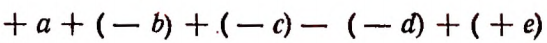
пишут просто
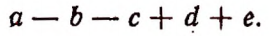
Когда мы рассматриваем выражение 8—5 как разность, то знак минус является знаком действия вычитания; когда же выражение 8—5 рассматривается как алгебраическая сумма, то знак минус перестает быть знаком действия и становится знаком, характеризующим отрицательность второго слагаемого. Переход от выражения
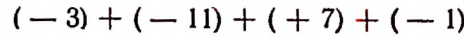
к выражению
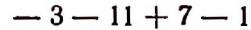
достигается следующим образом: в выражении
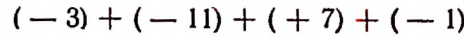
выбрасываются все знаки действия сложения и скобки, а числа, находящиеся в скобках, записываются одно за другим с их знаками.
Подобные одночлены и их приведение
Пусть в каждой коробке’ находится а спичек, а в каждой пачке b коробок; пусть, кроме того, в каждом ящике содержится а пачек и в каждом вагоне с ящиков.
При этих условиях можно, например, утверждать следующее:

Очевидно, что
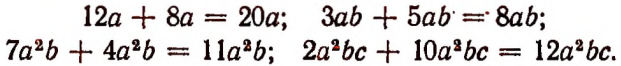
Пусть на складе имеется запас спичек. Этот запас есть величина, могущая изменяться в других противоположных направлениях: он может увеличиваться и уменьшаться.
Фраза «Запас спичек на складе изменился на 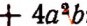 » будет означать, что на склад поступило 4 ящика спичек.
» будет означать, что на склад поступило 4 ящика спичек.
Фраза «Запас спичек на складе изменился на 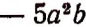 » означает, что со склада вывезли 5 ящиков спичек.
» означает, что со склада вывезли 5 ящиков спичек.
Пусть запас спичек на складе изменился первый раз на 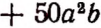 , второй раз на
, второй раз на 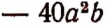 и третий раз на
и третий раз на 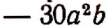 . Тогда итоговое изменение будет
. Тогда итоговое изменение будет
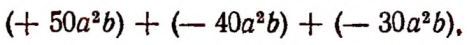
т. е. составит 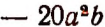 , что означает уменьшение запаса спичек на 20 ящиков. Очевидно, что
, что означает уменьшение запаса спичек на 20 ящиков. Очевидно, что
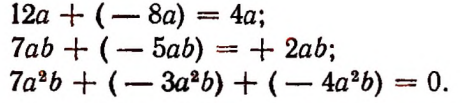
Определение. Одночлены называются подобными, если они отличаются друг от друга только числовыми коэффициентами или совсем не отличаются. Например, одночлены
подобны.
Подобны между собой и следующие одночлены:
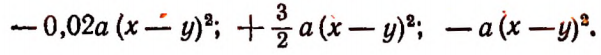
Точно так же подобны следующие одночлены:
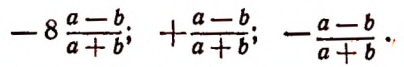
Сумму нескольких подобных одночленов можно записать в виде одного одночлена. Например,
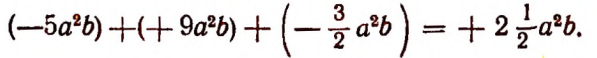
Определение. Операция замены суммы- нескольких подобных одночленов одним одночленом называется приведением подобных одночленов.
Теперь сформулируем правило приведения подобных одночленов и приведем его доказательство..
Если многочлен содержит несколько подобных членов, то их можно заменить одним членом, подобным каждому из них, приняв за его коэффициент алгебраическую сумму коэффициентов заменяемых членов.
Доказательство. Пусть имеется многочлен 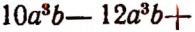
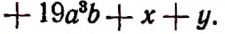 На основании распределительного закона
На основании распределительного закона
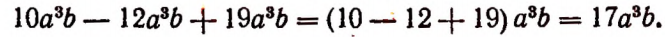
Следовательно,
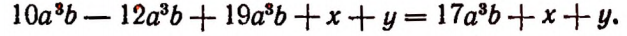
Примеры:
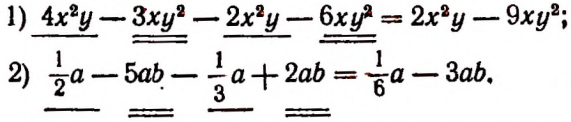
Сложение, вычитание и умножение одночленов
Сложение
Пусть имеется несколько одночленов: 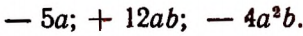 Суммой этих одночленов будет следующее выражение:
Суммой этих одночленов будет следующее выражение:
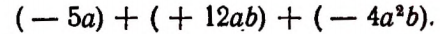
Последнюю сумму можно записать в следующем простом виде:
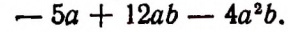
Отсюда вытекает правило:
Чтобы сложить одночлены, достаточно записать их один за другим с их знаками.
В соответствии с этим мы должны рассматривать, например выражение  как следующую сумму:
как следующую сумму:
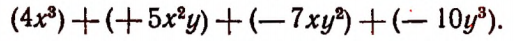
Примечание:
Два одночлена, отличающиеся только знаком, называются противоположными. Например, одночлены 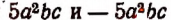 противоположны.
противоположны.
Сумма двух противоположных одночленов равна нулю.’Например,
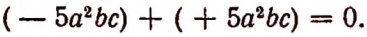
Вычитание
Пусть имеются два одночлена: 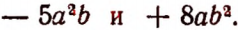 Разностью этих одночленов будет следующее выражение:
Разностью этих одночленов будет следующее выражение:

Вычитание любого числа можно заменить прибавлением числа, противоположного вычитаемому. Поэтому разность

мы можем записать в виде суммы
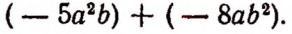
Эту сумму, как мы только что условились, можно записать в виде
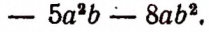
Отсюда вытекает следующее правило:
Чтобы вычесть одночлен, достаточно приписать его к уменьшаемому с противоположным знаком.
Например, разность между одночленами 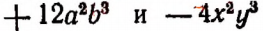 равна
равна 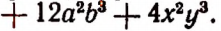
Умножение
Пусть имеются два одночлена
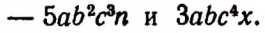
Произведением этих одночленов будет выражение
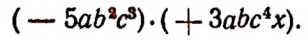
На основании сочетательного и переместительного законов умножения мы можем это произведение записать в следующем виде:
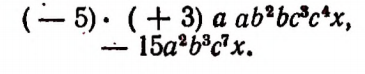
Умножение одночленов выполняется на основании переместительного и сочетательного законов умножения.
Другие примеры умножения одночленов:
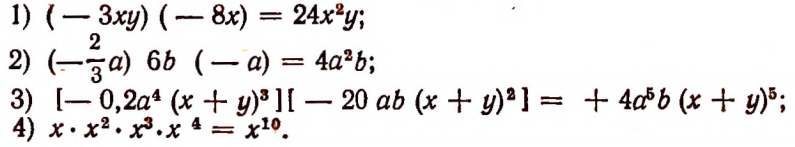
Сложение, вычитание и умножение многочленов
Под многочленом, например,
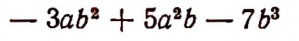
можно понимать следующую сумму одночленов:
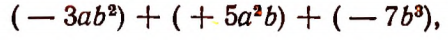
так как всякий многочлен можно рассматривать как алгебраическую сумму. Исходя из этого, мы будем говорить, что многочлен
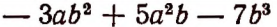
составлен из трех одночленов:
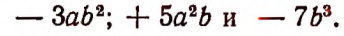
Эти одночлены называют членами многочлена
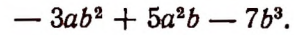
Например, членами многочлена
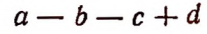
являются следующие одночлены:

Два многочлена называются противоположными, если члены одного из них противоположны членам другого.
Например, многочлены 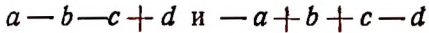 являются противоположными.
являются противоположными.
Сложение
Пусть имеется какое-нибудь алгебраическое выражение А и многочлен 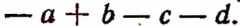 Суммой этих двух выражений называется выражение
Суммой этих двух выражений называется выражение
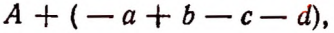
которое можно записать так:
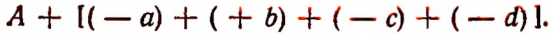
На основании сочетательного закона сложения эту сумму можно переписать в виде
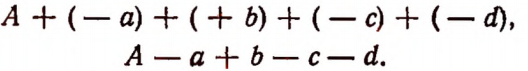
Отсюда вытекает следующее правило:
Чтобы прибавить многочлен, достаточно приписать все его члены с их знаками.
Например:
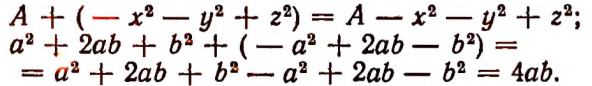
Значения двух противоположных многочленов при любых числовых значениях входящих в них букв будут числами противоположными, так как сумма двух противоположных многочленов всегда равна нулю.
Например:
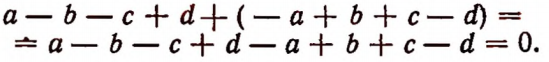
Вычитание
Пусть имеется какое-нибудь алгебраическое выражение А и многочлен 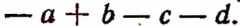 Разностью между этими выражениями будет выражение
Разностью между этими выражениями будет выражение
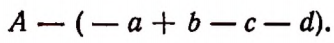
Вычитание любого числа можно заменить прибавлением числа, противоположного вычитаемому. Поэтому написанную выше разность можно представить в виде следующей суммы:

которая равна выражению
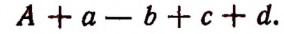
Отсюда вытекает правило:
Чтобы вычесть многочлен, достаточно приписать к уменьшаемому все его члены с противоположными знаками.
Например:
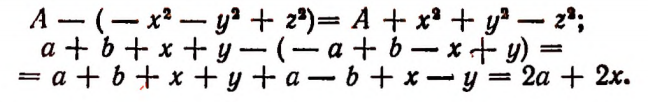
Умножение многочлена на одночлен
Пусть имеется многочлен 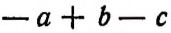 и одночлен
и одночлен 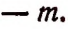 Произведением этих двух множителей будет выражение
Произведением этих двух множителей будет выражение
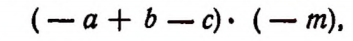
которое может быть записано в виде
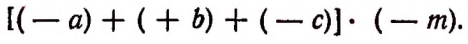
На основании распределительного закона умножения последнее произведение будет равно выражению
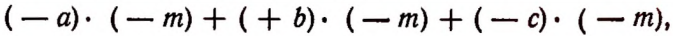
т. е. выражению
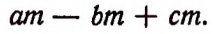
Отсюда вытекает следующее правило:
Чтобы, умножить многочлен на одночлен, достаточно умножить на этот одночлен каждый член многочлена и полученные произведения сложить. Например:
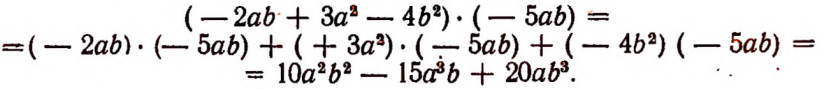
Умножение многочлена на многочлен
Пусть имеется два многочлена:
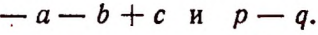
Их произведением называется выражение
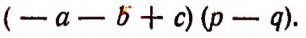
Рассматривая многочлен р — q как некоторое число и опираясь на распределительный закон умножения, мы можем написанное выше произведение представить в следующем виде:
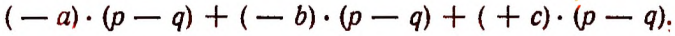
Опираясь на переместительный закон, перепишем последнее выражение в следующем виде:
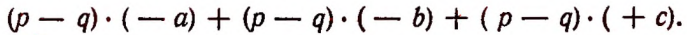
Применяя еще раз распределительный закон умножения, получим
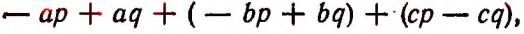
или
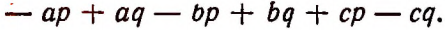
Итак, оказалось, что
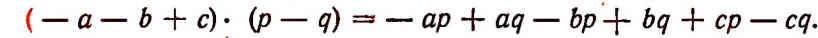
Отсюда вытекает правило:
Чтобы умножить многочлен на многочлен достаточно умножить каждый член одного многочлена на каждый член другого и все полученные произведения сложить.
Например:
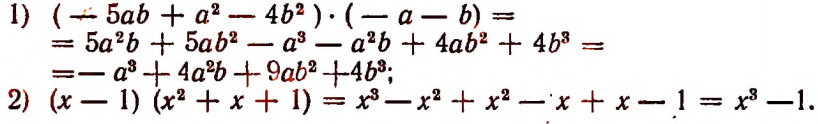
Раскрытие скобок
Чтобы раскрыть скобки, перед которыми стоит знак плюс, надо опустить этот знак плюс, опустить скобки и записать все члены, стоящие в скобках, с их знаками.
Это правило вытекает из правила сложения многочленов, сформулированного в § 9.
Примеры:
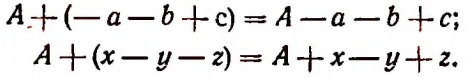
Из правила вычитания многочлена вытекает правило раскрытия скобок, перед которыми стоит знак минус.
Чтобы раскрыть скобки, перед которыми стоит знак минус, надо опустить этот знак минус, опустить скобки и записать все члены, стоящие в скобках, со знаками, противоположными их знакам.
Примеры:
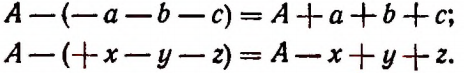
Заключение в скобки
При заключении данного многочлена в скобки перед ними можно ставить либо знак плюс, либо знак минус по своему усмотрению.
Чтобы заключить многочлен в скобки с поставленным перед скобками знаком плюс, надо внутри скобок все члены многочлена записать с их знаками.
Пример:
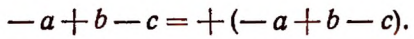
Чтобы заключить многочлен в скобки с поставленным перед скобками знаком минус, надо внутри скобок записать все его члены с противоположными знаками.
Это правило следует из правила вычитания многочленов, сформулированного в § 9.
Пример:

Примечание. В скобки можно заключать и часть членов многочлена.
Примеры:
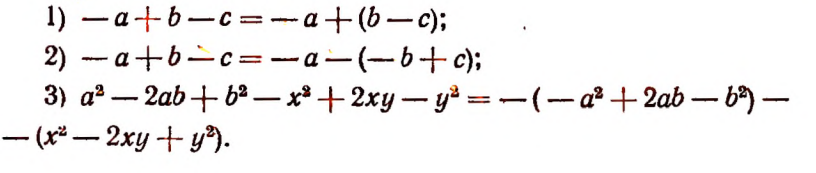
Основные формулы умножения
Алгебраическое равенство, выражающее какое-либо общее свойство чисел или связь между двумя или несколькими величинами, называется формулой.
Например, каждое из равенств
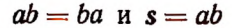
есть формула.
Равенство ab = ba выражает общее свойство чисел, а именно, что произведение двух чисел от перемены мест множителей не меняется.
Равенство s = ab устанавливает зависимость между тремя величинами s , a и b , например, между площадью прямоугольника s и длинами его сторон a и b .
Основными и часто применяемыми формулами умножения являются следующие:
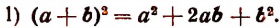
Квадрат суммы двух чисел равен квадрату первого кисла, плюс удвоенное произведение первого числа на второе, плюс квадрат второго числа.
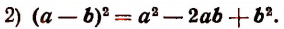
Квадрат разности двух чисел равен квадрату первого числа, минус удвоенное произведение первого числа на второе, плюс квадрат второго числа.
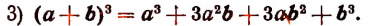
Куб суммы двух чисел равен кубу первого числа, плюс утроенное произведение квадрата первого числа на второе, плюс утроенное произведение первого числа на квадрат второго, плюс куб второго числа.
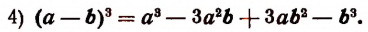
Куб разности двух чисел равен кубу первого числа, минус утроенное произведение квадрата первого числа на второе, плюс утроенное произведение первого числа на квадрат второго, минус куб второго числа.
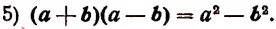
Произведение суммы двух чисел на их разность равно разности квадратов этих чисел.
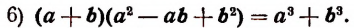
Произведение суммы двух чисел на неполный квадрат их разности равно сумме кубов этих чисел.
(Здесь неполным квадратом разности чисел а и b названо выражение 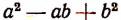 . Название это условное; оно принято потому, что выражение
. Название это условное; оно принято потому, что выражение 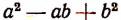 имеет внешнее сходство с выражением
имеет внешнее сходство с выражением 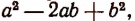 представляющим собой квадрат разности чисел а и b.)
представляющим собой квадрат разности чисел а и b.)
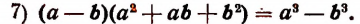
Произведение разности двух чисел на неполный квадрат их суммы равно разности кубов этих чисел.
(Здесь неполным квадратом суммы чисел а и b условно названо выражение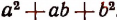 )
)
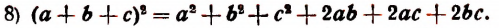
Квадрат многочлена равен сумме квадратов всех его членов, сложенной с удвоенными произведениями каждого члена на каждый из последующих.
Все эти формулы легко вывозятся путем умножения многочленов и приведения подобных членов. Например,
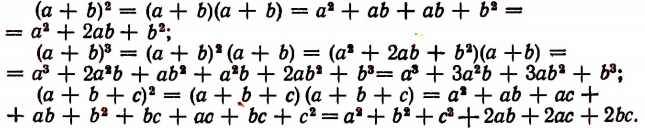
Остальные пять фюрмул предлагается учащемуся вывести самостоятельно.
Формула 8 верна для любого многочлена. Например,
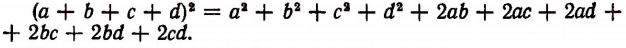
Применим формулу № 8 к частным случаям.
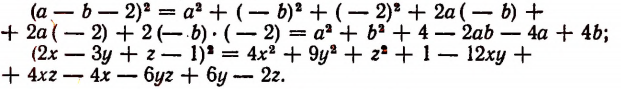
Формулу № 8 можно вывести еще и так:
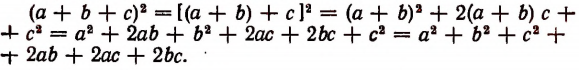
Во всяком равенстве
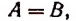
А называется левой частью равенства, а В — правой.
Обратим внимание на то. что во всех основных формулах умножения левая часть есть одночлен, а правая — многочлен.
Примеры применения основных формул умножения
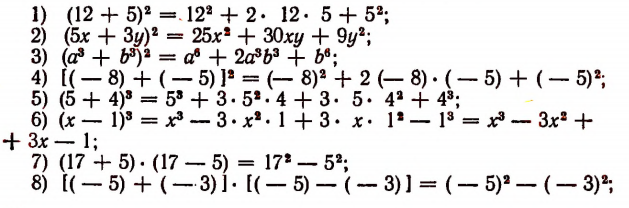
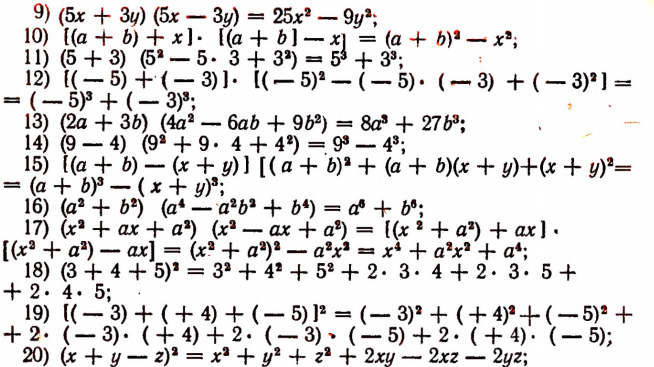
Рекомендуется самостоятельно убедиться, что 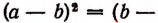
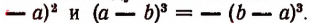
Основные формулы умножения многократно применяются при решении задач в дальнейшем.
Абсолютная величина числа
Как нам уже известно, абсолютной величиной положительного числа называется само это число. Абсолютной величиной отрицательного числа называется противоположное ему число.
Абсолютной величиной числа нуль называется само число нуль. Например, абсолютная величина числа + 17 будет + 17, причем абсолютной величиной числа — 17 будет тоже + 17.
Абсолютная величина числа х обозначается символом 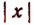 , т. е.
, т. е.
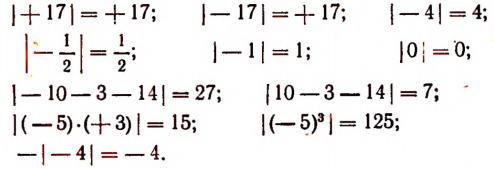
Абсолютная величина числа по определению никогда не может быть числом отрицательным, т, е.
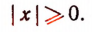
Знак  читается так: «больше или равно».
читается так: «больше или равно».
Запись 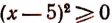 читается так: «
читается так: «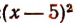 больше или равно нулю». Здесь равенство нулю будет иметь место тогда и только тогда, когда х = 5.
больше или равно нулю». Здесь равенство нулю будет иметь место тогда и только тогда, когда х = 5.
Запись 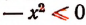 читается так: «
читается так: « меньше или равно нулю». Здесь равенство нулю будет тогда и только тогда, когда х = 0.
меньше или равно нулю». Здесь равенство нулю будет тогда и только тогда, когда х = 0.
Некоторые частные случаи:
В том случае, когда буква х обозначает собой положительное число, верно следующее равенство:
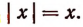
В том же случае, когда буква х представляет собой отрицательное число, будет верным следующее равенство: 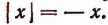 Например,
Например,
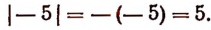
Сказанное можно записать короче так:
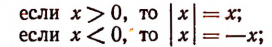
Очевидно, что при любом значении буквы а
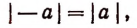
т. е. два противоположных числа всегда имеют одинаковую абсолютную величину.
При любых значениях буквы а и b значения выражений а — b и b — а представляют собой числа противоположные, т. е.
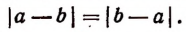
Легко понять, что
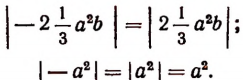
Равенство 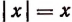 верно при всех положительных значениях х и при х = 0 и несправедливо при всех отрицательных значениях х .
верно при всех положительных значениях х и при х = 0 и несправедливо при всех отрицательных значениях х .
Равенство 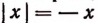 верно при всех отрицательных значениях х и при х = 0 и несправедливо при всех положительных значениях х .
верно при всех отрицательных значениях х и при х = 0 и несправедливо при всех положительных значениях х .
Если 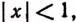 то буква х может принимать только значения, заключающиеся между — 1 и +1.
то буква х может принимать только значения, заключающиеся между — 1 и +1.
Если 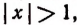 то х может принимать значения как больше +1, так и меньше —1.
то х может принимать значения как больше +1, так и меньше —1.
Если  то это значит, что
то это значит, что  , т. е, что х может принимать лишь значения от — 1 до + 1 включительно.
, т. е, что х может принимать лишь значения от — 1 до + 1 включительно.
Если 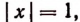 то либо х = 1, либо х = — 1.
то либо х = 1, либо х = — 1.
Если 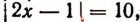 то либо 2х — 1 = 10, либо 2х — 1 =— 10.
то либо 2х — 1 = 10, либо 2х — 1 =— 10.
Свойства абсолютных величин
1. Абсолютная величина алгебраической суммы. Очевидно, что
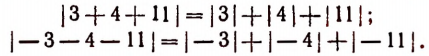
Обобщая это, замечаем, что если все числа a, b и с, одновременно положительны или отрицательны, то
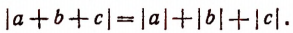
Поскольку очевидно также, что
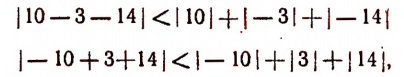
путем обобщения устанавливаем, что если среди чисел a, b и с имеются и положительные и отрицательные, то
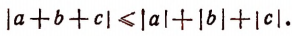
Если считать, что буквы a, b и с суть любые числа, то правильна следующая запись:
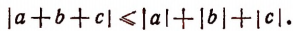
Этот результат формулируется словами так:
Абсолютная величина алгебраической суммы меньше или равна сумме абсолютных величин слагаемых.
Очевидно, что
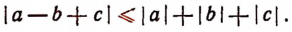
Здесь знак равенства имеет место тогда, когда все числа a, — b и с либо одновременно положительны, либо одновременно отрицательны. Если же среди чисел a, — b и с имеются и положительные и отрицательные, то знак равенства отпадает и остается только знак «меньше».
2. Абсолютная величина произведения. Очевидно, что
Из определения произведения следует, что
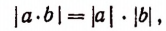
т. е. абсолютная величина произведения равна произведению абсолютных величин множителей.
3. Абсолютная величина дроби. Докажем, что абсолютная величина дроби равна абсолютной величине числителя, деленной на абсолютную величину знаменателя, т. е.
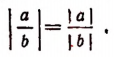
Действительно,
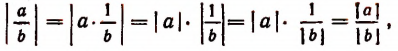
что и требовалось доказать.
Примеры:

4. Абсолютная величина степени. Абсолютная величина, n-й степени числа равна абсолютной величине основания этой степени, возведенной в n-ю степень, т. е.
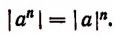
Действительно,
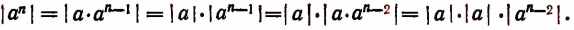
Продолжая этот процесс, мы получим в конце концов, что
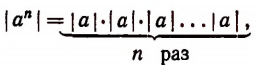
т. е. получим, что
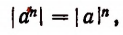
а это и требовалось доказать.
Примеры:
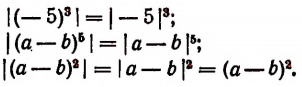
Примеры:
1. Найти значения выражения
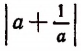
при следующих значениях буквы а:
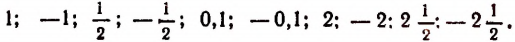
Примечание. Выражение 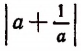 теряет смысл при а=0.
теряет смысл при а=0.
2. Найти значения выражения
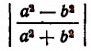
при следующих парах значений букв а и b:
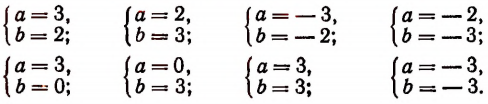
Примечание. Выражение 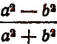 теряет смысл, если буквам а и b придать одновременно нулевые значения.
теряет смысл, если буквам а и b придать одновременно нулевые значения.
Замечание. Пусть 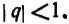 Тогда значение выражения
Тогда значение выражения 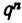 окажется столь угодно близким к нулю при достаточно большом значении буквы n. Например:
окажется столь угодно близким к нулю при достаточно большом значении буквы n. Например:
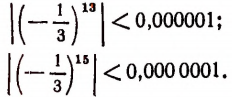
С помощью числа 0,000001 мы оцениваем степень близости к нулю чисел
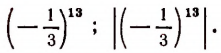
Точки числовой оси, соответствующие числам
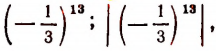
располагаются первая слева и вторая справа от начальной точки числовой оси на одинаковом очень малом удалении от этой начальной точки. С помощью числа 0,0000001 мы можем оценить близость к нулю чисел 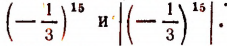
3. Найти значения выражения
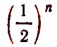
при следующих значениях буквы n:
Оцените значение этого выражения при n = 20; n = 100 и т. д.
Найти значения выражения
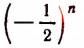
при следующих значениях буквы n: 
Оцените значение этого выражения при n = 20; n = 21; n = 100; n = 101 и т. д.
Понятие абсолютной величины числа, а также и свойства абсолютных величин имеют весьма широкое применение . С их помощью нередко разрешаются вопросы, весьма важные по их значимости и очень серьезные по степени их трудности.
Правила действий над алгебраическими выражениями
Деление степеней и одночленов
При делении степеней с одинаковыми основаниями показатели степеней вычитаются, если показатель степени делимого больше показателя степени делителя. Например,
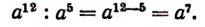
Справедливость этого легко доказать умножением
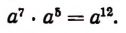
Оговорка, требующая, чтобы показатель степени делимого был больше показателя степени делителя, необходима. В самом деле, мы не можем писать
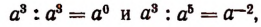
так как символы 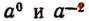 пока для нас смысла не имеют. Вопрос об этих символах будет рассмотрен на странице 161. Пока же равенство
пока для нас смысла не имеют. Вопрос об этих символах будет рассмотрен на странице 161. Пока же равенство 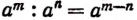 мы можем писать лишь при условии, что m > n, где m и n натуральные числа.
мы можем писать лишь при условии, что m > n, где m и n натуральные числа.
Примечание:
Равенство 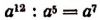 является верным при всяком значении буквы а, кроме а = 0. При а = 0 выражение
является верным при всяком значении буквы а, кроме а = 0. При а = 0 выражение 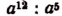 обращается в
обращается в  т. е. не имеет смысла, в то время как выражение
т. е. не имеет смысла, в то время как выражение 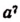 обращается в нуль.
обращается в нуль.
Деление одночленов
Правило деления одночленов проще всего уяснить на примерах. Поэтому приведем несколько примеров, в которых деление уже выполнено.
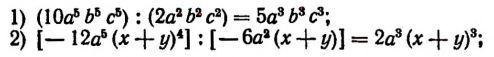
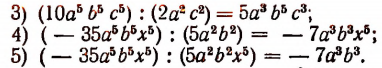
Верность этих равенств легко доказывается умножением частного на делитель.
Пусть имеются два целых алгебраических выражения. Говорят, что первое из них делится на второе нацело, если существует такое третье целое выражение, произведение которого на второе выражение дает первое. Например, 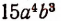 делится нацело на
делится нацело на 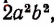 так как существует целое выражение
так как существует целое выражение 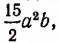 от умножения которого на
от умножения которого на 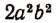 получается
получается 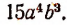
Если делитель содержит хоть одну букву, которую делимое вовсе не содержит или содержит с меньшим показателем, то де¬ление нацело невозможно.
Например, 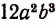 не делится нацело на
не делится нацело на 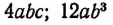 не делится нацело на
не делится нацело на 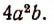
Если даны два таких одночлена, что каждое буквенное выражение, входящее во второй одночлен, входит и в первый и притом с не меньшим показателем, чем во второй, то при делении первого одночлена на второй получается целый одночлен. При этом числовой коэффициент частного получается делением числового коэффициента делимого на числовой коэффициент делителя.
Каждое буквенное выражение, входящее в делимое и не входящее в делитель, переходит в частное с неизменным показателем. Например, 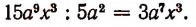
Каждое буквенное выражение, входящее в делимое с большим показателем, чем в делитель, входит в частное с показателем, равным разности его показателей в делимом и делителе.
Буквенное выражение, входящее в делимое и в делитель с одинаковыми показателями, вовсе не входит в результат деления (в частное).
Например,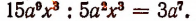
Наибольший общий делитель
Из арифметики известно, что наибольшим общим делителем произведений
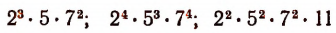
будет
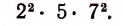
По аналогии с этим наибольшим общим делителем произведений
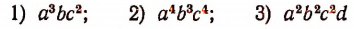
будет выражение
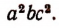
Наибольшим общим делителем произведений
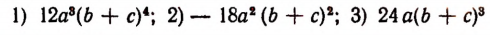
будет выражение
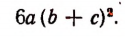
Наибольшим общим делителем таких произведений, как, например,
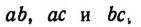
принято считать единицу.
Деление многочлена на одночлен
Частное от деления многочлена на одночлен равно сумме частных, полученных от деления на этот одно¬член каждого члена многочлена, т. е.
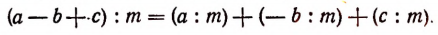
Правильность произведенного преобразования вытекает из того, что
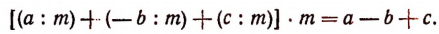
Примеры:
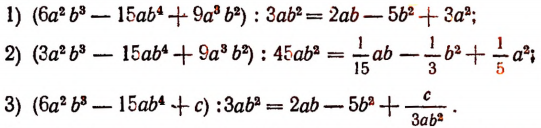
В первых двух примерах результатом деления оказалось целое алгебраическое выражение, а в третьем дробное.
Замечание:
Многочлен, не содержащий подобных членов, делится нацело на одночлен тогда и только тогда, когда каждый его член делится нацело на этот одночлен.
Многочлен всегда делится нацело на наибольший общий делитель его членов. Например, многочлен
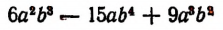
состоит из следующих членов.
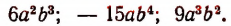
Наибольший общий делитель этих членов есть  Частное от деления многочлена
Частное от деления многочлена  будет
будет 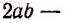
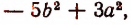 т. е. действительно целое выражение.
т. е. действительно целое выражение.
Разложение многочлена на множители
1. Мы уже видели некоторые применения алгебраических преобразований к решению задач.
В настоящем параграфе излагается еще одно специальное преобразование, которое называется разложением многочлена на множители.
Разложение целого многочлена на целые множители есть такая операция, с помощью которой мы представляем данный многочлен в виде произведения, тождественно равного данному многочлену, причем множители этого произведения должны быть некоторыми новыми целыми выражениями.
Приведем сначала несколько примеров уже выполненного разложения многочленов на множители:
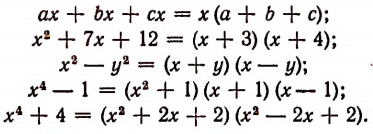
В верности каждого из этих равенств лето убедиться путем перемножения множителей, стоящих в его правой части. Однако сама операция разложения многочлена на множители, т. е. отыскание произведения, равносильного данному многочлену, не всегда является легкой задачей.
2. Существует четыре основных способа разложения многочленов на множители:
1) вынесения за скобки;
2) группировки;
3) применения основных формул умножения;
4) введения новых вспомогательных членов.
Кроме этих четырех основных способов, существуют и другие, специальные, которые изложены в последующих разделах курса алгебры.
Вынесение общего множителя за скобки
Этот способ заключается в следующем. Данный многочлен заменяют произведением общего наибольшего делителя всех его членов на частное, полученное от деления данного многочлена на этот общий делитель. Этот общий наибольший делитель называется множителем, выносимым за скобки.
Примеры:
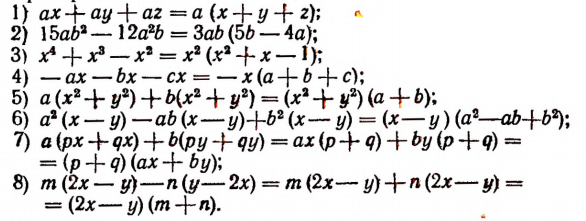
Примечание:
За скобки можно выносить и любой множитель. Например,
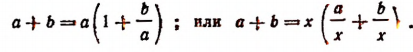
Последние два примера существенно отличаются от всех предыдущих. Во всех предыдущих примерах в скобках получались целые выражения, а в последних двух дробные.
Разложение на множители способом группировки
Этот способ заключается в следующем. Члены многочлена разбиваются на две или несколько групп с таким расчетом, чтобы каждую группу было бы возможно преобразовать в произведение, и так, чтобы эти произведения имели бы общий множитель. После этого применяется способ вынесения за скобки общего наибольшего делителя вновь образовавшихся членов.
Примеры:
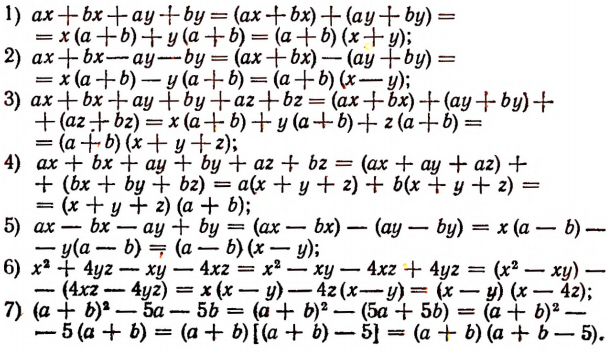
Разумеется, что способ группировки является пригодный не ко всякому многочлену.
Например, он не пригоден к многочлену 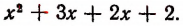 (Способ разложения таких многочленов на множители изложен на стр. 298)
(Способ разложения таких многочленов на множители изложен на стр. 298)
Многочлен 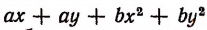 тоже нельзя разложить на множители способом группировки, но его и вообще нельзя разложить на целые множители.
тоже нельзя разложить на множители способом группировки, но его и вообще нельзя разложить на целые множители.
Применение основных формул умножения
В тех случаях, когда многочлен, подлежащий разложению на множители, имеет форму правой части какой-либо основной формулы умножения, то его разложение на множители достигается применением соответствующей основной формулы умножения, записанной в обратном порядке. Например, из формулы
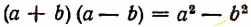
следует, что
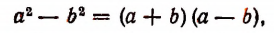
т. е. разность квадратов двух выражений равна произведению суммы этих выражений на их разность.
Примеры:
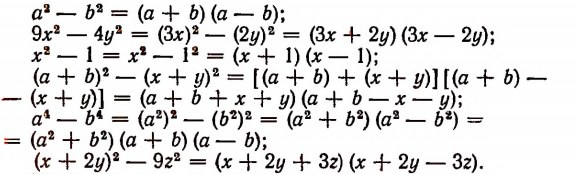
Из формулы
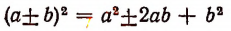
следует, что
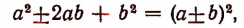
т. е. если многочлен содержит три члена, из которых два представляют собой квадраты, а третий член есть плюс (или минус) удвоенное произведение оснований этих квадратов, то этот многочлен можно заменить квадратом суммы (или квадратом разности).
Квадрат суммы или квадрат разности представляют собой по существу произведения. Поэтому применением основных формул умножения в данном случае мы по существу достигаем цели разложения многочлена на множители.
Аналогично применяют и остальные основные формулы умножения.
Примеры:
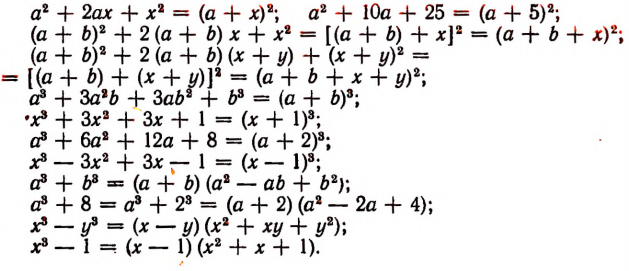
Введение новых вспомогательных членов
Способ введения новых вспомогательных членов заключается в том, что данный многочлен заменяется другим многочленом, ему тождественно равным, но содержащим иное число членов, причем это делается с таким расчетом, чтобы можно было применить к полученному многочлену способ группировки.
Примеры:
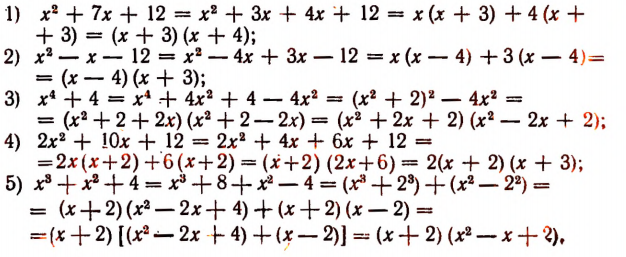
Некоторые более сложные примеры
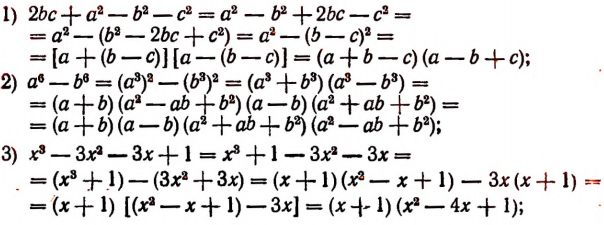
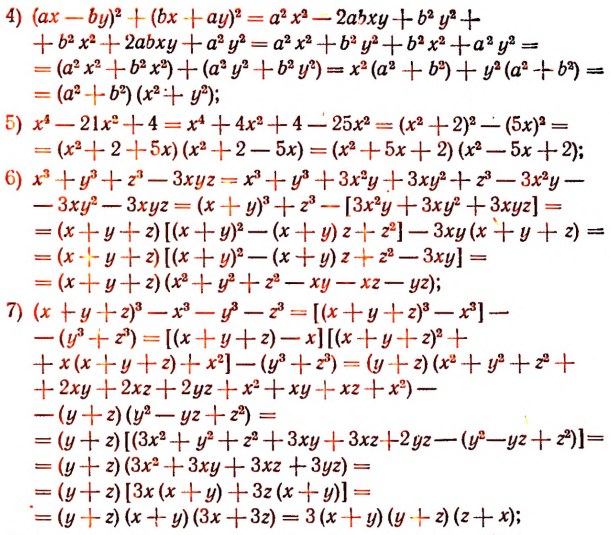
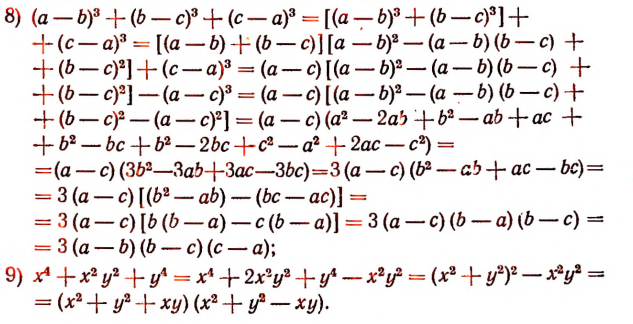
Некоторые дополнительные замечания
Не всякий многочлен разлагается на рациональные целые множители. Например, нельзя разложить на такие множители следующие многочлены:
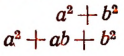
(сумма квадратов);
(неполный квадрат суммы);
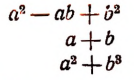
(неполный квадрат разности);
(сумма чисел а и b) ;
(сумма квадрата числа а и куба числа b).
Многочлен, не допускающий разложения на целые множители, называется неразложимым или неприводимым. Неприводимых многочленов существует сколько угодно.
Иногда приходится пользоваться разложением многочлена на нецелые множители. Например:
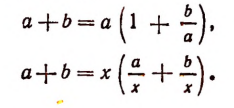
Умножение и деление расположенных многочленов
Многочлен n-й степени
Определение:
Выражение
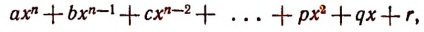
где 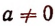 , а n — целое положительное число, называется многочленом n-й степени относительно х. При этом предполагается, что буква х может принимать любые значения, т. е. что буква х обозначает собой величину, могущую изменяться как угодно. Что же касается букв а, b, с, … , р, q, r, то они обозначают наперед выбранные известные числа, остающиеся неизменными при всех изменениях величины х. Буквы а, b, с, … , р, q, r называются коэффициентами многочлена. Буква же х называется независимой переменной. Если мы какую-либо величину называем независимой переменной, то это означает, что она может изменяться как угодно, независимо ни от чего.
, а n — целое положительное число, называется многочленом n-й степени относительно х. При этом предполагается, что буква х может принимать любые значения, т. е. что буква х обозначает собой величину, могущую изменяться как угодно. Что же касается букв а, b, с, … , р, q, r, то они обозначают наперед выбранные известные числа, остающиеся неизменными при всех изменениях величины х. Буквы а, b, с, … , р, q, r называются коэффициентами многочлена. Буква же х называется независимой переменной. Если мы какую-либо величину называем независимой переменной, то это означает, что она может изменяться как угодно, независимо ни от чего.
Если среди чисел b, с, … , р, q, r ни одно не равно нулю, то многочлен называется полным. В противном случае его называют неполным.
Примеры:


Во всех этих примерах предполагается, что 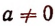 .
.
Числовое значение многочлена n-й степени (относительно переменной х) зависит от значения х. Если изменять значение х, и будет изменяться и значение самого многочлена. Например,
при х = 0 значение многочлена 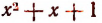 будет 1;
будет 1;

Выражение  называется многочленом, расположенным по убывающим степеням переменной х.
называется многочленом, расположенным по убывающим степеням переменной х.
Выражение же 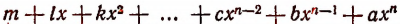 называется многочленом, расположенным по возрастающим степеням переменной х. Буква х в обоих случаях является независимой переменной.
называется многочленом, расположенным по возрастающим степеням переменной х. Буква х в обоих случаях является независимой переменной.
Член, содержащий независимую переменную в наивысшей степени, называется высшим членом.
Член, не зависящий от независимой переменной, называется свободным членом. В каждом из написанных выше многочленов свободным членом является m, а высшим членом 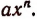
Если свободный член не равен нулю, то он называется низшим членом Многочлена. Если свободный член равен нулю, то низшим членом называется тот, который содержит наинизшую степень независимой переменной.
Примеры:
Выражение 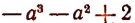 есть многочлен 3-й степени, расположенный по убывающим степеням переменной а, с коэффициентами — 1; —1; 0; 2.
есть многочлен 3-й степени, расположенный по убывающим степеням переменной а, с коэффициентами — 1; —1; 0; 2.
Выражение 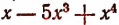 есть многочлен 4-й степени, расположенный по возрастающим степеням переменной х, с коэффициентами 0; 1; 0; —5; 1.
есть многочлен 4-й степени, расположенный по возрастающим степеням переменной х, с коэффициентами 0; 1; 0; —5; 1.
Выражение  есть многочлен 5-й степени, расположенный по убывающим степеням переменной а, с коэффициентами 1; 0; 0; 0; 0;
есть многочлен 5-й степени, расположенный по убывающим степеням переменной а, с коэффициентами 1; 0; 0; 0; 0; 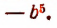
Выражение  можно рассматривать и как многочлен 5-й степени, расположенный по возрастающим степеням переменной b, с коэффициентами
можно рассматривать и как многочлен 5-й степени, расположенный по возрастающим степеням переменной b, с коэффициентами 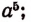 0; 0; 0; 0; —1.
0; 0; 0; 0; —1.
Многочлен 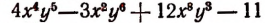 зависит от двух переменных х и у. Но мы можем его рассматривать как многочлен, зависящий только от одной переменной, например от х . Для этого надо только под буквой у понимать какое-нибудь выбранное число и при изменениях х оставлять у неизменным.
зависит от двух переменных х и у. Но мы можем его рассматривать как многочлен, зависящий только от одной переменной, например от х . Для этого надо только под буквой у понимать какое-нибудь выбранное число и при изменениях х оставлять у неизменным.
Если многочлен
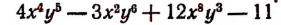
переписать в форме
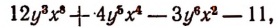
то получим многочлен 8-й степени, расположенный по убывающим степеням переменной х. Если же его переписать в форме
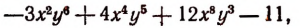
то получим многочлен 6-й степени, расположенный по убывающим степеням переменной у, с коэффициентами
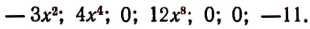
Выражение 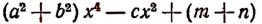 есть многочлен 4-й степени, расположенный по убывающим степеням переменной х, с коэффициентами
есть многочлен 4-й степени, расположенный по убывающим степеням переменной х, с коэффициентами
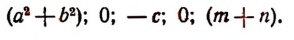
Умножение расположенных многочленов
Произведение 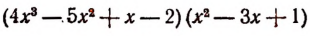 условимся записывать так:
условимся записывать так:
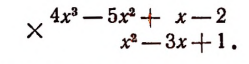
Покажем на примерах, как удобнее вести запись при умножении расположенных многочленов.
Примеры:
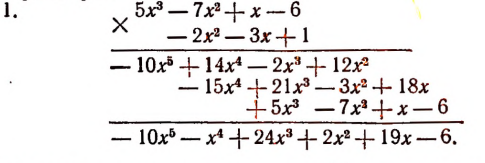
Последняя строка представляет собой произведение данных многочленов после приведения подобных членов.
Высший член произведения равен произведению высших членов перемножаемых многочленов; низший член равен произведению их низших членов.
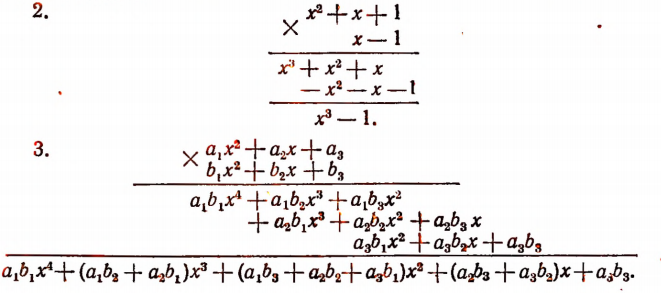
Полученное произведение есть многочлен 4-й степени, расположенный по убывающим степеням независимой переменной х, с коэффициентами
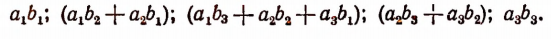
Деление расположенных многочленов
Деление многочлена n-й степени относительно x на многочлен k-й степени относительно x есть новое действие, которому необходимо дать определение, так как мы еще не знаем, что надо понимать под этим действием. Это определение мы дадим сначала на примере, а затем и в общем виде.
Определение на примере. Разделить многочлен 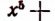
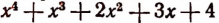 на многочлен
на многочлен 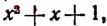 это значит найти два новых многочлена Q и R так, чтобы равенство
это значит найти два новых многочлена Q и R так, чтобы равенство
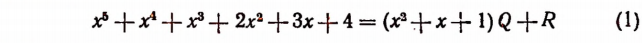
оказалось тождеством [и чтобы степень многочлена R была ниже степени делителя 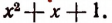
Если бы мы умели производить деление, таких многочленов, то нашли бы, что
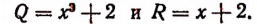
Действительно, при этих значениях Q и R равенство (1) обращается в тождество и при этом степень многочлена 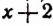 ниже степени делителя
ниже степени делителя 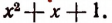
Получающийся в результате деления многочлен 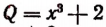 называется неполным частным, а второй многочлен
называется неполным частным, а второй многочлен 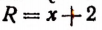 есть остаток.
есть остаток.
Определение общее. Разделить многочлен М на многочлен D, это значит найти два новых многочлена Q и R так, чтобы равенство
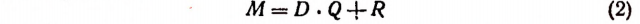
оказалось тождеством и чтобы степень многочлена R была ниже степени делителя D.
R называется остатком. Q называется неполным частным, если 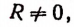 и полным частным, если R = 0. Однако как неполное частное, так и полное частное обычно называют просто частным.
и полным частным, если R = 0. Однако как неполное частное, так и полное частное обычно называют просто частным.
В том случае, когда остаток R равен нулю, равенство (2) принимает вид
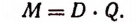
В этом случае говорят, что М делится на D, a Q является частным. Когда R не равно нулю, говорят, что М не делится па D.
Изучение деления многочленов начнем с рассмотрения примеров.
1. Пусть требуется найти частное от деления многочлена 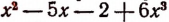 на многочлен
на многочлен 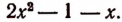
Расположив делимое и делитель по убывающим степеням независимой переменной х, выполним процесс деления пока без пояснений и без обоснования.
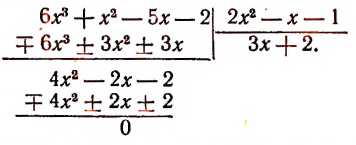
Первый остаток:
Второй остаток:
Последний (в данном примере второй) остаток оказался равным нулю. Мы скажем, что деление совершилось без остатка и в частном получилось 3х + 2. Правильность полученного частного можно проверить умножением. В самом деле,
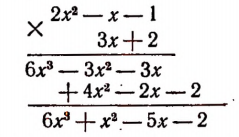
Теперь поясним, как производился процесс деления. Мы начали с того, что высший член делимого разделили на высший член делителя. Полученный результат приняли за первый член частного. Произведение делителя на этот первый член частного вычли из делимого. Получили первый остаток 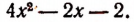 Высший член первого остатка разделили снова на высший член делителя. Получили второй член частного. Произведение делителя на этот второй член частного вычли из первого остатка. Получили второй остаток, оказавшийся равным нулю. На этом процесс деления прекратился.
Высший член первого остатка разделили снова на высший член делителя. Получили второй член частного. Произведение делителя на этот второй член частного вычли из первого остатка. Получили второй остаток, оказавшийся равным нулю. На этом процесс деления прекратился.
2. Применим указанную схему деления расположенных многочленов еще к нескольким примерам.
Пример:

Значит, 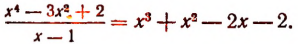
Пример:

Следовательно, 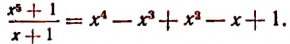
Пример:
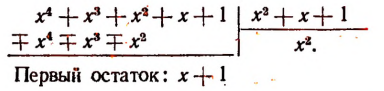
На этом процесс деления заканчивается, так как степень остатка ниже степени делителя.
Мы скажем, что при делении многочлена 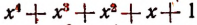 на многочлен
на многочлен 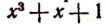 получается в частном
получается в частном  и в остатке х+1.
и в остатке х+1.
Правильность полученного частного и остатка можно проверить, если воспользоваться тем, что делимое равно произведению делителя на частное, сложенному с остатком.
Действительно, легко видеть, что сумма 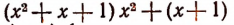 тождественно равна делимому
тождественно равна делимому 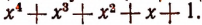
Пример:
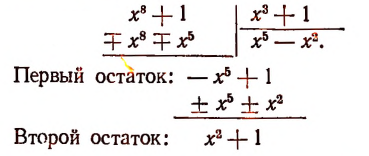
Деление прекращается, так как высший член последнего остатка не делится нацело на высший член делителя.
В частном получилось 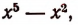 а в остатке
а в остатке 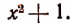
Проверка:
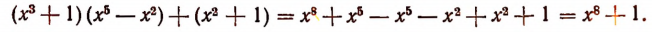
Рассмотрим еще несколько примеров деления многочленов с буквенными коэффициентами.
Пример:
Пусть требуется разделить многочлен
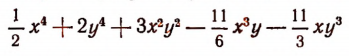
на многочлен 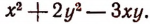 Примем за независимую переменную, например, величину у и расположим делимое и делитель по убывающим степеням этой величины. После этого станем производить деление:
Примем за независимую переменную, например, величину у и расположим делимое и делитель по убывающим степеням этой величины. После этого станем производить деление:

Пример:
Пусть требуется разделить 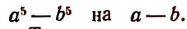 Примем за независимую переменную величину а. Так как делимое и делитель уже расположены по убывающим степеням этой величины, можно прямо приступить к делению:
Примем за независимую переменную величину а. Так как делимое и делитель уже расположены по убывающим степеням этой величины, можно прямо приступить к делению:
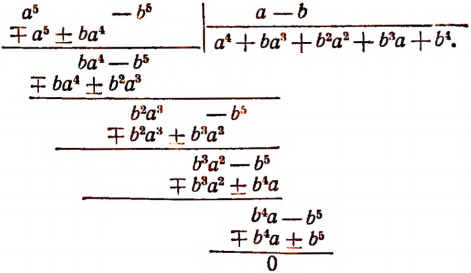
Значит,
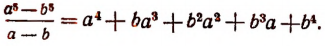
Пример:
Пусть требуется разделить многочлен 
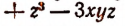 на многочлен
на многочлен 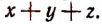 Примем за независимую переменную, например, величину х и расположим делимое и делитель по убывающим степеням этой величины. После этого произведем деление.
Примем за независимую переменную, например, величину х и расположим делимое и делитель по убывающим степеням этой величины. После этого произведем деление.
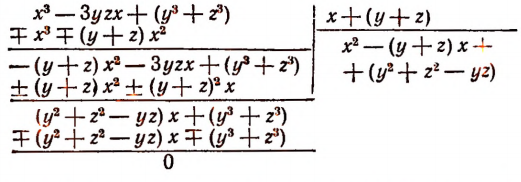
Деление произошло без остатка и в частном получилось
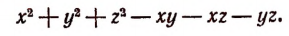
Таким образом,
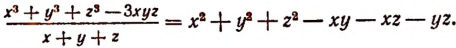
Пример:
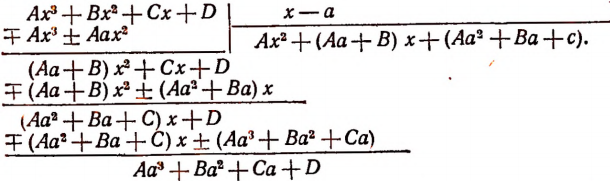
Деление прекращается, так как последний остаток вовсе не содержит буквы х, а поэтому не делится нацело на высший член делителя. Остаток при делении оказался равным
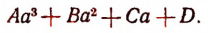
4. Теперь перейдем к обоснованию уже изложенного выше правила деления расположенных многочленов.
Пусть требуется разделить друг на друга два многочлена, расположенные по убывающим степеням какой-либо независимой переменной, например буквы х.
Предположим, что искомое частное есть целый относительно х многочлен (или одночлен) и что этот многочлен расположен тоже по убывающим степеням буквы х .
Из умножения расположенных многочленов известно, что высший член произведения равен произведению высшего члена множимого на высший член множителя. Значит, первый член частного ррвен частному от деления первого члена делимого на первый член д-лителя. После этого вычтем из делимого произведение делителя на найденный уже первый член частного. Результат этого вычитания назовем первым остатком. Если этот первый остаток окажется равным нулю, то это будет означать, что частное данных многочленов есть найденный целый одночлен. Если же этот первый остаток не окажется равным нулю, то он будет представлять собой произведение делителя на алгебраическую сумму остальных, еще не найденных членов частного. Поэтому второй член частного будет равен частному от деления высшего члена первого остатка на высший член делителя. Аналогичными рассуждениями и действиями мы будем получать и остальные члены частного, если они имеются.
Деление окажется выполненным нацело, если последний остаток окажется равным нулю. Если же мы дойдем до такого остатка, который не равен нулю и степень которого ниже степени делителя, то это будет означать, что частное от деления первоначально заданных многочленов не может быть целым многочленом.
В этом случае в результате деления мы получаем только часть частного, а именно только целую часть частного, а также в определенном виде и остаток.
Имея целую часть частного и остаток, мы можем частное двух данных многочленов записать в виде суммы целого выражения и некоторой дроби.
Например, при делении многочлена  на многочлен
на многочлен 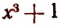 мы получили в частном
мы получили в частном  а в остатке
а в остатке  Поэтому
Поэтому
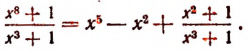
Выражение 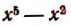 называется целой частью дроби
называется целой частью дроби 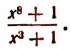
5. Деление расположенных многочленов можно производить и иначе, а именно, переписав предварительно члены делимого и делителя по возрастающим степеням независимой переменной.
Покажем на примере, как это делается.
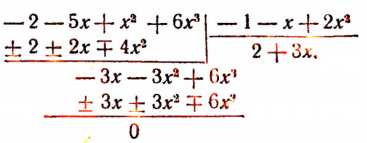
В том случае, когда при делении многочлена на многочлен остаток равен нулю, безразлично, как рас полагать многочлены — по убывающим или по возрастающим степеням.
В том же случае, когда остаток не равен нулю, лучше производить деление, располагая многочлены по убывающим степеням. При таком способе деления мы получим целую часть и вполне определенный остаток. Если же мы станем производить деление, расположив многочлены по возрастающим степеням, процесс деления никогда не закончится, сколько бы его ни продолжали. При таком способе получится бесконечноз множество различных выражений для частного и соответственно этому бесконечное множество различных выражений остатка. Приведем пример.
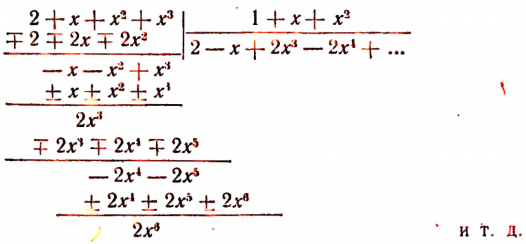
Процесс деления никогда не закончится.
Если остановиться на первом остатке, то частным будет число 2, а остатком 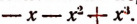 Если остановиться на втором остатке, то частным будет 2 — х, а остатком
Если остановиться на втором остатке, то частным будет 2 — х, а остатком 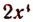 и т. д.
и т. д.
Так как заранее, вообще говоря, нельзя знать, будет ли остаток равным нулю или не будет, то лучше деление производить, располагая делимое и делитель по убывающим степеням независимой переменной.
Нахождение наибольшего общего делителя многочленов с помощью их разложения на неприводимые множители
Если каждый из двух многочленов делится без остатка на третий, то этот третий называется общим делителем первых двух многочленов.
Наибольшим общим делителем двух многочленов называется их общий делитель наивысшей степени.
Например, для многочленов
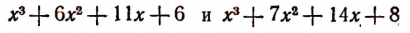
выражение x + 1 есть общий делитель, а выражение 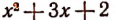 есть наибольший общий делитель.
есть наибольший общий делитель.
Приведем примеры на нахождение наибольшего общего делителя.
Пример:
Найти наибольший общий делитель многочленов
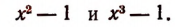
Пользуясь тем, что
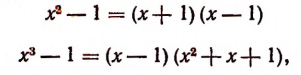
находим, что искомым наибольшим общим делителем будет х—1.
Пример:
Найти наибольший общий делитель многочленов
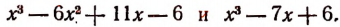
Пользуясь тем, что
находим искомый наибольший общий делитель:
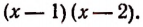
Аналогично можно находить наибольший общий делитель и нескольких многочленов.
Алгоритм Евклида для нахождения наибольшего общего делителя двух многочленов
В предыдущем параграфе было показано, как находить общий наибольший делитель двух многочленов с помощью разложения этих многочленов на неприводимые множители. Однако такое разложение на множители не всегда доступно. Алгоритм же Евклида для нахождения наибольшего общего делителя двух многочленов представляет собой такой способ, который позволяет во всех случаях находить общий наибольший делитель только с помощью конечного числа делений. Покажем этот алгоритм на примерах.
Пример:
Найти общий наибольший делитель многочленов
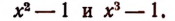
Разделим 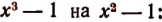
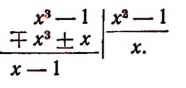
Теперь разделим делитель 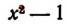 на остаток x—1:
на остаток x—1:
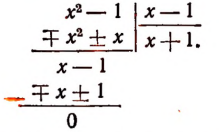
Деление здесь произошло без остатка. Значит, х—1 и будет искомым общим наибольшим делителем.
Пример:
Найти общий наибольший делитель многочленов
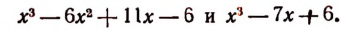
Произведем первое деление:
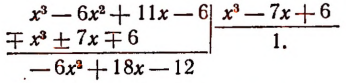
Произведем второе деление. Чтобы выполнить это деление, мы должны были бы разделить предыдущий делитель 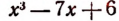 на остаток
на остаток 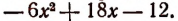
Но так как
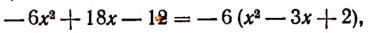
для удобства будем делить многочлен 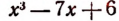 не на
не на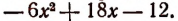 , а на
, а на 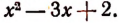
От такой замены решение вопроса не пострадает, так как наибольшие общие делителя двух многочленов, отличающиеся друг от друга лишь постоянным множителем, равноправны.
Итак, произведем второе деление в следующем виде:
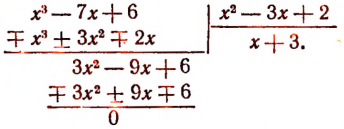
Остаток оказался равным нулю, значит, последний делитель, т. е. многочлен
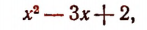
и будет искомым наибольшим общим делителем.
Пример:
Найти наибольший общий делитель многочленов
Первое деление:
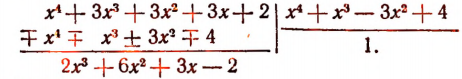
Второе деление:
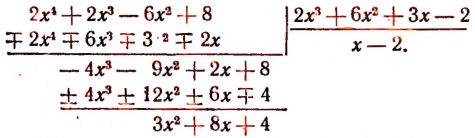
(Для удобства мы взяли здесь за делимое не 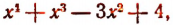 а
а 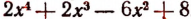 .)
.)
Третье деление:
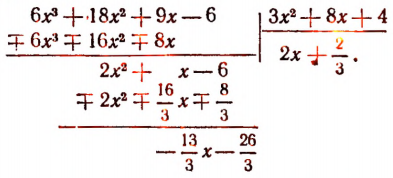
(Для удобства мы взяли здесь за делимое не 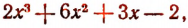 а
а 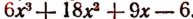 .)
.)
Четвертое деление:
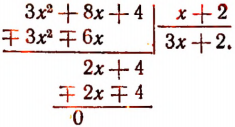
Для удобства мы взяли за делитель не 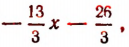 а х + 2, так как
а х + 2, так как 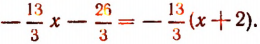
После четвертого деления остаток оказался равным нулю. Следовательно, последний делитель х + 2 и будет искомым наибольшим общим делителем.
Схема алгоритма Евклида такова. Один из двух многочленов делят на другой, степень которого не выше степени первого.
Далее, за делимое берут всякий раз тот многочлен, который служил в предшествующей операции делителем, а за делитель берут остаток, полученный при той же предшествующей операции. Этот процесс прекращается, как только остаток окажется равным нулю.
Алгоритм Евклида основан на следующем. Пусть М—делимое, D — делитель, Q — частное и R — остаток. Тогда
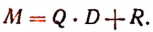
Из этого равенства следует, что наибольший общий делитель многочленов М и D будет тот же, что и наибольший общий делитель D и R (подробнее см. Г. М. Шапиро. Высшая алгебра). Упражнение. Найти наибольший общий делитель многочленов
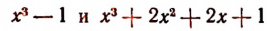
с помощью алгоритма Евклида и путем разложения данных многочленов на множители.
Отв. 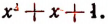
Преобразование числовых и алгебраических выражений
При решении почти любой школьной задачи приходится делать те или иные преобразования. Зачастую ее сложность полностью определяется степенью сложности и объемом преобразований, которые необходимо выполнить. Не так уж редки случаи, когда школьник оказывается не в состоянии решить задачу не потому, что не знает, как она решается, а потому, что он не может без ошибок, в разумное время произвести все необходимые преобразования и вычисления.
Примеры на преобразование числовых и алгебраических выражений важны не сами по себе (хотя среди них есть и содержательные), а как средство развития техники преобразований, можно даже сказать, культуры преобразований.
Заметим, что с заданиями «упростить выражение» мы достаточно часто сталкиваемся в школе; при этом всякий раз понятно, что надо сделать. Элементарный «здравый смысл» помогает нам определить, какое выражение проще, а какое сложнее, до каких пор следует упрощать заданное выражение.
Некоторые практические рекомендации
- Упростить выражение
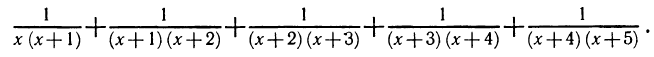
Решение:
Грубой тактической ошибкой была бы попытка сложить сразу все дроби, приведя их к общему знаменателю.
Сложим сначала первые две. Получим
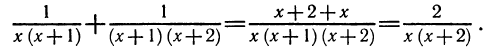
Прибавим третью:
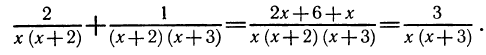
Продолжая этот процесс, получим в итоге 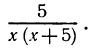
Замечание:
Легко проверить, что 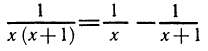 . Аналогичные равенства, очевидно, справедливы для остальных дробей. Заменив каждую дробь, входящую в данное выражение, на соответствующую разность (вместо того чтобы складывать дроби, каждую заменяем разностью!), получим в результате
. Аналогичные равенства, очевидно, справедливы для остальных дробей. Заменив каждую дробь, входящую в данное выражение, на соответствующую разность (вместо того чтобы складывать дроби, каждую заменяем разностью!), получим в результате 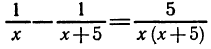 . Очевидно, что с помощью этого приема мы можем найти сумму, подобную рассмотренной, с любым числом слагаемых.
. Очевидно, что с помощью этого приема мы можем найти сумму, подобную рассмотренной, с любым числом слагаемых.
Важным элементом культуры преобразований, необходимым для решения всевозможных задач из любых разделов, является умение раскладывать на множители те или иные выражения. Как правило, цель достигается за счет удачной группировки слагаемых.
2. Упростить выражение 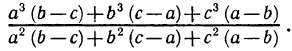 Р
Р
Решение:
Попробуем разложить на множители числитель и знаменатель. Начнем с числителя. Имеем
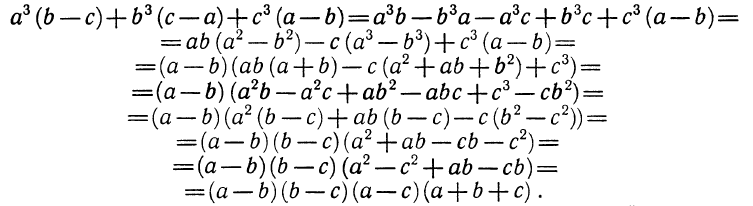
Раскладывая на множители знаменатель (проделайте аналогичные выкладки самостоятельно), получим 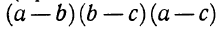 .
.
Таким образом, Данная дробь равна 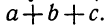
Замечание:
Теоретическим обоснованием того, что в числителе можно выделить множитель  служит равенство числителя нулю при
служит равенство числителя нулю при  .
.
Вообще, из двух взаимно обратных операций, как правило, выполнение одной технически существенно сложнее, чем выполнение другой. Именно такими являются действия умножения алгебраических выражений и разложение на множители. Аналогичная ситуация имеет место для операций возведения в степень и извлечения корня. Легко получить, что 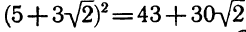 , и гораздо труднее «прочесть» это же равенство справа налево. Следует за помнить, что, если при решении задачи встретилось выражение вида
, и гораздо труднее «прочесть» это же равенство справа налево. Следует за помнить, что, если при решении задачи встретилось выражение вида 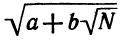 или
или 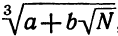 , необходимо попытаться «извлечь» соответствующий корень. Очень часто это можно сделать. Если подобное извлечение возможно, то найти его можно, например, подбором *. В старых учебниках алгебры встречается равенство
, необходимо попытаться «извлечь» соответствующий корень. Очень часто это можно сделать. Если подобное извлечение возможно, то найти его можно, например, подбором *. В старых учебниках алгебры встречается равенство
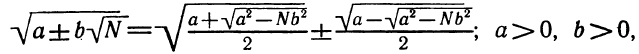
справедливость которого проверяется без труда. В некоторых случаях оно оказывается полезным при упрощении выражений, содержащих квадратные радикалы.
3. Упростить выражение 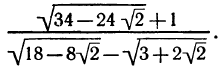
Решение:
Заметим, что 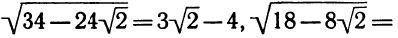
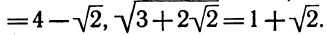 (Можно получить эти равенства под бором, а можно воспользоваться указанной выше формулой.) Таким образом, данная дробь приводится к виду
(Можно получить эти равенства под бором, а можно воспользоваться указанной выше формулой.) Таким образом, данная дробь приводится к виду 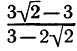 . Домножим числитель и знаменатель дроби на
. Домножим числитель и знаменатель дроби на 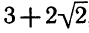 , получим в результате
, получим в результате
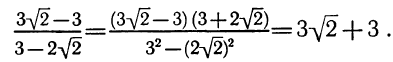
Замечание:
Обратите внимание на последний этап наших преобразований. Здесь использован часто встречающийся прием, который иногда называют «умножением на сопряженное выражение». В данном случае знаменатель имеет вид 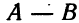 . Умножая числитель и знаменатель на
. Умножая числитель и знаменатель на 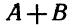 , получаем в знаменателе выражение
, получаем в знаменателе выражение 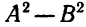 , которое оказывается равным 1.
, которое оказывается равным 1.
Замена переменных. Условные равенства
Переход к новым обозначениям, замена неизвестных — важнейший прием и метод, с помощью которого решаются самые различные задачи как элементарной, так и высшей математики. Для некоторых классов задач этот метод детально разработан, например для уравнений.
Замена переменных и переход к новым обозначениям могут использоваться как прием, облегчающий выкладки и делающий громоздкие алгебраические выражения компактными и обозримыми. Очень важно, чтобы этот прием и метод был прочно усвоен
- Например, чтобы упростить выражение
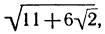 представим его в виде
представим его в виде 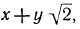 , откуда
, откуда 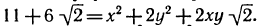 Поиск целых (рациональных) х и у сводится к решению системы
Поиск целых (рациональных) х и у сводится к решению системы 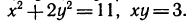 В данном случае пара целых х и у легко подбирается:
В данном случае пара целых х и у легко подбирается: 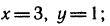 следовательно,
следовательно, 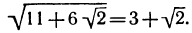
и освоен, так как идея замены переменных является сквозной.
Ограничимся рассмотрением одного примера.
4. Доказать, что если 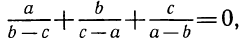 то и
то и 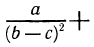
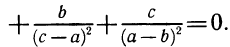 Доказать также, что из второго равенства следует первое.
Доказать также, что из второго равенства следует первое.
Решение:
Обозначим 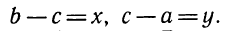 Перейдем к новым переменным
Перейдем к новым переменным 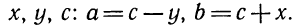 . В новых обозначениях
. В новых обозначениях
первое из данных в условии равенств примет вид
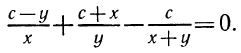
Оно легко преобразуется:
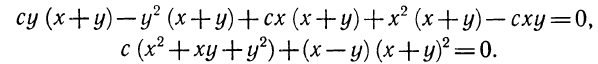
Второе равенство будет иметь вид
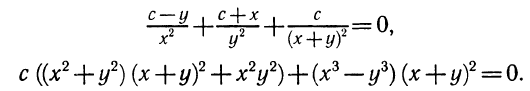
Коэффициент при с оказывается равным (проверьте!)
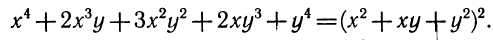
Таким образом, поскольку при  также
также 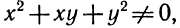 а
а 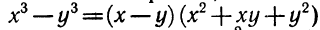 второе равенство преобразуется после сокращения на
второе равенство преобразуется после сокращения на  к тому же виду, что и первое.
к тому же виду, что и первое.
Приведенное решение содержит подсказку, позволяющую найти другое решение: левая часть второго равенства получается из левой части первого умножением на
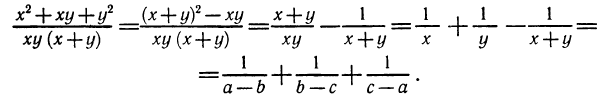
В самом деле,
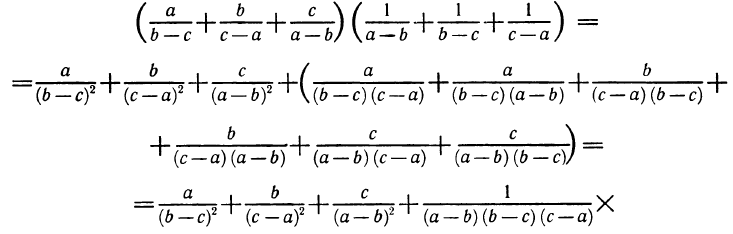
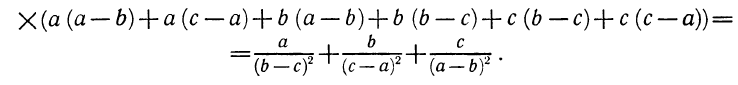
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

