Частные производные и дифференцируемость функций нескольких переменных

Пусть функция z=f(M) определена в некоторой окрестности точки
М(х; у). Придадим переменной х в точке М произвольное приращение 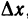, оставляя значение переменной у неизменным, т. е. перейдем на плоскости от точки М(х; у) к точке 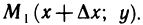При этом 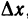таково, что точка 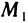лежит в указанной окрестности точки М. Тогда соответствующее приращение функции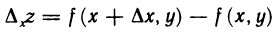

называется частным приращением функции по переменной х в точке М(х; у).

Из определения следует, что частная производная функции двух переменных по переменной х представляет собой обыкновенную производную функции одной переменной х при фиксированном значении переменной у. Поэтому частные производные вычисляют по формулам и правилам вычисления производных функций одной переменной.

Примеры: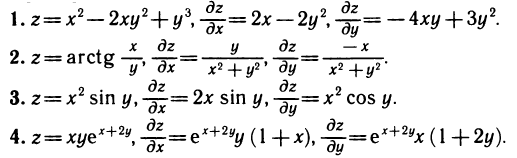

Отметим, что мы определили частные производные функции z=f(х, у) в такой точке М, в окрестности которой функция определена, т. е. во внутренней точке области определения функции. Если М (х; у) — граничная точка области определения функции, то 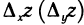может быть не определено, так как точка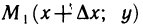 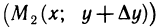может не принадлежать области определения функции ни при каком 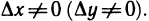Это, например, имеет место для точки 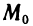на рис. 164. В этом случае, если существует частная производная 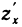во внутренних точках М области и существует 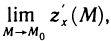то по определению полагают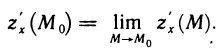

Аналогично определяется .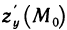

Определение дифференцируемости функции

Напомним, что полным приращением функции z=f(М) в точке М(х; у), соответствующим приращениям 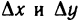переменных х и у, называется функция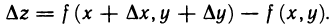

Пусть функция z=f(M) определена в некоторой окрестности точки М.

Определение:

Функция z=f(M) называется дифференцируемой в точке М, если ее полное приращение в этой точке может быть представлено в виде 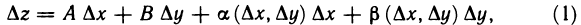где А и В — некоторые не зависящие от 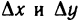числа, а 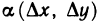и 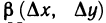— бесконечно малые при 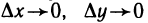функции.

Известно, что если функция одной переменной дифференцируема в некоторой точке, то она непрерывна и имеет производную в этой точке. Из существования производной функции одной переменной в данной точке следует дифференцируемость функции в этой точке. Выясним, как переносятся эти свойства на функции двух переменных.

Необходимые условия дифференцируемости

Теорема:

Если функция z=f(M) дифференцируема в точке М, то она непрерывна в этой точке.

Доказательство. Если функция z=f(M) дифференцируема в точке М, то, как следует из соотношения (1),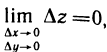

а это и означает, что функция непрерывна в точке М. ■

Теорема:

Если функция z=f(M) дифференцируема в точке М (х; у), то она имеет в этой точке частные производные 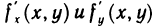, причем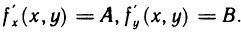

Доказательство:

Так как функция z=f(М)’ дифференцируема в точке М, то имеет место соотношение (1). Полагая 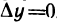, имеем 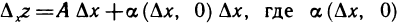— бесконечно малая при 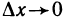функция. Разделив на 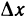и переходя к пределу при 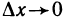, получаем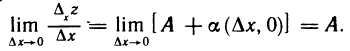

Следовательно, в точке М существует частная производная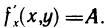

Аналогично доказывается, что в точке М существует частная производная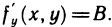

Обратные утверждения к теоремам 12.1 и 12.2 неверны, т. е. из непрерывности функции двух переменных в точке М, а также из существования ее частных производных в этой точке еще не следует дифференцируемость функции.

Например, функция 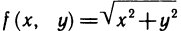непрерывна в точке (0;0), но не имеет в этой точке частных производных. В самом деле,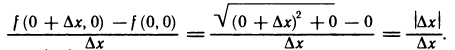

Но функция 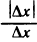не имеет предела при 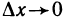. Следовательно, 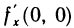не существует. Аналогично доказывается, что не существует 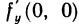. Так как данная функция не имеет частных производных в точке (0; 0), то она и не дифференцируема в данной точке. Функция
имеет частные производные по х и у в точке (0; 0). Это следует из того, что 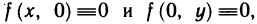следовательно, 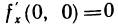и 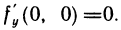Но f(x, у) не является непрерывной в этой точке, так как, например, вдоль прямой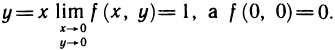

Следовательно, f(x, у) недифференцируема в точке (0; 0). И последний пример: функция 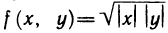непрерывна в точке (0; 0), так как 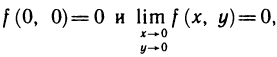и имеет частные производные по х и у в этой точке: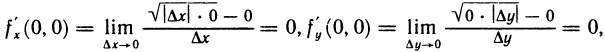

но, тем не менее, данная функция не является дифференцируемой в точке (0; 0). Действительно, полное приращение функции в точке
(0; 0) равно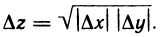

Если бы функция была дифференцируема в точке (0; 0), то, как следует из соотношения (1) и теоремы 12.2, выполнялось бы равенство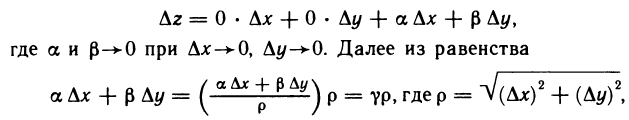
получаем, что 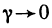при 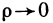[см. § 4 вывод формулы (3)]. Но в данном случае при любых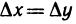 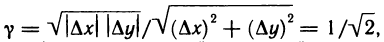т. е не является бесконечно малой функции при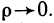

Таким образом, функция 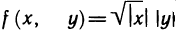непрерывна в точке (0; 0), имеет в этой точке частные производные и, тем не менее, не является дифференцируемой в этой точке.

Достаточные условия дифференцируемости

Теорема:

Если функция z=f(M) имеет частные производные в некоторой Ь-окрестности точки М и эти производные непрерывны в самой точке М, то функция дифференцируема в точке М.

Доказательство:

Придадим переменным х и у столь малые приращения 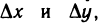чтобы точка 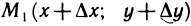не выходила за пределы указанной 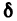-окрестности точки М. Полное приращение функции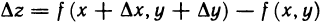

можно записать в виде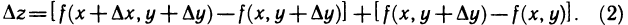

Выражение 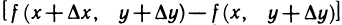можно рассматривать как приращение функции 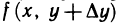одной переменной х (второй аргумент имеет постоянное значение, равное 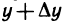). Так как согласно условию эта функция имеет производную 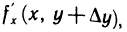то по теореме Лагранжа получаем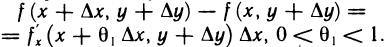

Рассуждая аналогично, для выражения 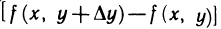имеем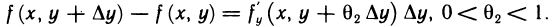

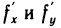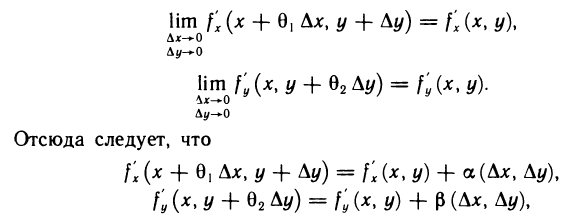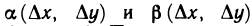Производные непрерывны в точке М (х; у), поэтому где — бесконечно малые функции при 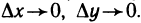Подставляя полученные выражения в формулу (2) для 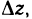находим 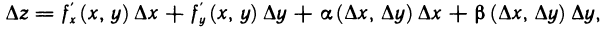а это и означает, что функция z=f(M) дифференцируема в точке М. ■

Следствие:

Из непрерывности частных производных следует непрерывность самой функции.

Теорема 12.3 имеет важное значение для установления дифференцируемости функций, поскольку непосредственная проверка дифференцируемости функции с помощью определения часто затруднительна, в то время как проверка непрерывности частных производных оказывается проще.

В заключение заметим, что понятие дифференцируемости для функций трех и более переменных вводится аналогично случаю функции двух переменных.

Производные сложных функций

Пусть z=f(x, у) — функция двух переменных х и у, каждая из которых, в свою очередь, является функцией независимой переменной t: 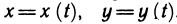. Тогда функция 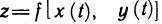является сложной функцией независимой переменной t, а переменные х и у — промежуточные переменные. Имеет место следующая теорема.

Теорема:

Если функции x=x(t) и y=y(t) дифференцируемы в точке t, а функция z=f(x, у) дифференцируема в точке 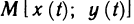, то сложная функция 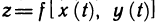также дифференцируема в точке t. При этом производная этой сложной функции вычисляется по формуле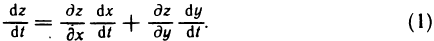

Доказательство:

Придадим переменной t произвольное приращение 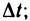тогда функции х(t) и у(t) получат соответственно приращения 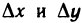, а функция z=f(x, у), в свою очередь, приращение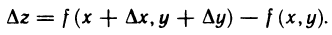

Так как функция z=f(x, у) дифференцируема в точке М (х; у), где 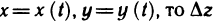можно записать в виде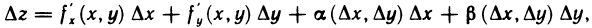
где 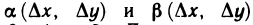— бесконечно малые функции при 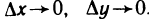Доопределим эти функции при 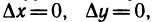положив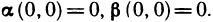

Разделив обе части равенства для 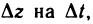получим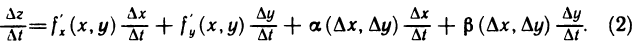

По условию, 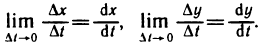Кроме того, так как функции x(t) и у(t) дифференцируемы в точке t, то они непрерывны в этой точке, т. е. 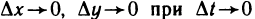и, как следствие, 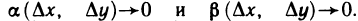Поэтому слагаемые 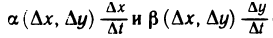стремятся к нулю при .

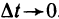Таким образом, доказано, что при 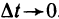существует предел правой части равенства (2), а следовательно, существует предел левой части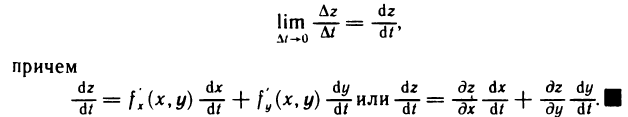

Замечание. Обратите внимание на то, когда в обозначениях производных пишется 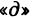и когда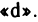

Примеры: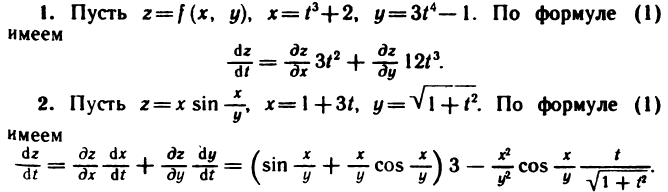

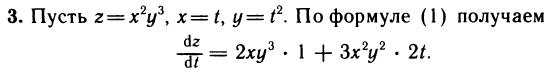
Учитывая, что 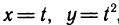находим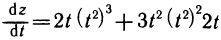

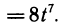
С другой стороны, можно найти 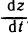выразив предварительно z через t. Имеем 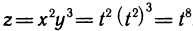откуда 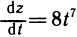что, безусловно, совпадает с результатом, полученным по формуле (1).

Если z=f(x, у), где у=ф(х), то 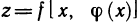— сложная функция х. На основании формулы (1), в которой роль t играет теперь х, получим

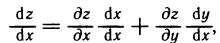
а так как 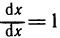, то

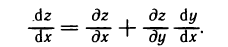
Аналогично решается вопрос о производной сложной функции, когда число промежуточных переменных больше двух. Например, если u=f(x, у, z), где х=х(t), y=y(t), z=z(t), то формула (1) принимает вид

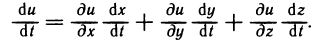
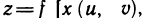
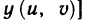Рассмотрим теперь более общий случай. Пусть z=f(х, у)— функция двух переменных х и у, которые, в свою очередь, зависят от двух или большего числа независимых переменных. Например, пусть . Тогда функция является сложной функцией независимых переменных и и v, а переменные х и у — промежуточные.

Если функции дифференцируемы в точке M'(u; v), а функция z=f(x, у) дифференцируема в точке М (х; у), где , то сложная функция 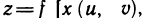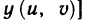дифференцируема в точке M(u, v), причем ее частные производные в этой точке находятся по формулам

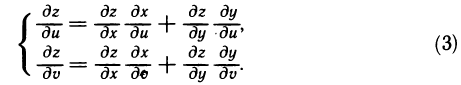
Дифференцируемость сложной функции доказывать не будем-Для вычисления же ее частных производных фиксируем значение одной из переменных и или v. Тогда попадаем в условия только что доказанной теоремы 12. 4. Из формулы (1) в обоих случаях вытекают формулы (3).

Примеры:

I. Пусть 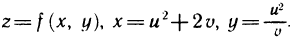По формулам (3) имеем

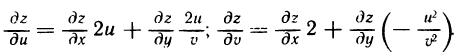
2. Пусть 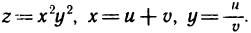По формулам (3) получаем

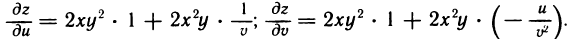
Подставьте самостоятельно в эти формулы выражения 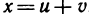, , 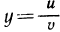с другой стороны, найдите и предварительно выразив z через 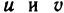, а затем сравните полученные результаты.

Пусть 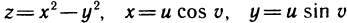. По формулам (3) имеем

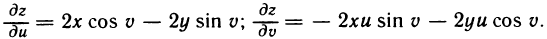
Если z=f(x), где 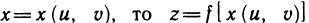— сложная функция, зависящая через переменную х от двух переменных и и у, и ее частные производные также находятся по формулам (3):

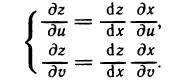
Обратите внимание на обозначения производных в этих формулах.

Формулы (3) можно обобщить на случай большего числа промежуточных переменных.

Например, если 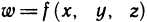— функция трех переменных х, у, z, а каждая из них зависит от и и у, то формулы (3) принимают вид

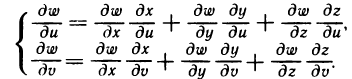
Дифференциал функции и его определение

Определение дифференциала:

Напомним, что если функция z=f(M) дифференцируема в точке М, то ее полное приращение в этой точке может быть представлено в виде

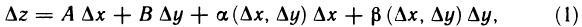
где 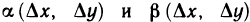— бесконечно малые функции при .

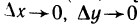Определение:

Дифференциалом dz дифференцируемой в точке М Функции z=f(M) называется линейная относительно приращений 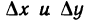часть полного приращения этой функции в точке М, т. е.

Используя теорему 12.2, выражение (2) можно переписать следующим образом:

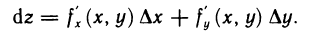
Дифференциалами независимых переменных х и у назовем приращения этих переменных: 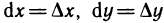. Тогда дифференциал функции можно записать в виде

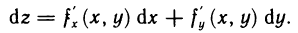
Из соотношений (1) и (2) следует, что разность между полным приращением и дифференциалом функции в точке М

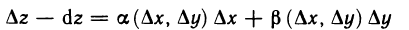
есть бесконечно малая при 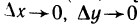более высокого порядка, чем 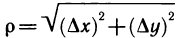— расстояние между точками М (х; у) и 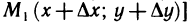. Действительно,

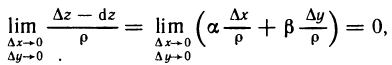
так как 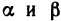— бесконечно малые, 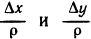— ограниченные
функции: 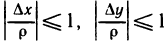. Отсюда получаем: 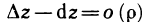или

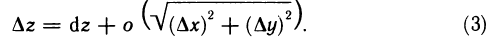
Отбрасывая при достаточно малых величину о (р), получаем приближенную формулу

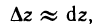
которую широко используют в приближенных вычислениях, так как легче вычислить дифференциал, чем полное приращение.

Касательная плоскость и нормаль к поверхности

Геометрический смысл дифференциала. Аналогично тому, как дифференциал функции одной переменной геометрически представляет собой приращение «ординаты касательной», дифференциал функции двух переменных есть приращение «аппликаты касательной плоскости». Введем понятие касательной плоскости к поверхности в точке 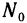. Плоскость, проходящая через точку 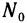поверхности, называется касательной плоскостью к поверхности в этой точке, если угол между секущей (прямой), проходящей через точку 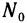и любую точку N поверхности, и плоскостью стремится к нулю, когда точка N стремится к точке .

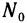Докажем, что касательная плоскость к поверхности в точк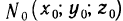е , где 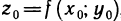определяется уравнением

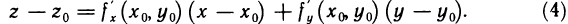
Действительно, из аналитической геометрии известно, что уравнение (4) определяет плоскость, проходящую через точку 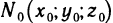и имеющую нормальный вектор 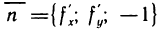. Чтобы установить, что эта плоскость является касательной, достаточно доказать, что угол ф между вектором 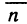и вектором 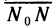любой секущей 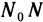стремится к 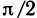, когда точка N стремится к 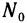. Координаты точки N’ обозначим через (х; у; z), где z=f(x, у). 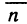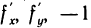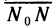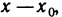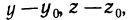Так как координаты вектора равны , а координаты вектора равны то

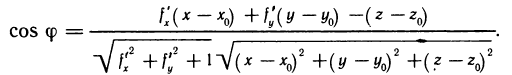
Но, как следует из соотношения (3), 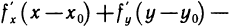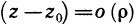, где 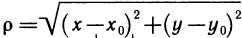. Поэтому

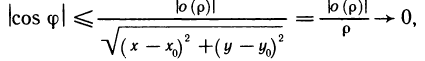
когда 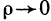. Отсюда следует, что 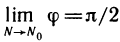, что и требовалось доказать.

Нормальный вектор 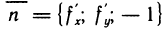касательной плоскости называют нормалью к поверхности z = f(x, у) в точке 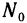. Пусть 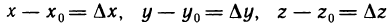; тогда из равенства (4) получаем, что приращение 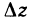«аппликаты касательной плоскости» определяется формулой

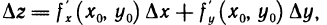
т. е. действительно совпадает с дифференциалом dz функции z=f(х,y).

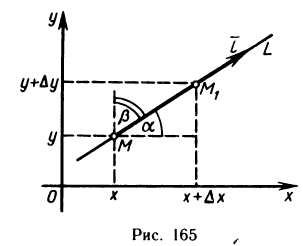
Производная по направлению. Градиент

Рассмотрим функцию z=f(M), определенную в некоторой окрестности точки М (х; у), и произвольный единичный вектор 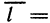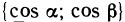(рис. 165).

Для характеристики скорости изменения функции в точке М(х; у) в направлении вектора 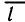введем понятие производной по направлению. Для этого проведем через точку М прямую L так, чтобы одно из направлений на ней совпадало с направлением вектора 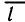, и возьмем на направленной прямой точку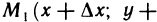 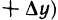. Обозначим величину отрезка 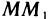через 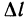, т. е.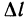 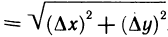, если точка М, расположена так, как на рис. 165, и 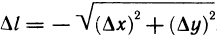, если точка М, расположена по другую сторону от точки М. Функция f(М) получит при этом приращение

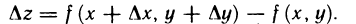
Определение:

Предел отношения 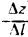при 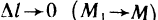, если он существует, называется производной функции z=f(M) в точке М (х; у) по направлению вектора 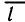и обозначается 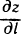, т. е.

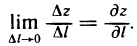
Предположим теперь, что функция f(М) дифференцируема в точке М. Тогда ее приращение в этой точке вдоль прямой L можно записать в виде

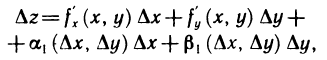
где 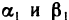— бесконечно малые функции при 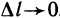. Разделив обе части равенства на 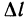и учитывая, что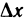 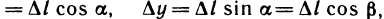получим

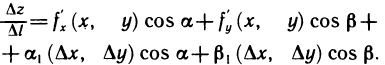
Переходя к пределу в этом равенстве при 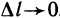, получаем формулу для производной по направлению

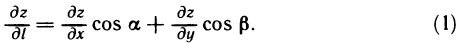
Из формулы (1) следует, что производная по направлению является линейной комбинацией частных производных, причем направляющие косинусы являются как бы весовыми множителями, показывающими вклад в производную по направлению соответствующей частной производной.

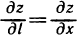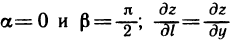В частности, при при 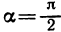и 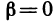. Отсюда следует, что частные производные по х и у являются частными случаями производной по направлению.

Пример:

Вычислить производную функции 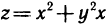в точке М(1; 2) по направлению вектора 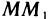, где 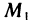— точка с координатами (3; 0).

Решение. Найдем единичный вектор 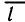, имеющий данное направление:

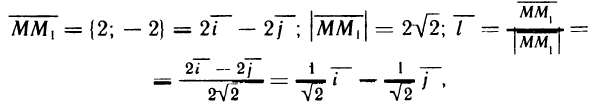
откуда 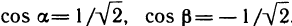. Вычислим частные производные функции в точке М (1; 2):

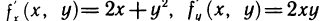, откуда 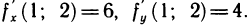По формуле (1) получим

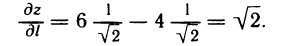
Определение:

Градиентом функции z=f(M) в точке М (х; у) называется вектор, координаты которого равны соответствующим частным производным 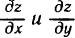и взятым в точке М (х; у).

Обозначение:

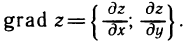
Используя понятие градиента функции и учитывая, что вектор 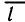имеет координаты 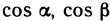, представим формулу (1) в виде скалярного произведения векторов grad z и :

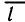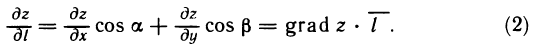
С другой стороны, по определению скалярного произведения имеем

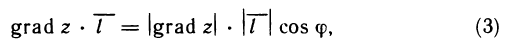
где 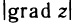— длина вектора grad z; ф—угол между векторами 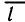и grad z. Сравнивая формулы (2) и (3) и учитывая, что 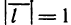, получаем

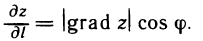
Из последнего равенства следует, что производная функции по направлению имеет наибольшую величину при cos ф= 1 (ф=0), т. е. когда направление вектора 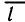совпадает с направлением gradz. При этом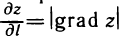

Таким образом, градиент функции z=f(M) в точке М(x: у) характеризует направление и величину максимальной скорости возрастания этой функции в данной точке.

Аналогично определяется производная по направлению для функции трех переменных u=f(x, у, z), выводится формула

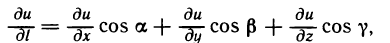
вводится понятие градиента

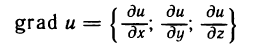
и исследуются его свойства.

Понятия производной по направлению и градиента функции играют важную роль во многих приложениях.

Частные производные

Частные производные высших порядков. Пусть частные производные 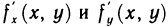функции z=f(M), определенной в окрестности точки М, существуют в каждой точке этой окрестности. В этом случае частные производные представляют собой функции двух переменных х и у, определенные в указанной окрестности точки М. Назовем их частными производными первого порядка.

В свою очередь, частные производные по переменным х и у от функций 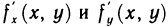в точке М, если они существуют, называются частными производными второго порядка от функции f (М) в этой точке и обозначаются следующими символами:

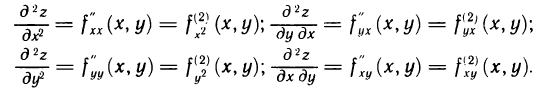
Частные производные второго порядка вида 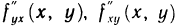называются смешанными частными производными.

Примеры:

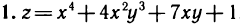
Имеем

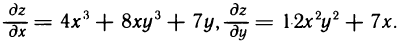
Следовательно,

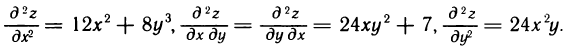
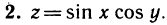
Имеем

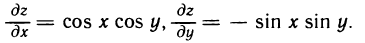
Следовательно,

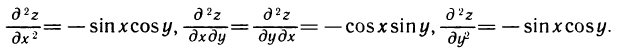
В обоих примерах смешанные частные производные 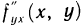и 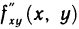равны. Но, вообще говоря, значения смешанных производных зависят от порядка, в котором производится дифференцирование. Так, например, функция

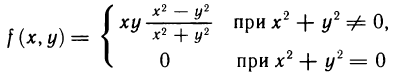
в точке (0; 0) имеет смешанные частные производные 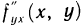и 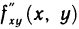, но они не равны друг другу. Действительно,

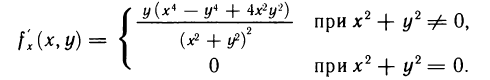
Следовательно,

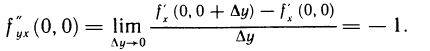
Проводя аналогичные вычисления, получим 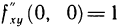. Таким образом,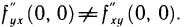

Ответ на вопрос о том, при каких условиях значения смешанных производных не зависят от того, в каком порядке производится дифференцирование, дает следующая теорема.

Теорема:

Если производные 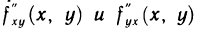существуют в некоторой 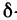-окрестности точки М (х; у) и непрерывны в самой точке М, то они равны между собой в этой точке, т. е. имеет место равенство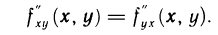

Доказательство:

Рассмотрим выражение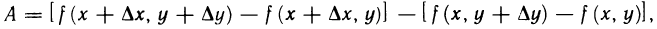

где 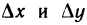— любые столь малые числа, что точка 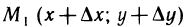находится в указанной 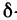-окрестности точки М. Введем вспомогательную функцию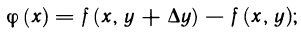
тогда выражение А можно рассматривать как приращение дифференцируемой на отрезке 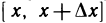функции одной переменной х:

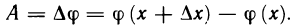
Поэтому, применяя к этой разности теорему Лагранжа, запишем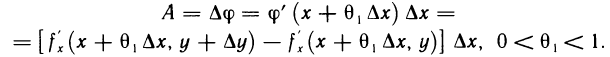

Выражение в квадратных скобках можно рассматривать как приращение дифференцируемой на отрезке 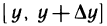функции 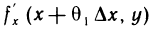одной переменной у. Применяя еще раз теорему Лагранжа (по переменной у), получаем

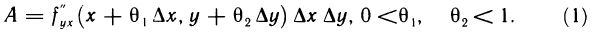
С другой стороны, если ввести вспомогательную функцию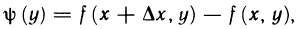

то, поступая аналогично, получим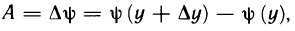

а затем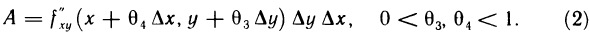
Сравнивая (1) и (2), получаем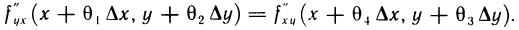

Переходя теперь в этом равенстве к пределу при 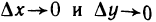и учитывая непрерывность частных производных 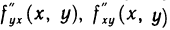в точке М, получим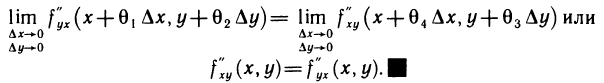

Аналогично частным производным второго порядка вводятся частные производные третьего, четвертого, …. n-го порядка и доказывается теорема типа 12.5 о равенстве смешанных производных любого порядка.

Дифференциалы высших порядков

Было введено понятие дифференциала дифференцируемой в точке М функции z=f(M) и получена формула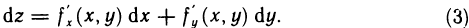

Будем называть dz дифференциалом первого порядка. Для удобства условимся обозначать дифференциалы не только символом d, но и символом (например, ).

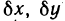Пусть функции 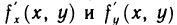дифференцируемы в точке М. Будем рассматривать dx и dy в выражении для dz как постоянные множители. Тогда функция dz представляет собой функцию только переменных х и у, дифференцируемую в точке М, и ее дифференциал имеет вид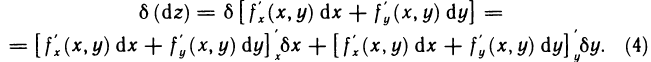

Дифференциал 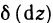от дифференциала dz в точке М, взятый при 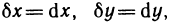называется дифференциалом второго порядка функции z=f(M) в точке М и обозначается 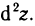В свою очередь, дифференциал 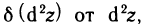взятый при 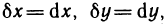называется дифференциалом третьего порядка функции z=f(M) и обозначается 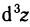и т. д. Дифференциал 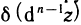от дифференциала 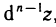, взятый при 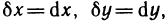называется дифференциалом
n-го порядка (или n-м дифференциалом) функции z=f(M) и обозначается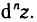

Итак, для n-го дифференциала функции z=f(M) справедлива формула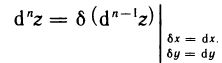

При нахождении второго (и последующих) дифференциалов обычно вычисление 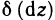и приравнивание дифференциалов аргументов 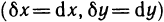производятся одновременно.

С помощью формулы (4) найдем выражение для дифференциала второго порядка: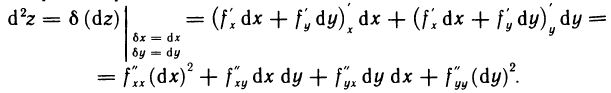

Если 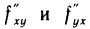непрерывны, то согласно теореме 12.5 слагаемые 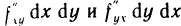равны, так что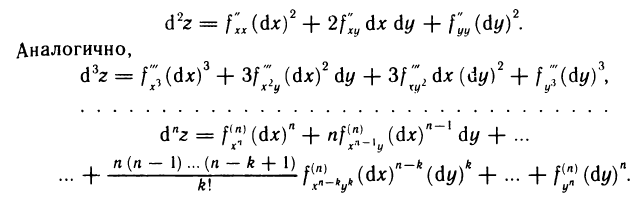

Формула для 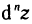напоминает разложение двучлена в n-й степени по формуле Ньютона. Поэтому выражение для 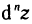символически можно записать в виде, более удобном для запоминания: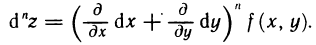

Примеры:
1. Найти 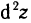для функции 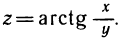Имеем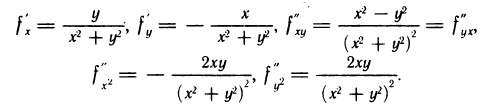

Следовательно,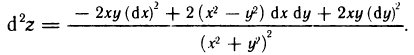

2. Найти 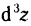для функции 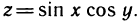Имеем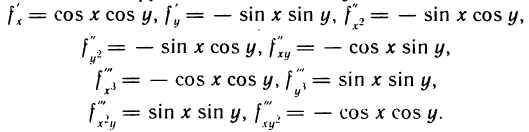Следовательно,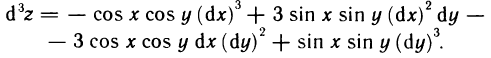

Формула Тейлора для функции двух переменных

Аналогично функции одной переменной функцию двух переменных можно представить в виде суммы многочлена n-й степени и некоторого остаточного члена. Докажем следующую теорему.

Теорема:

Пусть функции z=(х; у) непрерывна вместе со всеми частными производными до (n+1)-го порядка включительно в некоторой -окрестности точки М (х, у). Пусть точка 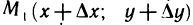принадлежит этой окрестности. Тогда приращение 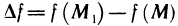этой функции в точке М можно представить в следующей форме: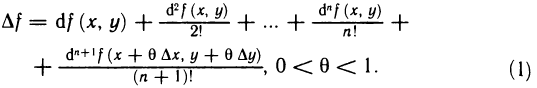

Формула (1) называется формулой Тейлора для функции z=f(x, y).

Доказательство:

Для доказательства введем вспомогательную функцию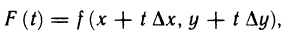

которая является сложной функцией независимой переменной t, изменяющейся в пределах от 0 до 1, и имеет (n+1)-ю производную по t на отрезке [0; 1].

Дифференцируя функцию F(t) по t, получаем 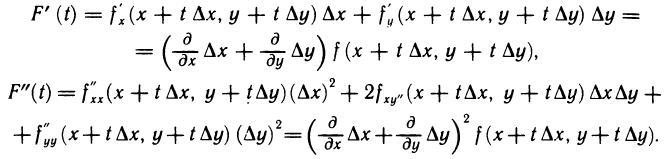По индукции найдем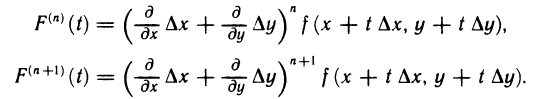

С другой стороны, применяя к функции F(t), как функции одной переменной t, формулу Маклорена (см. гл. 6, § 3, п. 3) и полагая t=1, получаем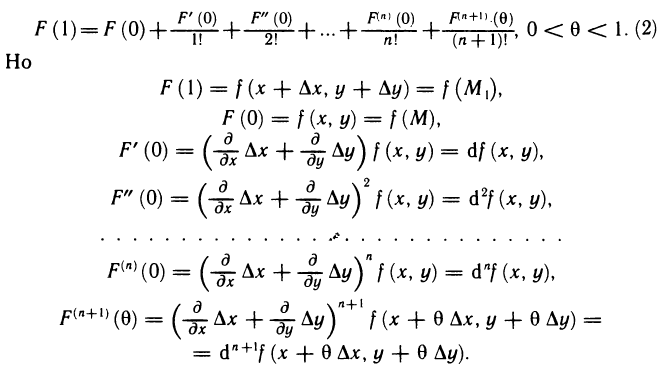

Учитывая эти равенства, из формулы (2) имеем 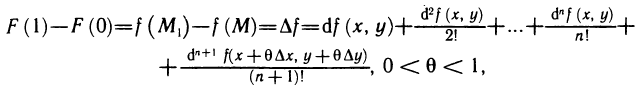т. е. получена формула (1). ■

Формула Тейлора для функции двух переменных напоминает формулу Тейлора для функции одной переменной. Но на самом деле, если раскрыть выражения для дифференциалов функции f(x, у) в формуле (1), то получим формулу более громоздкую и сложную, чем для функции одной переменной.

Формула Тейлора для функций большего числа переменных имеет аналогичный вид.

Замечание. При n=0 из (1) получается формула Лагранжа (или формула конечных приращений) для функции двух переменных 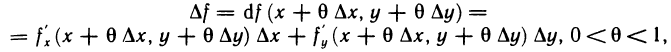из которой, в частности, следует, что если 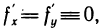то полное приращение функции тождественно равно нулю и функция f(x, у) является постоянной.

Экстремумы функции двух переменных и его определение

Пусть функция z=f(x, у) определена в некоторой окрестности точки .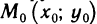

Определение:

Говорят, что функция z=f(x, у) имеет в точке 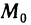локальный максимум (минимум), если существует такая окрестность точки 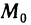, в которой для любой точки М (х; у) выполняется неравенство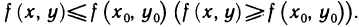

Точки локального максимума и локального минимума называются точками экстремума. Из определения следует, что если функция z = f(x, у) имеет экстремум в точке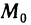, то полное приращение 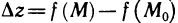этой функции в точке 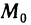удовлетворяет в некоторой окрестности точки 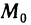одному из следующих условий: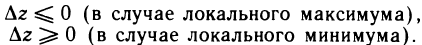

И обратно, если в некоторой окрестности точки 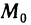выполняется одно из этих неравенств, то функция имеет экстремум в точке .

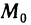Необходимые условия экстремума

Теорема:

Если функция f(x, у) имеет в точке 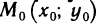экстремум и имеет в точке 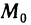частные производные первого порядка, то в этой точке частные производные первого порядка равны нулю, т. е.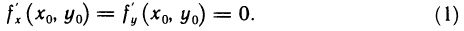

Доказательство:

Докажем, например, равенство нулю частной производной 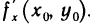. Для этого рассмотрим в окрестности точки 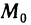только те точки, для которых 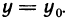. Получена функция 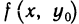одной переменной х, которая имеет в точке 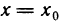экстремум и в точке 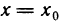производную 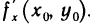. Следовательно, в этой точке выполняется необходимое условие экстремума функции одной переменной: 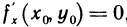, что и требовалось доказать.

Аналогично, рассматривая функцию 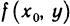одной переменной у, находим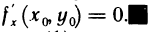

Условие (1) не является достаточным условием экстремума. Например, частные производные функции 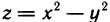равны нулю в точке (0; 0), однако эта функция не имеет экстремума в указанной точке, так как равна в ней нулю и ни в какой окрестности точки (0; 0) не сохраняет знак: если х=0, то z<0, а если у=0, то z> 0. Графиком функции 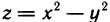является гиперболический параболоид (см. рис. 160).

Таким образом, условие (1) является только необходимым условием экстремума. Точки, в которых оно выполняется, будем по аналогии с функциями одной переменной называть точками возможного экстремума. Такие точки называются также стационарными.

Достаточные условия экстремума

Теорема:

Пусть в точке 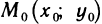возможного экстремума и некоторой ее окрестности функция f(х, у) имеет непрерывные частные производные второго порядка. Положим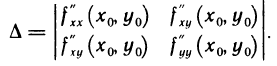

. Гхх{Х»Уо) f ху V 0» У о) уу V 0′

Тогда:
а) если 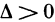, то в точке 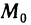функция имеет экстремум, причем при 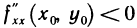— локальный максимум, при 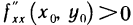— локальный минимум:
б) если , то в точке 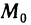нет экстремума.

Доказательство:

а) Пусть 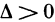. Введем следующие обозначения: 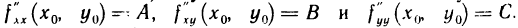По условию, 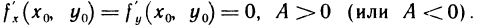Согласно формуле Тейлора (1) из § 7, взятой для n=1, полное приращение функции f(х, у) в точке 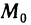можно записать в виде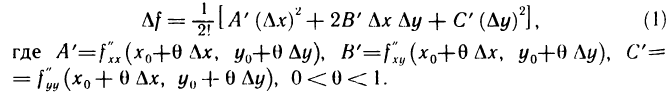

Из непрерывности частных производных второго порядка в точке 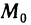следует: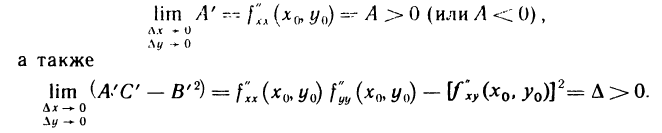

Поэтому для достаточно малых имеем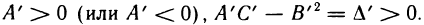

Так как 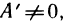то соотношение (1) можно переписать в виде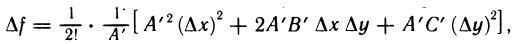
или, дополняя до полного квадрата,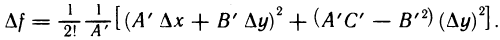

Выражение в квадратных скобках неотрицательно, поэтому если 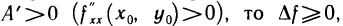и, следовательно, в точке 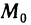локальный минимум; если же 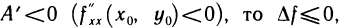и, следовательно, в точке 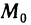локальный максимум, что и требовалось доказать.

б) Пусть теперь 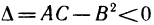и по-прежнему 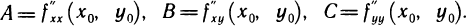Рассмотрим многочлен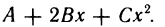

Так как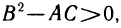

то можно указать два числа 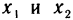такие, что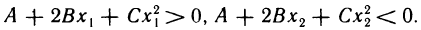

Полное приращение функции f(x, у) в точке 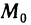, как и в п. а), запишем в виде (1). В силу непрерывности частных производных второго порядка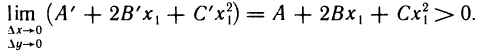

Следовательно, существует 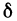-окрестность точки 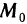такая, что если точка 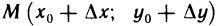принадлежит этой окрестности, то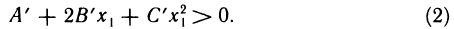

Рассмотрим теперь произвольную 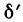-окрестность точки 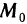такую, что 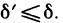Можно выбрать число t>0 столь малым, что точка 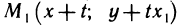будет принадлежать 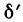-окрестности точки 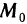. Полагая в (1) 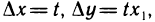в силу (2) получаем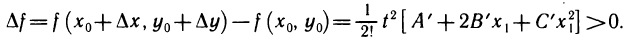

Рассуждая аналогично относительно значения 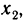получим, что в произвольной 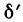-окрестности точки 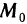существует точка 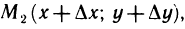для которой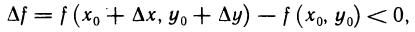
т. е. приращение функции f (х, у) в сколь угодно малой окрестности точки 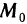не сохраняет знак и, следовательно, в точке 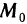нет экстремума. ■

Замечание:

Если 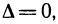то функция f (х, у) в точке 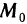возможного экстремума может иметь экстремум, но может и не иметь его.

Примеры:

1.Исследовать на экстремум функцию 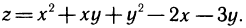Имеем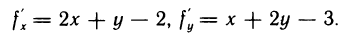
Найдем точки возможного экстремума. Для этого решим систему уравнений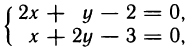

решения которой х=1/3, у=4/3. Следовательно, 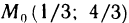— точка возможного экстремума.

Далее, 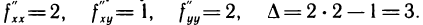Так как 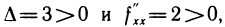то в точке 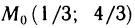данная функция имеет минимум.

2. Исследовать на экстремум функцию 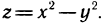Имеем 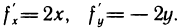Решая систему уравнений 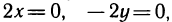получаем, что 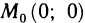— точка возможного экстремума. Так как 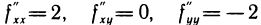и, следовательно, 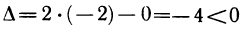, то в точке 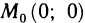экстремума нет.

3. Исследовать на экстремум функцию 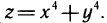Имеем 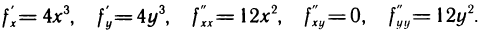Решая систему уравнений 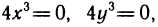находим, что 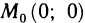— точка возможного экстремума. В этой точке 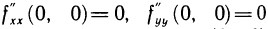и, следовательно, 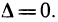Согласно замечанию в точке 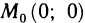экстремум может быть и может не быть. В данном случае экстремум есть, так как z>0 во всех точках, кроме 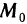и z=0 в точке 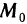, т. е. данная функция в точке 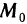имеет минимум.

4. Исследовать на экстремум функцию 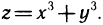Имеем 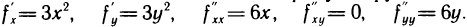Решая систему уравнений 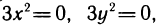находим, что 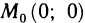— точка возможного экстремума. В этой точке 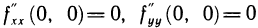и, следовательно, 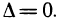В данном случае в точке 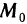экстремума нет.

В самом деле, 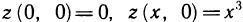откуда z>0 при х>0 и z<0 при х<0, т. е. в любой окрестности точки 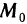данная функция имеет значения как большие, так и меньшие z (0, 0).

Метод наименьших квадратов

В различных исследованиях приходится использовать формулы, составленные на основании эксперимента. Одним из лучших способов получения таких формул является метод наименьших квадратов.

Пусть на основании эксперимента необходимо установить функциональную зависимость между двумя переменными величинами х и у. Например, между температурой и удлинением прямолинейного металлического стержня. По результатам измерений составим следующую таблицу:

Установим теперь вид функции y=f(x) по характеру расположения на координатной плоскости экспериментальных точек. Пусть, например, точки, взятые из таблицы, расположены так, как показано на рис. 166. В данном случае естественно предположить, что между х и у существует линейная зависимость, выражающаяся формулой

Ограничимся только случаем линейной зависимости.

Так как точки 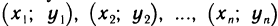не лежат точно на прямой, а лишь вблизи нее, то формула (1) является приближенной. Поэтому, подставляя значения координат точек в выражение 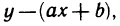получаем равенства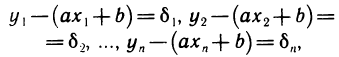
где 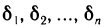— некоторые числа, которые назовем погрешностями.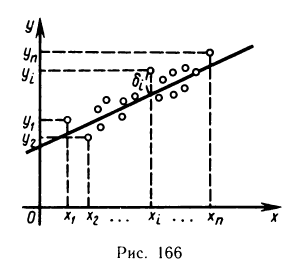

Поставим задачу подобрать коэффициенты а и b таким образом, чтобы эти погрешности были возможно меньше по абсолютной величине. Для решения этой задачи воспользуемся методом наименьших квадратов. Рассмотрим сумму квадратов погрешностей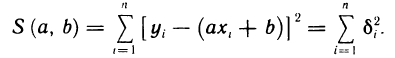

Здесь 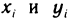— заданные числа, а коэффициенты а и b — неизвестные числа, подлежащие определению, исходя из условия минимума S (a, b), т. е. S (а, b) можно рассматривать как функцию двух переменных а и & и исследовать ее на экстремум.

Таким образом, задача свелась к нахождению значений а и b, при которых функция S (a, b) имеет минимум. Имеем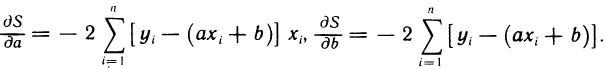

Приравнивая эти частные производные к нулю, получаем линейную систему двух уравнений с двумя неизвестными а и b: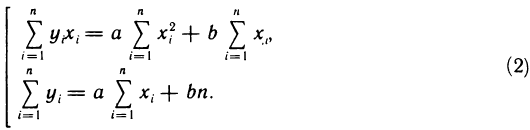

Система (2) называется нормальной системой метода наименьших квадратов. Из этой системы находим числа а и b и затем, подставляя их в уравнение (1), получаем уравнение искомой прямой.

Тот факт, что функция S (a, b) в найденной точке М (а; b) имеет минимум, легко устанавливается с помощью частных производных второго порядка. Имеем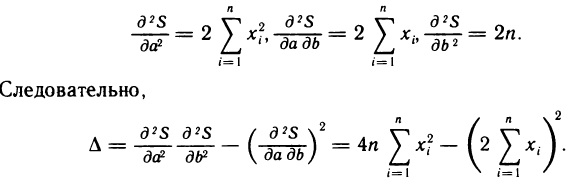

Это выражение можно записать в виде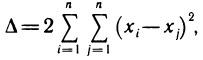

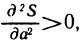откуда следует, что Так как то в точке М (а; b) функция S (а, b) имеет минимум.

Пример:

Пусть в результате эксперимента получены пять значений искомой функции у при пяти значениях аргумента Будем искать функциональную зависимость между х и у в виде линейной функции у=ах+b.

При составлении нормальной системы (2) для определения коэффициентов а и b предварительно вычислим: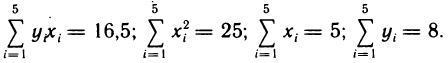
Система (2) принимает вид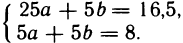

Решая эту систему, найдем: а=0,425, b=1,175. Следовательно, у=0,425х+1,175 — уравнение искомой прямой.

Частные производные функции нескольких переменных

Определение 12.1. Частной производной функции нескольких переменных по одной из этих переменных называется предел отношения соответствующего частного приращения функции к приращению рассматриваемой независимой переменной при стремлении приращения переменной к нулю (если этот предел существует).

Обозначения в случае 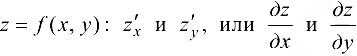, или .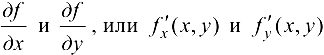

Таким образом, для функции 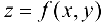по определению:

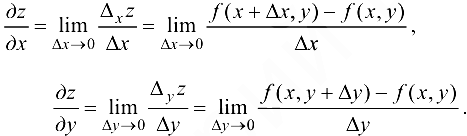
Согласно формулам (12.1) и (12.2), если для функции 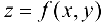вычисляется производная 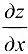, то переменная у считается постоянной; если же вычисляется производная 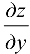, то переменная 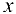считается постоянной. Следовательно, частное дифференцирование не требует никаких новых правил, и можно пользоваться известными формулами.

В общем случае, если 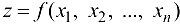и требуется найти 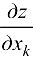, постоянными следует считать переменные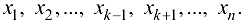

Пример:

Найти частные производные функции .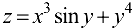

Ответ: .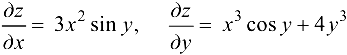

Пример:

Найти частные производные функции .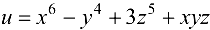

Ответ: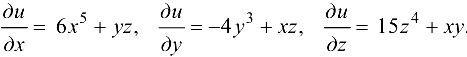

Геометрический смысл частных производных: геометрическим изображением функции 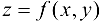является некоторая поверхность Р. Полагая 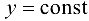, получим некоторую плоскую кривую 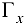(рис. 12.1). Пусть МК — касательная к кривой 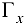в точке 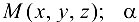— угол, образованный этой касательной с положительным направлением оси .

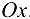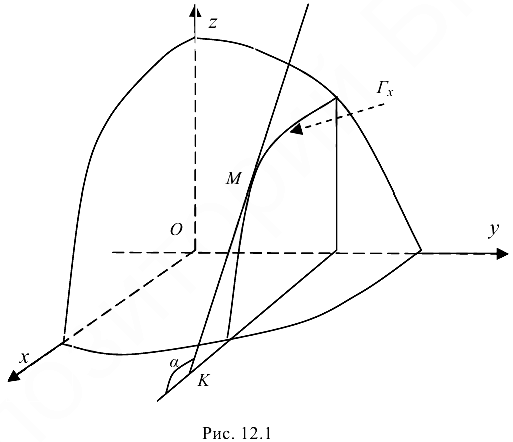
Так как 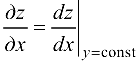, па основании геометрического смысла производной функции одной переменной, имеем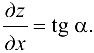

Аналогичный смысл имеет и .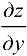

Эта лекция взята со страницы лекций по предмету математический анализ:

Предмет математический анализ

Возможно вам будут полезны эти страницы:

Функции нескольких переменных: определения и примеры с решением

Предел и непрерывность фнп: определение и примеры с решением

Частные производные высших порядков с примерами решения

Дифференцируемость фнп с примером решения

Решение заданий и задач по предметам:

• Математика
• Высшая математика
• Математический анализ
• Линейная алгебра

Дополнительные лекции по высшей математике:

1. Тождественные преобразования алгебраических выражений
2. Функции и графики
3. Преобразования графиков функций
4. Квадратная функция и её графики
5. Алгебраические неравенства
6. Неравенства
7. Неравенства с переменными
8. Прогрессии в математике
9. Арифметическая прогрессия
10. Геометрическая прогрессия
11. Показатели в математике
12. Логарифмы в математике
13. Исследование уравнений
14. Уравнения высших степеней
15. Уравнения высших степеней с одним неизвестным
16. Комплексные числа
17. Непрерывная дробь (цепная дробь)
18. Алгебраические уравнения
19. Неопределенные уравнения
20. Соединения
21. Бином Ньютона
22. Число е
23. Непрерывные дроби
24. Функция
25. Исследование функций
26. Предел
27. Интеграл
28. Двойной интеграл
29. Тройной интеграл
30. Интегрирование
31. Неопределённый интеграл
32. Определенный интеграл
33. Криволинейные интегралы
34. Поверхностные интегралы
35. Несобственные интегралы
36. Кратные интегралы
37. Интегралы, зависящие от параметра
38. Квадратный трехчлен
39. Производная
40. Применение производной к исследованию функций
41. Приложения производной
42. Дифференциал функции
43. Дифференцирование в математике
44. Формулы и правила дифференцирования
45. Дифференциальное исчисление
46. Дифференциальные уравнения
47. Дифференциальные уравнения первого порядка
48. Дифференциальные уравнения высших порядков
49. Дифференциальные уравнения в частных производных
50. Тригонометрические функции
51. Тригонометрические уравнения и неравенства
52. Показательная функция
53. Показательные уравнения
54. Обобщенная степень
55. Взаимно обратные функции
56. Логарифмическая функция
57. Уравнения и неравенства
58. Положительные и отрицательные числа
59. Алгебраические выражения
60. Иррациональные алгебраические выражения
61. Преобразование алгебраических выражений
62. Преобразование дробных алгебраических выражений
63. Разложение многочленов на множители
64. Многочлены от одного переменного
65. Алгебраические дроби
66. Пропорции
67. Уравнения
68. Системы уравнений
69. Системы уравнений высших степеней
70. Системы алгебраических уравнений
71. Системы линейных уравнений
72. Системы дифференциальных уравнений
73. Арифметический квадратный корень
74. Квадратные и кубические корни
75. Извлечение квадратного корня
76. Рациональные числа
77. Иррациональные числа
78. Арифметический корень
79. Квадратные уравнения
80. Иррациональные уравнения
81. Последовательность
82. Ряды сходящиеся и расходящиеся
83. Тригонометрические функции произвольного угла
84. Тригонометрические формулы
85. Обратные тригонометрические функции
86. Теорема Безу
87. Математическая индукция
88. Показатель степени
89. Показательные функции и логарифмы
90. Множество
91. Множество действительных чисел
92. Числовые множества
93. Преобразование рациональных выражений
94. Преобразование иррациональных выражений
95. Геометрия
96. Действительные числа
97. Степени и корни
98. Степень с рациональным показателем
99. Тригонометрические функции угла
100. Тригонометрические функции числового аргумента
101. Тригонометрические выражения и их преобразования
102. Преобразование тригонометрических выражений
103. Комбинаторика
104. Вычислительная математика
105. Прямая линия на плоскости и ее уравнения
106. Прямая и плоскость
107. Линии и уравнения
108. Прямая линия
109. Уравнения прямой и плоскости в пространстве
110. Кривые второго порядка
111. Кривые и поверхности второго порядка
112. Числовые ряды
113. Степенные ряды
114. Ряды Фурье
115. Преобразование Фурье
116. Функциональные ряды
117. Функции многих переменных
118. Метод координат
119. Гармонический анализ
120. Вещественные числа
121. Предел последовательности
122. Аналитическая геометрия
123. Аналитическая геометрия на плоскости
124. Аналитическая геометрия в пространстве
125. Функции одной переменной
126. Высшая алгебра
127. Векторная алгебра
128. Векторный анализ
129. Векторы
130. Скалярное произведение векторов
131. Векторное произведение векторов
132. Смешанное произведение векторов
133. Операции над векторами
134. Непрерывность функций
135. Предел и непрерывность функций нескольких переменных
136. Предел и непрерывность функции одной переменной
137. Производные и дифференциалы функции одной переменной
138. Дифференциальное исчисление функции одной переменной
139. Матрицы
140. Линейные и евклидовы пространства
141. Линейные отображения
142. Дифференциальные теоремы о среднем
143. Теория устойчивости дифференциальных уравнений
144. Функции комплексного переменного
145. Преобразование Лапласа
146. Теории поля
147. Операционное исчисление
148. Системы координат
149. Рациональная функция
150. Интегральное исчисление
151. Интегральное исчисление функций одной переменной
152. Дифференциальное исчисление функций нескольких переменных
153. Отношение в математике
154. Математическая логика
155. Графы в математике
156. Линейные пространства
157. Первообразная и неопределенный интеграл
158. Линейная функция
159. Выпуклые множества точек
160. Система координат