Оглавление:
Векторный базис в пространстве:
Пусть 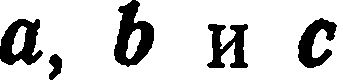 — тройка некомпланарных векторов. Тогда, как известно из школьного курса, любой вектор
— тройка некомпланарных векторов. Тогда, как известно из школьного курса, любой вектор 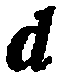 пространства может быть представлен, и притом единственным образом, в виде линейной комбинации данных векторов:
пространства может быть представлен, и притом единственным образом, в виде линейной комбинации данных векторов:
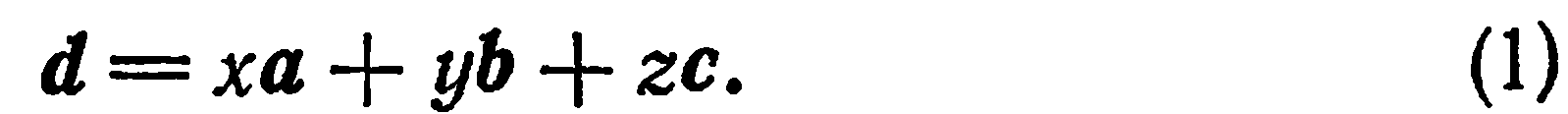
Определение:
Векторным базисом пространства называется тройка некомпланарных векторов, взятых в определенном порядке.
Очевидно, что существует бесконечное множество базисов пространства. Пусть 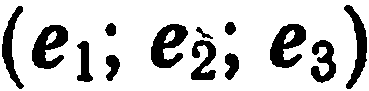 — один из них. Тогда любой вектор
— один из них. Тогда любой вектор  пространства может быть представлен единственным образом в виде
пространства может быть представлен единственным образом в виде
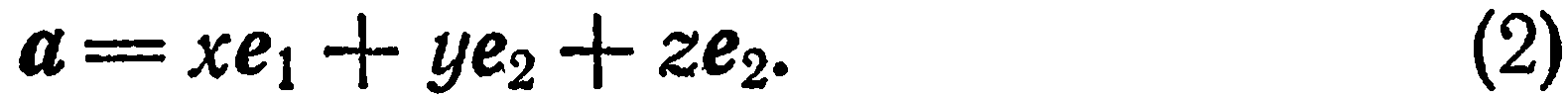
Это означает, что для любого вектора  существует и притом только одна тройка чисел
существует и притом только одна тройка чисел 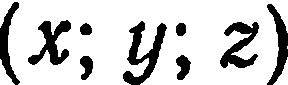 , удовлетворяющая равенству (2). Справедливо и обратное утверждение: тройка чисел
, удовлетворяющая равенству (2). Справедливо и обратное утверждение: тройка чисел 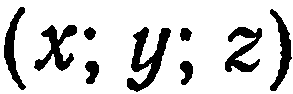 в данном базисе
в данном базисе 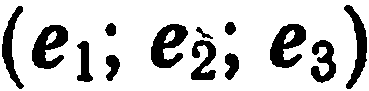 определяет единственный вектор
определяет единственный вектор  .
.
Числа  называются координатами вектора
называются координатами вектора  в базисе
в базисе
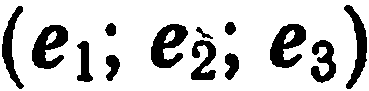 . Если вектор
. Если вектор  пространства задан своими координатами
пространства задан своими координатами  , то пишут
, то пишут 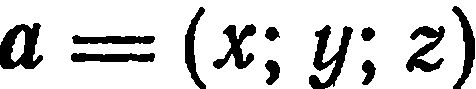 .
.
Определение:
Базис 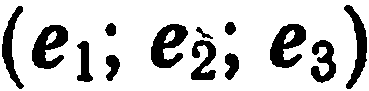 пространства называется прямоугольным, если базисные векторы единичны и попарно перпендикулярны^ т. е. если
пространства называется прямоугольным, если базисные векторы единичны и попарно перпендикулярны^ т. е. если
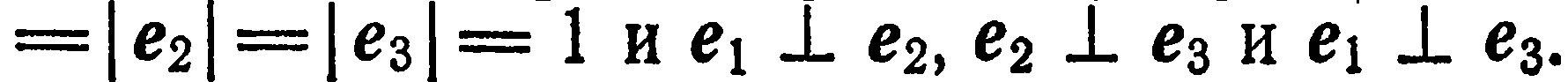
Базисные векторы прямоугольного базиса обозначают через 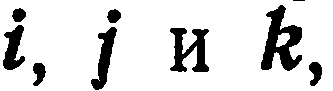 а разложение вектора
а разложение вектора 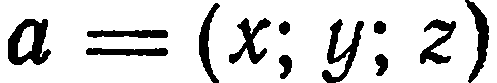 по базису
по базису 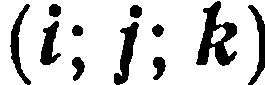 имеет вид
имеет вид 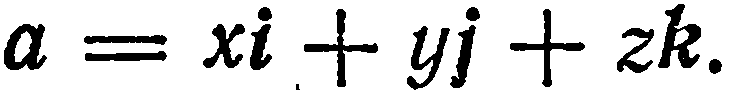
Пример:
Даны векторы:
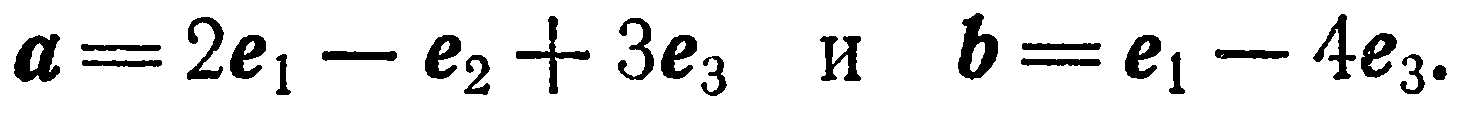
Найти координаты векторов 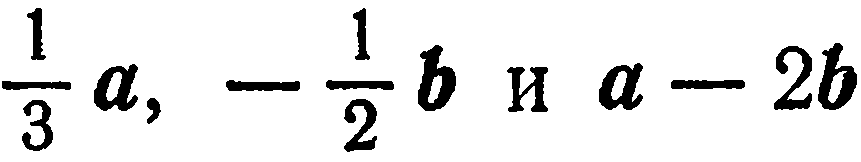 в базисе
в базисе 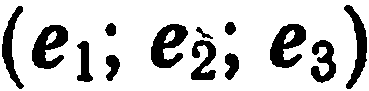 .
.
Решение. Имеем:

Применив правила действия над векторами, заданными координатами, находим:
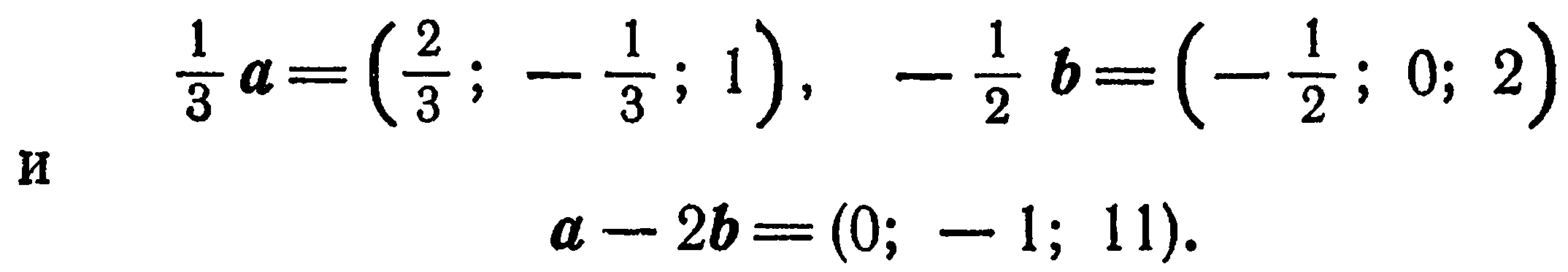
Пример:
Найти длину вектора 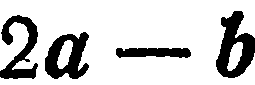 , если
, если 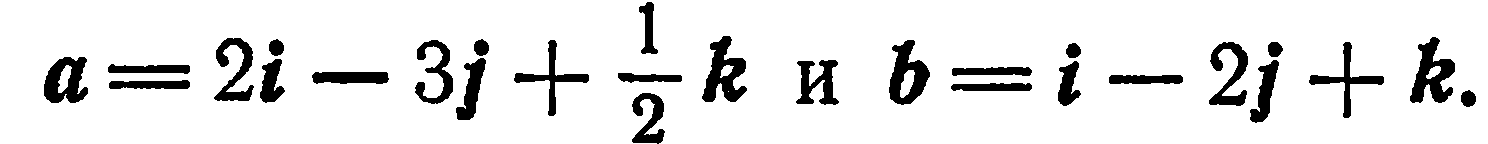
Решение:
Известно, что если 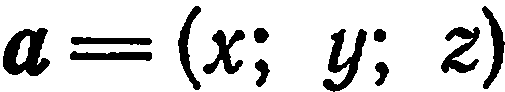 , то
, то 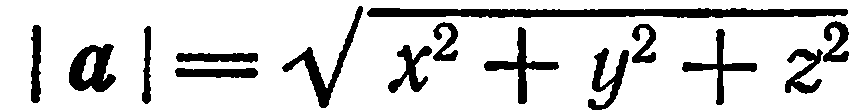 . Находим:
. Находим:
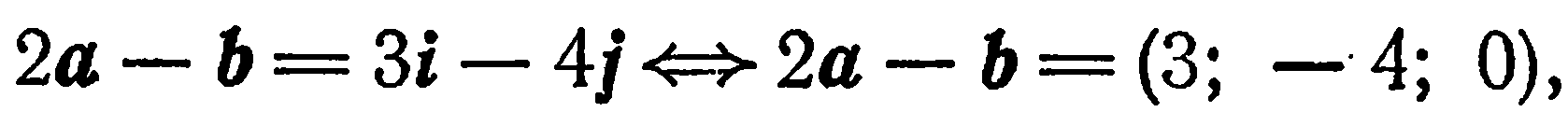
поэтому
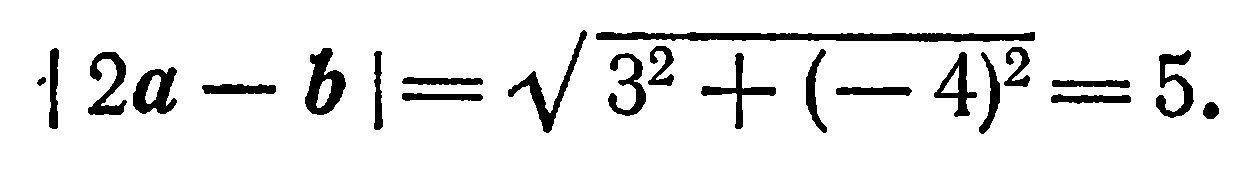
Прямоугольные координаты в пространстве
Определение:
Декартовой системой координат в пространстве называется совокупность фиксированной точки  и векторного базиса
и векторного базиса 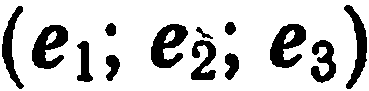 . Точка
. Точка  называется началом координат, прямые
называется началом координат, прямые 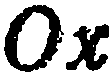
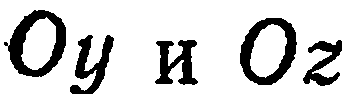 , проходящие через начало координат в направлении базисных векторов
, проходящие через начало координат в направлении базисных векторов 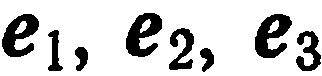 (рис. 32), называются осями координат:
(рис. 32), называются осями координат: 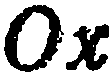 — ось абсцисс,
— ось абсцисс, 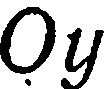 — ось ординат,
— ось ординат, 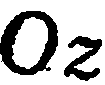 — ось апликат. При этом систему координат
— ось апликат. При этом систему координат 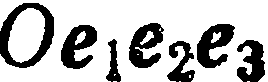 будем также обозначать
будем также обозначать  .
.
Пусть  — произвольная точка пространства. Тогда вектор
— произвольная точка пространства. Тогда вектор  называется радиусом-вектором относительно точки
называется радиусом-вектором относительно точки  . Координатами точки
. Координатами точки 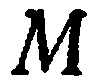 в декартовой системе координат называются координаты радиуса-вектора
в декартовой системе координат называются координаты радиуса-вектора  в базисе
в базисе 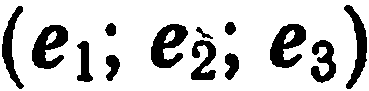 ; при этом
; при этом 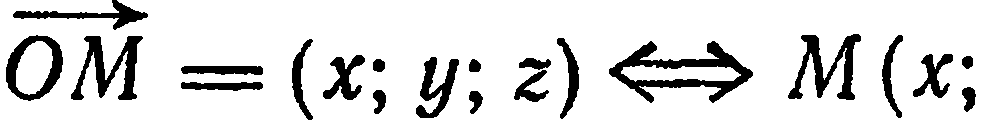
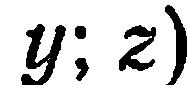 где
где  — абсцисса,
— абсцисса, 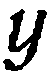 — ордината,
— ордината, 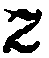 — апликата.
— апликата.
Определение:
Прямоугольной декартовой (или просто прямоугольной) системой координат в пространстве называется совокупность фиксированной точки  и прямоугольного базиса
и прямоугольного базиса 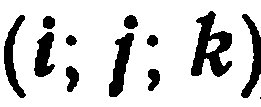 (рис. 33).
(рис. 33).
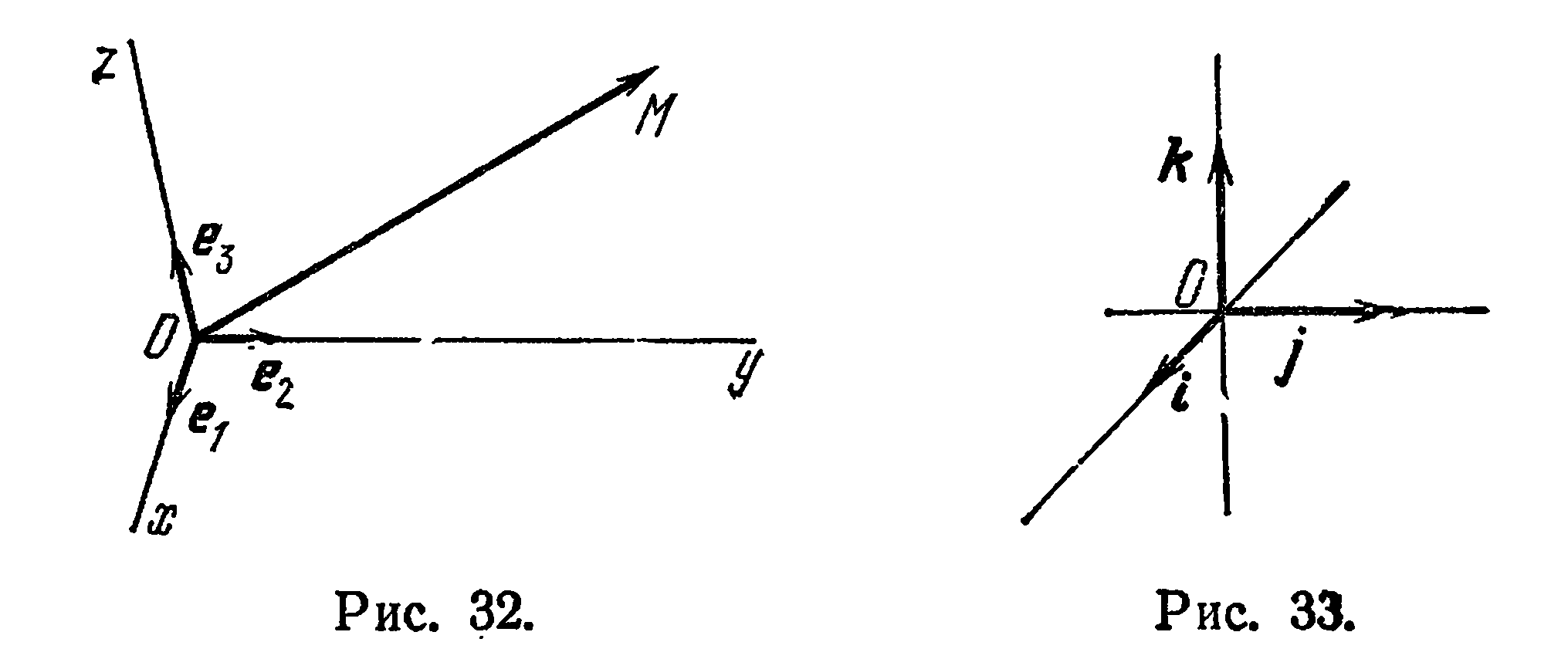
Прямоугольная система координат хорошо известна по школьному курсу, поэтому на ее описании мы здесь останавливаться не будем.
Введение прямоугольной системы координат в пространстве дает возможность решать много геометрических задач так, как это делалось в плоскости.
Например, можно показать, что координаты точки 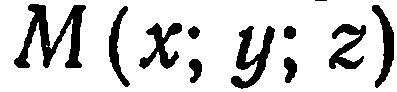 , делящей отрезок
, делящей отрезок 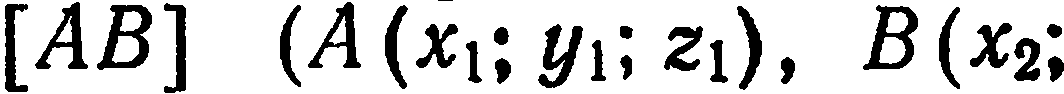
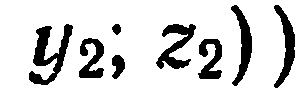 в данном отношении
в данном отношении 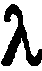 , определяются по формулам:
, определяются по формулам:
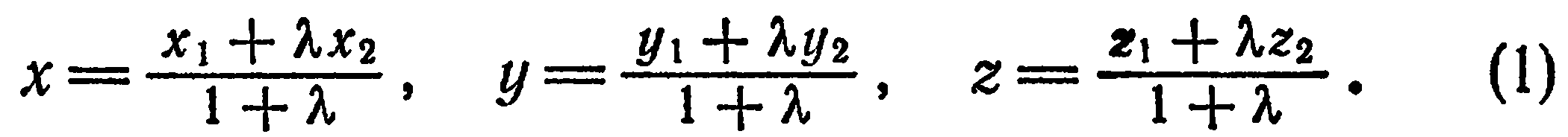
Понятие об уравнении поверхности и линии в пространстве
Пусть множество решений уравнения

не пусто. Тогда каждой тройке чисел  , являющейся решением уравнения (2), соответствует точка с координатами
, являющейся решением уравнения (2), соответствует точка с координатами 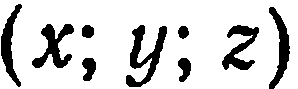 в некоторой прямоугольной системе координат. Множество всех точек пространства, координаты которых удовлетворяют уравнению (2), есть, вообще говоря, некоторая поверхность.
в некоторой прямоугольной системе координат. Множество всех точек пространства, координаты которых удовлетворяют уравнению (2), есть, вообще говоря, некоторая поверхность.
Обратно, пусть в пространстве заданы некоторая поверхность и прямоугольная система координат  .
.
Определение:
Уравнением данной поверхности в системе координат  называется такое уравнение с переменными
называется такое уравнение с переменными 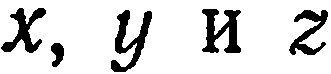 которому удовлетворяют координаты любой точки, лежащей на этой поверхности, и не удовлетворяют координаты любой точки, не лежащей на этой поверхности.
которому удовлетворяют координаты любой точки, лежащей на этой поверхности, и не удовлетворяют координаты любой точки, не лежащей на этой поверхности.
Пример:
Найти уравнение сферы радиуса 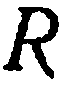 с центром в точке
с центром в точке 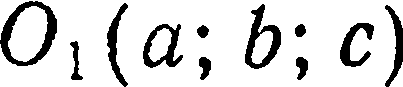 .
.
Решение:
Пусть 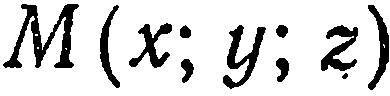 — произвольная точка на сфере; тогда
— произвольная точка на сфере; тогда
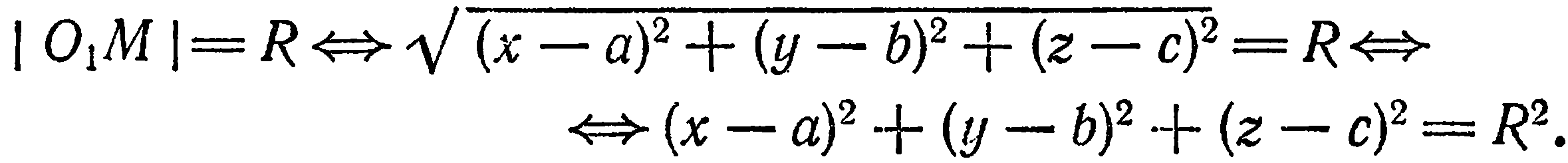
Уравнение 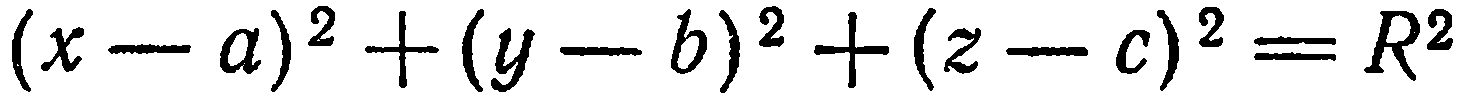 и есть искомое уравнение, так как координаты произвольной точки сферы ему удовлетворяют, и, как легко показать, координаты любой точки, не лежащей на сфере, не удовлетворяют этому уравнению (например,
и есть искомое уравнение, так как координаты произвольной точки сферы ему удовлетворяют, и, как легко показать, координаты любой точки, не лежащей на сфере, не удовлетворяют этому уравнению (например, 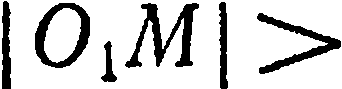
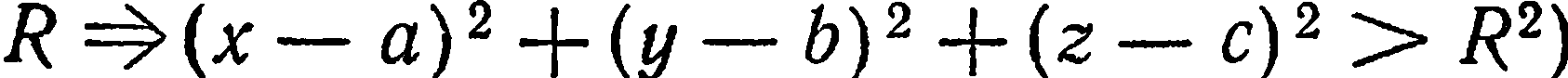
Линия в пространстве рассматривается как линия пересечения двух поверхностей, т. е. как множество точек, общих двум поверхностям. Так, если 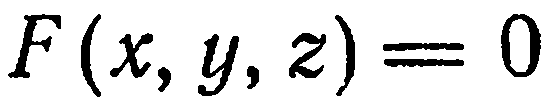 и
и 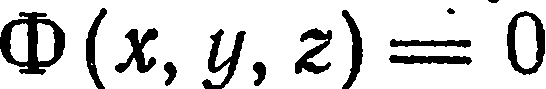 — уравнения двух поверхностей, пересекающихся по некоторой линии
— уравнения двух поверхностей, пересекающихся по некоторой линии 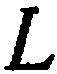 , то координаты точек этой линии удовлетворяют каждому из этих
, то координаты точек этой линии удовлетворяют каждому из этих
уравнений. Таким образом, система уравнений

определяет рассматриваемую линию 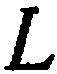 в пространстве.
в пространстве.
Например, система
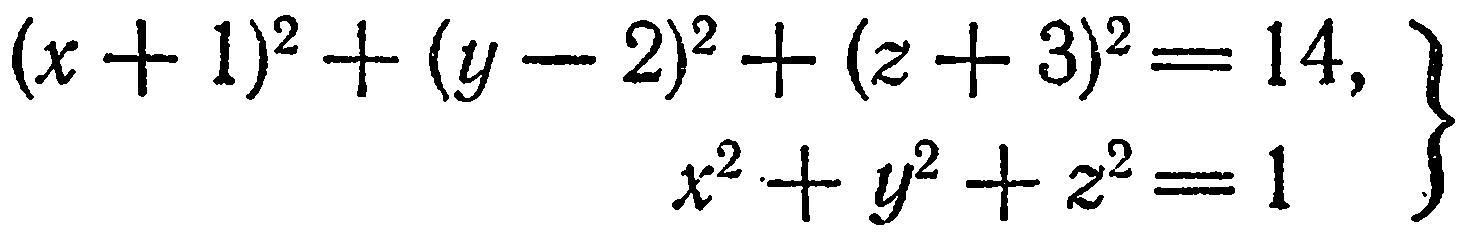
определяет окружность (как линию пересечения двух сфер).
Отметим, что если известно уравнение поверхности (линии), то относительно любой точки пространства можно решить вопрос: лежит эта точка на данной поверхности (линии) или нет?
Пример:
Лежит ли точка 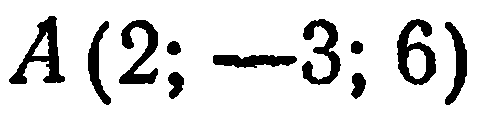 на поверхности
на поверхности 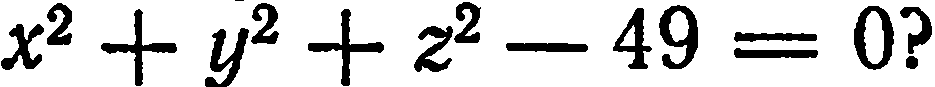
Решение:
Подставив в данное уравнение вместо текущих координат 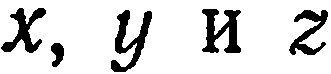 координаты точки
координаты точки 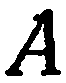 , получим: 4 + 9 + 36 — 49 = 49 — 49 = 0. Точка
, получим: 4 + 9 + 36 — 49 = 49 — 49 = 0. Точка 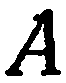 лежит на данной поверхности.
лежит на данной поверхности.
Уравнение плоскости, проходящей через данную точку с заданным нормальным вектором
Пусть в прямоугольной системе координат  задана некоторая точка
задана некоторая точка 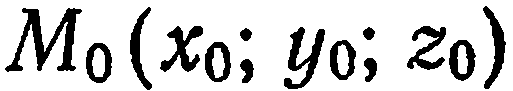 и ненулевой вектор
и ненулевой вектор 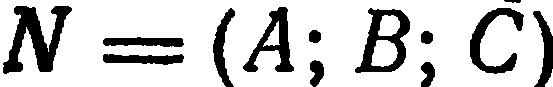 . Требуется составить уравнение плоскости
. Требуется составить уравнение плоскости  , проходящей через точку
, проходящей через точку 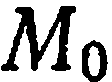 и
и
перпендикулярной вектору 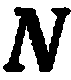 (рис. 34).
(рис. 34).
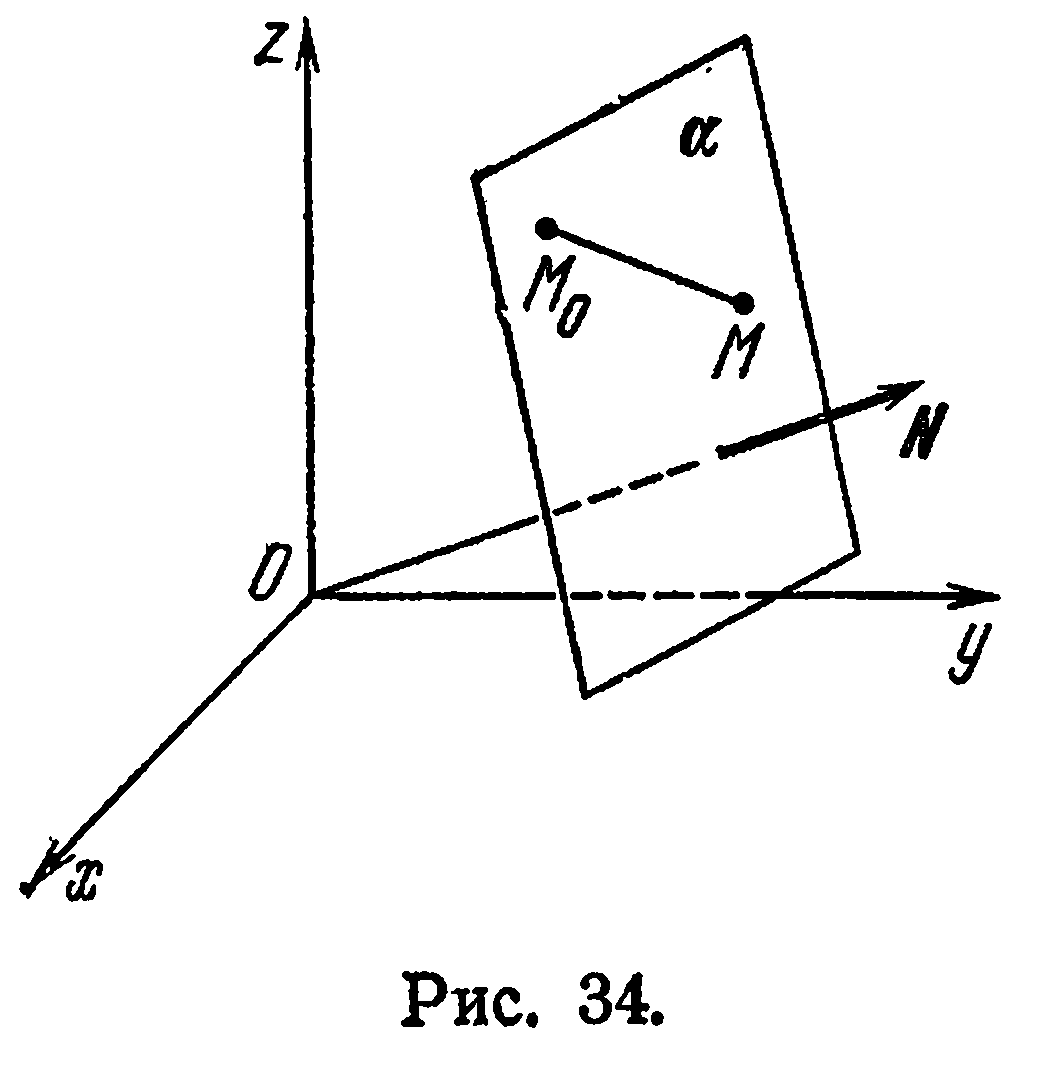
Определение:
Любой ненулевой вектор, перпендикулярный к плоскости  , называется нормальным вектором этой плоскости.
, называется нормальным вектором этой плоскости.
Очевидно, что положение плоскости  вполне определяется заданием точки
вполне определяется заданием точки  и вектора
и вектора 
Возьмем на плоскости  произвольную точку
произвольную точку 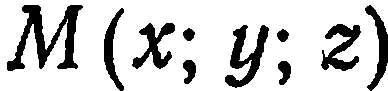 . Ясно, что
. Ясно, что  эквивалентно
эквивалентно 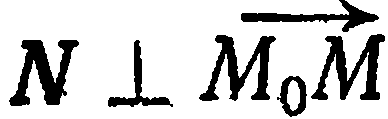 , что в свою очередь эквивалентно
, что в свою очередь эквивалентно

Учитывая, что 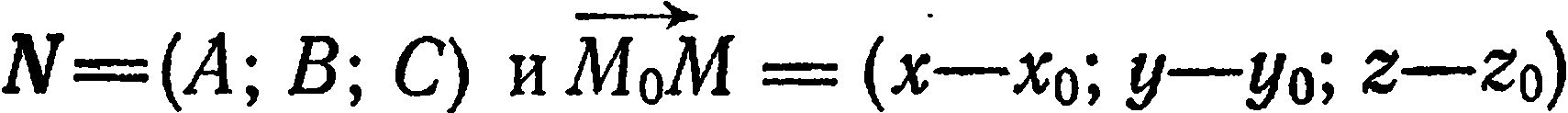 , запишем равенство (1) в координатной форме:
, запишем равенство (1) в координатной форме:
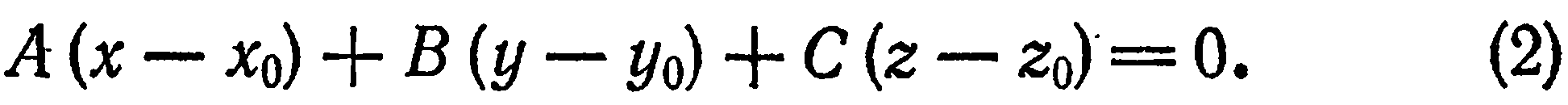
Уравнение (2) называется уравнением плоскости, проходящей через данную точку 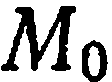 , с заданным нормальным вектором
, с заданным нормальным вектором 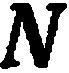 . Это —уравнение первой степени относительно текущих координат
. Это —уравнение первой степени относительно текущих координат 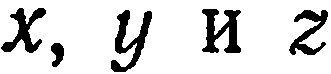 , поэтому можно сделать вывод: в прямоугольной системе координат каждая плоскость определяется уравнением первой степени относительно текущих координат.
, поэтому можно сделать вывод: в прямоугольной системе координат каждая плоскость определяется уравнением первой степени относительно текущих координат.
Заметим, что если коэффициентам 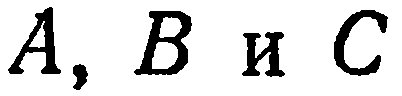 уравнения (2) придавать различные значения, то можно получить уравнение любой плоскости, проходящей через точку
уравнения (2) придавать различные значения, то можно получить уравнение любой плоскости, проходящей через точку 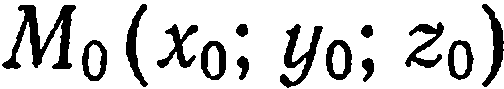 . Совокупность плоскостей, проходящих через данную точку, называют связкой плоскостей. Поэтому уравнение (2) называют и уравнением связки плоскостей.
. Совокупность плоскостей, проходящих через данную точку, называют связкой плоскостей. Поэтому уравнение (2) называют и уравнением связки плоскостей.
Пример:
Составить уравнение плоскости, проходящей через точку 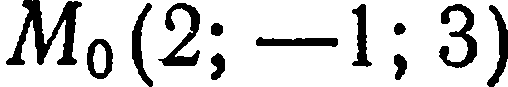 перпендикулярно вектору
перпендикулярно вектору  .
.
Решение:
Имеем 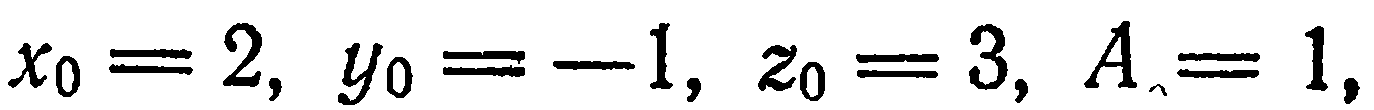
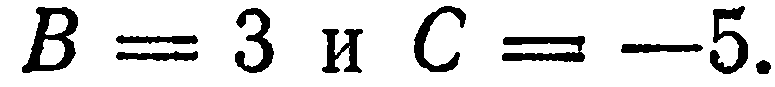 Подставив эти значения в уравнение
Подставив эти значения в уравнение
(2), получим
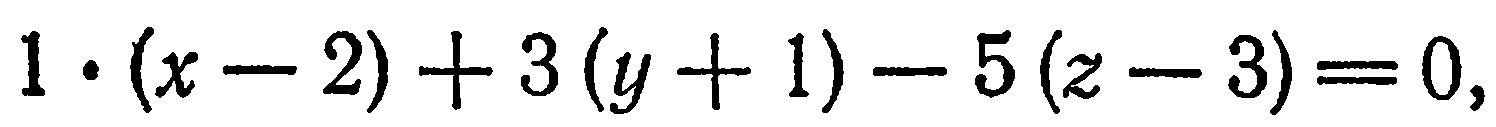
или
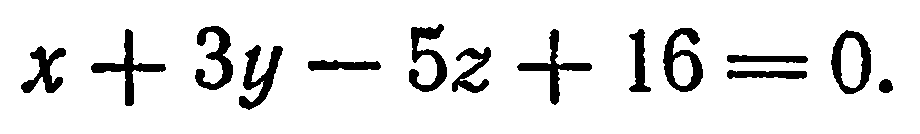
Общее уравнение плоскости и его частные случаи
В предыдущем параграфе мы показали, что в прямоугольной системе координат  каждая плоскость определяется уравнением первой степени относительно текущих координат
каждая плоскость определяется уравнением первой степени относительно текущих координат  . Теперь докажем обратное: всякое уравнение первой степени
. Теперь докажем обратное: всякое уравнение первой степени

в прямоугольной системе координат  определяет плоскость и притом единственную.
определяет плоскость и притом единственную.
Так как уравнение (1) является уравнением первой степени, то по крайней мере один из коэффициентов 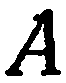 ,
, 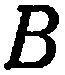 или
или  отличен от нуля. Допустим, для определенности, что
отличен от нуля. Допустим, для определенности, что 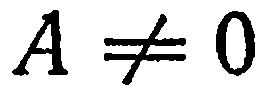 . Тогда уравнение (1) можно представить в виде
. Тогда уравнение (1) можно представить в виде
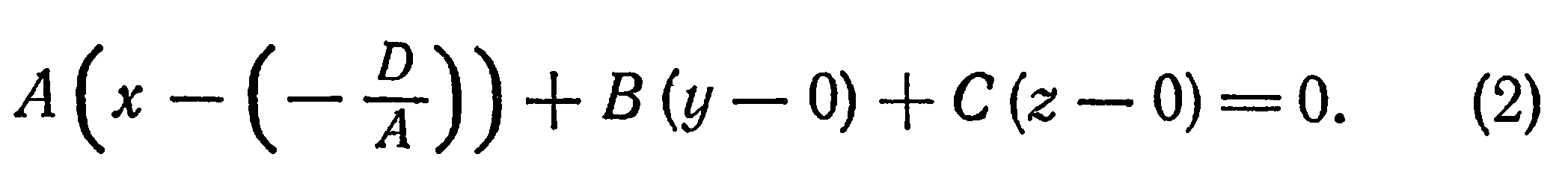
Это уравнение имеет вид уравнения (2) из предыдущего параграфа и, следовательно, оно определяет единственную плоскость, проходящую через точку 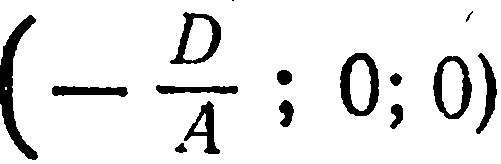 и перпендикулярную вектору
и перпендикулярную вектору 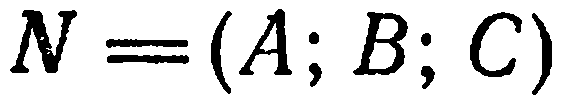 . Но тогда и уравнение (1), равносильное уравнению (2), определяет
. Но тогда и уравнение (1), равносильное уравнению (2), определяет
плоскость.
Уравнение (1) называется общим уравнением плоскости.
Рассмотрим некоторые частные случаи уравнения (1) (плоскость, определяемую этим уравнением, обозначим через  ).
).
1. Свободный член  равен 0. Тогда уравнение (1) имеет вид
равен 0. Тогда уравнение (1) имеет вид 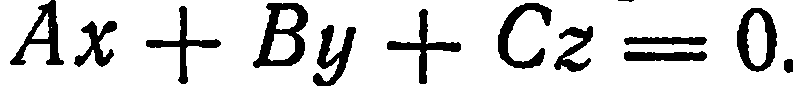 Этому уравнению удовлетворяют координаты точки
Этому уравнению удовлетворяют координаты точки 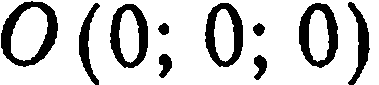 , следовательно, плоскость проходит через начало координат.
, следовательно, плоскость проходит через начало координат.
1. Один из коэффициентов при текущих координатах равен нулю. Пусть  . Тогда уравнение (1) примет вид
. Тогда уравнение (1) примет вид 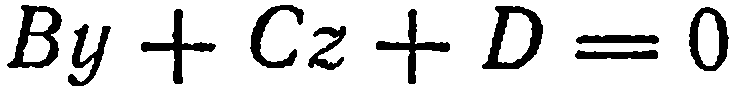 . В этом случае имеем
. В этом случае имеем 
Аналогично, 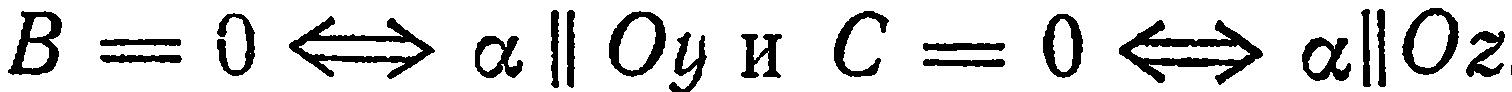 . Таким образом, если в уравнении плоскости отсутствует какой-либо член, содержащий координату
. Таким образом, если в уравнении плоскости отсутствует какой-либо член, содержащий координату  или
или  , то плоскость параллельна соответственно оси
, то плоскость параллельна соответственно оси  или
или 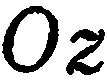 . Например, плоскость, определяемая уравнением
. Например, плоскость, определяемая уравнением 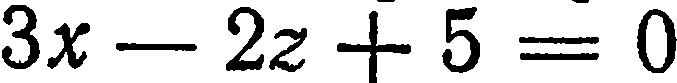 , параллельна оси
, параллельна оси  (здесь
(здесь  ).
).
1. Свободный член и один из коэффициентов при текущих координатах равны нулю. Пусть, например,  . Тогда (1) примет вид
. Тогда (1) примет вид  . Имеем:
. Имеем:  и, кроме того,
и, кроме того, 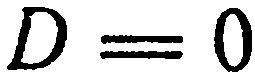 , т. е. плоскость
, т. е. плоскость  проходит через начало координат. Следовательно, плоскость проходит через ось
проходит через начало координат. Следовательно, плоскость проходит через ось 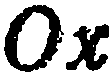 . Аналогично можно показать, что уравнения
. Аналогично можно показать, что уравнения 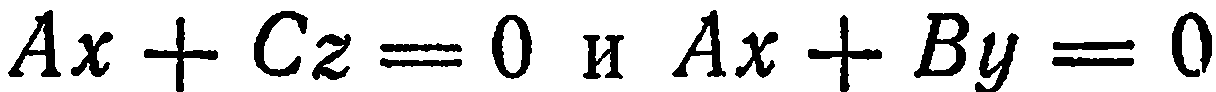 определяют плоскости, проходящие соответственно через оси
определяют плоскости, проходящие соответственно через оси  . Так, уравнение
. Так, уравнение  определяет плоскость, проходящую через ось
определяет плоскость, проходящую через ось 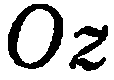 .
.
4. Два коэффициента при текущих координатах равны нулю. Пусть, например, 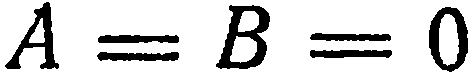 . Тогда уравнение (1) примет вид
. Тогда уравнение (1) примет вид 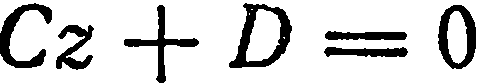 . Имеем:
. Имеем:

Следовательно, данная плоскость параллельна координатной плоскости  . Этот же вывод можно получить иначе. Имеем:
. Этот же вывод можно получить иначе. Имеем:
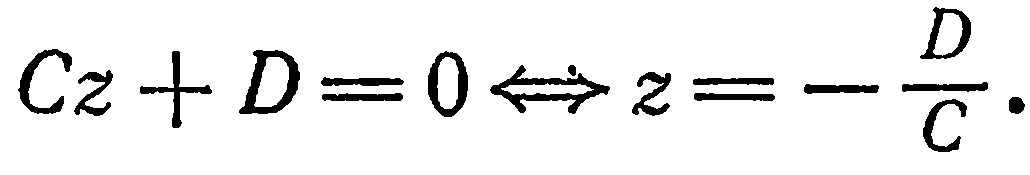
Положив
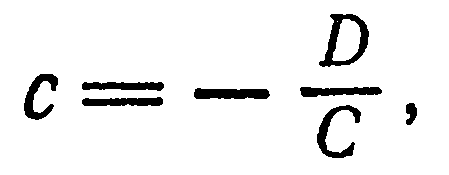
получим
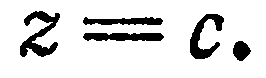
Это уравнение показывает, что все точки данной плоскости имеют одну и ту же апликату, т. е. данная плоскость параллельна плоскости 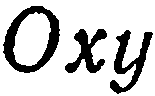 . Аналогично, уравнения
. Аналогично, уравнения 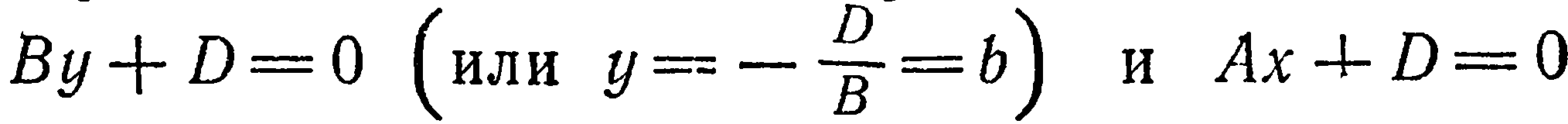
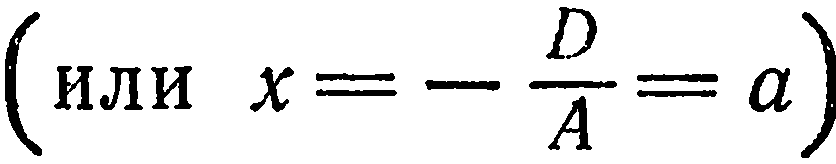
определяют плоскости, соответственно параллельные координатным плоскостям 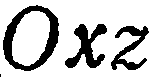 и
и  . Например, уравнение
. Например, уравнение 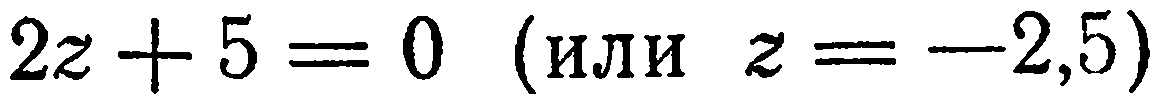 определяет плоскость, параллельную плоскости
определяет плоскость, параллельную плоскости 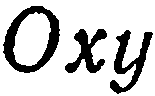 и расположенную ниже
и расположенную ниже 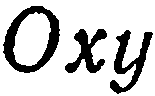 на расстоянии 2,5 ед.
на расстоянии 2,5 ед.
от нее.
5. Свободный член и два коэффициента при текущих координатах равны нулю. Пусть, например, 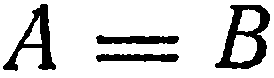
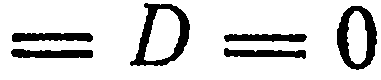 . Тогда уравнение (1) имеет вид
. Тогда уравнение (1) имеет вид 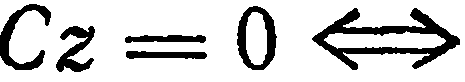
 . Это уравнение определяет плоскость, все точки которой имеют апликату, т. е. координатную плоскость
. Это уравнение определяет плоскость, все точки которой имеют апликату, т. е. координатную плоскость 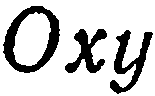 .
.
Аналогично, 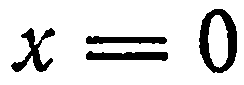 — уравнение плоскости
— уравнение плоскости 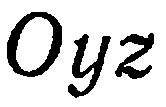 и
и  уравнение плоскости
уравнение плоскости 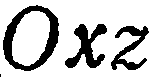 .
.
Пример:
Составить уравнение плоскости, проходящей через ось 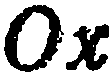 и через точку
и через точку 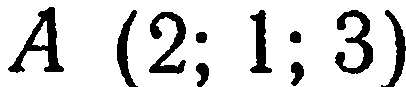 .
.
Решение. Так как искомая плоскость проходит через ось 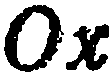 , то ее уравнение имеет вид
, то ее уравнение имеет вид  . Заменив в этом уравнении текущие координаты координатами точки
. Заменив в этом уравнении текущие координаты координатами точки 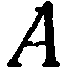 , получаем
, получаем 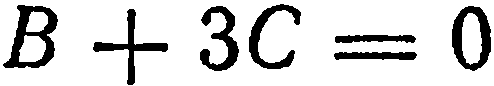 , откуда
, откуда 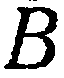
 . Подставив это значение
. Подставив это значение 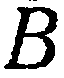 в уравнение
в уравнение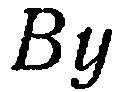
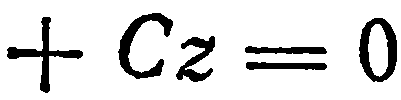 , находим
, находим  , или
, или 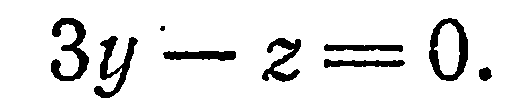
Пример:
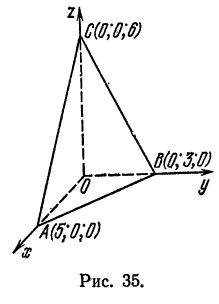
Построить плоскость
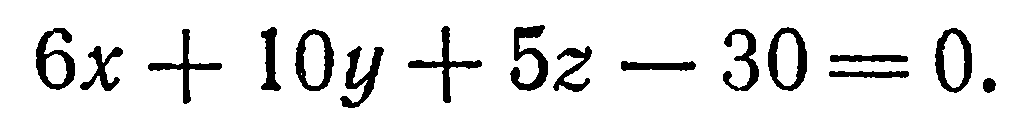
Решение:
Для построения плоскости достаточно построить три ее точки. Проще всего найти точки пересечения плоскости с осями координат. Положив в данном уравнении 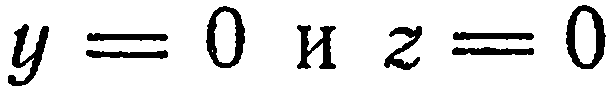 , найдем
, найдем  . Положив
. Положив 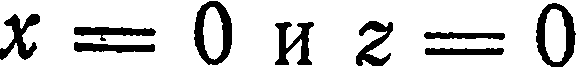 , находим
, находим  . Наконец, положив
. Наконец, положив 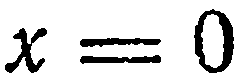 и
и  , находим
, находим 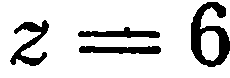 . Таким образом, данная
. Таким образом, данная
плоскость пересекает оси 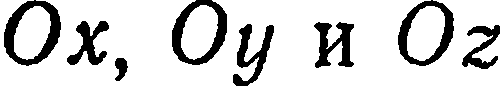 соответственно в точках
соответственно в точках 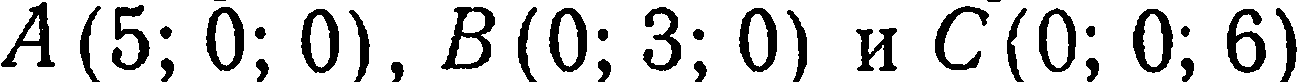 (рис.35).
(рис.35).
Пример:
Составить уравнение плоскости, проходящей через три точки 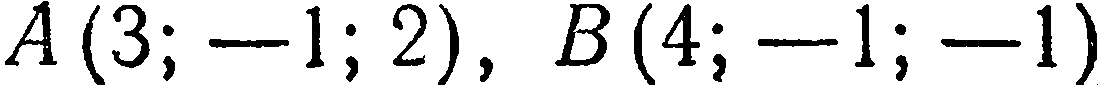 и
и 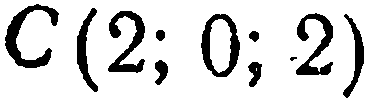 .
.
Решение:
Пусть искомое уравнение имеет вид (1). Так как каждая из данных точек принадлежит данной плоскости, то координаты этих точек удовлетворяет уравнению (1), т.-е.
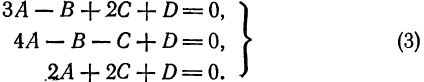
Решим эту систему, приняв за неизвестные коэффициенты 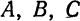 и считая
и считая 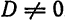 . Из второго уравнения имеем
. Из второго уравнения имеем
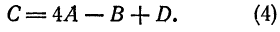
Подставив это значение 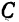 в остальные два уравнения системы (3), получаем:
в остальные два уравнения системы (3), получаем:
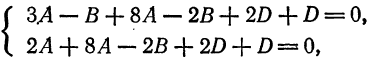
или
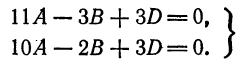
Отсюда 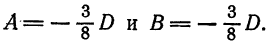 ходим По формуле (4) находим
ходим По формуле (4) находим
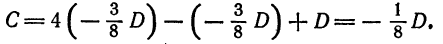
Заменив найденными значениями  соответствующие коэффициенты в уравнении (1), получаем
соответствующие коэффициенты в уравнении (1), получаем
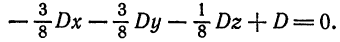
Отсюда
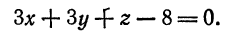
Уравнения прямой, проходящей через данную точку с заданным направляющим вектором
Пусть в прямоугольной системе координат 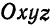 задана некоторая точка
задана некоторая точка 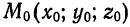 и ненулевой вектор
и ненулевой вектор 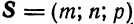 . Требуется составить уравнение прямой
. Требуется составить уравнение прямой 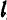 , проходящей через точку
, проходящей через точку 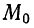 и параллельной вектору
и параллельной вектору 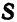 (рис. 36).
(рис. 36).
Определение:
Любой ненулевой вектор 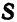 , колийеарный прямой
, колийеарный прямой 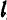 , называется направляющим вектором этой прямой.
, называется направляющим вектором этой прямой.
Положение прямой 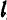 в пространстве вполне определяется заданием точки
в пространстве вполне определяется заданием точки 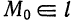 и вектора
и вектора 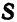 , параллельного прямой
, параллельного прямой 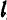 .
.
Возьмем на прямой 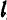 произвольную точку
произвольную точку 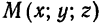 . Ясно, что условие принадлежности точки
. Ясно, что условие принадлежности точки 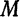 прямой
прямой 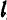 эквивалентно коллинеарности векторов
эквивалентно коллинеарности векторов 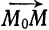 и
и 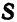 , т. е. пропорциональности их
, т. е. пропорциональности их
соответствующих координат. Следовательно,
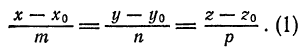
Уравнения (1) называются уравнениями прямой, проходящей через данную точку 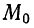 с заданным направляющим вектором
с заданным направляющим вектором 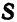
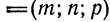 или каноническими уравнениями прямой
или каноническими уравнениями прямой 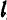
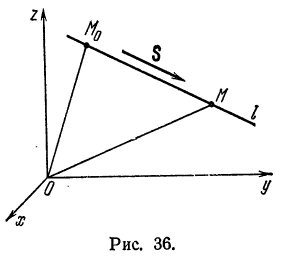
Пример:
Составить уравнения прямой, проходящей через точку 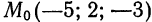 параллельно вектору,
параллельно вектору,
соединяющему точки 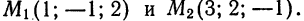
Решение:
За направляющий вектор искомой прямой примем вектор 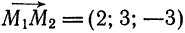 . Заменив в уравнениях (1)
. Заменив в уравнениях (1) 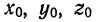 координатами точки
координатами точки 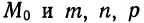 координатами вектора
координатами вектора 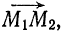 получим искомые уравнения
получим искомые уравнения
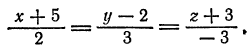
Отметим, что если прямая 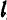 перпендикулярна какой-либо из координатных осей, то соответствующая координата направляющего вектора
перпендикулярна какой-либо из координатных осей, то соответствующая координата направляющего вектора 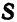 равна нулю. Например, если
равна нулю. Например, если 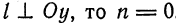 . Однако и в этом случае условимся формально записывать уравнения прямой в каноническом виде:
. Однако и в этом случае условимся формально записывать уравнения прямой в каноническом виде:
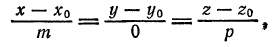
Пример:
Составить уравнения прямой, проходящей через точку 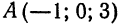 параллельно вектору
параллельно вектору 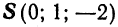 .
.
Решение:
Согласно уравнениям (1) имеем
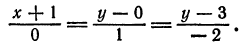
Другие формы уравнений прямой в пространстве
Параметрические уравнения прямой
В предыдущем параграфе мы показали, что точка 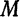 принадлежит прямой
принадлежит прямой 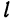 (рис. 36) в том и только в том случае, когда векторы
(рис. 36) в том и только в том случае, когда векторы 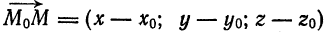 и
и 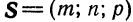 коллинеарны. А для этого необходимо и достаточно, чтобы
коллинеарны. А для этого необходимо и достаточно, чтобы

где 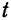 является параметром, принимающим всевозможные действительные значения в зависимости от положения точки на прямой
является параметром, принимающим всевозможные действительные значения в зависимости от положения точки на прямой 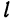 . Записав равенство (1) в координатной форме, получим
. Записав равенство (1) в координатной форме, получим
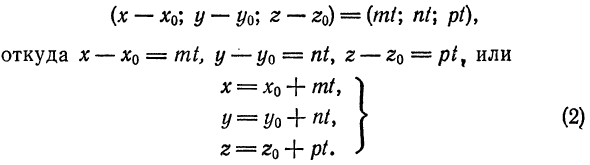
Уравнения (2) называются параметрическими уравнениями прямой.
Пример:
Найти точку пересечения прямой 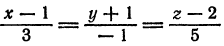 с плоскостью
с плоскостью 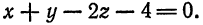
Решение:
Представим данные уравнения прямой в параметрическом виде, для чего перепишем их следующим образом:
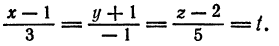
Отсюда
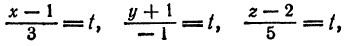
или
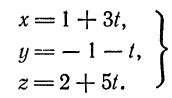
Очевидно, что. для нахождения координат искомой точки нужно решить систему
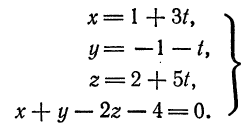
Заменив в последнем уравнении 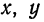 и
и 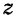 их значениями из первых трех уравнений, найдем
их значениями из первых трех уравнений, найдем
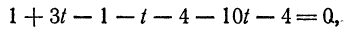
откуда 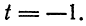 Подставив найденное значение
Подставив найденное значение 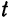 в параметрические уравнения прямой, получим:
в параметрические уравнения прямой, получим: 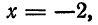
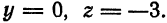 Следовательно, искомая точка имеет координаты (—2; 0; 3).
Следовательно, искомая точка имеет координаты (—2; 0; 3).
Уравнения прямой, проходящей через две данные точки
Пусть требуется найти уравнения прямой 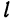 , проходящей через точки
, проходящей через точки 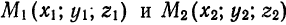 Так как вектор
Так как вектор 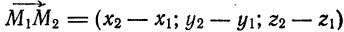 коллинеарен прямой
коллинеарен прямой 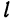 , то можно принять его за направляющий вектор. Искомые уравнения напишем как уравнения прямой, проходящей через точку
, то можно принять его за направляющий вектор. Искомые уравнения напишем как уравнения прямой, проходящей через точку 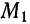 и имеющей
и имеющей
направляющий вектор 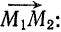
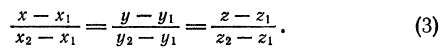
Пример:
Дан треугольник с вершинами 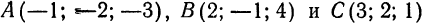 . Составить уравнения медианы
. Составить уравнения медианы 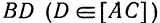 .
.
Решение:
Находим координаты точки 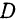 как середины отрезка
как середины отрезка 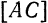 :
:
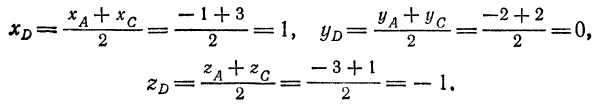
Напишем искомые уравнения как уравнения прямой, проходящей через точки 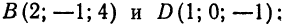
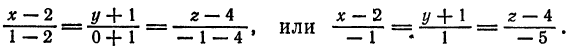
3. Общие уравнения прямой. Рассмотрим систему
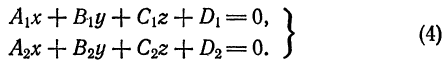
Каждое из уравнений системы (4) в прямоугольной системе координат 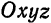 определяет плоскость Если нормальные векторы
определяет плоскость Если нормальные векторы 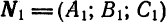 и
и 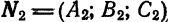 этих плоскостей не коллинеарны (т. е. плоскости не параллельны и не совпадают), то система (4) определяет некоторую прямую
этих плоскостей не коллинеарны (т. е. плоскости не параллельны и не совпадают), то система (4) определяет некоторую прямую 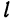 как линию пересечения двух плоскостей. Уравнения (4) называются общими уравнениями прямой.
как линию пересечения двух плоскостей. Уравнения (4) называются общими уравнениями прямой.
Пример:
Привести к каноническому виду общие уравнения прямой
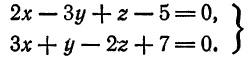
Решение:
Исключив сначала 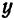 , а затем
, а затем 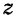 , получим уравнения
, получим уравнения 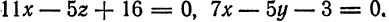 Разрешим каждое из уравнений относительно
Разрешим каждое из уравнений относительно 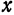
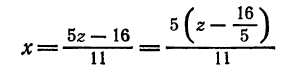
и
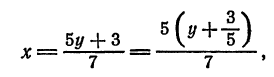
откуда
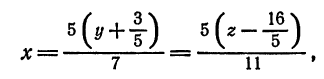
или
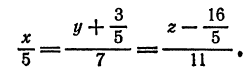
Некоторые задачи на прямую и плоскость в пространстве
Пусть прямая 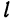 и плоскость
и плоскость 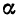 заданы соответственно своими уравнениями
заданы соответственно своими уравнениями
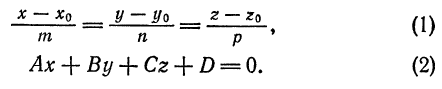
Решая задачи на прямую и плоскость, следует помнить, что для прямой (1) основной характеристикой является направляющий вектор 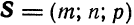 , а для плоскости (2) — нормальный вектор
, а для плоскости (2) — нормальный вектор 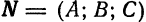 .
.
Мы рассмотрим несколько наиболее часто встречающихся задач на прямую и плоскость в пространстве.
Угол между прямой и плоскостью
Предположим сначала, что прямая 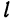 не параллельна плоскости
не параллельна плоскости 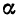 и не перпендикулярна ей.
и не перпендикулярна ей.
Непосредственно из рис. 37
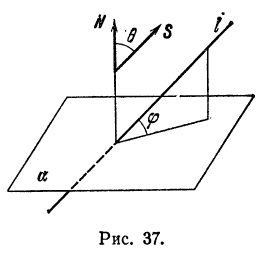
нетрудно заметить, что синус угла 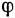 между прямой
между прямой 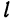 и плоскостью
и плоскостью 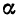 равен косинусу острого угла
равен косинусу острого угла 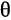 , образованного направляющим вектором
, образованного направляющим вектором 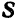 прямой
прямой 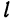 и нормальным вектором
и нормальным вектором 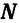 плоскости
плоскости 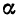 , т. е.
, т. е.
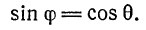
Но
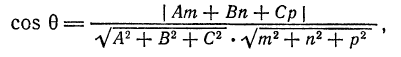
Следовательно
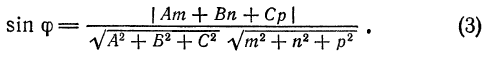
Пример:
Найти угол между прямой
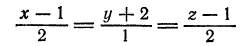
и плоскостью 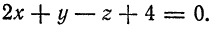
Решение:
Имеем: 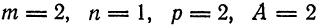
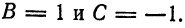 По формуле (3) находим
По формуле (3) находим
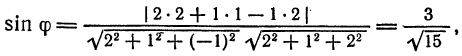
откуда 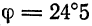 .
.
Условия параллельности прямой и плоскости
Прямая 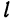 и плоскость
и плоскость 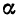 параллельны друг другу в том и только в том случае, когда векторы
параллельны друг другу в том и только в том случае, когда векторы 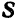 и
и 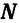 взаимно перпендикулярны. А для этого необходимо и достаточно, чтобы
взаимно перпендикулярны. А для этого необходимо и достаточно, чтобы 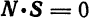 или, в координатной форме,
или, в координатной форме,
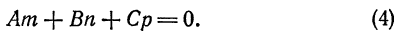
Мы видим, что формула (3) справедлива и в случае 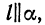 — она дает просто
— она дает просто 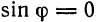 .
.
Пример:
При каком значении 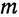 прямая
прямая
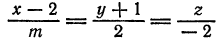
параллельна плоскости 
Решение:
По формуле (4) имеем
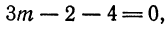
откуда 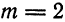 .
.
Условие перпендикулярности прямой и плоскости. Прямая 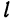 и плоскость
и плоскость 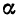 перпендикулярны в том и только в том случае, когда векторы
перпендикулярны в том и только в том случае, когда векторы 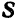 и
и 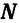 параллельны друг другу. А для этого необходимо и достаточно, чтобы их координаты были пропорциональны, т. е.
параллельны друг другу. А для этого необходимо и достаточно, чтобы их координаты были пропорциональны, т. е.

Из этих условий, в частности, следует, что формула (3) сохраняет смысл и при 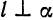 , так как (3) и (5) дают
, так как (3) и (5) дают 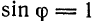 .
.
Пример:
При каких значениях 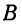 и
и 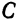 прямая
прямая
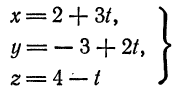
перпендикулярна плоскости 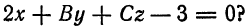
Решение:
Из уравнения прямой имеем 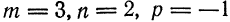 , а из уравнения плоскости
, а из уравнения плоскости 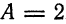 . Подставив эти значения в (5), получаем
. Подставив эти значения в (5), получаем
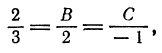
откуда 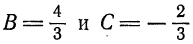
Уравнения прямой и плоскости в пространстве
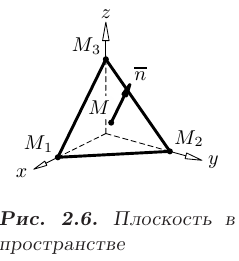
Уравнение плоскости, проходящей через точку пространства 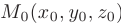 и имеющей нормальный вектор
и имеющей нормальный вектор 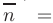
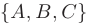 (см. рис. 2.6), записывается в виде
(см. рис. 2.6), записывается в виде
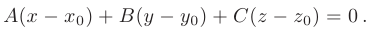
Это уравнение вытекает из условия ортогональности (см. п.2.4.) векторов 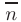 и
и
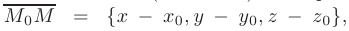
где 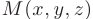 — произвольная точка плоскости.
— произвольная точка плоскости.
Обозначив

получим общее уравнение плоскости в пространстве:
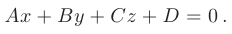
Если прямая параллельна вектору 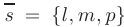 (называемому направляющим вектором) и проходит через точку
(называемому направляющим вектором) и проходит через точку 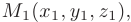 , то ее уравнения из условия коллинеарности векторов
, то ее уравнения из условия коллинеарности векторов 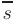 и
и 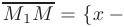
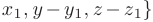 , (где
, (где 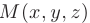 — произвольная точка прямой) примут вид
— произвольная точка прямой) примут вид
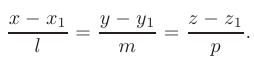
Эти уравнения называются каноническими уравнениями прямой линии в пространстве.
Уравнение прямой, проходящей через две точки пространства
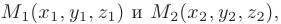
записывается в виде
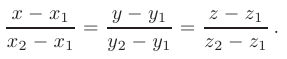
Направляющий вектор этой прямой 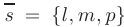 имеет координаты, равные соответственно
имеет координаты, равные соответственно
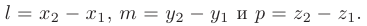
Интерпретируя координаты точек
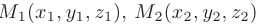
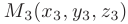
как координаты трех радиус-векторов
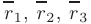
и используя условие компланарности векторов
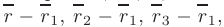
получим запись уравнения плоскости, проходящей через эти точки, в виде определителя третьего порядка
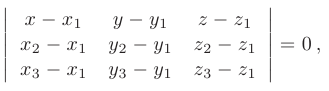
где 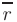 — радиус-вектор текущей точки
— радиус-вектор текущей точки 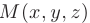 , лежащей в искомой плоскости.
, лежащей в искомой плоскости.
Пример:
Даны координаты вершин пирамиды 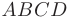 :
:
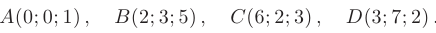
Требуется составить: 1) уравнения прямой 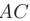 ; 2) уравнение плоскости, проходящей через точки
; 2) уравнение плоскости, проходящей через точки 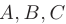 ; 3) канонические уравнения прямой, проходящей через точку
; 3) канонические уравнения прямой, проходящей через точку 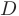 перпендикулярно плоскости
перпендикулярно плоскости 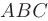 .
.
► 1. Составим уравнения прямой 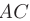 , используя приведенную в п. 2.6 формулу уравнений прямой, проходящей через две заданные точки пространства
, используя приведенную в п. 2.6 формулу уравнений прямой, проходящей через две заданные точки пространства
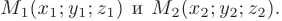
Подставив координаты точек 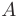 и
и 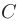 , получаем
, получаем
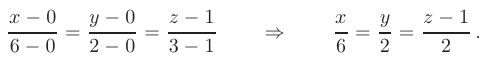
Окончательный вид уравнений прямой 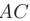 :
:
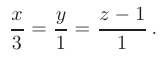
- Составим уравнение грани
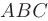 , используя формулу уравнения плоскости, проходящей через три заданные точки пространства
, используя формулу уравнения плоскости, проходящей через три заданные точки пространства
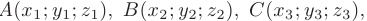
- приведенную в п. 2.6. Подставляя координаты точек
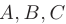 получаем
получаем
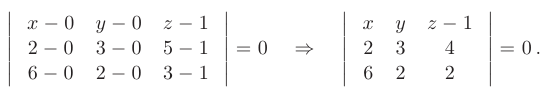
Раскладывая последний определитель по первой строке, выводим искомое уравнение плоскости, проходящей через три заданные точки пространства 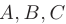 :
:
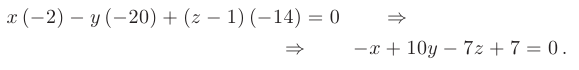
- В качестве направляющего вектора
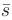 искомой прямой возьмем нормальный вектор плоскости
искомой прямой возьмем нормальный вектор плоскости 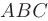 , т.е.
, т.е. 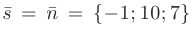 . Тогда уравнения искомой прямой согласно формуле канонических уравнений прямой, приведенной в п. 2.6 будут иметь вид
. Тогда уравнения искомой прямой согласно формуле канонических уравнений прямой, приведенной в п. 2.6 будут иметь вид
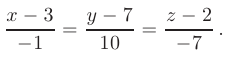
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
| Линейные операции над векторами в координатной форме в математике |
| Уравнение прямой на плоскости в математике |
| Уравнения линий второго порядка на плоскости в математике |
| Эллипс в математике |
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

