Оглавление:
Высшая алгебра — это раздел математики, изучающий алгебраические системы (также иногда называемые алгебраическими структурами), такие как группы, кольца, поля, модули, решётки, а также отображения между такими структурами.
Матрицы
Определение матрицы: Пусть даны прямоугольная система координат Oxyz и точка М с координатами 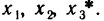 Рассмотрим радиус-вектор
Рассмотрим радиус-вектор 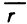 точки М:
точки М: 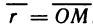 . Обозначим через
. Обозначим через 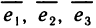 единичные базисные векторы; тогда вектор
единичные базисные векторы; тогда вектор 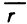 в данной системе координат запишется так:
в данной системе координат запишется так: 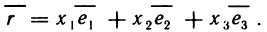
Преобразуем данную систему координат поворотом ее вокруг начала координат О и будем считать известными углы, которые образует каждая ось новой системы координат Ox’y’z’ с каждой осью старой. Обозначим через 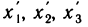 координаты точки М в новой системе координат, а через
координаты точки М в новой системе координат, а через 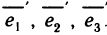 . единичные базисные векторы новых осей. Тогда вектор
. единичные базисные векторы новых осей. Тогда вектор 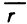 в новой системе координат запишется в виде
в новой системе координат запишется в виде 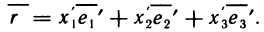
Приравнивая выражения для вектора 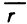 , получаем векторное равенство
, получаем векторное равенство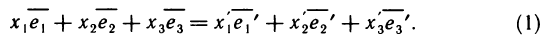
Рассмотрим преобразование координат точки М при повороте системы координат. Разложим векторы 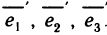 по старому базису:
по старому базису: 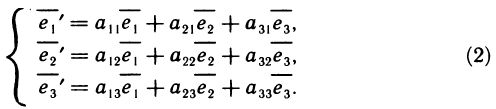
* — В этом параграфе координаты точки М обозначаются через 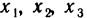 (вместо х, у, z).
(вместо х, у, z).
Каждый из векторов 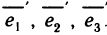 является единичным, поэтому для каждого из них коэффициентами разложения служат направляющие косинусы, т. е.
является единичным, поэтому для каждого из них коэффициентами разложения служат направляющие косинусы, т. е.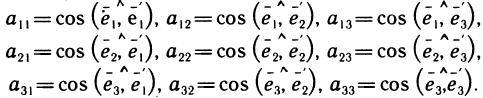
Заменяя в равенстве (1) векторы 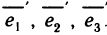 их разложениями (2) и группируя подобные члены, получаем
их разложениями (2) и группируя подобные члены, получаем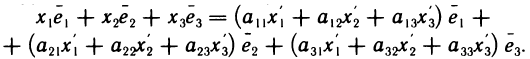
Отсюда, приравнивая коэффициенты при одинаковых базисных векторах, находим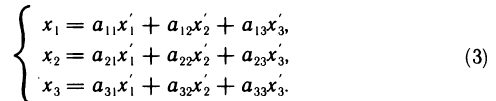
Следовательно, координаты 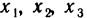 представляют собой линейные комбинации координат
представляют собой линейные комбинации координат 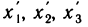 полностью определяемые совокупностью коэффициентов
полностью определяемые совокупностью коэффициентов 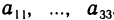 . Таким образом, мы пришли к понятию матрицы.
. Таким образом, мы пришли к понятию матрицы.
Определение:
Таблица, составленная из коэффициентов (3), записанная в виде 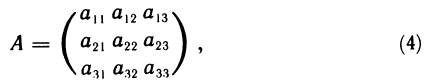
называется матрицей данного преобразования. Коротко матрицу обозначают так: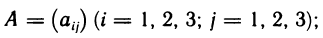
где 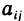 — элементы данной матрицы.
— элементы данной матрицы.
Элементы матрицы образуют столбцы и строки. Первый индекс (i) указывает номер строки, а второй (j) — номер столбца, на пересечении которых стоит элемент 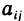 . Матрица (4) имеет три строки и три столбца.
. Матрица (4) имеет три строки и три столбца.
В высшей алгебре рассматриваются матрицы с любым числом строк и столбцов. Поэтому в общем виде матрица записывается следующим образом: 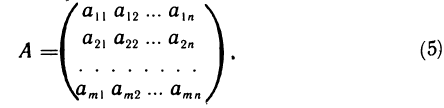
Если в матрице число строк равно числу столбцов (m=n), то матрица называется квадратной n-го порядка, а в противном случае — прямоугольной. Так , матрица (4) квадратная, третьего порядка. В матрице (5) m строк и n столбцов. Если m=1, b>1, то получаем однострочечную матрицу 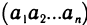 , которая называется вектор-строкой. Если же m>l, а n=1, то получаем одностолбцовую матрицу
, которая называется вектор-строкой. Если же m>l, а n=1, то получаем одностолбцовую матрицу 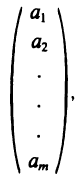
которая называется вектор-столбцом.
Две матрицы 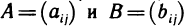 равны, если равны элементы, стоящие на одинаковых местах, т. е. если
равны, если равны элементы, стоящие на одинаковых местах, т. е. если 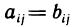 при всех i и j (при этом число строк (и аналогично столбцов) матриц A и В должно быть одинаковым).
при всех i и j (при этом число строк (и аналогично столбцов) матриц A и В должно быть одинаковым).
Свойства матриц
Матрицы подобно векторам можно складывать, умножать на число и друг на друга. Рассмотрим эти операции.
1°. Суммой двух матриц 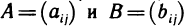 с одинаковым количеством m строк и n столбцов называется матрица
с одинаковым количеством m строк и n столбцов называется матрица 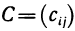 , элементы которой определяются равенством
, элементы которой определяются равенством 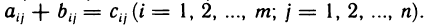 ,
,
Обозначение: А+В=С.
Пример 1. 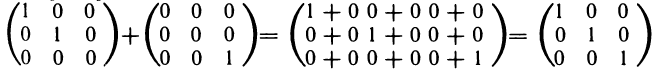
Аналогично определяется разность двух матриц.
2°. Произведением матрицы 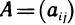 на число к называется матрица, у которой каждый элемент равен произведению соответствующего элемента матрицы А на число
на число к называется матрица, у которой каждый элемент равен произведению соответствующего элемента матрицы А на число 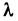 :
: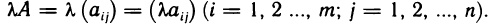
Пример:
3°. Произведением матрицы 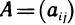 , имеющей m строк и k столбцов, на матрицу
, имеющей m строк и k столбцов, на матрицу 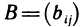 , имеющую k строк и п столбцов, называется матрица
, имеющую k строк и п столбцов, называется матрица 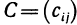 , имеющая m строк и n столбцов, У которой элемент
, имеющая m строк и n столбцов, У которой элемент 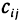 равен сумме произведений элементов i-й строки матрицы А и j-го столбца матрицы В, т. е.
равен сумме произведений элементов i-й строки матрицы А и j-го столбца матрицы В, т. е. 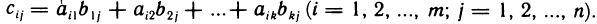
При этом число k столбцов матрицы А должно быть равно числу строк матрицы В. В противном случае произведение не определено. Произведение обозначается так: 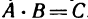 .
.
Пример: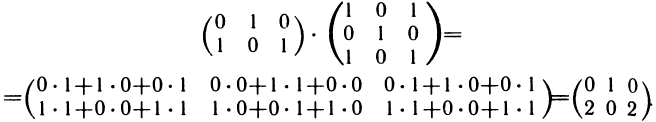
Пример 4. Пусть 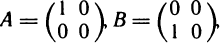 тогда
тогда 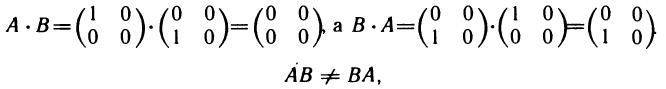 т. е. умножение матриц не обладает перестановочным свойством.
т. е. умножение матриц не обладает перестановочным свойством.
Замечание. Правило умножения легко запомнить, если сформулировать его в следующем виде: элемент 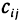 матрицы С, стоящей на пересечении i-й строки и j-го столбца, есть скалярное произведение i-й вектор-строки матрицы А и j-го вектор-столбца матрицы В.
матрицы С, стоящей на пересечении i-й строки и j-го столбца, есть скалярное произведение i-й вектор-строки матрицы А и j-го вектор-столбца матрицы В.
Непосредственной проверкой можно убедиться, что для суммы и произведения матриц справедливы следующие соотношения: 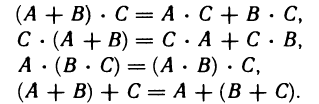
4°. Умножение на единичную матрицу. Совокупность элементов 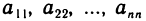 квадратной матрицы
квадратной матрицы 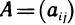 называется главной диагональю матрицы. Матрица, у которой элементы, стоящие на главной диагонали, равны единице, а все остальные элементы равны нулю, называется единичной матрицей и обозначается буквой Е.
называется главной диагональю матрицы. Матрица, у которой элементы, стоящие на главной диагонали, равны единице, а все остальные элементы равны нулю, называется единичной матрицей и обозначается буквой Е.
Так, единичной матрицей третьего порядка является матрица 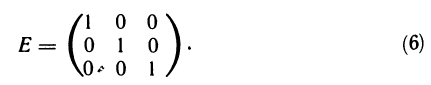
Единичная матрица обладает замечательным свойством, а именно: умножение квадратной матрицы любого порядка на соответствующую единичную матрицу не меняет матрицу. Это свойство и объясняет ее название «единичная»: при умножении матриц она обладает таким же свойством, как число 1 при умножении чисел.
Пример:
Пусть 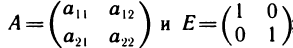 тогда согласно
тогда согласно
правилу умножения матриц имеем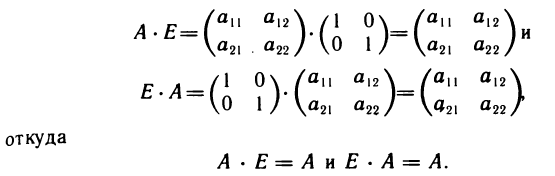
Заметим, что единичной матрице (6) соответствует следующее преобразование координат точки: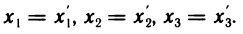
Такое преобразование называется тождественным. С понятием матрицы тесно связано понятие определителя.
Определители
Определение определителя: Пусть дана квадратная матрица третьего порядка, элементы которой для удобства обозначим через 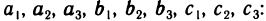

Определение:
Определителем третьего порядка, соответствующим матрице (1), называется число, обозначаемое символом 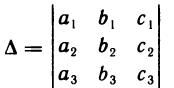
и определяемое равенством 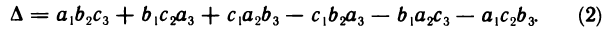
Числа 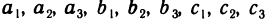 называются элементами определителя. Диагональ, образованная элементами
называются элементами определителя. Диагональ, образованная элементами 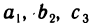 , называется главной, а диагональ, образованная элементами
, называется главной, а диагональ, образованная элементами 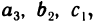 — побочной.
— побочной.
Чтобы запомнить, какие произведения в правой части равенства (2) берутся со знаком «+», а какие со знаком «—», полезно
использовать следующее правило треугольников: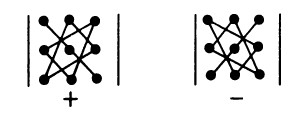
Это правило позволяет легко записать формулу (2) и вычислить данный определитель. Например, 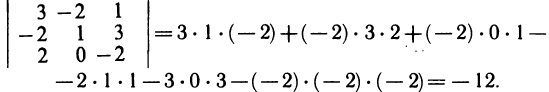
Свойства определителей
Сформулируем и докажем эти свойства для определителей третьего порядка, хотя они присущи и определителям любого порядка.
1°. Величина определителя не изменится, столбцы поменять местами, т. е. 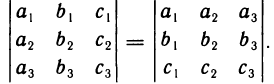
Для доказательства свойства достаточно применить к определителям, стоящим в левой и правой частях равенства, формулу (2) и убедиться в равенстве полученных выражений.
Свойство 1° устанавливает равноправность строк и столбцов определителя. Поэтому все дальнейшие свойства определителя будем формулировать и для строк, и для столбцов, а доказывать только для строк или только для столбцов.
2°. Перестановка двух столбцов или двух строк определителя равносильна умножению его на — 1. Например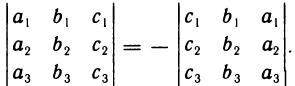
Это свойство доказывается аналогично предыдущему.
3°. Если определитель имеет два одинаковых столбца или две одинаковые строки, то он равен нулю.
В самом деле, при перестановке двух одинаковых столбцов определитель  не изменится, а согласно свойству 2 его знак изменится. Следовательно,
не изменится, а согласно свойству 2 его знак изменится. Следовательно, 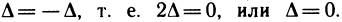 Например,
Например, 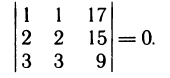
4°. Умножение всех элементов одного столбца или одной строки определителя на любое число 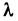 равносильно умножению определителя на это число
равносильно умножению определителя на это число 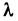 . Например,
. Например,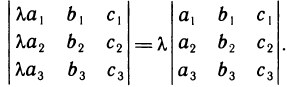
Для доказательства этого свойства достаточно заметить, что по формуле (2) определитель выражается в виде суммы, каждый член которой содержит множителем один элемент из каждой строки и из каждого столбца.
5°. Если все элементы некоторого столбца или некоторой строки определителя равны нулю, то и сам определитель равен нулю. Это свойство вытекает из предыдущего свойства (при 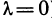 ).
).
6°. Если элементы двух столбцов или двух строк определителя пропорциональны, то определитель равен нулю.
Действительно, если элементы двух столбцов определителя пропорциональны, то согласно свойству 4° общий множитель элементов этих столбцов можно вынести за знак определителя, в результате остается определитель с двумя одинаковыми столбцами, равный нулю согласно свойству 3°. Например, 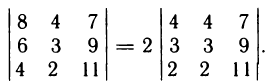
7°. Если каждый элемент n-го столбца (n-й строки) определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, из которых один в n-м столбце (n-й строке) имеет первые из упомянутых слагаемых, а другой — вторые; элементы, стоящие на остальных местах, у всех трех определителей одни и те же. Например,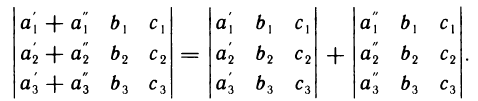
Для доказательства этого свойства достаточно применить к определителям, стоящим в левой и правой частях равенства, формулу (2) и убедиться в равенстве полученных выражений.
8°. Если к элементам некоторого столбца (строки) определителя прибавить соответствующие элементы другого столбца (строки), умноженные на любой общий множитель X, то величина определителя не изменится.
В самом деле, полученный в результате такого прибавления определитель согласно свойству 7° можно разбить на сумму двух определителей, первый из которых совпадает с исходным, а второй имеет два пропорциональных столбца и в силу свойства 6° равен нулю. Например, 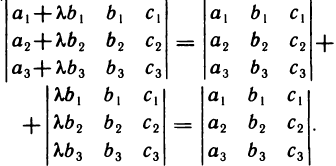
Для формулировки следующего свойства определителя познакомимся с понятиями алгебраического дополнения и минора. Минором некоторого элемента определителя называется определитель, получаемый из данного определителя вычеркиванием строки и столбца, на пересечении которых расположен этот элемент.
Например, минором элемента 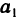 определителя
определителя  является определитель второго порядка
является определитель второго порядка 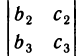 , минором элемента
, минором элемента 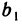 — определитель второго порядка
— определитель второго порядка 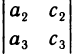 и т. д.
и т. д.
Алгебраическим дополнением некоторого элемента определителя называется минор этого элемента, умноженный на 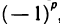 , где р — сумма номеров строки и столбца, на пересечении которых расположен этот элемент. Алгебраическое дополнение элемента обозначается такой же прописной буквой, что и сам элемент. Так, алгебраическое дополнение элемента
, где р — сумма номеров строки и столбца, на пересечении которых расположен этот элемент. Алгебраическое дополнение элемента обозначается такой же прописной буквой, что и сам элемент. Так, алгебраическое дополнение элемента 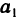 обозначается через
обозначается через 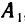 элемента
элемента  — через
— через  и т. д.
и т. д.
Если, например, элемент 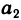 находится на пересечении первого столбца и второй строки, то для него р=1+2=3 и алгебраическим дополнением является
находится на пересечении первого столбца и второй строки, то для него р=1+2=3 и алгебраическим дополнением является 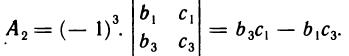
Таким образом, алгебраическое дополнение и минор одного и того же элемента отличаются только знаком.
9°. Определитель равен сумме произведений элементов какого-нибудь столбца или строки на их алгебраические дополнения.
Иначе говоря, имеют место следующие равенства: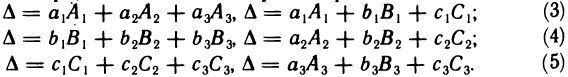
Чтобы доказать, например, первое из этих равенств, достаточно записать правую часть формулы (2) в виде 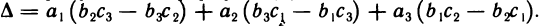
Величины, стоящие в скобках, являются алгебраическими дополнениями элементов 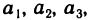 т. е.
т. е. 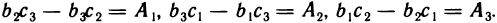
Отсюда и из предыдущего равенства получаем 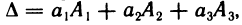
что и требовалось доказать. Равенства (3) — (5) доказываются аналогично.
Запись определителя по какой-нибудь из формул (3) — (5) называется разложением его по элементам некоторого столбца или некоторой строки (первая формула дает разложение по элементам первого столбца и т. д.).
Пример:
Вычислить определитель 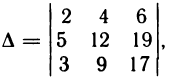
разлагая его по элементам первой строки.
Решение. Имеем 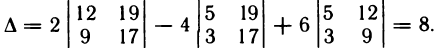
10°. Сумма произведений элементов какого-нибудь столбца или какой-нибудь строки определителя на алгебраические дополнения соответствующих элементов другого столбца или другой строки равна нулю.
Докажем, например, что сумма произведений элементов второго столбца на соответствующие алгебраические дополнения элементов первого столбца равна нулю. Для этого разложим определитель (1) по элементам первого столбца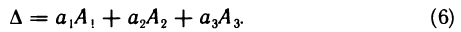
Алгебраические дополнения 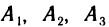 не зависят от самих элементов
не зависят от самих элементов 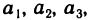 . Поэтому, если в обеих частях равенства (6) числа
. Поэтому, если в обеих частях равенства (6) числа 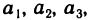 заменить произвольными числами
заменить произвольными числами 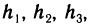 то получим верное равенство
то получим верное равенство 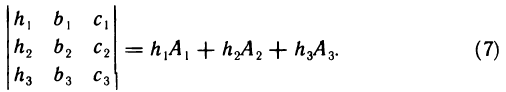
Если теперь в равенстве (7) в качестве 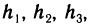 взять элементы
взять элементы 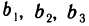 второго столбца и учесть, что согласно свойству 3° определитель с двумя одинаковыми столбцами равен нулю, то получим
второго столбца и учесть, что согласно свойству 3° определитель с двумя одинаковыми столбцами равен нулю, то получим 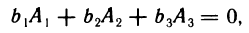
что и требовалось доказать.
Аналогично доказываются равенства 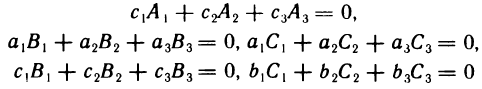
и шесть подобных равенств, относящихся не к столбцам, а к строкам: 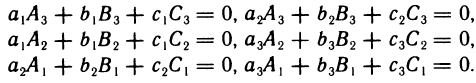
Исследование системы трех уравнений первой степени с тремя неизвестными
Теория матриц и определителей имеет широкое применение как в самой математике, так и в ее приложениях. Это очень удобный и часто используемый в самых разнообразных исследованиях математический аппарат.
Рассмотрим применение матриц и определителей к исследованию системы трех уравнений первой степени с тремя неизвестными х, у, z: 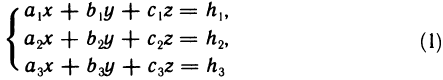
(коэффициенты 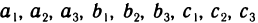 и свободные члены
и свободные члены 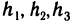 считаются заданными).
считаются заданными).
Тройка чисел 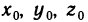 называется решением системы (1), если в результате подстановки этих чисел вместо х, у, z все три уравнения (1) обращаются в тождества.
называется решением системы (1), если в результате подстановки этих чисел вместо х, у, z все три уравнения (1) обращаются в тождества.
В дальнейшем основную роль будут играть следующие четыре определителя: 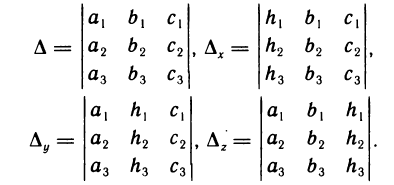
Определитель  называется определителем системы (1). Определители
называется определителем системы (1). Определители 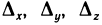 получаются из определителя системы
получаются из определителя системы  заменой свободными членами элементов соответственно первого, второго и третьего столбцов.
заменой свободными членами элементов соответственно первого, второго и третьего столбцов.
Рассмотрим отдельно два случая: когда определитель  системы отличен от нуля и когда этот определитель равен нулю.
системы отличен от нуля и когда этот определитель равен нулю.
Случай 1. 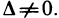 Докажем, что решение системы (1) существует и единственно. Для этого умножим обе части первого уравнения системы (1) на алгебраическое дополнение
Докажем, что решение системы (1) существует и единственно. Для этого умножим обе части первого уравнения системы (1) на алгебраическое дополнение 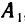 , второго— на
, второго— на 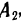 , третьего — на
, третьего — на 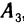 , а затем сложим эти уравнения. В результате получим
, а затем сложим эти уравнения. В результате получим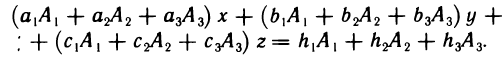
Отсюда на основании 9° и 10° свойств определителей имеем 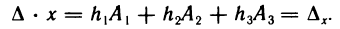
Аналогично найдем 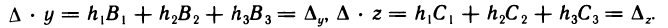
Таким образом, из системы (1) получена система уравнений 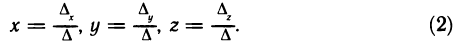
Формулы (2) называются формулами Крамера.
Чтобы доказать, что решение системы (1) существует, подставим вместо х, у, z значения, определяемые формулами Крамера, и убедимся, что все три уравнения (1) обращаются при этом в тождества. Проверим, например, что первое уравнение обращается в тождество. Имеем 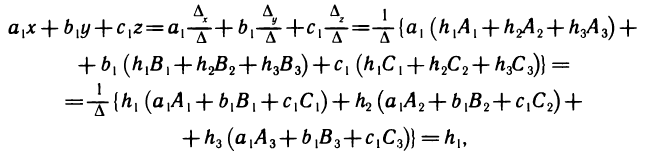 так как согласно свойству 9° определителей
так как согласно свойству 9° определителей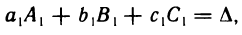
а согласно свойству 10°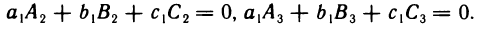
Итак, установлено, что первое уравнение системы (1) обращается в тождество. Аналогично можно показать, что в тождество обращаются второе и третье уравнения системы.
Таким образом, решение системы (1) существует. Формулы Крамера (2) доказывают также единственность решения системы (1), так как система (2) — следствие системы (1), и поэтому всякое решение системы (1) является решением и системы (2), т. е. выражается по формулам Крамера.
Все изложенное позволяет, сделать следующий вывод: если определитель  системы (1) отличен от нуля, то существует, и притом единственное, решение этой системы, и оно выражается формулами Крамера.
системы (1) отличен от нуля, то существует, и притом единственное, решение этой системы, и оно выражается формулами Крамера.
Пример:
Найти все решения системы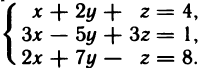
Решение:
Так как 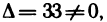 то данная система имеет единственное решение, определяемое формулами (2):
то данная система имеет единственное решение, определяемое формулами (2):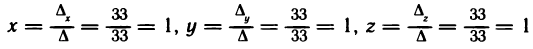
Следовательно, х=1, у=1, z=1— решение данной системы.
Случай 2. 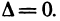 Пусть хотя бы один из определителей
Пусть хотя бы один из определителей 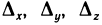 отличен от нуля. Тогда хотя бы одно из равенств (2) невозможно, т. е. система (2) не имеет решений, и поэтому не имеет решений и система (1), так как система (2)—следствие системы (1).
отличен от нуля. Тогда хотя бы одно из равенств (2) невозможно, т. е. система (2) не имеет решений, и поэтому не имеет решений и система (1), так как система (2)—следствие системы (1).
Пусть теперь 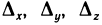 равны нулю. Сначала исследуем однородные системы.
равны нулю. Сначала исследуем однородные системы.
Однородной системой трех уравнений первой степени с тремя неизвестными называется система вида 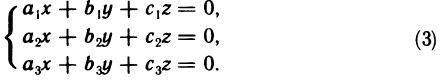
Очевидно, что эта система всегда имеет нулевое решение: х=0, у=0, z=0. Если 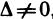 , то это решение является единственным (в силу случая 1).
, то это решение является единственным (в силу случая 1).
Покажем, что если определитель 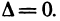 То система (3) имеет бесконечно много ненулевых решений. Доказательство проведем в два этапа.
То система (3) имеет бесконечно много ненулевых решений. Доказательство проведем в два этапа.
1) Предположим, что хотя бы один из миноров определителя  отличен от нуля. Пусть, например,
отличен от нуля. Пусть, например, 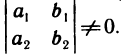 . Тогда однородную систему, составленную из двух первых уравнений (3), можно представить в виде
. Тогда однородную систему, составленную из двух первых уравнений (3), можно представить в виде 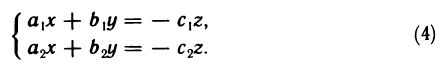
Рассмотрим алгебраические дополнения 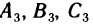 элементов третьей строки определителя:
элементов третьей строки определителя: 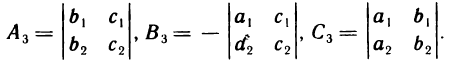
Так как, по условию, 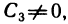 то для каждого z существует единственное решение системы (4). Его можно записать в виде
то для каждого z существует единственное решение системы (4). Его можно записать в виде 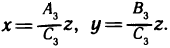 Положим
Положим 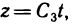 где t может принимать любые значения. Тогда очевидно, что однородная система (4) имеет бесконечно много решений, определяемых формулами
где t может принимать любые значения. Тогда очевидно, что однородная система (4) имеет бесконечно много решений, определяемых формулами 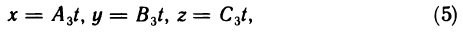
где t — произвольное число.
Осталось показать, что х, у и z, определяемые формулами (5), обращают в тождество и третье уравнение однородной системы (3). В самом деле, подставляя выражения для х, у, z по формулам (5) в левую часть третьего уравнения, находим 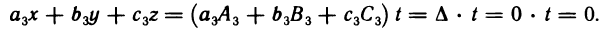
Таким образом, формулы (5) при любом t определяют решение однородной системы (3).
2) Предположим теперь, что все миноры определителя А равны нулю. Это значит, что коэффициенты всех трех уравнений (3) пропорциональны. Но тогда второе и третье уравнения (3) являются следствием первого и могут быть отброшены, а одно уравнение с тремя неизвестными 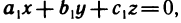 очевидно, имеет бесконечно много решений (двум неизвестным можно придавать произвольные значения, а третье неизвестное определять из уравнения).
очевидно, имеет бесконечно много решений (двум неизвестным можно придавать произвольные значения, а третье неизвестное определять из уравнения).
Итак, доказано, что однородная система (3) с определителем А, равным нулю, имеет бесконечно много решений.
Теперь рассмотрим систему (1), когда все четыре определителя 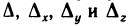 равны нулю. Докажем, что если в этом случае система (1) имеет хотя бы одно решение, то она имеет бесконечно много решений.
равны нулю. Докажем, что если в этом случае система (1) имеет хотя бы одно решение, то она имеет бесконечно много решений.
Пусть система (1) имеет решение 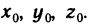 Тогда справедливы тождества
Тогда справедливы тождества
Вычитая почленно из уравнений (1) тождества (6), получаем систему уравнений, эквивалентную (1): 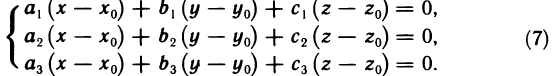
Это однородная система грех уравнений первой степени с неизвестными 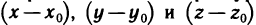 и определителем
и определителем  , равным нулю. Но согласно только что доказанному эта система имеет бесконечно много решений, следовательно, и система (1) имеет бесконечно много решений. Например, в случае, когда отличен от нуля минор
, равным нулю. Но согласно только что доказанному эта система имеет бесконечно много решений, следовательно, и система (1) имеет бесконечно много решений. Например, в случае, когда отличен от нуля минор 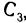 , в силу формул (5) решение системы (1) можно представить в виде
, в силу формул (5) решение системы (1) можно представить в виде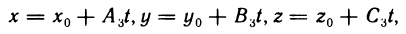
где t принимает любые значения. Тем самым утверждение доказано и можно сделать следующее заключение: если 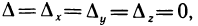 то система (1) либо совсем, не имеет решений, либо их бесконечно много.
то система (1) либо совсем, не имеет решений, либо их бесконечно много.
В качестве примера предлагаем самостоятельно рассмотреть следующие три системы: 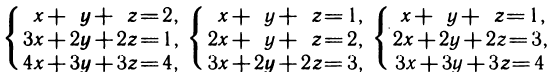
и убедиться в том, что первая из них не имеет решений 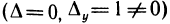 , вторая имеет бесконечно много решений
, вторая имеет бесконечно много решений 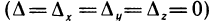 , определяемых формулами х= 1, y=t, z= —t, а третья не имеет решений
, определяемых формулами х= 1, y=t, z= —t, а третья не имеет решений 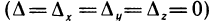 , но уже первые два уравнения этой системы не совместны, так как если умножить первое из них на 2 и вычесть из второго, то получим невозможное равенство 0=1.
, но уже первые два уравнения этой системы не совместны, так как если умножить первое из них на 2 и вычесть из второго, то получим невозможное равенство 0=1.
Матричная запись системы линейных уравнений. Понятие обратной матрицы
Рассмотрим снова систему уравнений (1) из § 3: 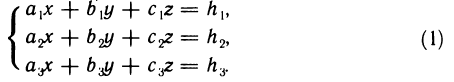
Введем следующие обозначения: 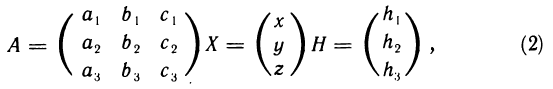
Тогда, используя правило умножения матриц, систему (1) можно записать в эквивалентном матричном виде 
где А — заданная матрица; Н — заданный вектор-столбец; X — неизвестный вектор-столбец. Решением уравнения (3) является такой вектор-столбец X, который обращает уравнение (3) в тождество.
Пусть определитель  матрицы А отличен от нуля. Тогда, как установлено в § 3,система (1) и, следовательно, система (3) имеют единственное решение, которое находится по формулам Крамера. Дадим теперь другую форму записи решения уравнения (3). Для этого введем понятие обратной матрицы.
матрицы А отличен от нуля. Тогда, как установлено в § 3,система (1) и, следовательно, система (3) имеют единственное решение, которое находится по формулам Крамера. Дадим теперь другую форму записи решения уравнения (3). Для этого введем понятие обратной матрицы.
Обратной для матрицы А называется такая матрица (обозначение 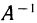 ), которая удовлетворяет условиям
), которая удовлетворяет условиям 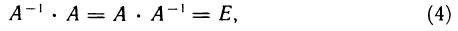
где Е — единичная матрица.
Докажем, что если определитель 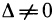 , то обратной для матрицы А является следующая матрица:
, то обратной для матрицы А является следующая матрица: 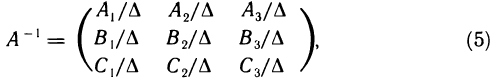
где, как и ранее, 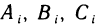 — алгебраические дополнения соответственно элементов
— алгебраические дополнения соответственно элементов 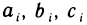 (i = 1, 2, 3). Для этого нужно доказать, что матрица (5) удовлетворяет условиям (4). Проверим, например, справедливость равенства
(i = 1, 2, 3). Для этого нужно доказать, что матрица (5) удовлетворяет условиям (4). Проверим, например, справедливость равенства 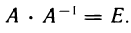
Умножая матрицу А на матрицу 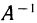 по правилу умножения матриц, получаем
по правилу умножения матриц, получаем 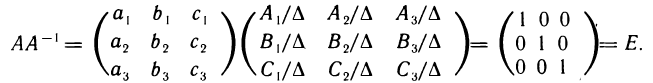
Здесь использован тот факт, что в силу свойств 9° и 10° определителя имеют место равенства 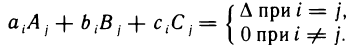
Поэтому, в частности, элемент матрицы 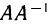 , стоящий на пересечении первой строки и первого столбца, равен
, стоящий на пересечении первой строки и первого столбца, равен 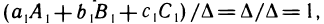 а элемент, стоящий на пересечении первой строки и второго столбца, равен
а элемент, стоящий на пересечении первой строки и второго столбца, равен 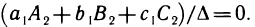
Можно убедиться в том, что и остальные элементы матрицы 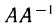 равны соответствующим элементам матрицы Е. Итак,
равны соответствующим элементам матрицы Е. Итак, 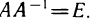 Аналогично можно доказать, что
Аналогично можно доказать, что 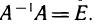
Таким образом, обратной для матрицы A является матрица 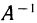 , определяемая формулой (5). Из равенств (4) следует, что матрица А — обратная для матрицы
, определяемая формулой (5). Из равенств (4) следует, что матрица А — обратная для матрицы 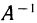 . Поэтому матрицы
. Поэтому матрицы 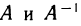 называются взаимнообратными.
называются взаимнообратными.
Замечание:
Если определитель матрицы A равен нулю (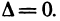 ), то обратная матрица не существует.
), то обратная матрица не существует.
Воспользуемся обратной матрицей для решения уравнения (3). Умножая уравнение (3) слева на матрицу 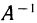 , получаем
, получаем
Так как 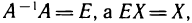 то из (6) следует равенство
то из (6) следует равенство 
Нетрудно убедиться в том, что выражение, полученное для X, действительно является решением уравнения (3). В самом деле, подставляя это выражение в уравнение (3), имеем 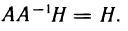
Это равенство является тождеством, так как 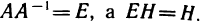
Итак, если 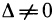 , то решение уравнения (3), значит и системы (1), можно записать в матричном виде (7). Это решение, конечно, то же самое, что было получено в § 3 по формулам Крамера. Этот факт, вытекающий из единственности решения системы (1) при
, то решение уравнения (3), значит и системы (1), можно записать в матричном виде (7). Это решение, конечно, то же самое, что было получено в § 3 по формулам Крамера. Этот факт, вытекающий из единственности решения системы (1) при 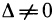 , можно непосредственно проверить, если подставить в формулу (7) выражение (5) для
, можно непосредственно проверить, если подставить в формулу (7) выражение (5) для 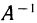 и выражения (2) для X и H. Тогда
и выражения (2) для X и H. Тогда 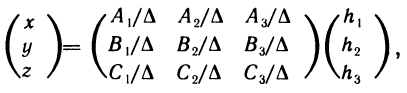
откуда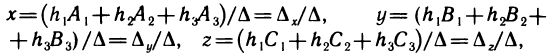 т. е. получили формулы Крамера.
т. е. получили формулы Крамера.
Пример:
Решить систему уравнений 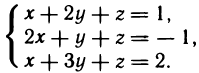
Решение:
Имеем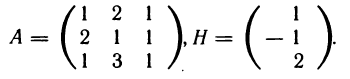
Определитель матрицы А равен 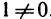 . Следовательно, матрица А имеет обратную. По формуле (5) находим
. Следовательно, матрица А имеет обратную. По формуле (5) находим 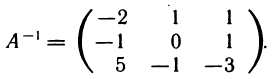
Используя матрицу 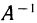 , по формуле (7) получаем
, по формуле (7) получаем 
откуда х=—1, у=1, z=0.
В заключение заметим, что при исследовании систем уравнений первой степени со многими неизвестными и во многих других задачах математики и ее приложений приходится иметь дело с матрицами и определителями произвольного n-го порядка (n = 2, 3, 4, 5, …). Теория матриц и определителей произвольного порядка строится аналогично изложенной теории матриц и определителей третьего порядка. Однако строгое ее построение требует введения дополнительных понятий и доказательства ряда сложных теорем. Желающие расширить и углубить свои знания могут познакомиться с этой теорией и с теорией систем уравнений первой степени со многими неизвестными по любому курсу высшей алгебры.
Высшая алгебра — решение заданий и задач по всем темам с вычислением
Понятие комплексного числа
1°. Комплексные числа появились из необходимости решить любое квадратное уравнение, в частности, уравнение 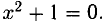
Обозначим через i символ, квадрат которого равен — 1, т. е.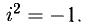 Тогда
Тогда 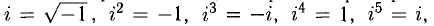 и т.д. Символ
и т.д. Символ 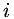 называется мнимой единицей. Введение мнимой единицы позволяет решать уравнения, которые раньше были неразрешимы, в частности квадратные уравнения с отрицательным дискриминантом.
называется мнимой единицей. Введение мнимой единицы позволяет решать уравнения, которые раньше были неразрешимы, в частности квадратные уравнения с отрицательным дискриминантом.
Например, если  если
если 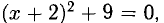 то
то 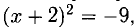 а тогда х + 2 = ±3i, или х =-2 ± Зi.
а тогда х + 2 = ±3i, или х =-2 ± Зi.
2°. Числа вида z = а + bi, где a и b — действительные числа, а 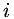 — мнимая единица, называются комплексными числами. При этом а называется действительной частью z (пишут a = Re z), a bi — мнимой частью z, b — коэффициент при мнимой единице
— мнимая единица, называются комплексными числами. При этом а называется действительной частью z (пишут a = Re z), a bi — мнимой частью z, b — коэффициент при мнимой единице 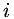 (пишут b = Im z).
(пишут b = Im z).
Числа 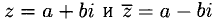 называются взаимно сопряженными. Число
называются взаимно сопряженными. Число 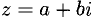 равно нулю, если а = 0 и b = 0.
равно нулю, если а = 0 и b = 0.
Два числа 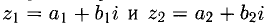 называются равными, (т.е.
называются равными, (т.е. 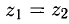 ) если
) если 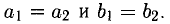
Геометрическое представление комплексных чисел. Тригонометрическая и показательная формы комплексного числа
1°. Число 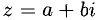 можно изобразить точкой на плоскости
можно изобразить точкой на плоскости 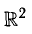 координатами (а, b). При этом действительные числа z = а (для них b = 0) лежат на оси Ох, а мнимые числа z = bi (для них а = 0) лежат на оси Оу.
координатами (а, b). При этом действительные числа z = а (для них b = 0) лежат на оси Ох, а мнимые числа z = bi (для них а = 0) лежат на оси Оу.
Поэтому ось Ох называется действительной осью, а Оу — мнимой осью. Числу z = 0 соответствует начало координат O(0,0).
2°. Положение точки (а, b) можно задать также при помощи полярных координат 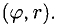 При этом
При этом 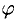 называется аргументом числа z и обозначается arg z, а r — модулем числа r и обозначается r= |z| (рис. 6.1).
называется аргументом числа z и обозначается arg z, а r — модулем числа r и обозначается r= |z| (рис. 6.1).
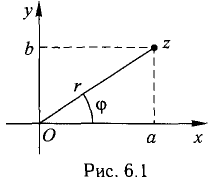
Имеют место формулы
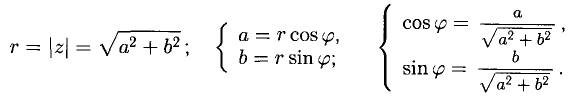
При этом если 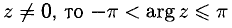 (иногда удобно считать, что
(иногда удобно считать, что 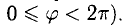
Примечание. Для числа z = 0 величина arg z не определена. Это равносильно тому, что числу z = 0 может соответствовать бесконечное множество аргументов, т. е. 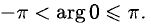
3°. Приведенные формулы позволяют записывать алгебраическое комплексное число 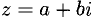 в тригонометрической форме:
в тригонометрической форме:
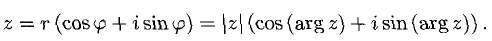
4°. Приняты обозначения (это формулы Эйлера)
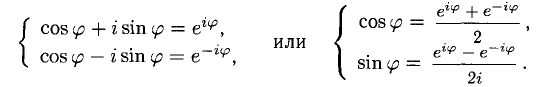
Тогда запись 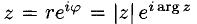 называется показательной формой комплексного числа.
называется показательной формой комплексного числа.
Например, для алгебраического числа z = — 3 + 4i имеем:
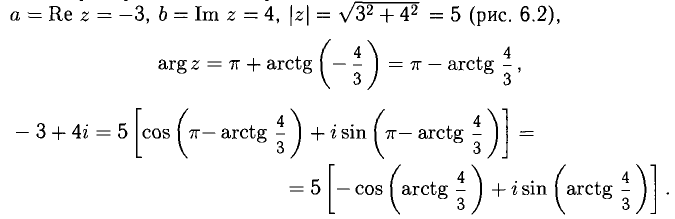
Любое из этих равенств может быть принято в качестве тригонометрической записи комплексного числа z = -3 + 4i, а из первого получаем показательную запись
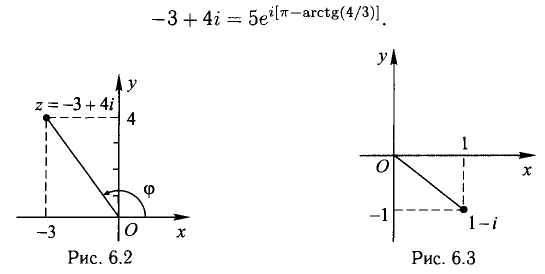
Примечание:
Ввиду периодичности косинуса и синуса (с периодом  ) принято обозначение
) принято обозначение  — произвольное целое число.
— произвольное целое число.
Это означает, что числу сопоставляется бесконечное множество аргументов, или тригонометрических углов, как это принято в тригонометрии.
сопоставляется бесконечное множество аргументов, или тригонометрических углов, как это принято в тригонометрии.
При этом arg z представляет собой частное значение Arg z, получаемое при п = 0; arg z называется главным значением Arg z.
Таким образом,
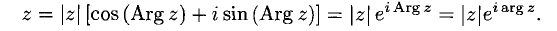
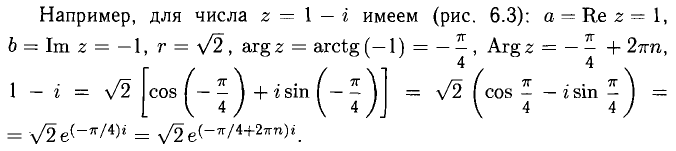
Арифметические действия с комплексными числами
1°. Арифметические действия с комплексными числами, заданными в алгебраической форме, выполняются как с выражениями, содержащими букву 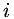 . При этом действие считается выполненным, если результат имеет вид алгебраического комплексного числа, т. е. а + b. Отсюда следует, в частности, что
. При этом действие считается выполненным, если результат имеет вид алгебраического комплексного числа, т. е. а + b. Отсюда следует, в частности, что
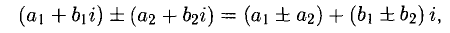
т. е. сложение и вычитание выполняются «покомпонентно».
Например,
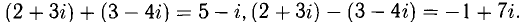
При умножении комплексных чисел следует учитывать, что 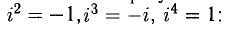
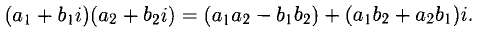
В частности, произведение двух комплексно сопряженных чисел есть действительное число:
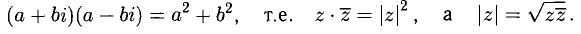
Например,
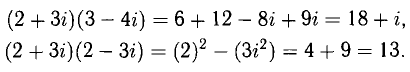
При делении комплексных чисел приходится умножать числитель и знаменатель дроби на выражение, сопряженное знаменателю. Например,
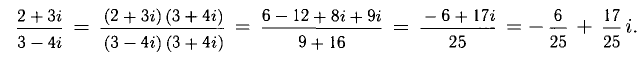
2°. Возведение комплексного числа в целую степень удобнее выполнять в показательной форме (мы используем действия со степенями в символической форме):
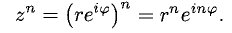
Из этого равенства следует, что при возведении в целую степень п комплексного числа:
- его модуль возводится в эту степень,
- его аргумент увеличивается в п раз.
Например, найдем 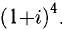 Имеем:
Имеем: 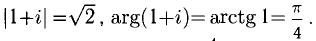
Следовательно,
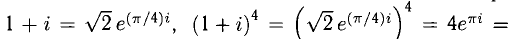
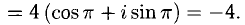
Примечание:
При возведении в степень п можно использовать формулу бинома Ньютона, но при больших п эта формула громоздка. Сравним:
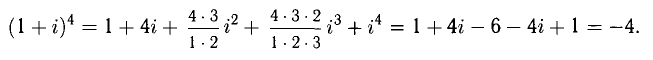
Извлечение корня из комплексного числа
1°. Пусть 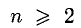 — целое положительное число. Если
— целое положительное число. Если 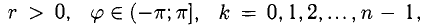 то комплексные числа
то комплексные числа 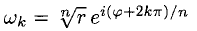 различны и имеют одну и ту же n-ю степень:
различны и имеют одну и ту же n-ю степень:
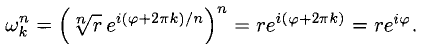
Например, если 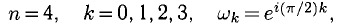 то
то
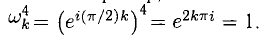
При этом
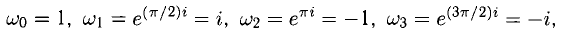
и каждое из этих чисел представляет одно из значений 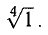
2°. Корнем степени п из комплексного числа 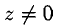 называется каждое комплексное число
называется каждое комплексное число 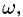 такое, что
такое, что 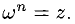 Из п. 1° следует, что существует множество
Из п. 1° следует, что существует множество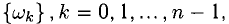 состоящее ровно из п различных чисел, таких, что
состоящее ровно из п различных чисел, таких, что 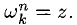 . Эти числа вычисляются по формуле
. Эти числа вычисляются по формуле
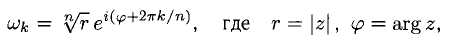
a 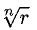 — известный арифметический корень степени п из положительного числа r.
— известный арифметический корень степени п из положительного числа r.
Например, найдем 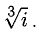 Имеем:
Имеем:
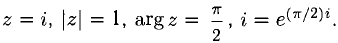
Тогда 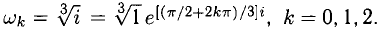 Отдельные значения
Отдельные значения 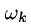 имеют вид
имеют вид
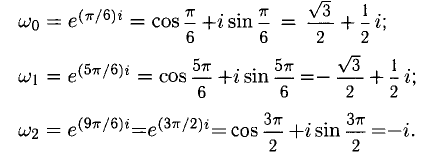
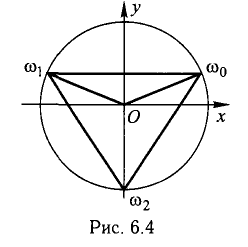
Предлагаем убедиться самостоятельно в том, что 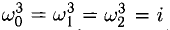 (делать это рекомендуется в алгебраической форме, возводя в куб по известной формуле сокращенного умножения).
(делать это рекомендуется в алгебраической форме, возводя в куб по известной формуле сокращенного умножения).
Примечание:
Пусть 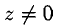 — данное комплексное число, п — целое положительное, п > 2. Тогда числа
— данное комплексное число, п — целое положительное, п > 2. Тогда числа 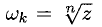 расположены в вершинах правильного n-угольника, вписанного в окружность радиуса
расположены в вершинах правильного n-угольника, вписанного в окружность радиуса 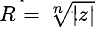 Одна из вершин этого многоугольника расположена на луче, образующем с осью Ох угол
Одна из вершин этого многоугольника расположена на луче, образующем с осью Ох угол 
Например, числа 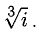 являются вершинами правильного треугольника
являются вершинами правильного треугольника 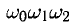 (рис. 6.4).
(рис. 6.4).
Примеры с решениями
Пример:
Даны числа:
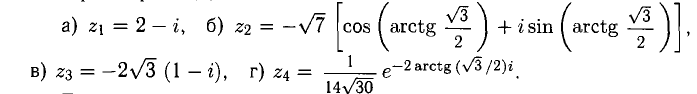
Требуется записать данные числа во всех формах.
Решение:
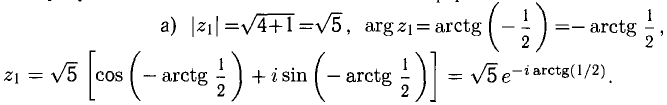
б) Вычислим 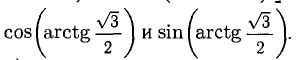 Положим
Положим 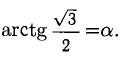 Тогда
Тогда 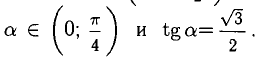 Следовательно,
Следовательно,
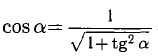
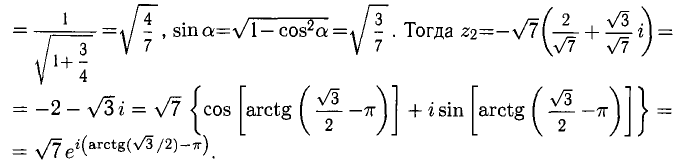
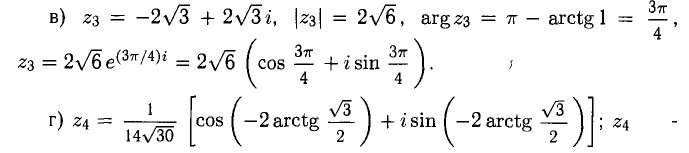
принадлежит четвертой четверти: 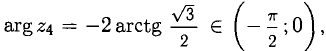 так как
так как 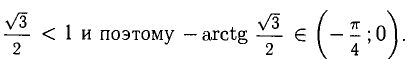
Вычислим сначала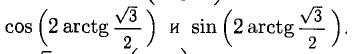 Положим
Положим
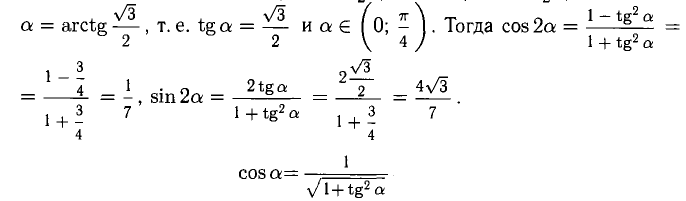
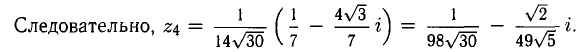
Пример:
Для данных предыдущего примера вычислить:
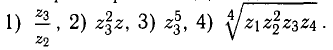
Решение:
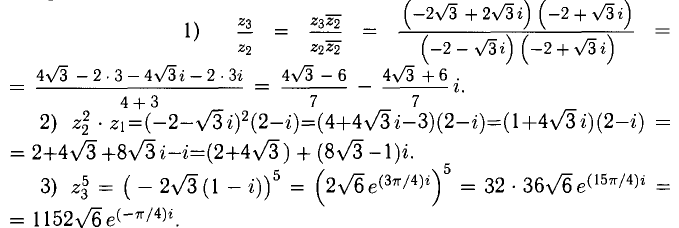
4) Чтобы найти 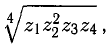 представим сначала подкоренное выражение в показательной форме:
представим сначала подкоренное выражение в показательной форме:
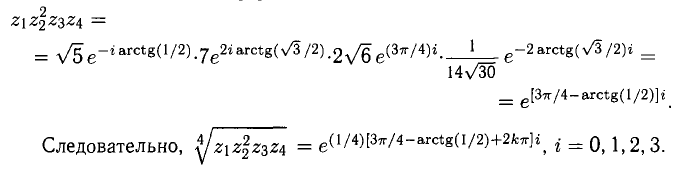
Разложение рациональной дроби на простейшие
1°. Простейшими дробями называются следующие дроби:
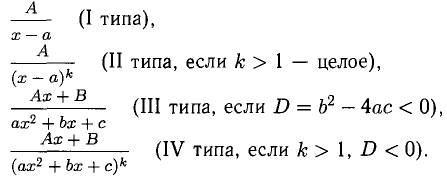
2°. Рациональной функцией (дробью) называется отношение двух
многочленов: 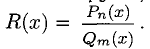
Если степень п числителя  меньше степени m знаменателя
меньше степени m знаменателя  , то такая дробь называется правильной. Если степень числителя больше или равна степени знаменателя, то дробь называется неправильной. Например,
, то такая дробь называется правильной. Если степень числителя больше или равна степени знаменателя, то дробь называется неправильной. Например, 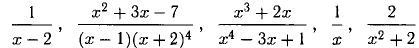 — и т. п. —правильные рациональные дроби, а
— и т. п. —правильные рациональные дроби, а 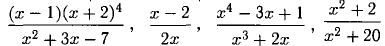 — неправильные дроби.
— неправильные дроби.
Теорема:
Каждая неправильная дробь равна сумме многочлена и правильной дроби.
Этот многочлен называется целой частью дроби и получается делением числителя на знаменатель, к примеру, «в столбик» («уголком»).
Например,
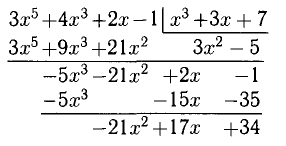
Результат запишем в виде
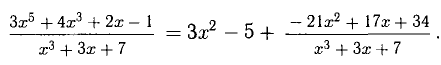
Теорема:
Правильная рациональная функция 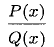 представляется единственным образом в виде суммы простейших дробей.
представляется единственным образом в виде суммы простейших дробей.
Разложение правильной дроби на сумму простейших производится по следующему правилу.
- Многочлен Q{x) следует разложить на простейшие множители.
- Каждому множителю Q(x) вида
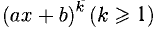 сопоставляется сумма из k дробей:
сопоставляется сумма из k дробей:
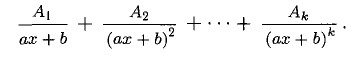
- Каждому множителю Q(x) вида
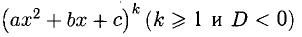 сопоставляется сумма k дробей вида
сопоставляется сумма k дробей вида
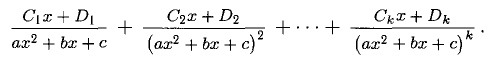
- Неизвестные коэффициенты числителей вычисляются методом неопределенных коэффициентов.
Этот метод вытекает из следующих теорем.
Теорема:
Две рациональные функции равны, если они имеют одинаковые числители и одинаковые знаменатели.
Теорема:
Два многочлена равны, если они имеют одинаковые степени, а их коэффициенты при одинаковых степенях равны между собой.
Теорема:
Два многочлена одинаковой степени п равны в том и только том случае, когда они принимают равные значения в системе из (n+ 1) различных точек.
Примеры с решениями
Пример:
Разложить на простейшие дроби: 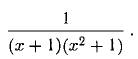
Решение:
Имеем
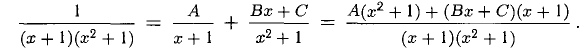
Применим теорему 3. Приходим к равенству
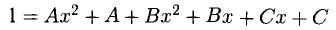
(знаменатели равных дробей одинаковы). А теперь применим теорему 4 — приравниваем коэффициенты при одинаковых степенях многочленов в правой и левой частях от знака равенства. В правой части имеем многочлен второй степени. Считаем, что в левой части имеем тоже многочлен второй степени с равными нулю коэффициентами при положительных степенях переменной х. Соответствующие равенства записываем в виде
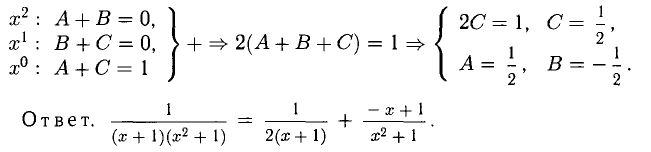
Пример:
Разложить на простейшие дроби: 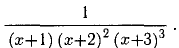
Решение:
Согласно теореме 2 имеем разложение
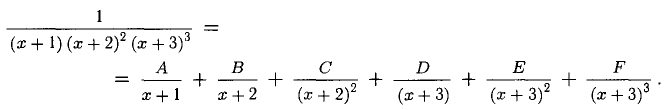
Правую часть этого равенства приводим к общему знаменателю. Согласно теореме 3 приходим к равенству
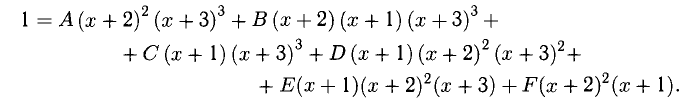
Неизвестные коэффициенты найдем, сочетая теоремы 4 и 5. Сначала действуем при помощи теоремы 5.
1) Положим х = -2 в полученном равенстве. Получаем равенство 1 = —С (все слагаемые правой части, кроме одного, обращаются в нуль). Отсюда С = — 1.
2) Положим теперь х =-1: 1 = 8А. Получаем А =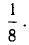
3) Положим х = -3, -2F = 1, F = 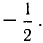
4) Положим х = 0: 1 = 108A + 54В + 21С + 36D + 12Е + 4F => 54В + 36D + 12Е = 16,5. Это уравнение будет использовано ниже.
Для определения остальных коэффициентов (с учетом уже полученных) используем теорему 4.
5) Приравниваем коэффициенты обеих частей при 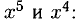
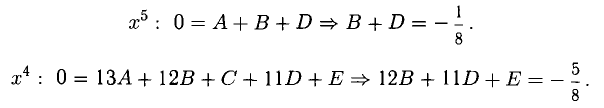
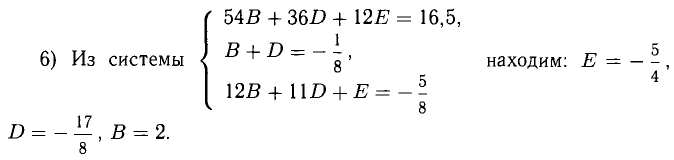
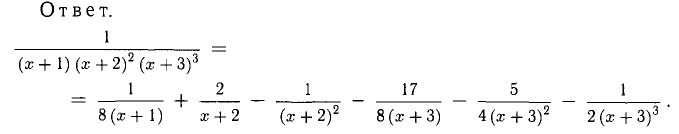
Примечание:
В дальнейших примерах мы опускаем раскрытие скобок в числителе правой дроби. Поиск коэффициентов при тех или иных степенях переменной выполняется, как правило, устно.
Пример:
Разложить на простейшие дроби:
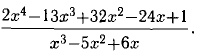
Решение:
1) Данная дробь неправильная, поэтому сначала выделим целую
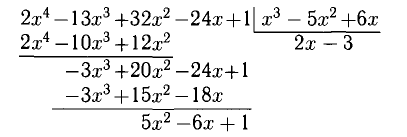
Получили
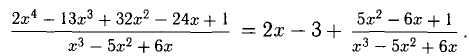
2) Остается разложить на простейшие дробь из правой части этого равенства, для чего предварительно ее знаменатель разложим на простые множители.
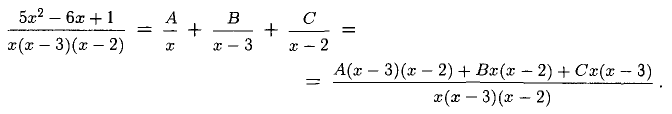
Приравниваем коэффициенты при одинаковых степенях числителей в правой и левой дробях. Это приводит к линейной системе из трех уравнений с тремя неизвестными А, В и С.
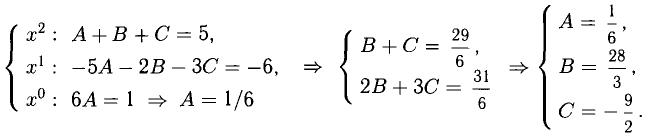
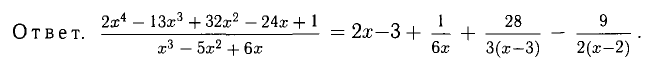
Дальнейшие примеры с краткими решениями разберите самостоятельно.
Пример:
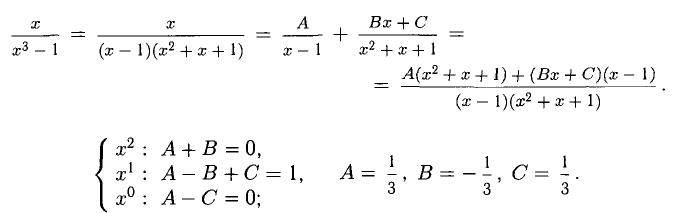
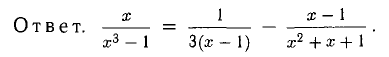
Пример:
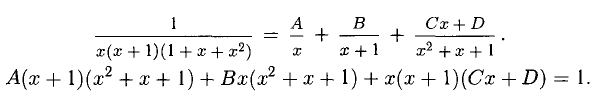
Имеем:
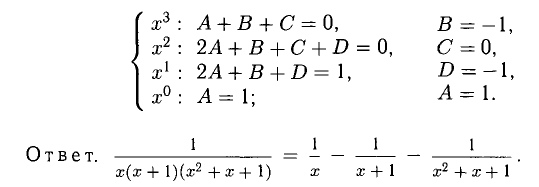
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

