Оглавление:
Величины, которые полностью определяются своим численным значением, называются скалярными. Примерами скалярных величин являются: площадь, длина, объем, температура, работа, масса.
Другие величины, например сила, скорость, ускорение, определяются не только своим числовым значением, но и направлением. Такие величины называют векторными. Векторная величина геометрически изображается с помощью вектора.
Вектор — это направленный прямолинейный отрезок, т. е. отрезок, имеющий определенную длину и определенное направление. Если А — начало вектора, а В — его конец, то вектор обозначается символом 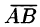 или
или 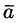 . Вектор
. Вектор 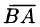 (у него начало в точке В, а конец в точке А) называется противоположным вектору
(у него начало в точке В, а конец в точке А) называется противоположным вектору 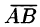 . Вектор, противоположный вектору
. Вектор, противоположный вектору 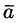 , обозначается —
, обозначается —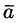 .
.
Длиной или модулем вектора 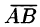 называется длина отрезка и обозначается |
называется длина отрезка и обозначается |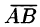 |. Вектор, длина которого равна нулю, называется нулевым вектором и обозначается
|. Вектор, длина которого равна нулю, называется нулевым вектором и обозначается 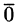 . Нулевой вектор направления не имеет.
. Нулевой вектор направления не имеет.
Вектор, длина которого равна единице, называется единичным вектором и обозначается через 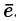 . Единичный вектор, направление которого совпадает с направлением вектора
. Единичный вектор, направление которого совпадает с направлением вектора 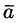 , называется ортом вектора
, называется ортом вектора 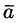 и обозначается
и обозначается 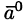 .
.
Векторы 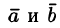 называются коллинеарными, если они лежат на одной прямой или на параллельных прямых; записывают
называются коллинеарными, если они лежат на одной прямой или на параллельных прямых; записывают 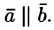 Коллинеарные векторы могут быть направлены одинаково или противоположно.
Коллинеарные векторы могут быть направлены одинаково или противоположно.
Нулевой вектор считается коллинеарным любому вектору. £5] Два вектора 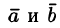 называются равными
называются равными 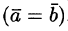 , если они коллинеарны, одинаково направлены и имеют одинаковые длины. Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, а начало вектора помещать в любую точку О пространства.
, если они коллинеарны, одинаково направлены и имеют одинаковые длины. Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, а начало вектора помещать в любую точку О пространства.
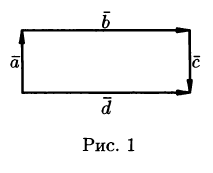
На рисунке 1 векторы образуют прямоугольник. Справедливо равенство 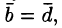 но
но 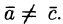 Векторы
Векторы 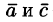 — противоположные,
— противоположные, 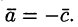
Равные векторы называют также свободными. Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Если среди трех векторов хотя бы один нулевой или два любые колли-неарны, то такие векторы компланарны.
Линейные операции над векторами
Под линейными операциями над векторами понимают операции сложения и вычитания векторов, а также умножение вектора на число.
Пусть 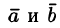 — два произвольных вектора. Возьмем произвольную точку О и построим вектор
— два произвольных вектора. Возьмем произвольную точку О и построим вектор 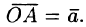 От точки А отложим вектор
От точки А отложим вектор 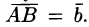 Вектор
Вектор 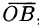 , соединяющий начало первого вектора с концом второго, называется суммой векторов
, соединяющий начало первого вектора с концом второго, называется суммой векторов 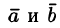 :
: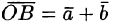 (см. рис. 2).
(см. рис. 2).
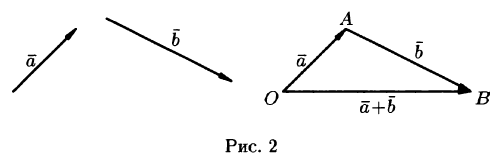
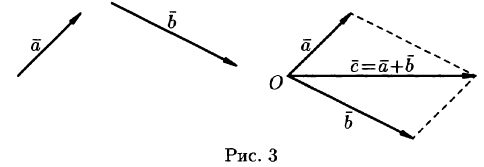
Это правило сложения векторов называют правилом треугольника. Сумму двух векторов можно построить также по правилу параллелограмма (см. рис. 3).
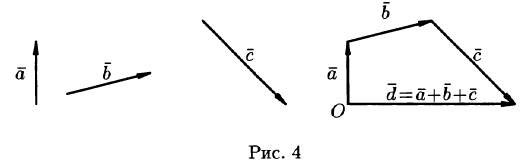
На рисунке 4 показано сложение трех векторов 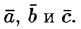
Под разностью векторов 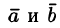 понимается вектор
понимается вектор 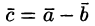 такой, что
такой, что 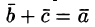 (см. рис. 5).
(см. рис. 5).
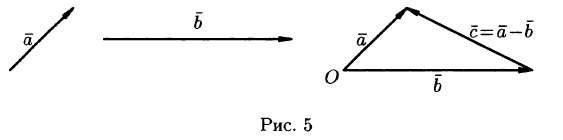
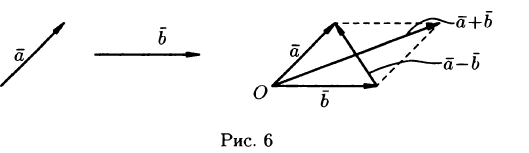
Отметим, что в параллелограмме, построенном на векторах 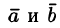 , одна направленная диагональ является суммой векторов
, одна направленная диагональ является суммой векторов 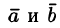 , а другая — разностью (см. рис. 6).
, а другая — разностью (см. рис. 6).
Можно вычитать векторы по правилу: 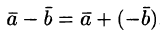 , т. е. вычитание векторов заменить сложением вектора
, т. е. вычитание векторов заменить сложением вектора 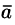 с вектором, противоположным вектору
с вектором, противоположным вектору 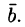
Произведением вектора 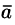 на скаляр (число)
на скаляр (число) 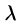 называется вектор
называется вектор 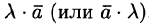 , который имеет длину
, который имеет длину 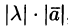 , коллинеарен вектору
, коллинеарен вектору 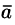 , имеет направление вектора
, имеет направление вектора 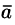 , если
, если 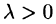 и противоположное направление, если
и противоположное направление, если 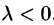 .Например, если дан вектор
.Например, если дан вектор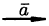 , то векторы
, то векторы 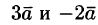 будут иметь вид
будут иметь вид 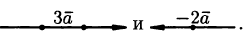
Из определения произведения вектора на число следуют свойства этого произведения:
1) если 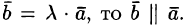 Наоборот, если
Наоборот, если 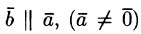 , то при некотором
, то при некотором 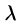 верно равенство
верно равенство 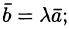
2) всегда 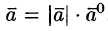 , т. е. каждый вектор равен произведению его модуля на орт.
, т. е. каждый вектор равен произведению его модуля на орт.
Линейные операции над векторами обладают следующими свойствами:
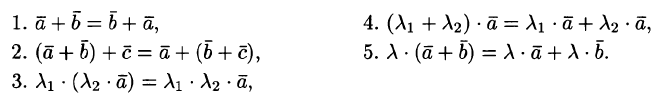
Эти свойства позволяют проводить преобразования в линейных операциях с вектором так, как это делается в обычной алгебре: слагаемые менять местами, вводить скобки, группировать, выносить за скобки как скалярные, так и векторные общие множители.
Проекция вектора на ось
Пусть в пространстве задана ось l, т. е. направленная прямая. Проекцией точки М на ось l называется основание 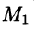 перпендикуляра
перпендикуляра 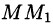 , опущенного из точки на ось.
, опущенного из точки на ось.
Точка 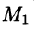 есть точка пересечения оси l с плоскостью, проходящей через точку М перпендикулярно оси (см. рис. 7).
есть точка пересечения оси l с плоскостью, проходящей через точку М перпендикулярно оси (см. рис. 7).
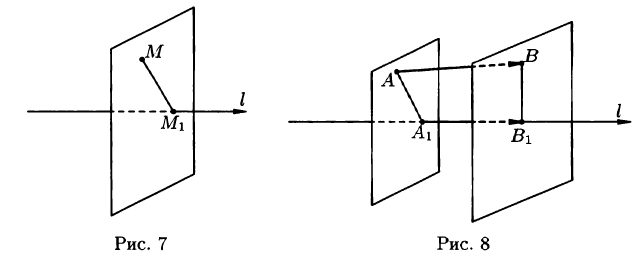
Если точка М лежит на оси l , то проекция точки М на ось совпадает с М.
Пусть 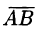 — произвольный вектор
— произвольный вектор 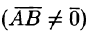 . Обозначим через
. Обозначим через 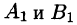 проекции на ось l соответственно начала А и конца В вектора
проекции на ось l соответственно начала А и конца В вектора 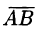 и рассмотрим вектор
и рассмотрим вектор 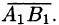
Проекцией вектора 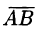 на ось l называется положительное число
на ось l называется положительное число 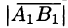 , если вектор
, если вектор 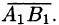 и ось l одинаково направлены и отрицательное число —если вектор
и ось l одинаково направлены и отрицательное число —если вектор 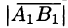 и ось l противоположно направлены (см. рис. 8). Если точки
и ось l противоположно направлены (см. рис. 8). Если точки 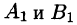 совпадают
совпадают 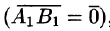 , то проекция вектора
, то проекция вектора 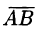 равна 0.
равна 0.
Проекция вектора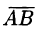 на ось l обозначается так:
на ось l обозначается так: 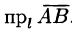 . Если
. Если 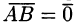 или
или 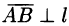 , то
, то 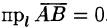 .
.
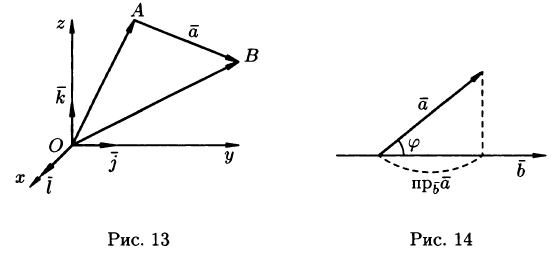
Угол 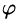 между вектором
между вектором 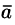 и осью l (или угол между двумя векторами) изображен на рисунке 9. Очевидно,
и осью l (или угол между двумя векторами) изображен на рисунке 9. Очевидно, 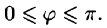
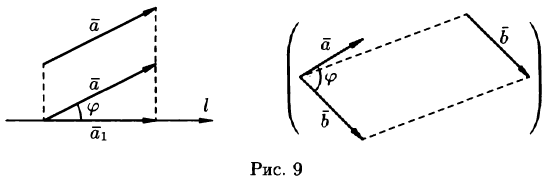
Рассмотрим некоторые основные свойства проекций. Свойство 1. Проекция вектора 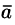 на ось l равна произведению модуля вектора
на ось l равна произведению модуля вектора 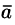 на косинус угла
на косинус угла 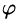 между вектором и осью, т. е.
между вектором и осью, т. е. 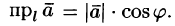
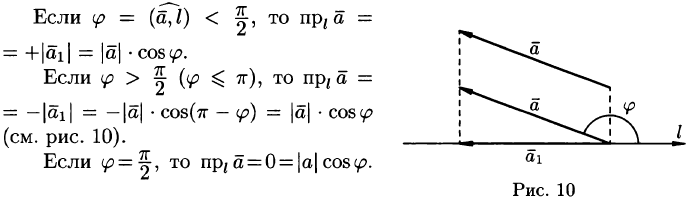
Следствие:
Проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол — прямой.
Следствие:
Проекции равных векторов на одну и ту же ось равны между собой.
Свойство 2. Проекция суммы нескольких векторов на одну и ту же ось равна сумме их проекций на эту ось.
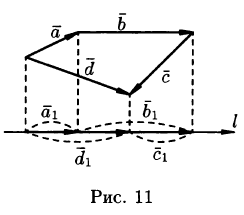
Пусть, например, 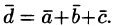 Имеем
Имеем 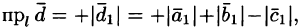 т. е.
т. е. 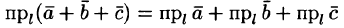 (см. рис. 11).
(см. рис. 11).
Свойство 3. При умножении вектора 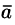 на число
на число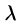 его проекция на ось также умножается на это число, т. е.
его проекция на ось также умножается на это число, т. е.
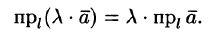
При 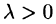 имеем
имеем
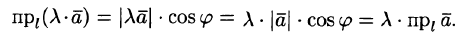
При 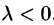 :
:
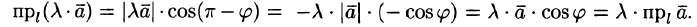
Свойство справедливо, очевидно, и при 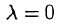 .
.
Таким образом, линейные операции над векторами приводят к соответствующим линейным операциям над проекциями этих векторов.
Разложение вектора по ортам координатных осей. Модуль вектора. Направляющие косинусы
Рассмотрим в пространстве прямоугольную систему координат Oxyz. Выделим на координатных осях Ох, Оу и Oz единичные векторы (орты), обозначаемые 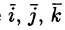 соответственно (см. рис. 12).
соответственно (см. рис. 12).
Выберем произвольный вектор а пространства и совместим его начало с началом координат: 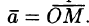
Найдем проекции вектора 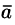 на координатные оси. Проведем через конец вектора
на координатные оси. Проведем через конец вектора 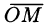 плоскости, параллельные координатным плоскостям. Точки пересечения этих плоскостей с осями обозначим соответственно через
плоскости, параллельные координатным плоскостям. Точки пересечения этих плоскостей с осями обозначим соответственно через 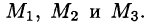 Получим прямоугольный параллелепипед, одной из диагоналей которого является вектор
Получим прямоугольный параллелепипед, одной из диагоналей которого является вектор 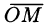 . Тогда
. Тогда 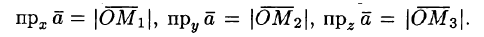 По определению суммы нескольких векторов находим
По определению суммы нескольких векторов находим 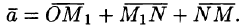 А так как
А так как 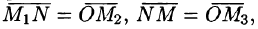 то
то
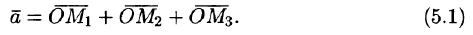
Но
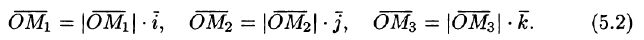
Обозначим проекции вектора 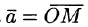 на оси Ох, Оу и Oz соответственно через
на оси Ох, Оу и Oz соответственно через
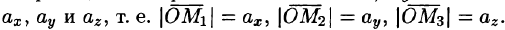
Тогда из равенств (5.1) и (5.2) получаем
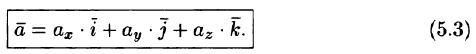
Эта формула является основной в векторном исчислении и называется разложением вектора по ортам координатных осей.
Числа 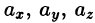 называются координатами вектора
называются координатами вектора 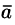 , т. е. координаты вектора есть его проекции на соответствующие координатные оси.
, т. е. координаты вектора есть его проекции на соответствующие координатные оси.
Векторное равенство (5.3) часто записывают в символическом виде: 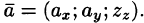
Зная проекции вектора 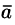 , можно легко найти выражение для модуля вектора. На основании теоремы о длине диагонали прямоугольного параллелепипеда можно написать
, можно легко найти выражение для модуля вектора. На основании теоремы о длине диагонали прямоугольного параллелепипеда можно написать 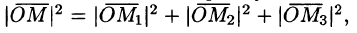

Отсюда
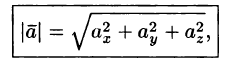
т. е. модуль вектора равен квадратному корню из суммы квадратов его проекций на оси координат.
Пусть углы вектора 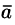 с осями Ох, Оу и Oz соответственно равны
с осями Ох, Оу и Oz соответственно равны 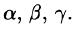 По свойству проекции вектора на ось, имеем
По свойству проекции вектора на ось, имеем
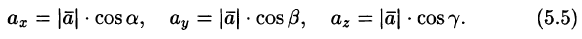
Или, что то же самое,
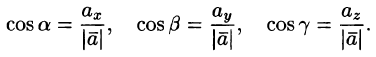
Числа 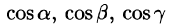 называются направляющими косинусами вектора
называются направляющими косинусами вектора 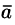 .
.
Подставим выражения (5.5) в равенство (5.4), получаем
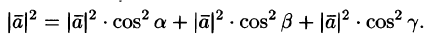
Сократив на 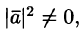 получим соотношение
получим соотношение
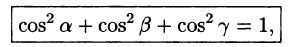
т. е. сумма квадратов направляющих косинусов ненулевого вектора равна единице.
Легко заметить, что координатами единичного вектора 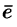 являются числа
являются числа 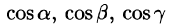 т. е.
т. е. 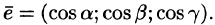 Итак, задав координаты вектора, всегда можно определить его модуль и направление, т. е. сам вектор.
Итак, задав координаты вектора, всегда можно определить его модуль и направление, т. е. сам вектор.
Действия над векторами, заданными проекциями
Пусть векторы 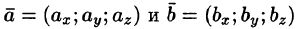 заданы своими проекциями на оси координат Ох, Оу , Oz или, что то же самое
заданы своими проекциями на оси координат Ох, Оу , Oz или, что то же самое
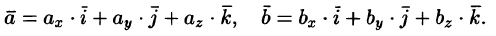
Линейные операции над векторами
Так как линейные операции над векторами сводятся к соответствующим линейным операциям над проекциями этих векторов, то можно записать:
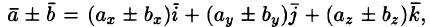 или кратко
или кратко 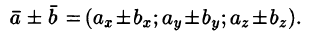 То есть при сложении (вычитании) векторов их одноименные координаты складываются (вычитаются).
То есть при сложении (вычитании) векторов их одноименные координаты складываются (вычитаются).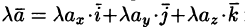 или короче
или короче 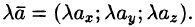 То есть при умножении вектора на скаляр координаты вектора умножаются на этот скаляр.
То есть при умножении вектора на скаляр координаты вектора умножаются на этот скаляр.
Равенство векторов
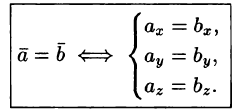
Из определения вектора как направленного отрезка, который можно передвигать в пространстве параллельно самому себе, следует, что два вектора 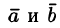 равны тогда и только тогда, когда выполняются равенства:
равны тогда и только тогда, когда выполняются равенства: 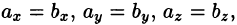 т. е.
т. е.
Коллинеарность векторов
Выясним условия коллинеарности векторов 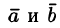 , заданных своими координатами.
, заданных своими координатами.
Так как 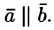 то можно записать
то можно записать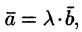 где
где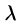 — некоторое число. То есть
— некоторое число. То есть
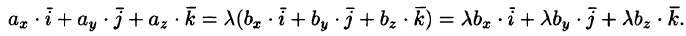
Отсюда
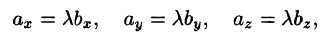
T.e.
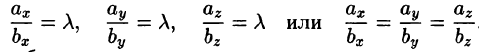
Таким образом, проекции коллинеарных векторов пропорциональны. Верно и обратное утверждение: векторы, имеющие пропорциональные координаты, коллинеарны.
Координаты точки
Пусть в пространстве задана прямоугольная декартова система координат Oxyz. Для любой точки М координаты вектора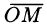 называются координатами точки М. Вектор
называются координатами точки М. Вектор 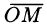 называется радиус-вектором точки М, обозначается г, т. е.
называется радиус-вектором точки М, обозначается г, т. е. 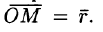 Следовательно, координаты точки — это координаты ее радиус-вектора
Следовательно, координаты точки — это координаты ее радиус-вектора
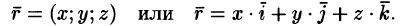
Координаты точки М записываются в виде М(х; у, z).
Координаты вектора
Найдем координаты вектора 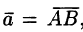 , если известны координаты точек
, если известны координаты точек 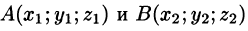 — Имеем (см. рис. 13):
— Имеем (см. рис. 13):
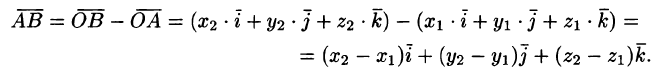
Следовательно, координаты вектора равны разностям соответствующих координат его конца и начала: 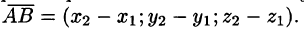
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

