Варианты уравнения прямой
На практике часто встречаются случаи, когда надо получить уравнение прямой не только с помощью приведенных выше общего и нормализованного уравнений. Рассмотрим некоторые такие случаи.
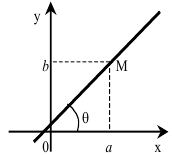
1. Известно, что прямая образует с 
угол 
и проходит через известную точку 
. Найти уравнение (прямая через точку по заданному направлению).
Так как 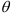известно, то 
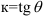. Тогда уравнение прямой
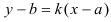
Это уравнение легко преобразуется в уже известные формы записи.
2. Известны точк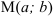и и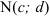 
. Найти уравнение проведенной через них прямой (прямая через две точки).
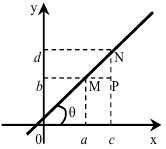
Из прямоугольного треугольника 
определяем
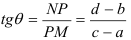
Тогда
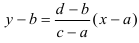
После преобразования получим
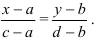
Ес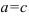ли 
или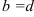 
, то следует использовать другую форму записи:
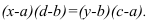
3. Известны отрезк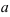и 
и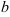 
, которые прямая отсекает от осей координат. Найти уравнение этой прямой (уравнение прямой в отрезках).
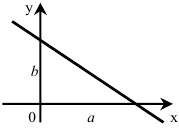
Искомое уравнение имеет вид
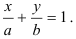
Отметим, что, если прямая параллельна ос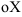и или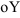 
, то такое уравнение составить нельзя — нет отрезка.
Остальные темы находится на этой странице и там же можно заказать любые работы по высшей математике:
Обратите внимание на эти страниц, возможно они вам будут полезны:
| Изгибы функции и их определение |
| Норма матрицы |
| Построение прямых. Расстояния |
| Абсолютные экстремумы функции двух переменных |
