Оглавление:
Дифференциальным уравнением порядка n называется уравнение вида 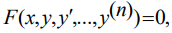 в котором обязательно наличие n-ой производной.
в котором обязательно наличие n-ой производной.
Задача Коши
Пусть имеем дифференциальное уравнение n-го порядка, разрешенное относительно старшей производной 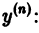
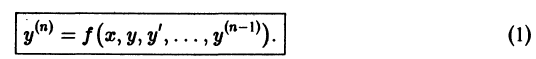
Возникает вопрос: какие надо задать условия, чтобы выделить определенное, частное решение уравнения (1)? Для дифференциального уравнения первого порядка
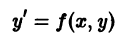
достаточно задать значение у0 частного решения при каком-то значении х0 независимой переменной х, т.е. задать точку 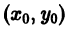 , через которую должна проходить интегральная кривая этого уравнения. Для уравнений высшего порядка этого уже недостаточно. Например, уравнение
, через которую должна проходить интегральная кривая этого уравнения. Для уравнений высшего порядка этого уже недостаточно. Например, уравнение
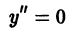
имеет решениями функции
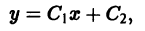
где 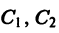 — произвольные постоянные. Уравнение
— произвольные постоянные. Уравнение
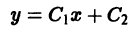
определяет двухпараметрическое семейство прямых на плоскости хОу, и, чтобы выделить определенную прямую, мало задать точку 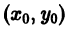 , через которую прямая должна проходить, — надо еще задать угловой коэффициент прямой
, через которую прямая должна проходить, — надо еще задать угловой коэффициент прямой
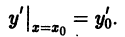
В общем случае дифференциального уравнения n-го порядка (1) для выделения частного решения надо задать n условий:
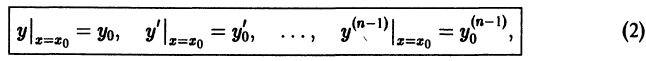
где 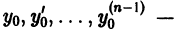 некоторые числа. Совокупность этих условий называется начальными условиями для дифференциального уравнения (1). Задача Коши для этого уравнения ставится так: найти решение дифференциального уравнения (1), удовлетворяющее заданным начальным условиям (2).
некоторые числа. Совокупность этих условий называется начальными условиями для дифференциального уравнения (1). Задача Коши для этого уравнения ставится так: найти решение дифференциального уравнения (1), удовлетворяющее заданным начальным условиям (2).
Сформулируем теорему существования и единственности решения задачи Коши.
Теорема:
Существования и единственности решения задачи Коши.
Пусть имеем дифференциальное уравнение n-го порядка, разрешенное относительно старшей производной,
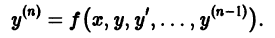
Если правая часть этого уравнения непрерывна как функция n + 1 аргументов  в некоторой окрестности
в некоторой окрестности 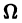 точки
точки 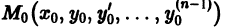 (на рис. 1 для n = 2), то найдется интервал
(на рис. 1 для n = 2), то найдется интервал 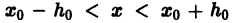 оси Ох, на котором существует по крайней мере одно решение
оси Ох, на котором существует по крайней мере одно решение 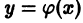 уравнения (1), удовлетворяющее начальным условиям
уравнения (1), удовлетворяющее начальным условиям
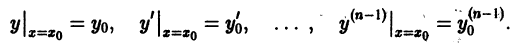
Если, кроме того, функция 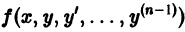 имеет ограниченные частные производные
имеет ограниченные частные производные 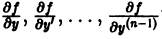 в указанной окрестности
в указанной окрестности  , то такое решение единственно.
, то такое решение единственно.
Так, для уравнения
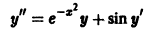
правая часть
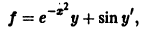
рассматриваемая как функция трех независимых переменных х, у, у’, непрерывна всюду и имеет ограниченные всюду производные
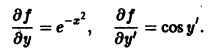
Поэтому, какова бы ни была тройка чисел 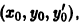 существует единственное решение этого уравнения, удовлетворяющее начальным условиям
существует единственное решение этого уравнения, удовлетворяющее начальным условиям
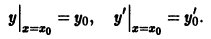
Определение:
Общим решением дифференциального уравнения n-го порядка
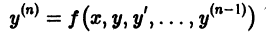
в некоторой области 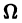 существования и единственности решения задачи Коши называется n-параметрическое семейство S функций
существования и единственности решения задачи Коши называется n-параметрическое семейство S функций 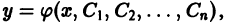 зависящих от х и n произвольных постоянных
зависящих от х и n произвольных постоянных 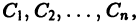 такое, что:
такое, что:
1) при любых допустимых значениях постоянных 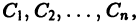 функция
функция
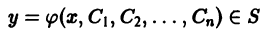
является решением дифференциального уравнения (1), т.е.
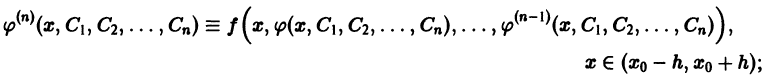
2) каковы бы ни были начальные условия
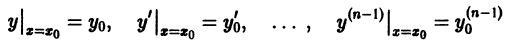
(лишь бы точка 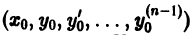 принадлежала области
принадлежала области 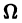 существования и единственности решения задачи Коши для уравнения (1)), можно так подобрать значения
существования и единственности решения задачи Коши для уравнения (1)), можно так подобрать значения 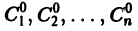 постоянных, чтобы решение
постоянных, чтобы решение
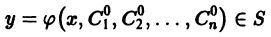
удовлетворяло заданным начальным условиям.
Решение, получаемое из общего при конкретных значениях постоянных 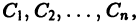 называется частным решением. Его график — кривую на плоскости хОу — называют интегральной кривой данного дифференциального уравнения.
называется частным решением. Его график — кривую на плоскости хОу — называют интегральной кривой данного дифференциального уравнения.
Соотношение 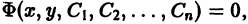 неявно определяющее общее решение, называют общим интегралом дифференциального уравнения (1).
неявно определяющее общее решение, называют общим интегралом дифференциального уравнения (1).
Задача:
Показать, что функция
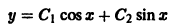
является общим решением уравнения
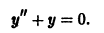
Уравнения высших порядков, допускающие понижение порядка
- Уравнение вида

где f(x) — известная непрерывная функция, интегрируется в квадратурах. Учитывая, что 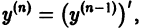 и интегрируя по х левую и правую части уравнения, получаем
и интегрируя по х левую и правую части уравнения, получаем
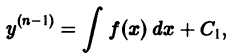
т. е. приходим к уравнению такого же вида, что и исходное; далее находим
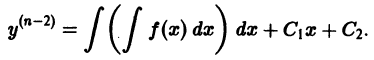
Через n шагов получим общее решение уравнения (1):
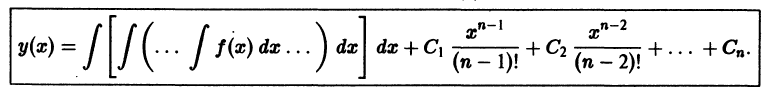
Пример:
Найти общее решение уравнения
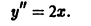
Последовательно интегрируя дважды, получаем искомое общее решение
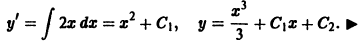
Бели уравнение не содержит искомой функции и ее производных до порядка к — 1 включительно, т. е. имеет вид
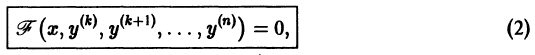
то порядок уравнения может быть снижен до порядка n — к заменой 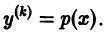 После такой замены уравнение принимает вид
После такой замены уравнение принимает вид
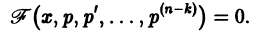
Пусть удалось проинтегрировать полученное уравнение:
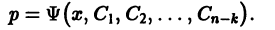
Замечая, что 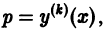 приходим к уравнению
приходим к уравнению
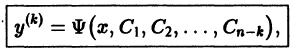
из которого у(х) находится k-кратным интегрированием.
Пример:
Найти общее решение уравнения
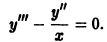
Положим 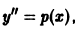 тогда
тогда
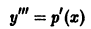
и данное уравнение примет вид
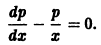
Разделяя переменные в последнем уравнении, найдем 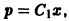 или
или
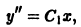
откуда легко получаем общее решение исходного уравнения:
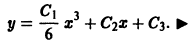
Пусть дифференциальное уравнение не содержит явно независимой переменной х, т. е. имеет вид

Порядок этого уравнения можно понизить на единицу подстановкой у’ = р(у), где р = р(у) рассматривается как новая неизвестная функция, а у принимается за независимую переменную. В этом случае все производные 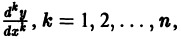 надо выразить через производные от функции р по у:
надо выразить через производные от функции р по у:
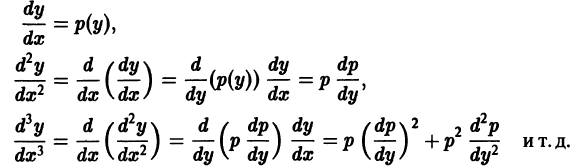
Мы видим, что любая производная 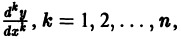 выражается через производные от р по у порядка не выше к -1, что приводит к понижению порядка уравнения на единицу.
выражается через производные от р по у порядка не выше к -1, что приводит к понижению порядка уравнения на единицу.
Пример:
Проинтегрировать уравнение

Положим у’ = р(у), тогда
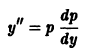
и данное уравнение принимает вид
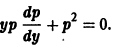
Сокращая на 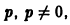 и разделяя переменные, найдем
и разделяя переменные, найдем

откуда
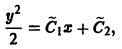
или

Случай р=0 дает решение
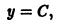
содержащееся в (**).
Всегда следует посмотреть, не является ли левая часть данного уравнения полным дифференциалом некоторого выражения. Так, уравнение (*) можно переписать в виде
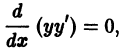
откуда находим:
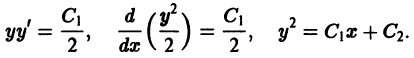
Часто встречающееся уравнение
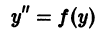
можно легко проинтефировать в квадратурах, если умножить обе его части на у’ (проделайте это!).
Замечание:
Рассмотрим уравнение второго порядка

линейное относительно искомой функции у(х) и ее производных у’ и у». Положим

где u(х), v(x) — новые функции, из которых одну мы можем выбирать произвольно. Подставляя у(х) в форме (5) в исходное уравнение (4), для функции u(х) получаем уравнение
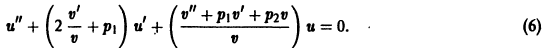
Если известно одно решение 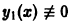 исходного уравнения (4), то можно взять
исходного уравнения (4), то можно взять 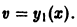 В уравнении (6) тогда исчезнет слагаемое, содержащее функцию u(х) (если
В уравнении (6) тогда исчезнет слагаемое, содержащее функцию u(х) (если 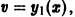 то
то
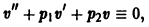
так как, по предположению, 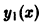 — решение уравнения (4)). Уравнение (6) примет тогда вид
— решение уравнения (4)). Уравнение (6) примет тогда вид
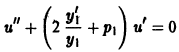
и легко интегрируется. В результате мы найдем общее решение исходного уравнения (4). Если положить

то в уравнении (6) исчезнет слагаемое с первой производной, и уравнение примет вид
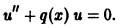
Такое преобразование полезно для качественного анализа уравнения и при использовании приближенных методов решения.
Рассмотрим, например, дифференциальное уравнение Бесселя
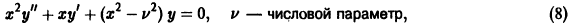
(его решения — функции Бесселя — играют важную роль во многих задачах физики); представим его в виде
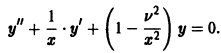
Здесь 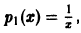 так что в силу (7) имеем
так что в силу (7) имеем
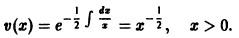
Полагая 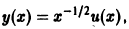 получаем для u(х) уравнение
получаем для u(х) уравнение
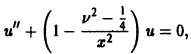
весьма удобное для изучения поведения функций Бесселя при больших значениях х.
Замечание:
При решении задачи Коши для уравнений высших порядков бывает целесообразно определять значения постоянных 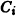 в процессе решения, а не после нахождения общего решения уравнения. Это связано с тем, что интегрирование порой значительно упрощается, когда постоянные
в процессе решения, а не после нахождения общего решения уравнения. Это связано с тем, что интегрирование порой значительно упрощается, когда постоянные 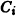 принимают конкретные числовые значения, в то время как при произвольных
принимают конкретные числовые значения, в то время как при произвольных 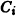 интегрирование затруднительно, а то и вообще невозможно в элементарных функциях.
интегрирование затруднительно, а то и вообще невозможно в элементарных функциях.
Рассмотрим, например, следующую задачу Коши:
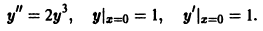
Полагая у’ = р(у), получаем
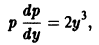
откуда 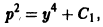 или
или
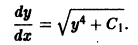
Разделяя переменные, найдем
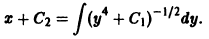
В правой части последнего равенства имеем интеграл от дифференциального бинома. Здесь m = 0, n = 4, 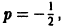 так что этот интеграл не выражается в виде конечной комбинации элементарных функций. Однако если использовать начальные условия, то
так что этот интеграл не выражается в виде конечной комбинации элементарных функций. Однако если использовать начальные условия, то 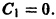 Это сразу дает
Это сразу дает
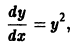
откуда, учитывая начальные условия, находим
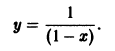
Задача:
Найти два решения задачи Коши для уравнения
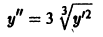
с начальными условиями у(0) = у'(0) = 0. Не противоречит ли этот факт теореме существования и единственности решения задачи Коши?
Линейные однородные дифференциальные уравнения n-го порядка
Линейным дифференциальным уравнением п-го порядка называется уравнение, линейное относительно неизвестной функции и всех ее производных. Оно имеет вид
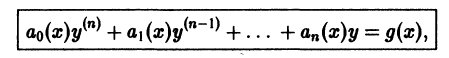
где 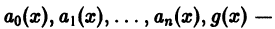 заданные на некотором интервале
заданные на некотором интервале  функции. Если g(х) = 0 на этом интервале, то уравнение называется линейным однородным, в противном случае уравнение называется неоднородным.
функции. Если g(х) = 0 на этом интервале, то уравнение называется линейным однородным, в противном случае уравнение называется неоднородным.
Пусть имеем линейное однородное дифференциальное уравнение
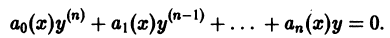
Если 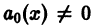 на некотором интервале, то разделив все члены данного уравнения на коэффициент
на некотором интервале, то разделив все члены данного уравнения на коэффициент 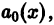 получим
получим
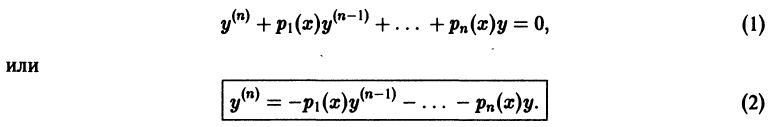
Если коэффициенты 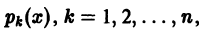 уравнения (1) непрерывны на отрезке [а,b], то правая часть уравнения (2) непрерывна по
уравнения (1) непрерывны на отрезке [а,b], то правая часть уравнения (2) непрерывна по 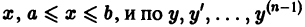 для любых значений
для любых значений 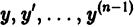 кроме того, имеет частные производные по
кроме того, имеет частные производные по 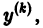 равные
равные 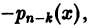 ограниченные на [а, b]. Поэтому в силу теоремы 1 получаем:
ограниченные на [а, b]. Поэтому в силу теоремы 1 получаем:
если коэффициенты 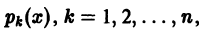 уравнения (1) непрерывны на [а, b], то, каковы бы ни были начальные условия
уравнения (1) непрерывны на [а, b], то, каковы бы ни были начальные условия
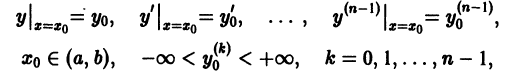
существует единственное решение уравнения (1), удовлетворяющее этим начальным условиям.
Напомним следующее понятие. Говорят, что на множестве Е задан оператор A со значениями в множестве F, если каждому элементу 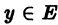 по некоторому закону поставлен в соответствие определенный элемент
по некоторому закону поставлен в соответствие определенный элемент 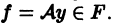 Множество Е называют областью определения оператора А.
Множество Е называют областью определения оператора А.
Пусть Е — линейное пространство. Оператор A, заданный на Е, называется линейным, если он аддитивен и однороден, т. е.
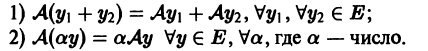
Представим линейное однородное уравнение (1) в виде
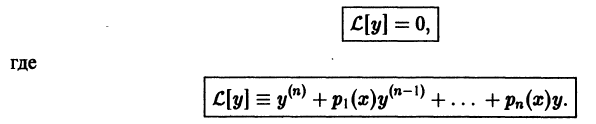
Нетрудно видеть, что 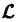 есть линейный дифференциальный оператор, определенный на линейном пространстве функций у(х), непрерывных на интервале (а, b), вместе со всеми производными до n-го порядка включительно. Дифференциальный характер оператора очевиден. Покажем его линейность, т. е. что
есть линейный дифференциальный оператор, определенный на линейном пространстве функций у(х), непрерывных на интервале (а, b), вместе со всеми производными до n-го порядка включительно. Дифференциальный характер оператора очевиден. Покажем его линейность, т. е. что
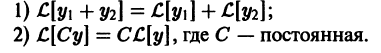
Имеем
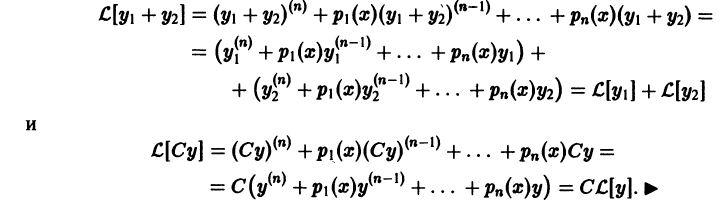
Как следствие получаем
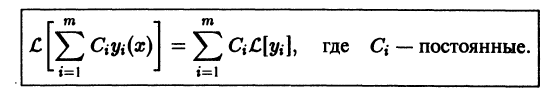
Установим некоторые свойства решений линейного однородного уравнения.
Теорема:
Если функция 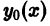 является решением линейного однородного дифференциального уравнения
является решением линейного однородного дифференциального уравнения
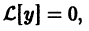
то функция 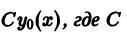 — произвольная постоянная, тоже является решением этого уравнения.
— произвольная постоянная, тоже является решением этого уравнения.
По условию,
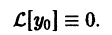
Надо доказать, что
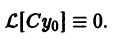
Пользуясь свойством однородности оператора 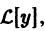 имеем
имеем
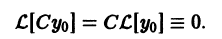
Это означает, что функция 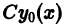 есть решение уравнения
есть решение уравнения 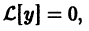
Теорема:
Если функции 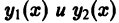 являются решениями линейного однородного уравнения
являются решениями линейного однородного уравнения
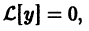
то сумма функций 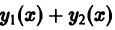 тоже является решением этого уравнения.
тоже является решением этого уравнения.
По условию, 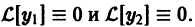 Надо доказать, что
Надо доказать, что
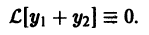
Последнее сразу вытекает из свойства аддитивности оператора 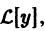
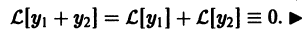
Следствие:
Линейная комбинация с произвольными постоянными коэффициентами
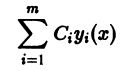
решений 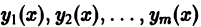 линейного однородного дифференциального уравнения
линейного однородного дифференциального уравнения
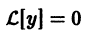
является решением того же уравнения.
Линейное однородное дифференциальное уравнение 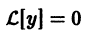 всегда имеет тривиальное решение
всегда имеет тривиальное решение 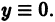 Из теорем 2 и З получаем: совокупность решений линейного однородного дифференциального уравнения
Из теорем 2 и З получаем: совокупность решений линейного однородного дифференциального уравнения 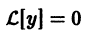 образует линейное пространство, нулем которого является функция
образует линейное пространство, нулем которого является функция 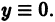
Теорема:
Если линейное однородное уравнение
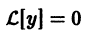
с действительными коэффициентами 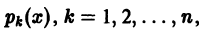 имеет комплексное решение
имеет комплексное решение
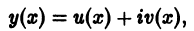
то действительная часть этого решения u(х) и его мнимая часть v(x) в отдельности являются решениями того же однородного уравнения.
Дано, что
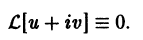
Надо доказать, что
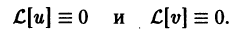
Пользуясь свойствами линейности оператора 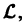 получаем
получаем
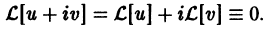
Отсюда следует, что 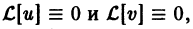 так как комплекснозначная функция действительного аргумента обращается тождественно в нуль тогда и только тогда, когда ее действительная и мнимая части тождественно равны нулю.
так как комплекснозначная функция действительного аргумента обращается тождественно в нуль тогда и только тогда, когда ее действительная и мнимая части тождественно равны нулю.
Линейно зависимые и линейно независимые системы функций
Пусть имеем систему функций 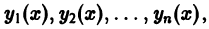 определенных на некотором интервале (а,b).
определенных на некотором интервале (а,b).
Определение:
Будем говорить, что система функций 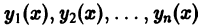 линейно зависима на интервале а < х < b, если существуют постоянные
линейно зависима на интервале а < х < b, если существуют постоянные 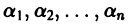 такие, что на этом интервале выполняется тождество по х:
такие, что на этом интервале выполняется тождество по х:
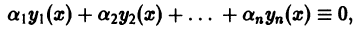
причем хотя бы одно из чисел 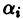 отлично от нуля.
отлично от нуля.
Если это тождество имеет место только при  то семейство функций
то семейство функций 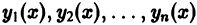 называется линейно независимым на интервале (а, Ь).
называется линейно независимым на интервале (а, Ь).
Рассмотрим примеры линейно зависимых и линейно независимых систем функций.
- Функции
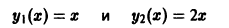
линейно зависимы на любом интервале (a, b), так как имеет место, например, тождество
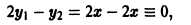
где 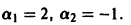
2. Функции
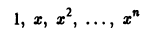
линейно независимы на любом интервале (а, b), так как тождество
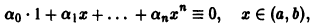
возможно лишь в случае, если 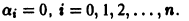
Если хоть одно из чисел 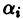 было бы отлично от нуля, то в левой част тождества стоял бы многочлен степени не выше n, который может иметь не более n различных корней и, следовательно, обращается в нуль не более чем в п точках рассматриваемого интервала.
было бы отлично от нуля, то в левой част тождества стоял бы многочлен степени не выше n, который может иметь не более n различных корней и, следовательно, обращается в нуль не более чем в п точках рассматриваемого интервала.
3. Функции
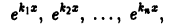
где  линейно независимы на любом интервале (а,b).
линейно независимы на любом интервале (а,b).
Для простоты ограничимся случаем n = 3. Допустим, что функции 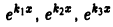 являются линейно зависимыми. Тогда имеет место тождество
являются линейно зависимыми. Тогда имеет место тождество
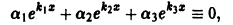
причем хотя бы одно из 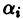 не равно нулю. Пусть для определенности
не равно нулю. Пусть для определенности 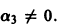 Разделив тождество на
Разделив тождество на 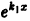 и продифференцировав, получим тождество
и продифференцировав, получим тождество
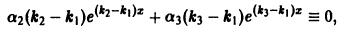
деля которое на 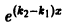 и дифференцируя результат по х, найдем
и дифференцируя результат по х, найдем
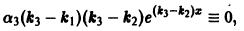
что невозможно, так как 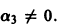 по предположению и
по предположению и  Значит, наше допущение неверно, и рассматриваемые функции являются линейно независимыми.
Значит, наше допущение неверно, и рассматриваемые функции являются линейно независимыми.
Замечание:
Линейная зависимость пары функций означает, что одна из функций получается из другой умножением на постоянную:
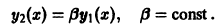
Вообще, если функции 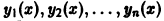 линейно зависимы на (a,b), то по крайней мере одна из них есть линейная комбинация остальных.
линейно зависимы на (a,b), то по крайней мере одна из них есть линейная комбинация остальных.
Задача:
Показать, что если система функций
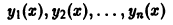
линейно независима на интервале (a, b), то и любая подсистема этой системы функций также линейно независима на (a, b).
Теорема:
Необходимое условие линейной зависимости функций. Если функции
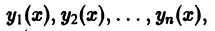
имеющие производные до порядка n — 1 включительно, Линейно зависимы на интервале (а, b), то на этом интервале определитель
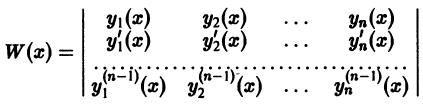
называемый определителем Вронского системы функций 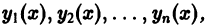 тождественно равен нулю:
тождественно равен нулю:
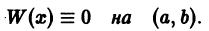
Ограничимся случаем n = 3. Пусть дважды дифференцируемые функции 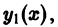
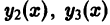 линейно зависимы на интервале (а, b). Значит, на (а, 6) выполняется тождество
линейно зависимы на интервале (а, b). Значит, на (а, 6) выполняется тождество
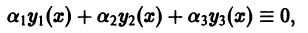
причем не все числа 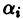 (i = 1, 2, 3) равны нулю. Для определенности будем считать, что
(i = 1, 2, 3) равны нулю. Для определенности будем считать, что 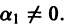 Разрешим тождество относительно
Разрешим тождество относительно 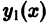 и дважды продифференцируем его:
и дважды продифференцируем его:
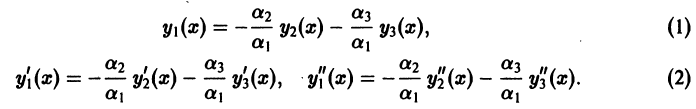
Составим определитель Вронского системы функций 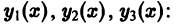
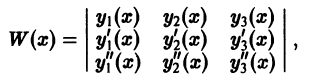
или, с учетом формул (1) и (2),
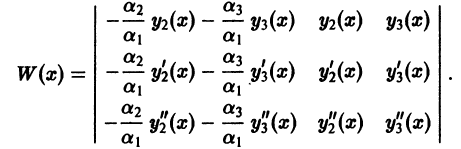
Первый столбец определителя является линейной комбинацией двух других при любом 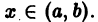 Такой определитель, как известно, равен нулю; следовательно
Такой определитель, как известно, равен нулю; следовательно 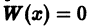
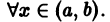
Рассуждением от противного легко доказывается следующая теорема.
Теорема:
Если определитель Вронского W(x) системы n функций не равен тождественно нулю в некотором интервале (а, b), то эти функции линейно независимы в этом интервале.
Для произвольной системы n — 1 раз дифференцируемых на (а,b) функций теорема, обратная теореме 5, неверна. Чтобы убедиться в этом, рассмотрим пример.
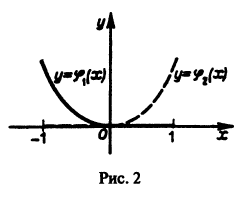
Для функций (рис. 2)
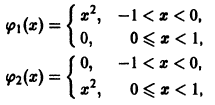
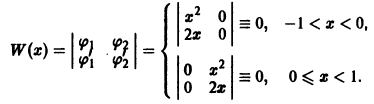
определитель Вронского на интервале (-1,1) тождественно равен нулю:
Однако, как легко видеть, функции 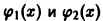 на интервале (-1,1) линейно независимы. Заметим, что в интервалах (-1,0) и (0,1) функции
на интервале (-1,1) линейно независимы. Заметим, что в интервалах (-1,0) и (0,1) функции 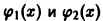 уже линейно зависимы. Можно несколько обобщить рассмотренный пример, взяв систему функций
уже линейно зависимы. Можно несколько обобщить рассмотренный пример, взяв систему функций
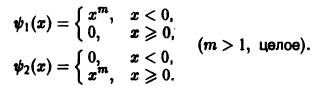
Эти функции линейно независимы в любом интервале, содержащем внутри себя точку х = 0, а вместе с тем их определитель Вронского тождественно равен нулю. При этом, скажем, функция 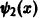 имеет всюду непрерывные производные, до порядка m — 1 включительно, и лишь производная m-го порядка терпит разрыв с конечным скачком в точке х = 0. Выбирая m достаточно большим, получаем систему функций, обладающих непрерывными производными любого нужного порядка.
имеет всюду непрерывные производные, до порядка m — 1 включительно, и лишь производная m-го порядка терпит разрыв с конечным скачком в точке х = 0. Выбирая m достаточно большим, получаем систему функций, обладающих непрерывными производными любого нужного порядка.
Задача:
Что можно сказать об определителе Вронского системы функций
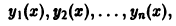
если только известно, что эти функции а) линейно зависимы; б) линейно независимы?
Теорема:
Необходимое условие линейной независимости решений. Если линейно независимые на интервале (а, b) функции 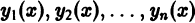 являются решениями линейного однородного дифференциального уравнения
являются решениями линейного однородного дифференциального уравнения
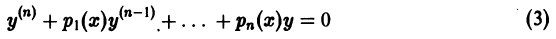
с непрерывными на [а, b] коэффициентами 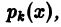 то определитель Вронского этой системы решений
то определитель Вронского этой системы решений
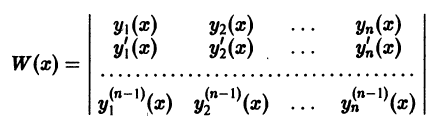
не может обратиться в нуль ни в одной точке интервала (а, b).
Ограничимся рассмотрением случая n = 3. Допустим, что в некоторой точке 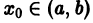 определитель Вронского равен нулю:
определитель Вронского равен нулю:
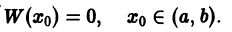
Составим систему трех линейных однородных алгебраических уравнений относительно 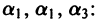
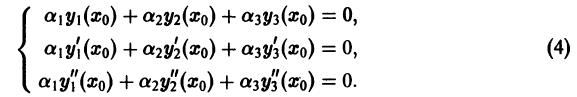
Определитель этой системы 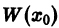 в силу допущения равен нулю, поэтому система имеет ненулевое решение
в силу допущения равен нулю, поэтому система имеет ненулевое решение  по крайней мере одно из чисел
по крайней мере одно из чисел 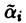 отлично от нуля.
отлично от нуля.
Рассмотрим функцию
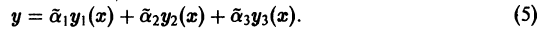
Она является линейной комбинацией решений 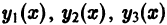 уравнения (3), и, значит, сама есть решение этого уравнения. Это решение в силу уравнений (4) удовлетворяет нулевым начальным условиям
уравнения (3), и, значит, сама есть решение этого уравнения. Это решение в силу уравнений (4) удовлетворяет нулевым начальным условиям
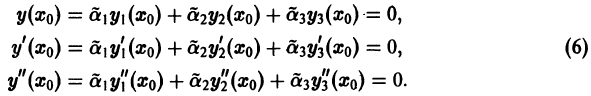
Таким начальным условиям, очевидно, удовлетворяет тривиальное решение 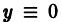 уравнения (3) и, по теореме о единственности решения, только это решение. Следовательно,
уравнения (3) и, по теореме о единственности решения, только это решение. Следовательно,
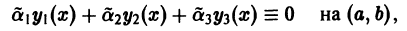
причем хотя бы одно из 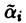 отлично от нуля. Таким образом, решения
отлично от нуля. Таким образом, решения 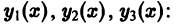 оказываются вопреки условию теоремы линейно зависимыми. Противоречие возникло в связи с допущением, что W(x) обращается в нуль в точке
оказываются вопреки условию теоремы линейно зависимыми. Противоречие возникло в связи с допущением, что W(x) обращается в нуль в точке 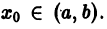 Значит, наше допущение неверно, и
Значит, наше допущение неверно, и 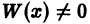 всюду в интервале (а, b).
всюду в интервале (а, b).
Из теорем 5 и 7 как следствие получаем следующую важную теорему.
Теорема:
Для того, чтобы частные решения 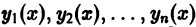 линейного однородного дифнциального уравнения (3) с непрерывными на отрезке [а, b] коэффициентами были линейно независимыми на интервале (a, b), необходимо и достаточно, чтобы определитель Вронского W(x) системы решений был отличен от нуля.
линейного однородного дифнциального уравнения (3) с непрерывными на отрезке [а, b] коэффициентами были линейно независимыми на интервале (a, b), необходимо и достаточно, чтобы определитель Вронского W(x) системы решений был отличен от нуля.
Необходимость условия прямо следует из теоремы 7.
Достаточность условия вытекает из того, что при линейной зависимости функций 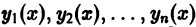 согласно теореме 5, имеем
согласно теореме 5, имеем 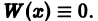 Поэтому если
Поэтому если 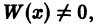 то функции
то функции 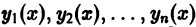 не могут быть линейно зависимыми, т. е. они в этом случае линейно независимы.
не могут быть линейно зависимыми, т. е. они в этом случае линейно независимы.
Задача:
Доказать, что два решения уравнения
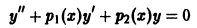
с непрерывными коэффициентами, имеющие максимум при одном и том же значении х, линейно зависимы.
Задача:
Доказать, что отношение двух любых линейно независимых решений уравнения
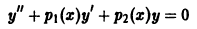
с непрерывными коэффициентами не может иметь точек максимума.
Задача:
Показать, что два линейно независимых решения 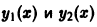 уравнения
уравнения
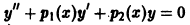
с непрерывными на отрезке [а, b] коэффициентами не могут обращаться в нуль при одном и том же значении 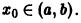
Структура общего решения линейного однородного дифференциального уравнения
Теорема:
О структуре общего решения линейного однородного дифференциального уравнения. Общим решением в области 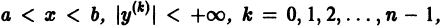 линейного однородного дифференциального уравнения
линейного однородного дифференциального уравнения
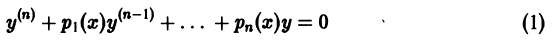
с непрерывными на отрезке [а, b] коэффициентами 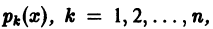 является линейная комбинация
является линейная комбинация

п линейно независимых на интервале (а, b) частных решений 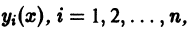 этого уравнения
этого уравнения 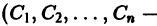 произвольные постоянные).
произвольные постоянные).
Будем исходить из определения общего решения и просто проверим, что семейство функций
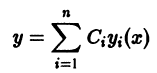
удовлетворяет условиям 1), 2) этого определения.
Функция у(х), определенная формулой (2), является решением дифференциального уравнения (1) при любых значениях постоянных 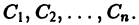 Это следует из того, что, как было установлено выше, любая линейная комбинация частных решений линейного однородного уравнения есть снова решение этого уравнения.
Это следует из того, что, как было установлено выше, любая линейная комбинация частных решений линейного однородного уравнения есть снова решение этого уравнения.
Для уравнения (1) при 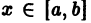 выполнены условия теоремой 1 существования и единственности решения задачи Коши; поэтому остается показать, что постоянные
выполнены условия теоремой 1 существования и единственности решения задачи Коши; поэтому остается показать, что постоянные 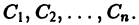 всегда можно подобрать так, чтобы удовлетворялись произвольно заданные начальные условия
всегда можно подобрать так, чтобы удовлетворялись произвольно заданные начальные условия
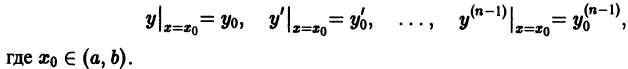
Ограничимся случаем, когда n = 3. Потребовав, чтобы решение
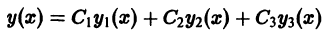
удовлетворяло поставленным начальным условиям, получим систему трех линейных алгебраических уравнений относительно 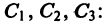
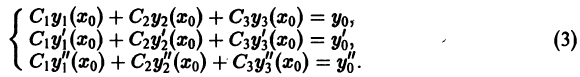
Определитель этой системы есть определитель Вронского 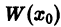 линейно независимой системы решений однородного уравнения (1), и, следовательно, отличен от нуля при любом
линейно независимой системы решений однородного уравнения (1), и, следовательно, отличен от нуля при любом 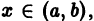 в частности при
в частности при 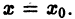 Поэтому система уравнений (3) однозначно разрешима относительно
Поэтому система уравнений (3) однозначно разрешима относительно 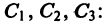 при любом
при любом 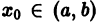 и при любых правых частях, т. е. при любых
и при любых правых частях, т. е. при любых 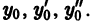 А это и означает возможность выбора таких значений
А это и означает возможность выбора таких значений 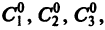 чтобы частное решение
чтобы частное решение
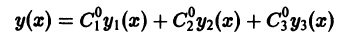
удовлетворяло поставленным начальным условиям, каковы бы они ни были.
Из теоремы 9 следует, что если известно п линейно независимых частных решений линейного однородного дифференциального уравнения n-го порядка, то всякое другое решение этого уравнения представляется в виде линейной комбинации этих частных решений и, значит, линейно зависимо с ними. Отсюда вытекает, что максимальное число линейно независимых решений однородного линейного дифференциального уравнения равно его порядку. Таким образом,
совокупность решений линейного однородного дифференциального уравнения образует линейное пространство, размерность которого равна порядку дифференциального уравнения.
Введем понятие фундаментальной системы решений.
Определение:
Совокупность любых п линейно независимых частных решений линейного однородного дифференциального уравнения n-го порядка называется его фундаментальной системой решений.
Теорема:
У каждого линейного однородного уравнения (1) с непрерывными коэффициентами  существует фундаментальная система решений (и даже бесконечное множество фундаментальных систем решений).
существует фундаментальная система решений (и даже бесконечное множество фундаментальных систем решений).
В самом деле, рассмотрим, например, однородное уравнение второго порядка

с непрерывными на отрезке {а, b] коэффициентами. Пусть 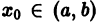 По теореме 1 уравнение (4) имеет решения
По теореме 1 уравнение (4) имеет решения

удовлетворяющие при 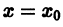 начальным условиям
начальным условиям
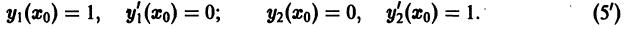
Определитель Вронского в точке 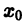 системы решений (5) отличен от нуля,
системы решений (5) отличен от нуля,
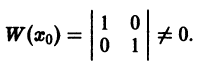
Следовательно, система решений (5) для уравнения (4) фундаментальна. Выбор начальных условий (5′) обеспечил построение одной фундаментальной системы. За начальные данные в точке  можно взять любую систему чисел:
можно взять любую систему чисел:

лишь бы определитель Вронского
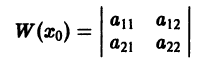
был отличен от нуля. Очевидно, таких систем чисел можно подобрать бесконечно много и построить бесконечно много фундаментальных систем решений для уравнения (4).
Задача:
Составить общее решение уравнения
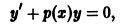
если известно ненулевое частное решение 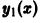 этого уравнения.
этого уравнения.
Теорема:
Если два уравнения вида
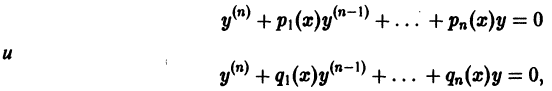
где функции 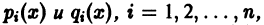 непрерывны на отрезке [a,b], имеют общую фундаментальную систему решений
непрерывны на отрезке [a,b], имеют общую фундаментальную систему решений 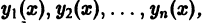 то эти уравнения совпадают, т. е.
то эти уравнения совпадают, т. е. 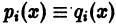 на отрезке [a, b].
на отрезке [a, b].
Таким образом, фундаментальная система решений вполне определяет линейное однородное уравнение (1), т.е. полностью определяет коэффициенты 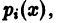 i = 1, 2,…, n, этого уравнения. Следовательно, можно поставить задачу о нахождении уравнения вида (1), имеющего заданную фундаментальную систему решений Представим дифференциальное уравнение с левой частью в виде определителя:
i = 1, 2,…, n, этого уравнения. Следовательно, можно поставить задачу о нахождении уравнения вида (1), имеющего заданную фундаментальную систему решений Представим дифференциальное уравнение с левой частью в виде определителя:
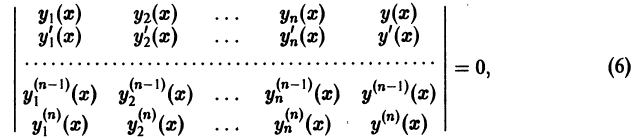
где у(х) — искомая функция, a 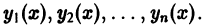 — заданная фундаментальная система решений. Уравнение (6) имеет в качестве решений функции
— заданная фундаментальная система решений. Уравнение (6) имеет в качестве решений функции
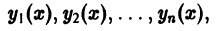
так как при подстановке вместо у(х) каждой из этих п функций два столбца определителя становятся тождественно равными и определитель обращается в нуль тождественно по 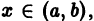 Разлагая определитель по элементам последнего столбца, получаем из (6) уравнение вида
Разлагая определитель по элементам последнего столбца, получаем из (6) уравнение вида
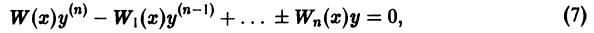
где W{х) — определитель Вронского системы функций 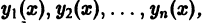 а
а
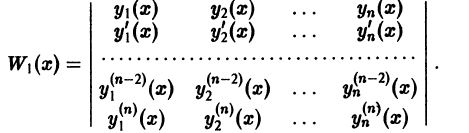
Определитель Вронского W(x) фундаментальной системы решений
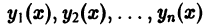
отличен от нуля во всем интервале (а, b). Разделив все члены уравнения (7) на 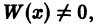 приведем это уравнение к виду (1):
приведем это уравнение к виду (1):
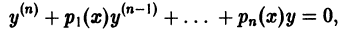
где, в частности, 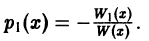
Можно показать, что если элементы 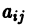 определителя
определителя  n-го порядка есть дифференцируемые функции аргумента х:
n-го порядка есть дифференцируемые функции аргумента х:
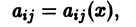
то производная определителя 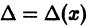 равна сумме n определителей:
равна сумме n определителей:
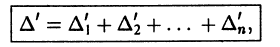
где 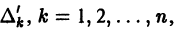 — определитель, получающийся из данного заменой элементов его k-ой строки производными от этих элементов. Например, для определителя Вронского системы функций
— определитель, получающийся из данного заменой элементов его k-ой строки производными от этих элементов. Например, для определителя Вронского системы функций 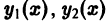 имеем
имеем
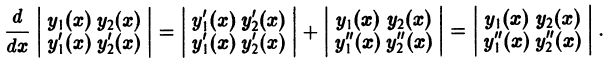
Нетрудно проверить, что 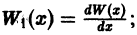 следовательно,
следовательно,
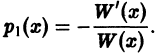
Интегрируя последнее равенство по х от X0 до х, получим формулу Остроградского— Лиувилля:
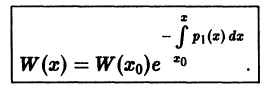
Задача:
Составить линейное дифференциальное уравнение второго порядка, имеющее решения
Показать, что функции 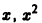 линейно независимы на интервале
линейно независимы на интервале 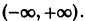 Убедиться в том, что определитель Вронского для этих функций равен нулю в точке х = 0. Почему это не противоречит необходимому условию линейной независимости системы решений линейного однородного дифференциального уравнения?
Убедиться в том, что определитель Вронского для этих функций равен нулю в точке х = 0. Почему это не противоречит необходимому условию линейной независимости системы решений линейного однородного дифференциального уравнения?
Линейные однородные дифференциальные уравнения с постоянными коэффициентами
Частный случай: уравнение второго порядка
Пусть имеем линейное однородное дифференциальное уравнение второго порядка

где р1, p2 — действительные числа. Чтобы найти общее решение этого уравнения, надо найти два его линейно независимых частных решения. Следуя Эйлеру, будем искать их в виде
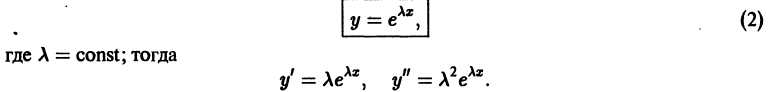
Подставляя эти выражения для у и ее производных в уравнение (1), получаем
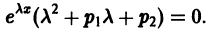
Так как 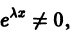 то должно выполняться равенство
то должно выполняться равенство
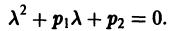
Следовательно, функция 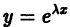 будет решением уравнения (1), т. е. будет обращать его в тождество по х, если
будет решением уравнения (1), т. е. будет обращать его в тождество по х, если 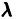 будет удовлетворять алгебраическому уравнению
будет удовлетворять алгебраическому уравнению

Уравнение (3) называется характеристическим уравнением по отношению к уравнению (1), а его левая часть 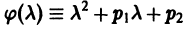 называется характеристическим многочленом.
называется характеристическим многочленом.
Уравнение (3) есть квадратное уравнение. Обозначим его корни через 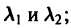 они могут быть
они могут быть
1) действительными и разными;
2) комплексными;
3) действительными и равными.
Рассмотрим каждый случай в отдельности.
- Если корни
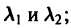 характеристического уравнения действительные и разные, то частными решениями уравнения (1) будут функции
характеристического уравнения действительные и разные, то частными решениями уравнения (1) будут функции
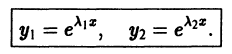
Эти решения линейно независимы 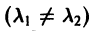 и, следовательно, образуют фундаментальную систему решений уравнения. Общее решение уравнения имеет вид
и, следовательно, образуют фундаментальную систему решений уравнения. Общее решение уравнения имеет вид
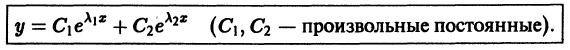
Пример:\
Найти общее решение уравнения
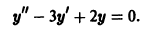
Составляем характеристическое уравнение:
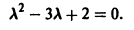
Оно имеет корни
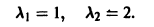
Отсюда получаем искомое общее решение
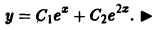
2. Пусть корни характеристического уравнения комплексные. Так как коэффициенты 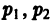 характеристического уравнения действительные, комплексные корни входят попарно сопряженными. Положим, что
характеристического уравнения действительные, комплексные корни входят попарно сопряженными. Положим, что
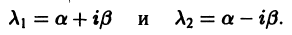
Частные решения дифференциального уравнения (1) можно записать в виде
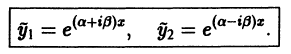
Это комплекснозначные функции действительного аргумента х, а мы будем заниматься лишь действительными решениями. С помощью формул Эйлера
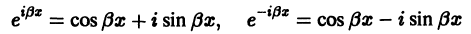
частные решения 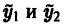 уравнения (1) можно представить в виде
уравнения (1) можно представить в виде
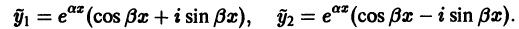
Воспользовавшись теоремой 4, получим, что частными решениями уравнения (1) будут также функции
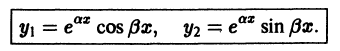
Эти решения линейно независимы, так как
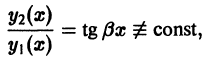
и, значит, составляют фундаментальную систему решений. Общее решение уравнения (1) в рассматриваемом случае имеет вид
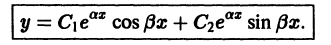
Пример:
Найти общее решение уравнения
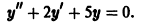
Составляем характеристическое уравнение:
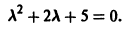
Оно имеет корни
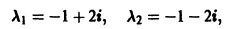
поэтому 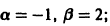 искомое общее решение
искомое общее решение
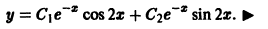
3. Пусть теперь корни характеристического уравнения действительные и равные. Одно частное решение
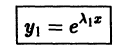
получаем сразу. Второе частное решение, линейно независимое с первым, будем искать в виде
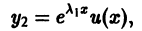
где u(х) — новая неизвестная функция. Дифференцируя, находим:
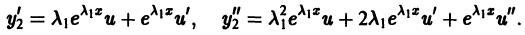
Подставляя полученные выражения в (1), получаем
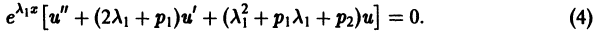
Так как 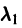 — корень характеристического уравнения, то
— корень характеристического уравнения, то
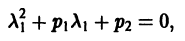
а так как 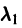 — двукратный корень, то и
— двукратный корень, то и
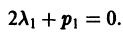
Следовательно, соотношение (4) примет вид
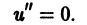
Отсюда
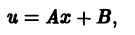
где А и В — постоянные. Можно, в частности, положить А = 1, В = 0; тогда
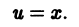
Таким образом, в качестве второго частного решения уравнения можно взять
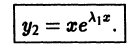
Это решение линейно независимо с первым, так как
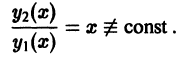
Решения 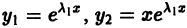 образуют фундаментальную систему решений уравнения (1), общее решение которого в этом случае имеет вид
образуют фундаментальную систему решений уравнения (1), общее решение которого в этом случае имеет вид
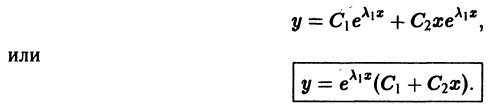
Пример:
Найти общее решение уравнения
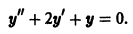
Характеристическое уравнение
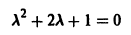
имеет кратные корни
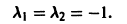
Поэтому общее решение исходного дифференциального уравнения:
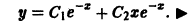
Замечание:
Пусть имеем линейное однородное дифференциальное уравнение (вообще, с переменными коэффициентами)
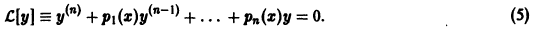
Пусть 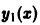 — частное решение уравнения. Введем новую искомую функцию u(х) соотношением
— частное решение уравнения. Введем новую искомую функцию u(х) соотношением
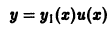
(разрешимым относительно u(х) в тех интервалах, где 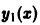 не обращается в нуль). Из этого соотношения найдем производные от у :
не обращается в нуль). Из этого соотношения найдем производные от у :
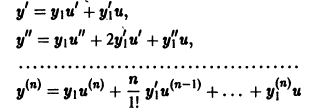
и подставим их в уравнение (5):
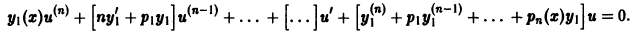
Для функции u(x) получаем опять уравнение порядка n, но коэффициент при u(х) есть 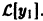 Он тождественно равен нулю, так как
Он тождественно равен нулю, так как 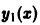 есть решение уравнения (5). Следовательно, в полученном уравнении порядок понизится, если ввести новую искомую функцию z(x) = u'(x). Разделив, кроме того, все члены последнего уравнения на
есть решение уравнения (5). Следовательно, в полученном уравнении порядок понизится, если ввести новую искомую функцию z(x) = u'(x). Разделив, кроме того, все члены последнего уравнения на 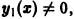 приведем его к виду
приведем его к виду
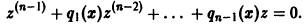
Итак, если известно частное решение уравнения (5), то задача интегрирования этого уравнения приводится к интегрированию линейного однородного уравнения порядка n — 1. Можно показать, что если известны два частных линейно независимых решения, то порядок уравнения может быть понижен на две единицы. Вообще, если известно r частных линейно независимых решений линейного однородного дифференциального уравнения, то порядок этого уравнения может быть понижен на r единиц.
Физические приложения: уравнение колебаний
Линейные дифференциальные уравнения с постоянными коэффициентами возникают в задачах о механических и электрических колебаниях. Рассмотрим уравнение свободных механических колебаний, причем независимой переменной будем считать время t:

где у — отклонение колеблющейся точки от положения равновесия, m — масса точки, h — коэффициент трения (считаем, что сила трения пропорциональна скорости), к > 0 — коэффициент упругости восстанавливающей силы (считаем, что эта сила пропорциональна отклонению). Характеристическое уравнение для (6)
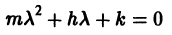
имеет корни
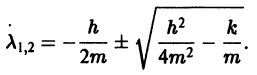
Если трение достаточно велико,  то эти корни действительные и отрицательные. Общее решение уравнения (6) в этом случае имеет вид
то эти корни действительные и отрицательные. Общее решение уравнения (6) в этом случае имеет вид

Так как 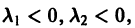 то из (7) заключаем, что при большом трении отклонение точки от положения равновесия с возрастанием t стремится к нулю, не совершая колебаний. Если трение мало,
то из (7) заключаем, что при большом трении отклонение точки от положения равновесия с возрастанием t стремится к нулю, не совершая колебаний. Если трение мало, 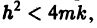 то характеристическое уравнение имеет комплексно сопряженные корни
то характеристическое уравнение имеет комплексно сопряженные корни 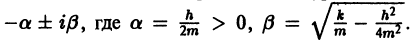 Общее решение уравнения (6) в этом случае определяется формулой
Общее решение уравнения (6) в этом случае определяется формулой
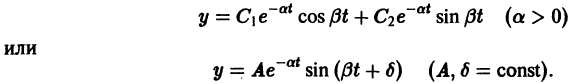
Отсюда видно, что в случае малого трения происходят затухающие колебания.
Пусть теперь трение отсутствует, т. е. h = 0. В этом случае характеристическое уравнение 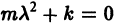 имеет чисто мнимые корни
имеет чисто мнимые корни 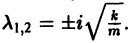 Решение уравнения (6) имеет вид
Решение уравнения (6) имеет вид
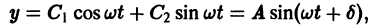
где 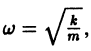 т. е. в этом случае происходят незатухающие гармонические колебания с частотой
т. е. в этом случае происходят незатухающие гармонические колебания с частотой 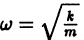 произвольными амплитудой А и начальной фазой
произвольными амплитудой А и начальной фазой 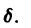
Задача:
При каких 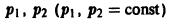
1) все решения уравнения
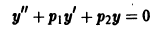
стремятся к нулю при 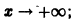
2) каждое решение уравнения
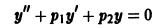
обращается в нуль на бесконечном множестве точек х?
Общий случай: уравнение произвольного порядка
Рассмотрим теперь линейное однородное дифференциальное уравнение произвольного порядка 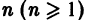 с постоянными коэффициентами
с постоянными коэффициентами
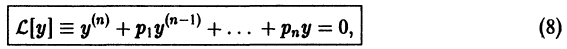
где  действительные числа. Общее решение дифференциального уравнения (8) находим так же, как и в случае уравнения второго порядка.
действительные числа. Общее решение дифференциального уравнения (8) находим так же, как и в случае уравнения второго порядка.
- Ищем решение в виде
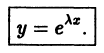
Подставляя вместо у величину 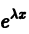 в уравнение (8), получаем
в уравнение (8), получаем
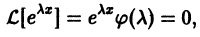
что приводит к характеристическому уравнению
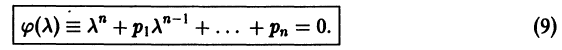
2, Находим корни
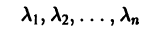
характеристического уравнения.
3. По характеру корней выписываем частные линейно независимые решения уравнения (8), руководствуясь тем, что:
а) Каждому действительному однократному корню 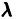 характеристического уравнения соответствует частное решение
характеристического уравнения соответствует частное решение
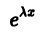
уравнения (8).
б) Каждой паре однократных комплексно сопряженных корней
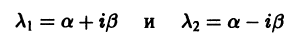
соответствуют два линейно независимых частных решения
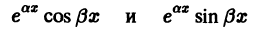
уравнения (8).
в) Каждому действительному корню 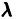 кратности r соответствует r линейно независимых частных решений
кратности r соответствует r линейно независимых частных решений
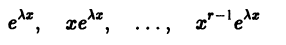
уравнения (8).
Рассмотрим случай в) подробнее. Пусть число 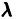 есть корень кратности г характеристического уравнения
есть корень кратности г характеристического уравнения 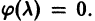 Функцию
Функцию 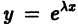 будем рассматривать как функцию двух аргументов:
будем рассматривать как функцию двух аргументов: 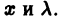 Она имеет непрерывные производные по х и по
Она имеет непрерывные производные по х и по 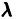 всех порядков, причем
всех порядков, причем
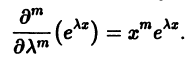
Поэтому частные производные функции 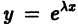 по х и по
по х и по 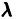 не зависят от порядка дифференцирования (операции дифференцирования функции у по x и по
не зависят от порядка дифференцирования (операции дифференцирования функции у по x и по 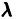 перестановочны), так что
перестановочны), так что
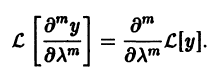
Воспользовавшись этой перестановочностью, а также тем, что
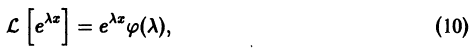
получим
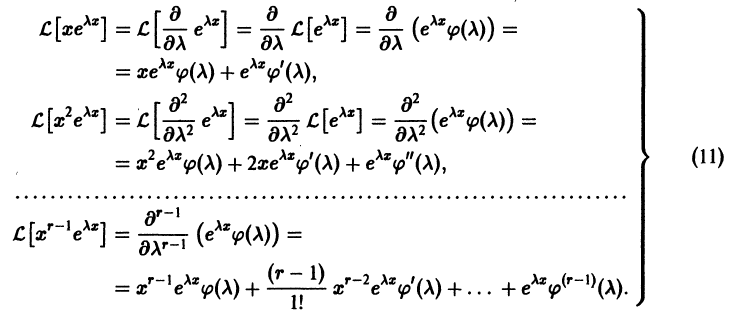
Если 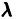 есть r-кратный корень характеристического уравнения
есть r-кратный корень характеристического уравнения 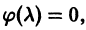 то
то
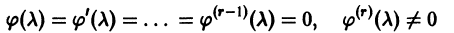
и, стало быть, правые части (10) и (11) тождественно по х равны нулю:
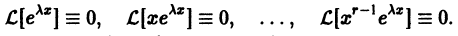
Это означает, что функции  являются в этом случае решениями уравнения (8). Легко проверить, что функции
являются в этом случае решениями уравнения (8). Легко проверить, что функции 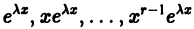 линейно независимы на любом интервале (а, b) изменения х.
линейно независимы на любом интервале (а, b) изменения х.
г) Приведенные в пункте в) рассуждения сохраняют силу и для комплексных корней. Поэтому каждой паре комплексно сопряженных корней 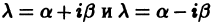 кратности
кратности 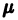 отвечает
отвечает 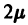 частных решений уравнения (8):
частных решений уравнения (8):
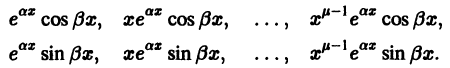
4. Число построенных таким образом частных решений уравнения (8) равно порядку п этого уравнения. Можно показать, что все эти решения линейно независимы в совокупности. Имея n линейно независимых частных решений 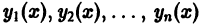 уравнения (8), получаем общее решение этого уравнения,
уравнения (8), получаем общее решение этого уравнения,
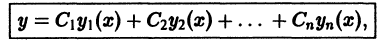
где 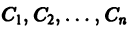 — произвольные постоянные. Пример 4. Найти общее решение уравнения
— произвольные постоянные. Пример 4. Найти общее решение уравнения
Пример:
Найти общее решение уравнения
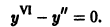
1. Составляем характеристическое уравнение:

2. Находим корни характеристического уравнения:
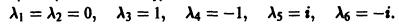
3. По характеру корней выписываем частные линейно независимые решения дифференциального уравнения:
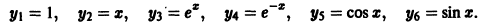
4. Общее решение дифференциального уравнения имеет вид
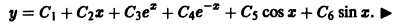
Схема решения линейного дифференциального уравнения с постоянными коэффициентами

Уравнения, приводящие к уравнениям с постоянными коэффициентами
Существуют линейные дифференциальные уравнения с переменными коэффициентами, которые с помощью замены переменных преобразуются в уравнения с постоянными коэффициентами. К их числу принадлежит уравнение Эйлера
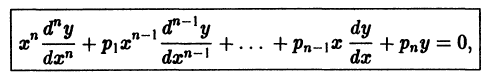
где 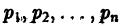 — постоянные числа. Ограничимся рассмотрением уравнения Эйлера 2-го порядка (оно встречается в задачах математической физики):
— постоянные числа. Ограничимся рассмотрением уравнения Эйлера 2-го порядка (оно встречается в задачах математической физики):
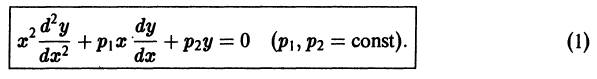
Положим 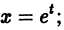 тогда
тогда
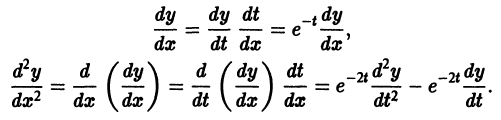
Подставляя выражения для  в (1), получим дифференциальное уравнение с постоянными коэффициентами
в (1), получим дифференциальное уравнение с постоянными коэффициентами
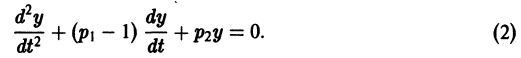
Последнее интегрируется обычным приемом: составляем характеристическое уравнение

находим его корни и по характеру корней выписываем общее решение уравнения (2), после чего возвращаемся к старой переменной х.
Пример:
Найти общее решение уравнения
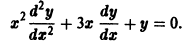
Замена переменной 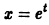 приводит к уравнению
приводит к уравнению
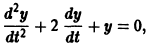
характеристическое уравнение которого
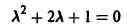
имеет корни 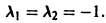 Общее решение преобразованного уравнения равно
Общее решение преобразованного уравнения равно
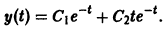
Учитывая, что 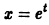 , для общего решения исходного уравнения получаем выражение
, для общего решения исходного уравнения получаем выражение
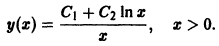
Замечание:
Для преобразованного уравнения (2) в случае действительных и различных корней характеристического уравнения (3) частные решения имеют вид
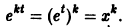
Поэтому можно сразу задаться этим видом частного решения. Подставляя 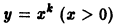 в уравнение (1), получим для к уравнение
в уравнение (1), получим для к уравнение

совпадающее с (3). Каждому простому действительному корню уравнения (4) отвечает частное решение
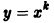
уравнения (1); двукратному корню отвечают два решения
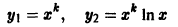
уравнения (1). Паре комплексных сопряженных корней 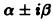 уравнения (4) будут соответствовать два решения
уравнения (4) будут соответствовать два решения
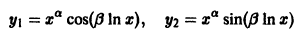
уравнения (1).
Замечание:
Уравнение
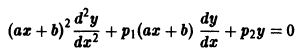
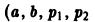 — постоянные числа) подстановкой
— постоянные числа) подстановкой 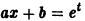 также приводится к уравнению с постоянными коэффициентами.
также приводится к уравнению с постоянными коэффициентами.
Линейные неоднородные дифференциальные уравнения
Линейное неоднородное дифференциальное уравнение n-го порядка имеет вид
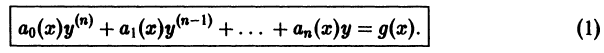
Здесь  — заданные на некотором интервале
— заданные на некотором интервале 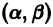 функции. Если
функции. Если 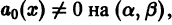 то после деления на
то после деления на 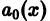 получим уравнение
получим уравнение
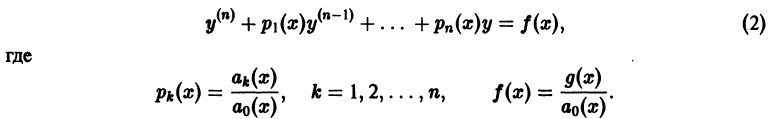
Из теоремы 1 существования и единственности решения задачи Коши получаем:
если на отрезке [а, b] коэффициенты 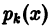 и правая часть f(х) уравнения (2) непрерывны, то это уравнение имеет единственное решение, удовлетворяющее условиям
и правая часть f(х) уравнения (2) непрерывны, то это уравнение имеет единственное решение, удовлетворяющее условиям
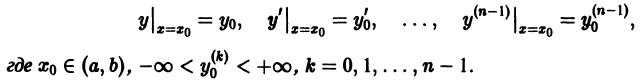
Уравнение (2) можно записать в виде

где, как и выше,
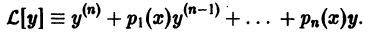
Теорема:
Если 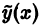 есть решение неоднородного уравнения
есть решение неоднородного уравнения
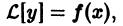
а 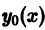 есть решение соответствующего однородного уравнения
есть решение соответствующего однородного уравнения
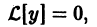
то сумма 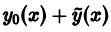 есть решение неоднородного уравнения.
есть решение неоднородного уравнения.
По условию, 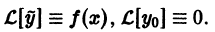 В силу линейности оператора
В силу линейности оператора 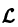 имеем
имеем
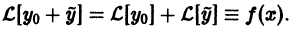
Это означает, что функция 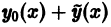 есть решение уравнения
есть решение уравнения 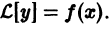
Теорема:
Если 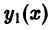 есть решение уравнения
есть решение уравнения
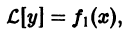
а 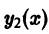 есть решение уравнения
есть решение уравнения
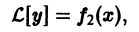
та функция 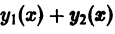 есть решение уравнения
есть решение уравнения
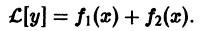
По условию, 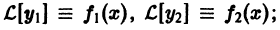 используя линейность оператора
используя линейность оператора 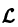 , получаем
, получаем
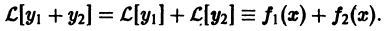
Последнее означает, что функция 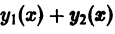 есть решение уравнения
есть решение уравнения 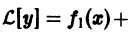
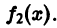
Теорема выражает так называемый принцип суперпозиции (наложения).
Теорема:
Если уравнение
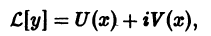
где все коэффициенты 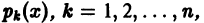 и функции U(x) и V(x) действительные, имеет решение
и функции U(x) и V(x) действительные, имеет решение 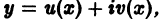 то действительная часть решения и(х) и его мнимая часть v(x) являются соответственно решениями уравнений
то действительная часть решения и(х) и его мнимая часть v(x) являются соответственно решениями уравнений
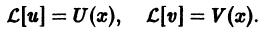
По условию имеем
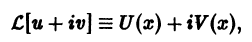
или
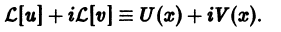
Отсюда получаем:
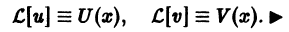
Теорема:
О структуре общего решения линейного неоднородного дифференциального уравнения.
Общее решение в области 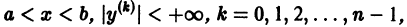 уравнения
уравнения
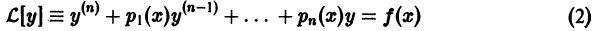
с непрерывными на отрезке [а, b] коэффициентами 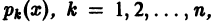 и правой частью f(x) равно сумме общего решения
и правой частью f(x) равно сумме общего решения
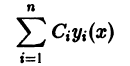
соответствующего однородного уравнения и какого-нибудь частного решения 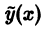 неоднородного уравнения, т. е.
неоднородного уравнения, т. е.
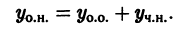
Надо доказать, что
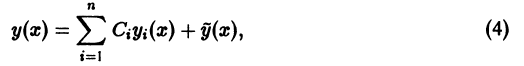
где 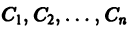 — произвольные постоянные, a
— произвольные постоянные, a 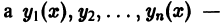 линейно независимые решения соответствующего однородного уравнения
линейно независимые решения соответствующего однородного уравнения  является общим решением неоднородного уравнения
является общим решением неоднородного уравнения
Будем исходить из определения общего решения и просто проверим, что семейство функций у(х), определяемое формулой (4), удовлетворяет условиям 1) и 2), содержащимся в этом определении.
В самом деле, функция у(х), определяемая формулой (4), является решением уравнения (2) при любых значениях постоянных, поскольку сумма какого-либо решения неоднородного уравнения и любого решения соответствующего однородного уравнения есть решение неоднородного уравнения 
Так как для уравнения (2) при 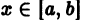 выполнены условия теоремы 1 существования и единственности решения задачи Коши, то остается показать, что подбором постоянных
выполнены условия теоремы 1 существования и единственности решения задачи Коши, то остается показать, что подбором постоянных 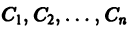 в (4) можно удовлетворить произвольно заданным начальным условиям
в (4) можно удовлетворить произвольно заданным начальным условиям
где 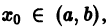 т.е. можно решить любую задачу Коши. Ограничимся случаем, когда n = 3. Потребовав, чтобы решение (4) удовлетворяло начальным условиям (5), приходим к системе уравнений для отыскания
т.е. можно решить любую задачу Коши. Ограничимся случаем, когда n = 3. Потребовав, чтобы решение (4) удовлетворяло начальным условиям (5), приходим к системе уравнений для отыскания 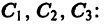
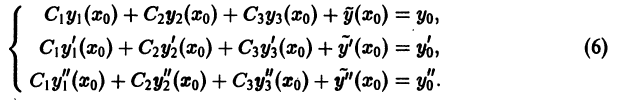
Эта линейная по отношению к 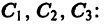 система трех уравнений с тремя неизвестными допускает единственное решение относительно
система трех уравнений с тремя неизвестными допускает единственное решение относительно 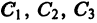 при произвольных правых частях, так как определитель этой системы есть определитель Вронского W(Xo) для линейно независимой системы решений соответствующего однородного уравнения и, следовательно, отличен от нуля в любой точке
при произвольных правых частях, так как определитель этой системы есть определитель Вронского W(Xo) для линейно независимой системы решений соответствующего однородного уравнения и, следовательно, отличен от нуля в любой точке 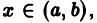 в частности в точке
в частности в точке 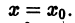 Значит, какова бы ни была тройка чисел
Значит, какова бы ни была тройка чисел 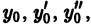 найдется решение
найдется решение 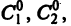
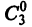 системы (6) такое, что функция
системы (6) такое, что функция
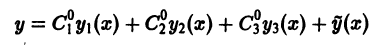
будет решением дифференциального уравнения (2), удовлетворяющим начальным условиям
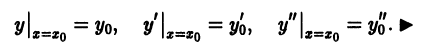
Из этой теоремы следует, что задача нахождения общего решения линейного неоднородного уравнения сводится к отысканию какого-либо частного решения этого неоднородного уравнения и общего решения соответствующего однородного уравнения.
Пример:
Найти общее решение уравнения
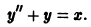
Нетрудно заметить, что функция
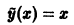
является частным решением данного неоднородного уравнения. Чтобы найти общее решение этого уравнения, остается отыскать общее решение соответствующего однородного уравнения

Это уравнение есть линейное однородное уравнение с постоянными коэффициентами. Характеристическое уравнение, соответствующее уравнению (*), есть
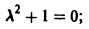
корни его 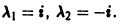 Поэтому общее решение уравнения (*) имеет вид
Поэтому общее решение уравнения (*) имеет вид
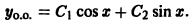
Общее решение исходного неоднородного уравнения:
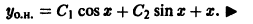
Интегрирование линейного неоднородного дифференциального уравнения методом вариации постоянных
Частный случай: уравнение второго порядка
Начнем для простоты со случая уравнения второго порядка. Пусть имеем дифференциальное уравнение
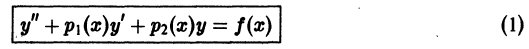
(функции 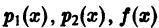 непрерывны на [а, b]) и пусть известна фундаментальная система
непрерывны на [а, b]) и пусть известна фундаментальная система 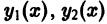 решений соответствующего однородного уравнения
решений соответствующего однородного уравнения
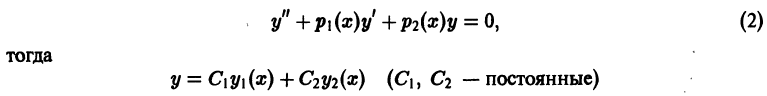
общее решение уравнения (2).
Заметим, что это предположение является весьма стеснительным, так как общего метода отыскания решений линейных однородных уравнений порядка 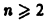 с переменными коэффициентами не существует.
с переменными коэффициентами не существует.
Для интегрирования неоднородного уравнения (1) применим метод вариации постоянных (метод Лагранжа), который состоит в следующем. Будем искать решение неоднородного уравнения (1) в виде
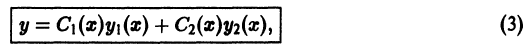
где 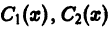 — новые неизвестные функции от х. Для их нахождения необходимы два уравнения, содержащие эти функции. Естественно, что функции
— новые неизвестные функции от х. Для их нахождения необходимы два уравнения, содержащие эти функции. Естественно, что функции 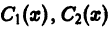 должны удовлетворять тому уравнению, которое получится, если в исходное уравнение подставить вместо у(х) выражение
должны удовлетворять тому уравнению, которое получится, если в исходное уравнение подставить вместо у(х) выражение 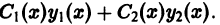
Наложим на функции 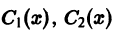 еще одно дополнительное условие. Продифференцируем (3),
еще одно дополнительное условие. Продифференцируем (3),
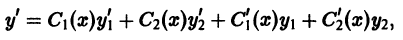
и в качестве дополнительного условия, налагаемого на С1, С2, возьмем следующее (целесообразность этого будет видна из дальнейшего):
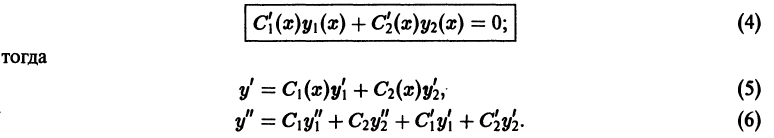
Подставляя выражения для 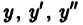 из (3), (5), (6) в исходное уравнение (1), после элементарной группировки слагаемых получаем
из (3), (5), (6) в исходное уравнение (1), после элементарной группировки слагаемых получаем
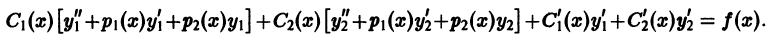
Выражения в квадратных скобках тождественно равны нулю, поскольку 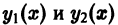 есть решения однородного уравнения (2). Следовательно, результат подстановки
есть решения однородного уравнения (2). Следовательно, результат подстановки  в (1) таков:
в (1) таков:
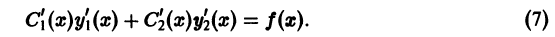
Значит, функция 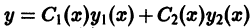 будет решением неоднородного дифференциального уравнения (1), если функции
будет решением неоднородного дифференциального уравнения (1), если функции 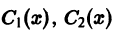 будут удовлетворять одновременно уравнениям (4) и (7), т. е. системе
будут удовлетворять одновременно уравнениям (4) и (7), т. е. системе
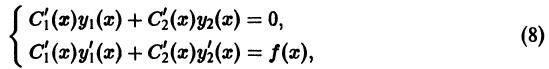
определитель которой есть определитель Вронского линейно независимых решений 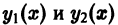 уравнения (2) и, следовательно, отличен от нуля всюду в интервале (а, b). Решаем эту систему как линейную алгебраическую систему относительно
уравнения (2) и, следовательно, отличен от нуля всюду в интервале (а, b). Решаем эту систему как линейную алгебраическую систему относительно 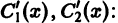
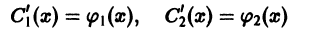
(здесь 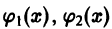 — известные функции) и интегрируем:
— известные функции) и интегрируем:
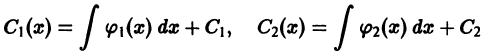
(здесь С1, С2 — постоянные интегрирования). Подставляя эти выражения для 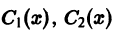 в (3), найдем общее решение неоднородного дифференциального уравнения (1):
в (3), найдем общее решение неоднородного дифференциального уравнения (1):
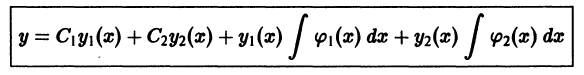
(C1, C2 — произвольные постоянные). Итак,
если известна фундаментальная система решений соответствующего однородного уравнения, то общее решение неоднородного уравнения может быть найдено с помощью квадратур.
Пример:
Найти общее решение уравнения
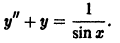
Рассмотрим однородное уравнение, соответствующее данному неоднородному:
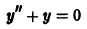
— это есть линейное уравнение с постоянными коэффициентами. Функции
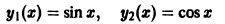
образуют его фундаментальную систему решений. Будем искать решение исходного уравнения в виде

Система (8) для определения 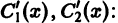 в данном случае примет вид
в данном случае примет вид
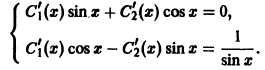
Решая эту систему относительно 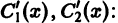 получаем:
получаем:
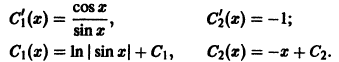
Подставляя найденные выражения для 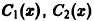 в (*), найдем общее решение данного уравнения:
в (*), найдем общее решение данного уравнения:
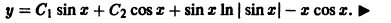
Общий случай: уравнение произвольного порядка
Для интегрирования линейного неоднородного дифференциального уравнения n-го порядка 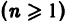
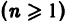
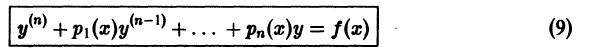
поступаем аналогично.
Пусть 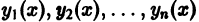 — известная фундаментальная система решений соответствующего однородного уравнения. Будем искать решение уравнения (9) в виде
— известная фундаментальная система решений соответствующего однородного уравнения. Будем искать решение уравнения (9) в виде

где 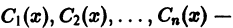 новые неизвестные функции.
новые неизвестные функции.
Чтобы найти п функций 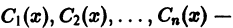 надо составить систему из п уравнений, содержащих эти функции. При составлении такой системы уравнений можно n — 1 уравнений взять произвольно и затем составить n-е уравнение, исходя из требования, чтобы функция у(х), определенная формулой (10), удовлетворяла уравнению (9). В качестве первых n — 1 уравнений возьмем следующие:
надо составить систему из п уравнений, содержащих эти функции. При составлении такой системы уравнений можно n — 1 уравнений взять произвольно и затем составить n-е уравнение, исходя из требования, чтобы функция у(х), определенная формулой (10), удовлетворяла уравнению (9). В качестве первых n — 1 уравнений возьмем следующие:
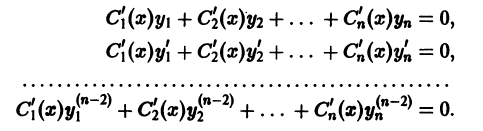
Тогда, чтобы функция у(х), определенная формулой (10), удовлетворяла уравнению (9), надо на функции 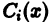 наложить условие
наложить условие
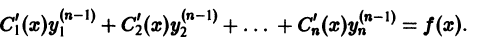
Для определения 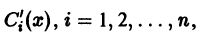 получаем систему
получаем систему
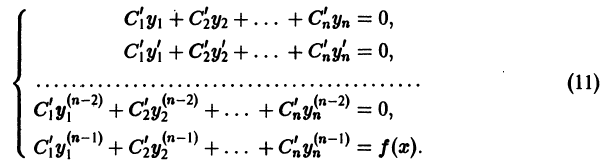
Определитель этой системы есть определитель Вронского фундаментальной системы решений однородного уравнения и, следовательно, отличен от нуля всюду в интервале (а, 6). Поэтому система (11) однозначно разрешима относительно 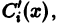 i = 1, 2, …, n. Решая ее, находим
i = 1, 2, …, n. Решая ее, находим 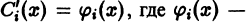 известные функции, откудa
известные функции, откудa
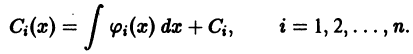
Подставляя найденные выражения для 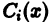 в (10), получаем общее решение у(х) исходного уравнения (9):
в (10), получаем общее решение у(х) исходного уравнения (9):
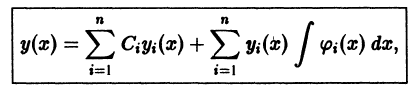
где 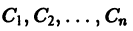 — произвольные постоянные.
— произвольные постоянные.
Неоднородные линейные дифференциальные уравнения с постоянными коэффициентами
В предыдущем параграфе был рассмотрен общий метод решения неоднородного линейного дифференциального уравнения — метод вариации постоянных. В случае дифференциального уравнения с постоянными коэффициентами частное решение неоднородного уравнения иногда бывает возможно найти проще — методом подбора. Рассмотрим некоторые виды уравнений, допускающие применение этого метода:
- Уравнение вида
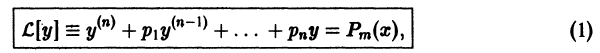
где 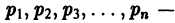 действительные числа,
действительные числа, 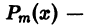 данный многочлен m-й степени,
данный многочлен m-й степени,
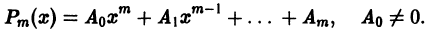
Характеристическое уравнение для соответствующего (1) однородного уравнения имеет вид
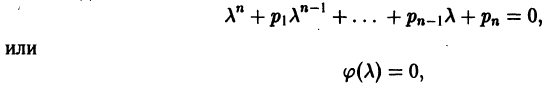
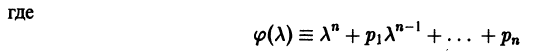
-характеристический многочлен.
Если коэффициент 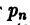 отличен от нуля, т. е.
отличен от нуля, т. е. 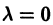 не является корнем характеристического уравнения
не является корнем характеристического уравнения 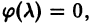 то существует частное решение
то существует частное решение 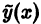 уравнения (1), имеющее тоже вид многочлена степени m. Действительно, беря
уравнения (1), имеющее тоже вид многочлена степени m. Действительно, беря 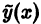 в виде
в виде
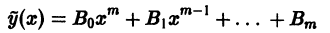
 неопределенные коэффициенты), подставляя его в уравнение (1) и сравнивая коэффициенты при одинаковых степенях х в левой и правой частях, получаем для определения коэффициентов
неопределенные коэффициенты), подставляя его в уравнение (1) и сравнивая коэффициенты при одинаковых степенях х в левой и правой частях, получаем для определения коэффициентов 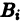 систему линейных алгебраических уравнений, которая всегда разрешима, если
систему линейных алгебраических уравнений, которая всегда разрешима, если 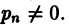 В самом деле, приравнивая коэффициенты при
В самом деле, приравнивая коэффициенты при 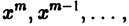 имеем:
имеем:
если  не является корнем характеристического уравнения
не является корнем характеристического уравнения  то существует частное решение
то существует частное решение  уравнения (1), имеющее вид многочлена, степень которого равна степени многочлена, стоящего в правой части уравнения (1):
уравнения (1), имеющее вид многочлена, степень которого равна степени многочлена, стоящего в правой части уравнения (1):
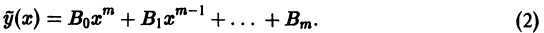
Предположим теперь, что 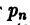 = 0, причем для большей общности допустим, что и
= 0, причем для большей общности допустим, что и
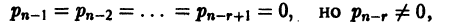
т.е. 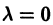 является г-кратным корнем
является г-кратным корнем 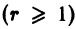 характеристического уравнения
характеристического уравнения 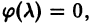 При этом уравнение (1) имеет вид
При этом уравнение (1) имеет вид
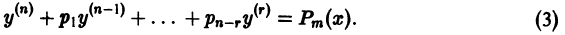
Полагая 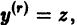 приходим к предыдущему случаю; следовательно, существует частное решение уравнения (3), имеющее вид
приходим к предыдущему случаю; следовательно, существует частное решение уравнения (3), имеющее вид
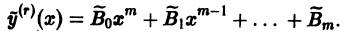
Отсюда получаем, что 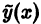 является многочленом степени m + r, причем члены, содержащие х в степени r — 1 и ниже, будут иметь произвольные постоянные коэффициенты, которые могут быть, в частности, выбраны равными нулю. Тогда частное решение примет вид
является многочленом степени m + r, причем члены, содержащие х в степени r — 1 и ниже, будут иметь произвольные постоянные коэффициенты, которые могут быть, в частности, выбраны равными нулю. Тогда частное решение примет вид
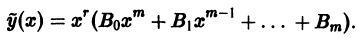
Итак,
если 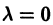 есть корень кратности
есть корень кратности 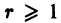 характеристического уравнения
характеристического уравнения 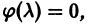 то частное решение
то частное решение 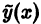 уравнения (1) надо искать в виде произведения
уравнения (1) надо искать в виде произведения 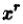 на многочлен
на многочлен 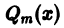 степени m с неопределенными коэффициентами:
степени m с неопределенными коэффициентами:
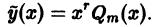
Пример:
Найти частное решение уравнения
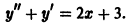
Характеристическое уравнение
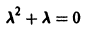
имеет корни 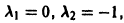 поэтому
поэтому 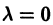 есть простой корень (r = 1) этого уравнения. В правой части многочлен первой степени (m = 1), поэтому частное решение неоднородного дифференциального уравнения следует искать в виде
есть простой корень (r = 1) этого уравнения. В правой части многочлен первой степени (m = 1), поэтому частное решение неоднородного дифференциального уравнения следует искать в виде
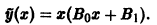
Подставляя 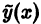 в уравнение и сравнивая коэффициенты при одинаковых степенях х, найдем, что
в уравнение и сравнивая коэффициенты при одинаковых степенях х, найдем, что 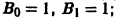 поэтому искомое частное решение будет
поэтому искомое частное решение будет
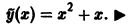
2. Уравнение вида
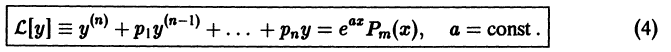
Частное решение 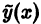 этого уравнения будем искать в виде
этого уравнения будем искать в виде
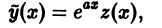
где z = z(x) — функция от х, которая должна быть определена из условия

Тогда имеем:
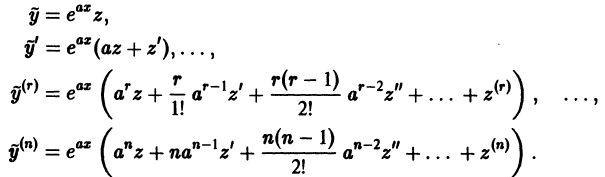
Умножим функции  соответственно на
соответственно на 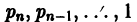 и сложим полученные результаты, группируя слагаемые по столбцам:
и сложим полученные результаты, группируя слагаемые по столбцам:
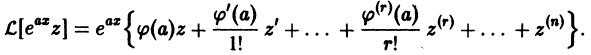
Здесь 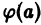 есть результат подстановки в характеристический многочлен
есть результат подстановки в характеристический многочлен 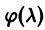 значения
значения 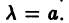 Отсюда следует, что для получения тождества (5) надо определить функцию z(x) как решение уравнения
Отсюда следует, что для получения тождества (5) надо определить функцию z(x) как решение уравнения
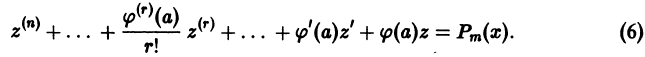
Это линейное неоднородное уравнение с постоянными коэффициентами, его правая часть — многочлен. Поэтому частное решение уравнения (6) надо искать в виде многочлена 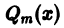 степени m, если
степени m, если 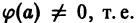 когда число а не есть корень характеристического уравнения
когда число а не есть корень характеристического уравнения 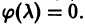 Если же число а окажется корнем характеристического уравнения кратности
Если же число а окажется корнем характеристического уравнения кратности 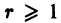 , то
, то
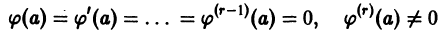
и решение уравнения (6) надо искать в виде 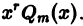 Поэтому частное решение
Поэтому частное решение 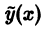 исходного уравнения (4) надо искать в виде
исходного уравнения (4) надо искать в виде

если число а не есть корень характеристического уравнения 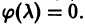 , и в виде
, и в виде

если число а есть корень характеристического уравнения кратности 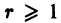 .
.
Здесь 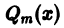 — многочлен степени m с неопределенными коэффициентами,
— многочлен степени m с неопределенными коэффициентами,
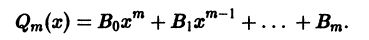
Пример:
Найти частное решение уравнения
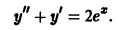
Характеристическое уравнение
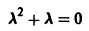
имеет корни 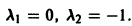 Правая часть уравнения представляет собой произведение
Правая часть уравнения представляет собой произведение 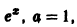 на многочлен нулевой степени (m = 0). Так как число а, равное единице, не является корнем характеристического уравнения, частное решение
на многочлен нулевой степени (m = 0). Так как число а, равное единице, не является корнем характеристического уравнения, частное решение 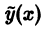 уравнения надо искать в виде
уравнения надо искать в виде
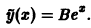
Подставляя 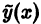 в уравнение, сокращая на
в уравнение, сокращая на 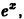 найдем В = 1, откуда
найдем В = 1, откуда
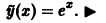
Пример:
Указать вид частного решения уравнения
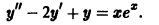
Характеристическое уравнениe
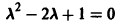
имеет корни 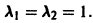 В данном случае
В данном случае
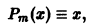
т.е. m = 1 и число а, равное единице, является двукратным корнем (r = 2) характеристического уравнения. Поэтому частное решение 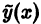 следует искать в виде
следует искать в виде
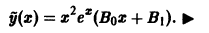
3. Приведенные выше рассуждения остаются справедливыми и при комплексном а. Поэтому, если правая часть линейного дифференциального уравнения
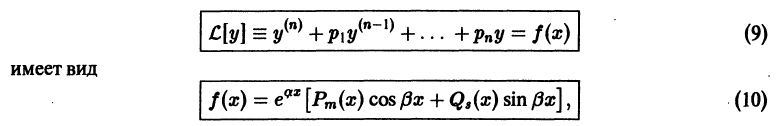
где 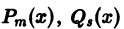 — многочлены степеней m и s соответственно, то поступим так. Преобразуем тригонометрические функции по формулам Эйлера к показательным:
— многочлены степеней m и s соответственно, то поступим так. Преобразуем тригонометрические функции по формулам Эйлера к показательным:
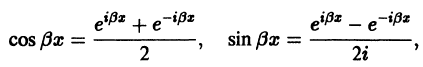
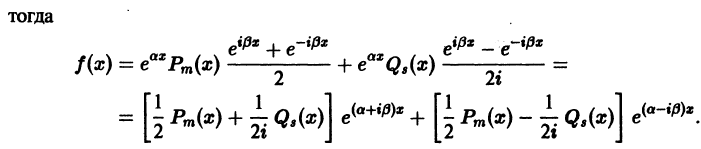
В квадратных скобках стоят многочлены, имеющие степень, равную наивысшей степени многочленов 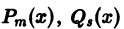 . Обозначив эти многочлены через М(х) и N(x), получим в правой части дифференциального уравнения выражение вида
. Обозначив эти многочлены через М(х) и N(x), получим в правой части дифференциального уравнения выражение вида
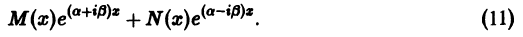
Для каждого слагаемого правой части можно применить указанное правило: если 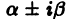 не являются корнями характеристического уравнения, то частное решение дифференциального уравнения можно искать в виде (11); если же числа
не являются корнями характеристического уравнения, то частное решение дифференциального уравнения можно искать в виде (11); если же числа 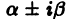 являются корнями характеристического уравнения кратности
являются корнями характеристического уравнения кратности 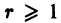 , то частное решение приобретает еще множитель
, то частное решение приобретает еще множитель 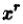 .
.
Если опять вернуться к тригонометрическим функциям, то это правило можно сформулировать так:
а) если числа 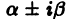 не являются корнями характеристического уравнения, то частное решение
не являются корнями характеристического уравнения, то частное решение 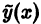 дифференциального уравнения (9) надо искать в виде
дифференциального уравнения (9) надо искать в виде
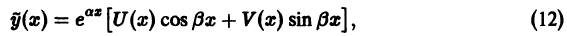
где U(х), V(x) — многочлены с неопределенными коэффициентами, степень каждого из которых равна наивысшей из степеней многочленов  .
.
Чтобы найти коэффициенты этих многочленов, надо подставить функцию 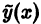 в дифференциальное уравнение и приравнять коэффициенты при одинаковых степенях х в левых и правых частях. При этом надо приравнять друг другу соответствующие коэффициенты тех многочленов, которые стоят множителями при cos
в дифференциальное уравнение и приравнять коэффициенты при одинаковых степенях х в левых и правых частях. При этом надо приравнять друг другу соответствующие коэффициенты тех многочленов, которые стоят множителями при cos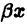 , и отдельно — коэффициенты многочленов при sin
, и отдельно — коэффициенты многочленов при sin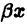 ;
;
б) если 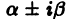 a±ip являются r -кратными корнями характеристического уравнения (резонансный случай), то частное решение
a±ip являются r -кратными корнями характеристического уравнения (резонансный случай), то частное решение 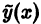 надо искать в виде
надо искать в виде
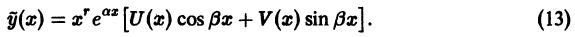
Замечание:
Указанные виды частных решений (12) и (13) сохраняются и в том случае, когда в правой части уравнения один из многочленов 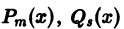 тождественно равен нулю, т.е. когда правая часть имеет вид
тождественно равен нулю, т.е. когда правая часть имеет вид
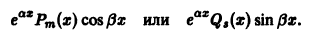
Пример:
Найти частное решение уравнения
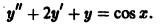
Характеристическое уравнение
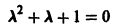
имеет корни 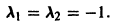 В данном случае
В данном случае 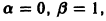 поэтому числа
поэтому числа 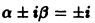 не являются корнями характеристического уравнения;
не являются корнями характеристического уравнения;
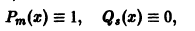
значит, частное решение уравнения следует искать в виде
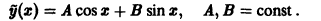
Подставляя функцию  в уравнение, получаем
в уравнение, получаем 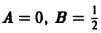 и, следовательно,
и, следовательно,
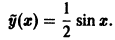
Пример:
Рассмотрим уравнение упругих колебаний без сопротивления при наличии периодической внешней силы

(независимой переменной считаем время t).
Общим решением однородного уравнения является функция
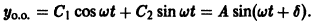
Если 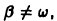 т.е. если частота внешней силы не совпадает с частотой w собственных колебаний системы, то частное решение неоднородного уравнения имеет вид
т.е. если частота внешней силы не совпадает с частотой w собственных колебаний системы, то частное решение неоднородного уравнения имеет вид
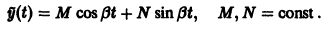
Подставляя это выражение в уравнение (*), найдем, что 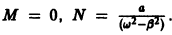 Общее решение уравнения (*) имеет в этом случае вид
Общее решение уравнения (*) имеет в этом случае вид
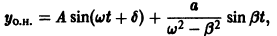
т. е. результирующее движение слагается из собственных колебаний с частотой w и вынужденных колебаний с частотой 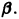
Если 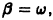 т.е. частота внешней силы совпадает с частотой собственных колебаний системы, то частное решение неоднородного уравнения (*) надо искать в виде
т.е. частота внешней силы совпадает с частотой собственных колебаний системы, то частное решение неоднородного уравнения (*) надо искать в виде

Подставляя 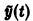 в (*), находим, что
в (*), находим, что

Общее решение уравнения (*) будет иметь вид
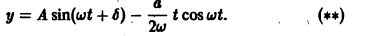
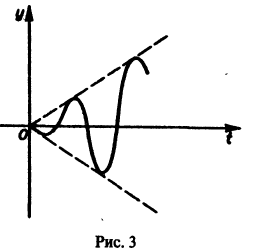
Второе слагаемое в правой части (**) показывает, что в этом случае амплитуда колебаний неограниченно возрастает при неограниченном возрастании времени t (рис. 3). Это явление, возникающее при совпадении частоты внешней силы с частотой собственных колебаний системы, называется резонансом.
Удобным для отыскания частных решений является следующий прием. Пусть имеем линейное неоднородное дифференциальное уравнение с действительными постоянными коэффициентами
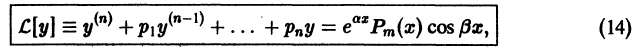
где 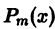 — заданный многочлен степени m с действительными коэффициентами,
— заданный многочлен степени m с действительными коэффициентами, 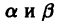 — действительные числа. Составим вспомогательное неоднородное уравнение с той же левой частью, что и у уравнения (14), и правой частью в виде комплекснозначной функции действительного переменного х:
— действительные числа. Составим вспомогательное неоднородное уравнение с той же левой частью, что и у уравнения (14), и правой частью в виде комплекснозначной функции действительного переменного х:
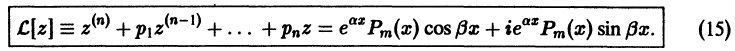
Правая часть уравнения (14) есть действительная часть правой части уравнения (15), и поэтому в силу теоремы 14 действительная часть u(x) решения 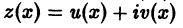 уравнения (15) будет решением исходного уравнения (14). Таким образом вопрос сводится к отысканию частного решения уравнения (15), которое можно переписать в виде
уравнения (15) будет решением исходного уравнения (14). Таким образом вопрос сводится к отысканию частного решения уравнения (15), которое можно переписать в виде

Из приведенных выше рассмотрений следует:
1) если число 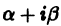 не является корнем характеристического уравнения
не является корнем характеристического уравнения
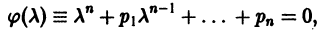
то частное решение уравнения (16) следует искать в виде

где Qm(x) — многочлен степени т с неопределенными коэффициентами,
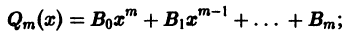
2) если 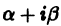 является корнем кратности r характеристического уравнения, то частное решение уравнения (16) имеет вид
является корнем кратности r характеристического уравнения, то частное решение уравнения (16) имеет вид

Замена тригонометрических функций показательной упрощает вычисления, так как после подстановки 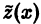 в уравнение (16) обе части уравнения можно сократить на
в уравнение (16) обе части уравнения можно сократить на 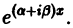 Комплексные коэффициенты
Комплексные коэффициенты 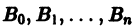 многочлена Qm(x) определяются путем подстановки решений (17) или (18) в уравнение (16) и приравнивания коэффициентов при одинаковых степенях х в левой и правой частях полученного равенства. Отделив действительную часть u(х) решений (17) или (18), найдем частное решение уравнения (14). В случае уравнения вида
многочлена Qm(x) определяются путем подстановки решений (17) или (18) в уравнение (16) и приравнивания коэффициентов при одинаковых степенях х в левой и правой частях полученного равенства. Отделив действительную часть u(х) решений (17) или (18), найдем частное решение уравнения (14). В случае уравнения вида

поступаем аналогично: 1) переходим к вспомогательному уравнению (16); 2) находим частное решение 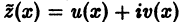 этого уравнения. Мнимая часть v(x) решения будет частным решением уравнения (19).
этого уравнения. Мнимая часть v(x) решения будет частным решением уравнения (19).
Пример 6. Найти частное решение уравнения

Составляем вспомогательное уравнение

Поскольку число 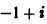 не является корнем характеристического уравнения
не является корнем характеристического уравнения
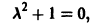
частное решение уравнения (**) ищем в виде
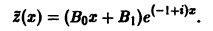
Подставляя 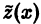 и
и
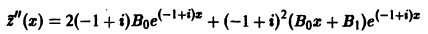
в уравнение (**) и сокращая на 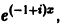 получаем
получаем
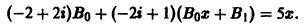
Приравнивая коэффициенты при одинаковых степенях х в левой и правой частях последнего равенства, найдем:
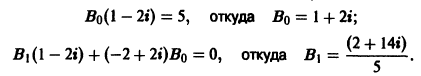
Поэтому для 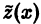 имеем формулу
имеем формулу
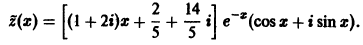
Отсюда получаем частное решение данного уравнения:
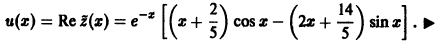
Применение степенных и обобщенных степенных рядов к интегрированию дифференциальных уравнений
Пусть имеем дифференциальное уравнение

и требуется найти решение этого уравнения, удовлетворяющее начальным условиям
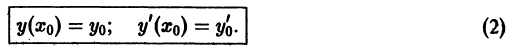
Предположим, что функция f аналитична в окрестности точки 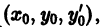 т. е. представляется степенным рядом по степеням
т. е. представляется степенным рядом по степеням 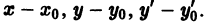 Тогда решение у(х) задачи Коши (1), (2) можно получить в виде ряда
Тогда решение у(х) задачи Коши (1), (2) можно получить в виде ряда
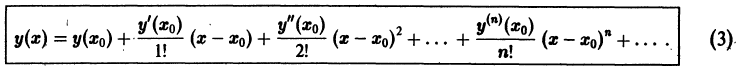
В самом деле, зная 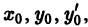 в силу самого уравнения (1) найдем
в силу самого уравнения (1) найдем 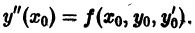 Дифференцируем уравнение (1) по х:
Дифференцируем уравнение (1) по х:

Подставляя в правую часть (4) значения 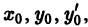 и только что найденное значение
и только что найденное значение 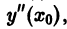 найдем
найдем 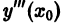 ) и т. д.
) и т. д.
Если ряд (3) сходится в некотором интервале 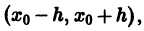 то он определяет там решение задачи (1), (2).
то он определяет там решение задачи (1), (2).
Пример:
Найти решение задачи Коши

В силу (*), (**) имеем
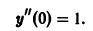
Дифференцируя (*), найдем
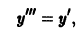
откуда у»‘(0) = у'(0) = 1, и вообще
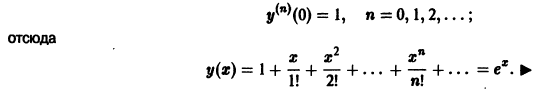
Рассмотрим линейное дифференциальное уравнение
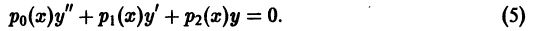
Теорема:
Об аналитичности решения. Если 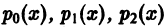 являются аналитическими функциями в окрестности точки
являются аналитическими функциями в окрестности точки 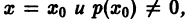 то решения уравнения (5) также являются аналитическими функциями в некоторой окрестности точки х = x0 и, следовательно, эти решения можно искать в виде ряда
то решения уравнения (5) также являются аналитическими функциями в некоторой окрестности точки х = x0 и, следовательно, эти решения можно искать в виде ряда
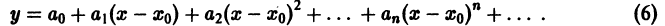
Пример:
Найти решение задачи
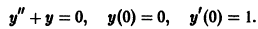
Решение будем искать в виде ряда
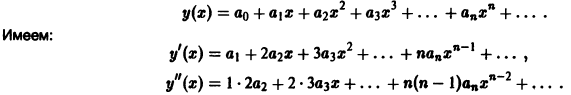
Подставим у(х) и у»(х) в данное уравнение и приравняем нулю коэффициенты при степенях х:
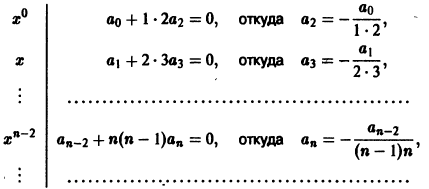
В силу начальных условий имеем 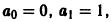 поэтому а2 = 0 и вообще
поэтому а2 = 0 и вообще
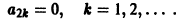
Далее имеем 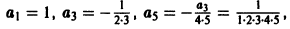 и вообще
и вообще
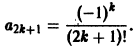
Окончательно получаем
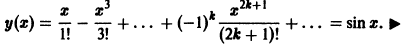
Пусть теперь коэффициент  обращается в нуль в точке х0.
обращается в нуль в точке х0.
Определение:
Точка х0 называется нулем порядка (кратности) m (m — целое положительное число) функции f(x), если f(х) представима в виде 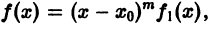 где
где 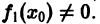
Теорема:
О разложимости решения в обобщенный стеленной ряд. Если в уравнении
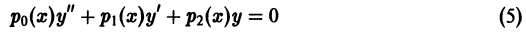
коэффициенты 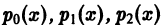 суть аналитические функции в окрестности точки Xо, причем X = Xo является нулем порядка то функции
суть аналитические функции в окрестности точки Xо, причем X = Xo является нулем порядка то функции 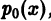 нулем порядка m — 1 или выше функции
нулем порядка m — 1 или выше функции 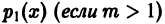 и нулем порядка m — 2 или выше функции
и нулем порядка m — 2 или выше функции 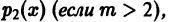 то существует по крайней мере одно нетривиальное решение уравнения (5) в виде суммы обобщенного степенного ряда
то существует по крайней мере одно нетривиальное решение уравнения (5) в виде суммы обобщенного степенного ряда
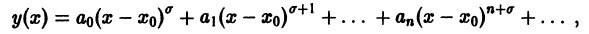
где 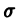 — некоторое действительное число, вообще говоря, не целое.
— некоторое действительное число, вообще говоря, не целое.
Уравнение Бесселя. Функции Бесселя
Дифференциальное уравнение Бесселя
Дифференциальным уравнением Бесселя называется уравнение вида
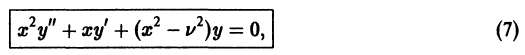
где v — действительное число. Это уравнение имеет особую точку х = 0 (коэффициент при старшей производной в (7) обращается в нуль при х = 0). Сравнивая (5) и (7), заключаем, что для уравнения Бесселя
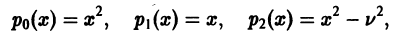
так что х = 0 является нулем второго порядка (m = 2) функции 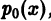 нулем первого порядка функции p1(x) и не является нулем функции
нулем первого порядка функции p1(x) и не является нулем функции 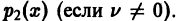 Поэтому в силу теоремы 17 существует решение уравнения (7) в виде обобщенного степенного ряда
Поэтому в силу теоремы 17 существует решение уравнения (7) в виде обобщенного степенного ряда
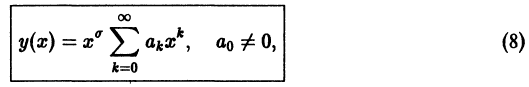
где 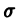 — характеристический показатель, подлежащий определению. Перепишем выражение (8) в виде
— характеристический показатель, подлежащий определению. Перепишем выражение (8) в виде
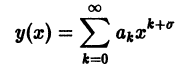
и найдем производные:
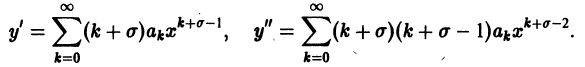
Подставим эти выражения в уравнение (7),
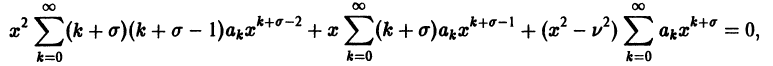
и приравнивая нулю коэффициенты при х в степени  получим систему уравнений
получим систему уравнений
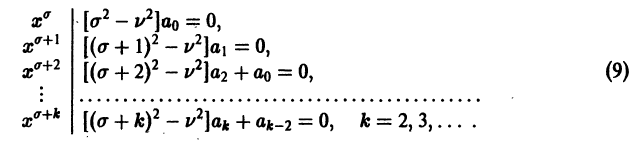
Так как 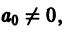 то из первого уравнения (9) следует, что
то из первого уравнения (9) следует, что 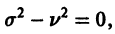 или
или
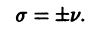
Теперь из второго уравнения (9) будем иметь
Рассмотрим сначала случай 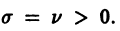 Перепишем
Перепишем 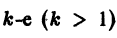 уравнение системы (9) в виде
уравнение системы (9) в виде
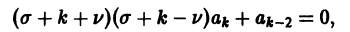
откуда получаем рекуррентную формулу для определения 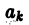 через
через 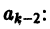
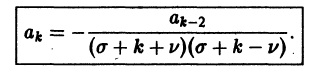
Учитывая, что a1 = 0, получаем отсюда а3 = 0 и вообще 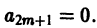 С другой стороны, каждый четный коэффициент может быть выражен через предыдущий по формуле
С другой стороны, каждый четный коэффициент может быть выражен через предыдущий по формуле
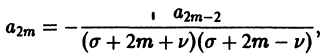
или, с учетом 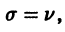
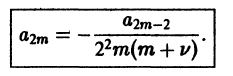
Последовательное применение этой формулы позволяет найти выражение 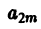 через
через 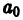 :
:
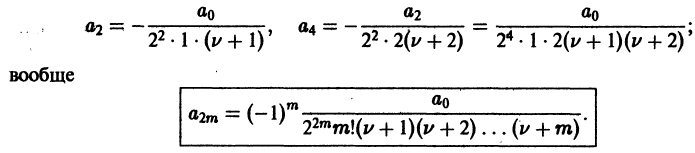
Подставим найденные значения коэффициентов в формулу (8),
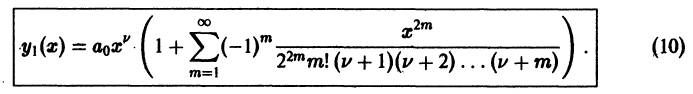
Нетрудно проверить, что ряд в правой части (10) сходится на полуоси х > 0 и определяет там функцию у1(х) — частное решение уравнения Бесселя.
Рассмотрим теперь второй случай, когда 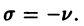 Если v не равно положительному целому числу, то можно написать второе частное решение, которое получается из выражения (10) заменой v на —v (в уравнение (7) v входит четным образом),
Если v не равно положительному целому числу, то можно написать второе частное решение, которое получается из выражения (10) заменой v на —v (в уравнение (7) v входит четным образом),
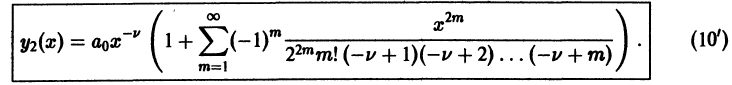
(Если v равно целому положительному числу, то решение (10′) теряет силу, так как начиная с некоторого числа один из множителей в знаменателе членов разложения (10′) будет равен нулю.) Ряд в правой части (10′) также сходится при всех значениях х > 0. Решения  линейно независимы. Действительно, их отношение
линейно независимы. Действительно, их отношение

не является постоянным.
Г-функция Эйлера и ее свойства
Для дальнейшего нам понадобятся некоторые свойства Г -функции Эйлера. Она определяется следующим образом:
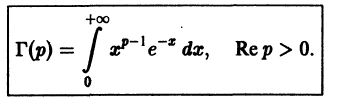
Интегрированием по частям получаем основное функциональное уравнение для Г-функции:
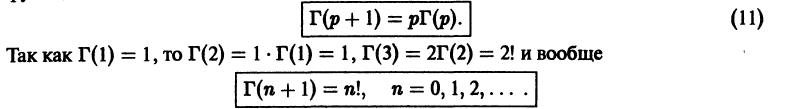
Можно показать еще, что
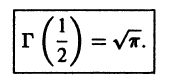
С помощью функционального уравнения (11) можно определить гамма-функцию для отрицательных значений аргумента. Записав уравнение (11) в виде 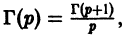 замечаем, что для малых р выполняется соотношение
замечаем, что для малых р выполняется соотношение 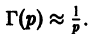
Аналогично, если m — положительное целое число, то для значений р, близких к числу -m, имеем
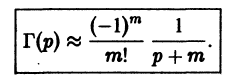
Можно показать, что 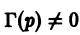 при всяком р, поэтому функция
при всяком р, поэтому функция 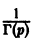 будет непрерывной для всех значений р, если положить
будет непрерывной для всех значений р, если положить
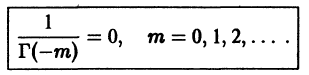
Возвратимся к решению уравнения Бесселя (7). Коэффициент 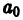 до сих пор оставался произвольным. Если
до сих пор оставался произвольным. Если 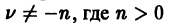 — целое число, то, полагая
— целое число, то, полагая

Подставляя это выражение для коэффициентов в (9), получаем
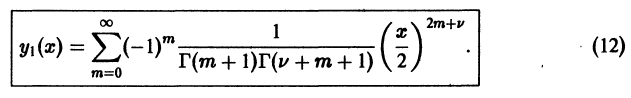
Ряд (12) определяет функцию
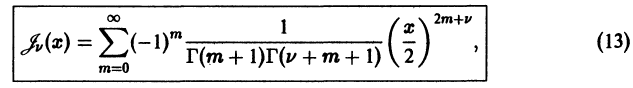
которая является решением уравнения Бесселя и называется функцией Бесселя первого рода v-го порядка.
Ряд
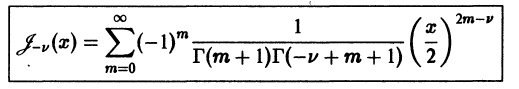
отвечает случаю 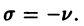 (v — нецелое) и определяет второе решение уравнения (7), линейно независимое с функцией
(v — нецелое) и определяет второе решение уравнения (7), линейно независимое с функцией 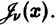
Итак, если v не равно целому числу 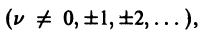 то функции
то функции 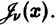
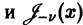 образуют фундаментальную систему решений уравнения Бесселя (7) и его общее решение имеет в этом случае вид
образуют фундаментальную систему решений уравнения Бесселя (7) и его общее решение имеет в этом случае вид
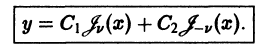
При v целом выполняется линейная зависимость

В самом деле, имеем
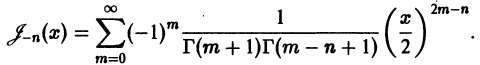
Первые n членов ряда исчезают, так как 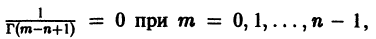
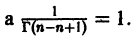 Введя обозначение m = к + n, находим
Введя обозначение m = к + n, находим
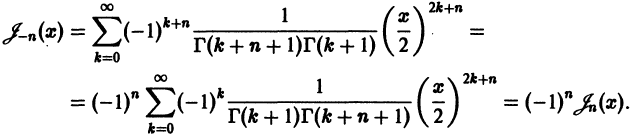
Выпишем ряды для функций Бесселя первого рода нулевого (n = 0) и первого (n = 1) порядков:
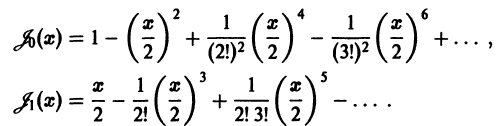
Функции 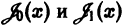 (рис. 4) часто встречаются в приложениях, и для них имеются подробные таблицы.
(рис. 4) часто встречаются в приложениях, и для них имеются подробные таблицы.
Рекуррентные формулы для функций Бесселя
Используя формулу
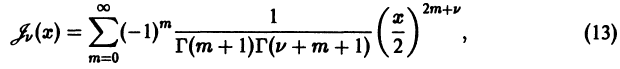
непосредственно проверкой убеждаемся в том, что
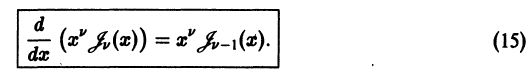
Точно таким же вычислением находим
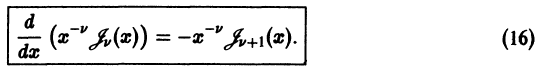
Раскрывая в левых частях формул (15) и (16) производные произведений, получаем соответственно равенства
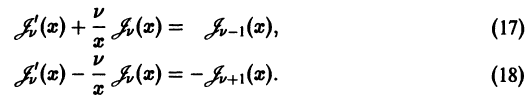
Складывая и вычитая (17) и (18), получим две важные рекуррентные формулы:
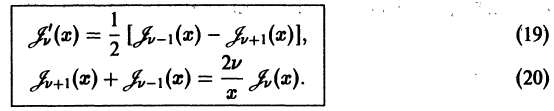
Формула (19) показывает, что производные функций Бесселя выражаются через бесселевы же функции. Из формулы (20) вытекает, что, зная 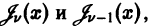 , можно найти
, можно найти 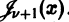 . В частности, все функции Бесселя целых номеров выражаются через две функции
. В частности, все функции Бесселя целых номеров выражаются через две функции 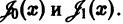 Здесь оказывается полезным соотношение (14). При v= 1 из (20) находим, например,
Здесь оказывается полезным соотношение (14). При v= 1 из (20) находим, например,
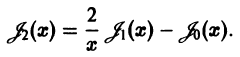
Функции Бесселя полуцелого индекса
Рассмотрим специальный класс бесселевых функций с индексом, равным половине нечетного целого числа. Этот класс встречается в приложениях и замечателен тем, что в рассматриваемом случае бесселевы функции могут быть выражены через элементарные. Так, при 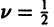 путем несложных преобразований находим
путем несложных преобразований находим
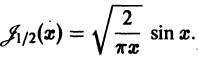
Аналогично, при 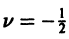 получаем
получаем
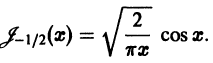
Обе эти формулы можно записать в виде
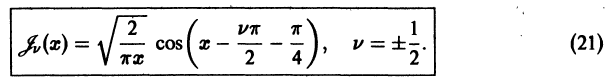
По рекуррентной формуле (20) подсчитываем, например,
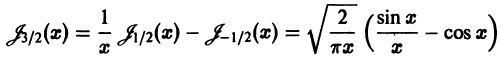
и т. д.
Нули бесселевых функций
При решении многих прикладных вопросов необходимо иметь представление о распределении нулей функций Бесселя. Нули функций  совпадают с нулями sin х и cos х соответственно. Можно показать, что для больших значений х имеет место асимптотическое представление (сравните с (21))
совпадают с нулями sin х и cos х соответственно. Можно показать, что для больших значений х имеет место асимптотическое представление (сравните с (21))
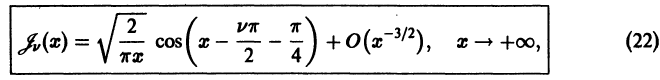
Символ 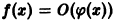 означает, что отношение
означает, что отношение 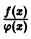 остается ограниченным при
остается ограниченным при  (см. главу VIII).
(см. главу VIII).
справедливое как для целых, так и для дробных v. Формула (22) показывает, как ведет себя функция Бесселя при возрастании аргумента. Это колеблющаяся функция, бесчисленное множество раз обращающаяся в нуль, причем амплитуда колебаний стремится к нулю при 
Распределение нулей функции Бесселя с целым положительным индексом, т. е. корней уравнения
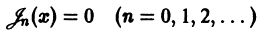
устанавливается следующей теоремой.
Теорема:
Функция 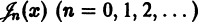 не имеет комплексных нулей, но имеет бесконечное множество действительных нулей, расположенных симметрично относительно точки х = 0, которая в случае n = 1,2,… принадлежит к их числу. Все нули функции простые за исключением точки х = 0, которая при n = 1,2,… является нулем кратности п соответственно.
не имеет комплексных нулей, но имеет бесконечное множество действительных нулей, расположенных симметрично относительно точки х = 0, которая в случае n = 1,2,… принадлежит к их числу. Все нули функции простые за исключением точки х = 0, которая при n = 1,2,… является нулем кратности п соответственно.
Ортогональность и норма функций Бесселя
Ортогональность функций Бесселя:
Рассмотрим дифференциальное уравнение
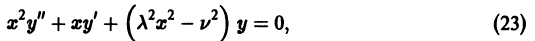
где 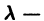 некоторый числовой параметр, отличный от нуля. Нетрудно проверить, что уравнению (23) удовлетворяет функция Бесселя
некоторый числовой параметр, отличный от нуля. Нетрудно проверить, что уравнению (23) удовлетворяет функция Бесселя 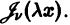 Перепишем уравнение (23) в виде
Перепишем уравнение (23) в виде
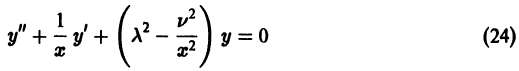
и обозначим 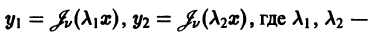 какие-либо значения параметра
какие-либо значения параметра 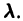 Тогда будем иметь тождества
Тогда будем иметь тождества
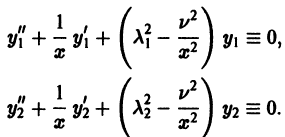
Умножая первое тождество на 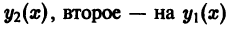 и вычитая одно из другого, получим
и вычитая одно из другого, получим
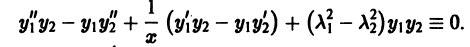
Умножив все члены последнего тождества на x, замечаем, что его можно записать в виде
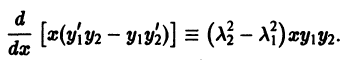
Интегрируя последнее тождество по ж в пределах от 0 до 1, будем иметь
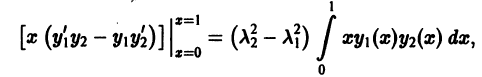
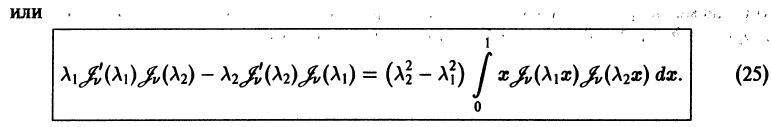
1. Пусть  Тогда из равенства (25) следует, что если
Тогда из равенства (25) следует, что если  есть нули функции
есть нули функции 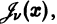 то левая часть (25), а значит, и правая, равны нулю, так чтo
то левая часть (25), а значит, и правая, равны нулю, так чтo
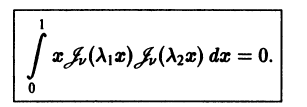
Это означает, согласно определению, что функции 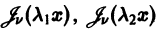 ортогональны с весом р(х) = х на отрезке [0,1].
ортогональны с весом р(х) = х на отрезке [0,1].
Бесселева функция 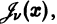 имеет счетное множество нулей
имеет счетное множество нулей
и, следовательно, система функций

есть ортогональная на отрезке [0,1] система с весом р(х) = х,
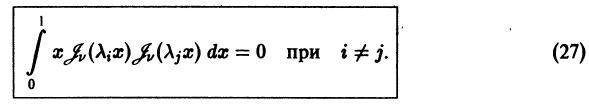
2. Если  являются корнями уравнения
являются корнями уравнения
то в этом случае при 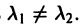 из (25) также имеем
из (25) также имеем
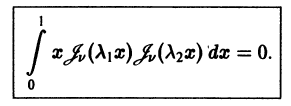
Следовательно, система функций 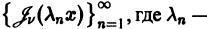 корни уравнения
корни уравнения 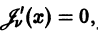 ортогональна на отрезке [0,1] с весом р(х) = х.
ортогональна на отрезке [0,1] с весом р(х) = х.
3. Пусть 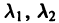 являются корнями уравнения
являются корнями уравнения
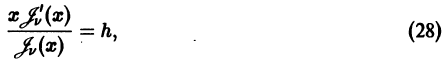
где h — некоторое фиксированное число. Уравнение (28) встречается в математической физике и при v > -1 имеет бесконечное множество положительных корней, но не имеет комплексных корней (исключая случай 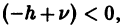 когда есть два чисто мнимых корня). Записав левую часть равенства (25) в виде
когда есть два чисто мнимых корня). Записав левую часть равенства (25) в виде
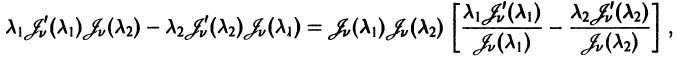
убеждаемся в ортогональности бесселевых функций по нулям линейной комбинации 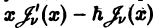 = 0 функции Бесселя и ее производной:
= 0 функции Бесселя и ее производной:
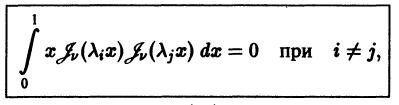
где  — корни уравнения (28).
— корни уравнения (28).
Норма функций Бесселя
Величина
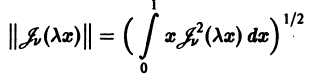
называется нормой функции Бесселя 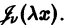
Пользуясь равенством (25), можно показать, что
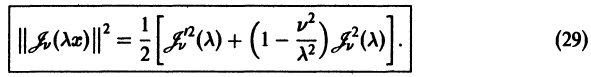
В частности, для 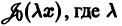 — нуль бесселевой функции, имеем
— нуль бесселевой функции, имеем
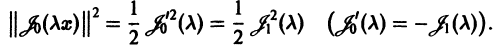
Функции Неймана (Вебера)
Всякое нетривиальное решение уравнения Бесселя
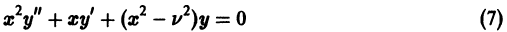
называют цилиндрической функцией. При v нецелом функции 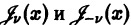 образуют функциональную систему решений уравнения Бесселя (7). При v = n — целом имеет место линейная зависимость
образуют функциональную систему решений уравнения Бесселя (7). При v = n — целом имеет место линейная зависимость
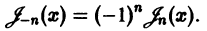
Чтобы к решению 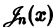 подыскать такое, которое ему не пропорционально, поступаем так: при нецелом v составляем функцию
подыскать такое, которое ему не пропорционально, поступаем так: при нецелом v составляем функцию
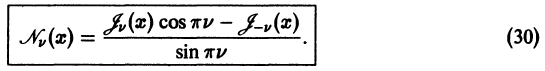
Она является линейной комбинацией решений линейного однородного уравнения (7) и, следовательно, сама есть решение этого уравнения. Переходя в (30) к пределу при  и пользуясь правилом Лопиталя, будем иметь
и пользуясь правилом Лопиталя, будем иметь
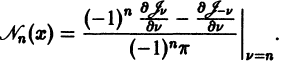
Характерное свойство функций  (функций Бесселя 2-го рода) — наличие особенности в начале координат (рис. 5)
(функций Бесселя 2-го рода) — наличие особенности в начале координат (рис. 5)
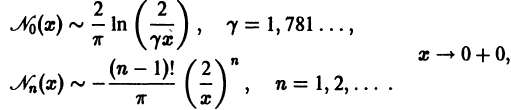
Найденное решение 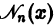 уравнения Бесселя (7) при v = n вместе с
уравнения Бесселя (7) при v = n вместе с 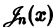 составляет фундаментальную систему решений уравнения
составляет фундаментальную систему решений уравнения
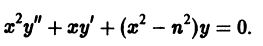
Функцию 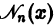 называют также функцией Неймана или функцией Вебера. При достаточно больших х
называют также функцией Неймана или функцией Вебера. При достаточно больших х
Таким образом, на больших расстояниях от начала координат цилиндрические функции 1 -го и 2-го рода относятся друг к другу как косинус и синус, но затухают с ростом ж благодаря множителю  Эти функции удобны для представления стоячих цилиндрических волн.
Эти функции удобны для представления стоячих цилиндрических волн.
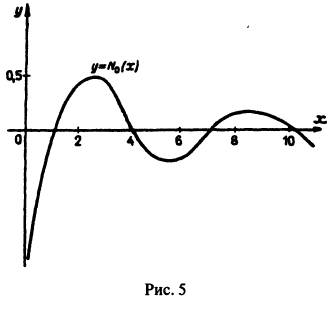
По аналогии с показательными функциями (формулы Эйлера) можно построить линейную комбинацию функций 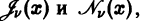 дающую функции, связанные с бегущими волнами. Так мы приходим к бесселевым функциям 3-го рода или функциям Ханкеля, определяемым соотношениями
дающую функции, связанные с бегущими волнами. Так мы приходим к бесселевым функциям 3-го рода или функциям Ханкеля, определяемым соотношениями
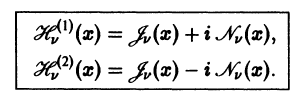
Дополнение к дифференциальным уравнениям высших порядков




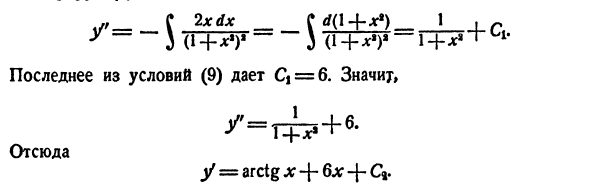

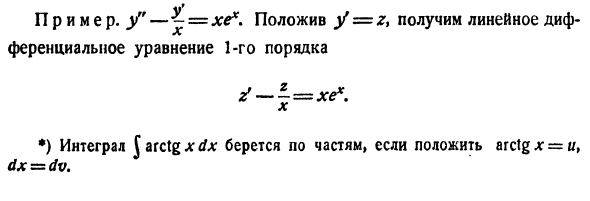

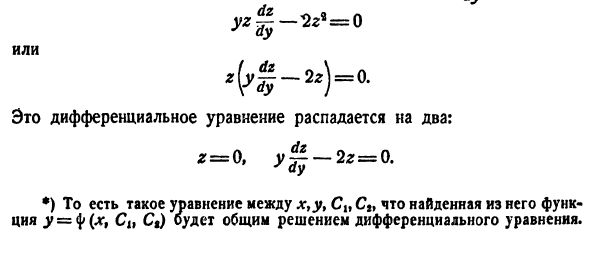

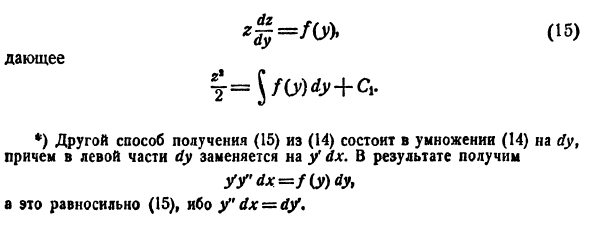

Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

