Оглавление:
Обобщением определенного интеграла на случай функции трех переменных является так называемый «тройной интеграл».
Теория тройного интеграла аналогична теории двойного интеграла. Поэтому изложим ее в несколько сокращенном виде.
Пусть в замкнутой области V пространства Oxyz задана непрерывная функция и = f(x;y;z). Разбив область V сеткой поверхностей на п частей 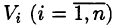 и выбрав в каждой из них произвольную точку
и выбрав в каждой из них произвольную точку 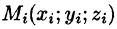 , составим интегральную сумму
, составим интегральную сумму 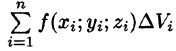 для функции
для функции 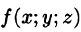 по области V (здесь
по области V (здесь 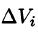 — объем элементарной области
— объем элементарной области 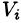 ).
).
Если предел интегральной суммы существует при неограниченном увеличении числа п таким образом, что каждая «элементарная область» 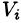 стягивается в точку (т. е. диаметр области
стягивается в точку (т. е. диаметр области 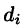 стремится к нулю, т.е.
стремится к нулю, т.е. 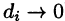 ), то его называют тройным интегралом от функции и = f(х;у;z) по области V и обозначают
), то его называют тройным интегралом от функции и = f(х;у;z) по области V и обозначают
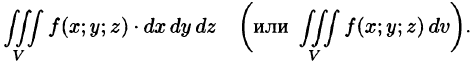
Таким образом, по определению, имеем:
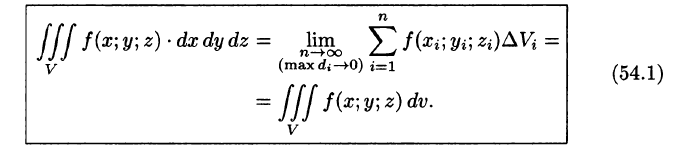
Здесь dv = dx dy dz — элемент объема.
Теорема:
Если функция и = f(x;y,z) непрерывна в ограниченной замкнутой области V, то предел интегральной суммы (54.1) при 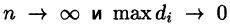 существует и не зависит ни от способа разбиения области V на части, ни от выбора точек
существует и не зависит ни от способа разбиения области V на части, ни от выбора точек 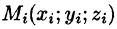 в них.
в них.
Тройной интеграл обладает теми же свойствами, что и двойной интеграл:
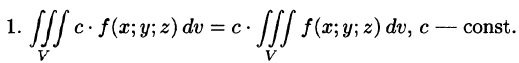
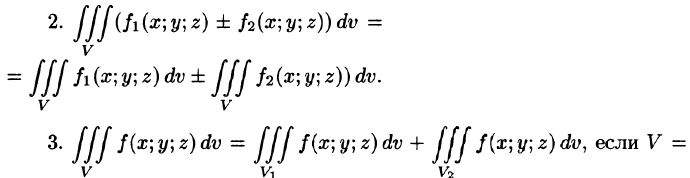
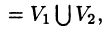
а пересечение 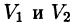 состоит из границы, их разделяющей.
состоит из границы, их разделяющей.
4. 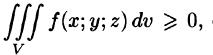 если в области V функция
если в области V функция 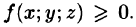
Если в области интегрирования 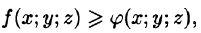 то и
то и
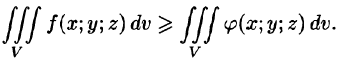
5.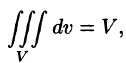 так как в случае
так как в случае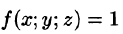 любая интегральная сумма имеет вид
любая интегральная сумма имеет вид 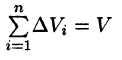 и численно равна объему тела.
и численно равна объему тела.
6. Оценка тройного интеграла:
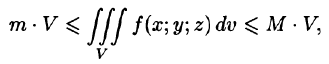
где m и М — соответственно наименьшее и наибольшее значения функции f(x;y;z) в области V.
7. Теорема о среднем значении: если функция f(x; у, z) непрерывна в замкнутой области V, то в этой области существует такая точка 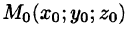 , что
, что
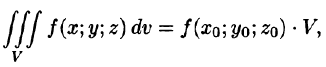
где V — объем тела.
Вычисление тройного интеграла в декартовых координатах
В декартовых координатах вычисление тройного интеграла сводится к последовательному вычислению трех определенных интегралов.
Пусть областью интегрирования V является тело, ограниченное снизу поверхностью 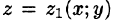 , сверху — поверхностью
, сверху — поверхностью 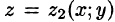 , причем
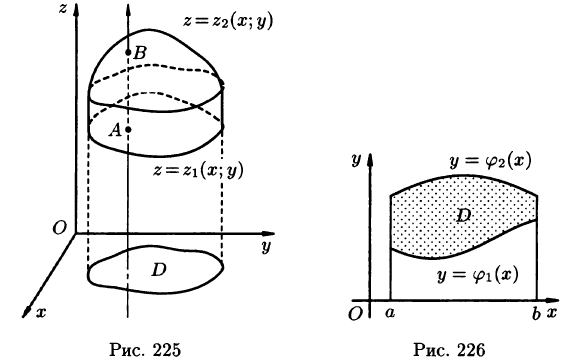
, причем 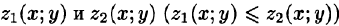 — непрерывные функции в замкнутой области D, являющейся проекцией тела на плоскость Оху (см. рис. 225). Будем считать область V — правильной в направлении оси Oz: любая прямая, параллельная оси Oz, пересекает границу области не более чем в двух точках. Тогда для любой непрерывной в области V функции f(х; у, z) имеет место формула
— непрерывные функции в замкнутой области D, являющейся проекцией тела на плоскость Оху (см. рис. 225). Будем считать область V — правильной в направлении оси Oz: любая прямая, параллельная оси Oz, пересекает границу области не более чем в двух точках. Тогда для любой непрерывной в области V функции f(х; у, z) имеет место формула
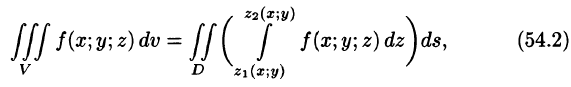
сводящая вычисление тройного интеграла к вычислению двойного интеграла от однократного (доказательство формулы (54.2) не приводим). При этом сначала вычисляется внутренний интеграл по переменной г при постоянных х и у в пределах изменения z. Нижней границей интеграла является аппликата точки А — точки входа прямой, параллельной оси Oz в область V, т. е. 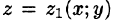 ; верхней границей — аппликата точки В — точки выхода прямой из области V, т. е.
; верхней границей — аппликата точки В — точки выхода прямой из области V, т. е. 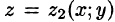 . Результат вычисления этого интеграла есть функция двух переменных: х и у.
. Результат вычисления этого интеграла есть функция двух переменных: х и у.
Если область D ограничена линиями 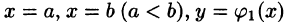 и
и 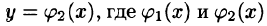 — непрерывные на отрезке [а, b] функции, причем
— непрерывные на отрезке [а, b] функции, причем 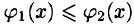 (см. рис. 226), то, переходя от двойного интеграла по области D к повторному, получаем формулу
(см. рис. 226), то, переходя от двойного интеграла по области D к повторному, получаем формулу
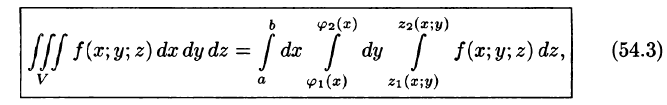
по которой вычисляется тройной интеграл в декартовых координатах.
Замечания:
- Если область V более сложная, чем рассмотренная, то ее следует разбить на конечное число таких областей (правильных), к которым можно применить формулу (54.3).
- Порядок интегрирования в формуле (54.3), при определенных условиях, может быть иным.
Пример:
Вычислить
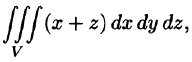
где V ограничена плоскостями х = 0, у =0, z = 1, x + y + z = 2 (рис. 227).
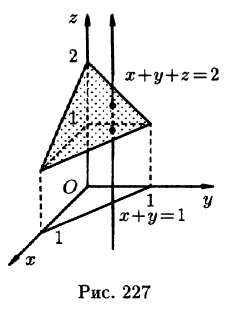
Решение:
Область V является правильной в направлении оси Oz (как, заметим, и в направлении осей Ох и Оу). Ее проекция на плоскость Оху является правильной в направлении оси Оу (и оси Ох). Согласно формуле (54.3), имеем:
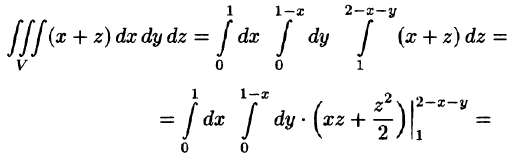
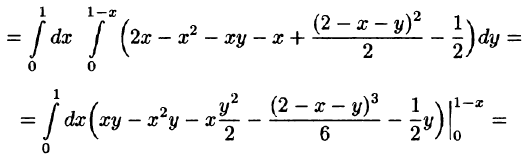
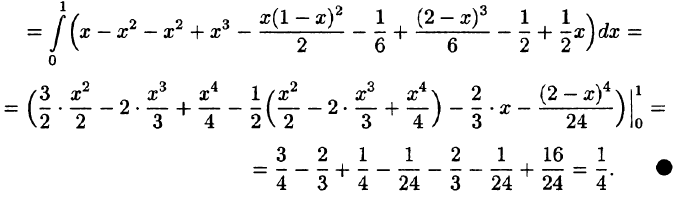
Замена переменных в тройном интеграле. Вычисление тройного интеграла в цилиндрических и сферических координатах
При вычислении тройного интеграла, как и двойного, часто применяется метод подстановки, т. е. совершается преобразование переменных.
Пусть совершена подстановка
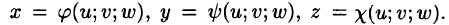
Если эти функции имеют в некоторой области 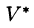 пространства Ouvw непрерывные частные производные и отличный от нуля определитель
пространства Ouvw непрерывные частные производные и отличный от нуля определитель
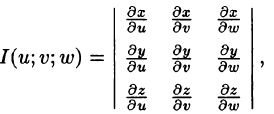
то справедлива формула замены переменных в тройном интеграле:
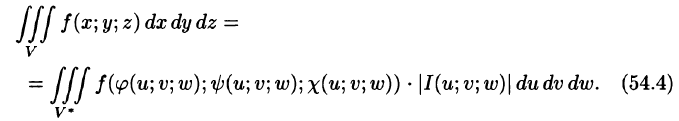
Здесь I(u; v;w) — определитель Якоби, или якобиан преобразования (примем без доказательства).
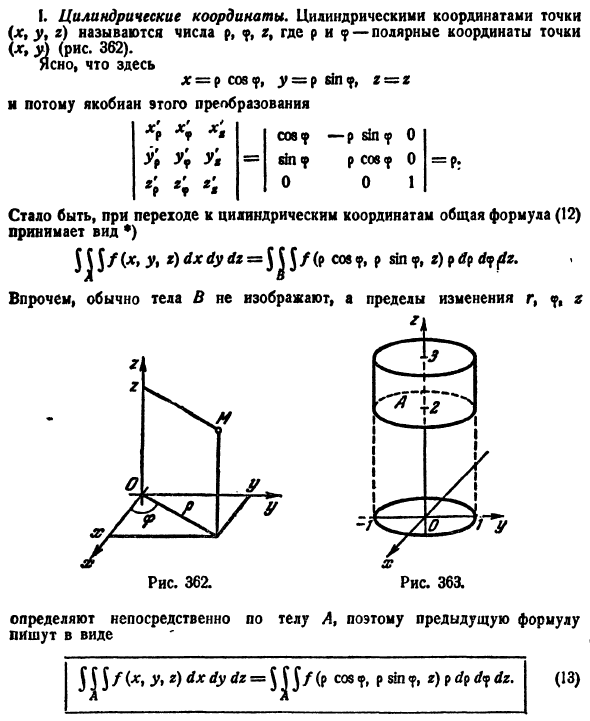
Для вычисления тройного интеграла часто используют так называемые цилиндрические координаты.
Положение точки М(х; у; z) в пространстве Oxyz можно определить заданием трех чисел 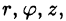 где r — длина радиуса-вектора проекции точки М на плоскость Оху,
где r — длина радиуса-вектора проекции точки М на плоскость Оху, 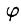 — угол, образованный этим радиусом-вектором с осью Ox, z — аппликата точки М (см. рис. 228).
— угол, образованный этим радиусом-вектором с осью Ox, z — аппликата точки М (см. рис. 228).
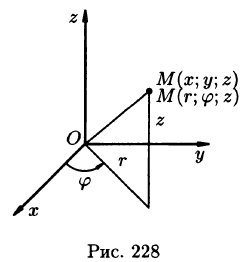
Эти три числа (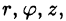 ) называются цилиндрическими координатами точки М.
) называются цилиндрическими координатами точки М.
Цилиндрические координаты точки связаны с ее декартовыми координатами следующими соотношениями:
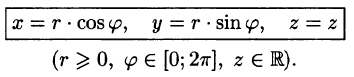
Возьмем в качестве и, v, w цилиндрические координаты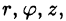 и вычислим якобиан преобразования:
и вычислим якобиан преобразования:
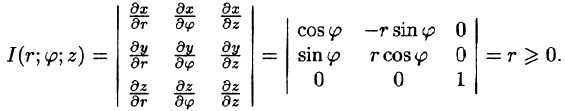
Формула замены переменных (54.4) принимает вид
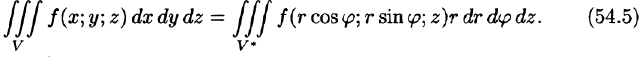
Таким образом, вычисление тройного интеграла приводится к интегрированию по r, по 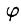 и по z аналогично тому, как это делается в декартовых координатах.
и по z аналогично тому, как это делается в декартовых координатах.
Замечание:
К цилиндрическим координатам бывает удобно перейти в случае, если область интегрирования образована цилиндрической поверхностью.
Пример:
Вычислить 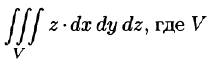 — область, ограниченная верхней частью конуса
— область, ограниченная верхней частью конуса 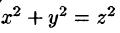 и плоскостью z = 1.
и плоскостью z = 1.
Решение:
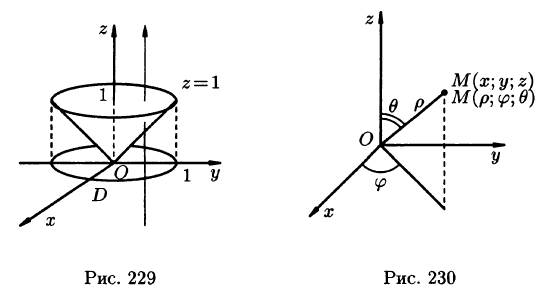
На рис. 229 изображена область интегрирования V. Вычислим интеграл путем перехода к цилиндрическим координатам: 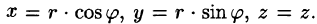 Здесь
Здесь 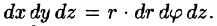 Уравнение конуса примет вид
Уравнение конуса примет вид 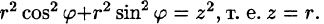 Уравнение окружности
Уравнение окружности 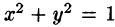 (границы области D) запишется так: r= 1. Новые переменные изменяются в следующих пределах: r— от 0 до 1,
(границы области D) запишется так: r= 1. Новые переменные изменяются в следующих пределах: r— от 0 до 1,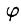 — от 0 до
— от 0 до 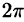 , a z — от r до 1 (прямая, параллельная оси Oz, пересекающая область D, входит в конус z =r и выходит из него на высоте z = 1).
, a z — от r до 1 (прямая, параллельная оси Oz, пересекающая область D, входит в конус z =r и выходит из него на высоте z = 1).
Таким образом, согласно формуле (54.5), получаем:
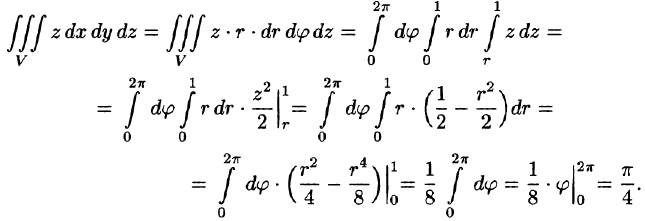
Заметим, что, не переходя к цилиндрическим координатам, получим:
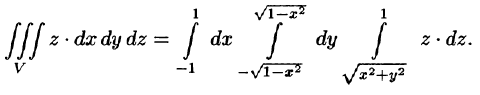
Сферическими координатами точки М(х; у; z) пространства Oxyz называется тройка чисел 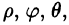 где р — длина радиуса-вектора точки
где р — длина радиуса-вектора точки 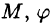 — угол, образованный проекцией радиуса-вектора
— угол, образованный проекцией радиуса-вектора 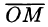 на плоскость Оху и осью Ох, в — угол отклонения радиуса-вектора
на плоскость Оху и осью Ох, в — угол отклонения радиуса-вектора 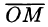 от оси Oz (см. рис. 230).
от оси Oz (см. рис. 230).
Сферические координаты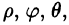 связаны с декартовыми координатами х, у, z соотношениями:
связаны с декартовыми координатами х, у, z соотношениями:
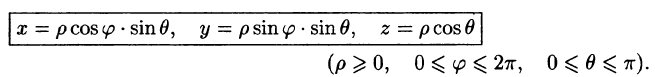
В некоторых случаях вычисление тройного интеграла удобно производить, перейдя к сферическим координатам. Для этого нужно воспользоваться формулой замены переменных в тройном интеграле (54.4). Так как якобиан преобразования
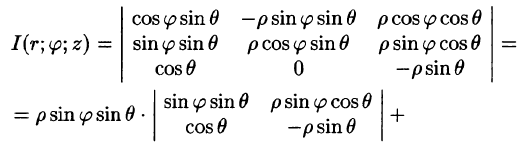
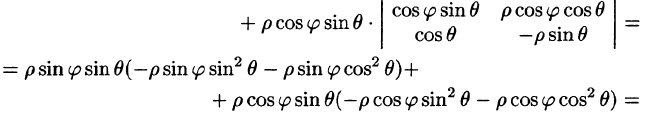
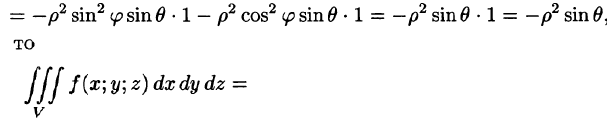
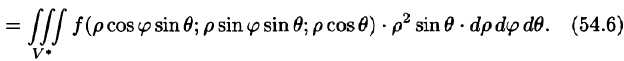
Замечание:
Переходить к сферическим координатам удобно, когда область интегрирования V есть шар (уравнение его границы 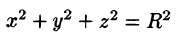 в сферических координатах имеет вид р = R) или его часть, а также если подынтегральная функция имеет вид
в сферических координатах имеет вид р = R) или его часть, а также если подынтегральная функция имеет вид 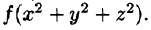
Пример 54.3. Вычислить
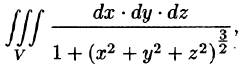
где V — шар 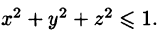
Решение:
Вычислим интеграл путем перехода к сферическим координатам: 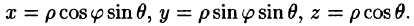 Тогда
Тогда
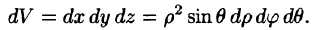
Граница области V — сфера и ее уравнение имеет вид р = 1, подынтегральная функция после замены переменных примет вид 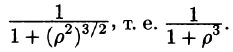 Новые переменные изменяются в следующих пределах: р —от 0 до 1, у — от 0 до
Новые переменные изменяются в следующих пределах: р —от 0 до 1, у — от 0 до 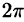 ,
, 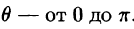 Таким образом, согласно формуле (54.6),
Таким образом, согласно формуле (54.6),
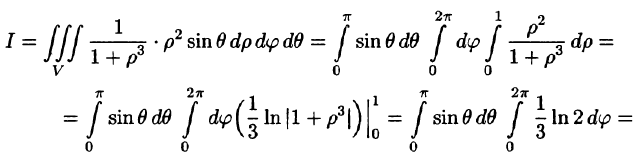
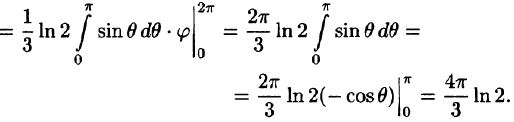
Некоторые приложения тройного интеграла Объем тела
Объем области V выражается формулой 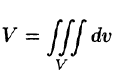 или
или 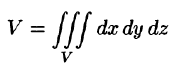 — в декартовых координатах,
— в декартовых координатах,

Масса тела
Масса тела m при заданной объемной плотности 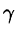 вычисляется с помощью тройного интеграла как
вычисляется с помощью тройного интеграла как
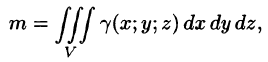
где 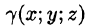 — объемная плотность распределения массы в точке M{x;y;z).
— объемная плотность распределения массы в точке M{x;y;z).
Статические моменты
Моменты 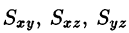 тела относительно координатных плоскостей Оху, Oxz, Oyz вычисляются по формулам
тела относительно координатных плоскостей Оху, Oxz, Oyz вычисляются по формулам
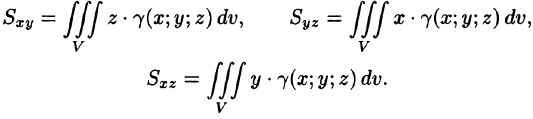
Центр тяжести тела
Координаты центра тяжести тела V находятся по формулам
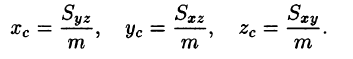
Моменты инерции тела
Моменты инерции тела относительно координатных плоскостей вычисляются по формулам
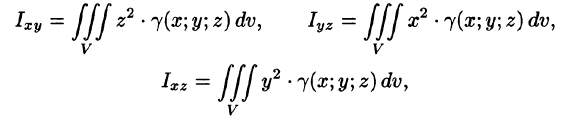
а моменты инерции относительно координатных осей:
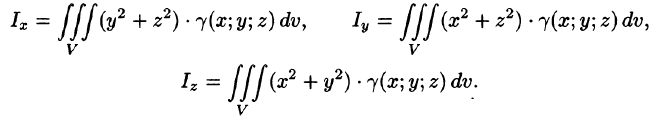
Пример:
Найти объем тела, ограниченного поверхностями
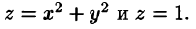
Решение:
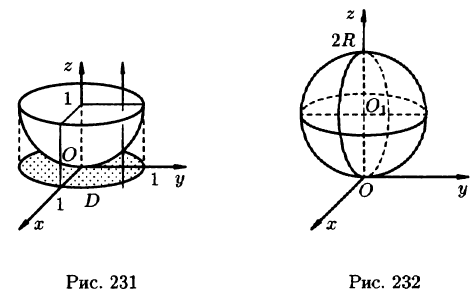
Данное тело ограничено сверху плоскостью z = 1, снизу — параболоидом 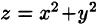 (см. рис. 231). Объем тела находим, используя цилиндрические координаты:
(см. рис. 231). Объем тела находим, используя цилиндрические координаты:
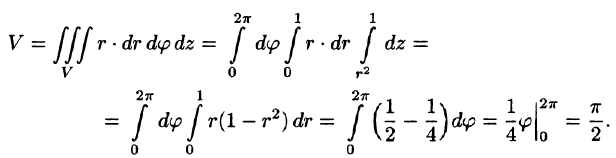
Пример:
Найти массу шара 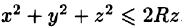 , если плотность в каждой точке шара обратно пропорциональна расстоянию от нее до начала координат (дополнительно: найти координаты центра тяжести).
, если плотность в каждой точке шара обратно пропорциональна расстоянию от нее до начала координат (дополнительно: найти координаты центра тяжести).
Решение:
Уравнение сферы 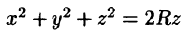 можно записать так:
можно записать так: 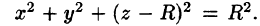 Центр шара расположен в точке
Центр шара расположен в точке 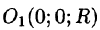 (см. рис. 232). Пусть M(x;y;z) — произвольная точка шара. Тогда, по условию, плотность
(см. рис. 232). Пусть M(x;y;z) — произвольная точка шара. Тогда, по условию, плотность 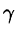 определяется формулой
определяется формулой
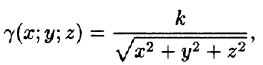
где k — коэффициент пропорциональности, 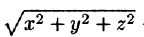 — расстояние от точки М до начала координат.
— расстояние от точки М до начала координат.
Итак,
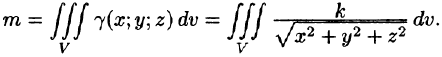
Вычислять интеграл будем в сферических координатах. Уравнение сферы 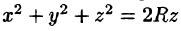 примет вид
примет вид 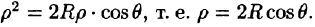
Поэтому сферические координаты будут изменяться в следующих пределах:
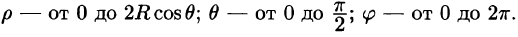
Подынтегральная функция примет вид 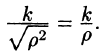 Поэтому
Поэтому
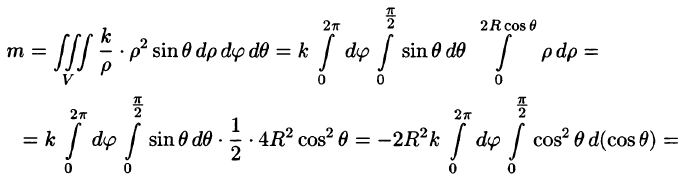
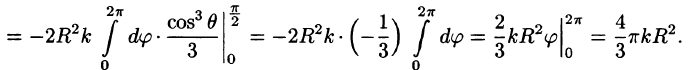
Из соображений симметрии следует, что 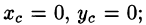 вычислив интеграл
вычислив интеграл 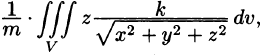 найдем
найдем 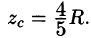 Итак, координаты центра тяжести
Итак, координаты центра тяжести 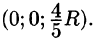
Тройной интеграл


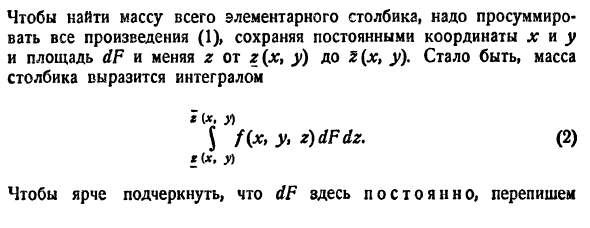

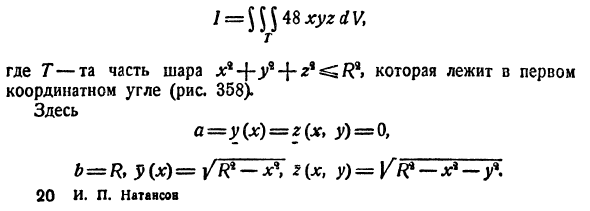

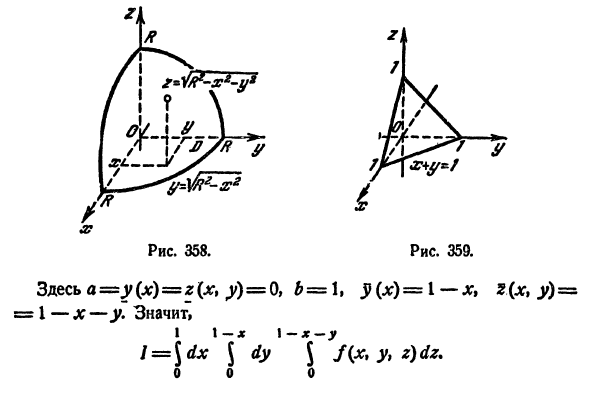

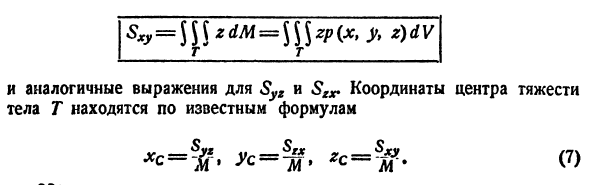










Смотрите также:
| Понятие о системах дифференциальных уравнений | Криволинейные интегралы |
| Двойной интеграл | Дальнейшие сведения из теории рядов |
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

