Оглавление:
Тождественные преобразования — это замена одного аналитического выражения другим, тождественно ему равным, но отличным по форме и преобразование (отображение в себя) некоторого множества, оставляющее на месте каждый его элемент
Опираясь на правила действий, изложенные в главе III, легко убедиться, что равенство
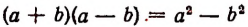
справедливо при любых значениях входящих в него букв.
То же самое можно сказать, например, и относительно каждого из следующих равенств:
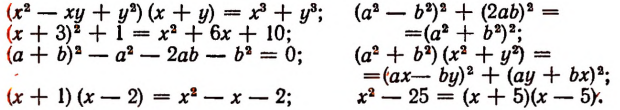
Равенство же
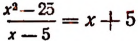
справедливо при всех значениях буквы х, кроме х = 5 . (При х = 5 правая часть принимает значение 10, а левая теряет смысл.)
Равенство
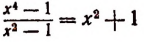
справедливо при всех значениях буквы х, кроме х=1 и х = — 1. (При х=1 и х = — 1 левая часть теряет смысл.) Равенство
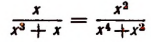
справедливо при любых значениях буквы х, кроме х = 0. (При х = 0 обе части этого равенства теряют смысл.)
Определение:
Равенство, справедливое при любых значениях букв, допустимых для его левой и правой частей, называется тождеством.
Любое из приведенных выше равенств является тождеством.
Тождеством называется также справедливое равенство, не содержащее букв (числовое тождество).
Равенство, составленное из двух совершенно одинаковых выражений, конечно, тоже является тождеством, например равенство
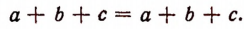
Но подобное тождество не содержит ничего интересного; оно говорит лишь о том, что всякое выражение равно самому себе.
Тождество, в котором левая и правая части совершенно одинаковы, назовем тривиальным. (Прилагательное, «тривиальный» происходит от латинского слова «trivialis», что означает «мало содержательный», «элементарный до очевидности», «мало интересный»).
Тривиальные тождества не представляют интереса, тождества же нетривиальные, напротив, представляют большой интерес. С их помощью решаются многочисленные теоретические и практические задачи. Заметим, кроме того, что каждое нетривиальное тождество выражает собой некоторое определенное свойство чисел. Например, тождество
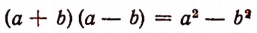
говорит о том, что произведение суммы двух любых чисел на их разность равняется разности квадратов этих чисел. Поясним это на примере.
Возьмем два каких-нибудь числа, скажем, + 10 и — 7; их сумма будет +3, а их разность + 17. Произведение суммы на разность будет +51.
С другой стороны, квадрат первого числа будет + 100, а квадрат второго + 49. Разность этих квадратов дает снова то же самое число +51.
Тождество
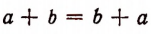
нетривиальное; оно выражает имеющий важное значение перемес-тительный закон сложения.
Определение:
Два выражения, равные друг другу, при любых допустимых значениях входящих в них букв, называются тождественно равными.
Примеры тождественно равных выражений:
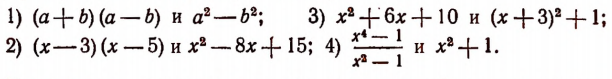
Легко видеть, что не всякие два выражения будут тождественно равными. Например, выражения 2а + 1 и а + 7 не будут тождественно равными. Их значения отличаются друг от друга, например, при а = 0.
Преобразование алгебраического выражения
В алгебре часто употребляется термин «преобразование выражения».
Что значит преобразовать выражение? Преобразовать данное выражение — значит составить новое выражение, отличающееся от данного, но ему тождественно равное.
Примеры:
Путем преобразования можно:
1) выражение 2а + 3b + 4а + 8b заменить тождественно равным ему выражением 6а+11b;
2) выражение (а +6) (а — b) заменить выражением 
3) выражение 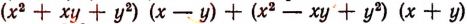 заменить выражением
заменить выражением 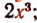
4) путем более сложных преобразований заменить выражение 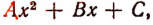 например, следующим выражением:
например, следующим выражением:
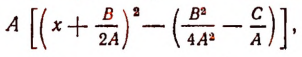
ему тождественно равным.
(Последнее преобразование называется «выделением полного квадрата из многочлена второй степени» и излагается в следующем параграфе.)
В первом и третьем примерах преобразование привело нас к более простому выражению, чем исходное; в четвертом же — к более громоздкому по сравнению с исходным.
Всякое преобразование делается в соответствии с той заранее поставленной целью, которая с помощью этого преобразования должна быть достигнута. Иначе говоря, всякое преобразование должно быть целенаправленным.
Часто употребляется термин «упростить выражение». Упростить выражение — это значит преобразовать его, вообще говоря, так, чтобы наиболее удобно было отыскивать его числовые значения. Как правило, упрощение выражения приводит его к новому выражению, содержащему меньшее число действий.
Например, находить значения выражения
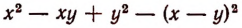
более удобно, если заменить это выражение тождественно равным ему выражением ху. Преобразование выражения 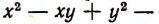
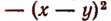 к виду ху является примером упрощения выражения. Выражение ху содержит лишь одно действие, а первоначальное — 8 действий.
к виду ху является примером упрощения выражения. Выражение ху содержит лишь одно действие, а первоначальное — 8 действий.
Преобразование алгебраических выражений является мощным средством, широко применяемым к решению самых разнообразных по содержанию и характеру задач.
В настоящем учебнике применения преобразований к решению задач содержатся во многих последующих главах.
Некоторые замечания:
1. Если в тождестве заменить какую-либо букву произвольным алгебраическим выражением, то получится опять же тождество. Например, заменяя в тождестве
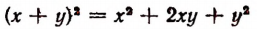
букву х выражением (а + b), а букву у выражением ab, получим новое тождество
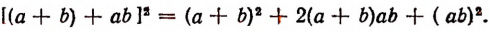
2. Каждым тождеством можно пользоваться двояко. Например, на основании тождества
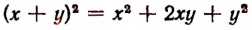
можно выражение 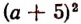 заменить выражением
заменить выражением
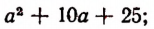
а в другом случае, скажем, выражение
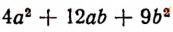
полезно заменить выражением
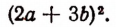
Пусть требуется вычесть из выражения 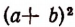 выражение
выражение 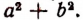 В этом случае целесообразно выражение
В этом случае целесообразно выражение 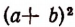 заменить выражением
заменить выражением 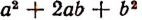 и тогда разность
и тогда разность
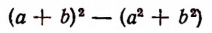
будет равна 2ab.
Пусть требуется вычислить значение выражения
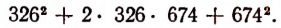
В этом случае для получения ответа целесообразно заменить данный многочлен выражением
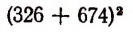
и этим самым гораздо легче обнаружить, что искомым ответом будет число 1 000 000.
Для того чтобы уметь применять тождество двояко, надо уметь и формулировать его двояко. Например, тождество
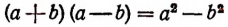
формулируется так: произведение суммы двух алгебраических выражений на их разность равно разности квадратов этих же алгебраических выражений.
Если же мы перепишем наше тождество в виде
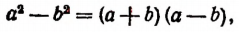
то его придется формулировать иначе, а именно: разность квадратов двух алгебраических выражений равна произведению суммы этих же выражений на их разность.
Выделение полного квадрата из многочлена 2-й степени
Выражение 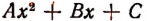 называется многочленом 2-й степени относительно величины х, записанным в общем виде. Здесь буква х может принимать любые значения, т. е. она обозначает собой величину, могущую изменяться как угодно. Что же касается букв А, В и С, то они обозначают собой наперед выбранные известные числа, остающиеся неизменными при всех изменениях величины х. Буквы А, В и С называются коэффициентами многочлена, причем предполагается, что
называется многочленом 2-й степени относительно величины х, записанным в общем виде. Здесь буква х может принимать любые значения, т. е. она обозначает собой величину, могущую изменяться как угодно. Что же касается букв А, В и С, то они обозначают собой наперед выбранные известные числа, остающиеся неизменными при всех изменениях величины х. Буквы А, В и С называются коэффициентами многочлена, причем предполагается, что 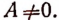 Буква же х называется независимой переменной. (Если мы здесь величину х называем «независимой переменной», то это значит, что она может изменяться как угодно, независимо ни от чего.)
Буква же х называется независимой переменной. (Если мы здесь величину х называем «независимой переменной», то это значит, что она может изменяться как угодно, независимо ни от чего.)
Выделение полного квадрата из многочлена 2-й степени является одним из важных преобразований, имеющим применения в ряде вопросов большой значимости. Это преобразование мы выполним сначала без пояснений, а затем дадим и пояснения.
Преобразование без пояснений:
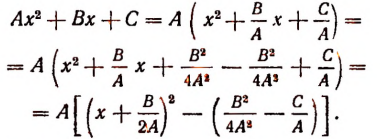
Пояснения:
1. Мы начали с того, что многочлен 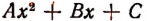 представили в виде произведения
представили в виде произведения
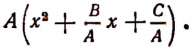
Законность этой операции вытекает из распределительного свойства умножения.
2. Вторая операция заключалась в том, что мы заменили внутри скобок выражение 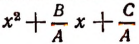 равным ему выражением
равным ему выражением
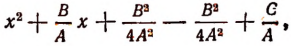
которое получилось введением двух новых вспомогательных членов 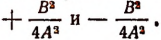
Вспомогательный член 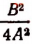 образован следующим образом: мы взяли множитель
образован следующим образом: мы взяли множитель 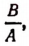 стоящий перед буквой х во втором члене многочлена
стоящий перед буквой х во втором члене многочлена 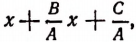 затем разделили этот множитель на два и получили выражение
затем разделили этот множитель на два и получили выражение 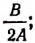 после этого выражение
после этого выражение 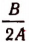 возвели в квадрат, т. е. умножили само на себя, в результате чего и получилось
возвели в квадрат, т. е. умножили само на себя, в результате чего и получилось 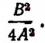
3. Далее, выражение 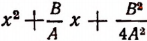 заменили тождественно равным ему выражением
заменили тождественно равным ему выражением 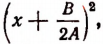 а остальные два члена многочлена заключили в скобки, поставив перед скобками знак минус.
а остальные два члена многочлена заключили в скобки, поставив перед скобками знак минус.
Примеры на выделение полного квадрата:
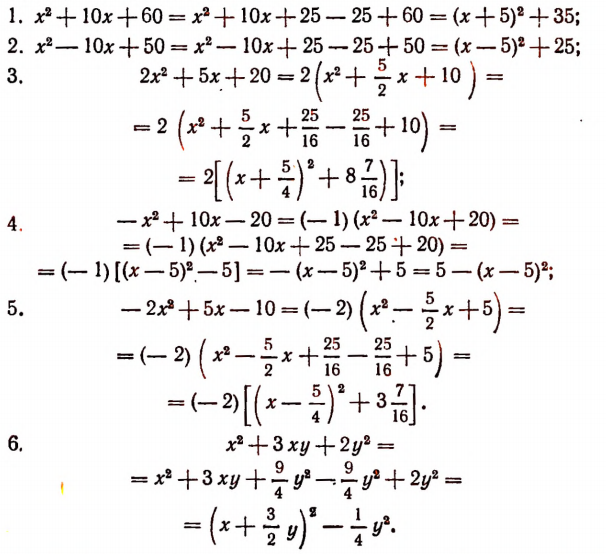
Выделение полного квадрата из многочлена 2-й степени будем называть ради краткости «выделением полного квадрата». Первые применения этого преобразования к решению задач показаны в следующей главе.
Возвышение в степень
Действие возвышения в степень: В начале курса мы уже видели, что возвышение в степень есть действие, посредством которого данное число (основание степени) берётся сомножителем столько раз, сколько единиц содержится в другом данном числе (показателе степени). 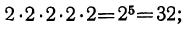
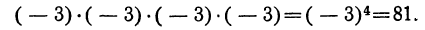
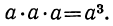
Вообще: 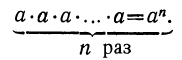
Степень отрицательного числа
При умножении относительных чисел мы видели, что произведение бывает положительно, если число отрицательных множителей чётное. В противном случае произведение будет отрицательным. Применяя это свойство к произведению равных отрицательных сомножителей, т. е. возвышению в степень отрицательного числа.
Чётная степень отрицательного числа положительна, нечётная — отрицательна.
Так: 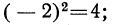
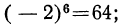
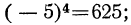
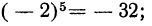
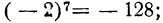
 и т. п.
и т. п.
Возвышение в степень одночленов
В первой части мы вывели правила возвышения одночлена в квадрат и куб. Покажем теперь, что по тем же правилам производится возвышение одночлена в любую степень.
а) Возвысим в степенью произведение abc. Пользуясь известными свойствами умножения, получим: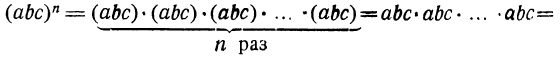
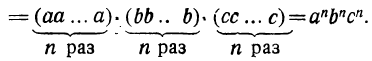
Чтобы возвысить в степень произведение, надо возвысить в эту степень каждый сомножитель отдельно и результаты перемножить.
б) Таким же способом найдём степень дроби 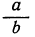 :
:
Чтобы возвысить в степень дробь, надо возвысить в эту степень отдельно числитель и знаменатель и первый результат разделить на второй.
в) Пусть требуется возвысить в степень n число 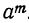 . Будем иметь:
. Будем иметь: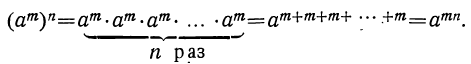
Чтобы возвысить степень какого-либо числа в другую степень, надо перемножить показатели степеней.
г) Возьмём теперь какой-либо одночлен, например 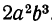 . Возвысим его в какую-либо степень n. Применяя выведенные правила, получим:
. Возвысим его в какую-либо степень n. Применяя выведенные правила, получим:
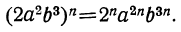
Чтобы возвысить в степень одночлен, надо возвысить в эту степень коэффициент, а показатели букв умножить на показатель степени, в которую возвышается одночлен.
Возвышение в квадрат многочлена
Вывод формулы: Пользуясь формулой 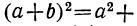
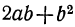 , мы можем возвысить в квадрат трёхчлен
, мы можем возвысить в квадрат трёхчлен 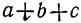 , рассматривая его как двучлен
, рассматривая его как двучлен 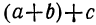 :
: 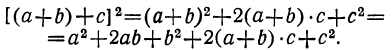
Таким образом, с прибавлением к двучлену a + b третьего члена с после возвышения суммы в квадрат прибавились два члена: 1) удвоенное произведение суммы первых двух членов на третий член и 2) квадрат третьего члена.
Теперь нетрудно четырёхчлен a + b + c + d возвысить в квадрат, принимая сумму a + b + c за один член: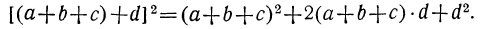
Подставляя вместо 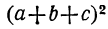 то выражение, которое мы нашли раньше, получим:
то выражение, которое мы нашли раньше, получим: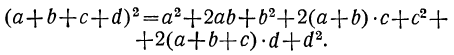
Мы опять замечаем, что с прибавлением нового члена к возвышаемому в квадрат многочлену к степени прибавляются два члена: 1) удвоенное произведение суммы прежних членов на новый член и 2) квадрат нового члена. Очевидно, что такое прибавление к степени двух членов будет идти и дальше по мере прибавления новых членов к возвышаемому в квадрат многочлену. Значит:
Квадрат многочлена равен квадрату 1-го члена, плюс удвоенное произведение 1-го члена на 2-й, плюс квадрат 2-го члена, плюс удвоенное произведение суммы первых двух членов на 3-й, плюс квадрат 3-го члена, плюс удвоенное произведение суммы первых трёх членов на 4-й, плюс квадрат 4-го члена и т. д.
Конечно, члены многочлена могут быть и отрицательными.
Если в правой части последнего равенства раскроем скобки, то получим после перестановки членов: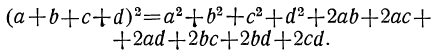
Можно поэтому предыдущее правило формулировать так:
Квадрат многочлена равен сумме квадратов всех его членов, сложенной с удвоенными произведениями каждого члена на каждый из последующих.
Замечание о знаках: В окончательном результате возвышения в квадрат многочлена со знаком плюс окажутся, во-первых, квадраты всех членов многочлена и, во-вторых, те удвоенные произведения, которые появились при умножении членов с одинаковыми знаками. Например: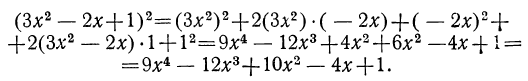
Понятие об иррациональных числах
Соизмеримые и несоизмеримые отрезки: Как известно из геометрии, общей мерой двух отрезков прямой называется такой отрезок, который в каждом из них содержится целое число раз без остатка. В геометрии разъясняется, что могут быть такие два отрезка, которые не имеют общей меры (например, сторона квадрата и его диагональ).
Два отрезка называются соизмеримыми или несоизмеримыми между собой, смотря по тому, имеют ли они общую меру или не имеют.
Понятие об измерении: Пусть требуется измерить длину отрезка AB (черт. 1) при помощи единицы длины CD. Для этого узнаем, сколько раз единица CD содержится в АВ.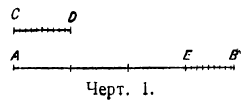
Пусть окажется, что она содержится в AB 3 раза с некоторым остатком EB (меньшим CD). Тогда число 3 будет приближённым результатом измерения с точностью до 1, и притом с недостатком, так как AB больше 3CD, но меньше 4CD (число 4 тоже можно назвать приближённым результатом измерения с точностью до 1, но с избытком). Желая получить более точный результат, узнаем, сколько раз в остатке EB содержится 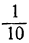 единицы CD. Положим, что эта доля содержится в EB более 8, но менее 9 раз. Тогда числа 3,8 и 3,9 будут приближёнными результатами измерения отрезка AB с точностью до
единицы CD. Положим, что эта доля содержится в EB более 8, но менее 9 раз. Тогда числа 3,8 и 3,9 будут приближёнными результатами измерения отрезка AB с точностью до 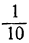 , первое число с недостатком, второе — с избытком. Желая получить ещё более точный результат измерения, узнаем, сколько раз в последнем остатке содержится доля единицы CD- Пусть эта доля содержится в остатке более 5 раз, но менее 6 раз. Тогда числа 3,85 и 3,86 будут приближёнными результатами измерения отрезка AB с точностью до
, первое число с недостатком, второе — с избытком. Желая получить ещё более точный результат измерения, узнаем, сколько раз в последнем остатке содержится доля единицы CD- Пусть эта доля содержится в остатке более 5 раз, но менее 6 раз. Тогда числа 3,85 и 3,86 будут приближёнными результатами измерения отрезка AB с точностью до 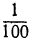 единицы. Можно продолжать такое измерение всё далее и далее. При этом возможны два случая:
единицы. Можно продолжать такое измерение всё далее и далее. При этом возможны два случая:
1) может случиться, что при последовательных измерениях с точностью до 0,1, 0,01, 0,001, … рано или поздно не получится никакого остатка;
2) может случиться, что с какой бы точностью до 0,1, 0,01, 0,001,… мы ни измеряли, остаток всегда будет получаться.
В первом случае в результате измерения получится конечная десятичная дробь. Во втором случае в результате измерения получится бесконечная десятичная дробь.
Конечная десятичная дробь получается лишь в том случае, если какая-нибудь десятичная доля единицы (одна десятая, или одна сотая, или одна тысячная и т. д.) является общей мерой измеряемого отрезка и единицы длины.
Если же измеряемый отрезок соизмерим с единицей длины, но ни 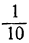 , ни
, ни 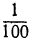 , ни
, ни 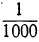 , вообще никакая десятичная доля единицы не является общей мерой измеряемого отрезка и единицы длины, то в результате измерения получается бесконечная периодическая десятичная дробь. Наконец, если измеряемый отрезок несоизмерим с единицей длины, то в результате измерения получается бесконечная непериодическая десятичная дробь.
, вообще никакая десятичная доля единицы не является общей мерой измеряемого отрезка и единицы длины, то в результате измерения получается бесконечная периодическая десятичная дробь. Наконец, если измеряемый отрезок несоизмерим с единицей длины, то в результате измерения получается бесконечная непериодическая десятичная дробь.
Иррациональные числа и их приближённые значения
Числа целые и дробные носят общее название рациональных чисел. Всякое рациональное число может быть записано в виде конечной десятичной дроби или в виде бесконечной периодической десятичной дроби; десятичные бесконечные непериодические дроби называются иррациональными числами. Рациональные числа служат мерой величин, соизмеримых с единицей, иррациональные числа — мерой величин, несоизмеримых с единицей.
Иррациональное число считается известным (или данным), если указан способ, посредством которого можно находить любое число его десятичных знаков.
Обрывая на каком-нибудь десятичном знаке бесконечную десятичную дробь, выражающую данное (рациональное или иррациональное) число, получаем приближённое значение этого числа с точностью до 0,1, 0,01, 0,001 и т. д. с недостатком. Увеличивая на 1 последний сохранённый десятичный знак, получим приближённое значение данного числа с той же точностью, но с избытком.
Примеры:
1) Записывая число 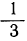 в виде бесконечной периодической дроби, 0,33333… и сохраняя первые четыре десятичных знака этой дроби, получим приближённое значение числа
в виде бесконечной периодической дроби, 0,33333… и сохраняя первые четыре десятичных знака этой дроби, получим приближённое значение числа 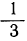 с точностью до 0,0001 с недостатком: 0,3333.
с точностью до 0,0001 с недостатком: 0,3333.
Приближённое значение этого числа с точностью до 0,0001 с избытком есть 0,3334.
2) Иррациональное число π, выражающее отношение длины окруж,-ности к диаметру, записывается в виде бесконечной десятичной дроби, первые 25 знаков которой суть: 3,1415926535897932384626433.
Приближённые значения числа π с точностью до 0,00001 суть 3,14159 (с недостатком) и 3,14160 (с избытком).
3) Возьмём иррациональное число, выражающееся следующей бесконечной непериодической десятичной дробью: 123,1010010001000010000010000001 … (между двумя последовательными единицами стоит один нуль, потом два нуля, потом три нуля и т. д.).
Приближённые значения этого иррационального числа с точностью до 0,000000000001 (т. е. до суть 123,101001000100 (с недостатком) и 123,101001000101 (с избытком).
Равенство и неравенство между иррациональными числами. Вещественные числа
Два иррациональных числа считаются равными, если они выражены десятичными дробями с соответственно одинаковыми цифрами. Из двух положительных иррациональных чисел больше то, которое при разложении в десятичную дробь содержит в себе большее число целых, или — при равенстве целых — большее число десятых, или — при равенстве целых и десятых — большее число сотых, и т. д. Например, число 2,745037… больше числа 2,745029 …, так как в первом 6-я цифра выражает число большее, чем 6-я цифра во втором при тождественности всех предыдущих цифр.
Это определение годится также и для сравнения иррационального числа с рациональным, если рациональное число разложено в десятичную дробь. Оно пригодно и для сравнения двух рациональных чисел, разложенных в десятичные дроби, если только десятичные дроби с периодом 9 заменять десятичными дробями, кончающимися нулями: например, надо вместо 2,39999 … брать 2,400000 ….
Заметим, что из приведённого определения неравенств следует:
Если α — какое-нибудь иррациональное число, a — какое нибудь приближённое значение числа α с недостатком, b— какое-нибудь приближённое значение числа α с избытком, то
α< α <b.
Иррациональные числа могут быть положительными и отрицательными, сообразно со смыслом измеряемой величины. Как и в случае рациональных чисел, из двух отрицательных’ вещественных чисел большим считают то, у которого абсолютная величина меньше; всякое отрицательное число меньше нуля, а нуль меньше всякого положительного числа.
Рациональные и иррациональные числа вместе называются вещественными, или действительными, числами.
10. Определение действий над иррациональными числами. Пусть а и β будут какие-нибудь данные положительные иррациональные числа (в нижеследующем примере 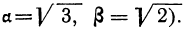 Пусть приближённые значения чисел α и β, взятые с недостатком, будут:
Пусть приближённые значения чисел α и β, взятые с недостатком, будут:
| до 0,1 | до 0,01 | до 0,001 | до 0,0001 | |
| для числа α | 1,7 | 1,73 | 1,732 | 1,7320 |
| для числа β | 1,4 | 1,41 | 1,414 | 1,4142 |
Соответствующие приближённые значения с избытком получаются из этих чисел посредством увеличения последнего десятичного знака на 1.
Тогда: а) Сложить α и β — значит найти число, которое было бы
больше каждой из сумм:
1,74-1,4=3,1
1,734-1,41=3,14
1,7324-1,414 = 3,146 1,73204-1,4142=3,1462 и т. д.
и меньше каждой из сумм:
1,84-1,5=3,3
1,744-1,42=3,16
1,7334-1,415=3,148
1,73214-1,4143=3,1464, т. е.:
Сложить числа α и β — значит найти такое третье число γ, которое было бы больше суммы любых приближённых их значений, взятых с недостатком, но меньше суммы любых приближённых значений, взятых с избытком.
Мы принимаем без доказательства, что такое число γ для любых двух вещественных чисел а и β существует, и притом только одно.
б) Беря приближённые значения чисел α и β, указанные выше, мы можем сказать, что произведение α ∙β есть число, которое
больше каждого из произве-
дений:
1,7-1,4=2,38
1,73-1,41=2,4393
1,732-1,414 = 2,449048
1,7320-1,4142 = 2,44939440 и т. д.
и меньше каждого из произведе-
ний:
1,8-1,5=2,70
1,74-1,42=2,4708
1,733-1,415 = 2,452195
1,7321-1,4143 = 2,44970903, т. е.:
Перемножить положительные числа α и β — значит найти такое третье число, которое было бы больше произведения их любых приближённых значений, взятых с недостатком, но меньше произведения их любых приближённых значений, взятых с избытком.
Мы примем без доказательства, что такое число существует, и притом только одно.
в) Возвысить иррациональное число а во вторую, третью, четвёртую и т. д. степень — значит найти произведение, составленное из двух, трёх, четырёх и т. д. сомножителей, равных 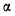 .
.
г) Обратные действия определяются для иррациональных чисел так же, как и для рациональных; так, вычесть из числа а число β — значит найти такое число х, чтобы сумма β+x равнялась а и т. п.
Если одно из чисел α или β — рациональное и выражается конечной десятичной дробью, то в указанных определениях вместо приближённых значений такого числа надо брать его точное значение.
Произведение иррационального числа на нуль принимается, как и для рационального числа, равным нулю.
Действия над отрицательными иррациональными числами производятся согласно правилам, данным для рациональных отрицательных чисел.
При более обстоятельном рассмотрении можно установить, что действия над иррациональными числами обладают теми же свойствами, какие принадлежат действиям над числами рациональными; например, сложение и умножение обладают свойствами переместительным и сочетательным; умножение и деление, кроме того, обладают ещё распределительным свойством. Свойства, выражаемые неравенствами, также сохраняются для чисел иррациональных; так, если α>β, то α+γ>β+γ, αγ>βγ (если γ>0) и αγ<βγ (если γ<0) и т. п.
Извлечение корня
Определение:
Корнем n-й степени из числа а называется такое число, которое, будучи возвышено в степень п, даёт а.
Корень n-й степени из числа а обозначается так: 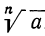 . Из самого определения следует, что
. Из самого определения следует, что 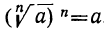 .
.
Это равенство может служить для проверки правильности произведённого действия извлечения корня. Пусть, например, мы нашли, что 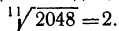 Для проверки возвысим 2 в одиннадцатую степень, получим
Для проверки возвысим 2 в одиннадцатую степень, получим 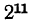 =2048. Значит, корень найден правильно. Точно так же
=2048. Значит, корень найден правильно. Точно так же 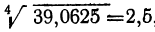 , так как
, так как 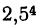 = 39,0625.
= 39,0625.
Приближённые корни любой степени
Мы уже говорили, что такое приближённые квадратные корни с точностью до 1, до 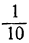 и т. д. Сказанное тогда о квадратном корне может быть применено к корню всякой другой степени. Например, приближённым значением
и т. д. Сказанное тогда о квадратном корне может быть применено к корню всякой другой степени. Например, приближённым значением 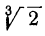 с точностью до
с точностью до 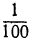 называется такая десятичная дробь, состоящая из целых, десятых и сотых, куб которой не больше 2, но если увеличим её на
называется такая десятичная дробь, состоящая из целых, десятых и сотых, куб которой не больше 2, но если увеличим её на 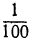 и возвысим в куб, то получим больше 2. Мы не будем выводить правила для нахождения точных и приближённых корней кубичных и других степеней, ограничимся только указанием следующего простого приёма для нахождения таких корней.
и возвысим в куб, то получим больше 2. Мы не будем выводить правила для нахождения точных и приближённых корней кубичных и других степеней, ограничимся только указанием следующего простого приёма для нахождения таких корней.
Пусть требуется найти 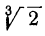 . Приближённые корни с точностью до 1 будут, очевидно, числа 1 (с недостатком), 2 (с избытком). Чтобы найти цифру десятых долей искомого корня, найдём в ряду: 1; 1,1; 1,2; 1,3; 1,4; 1,5; 1,6; 1,7; 1,8; 1,9 два таких рядом стоящих числа, чтобы куб левого числа был меньше 2, а куб правого — больше 2. Для этого возьмём из чисел нашего ряда среднее 1,5 и возвысим его в куб. Мы найдём:
. Приближённые корни с точностью до 1 будут, очевидно, числа 1 (с недостатком), 2 (с избытком). Чтобы найти цифру десятых долей искомого корня, найдём в ряду: 1; 1,1; 1,2; 1,3; 1,4; 1,5; 1,6; 1,7; 1,8; 1,9 два таких рядом стоящих числа, чтобы куб левого числа был меньше 2, а куб правого — больше 2. Для этого возьмём из чисел нашего ряда среднее 1,5 и возвысим его в куб. Мы найдём: 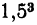 =3,375, что больше 2. Так как числа, стоящие направо от 1,5, при возвышении в куб дают результат ещё больший, то мы можем отбросить всю правую половину ряда и испытать только числа: 1; 1,1; 1,2; 1,3; 1,4.
=3,375, что больше 2. Так как числа, стоящие направо от 1,5, при возвышении в куб дают результат ещё больший, то мы можем отбросить всю правую половину ряда и испытать только числа: 1; 1,1; 1,2; 1,3; 1,4.
Возьмём среднее из них 1,2 и возвысим в куб. Получим 1,728, что меньше 2. Значит, испытанию подлежат теперь только числа 1,3 и 1,4. Возвысив в куб число 1,3, получим 2,197, что больше 2. Мы получили, таким образом, два числа: 1,2 и 1,3, которые разнятся между собой на 0,1 и между кубами которых заключается число 2. Это и будут приближённые кубичные корни из 2 с точностью до 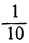 с недостатком и с избытком.
с недостатком и с избытком.
Если желаем найти цифру сотых, мы должны испытать следующие числа: 1,21; 1,22; 1,23; … ; 1,29. Взяв в этом ряду среднее число 1,25 и возвысив его в куб, найдём 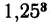 = 1,953125, что меньше 2. Значит, теперь надо испытать только числа: 1,26; 1,27; 1,28; 1,29. Так как
= 1,953125, что меньше 2. Значит, теперь надо испытать только числа: 1,26; 1,27; 1,28; 1,29. Так как 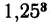 очень мало разнится от 2, то естественно попробовать, не будет ли 1,26
очень мало разнится от 2, то естественно попробовать, не будет ли 1,26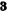 больше 2. И действительно, возвысив 1,26 в куб, получим 2,000376. Значит, искомый кубический корень из 2 с точностью до
больше 2. И действительно, возвысив 1,26 в куб, получим 2,000376. Значит, искомый кубический корень из 2 с точностью до 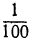 будет 1,25 (с недостатком) или 1,26 (с избытком). Если бы мы желали далее найти цифру тысячных, то должны были бы подобным же путём испытать числа ряда: 1,251; 1,252; 1,253; . . . ; 1,259.
будет 1,25 (с недостатком) или 1,26 (с избытком). Если бы мы желали далее найти цифру тысячных, то должны были бы подобным же путём испытать числа ряда: 1,251; 1,252; 1,253; . . . ; 1,259.
Конечно, приём этот утомителен (существуют более удобные способы), но из него ясно видно, что десятичные цифры приближённых корней любой степени могут быть найдены в каком угодно большом числе.
Для 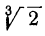 мы получили приближённые значения с недостатком: 1; 1,2; 1,25; 1,259; ….
мы получили приближённые значения с недостатком: 1; 1,2; 1,25; 1,259; ….
Составим бесконечную десятичную дробь 1,259 …. Эта бесконечная десятичная дробь выражает собой некоторое иррациональное число α, а числа: 1; 1,2; 1,25; 1,259; . . . представляют собой приближённые значения иррационального числа α, взятые с недостатком.
Куб иррационального числа α есть 2. Чтобы убедиться в этом, вспомним, что называется кубом иррационального числа α; α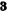 — это число, удовлетворяющее двум условиям: оно больше куба любого приближённого значения а, взятого с недостатком, и меньше куба любого приближённого значения α, взятого с избытком. Но число
— это число, удовлетворяющее двум условиям: оно больше куба любого приближённого значения а, взятого с недостатком, и меньше куба любого приближённого значения α, взятого с избытком. Но число 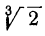 этим условиям удовлетворяет, так как
этим условиям удовлетворяет, так как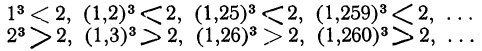
Значит, иррациональное число 1,259 .. . есть кубический корень 2.
Итак, после введения иррациональных чисел задача извлечения арифметического корня любой степени из любого положительного числа во всех случаях разрешима: такой корень всегда существует, и притом только один.
Замечание:
Действие извлечения корня является источником многочисленных примеров иррациональных чисел, которые приходится рассматривать в курсе элементарной алгебры. Однако было бы грубой ошибкой думать, что все иррациональные числа являются корнями из рациональных чисел или сводятся к этим корням при помощи алгебраических действий: существует бесконечно много иррациональных чисел, которые не являются корнями никакой степени ни из какого рационального числа и которые вообще не могут быть получены посредством алгебраических действий (сложения, вычитания, умножения, деления, возведения в степень, извлечения корня) над рациональными числами, в каком бы числе, в каком бы порядке и над какими бы рациональными числами мы эти действия ни совершали. Примером такого иррационального числа может служить число π.
Преобразование иррациональных выражений
Рациональные и иррациональные алгебраические выражения: Алгебраическое выражение называется рациональным относительно какой-нибудь буквы, входящей в это выражение, если эта буква не находится под знаком радикала; в противном случае выражение называется иррациональным относительно этой буквы. Например, выражение  есть рациональное относительно α и иррациональное относительно х.
есть рациональное относительно α и иррациональное относительно х.
Если говорят—„рациональное алгебраическое выражение“, не добавляя относительно каких букв, то предполагается, что оно рационально относительно всех букв, входящих в выражение.
Основное свойство радикала
Заметим, что корни (радикалы), о которых мы будем говорить в этой главе, разумеются только арифметические. Возьмём какой-нибудь радикал, например 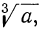 , и возвысим подкоренное число В какую-нибудь степень, например в квадрат; вместе с тем умножим показатель радикала на показатель той степени, в какую мы возвысили подкоренное число, т. е. в нашем случае умножим на 2. Тогда получим новый радикал
, и возвысим подкоренное число В какую-нибудь степень, например в квадрат; вместе с тем умножим показатель радикала на показатель той степени, в какую мы возвысили подкоренное число, т. е. в нашем случае умножим на 2. Тогда получим новый радикал 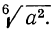 Докажем, что от этих двух операций величина радикала не изменилась.
Докажем, что от этих двух операций величина радикала не изменилась.
Предположим, что мы вычислили 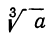 и получили некоторое число х. Тогда мы можем написать равенства: x=
и получили некоторое число х. Тогда мы можем написать равенства: x= 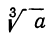 и x
и x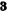 = α. Возвысим обе части последнего равенства в квадрат:
= α. Возвысим обе части последнего равенства в квадрат: 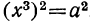 т. e.
т. e.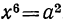 .
.
Из последнего равенства видно, что 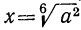 . Таким образом, одно и то же число х равно и
. Таким образом, одно и то же число х равно и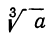 , и
, и 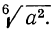 следовательно:
следовательно: 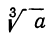 =
=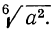
Подобно этому можно убедиться, что: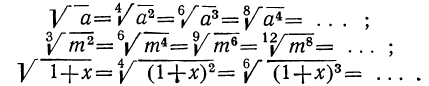
Величина радикала не изменится, если подкоренное выражение возвысим в какую-нибудь степень и вместе с тем показатель радикала умножим на показатель той степени, в которую возвысили подкоренное выражение.
Правило это короче выражают еще так:
Величина радикала не изменится, если показатель корня и показатель подкоренного выражения умножим (или разделим) на одно и то же число.
Следствия: а) Радикалы разных степеней можно привести к одинаковым показателям (подобно тому как дроби с разными знаменателями можно привести к одному знаменателю). Для этого достаточно найти общее кратное (лучше всего наименьшее) показателей всех радикалов и умножить показатель каждого из них на соответствующий дополнительный множитель, возвысив вместе с тем каждое подкоренное выражение в надлежащую степень.
Пример:
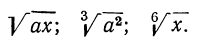
Наименьшее кратное показателей радикалов есть 6; дополнительные множители будут: для первого радикала 3, для второго 2 и для третьего 1. Тогда: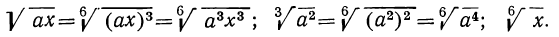
б) Если подкоренное выражение есть степень, показатель которой имеет общий множитель с показателем радикала, то на этот множитель можно разделить оба показателя.
Примеры:
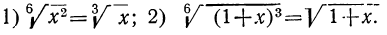
в) Если подкоренное выражение есть произведение нескольких степеней, показатели которых имеют один и тот же общий множитель с показателем радикала, то на этот множитель можно разделить все показатели.
Примеры:
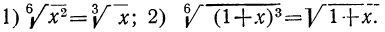
Извлечение арифметического корня из произведения, из степени и из дроби
а) Пусть надо извлечь арифметический корень степени п из произведения abc. Если бы требовалось произведение возвысить в степень, то, как мы видели, надо было бы возвысить в степень каждый сомножитель отдельно. Так как извлечение корня есть действие, обратное возвышению в степень, то надо ожидать, что и для извлечения корня из произведения надо извлечь его из каждого сомножителя отдельно, т. е. что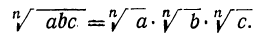
Чтобы убедиться в верности этого равенства, возвысим правую часть его в степень n: 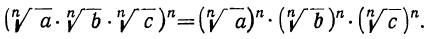
Но, по определении корня, 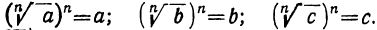
Следовательно, 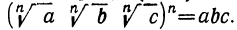
Если же n-я степень произведения 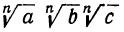 равна abc, то это значит, что произведение это равно корню n-й степени из abc. Значит:
равна abc, то это значит, что произведение это равно корню n-й степени из abc. Значит:
Чтобы извлечь корень из произведения, надо извлечь его из каждого сомножителя отдельно и результаты перемножить.
б) Легко убедиться проверкой, что 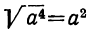 , потому что
, потому что 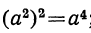 ;
;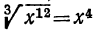 , потому что
, потому что 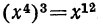 , и т. п.
, и т. п.
Вообще: 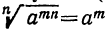 , потому что
, потому что 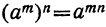 . Значит:
. Значит:
Чтобы извлечь корень из степени, показатель которой делится на показатель корня, надо разделить показатель степени на показатель корня.
в) Верны будут также и следующие равенства:
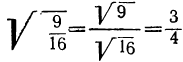 , потому что
, потому что 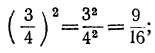
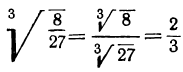 , потому что
, потому что 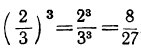 .
.
Вообще: 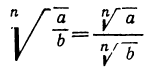 , потому что
, потому что 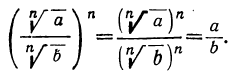 .
.
Чтобы извлечь корень из дроби, надо извлечь его из числителя и знаменателя отдельно и первый результат разделить на второй.
Примеры:
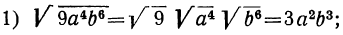
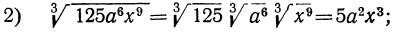
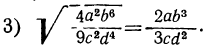
Простейшие преобразования радикалов
а) Вынесение множителей за знак корня. Если подкоренное выражение разлагается на такие множители, что из некоторых можно извлечь точный корень, то такие множители, по извлечении из них корня, могут быть написаны перед знаком корня (т. е. могут быть вынесены за знак корня); например: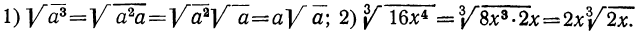
б) Подведение множителей под знак корня. Иногда бывает полезно, наоборот, подвести под знак корня множители, стоящие перед ним; для этого достаточно возвысить такие множители в степень, показатель которой равен показателю корня, а затем написать множители под знаком корня; например: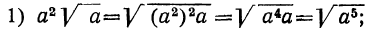
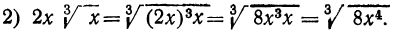
в) Освобождение подкоренного выражения от знаменателей.
Покажем это на следующих примерах:
1) 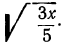 Чтобы из знаменателя можно было извлечь точный квадратный корень, умножим оба члена дроби на 5:
Чтобы из знаменателя можно было извлечь точный квадратный корень, умножим оба члена дроби на 5: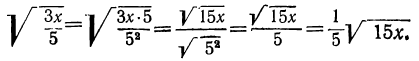
2) 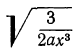 . Умножим оба члена дроби на 2, на а и на х, т. е. на 2ах:
. Умножим оба члена дроби на 2, на а и на х, т. е. на 2ах: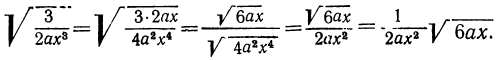
Замечание:
Если требуется извлечь корень из алгебраической суммы, то нельзя извлекать его из каждого слагаемого отдельно. Так: 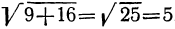 , тогда как
, тогда как 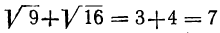 ; значит, действие извлечения корня по отношению к сложению (и вычитанию) не обладает распределительным свойством (как и возвышение в степень).
; значит, действие извлечения корня по отношению к сложению (и вычитанию) не обладает распределительным свойством (как и возвышение в степень).
Подобные радикалы
Подобными радикалами называются такие, у которых одинаковы подкоренные выражения и одинаковы показатели радикалов. Таковы, например, радикалы: 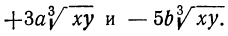
Чтобы определить, подобны ли между собой данные радикалы, следует предварительно упростить их, т. е. если возможно:
1) вынести из-под радикала те множители, из которых можно извлечь точный корень;
2) освободиться под радикалами от знаменателей дробей;
3) понизить степень радикала, сократив показатели радикала и подкоренного числа на их общий множитель, если такой есть.
По выполнении этих действий радикал приведётся к простейшему виду.
Примеры:
1) Радикалы 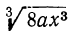 и
и 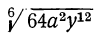 окажутся подобными, если упростим их:
окажутся подобными, если упростим их: 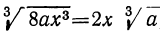 ;
; 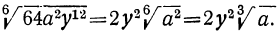
2) Три радикала 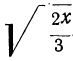 ,
, 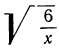 ,
, 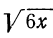 окажутся подобными, если освободимся под радикалами от знаменателей:
окажутся подобными, если освободимся под радикалами от знаменателей: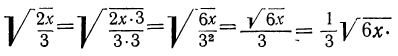
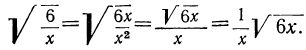
Действия над иррациональными одночленами
а) Сложение и вычитание. Чтобы сложить или вычесть иррациональные одночлены, соединяют их знаками плюс или минус и делают приведение подобных членов, если они окажутся.
Примеры: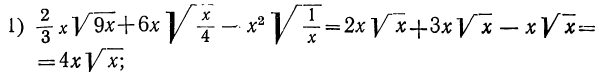
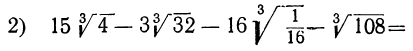
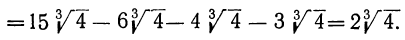
б) Умножение. Мы видели, что для извлечения корня из произведения надо извлечь его из каждого сомножителя отдельно; значит, наоборот:
Чтобы перемножить несколько корней одинаковой степени, надо перемножить подкоренные выражения и из произведения извлечь корень той же степени.
Так: 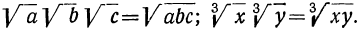
Если для перемножения даны радикалы с различными показателями, то их надо предварительно привести к одному показателю.
Если перед радикалами имеются коэффициенты, то их перемножают.
Примеры: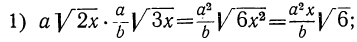
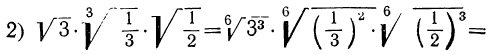
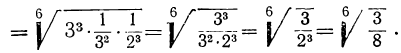
в) Деление. Мы знаем, что для извлечения корня из дроби надо извлечь его из числителя и знаменателя отдельно; значит, и наоборот: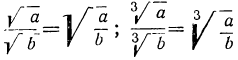 и т. д., т.е.:
и т. д., т.е.:
Чтобы разделить корни с одинаковыми показателями, надо разделить их подкоренные выражения и из частного извлечь корень той же степени.
Радикалы с различными показателями надо привести предварительно к одинаковым показателям. Если есть коэффициенты, то их делят.
Примеры: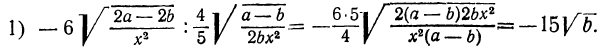
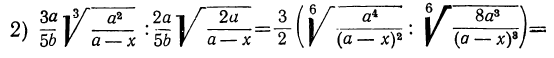
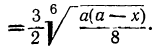
г) Возвышение в степень. Чтобы возвысить радикал в степень, надо возвысить в эту степень подкоренное выражение, оставив тот же показатель радикала.
Так: 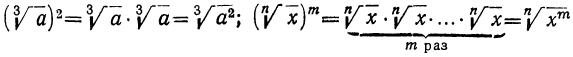
Примеры:
1) 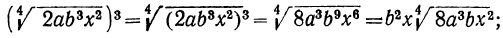
2) 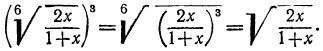
д) Извлечение корня. Чтобы извлечь корень из корня, надо перемножить показатели корней.
Так: 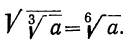
Чтобы убедиться в этом, положим, что 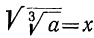 . Возвысим обе части этого равенства сначала в квадрат, а потом в куб:
. Возвысим обе части этого равенства сначала в квадрат, а потом в куб: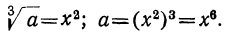
Отсюда видно, что 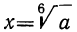 и, следовательно,
и, следовательно, 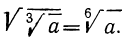
Пример:
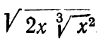
Подведём сомножитель 2х под знак радикала третьей степени:
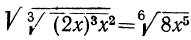
Заметим, что в этом примере (и в других, ему подобных) можно поступить иначе: заметив, что выражение, стоящее под знаком квадратного радикала, есть произведение, мы можем применить теорему об извлечении корня из произведения. Тогда получим: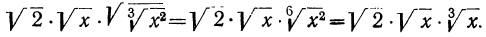
Приведя теперь радикалы к одинаковому показателю 6, найдём: 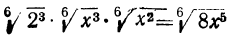
Действия над иррациональными многочленами производятся по тем же правилам, какие были выведены для многочленов рациональных. Например: 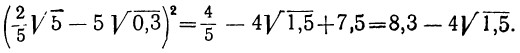
Освобождение знаменателя дроби от радикалов
При вычислении дробных выражений, знаменатели которых содержат радикалы, в некоторых случаях полезно предварительно преобразовать дробь так, чтобы знаменатель её не содержал радикалов. Пусть, например, надо вычислить: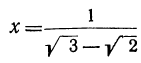
Мы можем производить вычисление или прямо по этой формуле, или же предварительно сделать её знаменатель рациональным, для чего достаточно умножить оба члена данной дроби на сумму 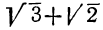 :
: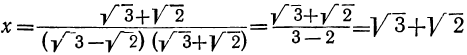 (2)
(2)
Формула (2) удобнее для вычисления, чем формула (1), во-первых, потому, что она содержит в себе всего три действия, а не четыре, как формула (1), а во-вторых, и потому, что при вычислении, которое по необходимости может быть только приближённое, погрешность результата сравнительно просто определяется по формуле (2). Так, найдя 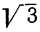 и
и 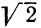 с точностью до половины тысячной доли, получим:
с точностью до половины тысячной доли, получим: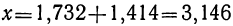
Результат этот точен до 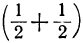 тысячной, т.е. до
тысячной, т.е. до 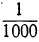 .
.
Примеры:
1) 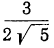 Умножим оба члена дроби на
Умножим оба члена дроби на 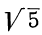 :
: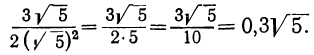
2) Если под знаком радикала стоит целое составное число, то иногда бывает полезно разложить его на простые сомножители с целью определить, каких сомножителей недостаёт в нём для того, чтобы оно было полным квадратом. Тогда достаточно умножить оба члена дроби на квадратный корень из произведения только недостающих сомножителей. Например: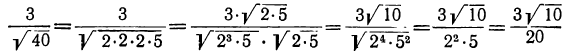
3) 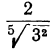 . Умножим оба члена дроби на
. Умножим оба члена дроби на 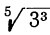 :
: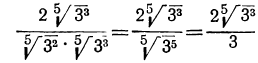
Вообще: 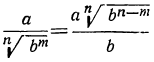 .
.
4) 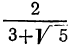 . Умножим оба члена дроби на разность
. Умножим оба члена дроби на разность 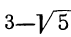 :
: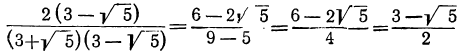
Вообще: 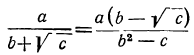
5) 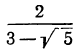 . Умножим оба члена дроби на сумму
. Умножим оба члена дроби на сумму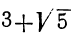 :
: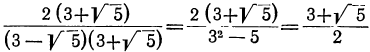
Вообще: 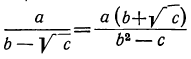
6) 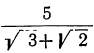 . Умножим оба члена дроби на
. Умножим оба члена дроби на 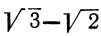 :
: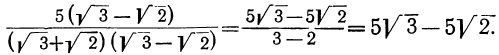
Вообще: 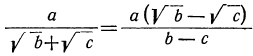
7) 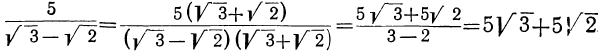
Вообще: 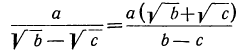 .
.
8) Если знаменатель есть двучлен с корнями третьей степени, то его можно сделать рациональным, основываясь на тождествах: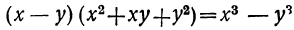 ;
;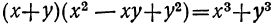 .
.
Пусть, например, знаменатель будет 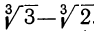 . Тогда, умножив числитель и знаменатель дроби на трёхчлен
. Тогда, умножив числитель и знаменатель дроби на трёхчлен 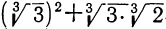
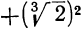 мы получим в знаменателе
мы получим в знаменателе 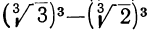 , т. е. 3 -2, или 1. Подобно этому найдём:
, т. е. 3 -2, или 1. Подобно этому найдём: 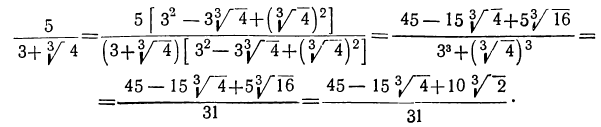
Иррациональные уравнения
Задача: Периметр прямоугольного треугольника равен 10 м, а один из его катетов равен 2 м; найти две другие стороны этого треугольника.
Обозначив второй катет буквой х, найдём, что гипотенуза должна равняться 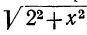 , и, следовательно, будем иметь уравнение:
, и, следовательно, будем иметь уравнение: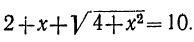
Мы получили уравнение, в котором под знак радикала входит неизвестное. Уравнения такого рода называются иррациональными.
Чтобы решить иррациональное уравнение, его надо предварительно освободить от радикалов, подкоренные выражения которых содержат неизвестное. Если в уравнение, как в нашей задаче, входит только один радикал, то освободиться от него можно таким образом: прежде всего уединим радикал, т. е. перенесём все члены, не содержащие радикала, в одну часть уравнения, оставив радикал в другой части: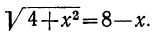
Теперь возвысим обе части уравнения в квадрат. Очевидно, что если равные числа мы возвысим в одну и ту же степень, то и получим равные числа; поэтому после возвышения в квадрат знак равенства сохраняется: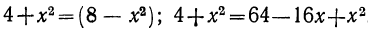
Решив это уравнение, найдём: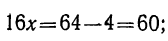
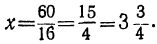
Тогда гипотенуза будет: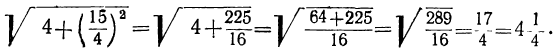
Пусть требуется решить ещё уравнение: 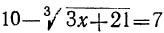 .
.
Уединим радикал и возвысим обе части уравнения в куб: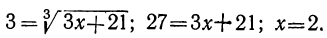
Проверка: 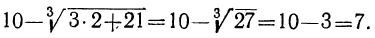
Посторонние решения: Возвышение частей уравнения в квадрат может ввести так называемые „посторонние» решения, т.е. такие, которые данному уравнению не удовлетворяют. Приведём этому пример. Пусть нам даны два уравнения: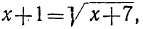 (1);
(1); 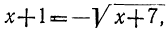 (2)
(2)
которые отличаются одно от другого только знаком перед радикалом. Возвысив в квадрат обе части каждого из этих уравнений, мы получим одно и то же уравнение: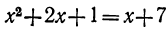 (3)
(3)
так как 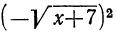 и
и 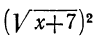 равны одному и тому же числу х+7.
равны одному и тому же числу х+7.
Уравнение (3) имеет два корня: —3 и 2. Число —3 удовлетворяет уравнению (2), но не удовлетворяет уравнению (1); наоборот, число 2 годно для уравнения (1), но не годится для уравнения (2).
Может оказаться, что уравнение (1) не имеет совсем решений; тогда уравнение (3) содержит только решения уравнения (2), и, значит, все они будут посторонние для уравнения (1).
Возвышение частей уравнения в квадрат может привести к новому уравнению, не равносильному с первоначальным.
Освобождение уравнения от двух квадратных радикалов
Пусть надо решить уравнение с двумя квадратными радикалами, подкоренные выражения которых содержат неизвестное: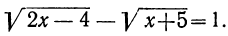
Желая освободиться от радикала 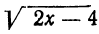 , уединим его:
, уединим его: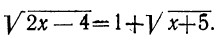
Теперь возвысим обе части этого уравнения в квадрат: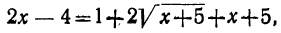
что даёт: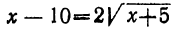
Наконец, освободим и последнее уравнение от радикала посредством вторичного возвышения в квадрат: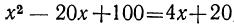 , или
, или 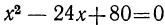 .
.
Решим это уравнение: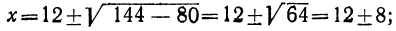
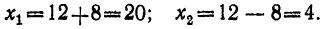
Подстановкой убеждаемся, что данное уравнение удовлетворяется только числом 20, а число 4 ему не удовлетворяет.
Решение задач с помощью преобразований
Задача:
Найти произведение чисел 1012 и 988 с помощью формулы
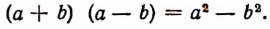
Решение:
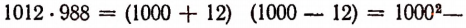
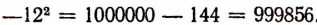
Задача:
Найти значение выражения
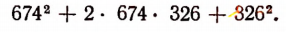
Решение:
На основании формулы
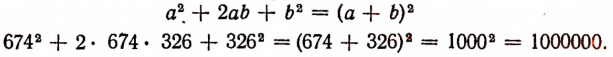
Задача:
Вывести удобное правило вычисления квадрата двузначного числа, оканчивающегося цифрой 5.
Решение:
Пусть число десятков двузначного числа равно а, а цифра единиц 5; тогда это двузначное число изобразится выражением 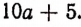
Очевидно, что
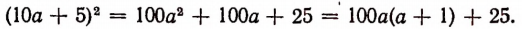
Отсюда вытекает следующее правило:
Чтобы найти квадрат двузначного числа, оканчивающегося цифрой 5, достаточно цифру десятков умножить на число, большее цифры десятков на единицу, и к полученному произведению приписать 25.
Например:
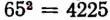 (42 мы получили, умножив 6 на 7),
(42 мы получили, умножив 6 на 7), 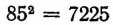 (72 мы получили, умножив 8 на 9).
(72 мы получили, умножив 8 на 9).
Задача:
Найти сумму кубов двух чисел, зная, что сумма этих чисел равна 10, а произведение равно 4.
Решение:
Обозначим первое число буквой х, а второе буквой у. Тогда по условию задачи
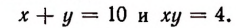
Чтобы найти искомую сумму кубов, т. е. значение выражения 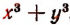 , сначала преобразуем это выражение следующим образом:
, сначала преобразуем это выражение следующим образом:
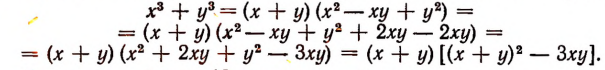
Зная, что 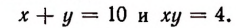 получим
получим
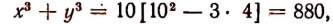
т.е. искомая сумма равна 880.
Задача:
Найти сумму четвертых степеней двух чисел, зная, что сумма этих чисел равна 10, а произведение равно 4.
Решение:
Обозначим первое число буквой х, а второе буквой у. Тогда
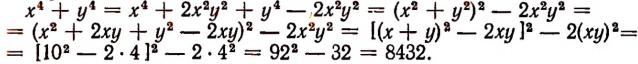
Для решения задач, помещенных в § 3, полезно предварительно разобрать несколько примеров на отыскание наименьшего и наибольшего значений выражений вида 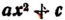 .
.
Наименьшее и наибольшее значение выражений
Наименьшее и наибольшее значение выражений вида 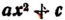
Пример:
Узнать, при каком значении буквы х выражение 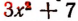 имеет наименьшее значение?
имеет наименьшее значение?
Решение:
Наименьшее значение, равное 7, получится при х = 0. При всех других положительных и отрицательных значениях буквы х выражение 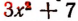 будет принимать значения, большие, чем 7.
будет принимать значения, большие, чем 7.
Пример:
Среди значений выражения 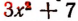 найти самое большее.
найти самое большее.
Решение:
Составим таблицу значений выражения 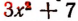 при различных значениях буквы х.
при различных значениях буквы х.

Из этой таблицы и самого выражения 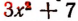 видно, что значения выражения
видно, что значения выражения 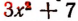 становятся сколь угодно большими, если букве х давать значения по абсолютной величине все большие и большие.
становятся сколь угодно большими, если букве х давать значения по абсолютной величине все большие и большие.
Следовательно, среди значений выражения 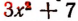 не имеется самого большего, т. е. выражение
не имеется самого большего, т. е. выражение 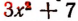 наибольшего значения не имеет.
наибольшего значения не имеет.
Пример:
Узнать, при каком значении буквы х выражение 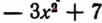 имеет наибольшее значение.
имеет наибольшее значение.
Решение:
Наибольшее значение, равное 7, получится при х = 0. При всех других положительных и отрицательных значениях буквы х выражение 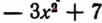 будет, принимать значения, меньшие, чем 7.
будет, принимать значения, меньшие, чем 7.
Пример:
Среди значений выражения 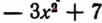 найти самое меньшее.
найти самое меньшее.
Решение:
Составим таблицу значений выражения 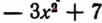
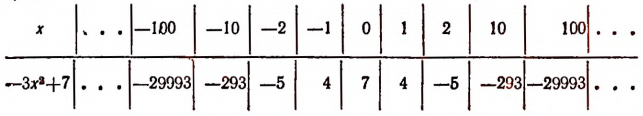
Из этой таблицы и из самого выражения 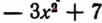 видно, что выражение
видно, что выражение 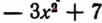 наименьшего значения не имеет.
наименьшего значения не имеет.
Нахождение наименьшего и наибольшего значения выражений
Задача:
Узнать, при каком значении буквы х выражение 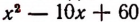 имеет наименьшее значение.
имеет наименьшее значение.
Решение:
Ясно, что выражение 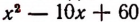 при разных числовых значениях буквы х принимает, вообще говоря, разные числовые значения. Например:
при разных числовых значениях буквы х принимает, вообще говоря, разные числовые значения. Например:
При х = 3 получается 39; При х = — 4 получается 116;
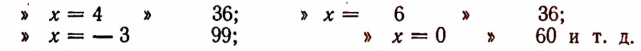
Чтобы решить поставленный вопрос, преобразуем данный многочлен путем выделения полного квадрата.
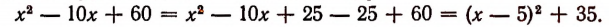
Теперь легко видеть, что наименьшее значение получится тогда, когда выражение 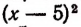 обратится в нуль, т. е. когда букве х будет дано значение 5.
обратится в нуль, т. е. когда букве х будет дано значение 5.
Итак, наименьшее значение выражения 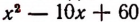 будет 35 и получится оно только тогда, когда мы дадим букве х значение 5.
будет 35 и получится оно только тогда, когда мы дадим букве х значение 5.
Задача:
Узнать, при каком значении буквы х многочлен 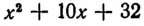 принимает наименьшее значение.
принимает наименьшее значение.
Решение:
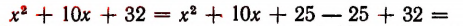
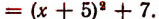 Отсюда видно, что многочлен
Отсюда видно, что многочлен 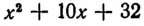 принимает наименьшее значение при х = — 5. (Это наименьшее значение равно 7.)
принимает наименьшее значение при х = — 5. (Это наименьшее значение равно 7.)
Задача:
Узнать, при каком значении буквы х выражение
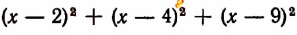
имеет наименьшее значение.
Очевидно, что
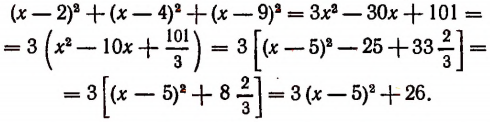
Из последнего выражения видно, что искомое наименьшее значение получается при х = 5 (оно равно 26).
Задача:
Число 14 требуется разбить на три части так, чтобы вторая часть была вдвое больше первой и чтобы сумма квадратов всех трех частей имела наименьшее значение;
Пусть первая часть есть х, тогда вторая часть будет 2 х , а третья 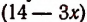 . Сумма квадратов всех трех частей изобразится выражением
. Сумма квадратов всех трех частей изобразится выражением 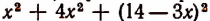 или выражением
или выражением 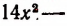
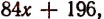 которое можно записать и в следующем виде:
которое можно записать и в следующем виде:
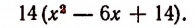
Теперь остается найти такое значение буквы х , при котором многочлен 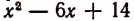 приобретет наименьшее значение. Для этого опять выделим полный квадрат:
приобретет наименьшее значение. Для этого опять выделим полный квадрат:
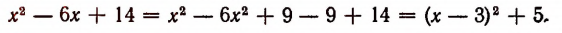
Отсюда
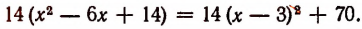
Искомое наименьшее значение получится при х = 3. Следовательно, число 14 надо разбить на следующие три части: 3; 6; 5.
При такой разбивке вторая часть будет вдвое больше первой и сумма квадратов всех трех частей будет иметь наименьшее значение, равное 70.
При всякой другой разбивке, при которой вторая часть будет вдвое больше первой, сумма квадратов трех частей будет оказываться числом, большим 70.
Задача:
Узнать, при каком значении буквы х многочлен
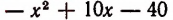 имеет наибольшее значение.
имеет наибольшее значение.
Решение:
Выделим полный квадрат:
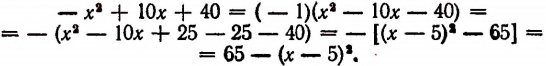
Из последнего выражения видно, что заданный многочлен 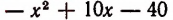 будет иметь наибольшее значение, равное 65, только тогда, когда букве х будет дано значение, равное 5.
будет иметь наибольшее значение, равное 65, только тогда, когда букве х будет дано значение, равное 5.
Задача:
Разделить данное число 12 на два слагаемых так, чтобы их произведение оказалось наибольшим.
Решение:
Обозначим одно из искомых слагаемых через х.
Тогда второе слагаемое будет 12 — х, а их произведение будет
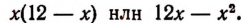
Таким образом, вопрос сводится к нахождению такого значения х , при котором многочлен 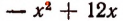 получит наибольшее значение.
получит наибольшее значение.
Преобразуем этот многочлен:
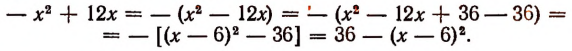
Последнее выражение принимает наибольшее значение при х = 6.
Стало быть, произведение слагаемых будет наибольшим, когда оба
слагаемых будут одинаковыми.
Задача:
Имеется запас досок, из которых можно построить
забор общей длиной 200 м. Требуется этим запасом досок огородить
с трех сторон прямоугольный двор, используя для четвертой стороны заводскую стену.
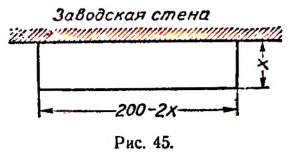
Спрашивается, какую длину надо взять для забора, перпендикулярного к заводской стене, и какую для забора, параллельного заводской стене, чтобы площадь двора оказалась наибольшей. (Легко проверить, что при различных выборах этих длин при постоянстве общей длины забора площадь двора будет, вообще говоря, различной)
Решение:
Пусть длина стороны двора, перпендикулярной
к заводской стене, будет х м (см. рис. 45). Тогда длина стороны, параллельной заводской стене, будет равна 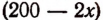 м, а площадь двора будет
м, а площадь двора будет 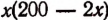 кв.м. или
кв.м. или 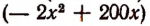 кв.м.
кв.м.
Таким образом, вопрос сводится к нахождению значения х , при котором многочлен 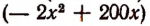 получит наибольшее значение.
получит наибольшее значение.
Преобразуем этот многочлен:
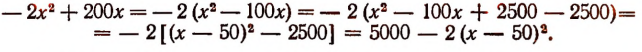
Последнее выражение принимает наибольшее значение при х = 50.
Стало быть, для получения наибольшей площади двора надо длину забора, перпендикулярного к заводской стене, взять равной 50 м, а длину забора, параллельного заводской стене, равной 100 м.
Задача:
Из пунктов А и В (рис. 46) по указанным стрелками направлениям выходят одновременно пароход и яхта; скорость парохода 36 км в час, а яхты 12 км в час. Расстояние между пунктами А и В равно 130 км. Узнать, через сколько часов расстояние между пароходом и яхтой окажется наименьшим.
На рисунке 46 точки С, D, Е и F обозначают положения парохода через один, два, три и четыре часа после начала движения.
Точки с, d, е и f обозначают положения яхты в те же моменты времени.
Сс — есть расстояние между пароходом и яхтой через один час;
Dd — расстояние через два часа;
Ее — расстояние через три часа и т. д.
Решение:
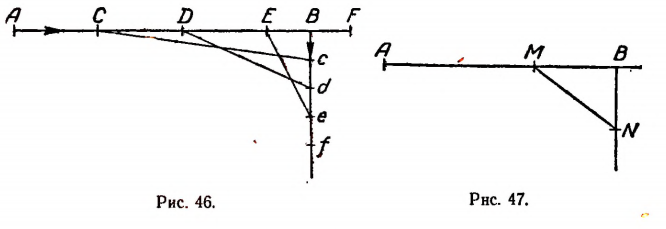
Отметим точками М и N положения парохода и яхты через х часов после их выхода из пунктов А и В (рис. 47). Тогда
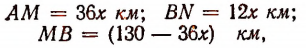
a MN будет представлять собой расстояние между пароходом и яхтой. Фигура MBN есть треугольник с прямым углом при вершине В.
На основании теоремы Пифагора *
*
Во всяком треугольнике с прямым углом квадрат стороны, лежащей против прямого угла, равен сумме квадратов остальных сторон. Под термином «квадрат стороны» следует понимать квадрат числа, выражающего длину стороны.
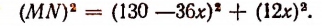
Для решения задачи достаточно узнать, при каком значении буквы х выражение 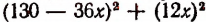 имеет наименьшее значение. Преобразуем это выражение:
имеет наименьшее значение. Преобразуем это выражение:
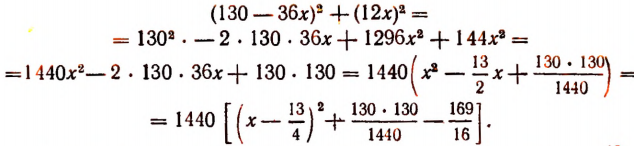
Последнее выражение имеет наименьшее значение при 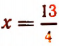 . Значит, расстояние между пароходом и яхтой окажется наименьшим спустя
. Значит, расстояние между пароходом и яхтой окажется наименьшим спустя 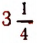 часа, т. е. спустя 3 часа 15 мин. после их выхода из пунктов А и В.
часа, т. е. спустя 3 часа 15 мин. после их выхода из пунктов А и В.
Задача:
Может ли выражение  принимать отрицательные значения?
принимать отрицательные значения?
Решение:
Преобразуем данное выражение следующим образом:
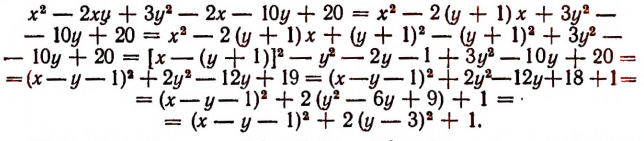
Выражение 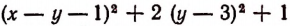 не может принимать отрицательных значений ни при каких значениях букв х и у положительных, отрицательных и нулевых). Поэтому и данное выражение
не может принимать отрицательных значений ни при каких значениях букв х и у положительных, отрицательных и нулевых). Поэтому и данное выражение  не может принимать отрицательных значений.
не может принимать отрицательных значений.
Задача:
Узнать, при каких значениях букв х и у выражение 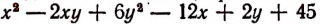 принимает наименьшее значение.
принимает наименьшее значение.
Решение:
Преобразуем данное выражение следующим образом:
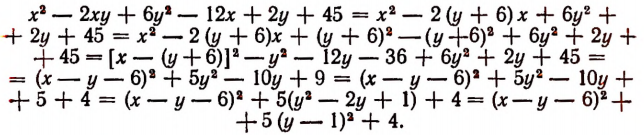
Это выражение имеет наименьшее значение лишь тогда, когда одновременно у — 1 = 0 и х — у — 6 = 0 , т. е. при у = 1 и х= 7.
Задача:
Узнать, при каких значениях букв х и у выражение 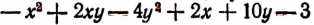 принимает наибольшее значение.
принимает наибольшее значение.
Решение:
Преобразуем данное выражение следующим об-
разом:
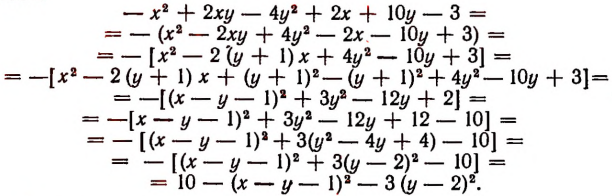
Данное выражение принимает наибольшее значение лишь тогда, когда одновременно у — 2 = 0 и х — у — 1 = 0, т. е. при у = 2 и х = 3.
Задача:
Две железные дороги АВ и CD перпендикулярны друг другу и пересекаются в пункте М, причем расстояния AM и СМ соответственно равны а и b км.
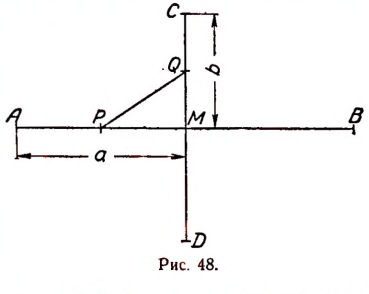
Из пунктов А и С по направлению к М одновременно выходят два поезда со скоростями v и
w км в час. Через сколько часов после отправления расстояние между поездами будет наименьшим?
Решение:
Отметим точками Р и Q положения поездов через х час. после отправления (рис. 48). Тогда 
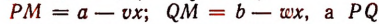 будет представлять собой расстояние между поездами.
будет представлять собой расстояние между поездами.
На основании теоремы Пифагора (см. сноску к решению задачи 8):
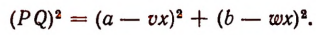
Для решения нашей задачи достаточно узнать, при каком значении буквы х выражение 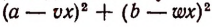 будет иметь наименьшее значение.
будет иметь наименьшее значение.
Преобразуем это выражение:
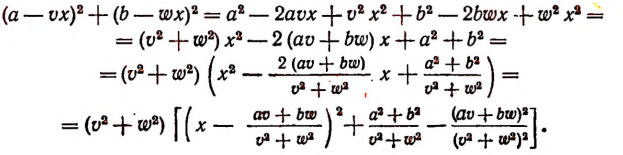
Последнее выражение имеет наименьшее значение при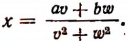 Значит, расстояние между поездами будет наименьшим через
Значит, расстояние между поездами будет наименьшим через 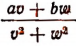 час после отправления.
час после отправления.
Доказательство теоремы Пифагора
Мы уже неоднократно пользовались теоремой Пифагора.
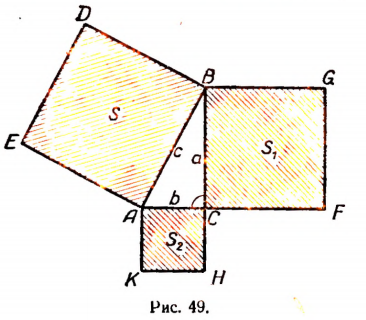
В древнее время эта теорема формулировалась так: «Площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах» (рис. 49).
На рисунке 49 площадь квадрата ABDE равна площади квадрата BCFG плюс площадь квадрата АКНС,
или, кратко, 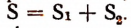
Современная формулировка теоремы Пифагора несколько иная, а именно: «Если стороны прямоугольного треугольника измерены одной и той же единицей длины, то квадрат числа, выражающего длину гипотенузы, равен сумме квадратов чисел, выражающих длины катетов», т. е. 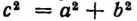 (рис. 50).
(рис. 50).
Различных доказательств теоремы Пифагора существует более семидесяти. Приведем здесь одно из них.
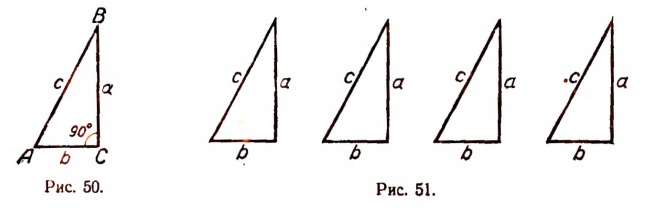
Возьмем четыре произвольных, но равных между собой прямоугольных треугольника с катетами а и b (а > b) и гипотенузой с (рис. 51).
Расположим эти треугольники последовательно так, как показано на рисунке 52.
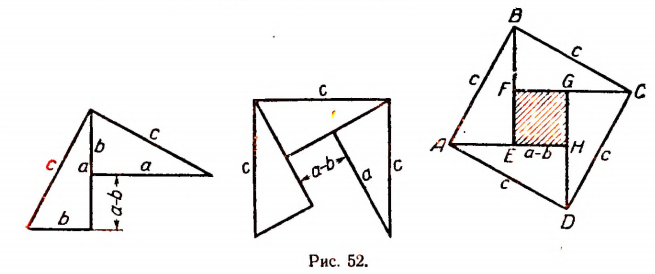
Фигура ABCD есть квадрат со стороной с, фигура EFGH — квадрат со cтороной а — b.
Площадь большого квадрата равна сумме площадей четырех треугольников и маленького квадрата. Поэтому
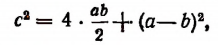
или после преобразований
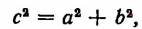
что и требовалось доказать.
Изложенное здесь доказательство теоремы Пифагора является лишь одyим из примеров применения алгебраических преобразований к решению геометрических задач.
Составление таблицы пифагоровых чисел
Тройка таких целых положительных чисел, что квадрат наибольшего из них равен сумме квадратов двух других, называется тройкой пифагоровых чисел. Например, тройка чисел 3, 4 и 5 есть тройка пифагоровых чисел, так как 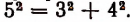
Решение:
Чтобы решить поставленную задачу, мы сначала убедимся в том, что равенство 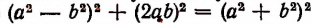 является тождеством. Действительно,
является тождеством. Действительно,
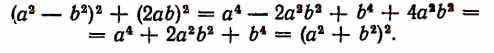
Теперь для получения троек пифагоровых чисел достаточно подставлять в каждое из трех выражений
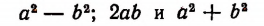
вместо букв а и b те или иные целые положительные числа, соблю¬дая неравенство а > b . Например, взяв а = 2 и b = 1, получим тройку пифагоровых чисел 3; 4; 5;
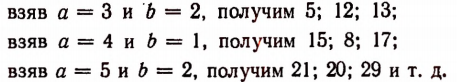
Таблица пифагоровых чисел
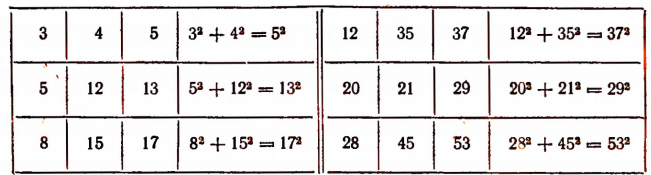
Эта таблица конца не имеет. Нетрудно было бы доказать, что указанным способом получаются все пифагоровы числа. Однако на доказательстве этого останавливаться не будем.
Тождественные преобразования — основные понятия и определения
Рациональные алгебраические выражения. Одночлены и многочлены
Буквенные обозначения, применяемые в алгебре, дают возможность записать общее правило решения множества однотипных задач в виде некоторой формулы. Такая формула показывает, какие действия (и в какой последовательности) следует произвести над определенными величинами, чтобы получить нужный результат. Так, сумма n членов геометрической прогрессии (см. (91.2)) задается формулой
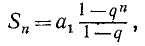
где 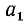 — первый член прогрессии, а q—ее знаменатель; площадь треугольника определяется формулой
— первый член прогрессии, а q—ее знаменатель; площадь треугольника определяется формулой
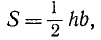
где h — высота треугольника, а b — его основание (201.1), и т. д.
Зная числовые значения величин (буквенных параметров) в правой части формулы, можно, выполняя указанные действия, найти числовое значение искомой величины. Правые части написанных формул дают нам примеры алгебраических выражений; другие примеры алгебраических выражений:
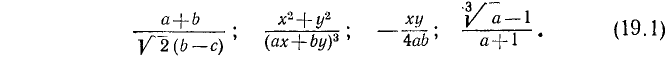
Нет необходимости в строгом определении понятия алгебраического выражения: этот термин можно применять всякий раз, когда дана запись, указывающая алгебраические действия, производимые над некоторыми числами и буквенными величинами.
Если в записи алгебраического выражения используют только рациональные (целые рациональные) действия над буквенными величинами, то оно называется рациональным (целым рациональным) алгебраическим выражением. Первые два выражения (19.1) рациональны.
При подстановке вместо букв указанных числовых значений данное алгебраическое выражение принимает определенное числовое значение (если все действия выполнимы).
Выражение (a + b) / (a—b) имеет смысл при всех значениях а и b, не равных между собой, т. е. при 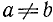 .
.
Выражение 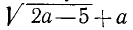 имеет смысл (везде, если не оговорено противное, мы ограничиваемся только действительной областью) при
имеет смысл (везде, если не оговорено противное, мы ограничиваемся только действительной областью) при 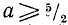 .
.
Например:
Найти значение алгебраического выражения (ах + b) / (bx—а) при следующих значениях а, b, х:
а) 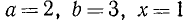 ;
;
б) 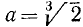 ,
, 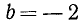 ,
, 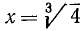 ;
;
в) 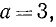
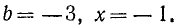
Решение:
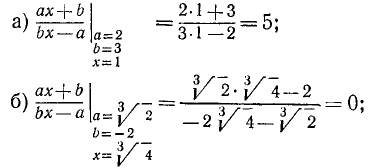
в) выражение не имеет смысла, так как знаменатель обращается в нуль.
Множество всех наборов числовых значений букв, входящих в данное алгебраическое выражение, часто называют областью допустимых значений (о. д. з.). В примере 1 области допустимых значений принадлежат любые тройки значений a, b, х при условии, что 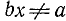 .
.
Два различных по виду алгебраических выражения могут тем не менее иметь равные числовые значения при любых допустимых значениях буквенных параметров (и одинаковые о. д. з.). Вот примеры такого рода:
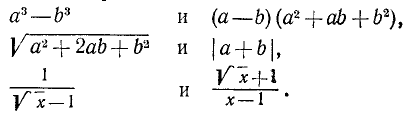
В таких случаях говорят, что эти алгебраические выражения тождественно равны и пишут:
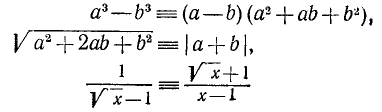
(часто вместо знака 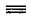 тождественного равенства употребляют просто знак равенства
тождественного равенства употребляют просто знак равенства 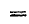 ).
).
В некоторых случаях о. д. з. двух алгебраических выражений могут различаться, но выражения все же равны при всех значениях буквенных параметров, при которых они оба. определены. Таковы выражения
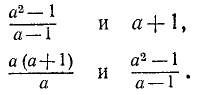
В первом случае левое выражение не определено при  (а правое определено). Во втором случае левое выражение не имеет смысла при
(а правое определено). Во втором случае левое выражение не имеет смысла при 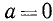 , а правое — при
, а правое — при  , в остальных же случаях они равны. В таких случаях равенства
, в остальных же случаях они равны. В таких случаях равенства
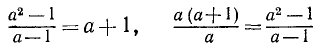
также часто называют тождественными, подразумевая при этом, что буквенные параметры принимают только значения, при которых имеют смысл оба выражения. Вообще, во избежание неясности лучше говорить так: «данные выражения тождественно равны при значениях буквенных параметров…», указывая область изменения этих параметров, в которой оба выражения принимают равные значения. Так, например, мы называем равенство
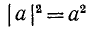
тождеством, подразумевая, что a — действительное число. При комплексном а это равенство уже не будет тождеством. Можно сказать, что равенство
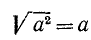
удовлетворяется тождественно для всех неотрицательных а (оно не будет тождеством, если рассматривать все действительные значения а).
Одним из основных навыков в области алгебры должно быть умение переходить от одного алгебраического выражения к другому, ему тождественному, более простому или удобному. Такой переход осуществляется с помощью тождественных преобразований. Практически при выполнении этих преобразований встречаются и случаи, когда происходят некоторые изменения о. д. з. На это всякий раз необходимо обращать внимание, так как иначе может быть допущена ошибка. Например, при решении уравнения
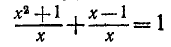
«тождественное» преобразование левой части
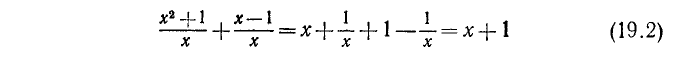
дало бы нам «решение» 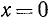 — значение, при котором исходное уравнение теряет смысл. Преобразование (19.2) изменяет о. д. з., и, выполняя его, следует исключить значение
— значение, при котором исходное уравнение теряет смысл. Преобразование (19.2) изменяет о. д. з., и, выполняя его, следует исключить значение 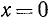 .
.
Простейшие алгебраические выражения суть одночлены и многочлены. Следующие алгебраические выражения:
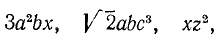
дают нам примеры одночленов. Вообще, одночленом называют выражение, получаемое при умножении числового множителя (коэффициента) на один или несколько буквенных сомножителей. Обычно при этом буквенные сомножители располагают в порядке алфавита, одинаковые сомножители объединяют вместе, пользуясь знаком возведения в степень:
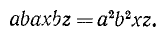
Произведение нескольких одночленов также есть одночлен.
Многочленом (полиномом) называют алгебраическое выражение, представленное как алгебраическая сумма нескольких одночленов, например:
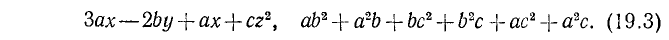
Одночлены, отличающиеся только числовым коэффициентом, называют подобными; так, в записи первого многочлена в (19.3) подобны одночлены 3ах и ах; такие одночлены можно объединить в один одночлен: Зах + ах — 4ах. При записи многочлена следует произвести это действие, называемое приведением подобных членов.
Сумма двух многочленов сама непосредственно является многочленом (в ней следует лишь привести подобные члены). Сформулируем также известные правила умножения одночлена на многочлен и умножения двух многочленов.
Чтобы умножить одночлен на многочлен, следует умножить на этот одночлен каждый член многочлена; чтбы умножить многочлен на многочлен, следует умножить каждый из одночленов, входящих в запись одного многочлена, на каждый из одночленов второго многочлена (и взять сумму полученных одночленов с учетом правила знаков).
Оба правила вытекают из применения распределительного закона умножения относительно сложения (1.6).
Пример:
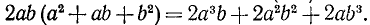
Пример:
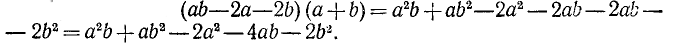
Формулы сокращенного умножения
В некоторых часто встречающихся случаях применяют формулы сокращенного умножения двух многочленов; напомним эти формулы.
а) Квадрат суммы и квадрат разности. Квадрат двучлена (бинома) а + b можно записать в виде
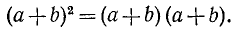
На основании правила умножения многочленов можно раскрыть стоящие справа скобки, а именно каждый член первого бинома умножить на каждый член второго бинома и результаты сложить. Получим
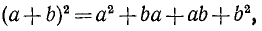
или после приведения подобных членов
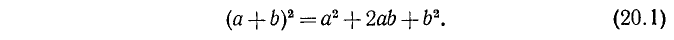
Формулу (20.1) иногда записывают в виде
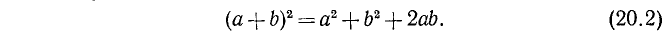
Заменив в формуле (20.1) (или (20.2)) b на — b , получим, соответственно, формулы для квадрата разности:
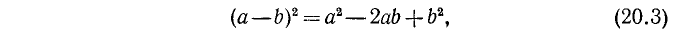
или
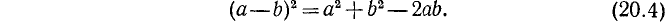
Формула (20.2) для квадрата двучлена (бинома) распространяется на случай, когда в квадрат возводится любой многочлен (полином). Покажем это для случая трехчлена. Имеем
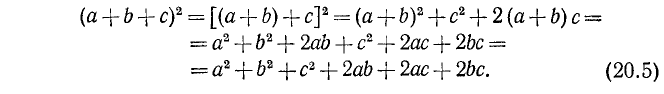
Вообще, квадрат алгебраической суммы нескольких слагаемых равен сумме квадратов этих слагаемых плюс сумма удвоенных попарных произведений этих слагаемых (с учетом правила знаков!).
Пример:
Раскрыть скобки в выражении 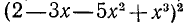 .
.
Решение:
Имеем
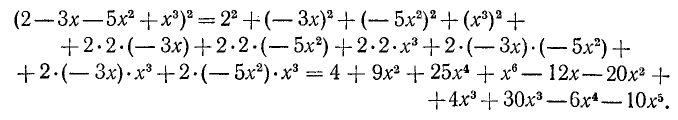
После приведения подобных членов запишем ответ:
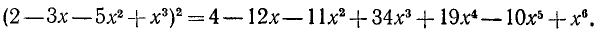
б) Куб суммы и куб разности. Чтобы вывести формулу для 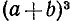 , заметим, что
, заметим, что
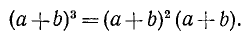
Но выражение для 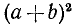 уже найдено — (20.2); поэтому
уже найдено — (20.2); поэтому
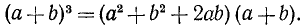
Перемножая почленно многочлены, стоящие в правой части этого равенства, получим
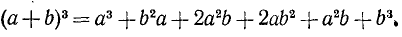
Последний результат можно переписать так:
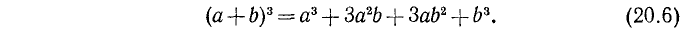
Заменив в формуле куба суммы (20.6) b через — b , напишем формулу куба разности:
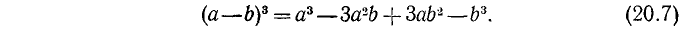
В некоторых случаях формулам (20.6) и (20.7) удобней придать следующий вид:
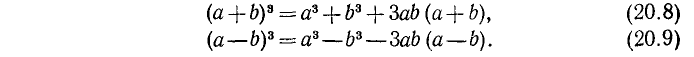
в) Разность квадратов. Следующая формула:
легко проверяется умножением двучленов в ее левой части.
г) Сумма и разность кубов. Также рекомендуется проверить самостоятельно следующие формулы:
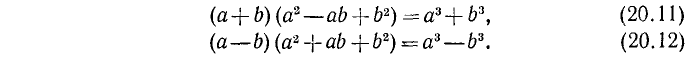
Трехчлены 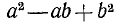 и
и 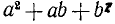
в левых частях равенств (20.11), (20.12) часто называют «неполным квадратом» разности или суммы соответственно.
Бином Ньютона
Под биномом Ньютона понимают формулу, дающую выражение степени 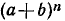 двучлена
двучлена 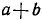 с любым натуральным показателем n. Мы можем записать выражения
с любым натуральным показателем n. Мы можем записать выражения 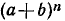 при n = 1, 2, 3 (используя формулы п. 20 для квадрата и куба суммы):
при n = 1, 2, 3 (используя формулы п. 20 для квадрата и куба суммы):
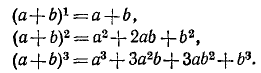
Можно подметить некоторую закономерность: при возведении бинома в степень n в правой части формулы получается сумма n — 1 слагаемых; каждое слагаемое содержит множители а и b в степенях, сумма показателей которых равна степени бинома. Для произвольного натурального n мы можем получить в правой части равенства, выражающего 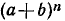 , слагаемые вида
, слагаемые вида 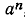 ,
, 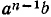 , … ,
, … , 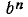 с некоторыми числовыми коэффициентами. Найдем еще
с некоторыми числовыми коэффициентами. Найдем еще 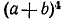 , проводя вычисление по некоторой удобной схеме. Именно, запишем
, проводя вычисление по некоторой удобной схеме. Именно, запишем
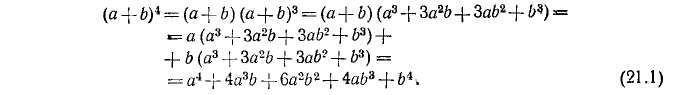
Мы провели вычисление таким образом, чтобы подобные члены оказались Записанными один под другим. Теперь видно, что коэффициенты формулы (21.1): 1, 4, 6, 4, 1 получаются из коэффициентов формулы для куба суммы следующим путем: записываем коэффициенты формулы для 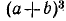 в две строки со сдвигом нижней строки вправо:
в две строки со сдвигом нижней строки вправо:
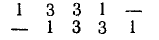
и складываем числа, подписанные одно под другим;
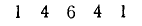
при этом и получатся коэффициенты формулы (21.1). Совершенно аналогично, для получения коэффициентов формулы, выражающей 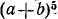 , пишем
, пишем
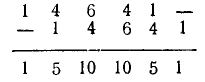
Теперь сама формула для пятой степени суммы напишется в виде
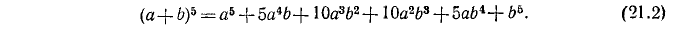
Можно весь этот процесс представить с помощью треугольника Паскаля:
коэффициенты:
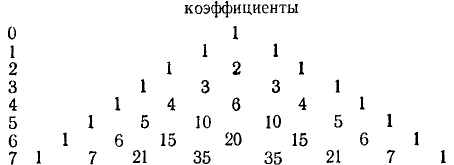
Каждая строка этой таблицы (за исключением первой) начинается и заканчивается единицей, любой другой элемент строки равен сумме соседних с ним элементов строки, расположенной над ней. Таким образом, таблица заполняется сверху вниз. Так, например, строка при n — 5 получается из строки при п — 4 по схеме:
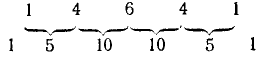
а строка при n = 6 — из строки при n = 5 аналогично по схеме
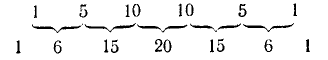
К сожалению, по указанной схеме неудобно находить коэффициенты в формуле для 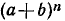 при больших значениях n, так как получить, например, десятую строку можно, лишь продолжив таблицу коэффициентов до десятой строки. Можно указать и общую формулу для любого из коэффициентов в выражении
при больших значениях n, так как получить, например, десятую строку можно, лишь продолжив таблицу коэффициентов до десятой строки. Можно указать и общую формулу для любого из коэффициентов в выражении 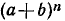 . Эту формулу мы сообщим здесь без вывода, она может быть доказана по индукции.
. Эту формулу мы сообщим здесь без вывода, она может быть доказана по индукции.
Первые два коэффициента при 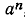 и
и 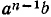 в разложении
в разложении 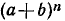 суть 1 и n; следующий коэффициент при
суть 1 и n; следующий коэффициент при 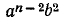 может быть получен по формуле
может быть получен по формуле 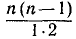 , следующий —при
, следующий —при 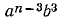 по формуле
по формуле 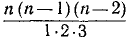 и т.д. Вообще, коэффициент при
и т.д. Вообще, коэффициент при 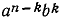 в выражении
в выражении 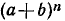 равен
равен
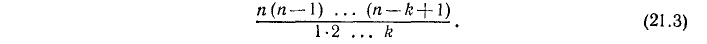
Здесь в числителе пишется произведение k последовательных чисел, начиная от n, расположенных в порядке убывания. В знаменателе, напротив, сомножители 1, 2 … k располагаются, начиная от единицы, в порядке возрастания. Найдем по этому правилу коэффициенты для 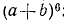
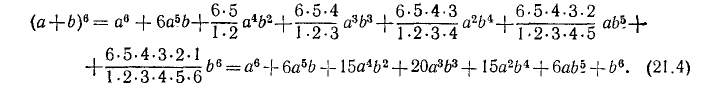
Отметим, что коэффициенты симметрично расположенных (от конца и начала) членов всегда оказываются рапными.
В общем виде можно записать формулу так:
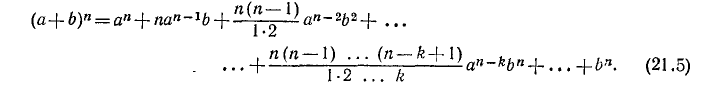
Эта формула называется формулой бинома Ньютона.
Пример:
Раскрыть выражение 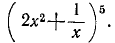
Решение:
По формуле бинома Ньютона находим
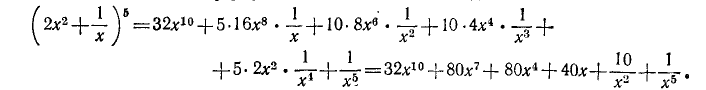
Пример:
Найти член бинома 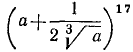 , содежащий а в степени 35/3.
, содежащий а в степени 35/3.
Решение:
Член бинома с номером k (считая от начала) содержит произведение
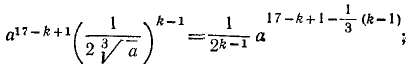
из условия задачи имеем 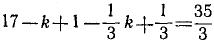 , откуда k = 5. Поэтому требуется написать член бинома с номером 5:
, откуда k = 5. Поэтому требуется написать член бинома с номером 5:

Разложение многочлена на множители
В некоторых случаях данный многочлен может быть представлен как произведение одночлена на многочлен или как произведение двух многочленов. В первом случае говорят, что за знак скобок можно вынести общий множитель, во втором,— что многочлен разлагается на множители. Нам известны некоторые приемы разложения многочлена на множители, в том числе метод группировки и применение формул сокращенного умножения. Ограничимся разбором нескольких типичных примеров (общего универсального мегода, чтобы узнать, разлагается ли многочлен на множители и найти их, не имеется).
Пример:
Разложить на множители 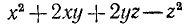 .
.
Решение:
Производим группировку слагаемых:
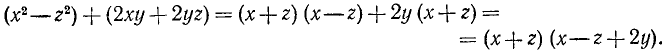
Мы применили здесь формулу разности квадратов (20.10) и прием вынесения общего множителя за скобку.
Пример:
Разложить на множители:
а) 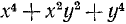 ; б)
; б) 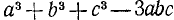 .
.
Решение:
а) Добавим и вычтем выражение 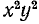 ; тогда получим
; тогда получим
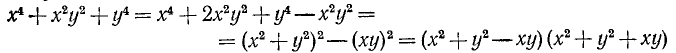
(применены формулы квадрата суммы (20.1), а затем разности квадратов (20.10)). Окончательно:
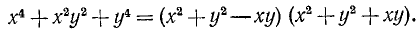
б) Добавим к нашему выражению и вычтем выражение 3ab (a + b), чтобы получить куб суммы по формуле (20.8):
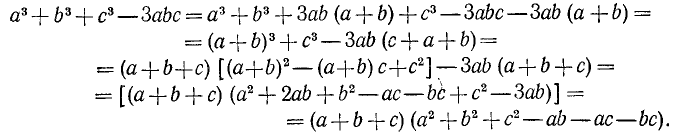
В некоторых случаях разложение на множители не удается в действительной области, но может быть осуществлено в комплексной области. Так, например, 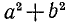 нельзя разложить на действительные множители, но
нельзя разложить на действительные множители, но
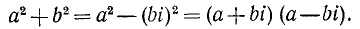
Сумма четвертых степеней 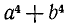 может быть разложена на множители так:
может быть разложена на множители так:
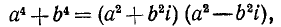
но она же разлагается и на действительные множители:
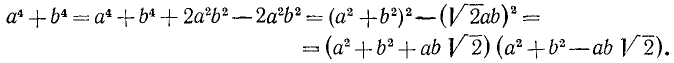
Дробные алгебраические выражения
Алгебраическое выражение в записи которого наряду с действиями сложения, вычитания и умножения используют также деление на буквенные выражения, называется дробным алгебраическим выражением. Таковы, например, выражения
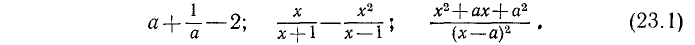
Алгебраической дробью мы называем алгебраическое выражение, имеющее вид частного от деления двух целых алгебраических выражений (например, одночленов или многочленов). Таковы, например, выражения
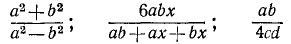
(и третье из выражений (23.1)).
Тождественные преобразования дробных алгебраических выражений имеют по большей части своей целью представить их и виде алгебраической дроби. Для отыскания общего знаменателя используется разложение на множители знаменателей дробей — слагаемых — с целыо отыскания их наименьшего общего кратного. При сокращении алгебраических дробей может нарушаться строгая тождественность выражений: необходимо исключать значения величин, при которых множитель, на который производится сокращение, обращается в нуль.
Приведем примеры тождественных преобразований дробных алгебраических выражений.
Пример:
Упростить выражение
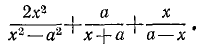
Решение:
Все слагаемые можно привести к общему знаменателю  (удобно при этом изменить знак в знаменателе последнего слагаемого и знак перед ним):
(удобно при этом изменить знак в знаменателе последнего слагаемого и знак перед ним):
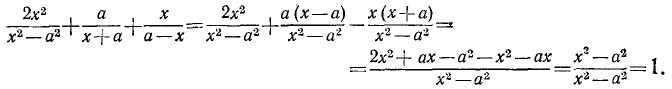
Наше выражение равно единице при всех значениях х, кроме  и
и 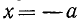 (при этих значениях оно не определено и сокращение дроби
(при этих значениях оно не определено и сокращение дроби 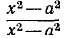 незаконно).
незаконно).
Пример:
Представить в виде алгебраической дроби выражение
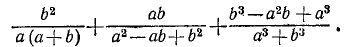
Решение:
За общий знаменатель можно принять выражение 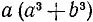 . Находим последовательно:
. Находим последовательно:
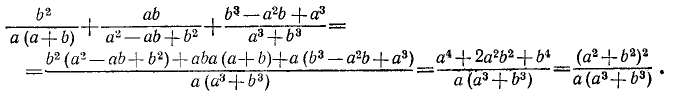
Иррациональные алгебраические выражения. Радикалы из алгебраических выражений
Алгебраические выражения, в записи которых используются не только четыре рациональных действия, но также знаки радикала (из буквенных выражений), мы называем иррациональными алгебраическими выражениями. Таковы, например, выражения
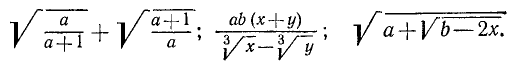
При определении о. д. з. иррациональных алгебраических выражений следует учитывать, что выражения, находящиеся под знаком радикала четной степени, не должны быть отрицательными, При отыскании числовых значений выражения при данных буквенных значениях параметров корни четной степени понимаются в арифметическом смысле.
Пример:
Найти о. д. з. выражения
и его значение при х = 5, а=1.
Решение:
О. д. з. определяем из условий 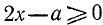 ,
, 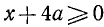 . Находим, что о. д. з. определяется неравенствами
. Находим, что о. д. з. определяется неравенствами 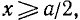
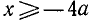 . При вычислении значения в заданной точке x = 5, а = 1 получаем
. При вычислении значения в заданной точке x = 5, а = 1 получаем
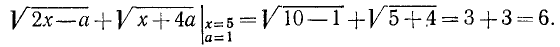
При преобразовании иррациональных алгебраических выражений используются все правила действий с корнями (гл. 1,§2). Рассмотрим сначала возможные упрощения выражения типа «корень из одночлена» или «корень из частного двух одночленов». Будем говорить, что корень приведен к простейшей форме, если: 1) он не содержит иррациональности в знаменателе, 2) в нем нельзя сократить его показатель с показателем подкоренного выражения и, наконец, 3) все возможные множители вынесены из-под корня. Всякий данный корень может быть приведен к простейшей форме, т. е. заменен тождественно равным ему, но таким, который отвечает всем трем перечисленным условиям.
Пример:
Привести к простейшей форме следующие корни (a > 0, b > 0):
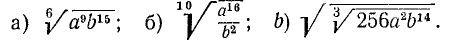
Решение:
а) Сокращаем на 3 показатель корня и показатель степеней каждого из сомножителей подкоренного выражения
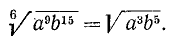
Выносим из-под знака корня множители а и 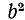 :
:
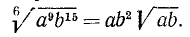
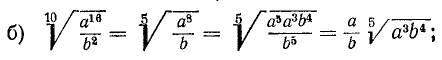
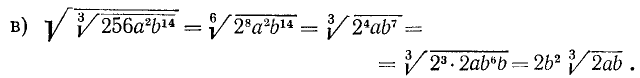
Корни, простейшие формы которых отличаются, быть может, лишь коэффициентами (числовыми или буквенными), принято называть подобными. Например, корни 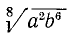 и
и 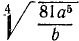 подобны, так как
подобны, так как 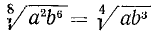 ,
, 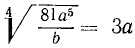
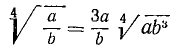 , а корни
, а корни 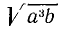 и
и 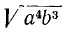 не подобны, так как
не подобны, так как 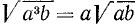 , а
, а 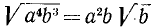 .
.
При сложении и вычитании подобных корней все они приводятся к простейшей форме, а затем корень выносится за скобки.
Пример:
Произвести указанные действия:
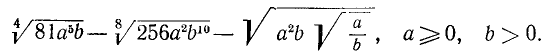
Решение:
Приведем каждый из корней к простейшей форме:
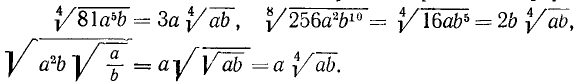
Теперь находим (все корни оказались подобными)
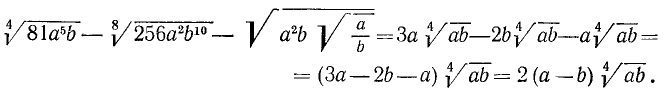
При вынесении сомножителей из-под знака корня четной степени необходимо помнить, что корень понимается в арифметическом смысле. Так, если знаки а, b не указаны, то следует писать не 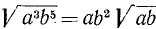 , а
, а 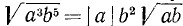 . Здесь о. д. з. состоит не только из значений
. Здесь о. д. з. состоит не только из значений  ,
,  , но и из значений
, но и из значений  ,
,  . Поэтому
. Поэтому
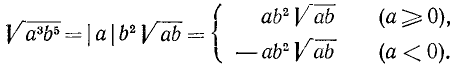
Пример:
Упростить выражение
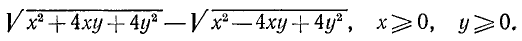
Находим
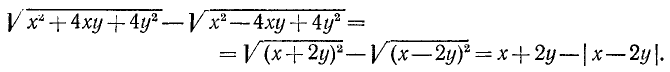
Возможны следующие случаи:
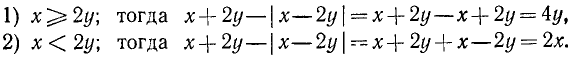
Итак,
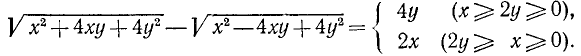
Если не предполагать заранее, что  ,
,  , то решение примера еще усложнится, так как придется записать ответ в общей форме:
, то решение примера еще усложнится, так как придется записать ответ в общей форме:
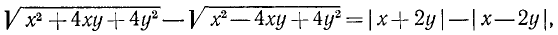
и затем разбирать четыре возможных случая: 1) 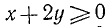 ,
, 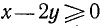 ; 2)
; 2) 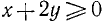 ,
, 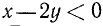 ; 3)
; 3) 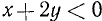 ,
, 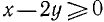 ; 4)
; 4) 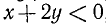 ,
, 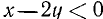 . Предоставляем завершить этот разбор читателю
. Предоставляем завершить этот разбор читателю
В примере, который мы сейчас решали, подкоренные выражения представлялись как точные квадраты некоторых двухчленов очевидным способом. В некоторых случаях такое представление подкоренного выражения производится не столь очевидным образом. Так, иногда можно упростить радикалы вида
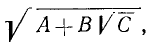
записав 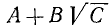 в виде точного квадрата.
в виде точного квадрата.
Пример:
Упростить выражение
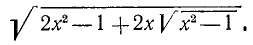
Решение:
Подкоренное выражение перепишем в виде
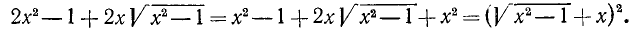
Теперь имеем
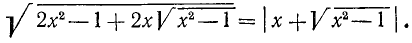
О. д. з. нашего выражения состоит из интервалов 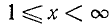 ,
, 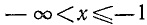 . Нетрудно заметить, что
. Нетрудно заметить, что 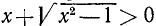 при
при  , а при
, а при 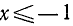
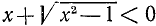 . Поэтому окончательно имеем
. Поэтому окончательно имеем

Пример:
Упростить числовые выражения: 1) 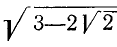 ; 2)
; 2) 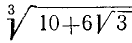 .
.
Решение:
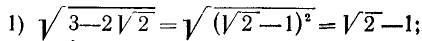
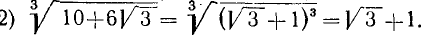
В последнем случае удается записать подкоренное выражение как точный куб.
Освобождение от иррациональности в знаменателе дроби
При преобразовании дробного алгебраического выражения, в знаменателе которого записано иррациональное выражение, обычно стремятся представить дробь так, чтобы ее знаменатель был рациональным. Если А, В, С, D, … — некоторые алгебраические выражения, то можно указать правила, с помощью которых можно освободиться от знаков радикала в знаменателе выражений вида
Во всех этих случаях освобождение от иррациональности производится умножением числителя и знаменателя дроби на множитель, выбранный так, чтобы его произведение на знаменатель дроби было рациональным.
1) Для освобождения от иррациональности в знаменателе дроби вида 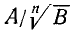 умножаем числитель и знаменатель на
умножаем числитель и знаменатель на 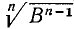 .
.
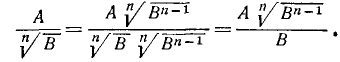
Пример:
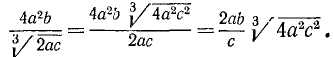
2) В случае дробей вида 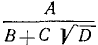 ,
, 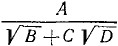 умножаем числитель и знаменатель на иррациональный множитель
умножаем числитель и знаменатель на иррациональный множитель 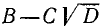 или
или 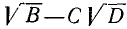 соответственно, т. е. на сопряженное иррациональное выражение.
соответственно, т. е. на сопряженное иррациональное выражение.
Смысл последнего действия состоит в том, что в знаменателе произведение суммы на разность преобразуется в разность квадратов, которая уже будет рациональным выражением.
Пример:
Освободиться от иррациональности в знаменателе выражения:
а) 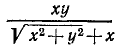 ; б)
; б) 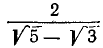 .
.
Решение:
а) Умножаем числитель и знаменатель дроби на выражение 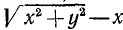 . Получаем (при условии, что
. Получаем (при условии, что 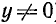 )
)
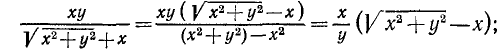
б)
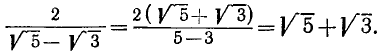
3) В случае выражений типа
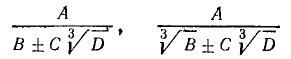
знаменатель рассматривается как сумма (разность) и умножается на неполный квадрат разности (суммы), чтобы получить сумму (разность) кубов ((20.11), (20.12)). На тот же множитель умножается и числитель.
Пример:
Освободиться от иррациональности в знаменателе выражений:
а) 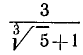 ; б)
; б) 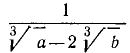 .
.
Решение:
а) Рассматривая знаменатель данной дроби как сумму чисел 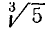 и 1, умножим числитель и знаменатель на неполный квадрат разности этих чисел:
и 1, умножим числитель и знаменатель на неполный квадрат разности этих чисел:
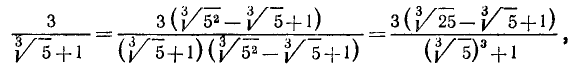
или окончательно:
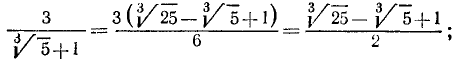
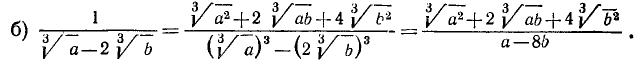
В некоторых случаях требуется выполнить преобразование противоположного характера: освободить дробь от иррациональности в числителе. Оно проводится совершенно аналогично.
Пример:
Освободиться от иррациональности в числителе, дроби 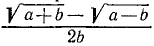 .
.
Решение:
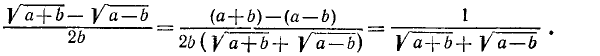
Коэффициент и показатель степени. Одночлены и многочлены
Пусть требуется сложить несколько слагаемых, среди которых могут быть и одинаковые; например,  ,
, 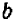 ,
, 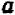 ,
, 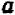 и
и 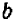 .
.
Мы напишем сумму: 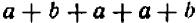
Пользуясь законами сложения, переместительным и сочетательным, можно внести в эту запись порядок: 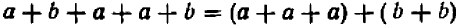 .
.
Повторить число 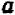 три раза слагаемым — значит то же, что умножить его на
три раза слагаемым — значит то же, что умножить его на 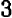 ; поэтому
; поэтому 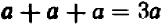 .
.
Таким же образом 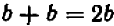 .
.
Итак, при любых значениях 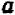 и
и 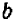 можно нашу сумму записать более кратко:
можно нашу сумму записать более кратко: 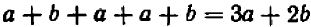 .
.
Пусть требуется перемножить несколько чисел, среди которых необязательно все — различные; например, 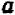 ,
, 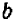 ,
, 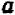 ,
, 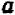 и
и 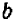 .
.
Мы напишем произведение 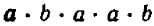 или
или 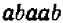 .
.
Пользуясь законами умножения, переместительным и сочетательным, можно дальше следующим образом упорядочить эту запись 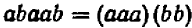 .
.
Ради сокращения приняты обозначения: 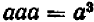 ,
, 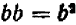 .
.
Вообще, если одно и то же число (или какое угодно выражение) нужно взять множителем несколько раз, то пишут его только один раз, а сколько раз оно повторяется множителем, обозначают маленькой цифрой, стоящей правее и выше числа (или выражения).
Таким образом, в нашем примере получается запись: 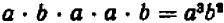 .
.
Например, подставляя значения 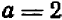 ,
, 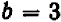 , получим:
, получим: 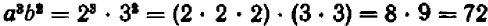 .
.
Если требуется перемножить несколько величин, из которых одни могут быть выражены числами, другие — буквами, то обыкновенно сначала пишут произведение числовых множителей, затем буквенные множители в алфавитном порядке. Например, если нужно перемножить 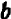 ,
, 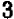 ,
,  ,
,  ,
, 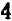 и
и 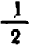 , то получается произведение:
, то получается произведение: 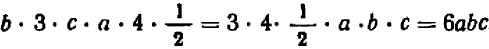 .
.
Каждое выражение, представляющее собою произведение числового множителя и одного или нескольких буквенных множителей, называется одночленом. Числовой множитель в одночлене называется коэффициентом.
Так, в одночлене 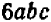 коэффициент равен
коэффициент равен  ; выражение же
; выражение же 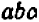 называют иногда буквенной частью одночлена.
называют иногда буквенной частью одночлена.
Коэффициент может быть целым или дробным, положительным или отрицательным.
Если нужно некоторую величину умножить на дробь, достаточно умножить ее на числитель дроби и разделить на ее знаменатель. Поэтому, скажем, 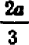 означает то же, что и
означает то же, что и 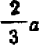 : выражение
: выражение 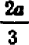 можно считать одночленом, имеющим коэффициент
можно считать одночленом, имеющим коэффициент 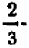 .
.
Точно также одно и то же означают записи: 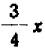 и
и 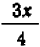 или еще
или еще 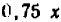 , и одинаково употребительны.
, и одинаково употребительны.
Если коэффициент не выписан (как, например, в одночлене 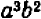 ), то его, очевидно, следует считать равным единице.
), то его, очевидно, следует считать равным единице.
Значок, указывающий, сколько раз то или иное число (или выражение) должно быть взято множителем, называется «показателем степени» при этом числе (или выражении). Например, в одночлене 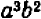 показатель при
показатель при 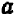 равен
равен  , показатель при
, показатель при 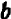 равен
равен 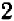 . Показатель степени при каком-нибудь выражении — целое положительное число.
. Показатель степени при каком-нибудь выражении — целое положительное число.
Если показатель не выписан (например, 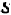 при выражении
при выражении 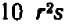 ), то его, очевидно, нужно считать равным единице.
), то его, очевидно, нужно считать равным единице.
Несколько (не менее двух) одночленов, соединенных между собою знаками 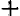 или
или  , образуют выражение, называемое многочленом.
, образуют выражение, называемое многочленом.
Сами одночлены, из которых образован многочлен, короче называются членами этого многочлена. Смотря по числу членов, различают двучлены, трехчлены и т. д. Если в многочлене есть члены, не содержащие буквенных множителей, то такие члены называются свободными.
Так, выражение 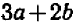 есть многочлен (двучлен), членами которого являются
есть многочлен (двучлен), членами которого являются 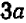 и
и 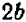 . Выражение
. Выражение 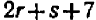 — тоже многочлен (трехчлен), членами которого являются
— тоже многочлен (трехчлен), членами которого являются 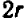 ,
, 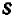 и
и 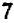 ; из них последний — свободный член.
; из них последний — свободный член.
Мы знаем, что вычитание может быть всегда заменено сложением. Поэтому, если несколько выражений соединены между собою знаками 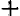 или
или  , то полученный результат называется алгебраической суммой и может быть записан также в виде обыкновенной (арифметической) суммы. Например:
, то полученный результат называется алгебраической суммой и может быть записан также в виде обыкновенной (арифметической) суммы. Например: 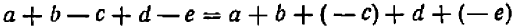 .
.
Итак, можно сказать кратко: многочлен есть алгебраическая сумма одночленов.
Знаки минус (если такие есть) обыкновенно относят к коэффициентам: так, вместо 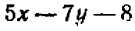 можно было бы написать
можно было бы написать 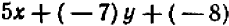 .
.
Таким образом, следует считать, что в трехчлене 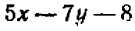 коэффициенты при
коэффициенты при 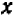 и при
и при 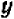 суть
суть 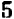 и
и 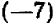 , а свободный член равен
, а свободный член равен 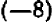 .
.
Возведение в степень
Повторное умножение одного и того же числа самого на себя называется возведением в степень.
Пусть 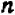 — целое положительное число. Тогда выражение
— целое положительное число. Тогда выражение 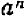 обозначает произведение
обозначает произведение 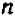 множителей, из которых каждый равен
множителей, из которых каждый равен 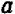 ; оно носит название
; оно носит название 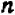 -й степени
-й степени 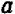 и читается «
и читается «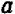 в степени
в степени 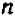 ». Само
». Само 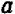 при этом называется основанием степени, тогда как
при этом называется основанием степени, тогда как 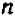 (как мы уже видели) — показателем степени.
(как мы уже видели) — показателем степени.
Как мы знаем, вторая степень числа 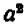 , т. е.
, т. е. 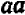 , называется также квадратом числа
, называется также квадратом числа  (читается «
(читается « -квадрат»). Это объясняется тем, что формула
-квадрат»). Это объясняется тем, что формула 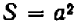 дает площадь квадрата со стороной
дает площадь квадрата со стороной 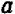 .
.
Точно так же третья степень числа 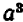 , т.е.
, т.е. 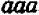 , называется иначе кубом числа
, называется иначе кубом числа 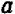 (читается «
(читается «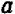 -куб»).
-куб»).
Это объясняется тем, что формула 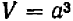 дает объем куба со стороной
дает объем куба со стороной  .
.
Умножение одночленов
Пусть нужно умножить 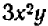 на
на 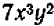 . С помощью переместительного и сочетательного законов умножения мы получим:
. С помощью переместительного и сочетательного законов умножения мы получим: 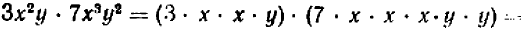
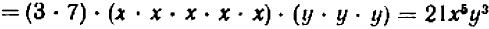 .
.
Сложение и вычитание одночленов
Пусть нужно сложить одночлены 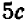 и
и 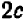 . Мы получим:
. Мы получим: 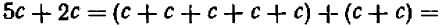
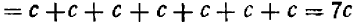 .
.
Если слагаемые одинаковы или одночлены отличаются только своими коэффициентами (или не отличаются совсем), то сумму одночленов можно также написать в виде’одночлена с той же буквенной частью и коэффициентом, равным сумме коэффициентов данных одночленов; например: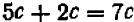 ,
, 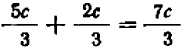 .
.
Это правило следует из распределительного закона умножения: действительно, достаточно в тождестве 
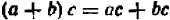 переставить левую и правую части и потом положить
переставить левую и правую части и потом положить 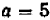 ,
,  , чтобы получить равенство
, чтобы получить равенство 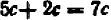
Подобно сложению делается и вычитание. Например: 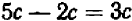 .
.
В самом деле, мы можем пользоваться прежним правилом, относя знак минус к коэффициенту; другими словами, под «суммой» понимая «алгебраическую сумму»: 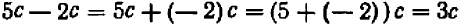 .
.
Члены алгебраической суммы называются подобными, если они имеют одинаковые буквенные части и различаются, следовательно, разве только коэффициентами.
Мы уже умеем складывать и вычитать одночлены, которые подобны между собою. Для того, чтобы сложить несколько каких угодно одночленов, достаточно собрать вместе (на основе переместительного и сочетательного законов сложения) все члены, подобные между собой, и затем (на основе распределительного закона) соединить их в один член. Например: 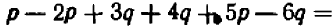
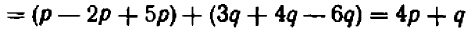 .
.
Такого рода упрощение алгебраической суммы называется приведением подобных членов.
Сложение и вычитание многочленов
Чтобы прибавить многочлен, достаточно прибавить каждый его член в отдельности.
Чтобы вычесть многочлен, достаточно вычесть каждый его член в отдельности.
Так, например:
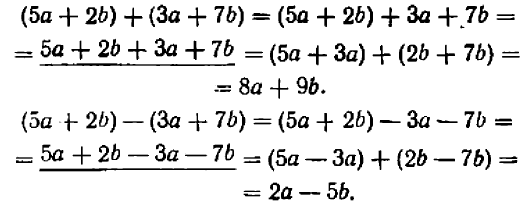
И точно также:
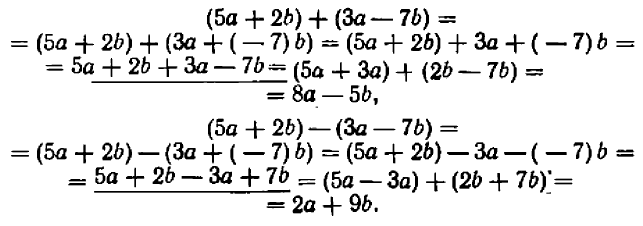
Прежде чем выполнить сложение или вычитание данных многочленов, мы должны заключить их в скобки; выполняя же эти действия, мы скобки устраняем, или, как говорят, «раскрываем».
Из приведенных примеров видно, что правило сложения или вычитания многочленов можно сформулировать как «правило раскрытия скобок».
Раскрывая скобки, нужно перед каждым членом: сохранять прежний знак, если перед скобками стоит плюс (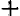 ); менять знак на противоположный, если перед скобками стоит минус (
); менять знак на противоположный, если перед скобками стоит минус ( ).
).
Умножение многочлена на одночлен
Чтобы умножить алгебраическую сумму нескольких членов на некоторый множитель, достаточно на этот множитель умножить каждый из членов и результаты сложить. Это следует непосредственно из распределительного закона.
Примеры:
1)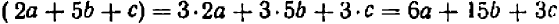
2)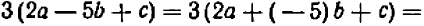
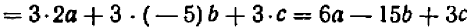
3)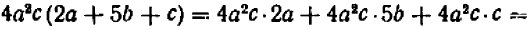
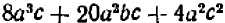
Если нужно умножить многочлен на некоторый множитель, то приходится заключать многочлен в скобки; после же умножения скобки исчезают. Поэтому, вместо того чтобы сказать: «умножим многочлен на одно член», говорят короче: «раскроем скобки».
Равенства, получающиеся в результате выполнения простейших действии над одночленами и многочленами (сложение, вычитание, умножение), являются тождествами, так как справедливы при каких угодно значениях входящих букв.
Буквенные подстановки
Предположим, что у нас имеется тождество, содержащее некоторую букву. Если вместо этой буквы подставить в обеих частях тождества одно и то же алгебраическое выражение, содержащее новые буквы или ту же букву, то получим опять тождество. Тот же результат получится, если тождество содержит несколько букв и мы вместо каждой буквы подставим свое данное выражение.
Пример:
Сделав в тождестве 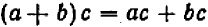 замены, выражающиеся равенствами
замены, выражающиеся равенствами 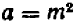 ,
, 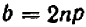 ,
, 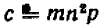 , получим тождество
, получим тождество 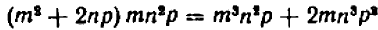 .
.
Пример:
Заменяя в тождестве  буквы
буквы  и
и 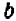 выражениями
выражениями 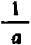 и
и 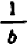 , получаем тождество
, получаем тождество 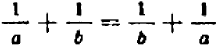 .
.
Предыдущее замечание делает излишним запоминание четырех различных распределительных законов:
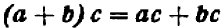 (1)
(1)
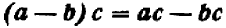 (2)
(2)
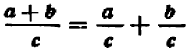 (3)
(3)
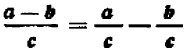 (4)
(4)
Достаточно, в самом деле, запомнить формулу (1): формула (2) из нее получается посредством за мены 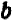 на
на 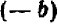 , формула (3) посредством замены
, формула (3) посредством замены 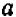 на
на 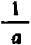 ,формула (4) посредством одновременной замены
,формула (4) посредством одновременной замены 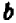 на
на 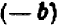 и
и 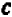 на
на 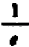 .
.
Из того же распределительного закона (1) следуют также формулы, выражающие правила сложения или вычитания суммы и разности:
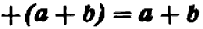 (5)
(5)
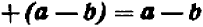 (6)
(6)
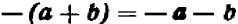 (7)
(7)
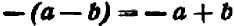 (8)
(8)
Именно, тождества (5) и (6) получаются из тождеств (1) и (2) посредством замены 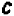 через
через 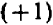 ; тождества (7) и (8)— из них же посредством замены
; тождества (7) и (8)— из них же посредством замены 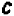 через
через 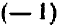 .
.
Умножение многочлена на многочлен
При умножении многочлена на многочлен также получается многочлен. Этот результат следует из распределительного закона, на который при выполнении действия приходится ссылаться несколько раз.
Предположим, что требуется умножить двучлен 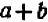 на двучлен
на двучлен 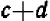 . Заменяя в тождестве
. Заменяя в тождестве 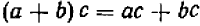
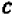 через
через 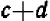 мы получаем тождество
мы получаем тождество 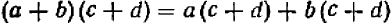 . Дальше остается раскрыть скобки в правой части, и мы получаем окончательно:
. Дальше остается раскрыть скобки в правой части, и мы получаем окончательно: 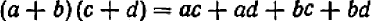 .
.
Это тождество мы запишем также в следующей форме: 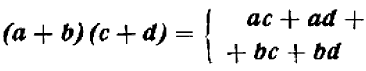 (1)
(1)
Умножим теперь двучлен 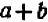 на трехчлен
на трехчлен 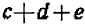 . Заменяя в тождестве (1)
. Заменяя в тождестве (1)  через
через  , мы придем к новому тождеству:
, мы придем к новому тождеству: 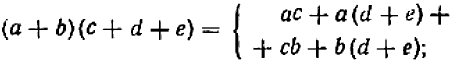 ; раскрывая скобки справа, получим окончательно:
; раскрывая скобки справа, получим окончательно: 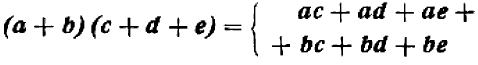 (2).
(2).
Посмотрим дальше, как умножить трехчлен 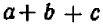 на трехчлен
на трехчлен 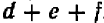 . По формуле (2) мы получаем
. По формуле (2) мы получаем 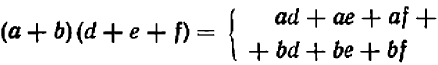 ;
;
Заменяя теперь 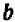 через
через 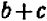 , будем иметь:
, будем иметь: 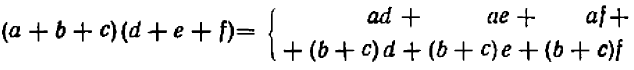 и остается раскрыть скобки справа. Результат можно записать в следующей форме:
и остается раскрыть скобки справа. Результат можно записать в следующей форме: 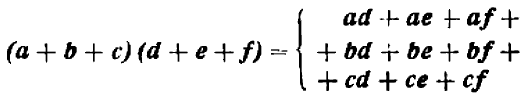 (3)
(3)
Тождества (1), (2) и (3) соответствуют лишь частным случаям умножения многочлена на многочлен; тем не менее они позволяют подметить общее правило, по которому следует выполнять это действие. Вместе с тем предыдущие рассуждения показывают, как шаг за шагом это правило может быть доказано для любого числа членов в каждом из перемножаемых многочленов.
Чтобы умножить многочлен на многочлен, достаточно умножить каждый член многочлена-множимого на каждый член многочлена-множителя и затем составить сумму полученных одночленов.
Кроме того, необходимо сделать приведение подобных членов, если таковые окажутся.
Квадрат суммы и разности
Часто приходится некоторый двучлен (сумму или разность) умножать, сам на себя — возводить в квадрат.
Проверьте сами правильность следующих умножений; подробно объясните каждый шаг.
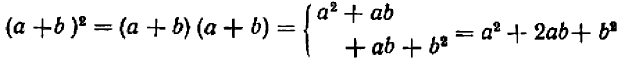
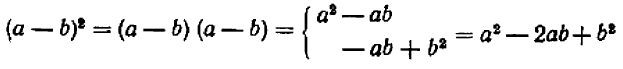
Запишем, прочтем словами и постараемся запомнить полученные формулы:
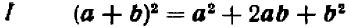
Квадрат суммы двух слагаемых равен квадрату первого слагаемого» плюс удвоенное произведение первого слагаемого на второе, плюс квадрат второго слагаемого.
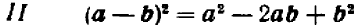
Квадрат разности двух слагаемых равен квадрату уменьшаемого, минус удвоенное произведение уменьшаемого на вычитаемое, плюс квадрат вычитаемого.
Формулы  и
и  представляют собою тождества: они справедливы при всевозможных значениях букв
представляют собою тождества: они справедливы при всевозможных значениях букв 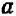 и
и 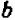 ; остаются справедливыми также при подстановке вместо
; остаются справедливыми также при подстановке вместо 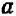 и
и 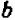 каких угодно буквенных выражений.
каких угодно буквенных выражений.
Положим, например, 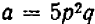 ,
, 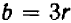 . Получится:
. Получится:
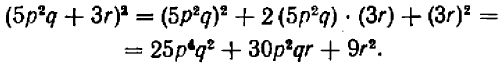
Обратите внимание, что, заменяя в формуле 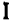
 через
через  , мы получаем формулу
, мы получаем формулу 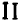 :
: 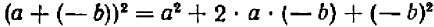 , т.е.
, т.е. 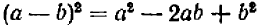 .
.
Произведение суммы на разность
Очень важно также уметь без потери времени умножить сумму двух чисел или выражений на их же разность.
Производя умножение 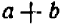 на
на  обычным способом, мы получаем:
обычным способом, мы получаем: 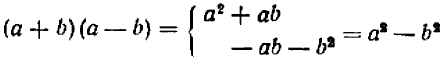
Таким образом, при всех значениях букв 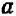 и
и 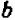 справедлива формула, которую тоже необходимо запомнить:
справедлива формула, которую тоже необходимо запомнить:
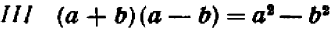
Произведение суммы двух чисел (величин) на их разность равно разности их квадратов.
Положим, например, 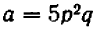 ,
, 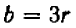 . Будем иметь:
. Будем иметь:
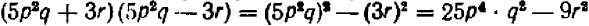
Куб суммы и разности
Пользуясь формулами 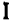 и
и 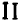 («квадрат суммы и разности», легко получить формулы для «куба суммы и разности».
(«квадрат суммы и разности», легко получить формулы для «куба суммы и разности».
Именно:
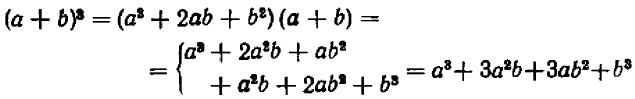
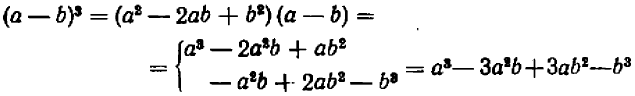
В окончательном виде формулы таковы:
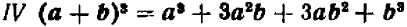
Куб суммы двух слагаемых равен сумме: 1) куба первого слагаемого, 2) утроенного произведения квадрата первого слагаемого на второе слагаемое, 3) утроенного произведения первого слагаемого на квадрат второго слагаемого и 4) куба второго слагаемого.
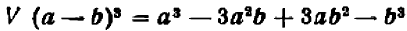
Куб разности равен сумме: 1) куба уменьшаемого. 2) взятого с обратным знаком утроенного произведения квадрата уменьшаемого на вычитаемое, 3) утроенного произведения уменьшаемого на квадрат вычитаемого и 4) взятого с обратным знаком куба вычитаемого.
Для облегчения запоминания важно заметить, что в обеих формулах  и
и  сумма показателей во всех членах равна
сумма показателей во всех членах равна  , причем показатели при
, причем показатели при 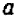 от члена к члену убывают, а показатели при
от члена к члену убывают, а показатели при 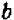 возрастают: запомнить же коэффициенты
возрастают: запомнить же коэффициенты 
не представляет труда.
Формула 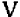 получается из формулы
получается из формулы 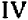 посредством замены
посредством замены  на
на  , что влечет за собой чередование знаков начиная с плюса.
, что влечет за собой чередование знаков начиная с плюса.
Пример:
При 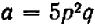 ,
, 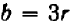 , мы получаем:
, мы получаем:
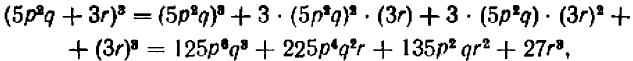
и точно так же
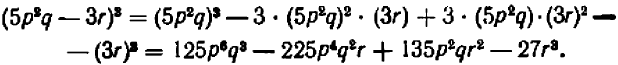
Разность и сумма кубов
Нетрудно проверить правильность следующих умножений:
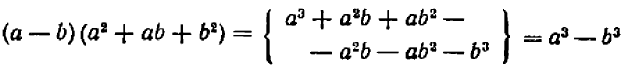
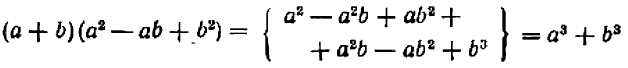
Отсюда следуют формулы:
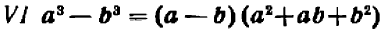
Разность кубов двух чисел (выражений) равна произведению разности самих чисел на сумму: 1) квадрата первого числа, 2) произведения обоих чисел и 3) квадрата второго числа.
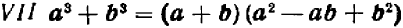
Сумма кубов двух чисел (выражений) равна произведению суммы самих чисел на сумму: 1) квадрата первого числа, 2) взятого с обратным знаком произведения обоих чисел и 3) квадрата второго числа.
Обратите внимание, что сумма показателей в каждом из трех членов второго произведения в правой части формул 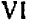 и
и 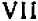 равна
равна  .
.
Формула 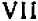 получается из формулы
получается из формулы 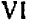 после замены
после замены 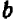 на
на 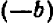 .
.
Пример:
Полагая 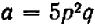 ,
, 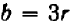 , получим:
, получим:
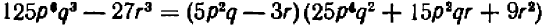
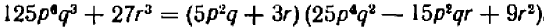
Деление на одночлен
Пусть нужно разделить одночлен 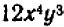 на одночлен
на одночлен 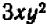 . Мы получаем, пользуясь сокращениями дробей:
. Мы получаем, пользуясь сокращениями дробей: 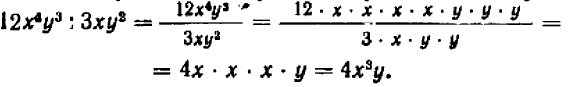
В результате может в иных случаях получится и дробь. Например: 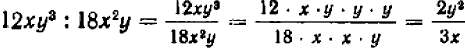
Пусть теперь требуется разделить многочлен на одночлен: например, 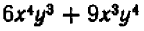 на
на 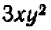 .
.
Согласно распределительному закону деления имеет место тождество 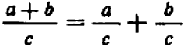 ; полагая
; полагая 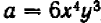 ,
, 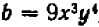 ,
, 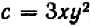 , мы сейчас же получим
, мы сейчас же получим 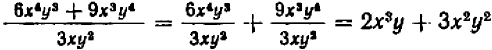 .
.
Вот другой пример: нужно разделить 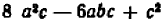 на
на 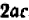 . Мы будем иметь:
. Мы будем иметь: 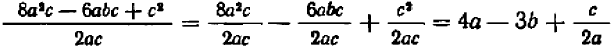
Здесь выполнить деление «нацело» не удается.
Разложение многочлена на множители
Если в курсе арифметики мы встречаемся с произведением нескольких числовых множителей, то по большей части, не медля, производим умножение: 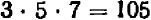 .
.
Но нередко в арифметике же, напротив, бывает нужно представить данное число в виде произведения множителей; так, мы пишем, например: 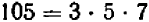 .
.
Точно так же в алгебре не всегда целесообразно перемножать данные выражения, а иногда требуется представить данное буквенное выражение в виде произведения множителей.
Сделать это не представляет труда в случае одно члена; так, например, 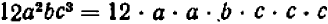 .
.
Займемся теперь многочленами. В общем случае разложение многочлена на множители может представить затруднения; мы ограничимся указанием простейших приемов.
1. Самый простой прием разложения многочлена на множители заключается в вынесении за скобки одночлена, являющегося произведением числовых и буквенных множителей, входящих во все члены данного многочлена. Это преобразование — обратное умножению многочлена на одночлен, и тоже непосредственно вытекает из распределительного закона умножения; надо лишь переставить левую и правую части: 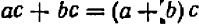 .
.
Если нужно, скажем, разложить на множители двучлен  , то мы получим:
, то мы получим: 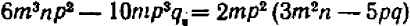 .
.
Здесь мы имеем: 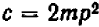 ,
, 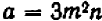 ,
, 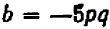 .
.
При вынесении одночлена за скобки надо, очевидно, на него делить данное выражение.
2. Более общий прием разложения заключается в группировке членов, выполняемой с таким расчетом, чтобы по вынесении за скобки одночленных множителей в каждой группе в скобках оставался в разных группах один и тот же многочлен, который и выносится вслед за тем, в свою очередь, за скобки. Так мы получаем, например, разложение:
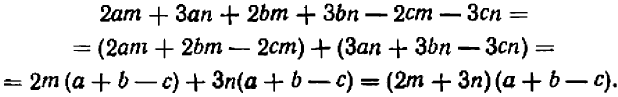
Иногда возможность разложения, усматривается не посредственно: 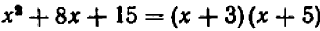 .
.
3. Довольно часто при разложении многочлена на множители удается воспользоваться основными формулами умножения I — VII. Например:
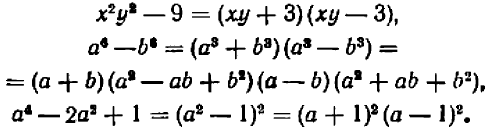
Выделение квадрата из трехчлена
Следующий прием преобразования («выделение квадрата») в некоторых случаях приводит к разложению на множители; вместе с тем он представляет и самостоятельный интерес.
Пример:
Дано выражение 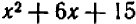 . Оно не составляет «квадрата суммы», но если бы третий член был не
. Оно не составляет «квадрата суммы», но если бы третий член был не 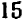 , а
, а 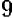 , то мы имели бы квадрат суммы. Исходя из этого соображения, в данном трехчлене
, то мы имели бы квадрат суммы. Исходя из этого соображения, в данном трехчлене 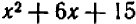 можно «выделить квадрат» следующим образом:
можно «выделить квадрат» следующим образом: 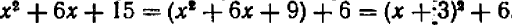 .
.
Пример:
Дано выражение 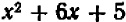 . Оно не составляет «квадрата суммы», но если бы третий член был не
. Оно не составляет «квадрата суммы», но если бы третий член был не 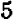 , а
, а 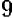 , то мы имели бы квадрат суммы
, то мы имели бы квадрат суммы 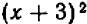 . Исходя из этого, «выделяем квадрат»:
. Исходя из этого, «выделяем квадрат»: 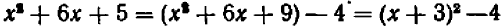 .
.
Но в этом примере можно произвести и разложение на множители, так как мы получили «разность квадратов»:
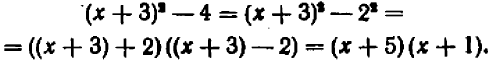
Итак, мы получаем: 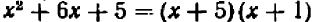 .
.
О возможности такого разложения можно было бы догадаться и сразу!
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

