Оглавление:
Иллюстрация теоремы Безу на примерах:
Пусть требуется, например, разделить многочлен 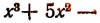
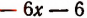 на двучлен х—2.
на двучлен х—2.
Можно предсказать, что остаток при этом делении будет равен 10. Проверим это:
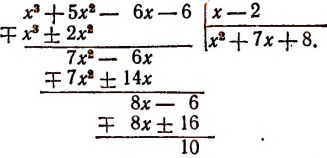
Предсказание было сделано следующим образом.
Рассматривая делитель х—2, мы видим, что в нем из независимой переменной х вычитается число 2. Это число 2 мы подставили в делимое вместо переменного х и получили 10, т. е. как раз остаток.
Действительно,
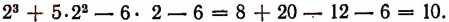
Таким образом, оказалось, что остаток от деления многочлена на х—2 равен значению делимого при х = 2.
Это правило определения остатка, сформулированное в общем виде, и будет являться теоремой Безу.
При делении многочлена 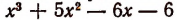 на х — 3 остаток будет равен:
на х — 3 остаток будет равен:
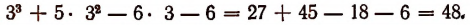
(Проверьте это непосредственным делением.)
При делении многочлена 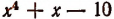 на х + 2, т. е. на х—(— 2), остаток будет равен:
на х + 2, т. е. на х—(— 2), остаток будет равен:
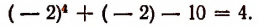
(Проверьте это непосредственным делением.)
При делении многочлена 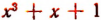 на х — i остаток равен
на х — i остаток равен 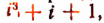 т. е. единице (проверьте это непосредственно делением).
т. е. единице (проверьте это непосредственно делением).
Приведенные примеры никак не могут рассматриваться как доказательства теоремы Безу: они даны лишь для того, чтобы облегчить понимание самой формулировки теоремы Безу.
Формулировка и доказательство теоремы Безу
При делении многочлена п-й степени относительно х, расположенного по убывающим степеням х, на двучлен (х — а остаток равен значению делимого при х = а
буква а может обозначать любое действительное или мнимое число, т. е. любое комплексное число).
Прежде чем доказывать теорему, сделаем несколько подготовительных пояснений.
1. В формулировке теоремы не случайно сказано: «расположенного по убывающим степеням х».
Если производить деление, расположив делимое и делитель по возрастающим степеням х, то тогда нельзя утверждать, что остаток всегда будет равен значению делимого при х = а.
Например, если многочлен 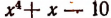 расположить по возрастающим степеням х и делить его на 2 + х, т. е. производить деление так:
расположить по возрастающим степеням х и делить его на 2 + х, т. е. производить деление так:
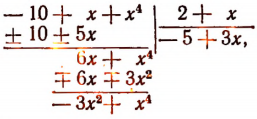
то мы никогда не получим остатка, равного числу 4, т. е. значению делимого при x = — 2.
2. Мы знаем, что существуют такие алгебраические выражения, которые теряют смысл при некоторых отдельных значениях входящих в него букв. Например, 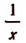 теряет смысл при x = 0; выражение
теряет смысл при x = 0; выражение 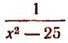 теряет смысл при x = 5 и при x = — 5.
теряет смысл при x = 5 и при x = — 5.
Заметим, что многочлен любой целой положительной степени никогда не теряет смысла. При всяком значении переменной он принимает определенное значение.
3. Произведение двух множителей, из которых один обращается в нуль, а другой принимает определенное значение, всегда равно нулю. Если же один множитель обращается в нуль, а другой теряет смысл, то о таком произведении нельзя говорить, что оно равно нулю. О таком произведении ничего определенного сказать нельзя. В каждом отдельном случае необходимо особое исследование.
Рассмотрим, например, произведение
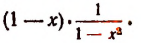
При х = 1 первый множитель обращается в нуль, а второй теряет смысл. Нельзя утверждать, что это произведение при х = 1 равно нулю.
Очевидно, что
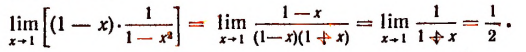
Итак, при х = 1 само произведение 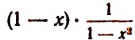 смысла не имеет. Но его предел имеет смысл, а именно равен
смысла не имеет. Но его предел имеет смысл, а именно равен 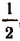 , а не нулю, как это ошибочно можно было предположить.
, а не нулю, как это ошибочно можно было предположить.
Доказательство теоремы Безу
Пусть f(x) обозначает собой произвольный многочлен n-й степени относительно переменной х, расположенный по убывающим степеням х, и пусть при делении на двучлен х — а получилось в частном q(x), а в остатке R (см. схему деления):
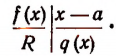
Очевидно, что q(х) будет некоторый многочлен (п — 1)-й степени относительно х, а остаток R будет величиной постоянной, т. е. не зависящей от х.
Если бы остаток R был многочленом хотя бы первой степени относительно х, то это означало бы, что процесс деления не доведен до конца. Итак, R от х не зависит
По свойству деления (делимое равно произведению делителя на частное плюс остаток) получим тождество
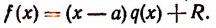
Это равенство справедливо прн всяком значении х, значит, оно будет справедливым и при х = а.
Подставляя в левую и правую части этого равенства вместо переменной х число а, получим:
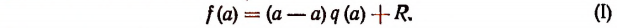
Здесь символ f(a) обозначает собой уже не f(x) т.е. не многочлен относительно х, а значение этого многочлена при х = a.
q(а) обозначает значение q(x) при х = а.
Остаток R остался таким, каким он был раньше, так как R от х не зависит.
Произведение (а — a)q(a) равно нулю, так как множитель (а — а) равен нулю, а множитель q(a) есть определенное число. (Многочлен q(x) ни при каком определенном значении х не теряет смысла.)
Поэтому из равенства (I) получим:

что и требовалось доказать.
Пример:
При делении многочлена 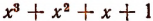 на х —i остаток равен
на х —i остаток равен 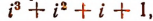 т. е. нулю.
т. е. нулю.
Следствия из теоремы Безу
Следствие 1. Если многочлен делится без остатка на х — а, то а необходимо будет корнем этого многочлена.
Следствие 2. Если а есть корень какого-либо многочлена, то это условие будет достаточным для делимости этого многочлена без остатка на х — а.
Эти два следствия можно объединить и выразить следующим образом:
Для делимости многочлена на x — а необходимо и достаточно, чтобы а было корнем этого многочлена.
Применения теоремы Безу
Поинтересуемся делимостью выражений вида 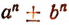 на двучлены вида а±b (здесь п — натуральное число).
на двучлены вида а±b (здесь п — натуральное число).
В выражении 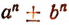 примем а за независимую переменную, а b за постоянную. Тогда выражение
примем а за независимую переменную, а b за постоянную. Тогда выражение 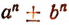 будет многочленом п-й степени относительно переменной а, расположенным по убывающим степеням этой переменной.
будет многочленом п-й степени относительно переменной а, расположенным по убывающим степеням этой переменной.
а) При делении 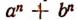 на а + b остаток будет равен:
на а + b остаток будет равен:
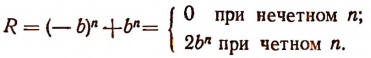
Значит, 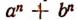 делится без остатка на а+b лишь тогда, когда п — число нечетное.
делится без остатка на а+b лишь тогда, когда п — число нечетное.
б) При делении 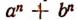 на а — b имеем
на а — b имеем
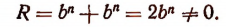
Значит, 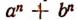 не делится на а — b.
не делится на а — b.
в) При делении  на a+b имеем
на a+b имеем
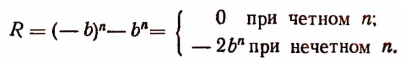
Значит,  делится на а + b лишь тогда, когда п — число четное.
делится на а + b лишь тогда, когда п — число четное.
г) При делении  на а — b получаем
на а — b получаем
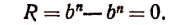
Значит,  всегда делится на а — b.
всегда делится на а — b.
Другие важные применения теоремы Безу изложены в следующих главах.
Правило Горнера. Правило Горнера позволяет вычислять коэффициенты частного и остаток при делении многочлена, расположенного по убывающим степеням х, на двучлен х — а, не производя самого деления. При делении многочлена
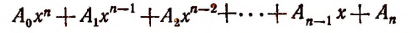
на двучлен x — а в частном получим многочлен степени (п — 1):
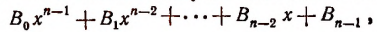
а в остатке — некоторое число R.
По свойству деления
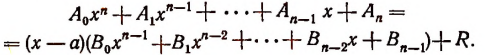
Раскрыв скобки в правой части этого равенства и объединив члены с одинаковыми степенями х, получим тот же многочлен, что и в левой части.
Приравнивая коэффициенты при одинаковых степенях х, найдем, что
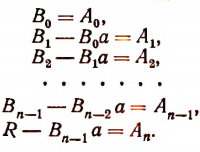
Отсюда
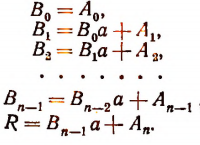
Вычисления можно располагать так: коэффициенты делимого:

коэффициенты частного и остаток:
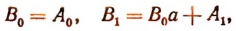
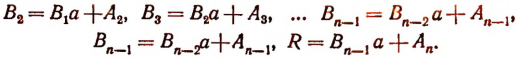
Примеры:
1. С помощью правила Горнера найти частное и остаток при делении многочлена
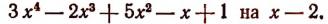
Решение:
2. Разделить 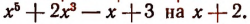
Решение:
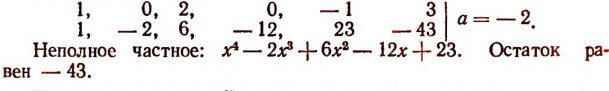
Пользуясь правилом Горнера, легко найти частное
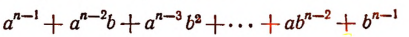
от деления
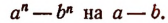
Отсюда вытекает формула
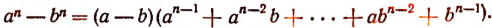
Аналогично можно получить и формулу
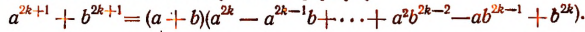
Теорема Гаусса
Если бы мы не знали никаких других чисел, кроме натуральных, то сказали бы, что уравнение 2х— 3 = 0 не имеет ни одного корня, так как нет ни одного натурального числа, которое удовлетворяло бы этому уравнению.
Уравнение 2х + 3 =0 не имеет ни одного корня в области положительных чисел.
Уравнение 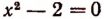 не имеет ни одного корня в области рациональных чисел.
не имеет ни одного корня в области рациональных чисел.
Уравнение 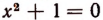 не имеет ни одного корня в области действительных чисел.
не имеет ни одного корня в области действительных чисел.
Выражение
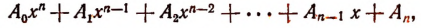
в котором х есть независимая переменная, 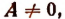 п — натуральное число и коэффициенты
п — натуральное число и коэффициенты 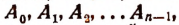
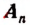 — любые комплексные числа, называется целой рациональной функцией п-й степени.
— любые комплексные числа, называется целой рациональной функцией п-й степени.
Корнем данной целой рациональной функции называется такое значение (действительное или мнимое) переменной х, при котором эта целая рациональная функция обращается в нуль.
В области действительных чисел не всякая целая рациональная функция имеет корень. Например, целая рациональная функция
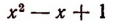
не имеет ни одного действительного корня.
В связи с этим возникает следующий важный вопрос. Можно ли утверждать, что среди комплексных чисел найдется хоть одно число, являющееся корнем целой рациональной функции
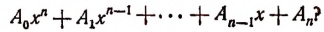
Этот вопрос на протяжении длительного исторического периода оставался неразрешенным. В 1799 году Гаусс в возрасте 22 лет дал первое строгое доказательство теоремы о существовании корня целой рациональной функции.
Теорема Гаусса гласит: Всякая целая рациональная функция с любыми комплексными коэффициентами имеет по крайней мере один корень (действительный или мнимый).
В настоящее время существует несколько различных доказательств этой фундаментальной теоремы алгебры, но все они сложны и не входят в курс элементарной алгебры.
Теорема Гаусса еще раз свидетельствует нам ту общность в решении различных вопросов, которую придает им введение в науку комплексных чисел.
Свойства целой рациональной функции
Теорема Гаусса позволяет открыть и доказать другие важные свойства целой рациональной функции.
1. Всякую целую рациональную функцию п-й степени можно представить в виде произведения коэффициента высшего члена на п линейных множителей, т. е.
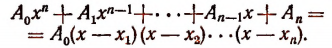
Эти линейные множители могут быть все действительными или все мнимыми и могут быть частью действительными и частью мнимыми.
Доказательство:
Функцию
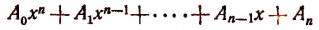
обозначим для краткости буквой М. По теореме Гаусса М имеет по крайней. мере один корень х, (действительный или мнимый). Тогда по следствию из теоремы Безу многочлен М должен делиться без остатка на  .
.
Обозначив буквой  частное от этого деления, получим:
частное от этого деления, получим:
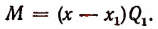
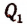 будет целой рациональной функцией (п— 1)-й степени с коэффициентом при высшем члене, равном
будет целой рациональной функцией (п— 1)-й степени с коэффициентом при высшем члене, равном 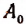 .
.
По теореме Гаусса функция 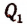 также будет иметь по крайней мере один корень.
также будет иметь по крайней мере один корень.
Обозначив этот корень буквой 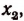 получим:
получим:
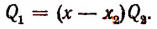
Число 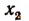 может оказаться отличным от xv но может оказаться и равным ему. Для нас это безразлично.
может оказаться отличным от xv но может оказаться и равным ему. Для нас это безразлично.
Применяя такие же рассуждения к функции 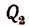 , получим:
, получим:
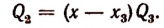
Степени функций 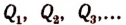 будут соответственно
будут соответственно
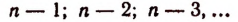
Продолжая этот процесс, мы придем к равенству

где 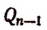 есть функция вида
есть функция вида 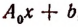 , где b — постоянная. Но
, где b — постоянная. Но
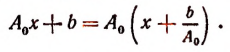
Обозначив корень функции 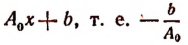 буквой
буквой 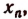 получим, что
получим, что
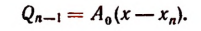
Пользуясь полученными равенствами, найдем последовательно:
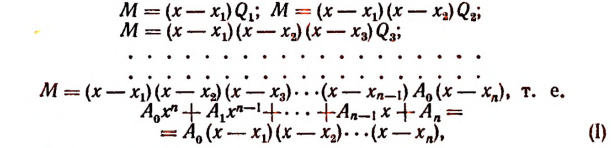
что и требовалось доказать.
Из равенства (I) непосредственно видно, что числа 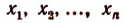 являются корнями данной целой рациональной функции.
являются корнями данной целой рациональной функции.
Правая часть равенства (I) не может обратиться в нуль ни при каком значении переменной х, отличном от значений
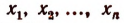
Следовательно, целая рациональная функция п-й степени не может иметь более п корней.
Если все числа 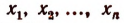 окажутся различными, то функция будет иметь ровно п различных корней.
окажутся различными, то функция будет иметь ровно п различных корней.
Если же среди чисел 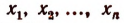 окажутся равные, то различных корней будет меньше чем п.
окажутся равные, то различных корней будет меньше чем п.
Пусть оказалось, что
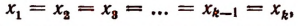
а остальные корни отличны от 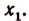 В этом случае говорят, что
В этом случае говорят, что 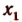 есть корень кратности k. Например, функция
есть корень кратности k. Например, функция 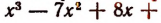
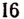 разлагается на множители
разлагается на множители

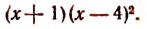
Значит, число — 1 есть простой ксрень, а число 4 есть корень кратности 2 или двукратный корень.
2. Если целая рациональная функция с действительными коэффициентами имеет комплексный корень  то она обязательно будет иметь и корень
то она обязательно будет иметь и корень 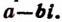
Доказательство. Выражение
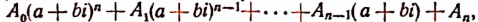
в котором  —действительные числа, будет представлять собой некоторое комплексное число Р + Qi, т. е.
—действительные числа, будет представлять собой некоторое комплексное число Р + Qi, т. е.

Заменив в последнем равенстве i числом —i, получим:

Теперь допустим, что 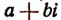 есть корень целой рациональной функции
есть корень целой рациональной функции
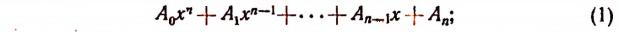
тогда окажется, что P + Qi = 0. Отсюда следует, что Р = 0 и Q = 0. Но в таком случае окажется равным нулю и выражение Р—Qi, т. е. окажется корнем целой рациональной функции (1) и число  что и требовалось доказать.
что и требовалось доказать.
3. Всякая целая рациональная функция с действительными коэффициентами степени выше 2-й разложима либо на действительные линейные множители, либо на действительные множители 2-й степени, либо на действительные множители, среди которых имеются и линейные и второй степени. (Доказательство 3-го свойства опускается.)
Примеры разложения целой рациональной функции с действительными коэффициентами степени выше второй на действительные неприводимые множители
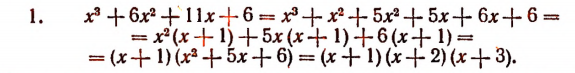
Получилось разложение на действительные линейные множители.
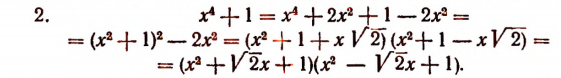
Получилось разложение на действительные множители 2-й степени.
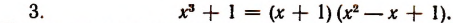
Получился один множитель линейный, а другой 2-й степени.
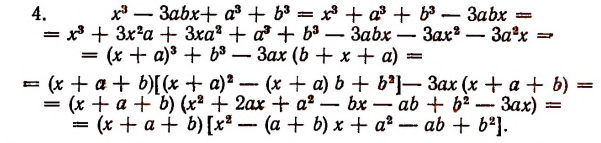
Получился один множитель линейный, а другой 2-й степени.
Теоретически доказано (как уже отмечалось), что всякая целая рациональная функция с действительными коэффициентами степени выше 2-й разложима на действительные множители 1-й и 2-й степени.
Однако осуществление этого разложения не всегда достигается легко. Например, попробуем разложить на множители
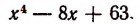
Решим эту задачу двумя способами.
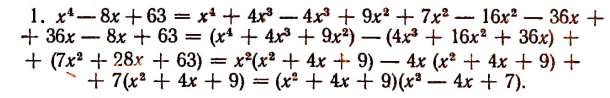
(Полученные многочлены 2-й степени имеют мнимые корни, а потому неразложимы на действительные линейные множители.)
Изложенный способ носит слишком искусственный характер. Его трудно придумать.
Второй способ, изложенный ниже, будет менее искусственным.
2. Прежде всего исследуем характер корней многочлена 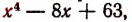 или, что то же самое, характер корней уравнения
или, что то же самое, характер корней уравнения
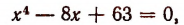
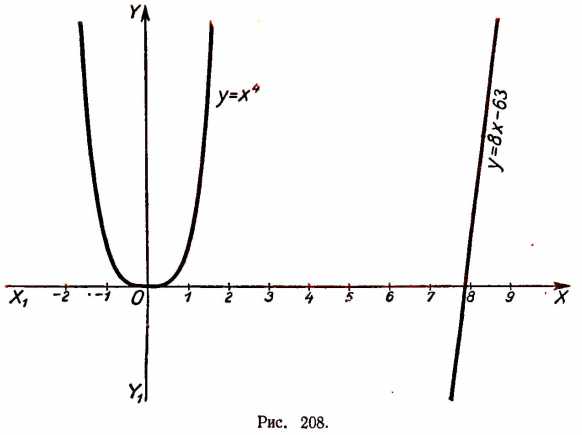
Переписав это уравнение в виде
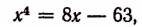
построим графики функций 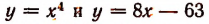 (рис. 208). Графики не пересекаются. Следовательно, корни уравнения
(рис. 208). Графики не пересекаются. Следовательно, корни уравнения
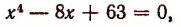
а значит, и многочлена
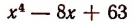
будут все мнимыми. Поэтому среди действительных множителей, на которые разлагается этот многочлен, не может быть ни одного линейного.
Итак, выяснено, что действительными множителями разложения многочлена 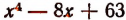 будут только многочлены 2-й степени. Таких множителей будет два, так как данный многочлен имеет 4-ю степень.
будут только многочлены 2-й степени. Таких множителей будет два, так как данный многочлен имеет 4-ю степень.
Таким образом, будем иметь, что
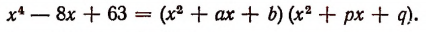
Остается определить а, b, р и q.
Перемножив многочлены, стоящие в правой части последнего равенства, получим:
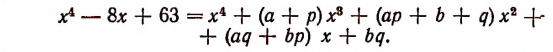
Но поскольку нам необходимо, чтобы правая часть этого равенства превратилась в такой же многочлен, который стоит в левой части, потребуем выполнения следующих условий:
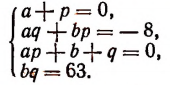
Получилась система четырех уравнений с четырьмя неизвестными a, b, р, q.
Из первого уравнения
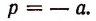
Подставив во второе и третье уравнение — а вместо р, получим систему:
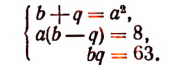
Из второго уравнения этой системы
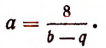
Подставив это в первое уравнение, получим систему:
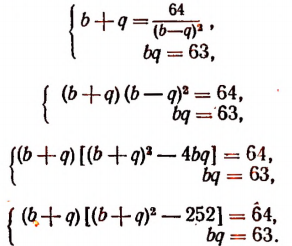
Обозначим b + q буквой z. Тогда первое уравнение последней системы примет вид:
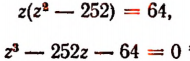
Делителями числа 64 являются: ± 1; ± 2; ± 4; ± 8; ± 16; ± 32; ± 64.
Испытывая эти делители, обнаружим, что число 16 является корнем уравнения
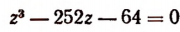
Значит, мы можем взять b + q = 16. Кроме того, bq = 63. Отсюда примем b = 7 и q = 9. Пользуясь равенством
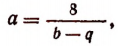
получим, что а = —4. Наконец, из равенства р = —а найдем, что р = — 4.
Теперь задача решена полностью. Мы получили:
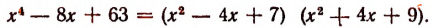
Имея это разложение, мы легко обнаруживаем все корни многочлена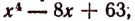 или, что то же самое, все корни уравнения
или, что то же самое, все корни уравнения
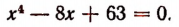
Этими корнями будут комплексные числа
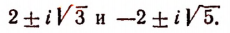
Формулы Виета
Было доказано, что целая рациональная функция разлагается иа множители по формуле:
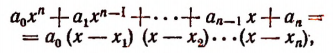
где 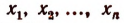 — суть корни целой рациональной функции. Выполняя умножение в правой части этой формулы, получим:
— суть корни целой рациональной функции. Выполняя умножение в правой части этой формулы, получим:
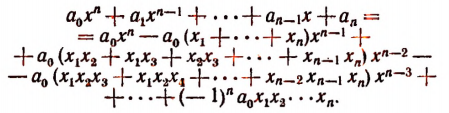
Сравнивая коэффициенты при одинаковых степенях буквы х в левой и правой частях последнего равенства, получим формулы:
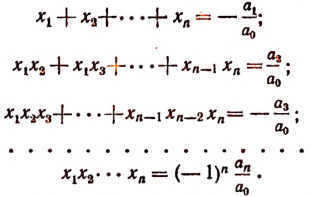
Эти формулы носят название формул Виета, по имени открывшего их замечательного французского математика Франсуа Виета. Оии связывают корни и коэффициенты целой рациональной функции. Например, для
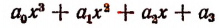
получим
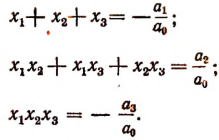
Для приведенной функции
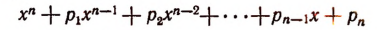
формулы Виета принимают вид:
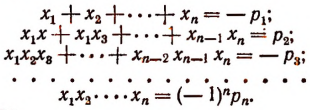
Например, для
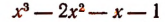
получим:
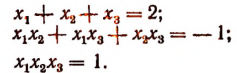
Примеры:
1. Не решая уравнения
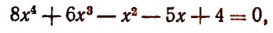
найти сумму и произведение его корней.
Решение:
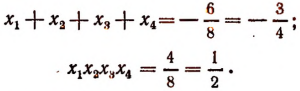
2. Пусть 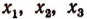 — корни уравнения
— корни уравнения
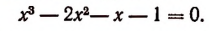
Составить новое уравнение, корнями которого были бы числа:
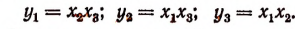
Решение:
Согласно формулам Виета
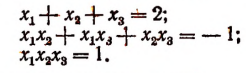
Теперь найдем значения трех выражений:
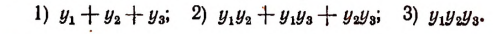
Легко видеть, что
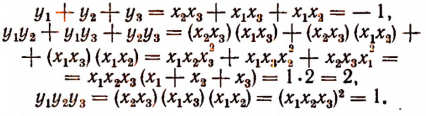
Искомым уравнением будет
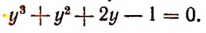
3. Сторонами треугольника являются корни уравнения
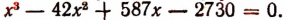
Не решая этого уравнения, найти площадь треугольника.
Решение:
Обозначим корни данного уравнения через 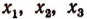 . Тогда согласно формулам Виета
. Тогда согласно формулам Виета 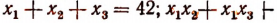
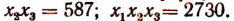
По формуле Герона
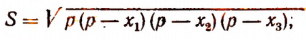
где
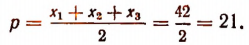
Следовательно
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

