Соединения в комбинаторике с примерами решения и образцами выполнения

Оглавление:

Группы, составленные из каких-либо предметов (безразлично какой природы, например букв, чисел, геометрических фигур, цветных флажков и т. п.), называются соединениями.

Сами предметы, из которых составляются соединения, называются элементами.

Различают три основных типа соединений: размещения, перестановки и сочетания.

Размещения

Пусть имеется п каких-либо различных элементов. Ради краткости обозначим их различными буквами:

а; b; с, …; h; k; l.

Определение:

Размещениями из п элементов по р в каждом называются такие соединения, из которых каждое содержит р элементов, взятых из числа данных п элементов, и которые отличаются друг от друга либо самими элементами (хотя бы одним), либо лишь порядком их расположения.

Примеры:

Из одного элемента а можно составить лишь одно размещение.

Из двух элементов а и b можно составить два размещения по одному элементу и два размещения по два элемента ab, bа.

Из трех элементов а, b, с можно составить три размещения по одному элементу; шесть размещений по два элемента ab, ас, bа, be, са, cb; шесть размещений по три элемента abc, acb, bac, bca, cab, cba.

Из четырех элементов а, b, с, d можно составить 4 размещения по одному элементу:

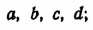
12 размещений по два элемента:

ab, ас, ad; са, cb, cd;
ba, bc, bd; da, db, dc

24 размещения по три элемента:

abc, abd, acb, acd, adb, adc, bac, bad
bca, bcd, bda, bdc, cab, cad, cba, cbd
cda, cdb, dca, dcb, dba, dbc, dca, dcb

24 размещения по четыре элемента:

abcd, abdc, acbd, acdb, adbc, adcb, bacd, badc
bcad, bcda, bdac, bdca, cabd, cadb, cbad, cbda
cdab, cdba, dcab, dcba, dbac, dbca, dcab, dcba

По поводу размещений могут быть поставлены две основные задачи.

1. Имеется п элементов. Составить из них всевозможные размещения по р в каждом.

2. Имеется п элементов. Не составляя из них всевозможных размещений по р в каждом, определить, сколько таких различных размещений можно составить.

Начиная изложение теории размещений, мы не можем решить вторую задачу вне связи с первой. Но в дальнейшем, когда вторая задача будет решена в общем виде, мы уже не будем нуждаться в составлении самих размещений, а будем прямо подсчитывать число размещений в любом случае с помощью выведенного правила.

Число размещений из п элементов по р в каждом обозначается символом Соединения

Вывод формулы числа размещений

Пусть имеется п элементов а, b, с,…, h, k, l. Очевидно, что размещений из п элементов по одному будет п. Следовательно,

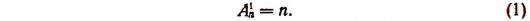
Чтобы определить число размещений из п элементов по два, сначала составим все такие размещения.

Воспользуемся уже имеющимися размещениями по одному:

а, b, с,…, h, k, l

Возьмем из этих размещений только первое, т. е. элемент а, и станем присоединять к нему по очереди каждый из остальных элементов. Тогда получим первую строчку размещений по два:

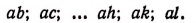
Поступая также с каждым из остальных размещений по одному, получим записанную ниже колонку всех размещений из n элементов по два:

Число размещений в каждой строке равно n — 1, а всех строк n. Следовательно,

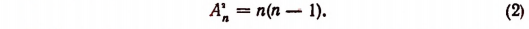
Чтобы найти число размещений по три, воспользуемся уже имеющимися размещениями по два.

Возьмем из предыдущей колонки первое размещение по два и станем присоединять к нему по очереди каждый из (n — 2) оставшихся элементов. Тогда получим первую строчку размещений по три:

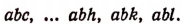
Поступая также с каждым из остальных размещений по два, получим записанную ниже колонку всех размещений из n элементов по три:

В каждой строке (n — 2) размещения, а всех строк n(n — 1). Следовательно,

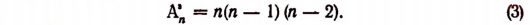
Пользуясь методом математической индукции, можно доказать, что закономерность, наблюдаемая в формулах (1), (2) и (3), обладает общностью, т. е. доказать справедливость формулы

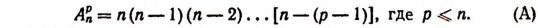
Допустим, что формула (А) справедлива при р = k, т. е. предположим справедливым следующее равенство:

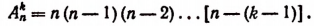
Докажем, что в таком случае будет справедливым и равенство

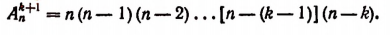
Мы допустили, что число всех размещений из n элементов по k элементов равно произведению

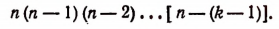
Возьмем одно из этих размещений k-гo порядка и станем присоединять к нему по очереди каждый из оставшихся (п — k) элементов, не вошедших во взятое нами размещение. Тогда мы получим (п — k) размещений (k + 1)-го порядка.

Таким способом из каждого размещения k-гo порядка можно образовать (п — k) размещений (k + 1)-го порядка.

Но число всех размещений k-гo порядка по нашему предположению равно произведению

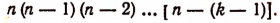
Следовательно, из всех размещений k-гo порядка можно составить указанным выше способом столько размещений (k + 1)-го порядка, сколько единиц окажется в произведении

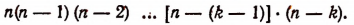
Легко понять, что изложенным способом мы получим все размещения (k + 1)-го порядка, взятые только по одному разу. Поэтому окажется, что

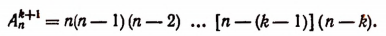
Таким образом, из предположения, что формула (А) верна для р = k, мы пришли к тому, что эта формула оказалась верной и при р = k + 1. Но поскольку формула (А) верна, как это мы видели при р = 1, то, значит, она верна всегда, т. е. при любом натуральном значении р, меньшем или равном п.

Число множителей в правой части формулы (А) равно р. Эту формулу можно записывать и так:

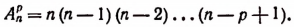
Примеры:

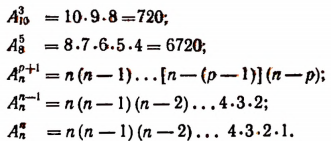
Из последних двух формул следует, что

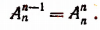
Перестановки

Определение:

Перестановками из п элементов называются такие соединения, из которых каждое содержит все п элементов и которые отличаются друг от друга лишь порядком расположения элементов.

Число перестановок из одного элемента равно единице. Число перестановок из двух элементов a, b равно двум: ab; bа.

Число перестановок из трех элементов a, b, с равно шести: abc, acb; bac; bca; cab; cba.

Число перестановок из n элементов обозначается символом 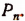Соединения Число перестановок из п элементов — это то же самое, что число размещений из п элементов по п в каждом. Поэтому

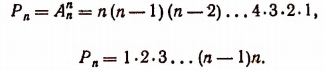
Число всех перестановок из п элементов равно произведению последовательных натуральных чисел от 1 до п включительно. Из формулы 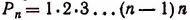Соединения следует, что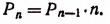

Примеры:

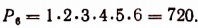
Сколькими различными способами могут разместиться на скамейке 10 человек?

Отв. 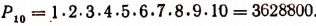Соединения

Понятие факториала

Произведение я натуральных чисел от 1 до n обозначается сокращенно n!, т. е.

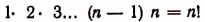Соединения (читается n факториал).

Например,

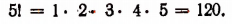
Выражение 5! читается: пять факториал.

2!= 2; 1! = 1.

Формулу числа перестановок теперь можно записать так:

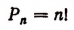
Умножив и разделив произведение

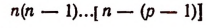
на (n — р)!, получим:

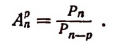
Сочетания

Определение. Сочетаниями из п элементов по р в каждом называются такие соединения, из которых каждое содержит р элементов, взятых из числа данных п элементов, и которые отличаются друг от друга по крайней мере одним элементом.

Примеры.

Из одного элемента можно составить лишь одно сочетание. Из двух элементов а и b можно составить два сочетания по одному элементу а, b и лишь одно сочетание по два элемента ab.

Из трех элементов а, b, с можно составить: 3 сочетания по одному элементу:

а, b; с;

3 сочетания по два элемента:

ab; ас; bc;

одно сочетание по три элемента:

abc.

Из четырех элементов а, b, с, d можно составить: 4 сочетания по одному элементу:

а; b; с; d;

6 сочетаний по два элемента:

ab; ас; ad; bc; bd; cd;

4 сочетания по три элемента:

abc; abd, acd; bcd;

одно сочетание по 4 элемента:

abcd.

Соединение abc и соединение cab представляют собой одно и то же сочетание. Если же взять abc и abd или bcd, то это будут различные сочетания.

Число сочетаний из п элементов по р в каждом обозначается символом 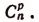Соединения

Вывод формулы числа сочетаний

Если в каждом сочетании из п элементов по р сделать всевозможные перестановки, то образуются всевозможные размещения из п элементов по р. Поэтому

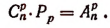
Отсюда

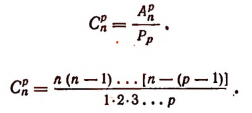
Заметим, что в выражении п (п—1)(n — 2)… каждый последующий множитель на единицу меньше предыдущего. Так, например.

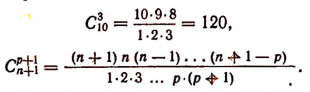
Задача. Сколькими способами можно выбрать три лица на три одинаковые должности из десяти кандидатов.

Отв.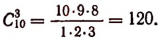 Соединения

Другой вид формулы числа сочетаний

Умножим числитель и знаменатель правой части формулы

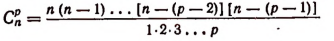
на произведение

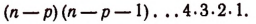
Тогда получим:

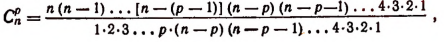
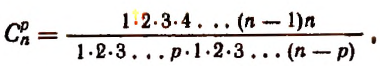
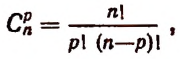
или

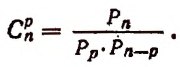
Например,

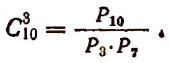
Два основных свойства числа сочетаний

Первое свойство: 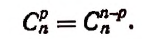Соединения

Доказательство:

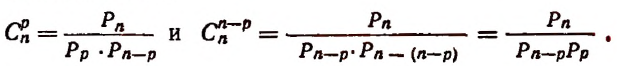
Отсюда

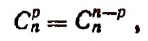
что и требовалось доказать.

Пример:

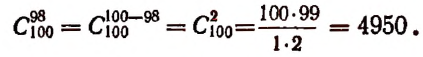
Второе свойство: 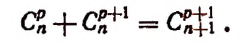Соединения

Доказательство:

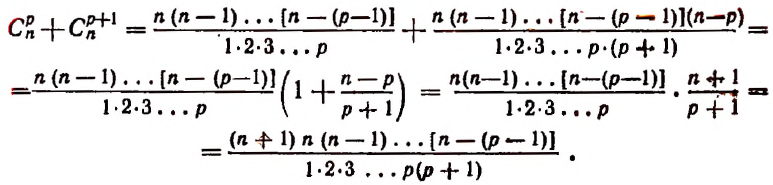
Но последнее выражение как раз и представляет собой 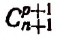Соединения . Поэтому

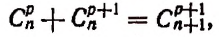
что и требовалось доказать.

Если воспользоваться формулой 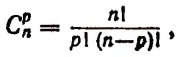Соединения то доказательство второго свойства можно изложить так:

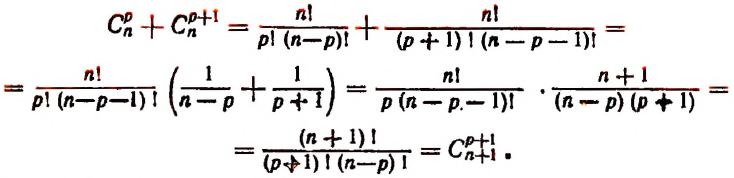
Так, например,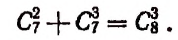 Соединения

Символ 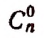Соединения не имеет смысла. Но в целях единообразной формы записи, с которой нам придется встречаться, мы примем по определению

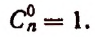
При наличии этого определения мы можем формулу

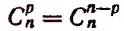
применять и тогда, когда 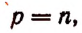Соединения т. е. писать

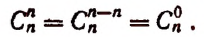
Эта запись будет правильной, так как

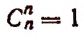Соединения и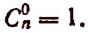

Аналогично этому принимают по определению

хотя символ 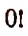Соединения сам по себе смысла не имеет.

Соединения с повторениями

Перестановки с повторениями

Пусть мы имеем 5 элементов, среди которых имеется три одинаковых элемента:

а, а, а, Ь, с.

Перестановками из этих 5 элементов будут такие соединения, из которых каждое содержит все эти 5 элементов и которые будут отличаться друг от друга, следовательно, лишь порядком расположения Зтих пяти элементов.

Отсюда понятно, что элемент а будет входить в каждое соединение три раза.

Всевозможными перестановками из этих пяти элементов будут следующие:

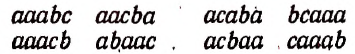
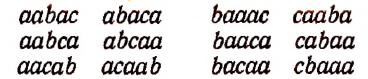
Эти перестановки будут перестановками с повторениями потому, что в каждое соединение один и тот же элемент а входит три раза, т. е. столько раз, сколько раз он имелся среди данных пяти элементов.

Из написанной выше таблицы видно, что число перестановок из 5 элементов

а, а, а, b, с,

т. е. перестановок с повторениями, равно 20.

Если же все 5 элементов были бы различными, то, как нам уже известно, число перестановок равнялось бы не 20, а числу 5!, т. е. 120.

Пусть мы не знаем число перестановок с повторениями из 5 элементов

а, а, а, b, с,

Обозначим это неизвестное число буквой х. Теперь вообразим, что в группе а, а, а, b, с вместо трех одинаковых элементов а, а, а мы взяли три различных элемента 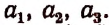Соединения Тогда имеющееся число перестановок х увеличится в 3! раза *. Но при этом число всех перестановок окажется равным числу перестановок из 5 различных элементов, т. е. будет равно числу 5! Таким образом,

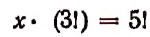
Отсюда

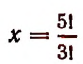
Формула числа перестановок с повторениями

Пусть имеется п элементов, среди которых имеется 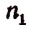Соединения одинаковых элементов.

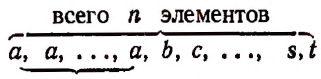
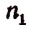Соединения одинаковых элементов

Число перестановок с повторениями из этих n элементов обозначим буквой х.

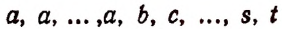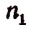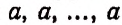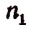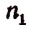Теперь вообразим, что в группе Соединения вместо одинаковых элементов мы взяли различных элементов Тогда имеющееся число перестановок х увеличится во столько раз, сколько перестановок можно сделать из Соединения элементов, т. е. увеличится в 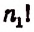раз. Но тогда число всех перестановок окажется равным числу перестановок из n различных элементов, т. е. будет равно числу 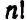. Поэтому

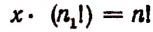
Отсюда

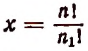
Если теперь рассматривать как одинаковые еще 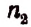Соединения элемента 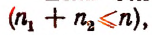то число различных перестановок с повторениями из таких n элементов будет

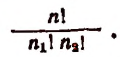
Примеры:

Сколько различных шестизначных чисел можно записать c помощью цифр 1; 1; 1; 2; 2; 2?

Отв. 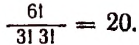Соединения

2. Различных перестановок букв можно сделать в слове;

замок — 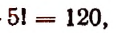Соединения ротор —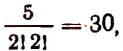

топор —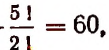 Соединения колокол —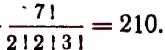

3. Я помню, что нужный мне телефонный адрес начинается с буквы К и содержит три «четверки» и две «пятерки». Однако расположение этих пяти цифр я позабыл. Спрашивается, сколько надо сделать проб, чтобы с гарантией связаться с нужным мне абонентом. (Предполагается, что на каждый телефонный вызов каждый вызываемый абонент будет отвечать при первом же его вызове.)

Из теории, изложенной выше, видно, что таких проб достаточно сделать

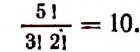
Размещения с повторениями

Сначала поясним на примере, какие соединения называются размещениями с повторениями.

Пусть имеется 4 различных элемента а, b, с, d и пусть требуется составить из этих 4-х элементов размещения с повторениями по два элемента.

Поскольку здесь речь идет о размещениях по два элемента, то, значит, каждое соединение, которое мы будем составлять, должно содержать по два элемента.

Если бы мы составляли размещения без повторений, то все элементы, входящие в любое размещение, обязательно должны были бы быть различными.

Например, размещениями без повторений из 4-х элементов а, b, c, d по два элемента были бы следующие:

Размещениями же с повторениями из этих 4-х элементов по два элемента будут следующие:

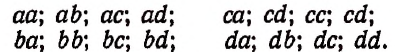
Размещение с повторениями из m элементов по Соединения элементов может содержать любой элемент сколько угодно раз от 1 до р включительно либо не содержать его вовсе.

Другими словами, каждое размещение с повторениями из m элементов по р элементов может состоять не только из р различных элементов, но из р каких угодно и как угодно повторяющихся элементов.

Соединения, отличающиеся друг от друга хотя бы порядком расположения элементов, считаются различными размещениями.

Число размещений с повторениями из m элементов по р элементов будем обозначать символом

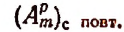
Формула для числа размещений с повторениями

Пусть мы имеем сколько угодно комплектов m различных элементов:

Пусть теперь требуется узнать, сколько можно составить всевозможных размещений по р элементов с повторениями из различных элементов, если каждый из этих различных элементов имеется в нашем распоряжении в достаточном количестве.

Возьмем р комплектов данных m различных элементов:

Поставим на первое место какой-либо элемент 1-й строки, на второе место, независимо от этого, какой-либо элемент 2-й строки н т. д. и, наконец, на Соединения место какой-либо элемент 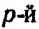строки. Соединяя каждый элемент 1-й строки с каждым элементом 2-й строки, получим 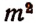соединений по два, т. е.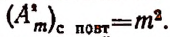

Присоединяя к каждому из этих 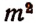Соединения соединений каждый элемент 3-й строки, получим 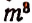соединений по 3 н т. д.

Присоединяя к каждому из 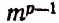Соединения со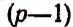единений по каждый элемент 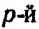строки, получим 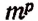соединений по р.

Эти 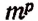Соединения соединений по р как раз и будут представлять всевозможные размещения по р элементов с повторениями из m различных элементов.

Следовательно, число размещений по р элементов с повторениями из m различных элементов равно 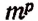, т. ,е.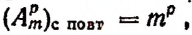

Примеры:

Из цифр 1, 2, 3, 4, 5 можно составить 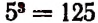трехзначных чисел, если в одном и том же числе могут попадаться и одинаковые цифры.
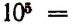
Из цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 можно составить 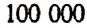телефонных номеров, если в одном и том же номере могут попадаться и одинаковые цифры.

Отсюда видно, что на каждую из 10 букв — А, Б, В, Г, Д, Е, Ж, И, К, Л — приходится телефонных номеров 100 000. Следовательно, центральная телефонная станция г. Москвы может обслуживать непосредственно не более одного миллиона абонентов.

Сочетания с повторениями

Сначала поясним на примере, какие соединения называются сочетаниями с повторениями.

Пусть имеется 5 различных элементов а, b, с, d, е и пусть требуется составить из этих 5 элементов сочетания с повторениями по 3 элемента.

Поскольку здесь речь идет о сочетаниях по три элемента, то, значит, каждое соединение, которое мы будем составлять, должно содержать по три элемента и одно от другого должно отличаться по крайней мере одним элементом.

Если бы мы составляли сочетания без повторений, то все элементы, входящие в любое сочетание, обязательно должны были бы быть различными.

Например, сочетания без повторений из 5 элементов а, b, с, d, е по три элемента были бы следующие:

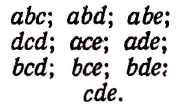
Сочетания же с повторениями из этих 5 элементов по три элемента будут следующими:

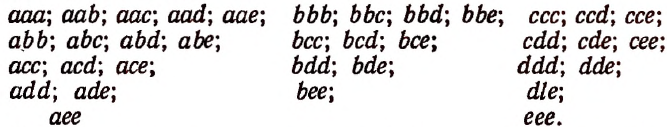
Сочетание с повторениями из m элементов по Соединения элементов может содержать любой элемент сколько угодно раз от 1 до р включительно, либо не содержать его вовсе.

Другими словами, каждое сочетание с повторениями из m элементов по р элементов может состоять не только из р различных элементов, но из р каких угодно и как угодно повторяющихся элементов.

Во всех случаях два соединения по р элементов не считаются различными сочетаниями, если они отличаются друг от друга только порядком расположения элементов.

Число сочетаний с повторениями из m элементов по р элементов будем обозначать символом

Формула числа сочетаний с повторениями

Чтобы составить всевозможные сочетания с повторениями из m различных элементов по р элементов, воспользуемся следующей таблицей:

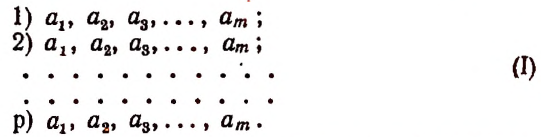
Из первой строки возьмем какой-либо произвольный элемент; из второй строки возьмем элемент, расположенный либо непосредственно над взятым элементом из первой строки, либо справа от него; из третьей строки возьмем элемент, расположенный либо непосредственно над взятым элементом из второй строки, либо справа от него и т. д.

Совершив этот процесс с каждым элементом первой строки, мы получим всевозможные сочетания с повторениями из m различных элементов по р элементов.

Число всевозможных соединений, которые мы составили указанным выше способом, пользуясь таблицей (I), будет таким же, как если бы мы тем же способом стали бы составлять соединения, пользуясь следующей таблицей:

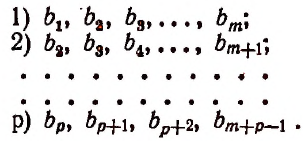
Но эти последние соединения представляли бы собой всевозможные сочетания без повторений из 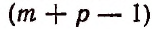различных элементов по р элементов.

Следовательно, число сочетаний с повторениями из m различных элементов по р элементов равно числу сочетаний без повторений из 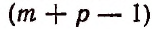Соединения различных элементов по р элементов, т. е.

Примеры:

Найти число сочетаний с повторениями из четырех элементов а, b, с, d по 3 элемента.

Искомое число будет 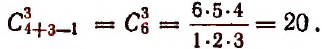Соединения

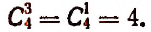
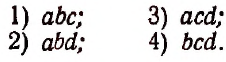
Число же различных сочетаний из 4-х элементов а, b, с, d по 3 элемента без повторений равно Соединения

2. Найти число неподобных между собой членов разложения

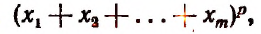
получающихся после возведения в степень.

Так как

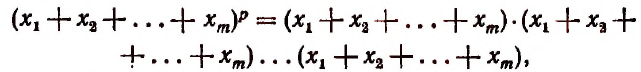
то искомое число будет равно числу сочетаний с повторениями из m различных элементов Соединения по р элементов, т. е. равно

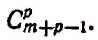
В частности, в разложении

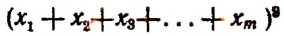
будет неподобных членов

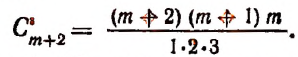
В разложении 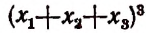Соединения неподобных членов будет

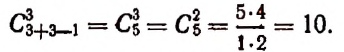
(Последний результат проверьте непосредственным возведением в куб многочлена 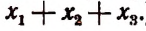Соединения )

Что такое соединения и математика

Различные группы, составленные из каких-либо предметов и отличающиеся одна от другой или порядком этих предметов, или самими предметами, называются вообще соединениями.

Если, например, из 10 различных цифр: 0, 1, 2, 3, …, 9 будем составлять группы по нескольку цифр в каждой, например такие: 123, 312, 8056, 5630,42 и т. п., то будем получать различные соединения из этих цифр. Из них некоторые, например 123 и 312, различаются только порядком предметов, другие же, например 8056 и 312, разнятся входящими в них предметами (и даже числом предметов).

Предметы, из которых составляются соединения, называются элементами. Элементы будем обозначать буквами а, b, с, … .

Соединения могут быть трёх родов: размещения, перестановки и сочетания. Рассмотрим их отдельно.

Размещения

Пусть число предметов, из которых мы составляем различные соединения, равно трём (например, 3 карты); обозначим эти предметы a, b и с. Из них можно составить соединения по одному:
а, b, с
по два:
ab, ас, be, ba, са, cb;
по три:
abc, acb, bас, bca, cab, cba.

Возьмём из этих соединений соединения по 2. Они отличаются одно от другого либо предметами, например ab и ас, либо порядком предметов, например ab и bа, но число предметов в них одно и то же. Такие соединения называются размещениями из трёх элементов по два.

Размещениями из m элементов по n называются такие соединения, из которых каждое содержит n элементов, взятых из данных m элементов, и которые отличаются одно от другого или элементами, или порядком элементов (значит, предполагается, что n ≤ m). Так, написанные выше соединения по 3 будут размещения из трёх элементов по 3 (различаются только порядком), соединения по 2 будут размещения из трёх элементов по 2 (различаются или предметами, или порядком).

Размещения из данных т элементов могут быть по 1, по 2, по 3, .. . и, наконец, по m.

Определим число всевозможных размещений, которые можно составить из m элементов по n, не составляя самих размещений. Число это принято обозначать так: 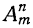Соединения (здесь А есть начальная буква французского слова „arrangement“, что значит „размещение“ ). Чтобы найти это число, рассмотрим приём, посредством которого можно составлять всевозможные размещения.

Пусть нам дано т элементов: а, b, с, . . ., k, l. Сначала составим из них все размещения по 1. Их, очевидно, будет m. Значит, 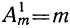Соединения . Теперь составим все размещения по 2. Для этого к каждому из ранее составленных размещений по 1 приставим последовательно все оставшиеся m— 1 элементов по 1. Так, к элементу а приставим последовательно оставшиеся элементы: b, с,… , k, l; к элементу b приставим последовательно оставшиеся элементы а, с,. . . , k, l и т. д. Тогда получим следующие размещения по 2:

Так как всех элементов m, то из каждого размещения по одному элементу мы получим m — 1 размещений по 2, а всего их будет (m— 1)m. Очевидно, что других размещений по 2 быть не может. Значит:
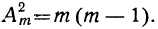
Соединения

Чтобы составить теперь размещения по 3, берём каждое из составленных сейчас размещений по 2 и приставляем к нему последовательно по одному все m — 2 оставшихся элементов. Тогда получим следующие размещения по 3:

Так как число всех размещений по 2 равно m (m — 1) и из каждого получается (m — 2) размещения по 3, то всех таких размещений окажется:
(m — 2) [m (m — l)]=m (m — 1) (m — 2).

Таким образом: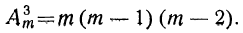
Соединения

Подобно этому получим: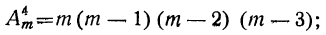
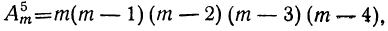
Соединения

и вообще: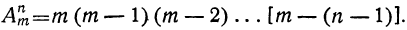

Такова формула числа размещений; её можно высказать так:

Число всевозможных размещений из m элементов по n равно произведению n последовательных целых чисел, из которых большее есть m.

Таким образом: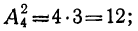
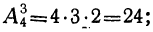
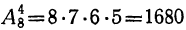Соединения и т. п.

Задачи:

1) В классе 10 учебных предметов и 5 разных уроков в день. Сколькими способами могут быть распределены уроки в день?

Всевозможные распределения уроков в день представляют собой, очевидно, всевозможные размещения из десяти элементов по 5; поэтому всех способов распределения должно быть: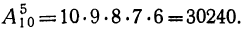
Соединения

2) Сколько можно образовать целых чисел, из которых каждое выражалось бы тремя различными значащими цифрами?

Искомое число есть число размещений из 9 значащих цифр по 3; следовательно, оно равно 9∙8∙7=504.

3) Сколько можно образовать целых чисел, из которых каждое изображалось бы тремя различными цифрами?

Из 10 цифр: 0, 1, 2, 3,…, 9 можно составить размещений по три 10∙9∙8=720; но из этого числа надо исключить число тех размещений по 3, которые начинаются с цифры 0. Таких размещений будет столько, сколько можно составить размещений по 2 из 9 значащих цифр, т. е. 9∙8=72; следовательно, искомое число 720 — 72=648.

Перестановки

Если размещения из m элементов взяты по m (т. е. различаются только порядком элементов), то такие размещения называются перестановками. Например, перестановки из двух элементов α, b будут размещения из 2 по 2, т. е. ab и bа, перестановки из трёх элементов а, b, с будут размещения из 3 по 3, т. е. abc, acb, bac, bca, cab, cba и т. п.

Число всевозможных перестановок из т элементов обозначается 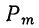Соединения (здесь P есть начальная буква французского слова „permutation» , что значит „перестановка»).

Так как перестановки из m элементов — это размещения из m по m, то формула числа перестановок будет такая:
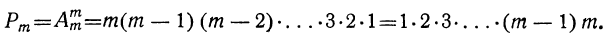
Соединения

Число всевозможных перестановок из m элементов равно произведению натуральных чисел от 1 до m.

Задачи:

1) Сколько девятизначных чисел можно написать девятью разными значащими цифрами?

Искомое число есть
P₉= 1∙2∙3∙4∙5∙6∙7∙8∙9=362880.

2) Сколькими способами можно разместить 12 лиц за столом, на котором поставлено 12 приборов?

Число способов равно:
1∙2∙3∙…∙ 12 = 479001600.

Замечание. Произведение натуральных чисел от 1 до m включительно (обозначается сокращённо так: m!) растёт чрезвычайно быстро с возрастанием m; так, при m = 12 оно даёт 479001600, при m= 100 оно выражается числом, требующим 158 цифр для своего изображения.

Сочетания

Если из всех размещений, которые можно составить из т элементов по n, мы отберём только те, которые одно от другого разнятся по крайней мере одним элементом, то получим соединения, которые называются сочетаниями.

Например, из четырёх элементов а, b, с и d сочетания по 3 будут:
abc, abd, acd, bcd.

Если в каждом из этих сочетаний сделаем всевозможные перестановки, то получим всевозможные размещения из четырёх элементов по 3:

abc
acb
bас
bса
cab
cba

abd
adb
bad
bda
dab
dba

acd
adс
cad
cda
dac
dca

bed
bdc
cbd
cdb
dbc
deb

Число таких размещений равно, очевидно, 6∙4=24.

Таким образом, число всех размещений из m элементов по n равно числу всех сочетаний из m элементов по n, умноженному на число всех перестановок, какие можно сделать из n элементов, т. е.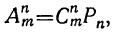
Соединения
где 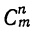означает число всех сочетаний из m по n (С есть начальная буква французского слова „combinaison», что значит „сочетание»).

Отсюда выводим следующую формулу числа сочетаний: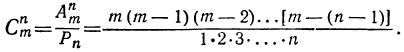
Соединения
Например: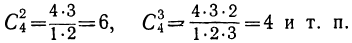

Примеры:

1) Из 10 кандидатов на одну и ту же должность должны быть выбраны трое. Сколько может быть разных случаев выборов?

Искомое число, очевидно, составляет число всевозможных сочетаний из десяти элементов по 3, т. е.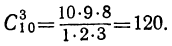
Соединения

2) Сколькими способами можно выбрать 13 карт из колоды в 52 карты?

Искомое число представляет собой число сочетаний из 52 по 13, т. е.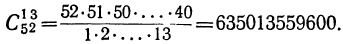
Соединения

Другой вид формулы числа сочетаний

Формулу числа сочетаний можно привести к другому виду, если умножим числитель и знаменатель её на произведение 1∙2∙3… (m — n); тогда в числителе получим произведение m (m — 1) … [m — (n — 1)]∙1 ∙2∙3∙ … ∙(m-n), которое, переставив сомножители, можно написать:
1∙2∙3∙ … ∙(m — n) [m — (n — 1)] … m.

Следовательно: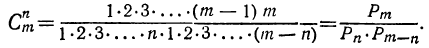
Соединения

Свойство сочетаний

Заменив в этой формуле n на m — n, получим: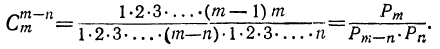
Соединения

Сравнивая эту формулу с предыдущей, находим: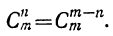
Соединения

К этому выводу приводит и такое простое рассуждение: если из m элементов отберём какие-нибудь n элементов, чтобы составить из них одно сочетание, то совокупность оставшихся элементов составит одно сочетание из m — n элементов. Таким образом, каждому сочетанию из n элементов соответствует одно сочетание из m— n элементов, и наоборот; значит:
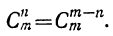
Соединения

Это соотношение позволяет упростить нахождение числа сочетаний из m элементов по n, когда n превосходит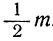 Соединения . Например: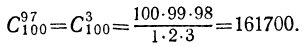

Соединения и Бином Ньютона

Размещения

Имеется m элементов (т. е. предметов, букв, цифр, чисел и т. д.). Выберем из них какие-нибудь k элементов (k ≤ m) и расположим эти k элементов в каком-нибудь порядке, т. е. так, чтобы было известно, какой элемент находится на первом месте, какой — на втором и т. д.

Определение:

Расположенная совокупность k элементов, взятых из данных m элементов, называется размещением из m элементов по k.

По определению, два размещения из т элементов по k являются различными, если они отличаются или самими элементами, или порядком их расположения.

Число всевозможных размещений из т элементов по k обозначается знаком 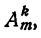Соединения , где m показывает число всех элементов, a k — число элементов, входящих в каждое размещение. Задача состоит в отыскании общей формулы для подсчета 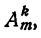. Решение задачи разобьем на две части. В первой части рассмотрим несколько частных случаев с тем, чтобы на основе их построить гипотезу для общего случая. Во второй части проверим гипотезу методом математической индукции.

Случай 1. k = 1. Пусть m = 5, т. е. имеется 5 элементов: а₁, а₂ ,а₃, а₄, а₅. В каждое размещение по одному элементу входит либо a₁ , либо а₂ , либо a₃ либо а₄ либо а₅. Таким образом, 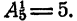Соединения . Очевидно, что и при всяком m.

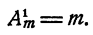
Случай 2. k = 2. Пусть m = 4, т. е. имеется 4 элемента: а₁, а₂ ,а₃, а₄ . Для того чтобы составить все размещения из этих элементов по 2, выпишем сначала все размещения по 2, у которых на первом месте находится элемент а₁ . Получим строку

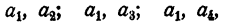
содержащую три размещения. Выпишем теперь все размещения по 2, у которых на первом месте находится элемент а₂ . Получим строку

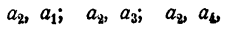
содержащую еще три размещения. Далее имеем строку

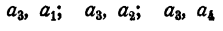
и, наконец, строку

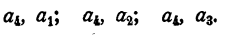
Всего имеем 4 строки, в каждой из которых содержится три размещения из 4 элементов по 2. Таким образом,

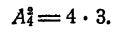
Если бы m = 10, то, поступая таким же образом, мы получили бы 10 строк, в каждой из которых содержалось бы по 9 размещений из 10 элементов по 2:

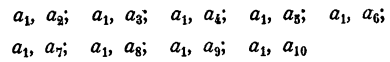
и т. д. Таким образом,

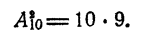
Все это наводит на гипотезу, что при всяком m.

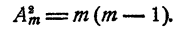
Рассматривая, если потребуется, еще и другие примеры, можно ваметить, что 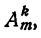Соединения равно произведению k последовательных целых чисел, наибольшее из которых m, т. е. при любом m и при любом k (конечно, k ≤ m)

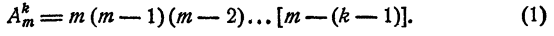
Рассуждения, которые были проведены, не являются доказательством того, что формула (1) верна. Эти рассуждения дали лишь возможность построить гипотезу. Нужно еще доказать, что гипотеза эта верна.

Теорема:

Число размещений из m элементов по k может, быть вычислено по формуле

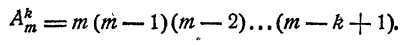
Доказательство:

Доказательство проводится методом математической индукции, причем индукция ведется по k

При k = 1 утверждение справедливо, так как непосредственно видно, что 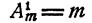Соединения и по формуле (1)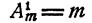

Допустим, что утверждение справедливо при k = n, где n < m, т. е.

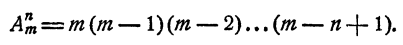
Докажем, что тогда утверждение должно быть справедливым и при k = n + 1, т. е.

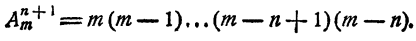
Для получения размещений из от элементов по n + 1 возьмем все размещения из m элементов по n и к каждому из них на (n + 1)-е место припишем каждый из остальных n — m элементов. Таким путем получим 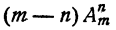Соединения размещений.

Если мы теперь докажем, что ни одно размещение из от элементов по n + 1 нами не пропущено и ни одно из этих размещений не выписано дважды, теорема будет доказана.

Возьмем произвольное размещение A из m элементов по n + 1. Пусть в размещении А на (n + 1)-м месте находится элемент 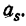Соединения . Отбросим этот элемент, получим размещение A₁ из m элементов по n. Так как мы брали все размещения из m элементов по n, взято и размещение A₁. К этому размещению на (n + 1)-е место мы приписывали каждый из остальных элементов, значит, приписали и элемент 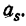Соединения . Выходит, что ни одно размещение из m элементов по n + 1 нами не пропущено.

Допустим теперь, что размещение A из m элементов по n + 1 нами получено дважды. Вычеркнем в каждом из этих размещений элемент, находящийся на последнем месте. Получим одно и то же размещение A₁ из m элементов по n. Выходит, что к одному и тому же размещению A₁, два раза в конце был приписан один и тот же элемент, Это противоречит способу, посредством которого составлялись размещения из от элементов по n + 1.

Итак,

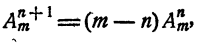
но

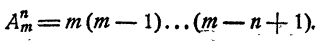
Значит,

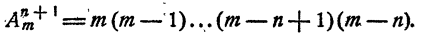
Утверждение справедливо при k = 1, и из справедливости его при k = n следует его справедливость при k = n + 1.

Теорема доказана.

Пример:

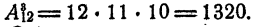
Соединения

Пример:

Сколько различных двузначных чисел можно записать при помощи цифр 1, 2, 3 и 4, если ни одна цифра не входит в изображение числа дважды?

Решение:

Искомое число равно

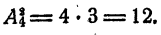
Перестановки

Размещения из m элементов по m называются перестановками из от элементов. Таким образом, две различные перестановки из данных m элементов не могут отличаться одна от другой элементами, а отличаются только порядком расположения элементов.

Определение:

Расположенная совокупность m элементов называется перестановкой из m элементов.

Число всевозможных различных перестановок из m элементов обозначается знаком 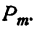Соединения . По определению,

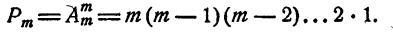
Произведение 1.2…m первых m натуральных чисел обозначается m (читается: m факториал). Таким образом, 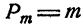Соединения

Пример:

Сколько четырехзначных чисел можно записать при помощи цифр .1, 2, 3, 4, если каждая цифра входит в изображение числа только один раз?

Решение:

Искомое число равно числу всевозможных перестановок из четырех элементов

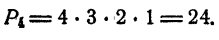
Сочетания

Определение. Сочетанием из m элементов по k называется совокупность, образованная любыми k элементами из данных m. Два сочетания из m элементов по k считаются различными тогда и только тогда, когда они отличаются по крайней мере одним элементом.

В отличие от размещений, где существенное значение имеет порядок, в котором расположены элементы, в сочетаниях порядок расположения элементов не имеет значения.

Число всевозможных сочетаний из m элементов по k обозначается знаком 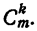Соединения

Теорема:

Число всевозможных сочетаний из m элементов по k может быть вычислено по формуле

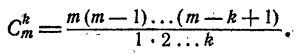
Доказательство:

Предположим, что мы составили таблицу всех сочетаний из m элементов по k. Назовем ее таблицей 1. Возьмем каждое из сочетаний таблицы 1 и всеми возможными способами переставим в нем элементы. Получим всего 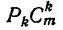Соединения размещений, которые и запишем в таблицу 2. Покажем, что в таблице 2 содержатся все размещения из m элементов по k и при этом ни одно размещение не содержится дважды.

Пусть А — произвольное размещение из m элементов по k. Если не обращать внимания на порядок расположения элементов, то А представляет собой некоторое сочетание С из m элементов по k.

Так как в таблице 1 содержатся все сочетания из m элементов no k, в ней содержится и это сочетание С. 3 сочетании С мы переставляли элементы всеми возможными способами. Следовательно, размещение А содержится в таблице 2.

Возьмем теперь два каких-нибудь размещения из таблицы 2. Если они получены из разных сочетаний, то они отличаются друг, от друга элементами. Если они происходят от одного сочетания, они отличаются порядком расположения элементов. В обоих случаях эти размещения различны.

Отсюда вытекает, что

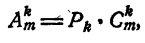
т. е.

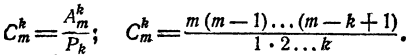
Формула для 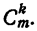Соединения может быть преобразована. Умножим числитель и знаменатель на (m — k) Получим

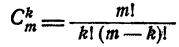
Пример:

В классе 30 учащихся. Сколькими способами можно назначить двух дежурных из них?

Решение:

Искомое число равно числу сочетаний из 30 элементов по 2.

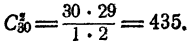
Ответ. 435.

Теорема:

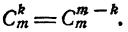
Соединения

Доказательство:

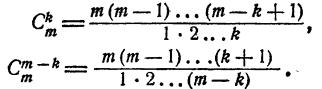
Разделим почленно

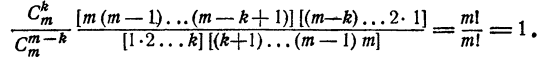
Эту теорему можно доказать и иначе.

Выбирая какие-нибудь k элементов из данных m, мы составляем некоторое сочетание из m элементов по k. Остальные m — k элементов образуют сочетание из т элементов по m — k.

Таким образом, каждому сочетанию из m элементов по k соответствует одно сочетание из m элементов по m — k и наоборот. Значит число сочетаний из m элементов по k равно числу сочетаний из m элементов по m — k.

Пример:

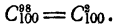
Соединения

Некоторые суммы и их свойства

Пусть

— некоторые числа. Пусть 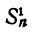Соединения , обозначает сумму всех этих чисел, 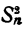обозначает сумму всевозможных произведений этих чисел, взятых по два, 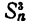обозначает сумму всевозможных произведений этих чисел, взятых по три, ит. д, Вообще означает сумму всевозможных произведений этих чисел, взятых по k. Таким образом, 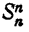Соединения обозначает произведение этих чисел

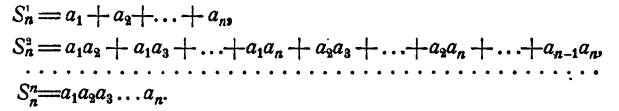
Присоединим к числам (1) еще какое-нибудь число 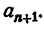Соединения . Получим n+1 чисел

Пусть 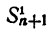Соединения обозначает сумму всех чисел (2), 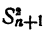обозначает сумму всевозможных произведений чисел (2), взятых по два, 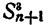обозначает сумму всевозможных произведений чисел (2), взятых по три, и т. д. Вообще 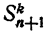Соединения обозначает сумму всевозможных произведений чисел (2), взятых по k. Таким образом, 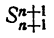обозначает произведение чисел (2).

Рассматриваемые суммы обладают следующими свойствами,

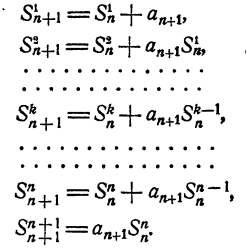
Свойство:

При любом k (1 ≤ k ≤ n) в сумме 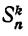Соединения содержится слагаемых.

Свойство:

Если 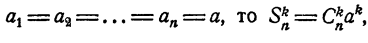Соединения , где 1 ≤ k ≤ n .

Свойства 2 и 3 непосредственно вытекают из способа составления рассматриваемых сумм. Остается доказать справедливость свойства 1.

Возьмем какое-нибудь слагаемое, входящее в 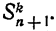Соединения Такое слагаемое является произведением k чисел, взятых из (2). Возможно одно из двух: либо число 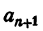в это слагаемое не входит в качестве сомножителя, либо 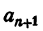в него сомножителем входит.

На этом основании разобьем все слагаемые, входящие в 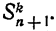Соединения , на две группы: к первой группе отнесем те из них, которые не содержат число 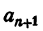в качестве сомножителя, ко второй группе отнесем те слагаемые, которые содержат число 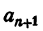Соединения в качестве сомножителя. Сумма слагаемых первой группы есть 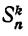, так как эта сумма состоит из всевозможных произведений чисел совокупности (1), взятых по k.

Из суммы, которую составляют слагаемые второй группы, вынесем за скобки 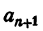Соединения . В скобке останется сумма всевозможных произведений чисел совокупности (1), взятых по k — 1.

Таким образом,

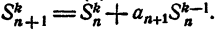
Следствие:

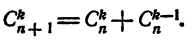
О произведении двучленов, первые члены которых одинаковы

Рассмотрим произведение n двучленов, имеющих один и тот же первый член:

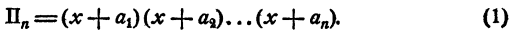
При n = 2 имеем

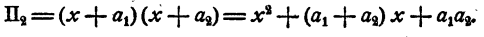
При n = 3 имеем

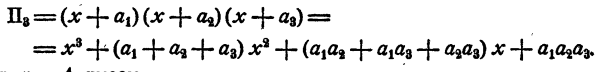
Эти результаты можно записать короче:

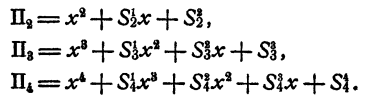
Из рассмотрения П₂, П₃, П₄ можно высказать следующую гипотезу: при любом натуральном n

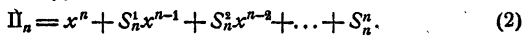
Докажем, что формула (2) справедлива. Доказательство проводится методом математической индукции. При n = 1 произведение (1) имеет вид х + a₁. Правая часть формулы (2) при n= 1 тоже равна х + a₁ . Предположим, что формула (2) справедлива при n = k, где k — какое-нибудь натуральное число, т. е.

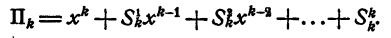
Докажем, что тогда формула (2) справедлива и при n = k + 1, т. е.

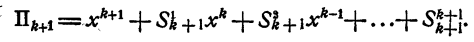
Действительно,

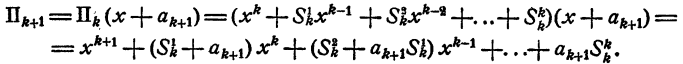
На основании свойства 1 § 4

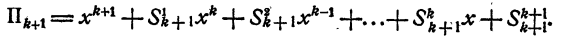
Утверждение доказано.

Натуральная степень бинома (формула Ньютона)

Теорема. При любом натуральном n

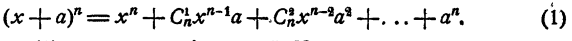
Равенство (1) называется формулой Ньютона.

Доказательство. Положим в формуле (2) § 5

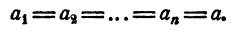
Тогда на основании свойства 3 § 4 имеем формулу (1).

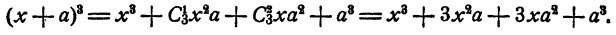
Пример:

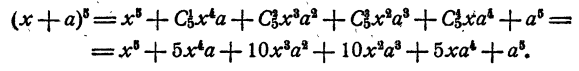
Свойства разложения по формуле Ньютона

1.Члены разложения расположены по убывающим степеням буквы х и по возрастающим степеням буквы а. Показатели буквы х последовательно уменьшаются на единицу, начиная от n(в первом члене) и до нуля (в последнем члене). Показатели буквы а последовательно увеличиваются на единицу, начиная от нуля (в первом члене) и до n (в последнем).

Сумма показателей при х и а постоянна и равна в каждом члене n— показателю степени бинома.

2. Число членов разложения равно n + 1, т. е. на единицу больше показателя степени бинома.

3. Коэффициенты разложения суть

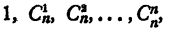
т. е. коэффициент первого члена равен единице, а коэффициенты членов, начиная со второго, равны числу сочетаний из n по k, где к— число предшествующих членов.

4. Все члены разложения, начиная со второго, можно получить по формуле

придавая k последовательно значения 1, 2,… , n.

Равенство (1) называется формулой общего члена разложения. Например, при k = 1 получаем второй член разложения

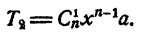
5. Коэффициенты крайних членов и членов, равноудаленных от крайних, равны между собой. Действительно, коэффициенты первого и последнего членов равны единице. Коэффициент члена 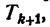Соединения т. е. (k + 1)-го члена, считая с начала, равен 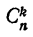Коэффициент члена 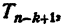т. е. (k + 1)-го члена, считая с конца, равен к. В § 3 показано, что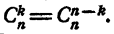

Это свойство можно объяснить и так. Рассмотрим

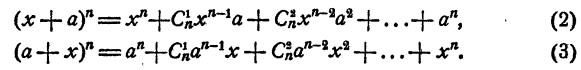
Коэффициенты членов разложения (2) равны коэффициентам соответствующих членов разложения (3), т. е. k-й член разложения (2) имеет тот же коэффициент, что и k-й член разложения (3). Но разложение (3) получается из разложения (2), если все члены разложения (2) написать в обратном порядке, и следовательно, k-й член разложения (3), считая с начала, есть k-й член разложения (2), считая с конца.

6. Если показатель степени бинома есть нечетное число, разложение содержит четное число членов. Коэффициенты второй половины членов в этом случае те же, что и коэффициенты первой половины членов, но расположены в обратном порядке.

Если показатель степени бинома есть число четное, разложение содержит нечетное число членов. В этом случае в середине разложения будет коэффициент, который не повторяется, а с обеих сторон от него коэффициенты равны, но расположены в обратном порядке.

7. Вычисление коэффициентов разложения можно вести по следующему правилу. Для того чтобы из коэффициента k-го члена разложения получить коэффициент следующего (k + 1)-го члена, достаточно коэффициент k-го члена умножить на показатель степени при х в этом члене и разделить на число членов, предшествующих определяемому.

Действительно, коэффициент k-то члена есть 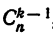Соединения , а коэффициент (k + 1)-го члена есть :

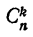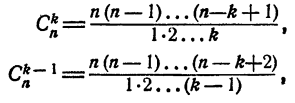
отсюда

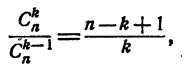
т. е.

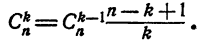
Число n — k + 1 есть показатель степени при х в k-м члене, k — число членов, предшествующих определяемому (k + 1)-му члену.

Пример:

Определить все члены разложения

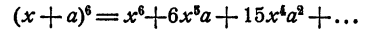
Решение:

Чтобы найти коэффициент четвертого члена, достаточно 15 (коэффициент третьего члена) умножить на 4 (показатель степени при х в третьем члене) и разделить на 3 (число членов, предшествующих определяемому четвертому). Имеем

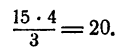
Значит

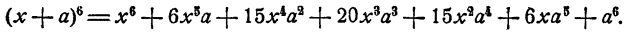
Коэффициенты последних трех членов равны коэффициентам первых трех, но расположены в обратном порядке.

8. Сумма всех коэффициентов разложения (х + а)ⁿ равна 2ⁿ. Положим в формуле Ньютона х = а= 1. Получим

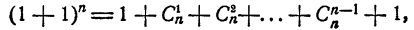
т. е

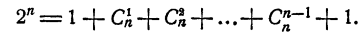
9. Разложение (x — а)ⁿ получается из разложения (x + a)ⁿ посредством умножения на -1 членов, находящихся на четных местах. Имеем

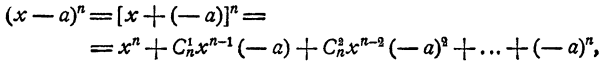
т. е

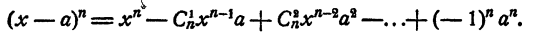
10. Сумма коэффициентов членов разложения (x + а)ⁿ , находящихся на четных местах, равна сумме коэффициентов членов, находящихся на нечетных местах. Рассмотрим разложение

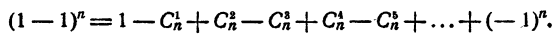
Так как левая часть этого равенства равна нулю, то

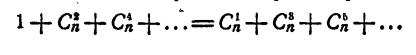
Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике: