Смешанное произведение векторов с примерами решения и образцами выполнения

Определение смешанного произведения, его геометрический смысл:

Рассмотрим произведение векторов 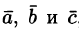, составленное следующим образом: 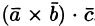. Здесь первые два вектора перемножаются векторно, а их результат скалярно на третий вектор. Такое произведение называется векторно-скалярным, или смешанным, произведением трех векторов. Смешанное произведение представляет собой некоторое число.

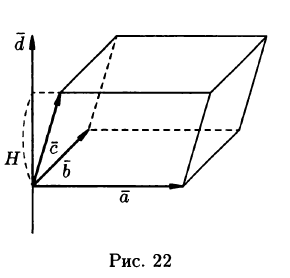
Выясним геометрический смысл выражения 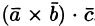. Построим параллелепипед, ребрами которого являются векторы 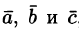и вектор 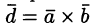(см. рис. 22).

Имеем: 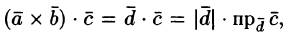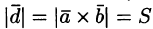, где S — площадь параллелограмма, построенного на векторах 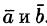, 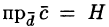для правой тройки векторов и 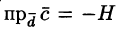для левой, где H высота параллелепипеда. Получаем:

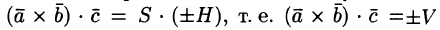
где V — объем параллелепипеда, образованного векторами .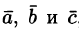

Таким образом, смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком «плюс», если эти векторы образуют правую тройку, и со знаком «минус», если они образуют левую тройку.

Свойства смешанного произведения

1.Смешанное произведение не меняется при циклической перестановке его сомножителей, т. е.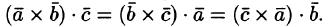 Действительно, в этом случае не изменяется ни объем параллелепипеда, ни ориентация его ребер.

2. Смешанное произведение не меняется при перемене местами знаков векторного и скалярного умножения, т. е. .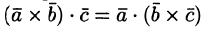

Действительно, 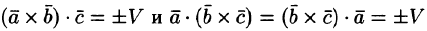Знак в правой части этих равенств берем один и тот же, так как тройки векторов 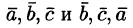— одной ориентации.

Следовательно, 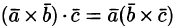. Это позволяет записывать смешанное произведение векторов 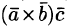. в виде 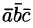без знаков векторного, скалярного умножения.

3. Смешанное произведение меняет свой знак при перемене мест любых двух векторов-сомножителей, т. е.

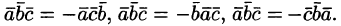
Действительно, такая перестановка равносильна перестановке сомножителей в векторном произведении, меняющей у произведения знак.

4. Смешанное произведение ненулевых векторов 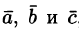равно нулю тогда и только тогда, когда они компланарны.

Если 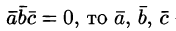— компланарны.

Допустим, что это не так. Можно было бы построить параллелепипед с объемом 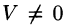. Но так как 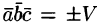, то получили бы, что 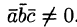. Это противоречит условию: .

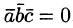Обратно, пусть векторы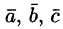 — компланарны. Тогда вектор 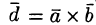будет перпендикулярен плоскости, в которой лежат векторы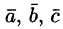, и, следовательно, 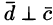. Поэтому 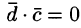, т. е. .

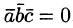Выражение смешанного произведения через координаты

Пусть заданы векторы 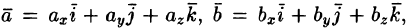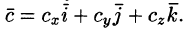Найдем их смешанное произведение, используя выражения в координатах для векторного и скалярного произведений:

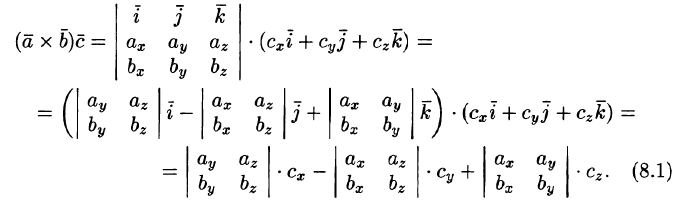
Полученную формулу можно записать короче:

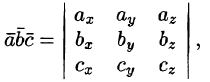
так как правая часть равенства (8.1) представляет собой разложение определителя третьего порядка по элементам третьей строки. Итак, смешанное произведение векторов равно определителю третьего порядка, составленному из координат перемножаемых векторов.

Некоторые приложения смешанного произведения

Определение взаимной ориентации векторов в пространстве

Определение взаимной ориентации векторов 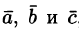основано на следующих соображениях. Если 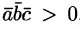, то 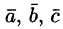— правая тройка; если 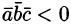, то 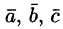— левая тройка.

Установление компланарности векторов

Векторы 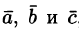компланарны тогда и только тогда, когда их смешанное произведение равно нулю :

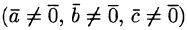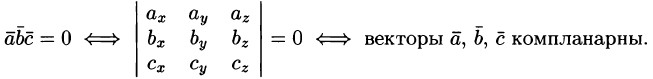
Определение объемов параллелепипеда и треугольной пирамиды

Нетрудно показать, что объем параллелепипеда, построенного на векторах 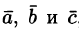вычисляется как 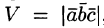, а объем треугольной пирамиды, построенной на этих же векторах, равен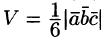

Пример:

Вершинами пирамиды служат точки A(1; 2;3), B(0; -1; 1), С(2;5;2) и D(3;0; -2). Найти объем пирамиды.

Решение:

Находим векторы :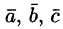

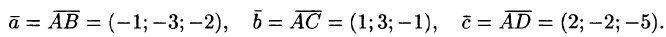
Находим :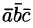

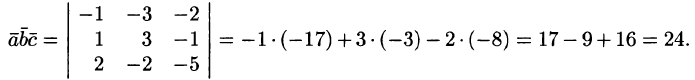
Следовательно,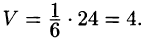

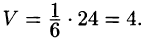
Определение смешанного произведения, его геометрический смысл

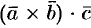Рассмотрим произведение векторов , и , составленное следующим образом: . Здесь первые два вектора перемножаются векторно, а их результат скалярно на третий вектор. Такое произведение называется векторно-скалярным, или смешанным, произведением трех векторов. Смешанное произведение представляет собой некоторое число.

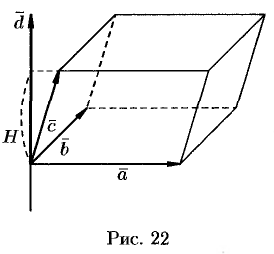
Выясним геометрический смысл выражения 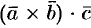. Построим параллелепипед, ребрами которого являются векторы , , и вектор 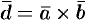(см. рис. 22).

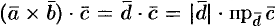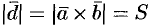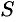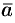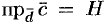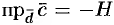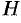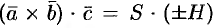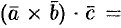
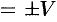Имеем: , , где — площадь параллелограмма, построенного на векторах и , для правой тройки векторов и для левой, где — высота параллелепипеда. Получаем: , т. е. , где 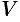— объем параллелепипеда, образованного векторами , и .

Таким образом, смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком «плюс», если эти векторы образуют правую тройку, и со знаком «минус», если они образуют левую тройку.

Свойства смешанного произведения

1. Смешанное произведение не меняется при циклической перестановке его сомножителей, т. е. .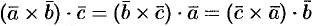

Действительно, в этом случае не изменяется ни объем параллелепипеда, ни ориентация его ребер.

2. Смешанное произведение не меняется при перемене местами знаков векторного и скалярного умножения, т. е. .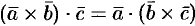

Действительно, 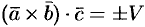и 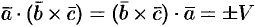. Знак в правой части этих равенств берем один и тот же, так как тройки векторов , , и , , — одной ориентации.

Следовательно, 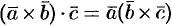. Это позволяет записывать смешанное произведение векторов 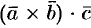в виде 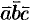без знаков векторного, скалярного умножения.

3.Смешанное произведение меняет свой знак при перемене мест любых двух векторов-сомножителей, т. е. .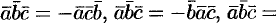

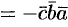Действительно, такая перестановка равносильна перестановке сомножителей в векторном произведении, меняющей у произведения знак.

4. Смешанное произведение ненулевых векторов , и равно нулю тогда и только тогда, когда они компланарны.

Если 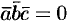, то , , — компланарны.

Допустим, что это не так. Можно было бы построить параллелепипед с объемом 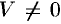. Но так как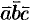 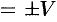, то получили бы, что 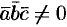. Это противоречит условию: .

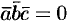Обратно, пусть векторы , , — компланарны. Тогда вектор 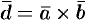будет перпендикулярен плоскости, в которой лежат векторы , , , и, следовательно, 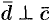. Поэтому 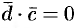, т. е. .

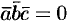Другие темы по высшей математике возможно вам они будут полезны:

Некоторые приложения скалярного произведения

Векторное произведение векторов и его свойства

Основные приложения метода координат на плоскости

Линии на плоскости

Решение заданий и задач по предметам:

• Математика
• Высшая математика
• Математический анализ
• Линейная алгебра

Дополнительные лекции по высшей математике:

1. Тождественные преобразования алгебраических выражений
2. Функции и графики
3. Преобразования графиков функций
4. Квадратная функция и её графики
5. Алгебраические неравенства
6. Неравенства
7. Неравенства с переменными
8. Прогрессии в математике
9. Арифметическая прогрессия
10. Геометрическая прогрессия
11. Показатели в математике
12. Логарифмы в математике
13. Исследование уравнений
14. Уравнения высших степеней
15. Уравнения высших степеней с одним неизвестным
16. Комплексные числа
17. Непрерывная дробь (цепная дробь)
18. Алгебраические уравнения
19. Неопределенные уравнения
20. Соединения
21. Бином Ньютона
22. Число е
23. Непрерывные дроби
24. Функция
25. Исследование функций
26. Предел
27. Интеграл
28. Двойной интеграл
29. Тройной интеграл
30. Интегрирование
31. Неопределённый интеграл
32. Определенный интеграл
33. Криволинейные интегралы
34. Поверхностные интегралы
35. Несобственные интегралы
36. Кратные интегралы
37. Интегралы, зависящие от параметра
38. Квадратный трехчлен
39. Производная
40. Применение производной к исследованию функций
41. Приложения производной
42. Дифференциал функции
43. Дифференцирование в математике
44. Формулы и правила дифференцирования
45. Дифференциальное исчисление
46. Дифференциальные уравнения
47. Дифференциальные уравнения первого порядка
48. Дифференциальные уравнения высших порядков
49. Дифференциальные уравнения в частных производных
50. Тригонометрические функции
51. Тригонометрические уравнения и неравенства
52. Показательная функция
53. Показательные уравнения
54. Обобщенная степень
55. Взаимно обратные функции
56. Логарифмическая функция
57. Уравнения и неравенства
58. Положительные и отрицательные числа
59. Алгебраические выражения
60. Иррациональные алгебраические выражения
61. Преобразование алгебраических выражений
62. Преобразование дробных алгебраических выражений
63. Разложение многочленов на множители
64. Многочлены от одного переменного
65. Алгебраические дроби
66. Пропорции
67. Уравнения
68. Системы уравнений
69. Системы уравнений высших степеней
70. Системы алгебраических уравнений
71. Системы линейных уравнений
72. Системы дифференциальных уравнений
73. Арифметический квадратный корень
74. Квадратные и кубические корни
75. Извлечение квадратного корня
76. Рациональные числа
77. Иррациональные числа
78. Арифметический корень
79. Квадратные уравнения
80. Иррациональные уравнения
81. Последовательность
82. Ряды сходящиеся и расходящиеся
83. Тригонометрические функции произвольного угла
84. Тригонометрические формулы
85. Обратные тригонометрические функции
86. Теорема Безу
87. Математическая индукция
88. Показатель степени
89. Показательные функции и логарифмы
90. Множество
91. Множество действительных чисел
92. Числовые множества
93. Преобразование рациональных выражений
94. Преобразование иррациональных выражений
95. Геометрия
96. Действительные числа
97. Степени и корни
98. Степень с рациональным показателем
99. Тригонометрические функции угла
100. Тригонометрические функции числового аргумента
101. Тригонометрические выражения и их преобразования
102. Преобразование тригонометрических выражений
103. Комбинаторика
104. Вычислительная математика
105. Прямая линия на плоскости и ее уравнения
106. Прямая и плоскость
107. Линии и уравнения
108. Прямая линия
109. Уравнения прямой и плоскости в пространстве
110. Кривые второго порядка
111. Кривые и поверхности второго порядка
112. Числовые ряды
113. Степенные ряды
114. Ряды Фурье
115. Преобразование Фурье
116. Функциональные ряды
117. Функции многих переменных
118. Метод координат
119. Гармонический анализ
120. Вещественные числа
121. Предел последовательности
122. Аналитическая геометрия
123. Аналитическая геометрия на плоскости
124. Аналитическая геометрия в пространстве
125. Функции одной переменной
126. Высшая алгебра
127. Векторная алгебра
128. Векторный анализ
129. Векторы
130. Скалярное произведение векторов
131. Векторное произведение векторов
132. Операции над векторами
133. Непрерывность функций
134. Предел и непрерывность функций нескольких переменных
135. Предел и непрерывность функции одной переменной
136. Производные и дифференциалы функции одной переменной
137. Частные производные и дифференцируемость функций нескольких переменных
138. Дифференциальное исчисление функции одной переменной
139. Матрицы
140. Линейные и евклидовы пространства
141. Линейные отображения
142. Дифференциальные теоремы о среднем
143. Теория устойчивости дифференциальных уравнений
144. Функции комплексного переменного
145. Преобразование Лапласа
146. Теории поля
147. Операционное исчисление
148. Системы координат
149. Рациональная функция
150. Интегральное исчисление
151. Интегральное исчисление функций одной переменной
152. Дифференциальное исчисление функций нескольких переменных
153. Отношение в математике
154. Математическая логика
155. Графы в математике
156. Линейные пространства
157. Первообразная и неопределенный интеграл
158. Линейная функция
159. Выпуклые множества точек
160. Система координат