Оглавление:
Некоторые способы приближения функций:
При изучении функций применяются различные методы представления данной функции при помощи более простых функций, свойства которых являются известными.
Вопрос о том, какими «базовыми» функциями 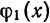 ,
,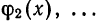 и какими выражениями от этих функций «аппроксимировать» данную функцию
и какими выражениями от этих функций «аппроксимировать» данную функцию 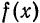 , зависит от свойств функции
, зависит от свойств функции 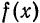 и от того, каким образом мы будем оценивать характер приближения, т. е. как будем
и от того, каким образом мы будем оценивать характер приближения, т. е. как будем
измерять «близость» функций.
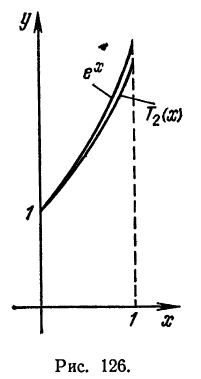
Так, например, при вычислении значений функции 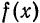 бывает удобно аппроксимировать ее при помощи многочленов
бывает удобно аппроксимировать ее при помощи многочленов  т. е. разложить функцию
т. е. разложить функцию 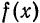 в степенной ряд:
в степенной ряд:
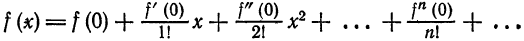
Различаются три основных способа приближения (аппроксимации) функций.
Локальное приближение — это такой вид приближения функции 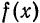 в окрестности некоторой точки
в окрестности некоторой точки 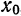 , при котором качество аппроксимации улучшается при переходе к точкам, близким к
, при котором качество аппроксимации улучшается при переходе к точкам, близким к 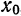 . Хорошим аппаратом для локального приближения функций
. Хорошим аппаратом для локального приближения функций
(имеющих производные любого порядка) служат ряды Тейлора.
На рис. 126 представлены графики функций 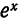 и
и 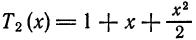 на отрезке
на отрезке 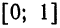 . Подсчеты показывают, что для различных значений x отрезка [0; 1] погрешность незначительна вблизи точки x = 0 и возрастает при удалении от нее:
. Подсчеты показывают, что для различных значений x отрезка [0; 1] погрешность незначительна вблизи точки x = 0 и возрастает при удалении от нее:
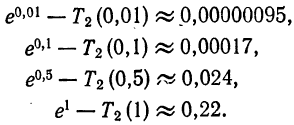
Равномерное приближение — это такой способ аппроксимации функции  с помощью другой функции
с помощью другой функции  на отрезке [a; b], при котором погрешности в любых точках этого отрезка имеют примерно один и тот же порядок малости.
на отрезке [a; b], при котором погрешности в любых точках этого отрезка имеют примерно один и тот же порядок малости.
Например, многочлен 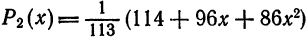 равномерно приближает функцию
равномерно приближает функцию 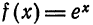 на отрезке [0; 1]. Подсчеты
на отрезке [0; 1]. Подсчеты
показывают, что
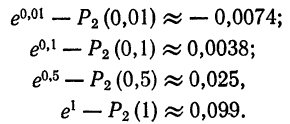
График многочлена 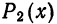 в масштабах рис. 126 практически не отличается от графика функции
в масштабах рис. 126 практически не отличается от графика функции 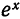 .
.
В случаях локальной и равномерной аппроксимаций в качестве
оценки «близости» двух функций  и
и  берется поточечное максимальное отклонение функций, т. е. максимум модуля разности значений этих функций во всех точках рассматриваемого отрезка:
берется поточечное максимальное отклонение функций, т. е. максимум модуля разности значений этих функций во всех точках рассматриваемого отрезка:
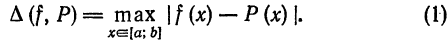
Аппроксимация такого вида называется поточечной или аппроксимацией в обычном смысле.
Приближение в среднем (приближение по среднему квадратическому отклонению). Если данная функция  имеет на отрезке [а ; b] резкие колебания, то равномерное (тем более локальное) приближение может оказаться малопригодным для представления
имеет на отрезке [а ; b] резкие колебания, то равномерное (тем более локальное) приближение может оказаться малопригодным для представления
такой функции на отрезке. На рис. 127 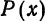 изображает лучшее равномерное приближение функции
изображает лучшее равномерное приближение функции  по сравнению с Q(x). Из этого рисунка видно, что функция Q(x), несмотря на то, что в некоторых точках и отличается сильно от
по сравнению с Q(x). Из этого рисунка видно, что функция Q(x), несмотря на то, что в некоторых точках и отличается сильно от 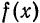 , может быть рассмотрена все же
, может быть рассмотрена все же
как лучшее приближение для  в среднем, на всем рассматриваемом отрезке для уточнения смысла приближения в среднем вводим понятие среднего квадратического отклонения функций.
в среднем, на всем рассматриваемом отрезке для уточнения смысла приближения в среднем вводим понятие среднего квадратического отклонения функций.
Определение:
Средним квадратическим отклонением функций  и Q(x) на отрезке [а ; b] называется величина
и Q(x) на отрезке [а ; b] называется величина
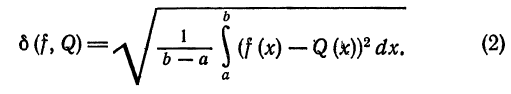
Нахождение наилучших приближений в среднем, т.е, оцененных по среднему квадратическому отклонению играет большую роль в-решении многих технических задач.
Пример:
Найти поточечное и среднее квадратиченское: отклонения функции 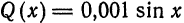 от функций
от функций 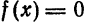 на отрезке
на отрезке 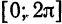
Решение:
По формуле (1) находим поточечное отклонение
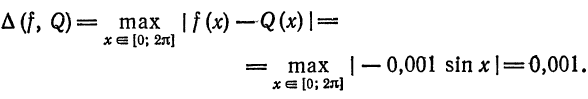
Среднее квадратическое отклонение вычислим по формуле (2):
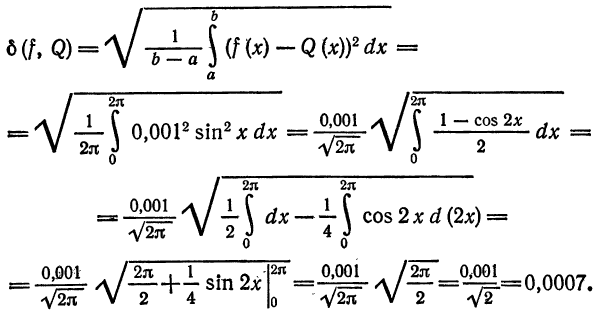
Для среднего квадратического отклонения и потокчечного отклонения двух функций на отрезке имеет место следующее утверждение: среднее квадратическое отклонение двух функций не превосходит поточечного отклонения на том же отрезке:
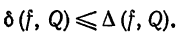
В самом деле,
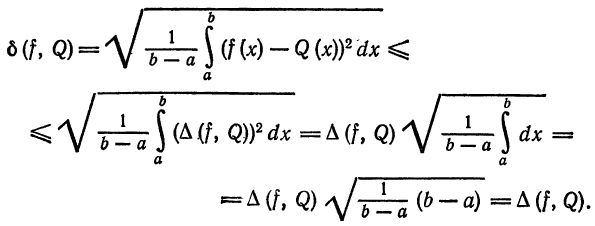
Ортогональные системы функций. Обобщенные многочлены Фурье
Часто в качестве базовых функций, при помощи которых строятся приближения для рассматриваемых функций, служат так называемые ортогональные системы функций.
Определение:
Система отличных от нулей функций
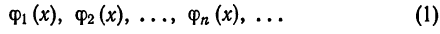
называется ортогональной на отрезке [a ; b], если для любых 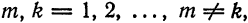 имеет место
имеет место
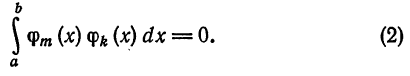
Если к тому же
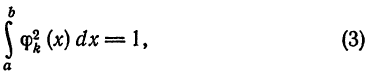
для всех 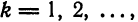 то система (1) называется ортонормированной.
то система (1) называется ортонормированной.
Любую ортогональную систему функций (1) можно ортонормировать. Для этого достаточно каждую функцию 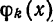 разделить на
разделить на
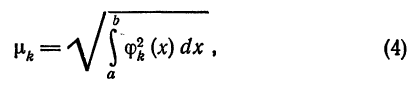
т. е. взять функции
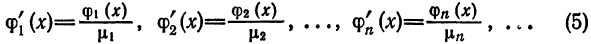
В самом деле, для функций 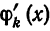 при
при 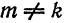 имеем:
имеем:
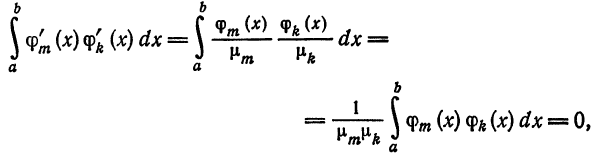
т. е. система (5) также ортогональна. Кроме того,
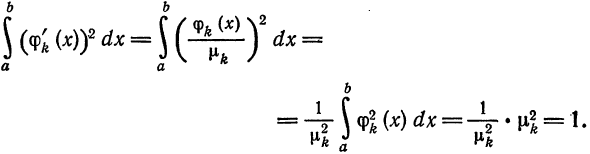
Следовательно, система (5) ортонормирована.
Числа 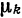 называются нормирующими множителями.
называются нормирующими множителями.
Пример:
Покажем, что система тригонометрических функций
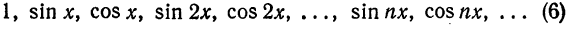
является ортогональной системой функций на отрезке 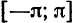
Для этого надо показать, что интегралы
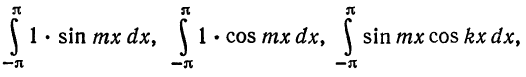
при любых 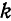 и m, а также интегралы
и m, а также интегралы
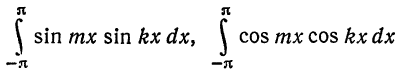
при 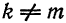 равны нулю. Имеем:
равны нулю. Имеем:
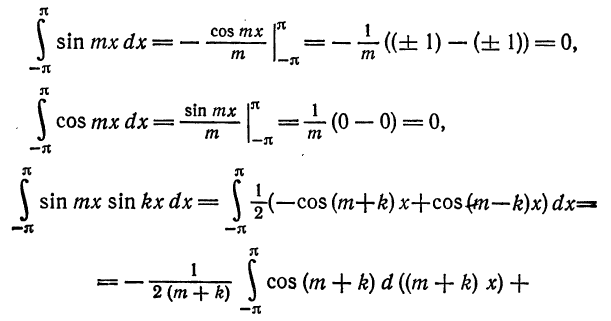
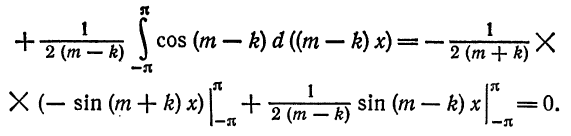
При помощи формул
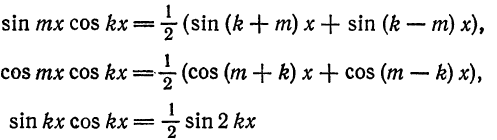
аналогично доказывается, что остальные интегралы также равны нулю.
Пример:
Можно показать, что следующие многочлены, известные под названием многочленов Лежандра, составляют ортогональную систему на отрезке 
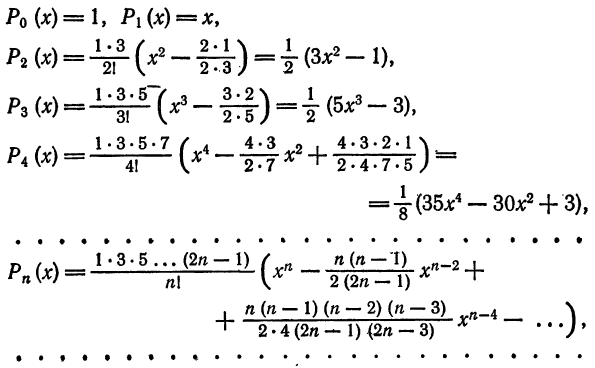
Легко видеть, что подсистема любой ортогональной системы функции также ортогональна на том же отрезке. В самом деле, если равенства (2) выполняются для всех функций системы, то они выполняются и для всех функций некоторой ее подсистемы. Учитывая это замечание и ортогональность системы (6), можем указать новые примеры ортогональных систем функций.
Пример:
Система функций
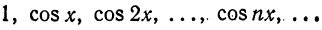
ортогональна на отрезке 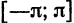 . Пример 4. Система функций
. Пример 4. Система функций

ортогональна на отрезке 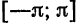 .
.
Определение:
Выражение
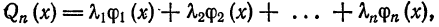
где  — числовые коэффициенты, называется обобщенным многочленом n-го порядка относительно системы функций
— числовые коэффициенты, называется обобщенным многочленом n-го порядка относительно системы функций 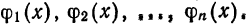
Например, выражение
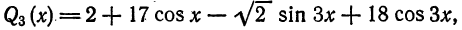
является обобщенным многочленом относительно системы (6).
Определение:
Пусть дана ортогональная система (1) на отрезке
[a ; b]. Величины
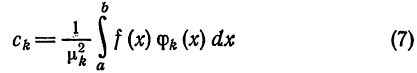
называются обобщенными коэффициентами Фурье для функции 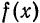 относительно системы ортогональных функций (1).
относительно системы ортогональных функций (1).
Если система (1) ортонормирована, то в силу
формул (4) и (3) 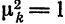 и тогда
и тогда
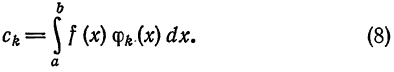
Определение:
Обобщенный многочлен
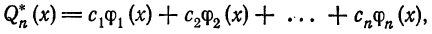
взятый с соответствующими, обобщенными коэффициентами Фурье, называется обобщенным многочленом Фурье n-го порядка для функции 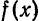 относительно, системы ортогональных функций (1),
относительно, системы ортогональных функций (1),
Пример:
Составить обобщенный многочлен Фурье второго порядка для функции 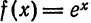 относительно системы многочленов Лежандра.
относительно системы многочленов Лежандра.
Решение. Пусть
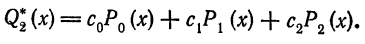
Имеем:
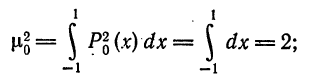
тогда
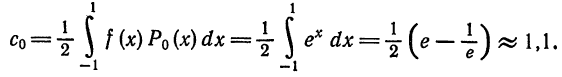
Далее,
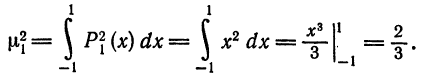
Следовательно,
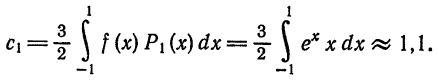
Аналогично,
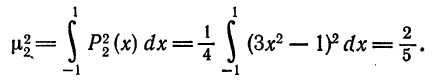
Следовательно,
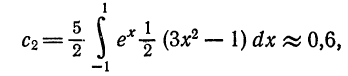
т. e.
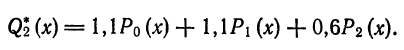
Роль обобщенных многочленов Фурье в теории приближения функций выражается в следующей теореме.
Теорема:
Для каждого n среди всех обобщенных многочленов n-го порядка
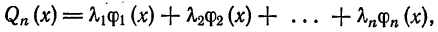
где
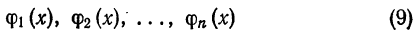
— ортонормированием система функций на [а; b], наилучшее среднее квадратическое приближение функции 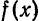 на [а; b] дает соответствующий обобщенный многочлен Фурье п-го порядка
на [а; b] дает соответствующий обобщенный многочлен Фурье п-го порядка
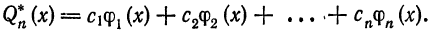
Доказательство:
Имеем:
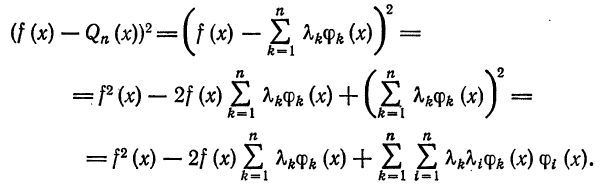
Интегрируя полученное равенство почленно и учитывая соотношения (2), (3) и (8), найдем:
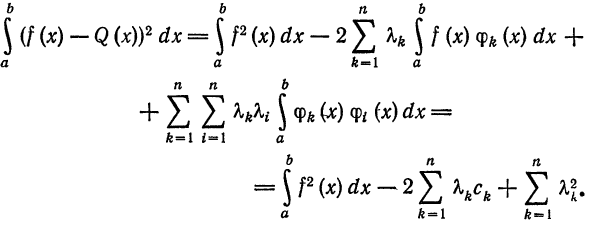
В полученном выражении добавим и вычтем 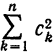 ; тогда
; тогда
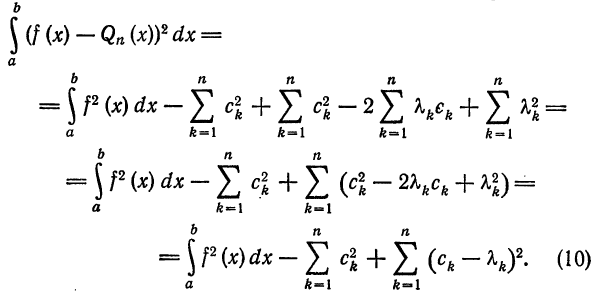
Первые два члена выражения из правой части равенства (10) не зависят от взятого обобщенного много члена 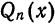 , а третий (неотрицательный) член
, а третий (неотрицательный) член 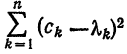 зависит от него. Это выражение, а следовательно, и интеграл
зависит от него. Это выражение, а следовательно, и интеграл 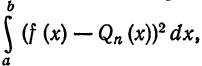 получит наименьшее значение тогда, когда
получит наименьшее значение тогда, когда 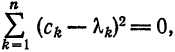 т. е. когда
т. е. когда  другими словами, когда
другими словами, когда 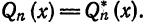 Теорема доказана.
Теорема доказана.
Аналогично доказывается эта теорема для любой ортогональной системы (1), только вместо равенства (8) надо будет использовать равенство (7).
Таким образцом, для функции 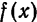 и ее обобщенного многочлена Фурье n-го порядка
и ее обобщенного многочлена Фурье n-го порядка 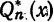 относительно системы ортогональных функций имеем:
относительно системы ортогональных функций имеем:
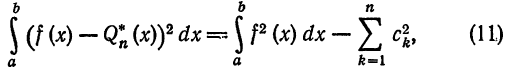
или
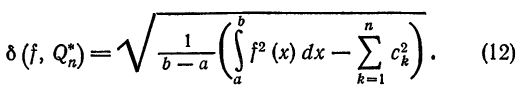
Обобщенные ряды Фурье
Пусть дана бесконечная ортогональная на отрезке [а; b] система функций
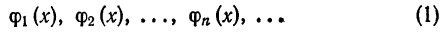
Определение:
Ряд
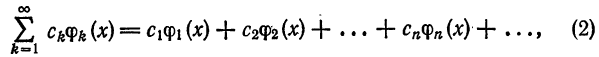
где
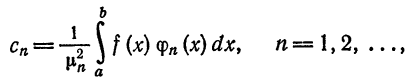
называется обобщенным рядом Фурье для функции 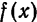 относительно системы (1) на отрезке [а; b].
относительно системы (1) на отрезке [а; b].
Обращаем внимание на то, что коэффициенты 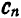 в (2) — это обобщенные коэффициенты Фурье, которые вычисляются по формулам (7) § 2.
в (2) — это обобщенные коэффициенты Фурье, которые вычисляются по формулам (7) § 2.
Таким образом, при заданной системе ортогональных функций каждая функция 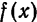 порождает вполне определенный обобщенный ряд Фурье (2). В этом смысле будем писать
порождает вполне определенный обобщенный ряд Фурье (2). В этом смысле будем писать
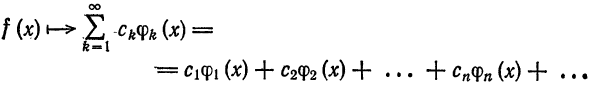
Частичные суммы ряда (2) совпадают с обобщенными многочленами Фурье 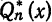 y которые, как мы знаем, дают наилучшее приближение в среднем к
y которые, как мы знаем, дают наилучшее приближение в среднем к 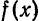 .
.
Из формулы (12) §2 видно, что при возрастании n среднее квадратическое отклонение 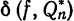 , вообще говоря, убывает.
, вообще говоря, убывает.
Определение:
Обобщенный ряд Фурье (2) называется сходящимся в среднем к функции 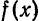 , если
, если 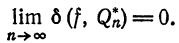
Из формулы (11) § 2 видно, что необходимым и достаточным условием сходимости в среднем ряда (2) к порождающей функции 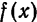 является выполнение условия
является выполнение условия
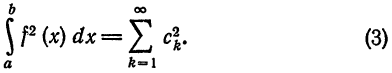
Это равенство известно под названием равенства Ляпунова — Парсеваля или уравнения замкнутости. Равенство Ляпунова — Парсеваля имеет место, в частности, для тригонометрических ортогональных систем из примеров 1, 3, 4 § 2 и любой ограниченной на [а; b] функции 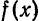 с конечным числом точек разрыва первого
с конечным числом точек разрыва первого
рода. В § 1 мы показали, что среднее квадратическое отклонение 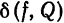 не превосходит поточечного отклонения
не превосходит поточечного отклонения 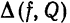 , т. е.
, т. е. 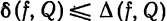 . Отсюда следует, что если обобщенный ряд Фурье (2) сходится в обычном смысле (поточечно) к порождающей функции
. Отсюда следует, что если обобщенный ряд Фурье (2) сходится в обычном смысле (поточечно) к порождающей функции 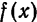 , то он сходится к
, то он сходится к 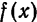 и в среднем, т. е.
и в среднем, т. е.
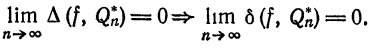
Обратное утверждение, вообще говоря, не имеет места, так как ряд (2) может сходиться в среднем к функции 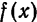 , но не сходиться поточечно. Следовательно, для поточечной сходимости требуется выполнение более сильных условий, чем для сходимости в среднем.
, но не сходиться поточечно. Следовательно, для поточечной сходимости требуется выполнение более сильных условий, чем для сходимости в среднем.
Во многих инженерно-технических приложениях основную ценность представляют именно приближения в среднем для рассматриваемых функций. Аппаратом для получения таких приближений служат обобщенные ряды Фурье и их частичные суммы — обобщенные
многочлены Фурье.
Докажем теорему об единственности представления функции в виде обобщенного ряда.
Теорема:
Если функция 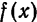 представляется в виде обобщенного ряда по ортогональной системе функций
представляется в виде обобщенного ряда по ортогональной системе функций
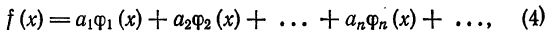
то этот ряд совпадает с обобщенным рядом Фурье для функции 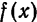 .
.
Докажем теорему в предположениях, что выражение (4) можно почленно интегрировать.
Для определения коэффициента 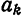 умножим (4) на
умножим (4) на 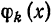 :
:
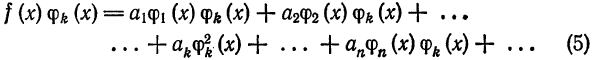
Интегрируя (5) получим
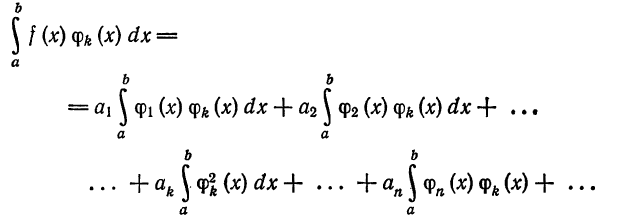
Так как система  ортогональна, то
ортогональна, то 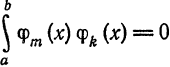 при
при 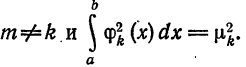
Следовательно,
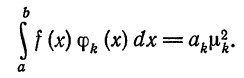
Отсюда
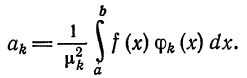
Учитывая формулу (7) § 2, имеем 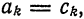 т. е. ряд (4) совпадает с обобщенным рядом Фурье. Изложенная в этом параграфе общая теория применима к любой конкретной системе ортогональных
т. е. ряд (4) совпадает с обобщенным рядом Фурье. Изложенная в этом параграфе общая теория применима к любой конкретной системе ортогональных
функций. В частности, если в качестве «базовых» функций взять тригонометрическую систему из примера 1 § 2, получим разложение (на отрезке 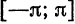 ) функции по синусам и косинусам; если взять систему функций из примера 2 § 2, получим разложение (на [—1; 1])
) функции по синусам и косинусам; если взять систему функций из примера 2 § 2, получим разложение (на [—1; 1])
функции по многочленам Лежандра; если взять систему функций примеров 3 и 4 § 2, то получим соответственно разложение (на 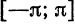 ) функции только по косинусам, или только по синусам. Понятно, что можно разлагать функции и по другим ортогональным системам.
) функции только по косинусам, или только по синусам. Понятно, что можно разлагать функции и по другим ортогональным системам.
Разложение функций в ряды Фурье по тригонометрическим системам играет большую роль как в
математике, так и в ее приложениях (особенно в электротехнике), поэтому мы остановимся на них подробнее.
Тригонометрические ряды Фурье
Разложение функций в ряд Фурье на отрезке 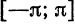 . Во многих технических задачах возникает необходимость представлять произвольные функции через простейшие периодические функции. Такие задачи часто возникают в электротехнике: представить ток,
. Во многих технических задачах возникает необходимость представлять произвольные функции через простейшие периодические функции. Такие задачи часто возникают в электротехнике: представить ток,
изменяющийся по сложному закону  , через простые
, через простые
синусоидальные токи 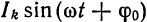 . Математическим
. Математическим
аппаратом для исследования таких задач служат ряды Фурье относительно тригонометрической системы ортогональных функций на отрезке 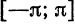 (пример 1 § 2):
(пример 1 § 2):
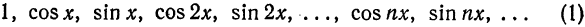
Обобщенные многочлену Фурье, обобщенные коэффициенты Фурье, обобщенные ряды Фурье для функции 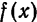 относительно системы (1) называются соответственно просто многочленами Фурье, коэффициентами Фурье, рядами Фурье.
относительно системы (1) называются соответственно просто многочленами Фурье, коэффициентами Фурье, рядами Фурье.
Многочленом Фурье (или тригонометрическим многочленом) n-го порядка функции 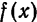 называется тригонометрический многочлен вида
называется тригонометрический многочлен вида
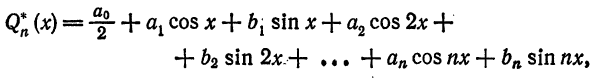
где 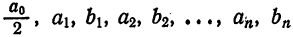 — коэффициенты Фурье. Вычислим коэффициенты Фурье в соответствии с формулой (7) § 2. Имеем
— коэффициенты Фурье. Вычислим коэффициенты Фурье в соответствии с формулой (7) § 2. Имеем
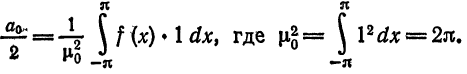
Следовательно,  или
или
Для коэффициентов  обозначим соответствующий нормирующий множитель через
обозначим соответствующий нормирующий множитель через  и по формуле (4)
и по формуле (4)
§ 2 получим
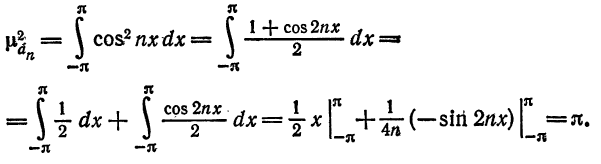
Следовательно,
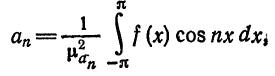
или
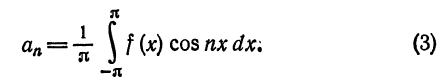
Аналогично показывается, что 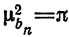 , следовательно,
, следовательно,
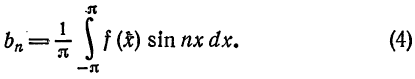
Таким образом, каждой функции 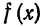 на отрезке
на отрезке 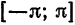 сопоставляется ряд Фурье
сопоставляется ряд Фурье
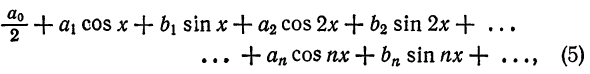
т. е.
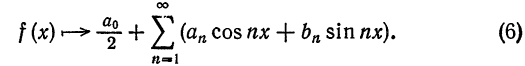
Определение:
Ряд
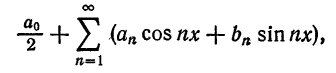
где
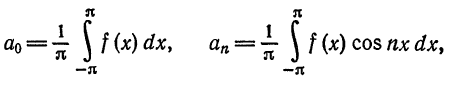
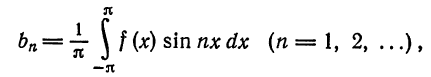
называется рядом Фурье (или тригонометрическим рядом) для функции 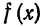 на отрезке
на отрезке 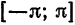 .
.
Пример:
Составить ряд Фурье для функции 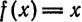 на отрезке
на отрезке 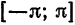
Решение По формуле (2) имеем
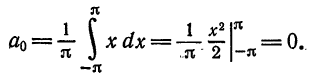
По формуле (3); получаем
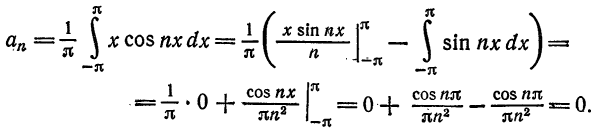
Далее, по формуле (4)
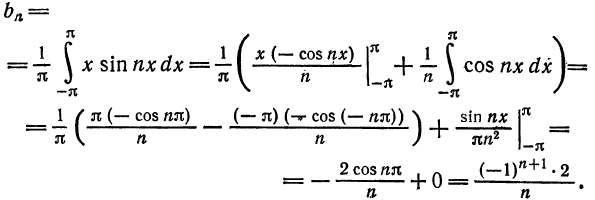
Следовательно,
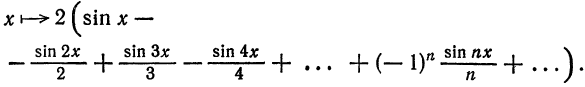
Ряд (5) может сходиться к функции 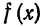 в среднем или поточечно (в обычном смысле) Так как равными считаются функции, значения которых равны в каждой точке, то в (6) стрелка может быть заменена знаком
в среднем или поточечно (в обычном смысле) Так как равными считаются функции, значения которых равны в каждой точке, то в (6) стрелка может быть заменена знаком
равенства только в том случае, если ряд сходится поточечно к функции  на всем рассматриваемом промежутке.
на всем рассматриваемом промежутке.
Для формулировки условий сходимости ряда (5) к функции введем понятие кусочно-непрерывных функций.
Функция  называется кусочно-непрерывной на отрезке [а; b], если она имеет лишь конечное число точек разрыва первого рода (см. рис. 128, на котором жирными точками обозначено значение функции в точках разрыва).
называется кусочно-непрерывной на отрезке [а; b], если она имеет лишь конечное число точек разрыва первого рода (см. рис. 128, на котором жирными точками обозначено значение функции в точках разрыва).
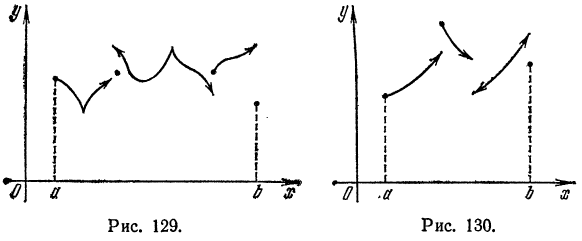
Функция 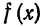 называется кусочно-дифференцируемой или кусочно-гладкой на отрезке [а; b], если ее производная является кусочно-непрерывной функцией на [а; b] (см. рис. 129).
называется кусочно-дифференцируемой или кусочно-гладкой на отрезке [а; b], если ее производная является кусочно-непрерывной функцией на [а; b] (см. рис. 129).
Приводим достаточное условие сходимости в среднем ряда Фурье к порождающей функции.
Теорема:
Ряд Фурье (5) сходится в среднем к порождающей функции 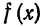 , если функция
, если функция 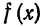 кусочно-непрерывна на отрезке
кусочно-непрерывна на отрезке 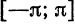 .
.
Следующие теоремы Дирихле представляют собой достаточные условия поточечной сходимости ряда к порождающей функции, за исключением, быть может, точек разрыва и границ отрезка.
Теорема:
Если функция 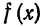 кусочно-дифференцируема на отрезке
кусочно-дифференцируема на отрезке  , то ряд Фурье функции
, то ряд Фурье функции  сходится во всех точках
сходится во всех точках 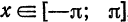 , причем в точках непрерывности функции
, причем в точках непрерывности функции 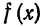 его сумма равна
его сумма равна 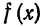 в точках разрыва функции
в точках разрыва функции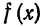 его сумма равна
его сумма равна 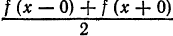 на концах отрезка его сумма равна
на концах отрезка его сумма равна 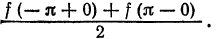
Функция 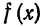 называется кусочно-монотонной на отрезке [а; b] если его можно разбить на конечное число интервалов так, что на каждом из интервалов функция монотонна (см. рис. 130).
называется кусочно-монотонной на отрезке [а; b] если его можно разбить на конечное число интервалов так, что на каждом из интервалов функция монотонна (см. рис. 130).
Теорема:
Если функция 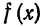 кусочно-монотонна и ограничена на отрезке
кусочно-монотонна и ограничена на отрезке 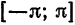 , то ряд Фурье для этой функции сходится во всех точках
, то ряд Фурье для этой функции сходится во всех точках  , причем в точках непрерывности его сумма равна
, причем в точках непрерывности его сумма равна 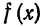 , в точках разрыва функции
, в точках разрыва функции 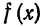 его сумма равна
его сумма равна 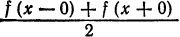 а на концах отрезка его сумма равна
а на концах отрезка его сумма равна 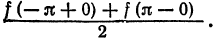
Сформулированные теоремы мы принимаем без доказательства.
Таким образом, если функция 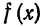 кусочно-дифференцируема или ограничена и кусочно-монотонна на отрезке
кусочно-дифференцируема или ограничена и кусочно-монотонна на отрезке 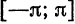 , то на этом отрезке имеет место разложение
, то на этом отрезке имеет место разложение
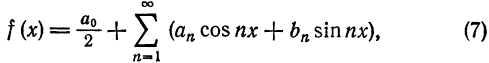
причем коэффициенты 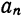 и
и 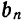 вычисляются по формулам (2), (3) и (4). Равенство (7) может нарушиться только в точках разрыва функции
вычисляются по формулам (2), (3) и (4). Равенство (7) может нарушиться только в точках разрыва функции 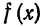 и на концах отрезка
и на концах отрезка 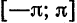 .
.
Пример:
Так как функция  дифференцируема на отрезке
дифференцируема на отрезке  , то из примера 1 получаем разложение
, то из примера 1 получаем разложение
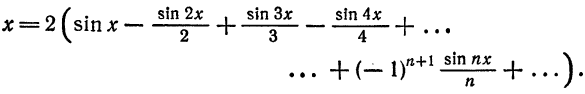
Заметим, что значение полученного ряда в концах интервала равно
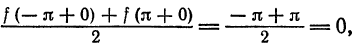
следовательно, сумма ряда равна значению порождающей функции 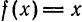 для всех точек интервала
для всех точек интервала 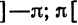
Заметим, что.большинство функций, которые встречаются в математике и ее приближениях, являются
кусочно-дифференцируемыми, а часто просто дифференцируемыми функциями, поэтому для них ряд Фурье сходится к порождающей функции в обычном смысле.
Скорость сходимости ряда Фурье к порождающей функции зависит от свойств данной функции. Оказывается, что чем выше «степень гладкости» данной функции, т. е. чем более высокого порядка непрерывные производные она имеет, тем больше скорость сходимости ее ряда Фурье.
Приводим, также без доказательства, следующую оценку скорости сходимости ряда Фурье.
Теорема:
Если 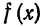 — непрерывная функция имеющая непрерывные производные до (т — 1)—го порядка включительно, а производная m-го порядка
— непрерывная функция имеющая непрерывные производные до (т — 1)—го порядка включительно, а производная m-го порядка 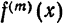 кусочно-непрерывна на
кусочно-непрерывна на 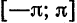 , то
, то
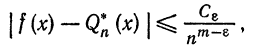
где 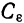 — некоторая постоянная, а
— некоторая постоянная, а 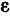 — сколько угодно малое действительное число.
— сколько угодно малое действительное число.
Разложение функций в ряд Фурье на произвольном отрезке
Пусть функция 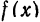 определена на отрезке
определена на отрезке 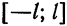 . Тогда подстановкой
. Тогда подстановкой 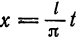 переходим к функции
переходим к функции 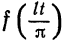 , которая определена на отрезке
, которая определена на отрезке 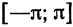 . В самом деле, если
. В самом деле, если 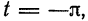 то
то 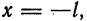 если
если 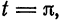 то
то  и при
и при 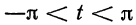 имеем
имеем 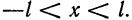
Предположим, например, что исходная функция 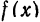 кусочно-дифференцируема на отрезке
кусочно-дифференцируема на отрезке 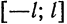 . Тогда и полученная функция
. Тогда и полученная функция 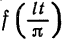 на отрезке
на отрезке 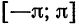 будет кусочно-дифференцируемой. Разлагая функцию
будет кусочно-дифференцируемой. Разлагая функцию 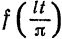 в ряд Фурье на отрезке
в ряд Фурье на отрезке 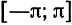 , получим (всюду, за исключением, быть может, точек разрыва функции и
, получим (всюду, за исключением, быть может, точек разрыва функции и
концов отрезка  ):
):
где
Перейдем теперь к переменной  Имеем
Имеем 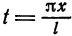 ,
, 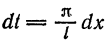
и при этом 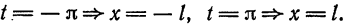
Итак,
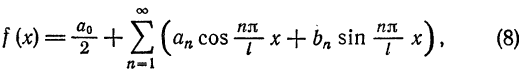
где
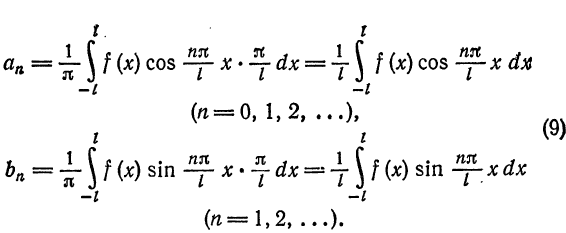
Таким образом, функцию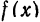 , определенную на отрезке
, определенную на отрезке 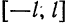 , можно разложить в ряд Фурье (8), коэффициенты которого вычисляются по формулам (9), Равенство (8) может нарушиться лишь в точках разрыва функции и на концах отрезка
, можно разложить в ряд Фурье (8), коэффициенты которого вычисляются по формулам (9), Равенство (8) может нарушиться лишь в точках разрыва функции и на концах отрезка 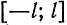 .
.
Пример:
Разложить функцию 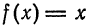 на интервале
на интервале 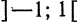 . в ряд Фурье. Решение. По формуле (8) при
. в ряд Фурье. Решение. По формуле (8) при 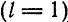 имеем
имеем
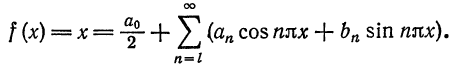
Вычислим коэффициенты ряда по формулам (9):
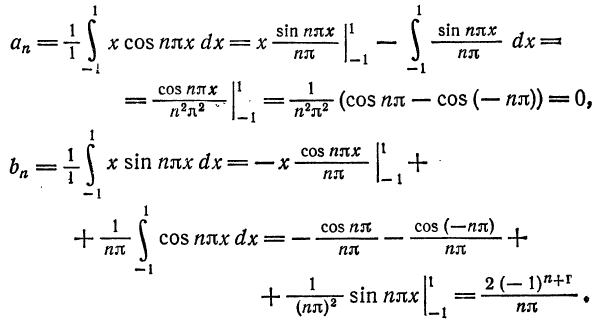
Таким образом,
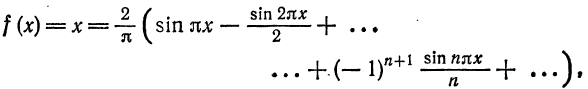
для 
Разложение в ряд Фурье периодических функций
Если данная функция  является периодической с периодом
является периодической с периодом 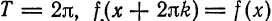 , и для нее имеет место разложение (7) в ряд Фурье на отрезке
, и для нее имеет место разложение (7) в ряд Фурье на отрезке 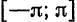 , то оно справедливо и на всей прямой
, то оно справедливо и на всей прямой 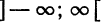 .
.
В самом деле; сумма тригонометрического ряда Фурье
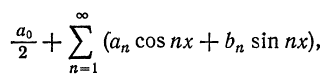
если она существует, является периодической функцией с периодом 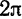 . Это следует из того, что
. Это следует из того, что
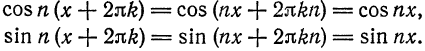
Аналогично, если функция 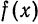 имеет период T = 2l,
имеет период T = 2l, 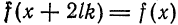 , то разложение (8) имеет место для всей прямой.
, то разложение (8) имеет место для всей прямой.
Так как для периодической функции периода T интегралы по любым отрезкам длины T равны между собой
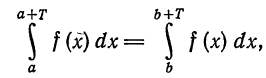
то для вычисления коэффициентов Фурье периодической функции можно интегрировать по любому отрезку
длины T. Так, если функция имеет период  , то в формулах
, то в формулах
(2) — (4) (в формулах (9)) вместо 
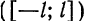 можно взять интегралы по отрезку
можно взять интегралы по отрезку 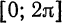
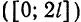
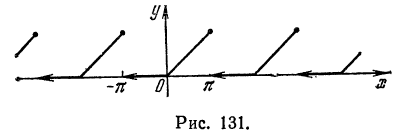
Пример:
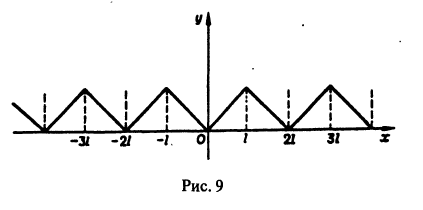
Разложить в ряд Фурье периодическую функцию 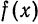 , определенную следующим образом:
, определенную следующим образом:
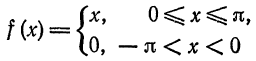
и 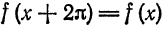 (рис. 131).
(рис. 131).
Решение:
Данная функция кусочно-дифференцируема, следовательно,
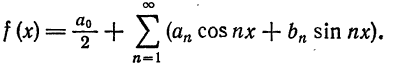
При этом
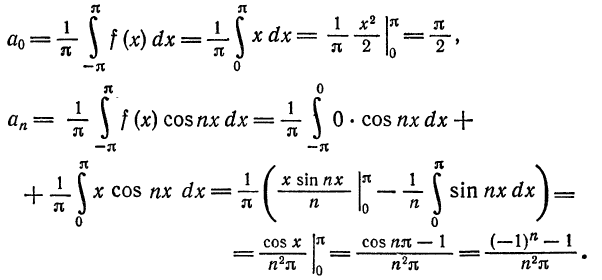
Отсюда 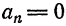 при n четном и
при n четном и 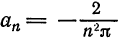 при n нечетном.
при n нечетном.
Аналогичными вычислениями находим
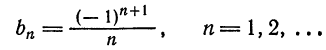
Следовательно,
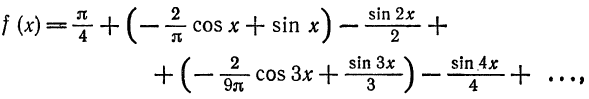
или
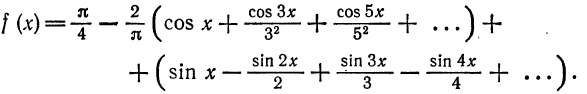
В точках 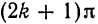 данная функция терпит разрыв, следовательно, в этих точках ряд принимает значение, отличное от значения функции. Так, при
данная функция терпит разрыв, следовательно, в этих точках ряд принимает значение, отличное от значения функции. Так, при 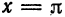 функция
функция 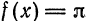 , в то время как сумма ряда равна
, в то время как сумма ряда равна 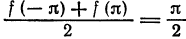 при
при 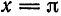 получаем
получаем
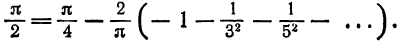
Отсюда
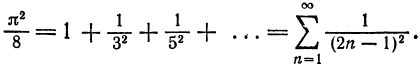
О том, что ряд  сходится можно определить при помощи признаков сходимости числовых рядов (например, интегрального). Здесь же мы в качестве побочного результата получили сумму этого ряда.
сходится можно определить при помощи признаков сходимости числовых рядов (например, интегрального). Здесь же мы в качестве побочного результата получили сумму этого ряда.
Разложение в ряд Фурье четных и нечетных функций
Сделаем два замечания, необходимых для дальнейшего.
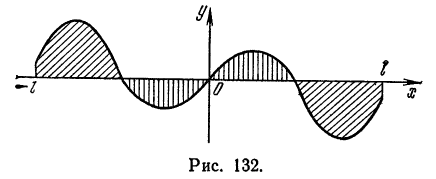
1) Рассмотрим нечетную на отрезке  функцию
функцию  , т. е. такую, что
, т. е. такую, что  .
.
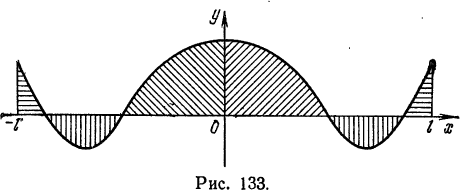
Из геометрических соображений ясно (см., например, рис. 132), что
2) Если функция  , четная, т. е.
, четная, т. е.  , то, очевидно (см., например, рис. 133),
, то, очевидно (см., например, рис. 133),
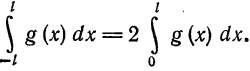
Рассмотрим разложение в ряд Фурье нечетных функций.
Пусть  — нечетная, кусочно-дифференцируемая функция на отрезке
— нечетная, кусочно-дифференцируемая функция на отрезке  . Следовательно, для
. Следовательно, для  имеет место разложение (7). Так как в этом случае
имеет место разложение (7). Так как в этом случае 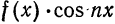 — нечетная функция:
— нечетная функция:
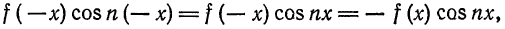
а произведение 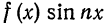 является четной функцией:
является четной функцией:
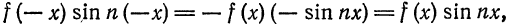
то для коэффициентов ряда Фурье получим:
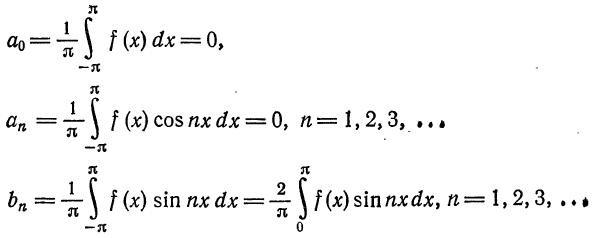
Отсюда следует, что разложение нечетной функция 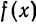 в ряд Фурье имеет вид
в ряд Фурье имеет вид
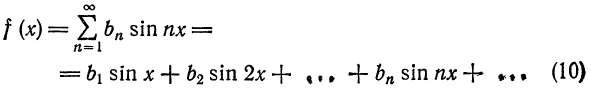
Аналогично, для четных функций 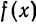 , получаем разложение
, получаем разложение
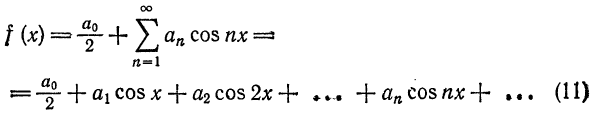
Таким образом, если функция f(x)] нечетная, то ее ряд Фурье содержит только члены с синусами; если 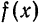 четная, то ее ряд Фурье содержит свободный член и только члены с косинусами. Подобные разложения можно получить для четных и нечетных функций, определенных на отрезке
четная, то ее ряд Фурье содержит свободный член и только члены с косинусами. Подобные разложения можно получить для четных и нечетных функций, определенных на отрезке 
Разложение произвольных функций в ряды Фурье
Пусть дана кусочно-дифференцируемая функция  определенная на отрезке
определенная на отрезке 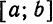 . Перенеся начало координат в середину отрезка
. Перенеся начало координат в середину отрезка 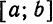 , мы получим новую систему координат, относительно которой область определения функции
, мы получим новую систему координат, относительно которой область определения функции 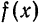 имеет вид
имеет вид 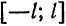 , где
, где 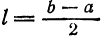 Следовательно, для функции
Следовательно, для функции 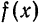 можно получить разложение в ряд Фурье вида (8).
можно получить разложение в ряд Фурье вида (8).
Если перенести начало координат в точку 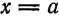 , то область определения функции
, то область определения функции 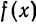 . будет иметь вид
. будет иметь вид 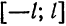 , где
, где 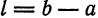 . Продолжим «нечетным образом» функцию
. Продолжим «нечетным образом» функцию 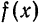 на отрезок
на отрезок 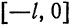 , т. е. определим функцию
, т. е. определим функцию
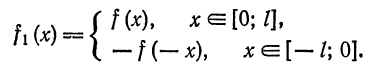
Функция 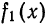 является нечетной, следовательно,она разлагается в ряд Фурье только по синусам. Рассматривая разложение функции
является нечетной, следовательно,она разлагается в ряд Фурье только по синусам. Рассматривая разложение функции 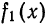 только на отрезке
только на отрезке 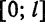 , получим разложение для данной функции
, получим разложение для данной функции  в ряд Фурье только по синусам.
в ряд Фурье только по синусам.
Продолжая «четным образом» функцию  на отрезок
на отрезок  , т. е. введя в рассмотрение функцию
, т. е. введя в рассмотрение функцию
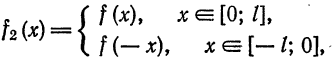
которая является четной, аналогично получим разложение данной функции в ряд Фурье только по косинусам.
Таким образом, любая функция  , определенная на произвольном отрезке
, определенная на произвольном отрезке  и удовлетворяющая на этом отрезке условиям теоремы 2 или теоремы 3, может быть разложена в ряд Фурье по синусам и косинусам, а также только по синусам, или только по косинусам.
и удовлетворяющая на этом отрезке условиям теоремы 2 или теоремы 3, может быть разложена в ряд Фурье по синусам и косинусам, а также только по синусам, или только по косинусам.
Заметим, что возможность таких разложений была указана в § 3 из общих соображений относительно обобщенных рядов Фурье.
Практический гармонический анализ
Теория разложения функций в тригонометрические ряды Фурье называется также гармоническим анализом. Под практическим гармоническим анализом понимается представление конкретных функций, возникающих при решении практических задач, в виде ряда
Фурье, коэффициенты которого, как правило, вычисляются приближенным образом. В большинстве случаев функции, описывающие исследуемый процесс, даны в виде экспериментальных данных или графиков, которые вычерчиваются самопишущим прибором. В таких случаях коэффициенты Фурье вычисляются при помощи приближенных методов интегрирования. Для приближенного вычисления интегралов
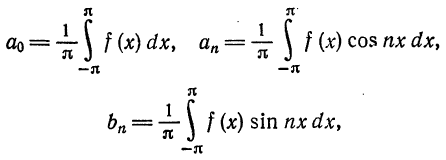
применяется какой-либо из методов численного интегрирования. Применим, например, формулу прямоугольников (1) § 8 гл. 8. Разделим отрезок  на n равных частей с помощью точек
на n равных частей с помощью точек 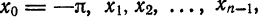 при этом шаг деления равен
при этом шаг деления равен 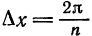 Обозначим через
Обозначим через  значения функции
значения функции 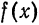 в точках деления. Тогда
в точках деления. Тогда
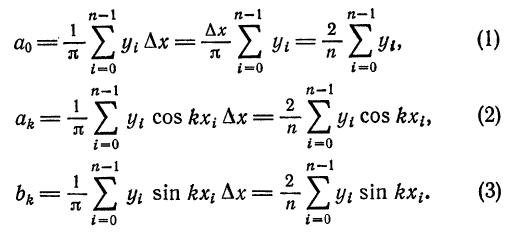
Для облегчения ручных вычислений коэффициентов Фурье разработаны различные схемы и шаблоны, в более сложных случаях вычисления проводятся на ЭВМ
Пример:
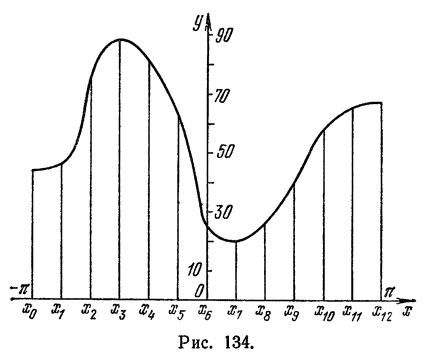
Найти тригонометрический многочлен второго порядка для функции, заданной графически на рис. 134.
Решение:
Делим отрезок 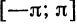 на 12 частей. Следовательно, шаг деления равен
на 12 частей. Следовательно, шаг деления равен 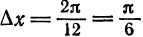 Из графика функции непосредственным измерением ординат находим:
Из графика функции непосредственным измерением ординат находим:
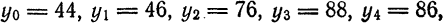
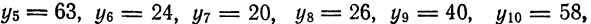
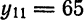
Тогда по формуле (1)
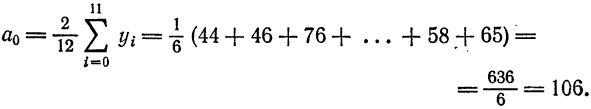
По формуле (2) имеем
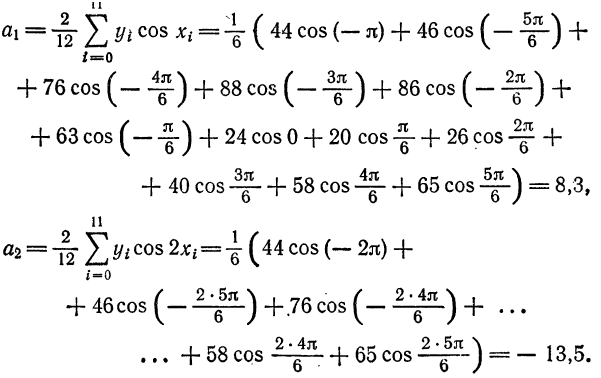
По формуле (3) вычислим 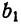 и
и 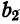 :
:
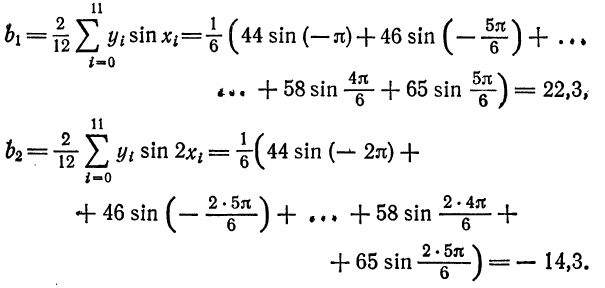
Таким образом,
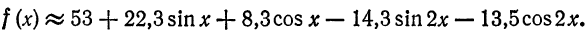
Если функция  задана аналитически, то для вычисления коэффициентов Фурье часто могут быть применены методы точного интегрирования (см. примеры 1, 2, 3,4 §4).
задана аналитически, то для вычисления коэффициентов Фурье часто могут быть применены методы точного интегрирования (см. примеры 1, 2, 3,4 §4).
В электротехнике и радиотехнике нередко встречаются периодические функции, имеющие точки разрыва первого рода внутри отрезка  и на его границах. Рассмотрим некоторые примеры разложения в ряд Фурье таких функций.
и на его границах. Рассмотрим некоторые примеры разложения в ряд Фурье таких функций.
Пример:
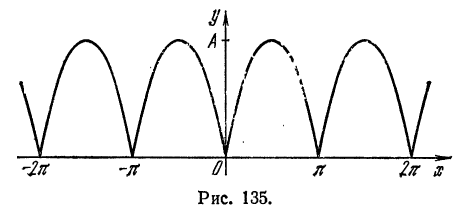
Разложить в ряд Фурье кривую двухполупериодного выпрямленного синусоидального тока
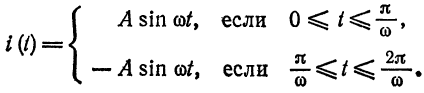
Решение:
Данная функция может быть представлена в виде 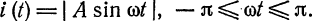 Заменяем
Заменяем 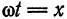 и распространяем функцию периодически на всю прямую (рис. 135). Тогда
и распространяем функцию периодически на всю прямую (рис. 135). Тогда 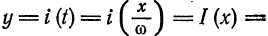
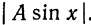 Так как полученная функция
Так как полученная функция 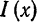 четная, то
четная, то 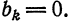 Вычислим коэффициенты
Вычислим коэффициенты 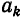 :
:
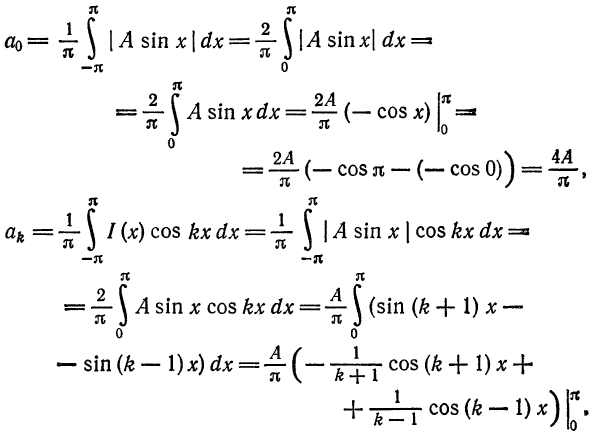
При 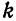 нечетном
нечетном 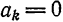 ; при
; при 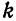 четном
четном 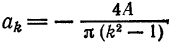 Функция
Функция 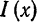 разлагается в ряд Фурье
разлагается в ряд Фурье
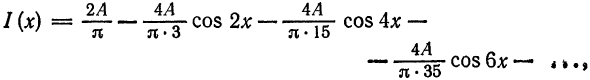
а исходная функция, следовательно, — в ряд Фурье
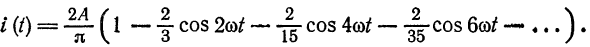
Пример:
Разложить в ряд Фурье кривую однополупериодного выпрямленного синусоидального тока
Решение:
Положим 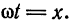 Тогда
Тогда
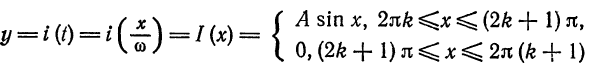
(рис. 136). Имеем:
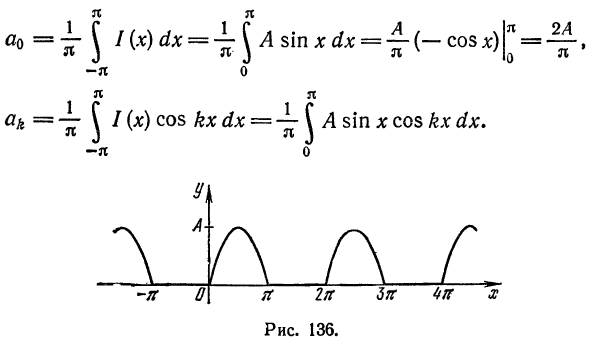
Из примера 2 известно, что при 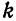 нечетном
нечетном 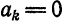 , при
, при 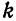 четном
четном 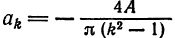 Далее,
Далее,
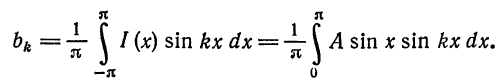
Если 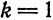 , то
, то
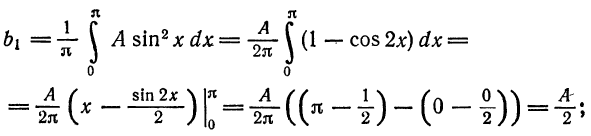
если 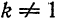 , то
, то 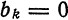 .
.
Функция 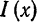 разлагается в ряд Фурье:
разлагается в ряд Фурье:
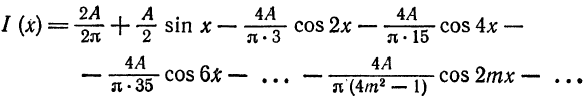
Следовательно,
Пример:
Разложить в ряд Фурье периодическую функцию 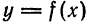 с периодом
с периодом 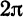 , которая определена следующим образом (рис. 137):
, которая определена следующим образом (рис. 137):

Решение:
Функция 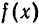 удовлетворяет условиям теорем Дирихле и, значит, разлагается в ряд Фурье.
удовлетворяет условиям теорем Дирихле и, значит, разлагается в ряд Фурье.
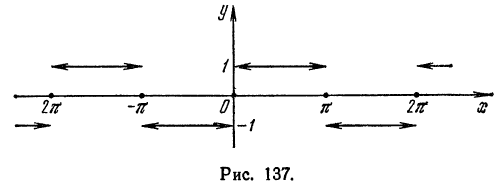
Вычислим ее коэффициенты Фурье. Так как 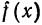 нечетна, то
нечетна, то 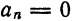 для всех n. Далее,
для всех n. Далее,
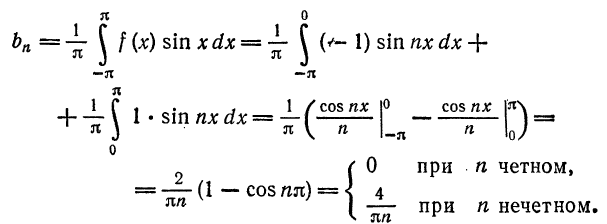
Следовательно,
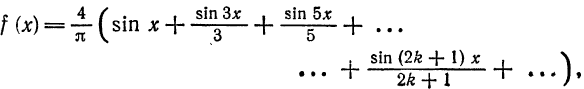
где 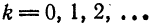
Пример:
Разложить в ряд Фурье периодическую функцию 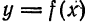 с периодом 2l, заданную на отрезке [—l;l] формулой
с периодом 2l, заданную на отрезке [—l;l] формулой 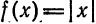
(рис. 138).
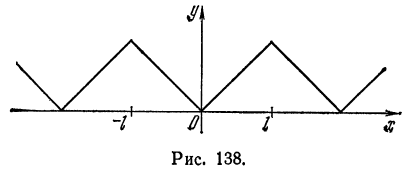
Решение:
Так как рассматриваемая функция четная, то 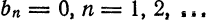 Далее,
Далее,
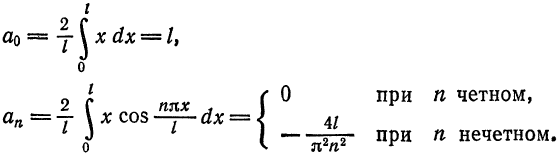
Следовательно, на отрезке 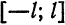
Пример:
Разложить функцию 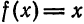 на отрезке
на отрезке 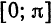 в ряд по синусам.
в ряд по синусам.
Решение:
Продолжая эту функцию нечетным образом на 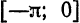 , будем иметь
, будем иметь 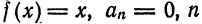
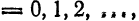 и
и
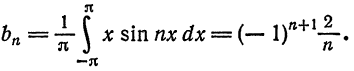
Следовательно, во всех точках промежутка 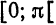 имеет место разложение:
имеет место разложение:
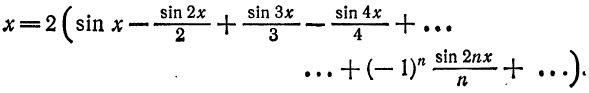
В точке 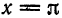 равенство нарушается: значение функции равно
равенство нарушается: значение функции равно 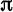 , а сумма ряда — 0.
, а сумма ряда — 0.
Пример:
Разложить функцию 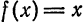 на отрезке
на отрезке 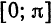 в ряд по косинусам.
в ряд по косинусам.
Решение:
Продолжая эту функцию четным образом на 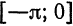 , получим
, получим 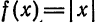 (см. пример 5). Имеем:
(см. пример 5). Имеем:
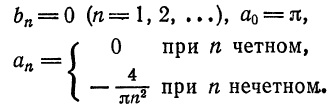
Следовательно, на отрезке 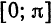
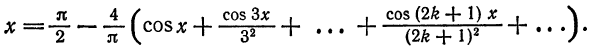
Дополнение к рядам Фурье










Смотрите также:
Решение задач по математическому анализу
Решение рядов Фурье
Тригонометрические ряды
Определение:
Функция f(x), определенная на неограниченном множестве D, называется периодической, если существует число 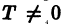 такое, что для каждого
такое, что для каждого 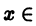 D выполняется условие
D выполняется условие
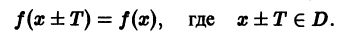
Наименьшее из таких чисел Т называется периодом функции f(х).
Пример:
Функция
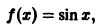
определенная на интервале 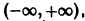 является периодической, так как существует число
является периодической, так как существует число  такое, что для всех
такое, что для всех 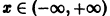 выполняется условие
выполняется условие
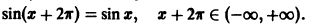
Таким образом, функция sinx имеет период 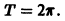 То же самое относится и к функции
То же самое относится и к функции
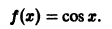
Пример:
Функция
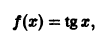
определенная на множестве D чисел
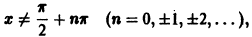
является периодической, так как существует число  , а именно, Т =
, а именно, Т = 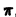 , такое, что для
, такое, что для 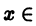 D имеем
D имеем 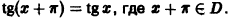
Определение:
Функциональный ряд вида
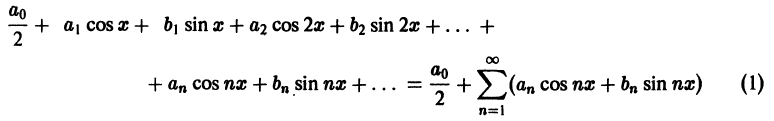
называется тригонометрическим рядом, а постоянные 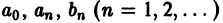 называются коэффициентами тригонометрического ряда (1).
называются коэффициентами тригонометрического ряда (1).
Частичные суммы Sn(x) тригонометрического ряда (1) являются линейными комбинациями функций из системы функций

которая называется тригонометрической системой. Так как членами этого ряда являются периодические функции с периодом 2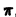 , то в случае сходимости ряда (1) его сумма S(х) будет периодической функцией с периодом Т = 2
, то в случае сходимости ряда (1) его сумма S(х) будет периодической функцией с периодом Т = 2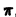 :
:
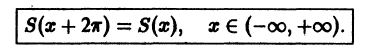
Определение:
Разложить периодическую функцию f(x) с периодом Т = 2 в тригонометрический ряд (1) означает найти сходящийся тригонометрический ряд, сумма которого равна функции f(х).
в тригонометрический ряд (1) означает найти сходящийся тригонометрический ряд, сумма которого равна функции f(х).
Ортогональность тригонометрической системы
Определение:
Функции f(х) и g(х), непрерывные на отрезке [а, b], называются ортогональными на этом отрезке, если выполнено условие
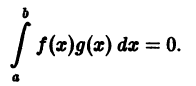
Например, функции 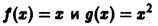 ортогональны на отрезке [-1,1], так как
ортогональны на отрезке [-1,1], так как
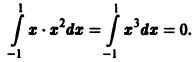
Определение:
Конечная или бесконечная система функций
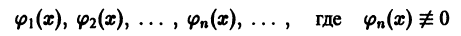
(n = 1, 2,…), интегрируемых на отрезке [а, b], называется ортогональной системой на отрезке [а, b], если для любых номеров тип таких, что 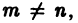 выполняется равенство
выполняется равенство
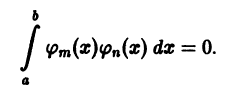
Теорема:
Тригонометрическая система
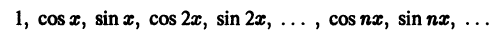
ортогональна на отрезке 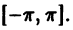
При любом целом 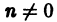 имеем
имеем
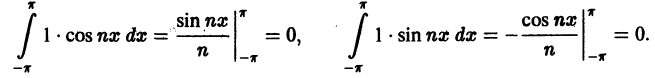
С помощью известных формул тригонометрии
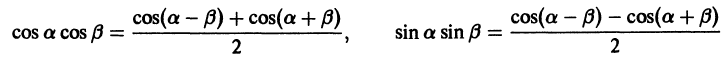
для любых натуральных 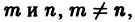 находим:
находим:
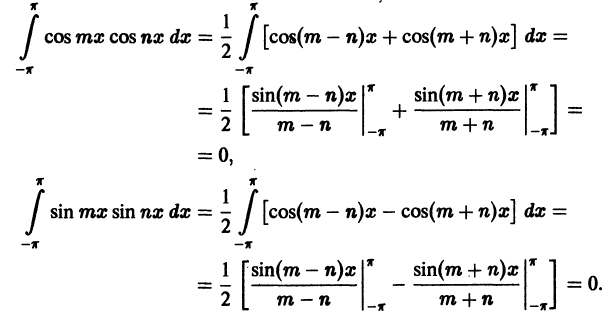
Наконец, в силу формулы
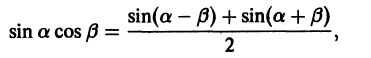
для любых целых m и n получаем
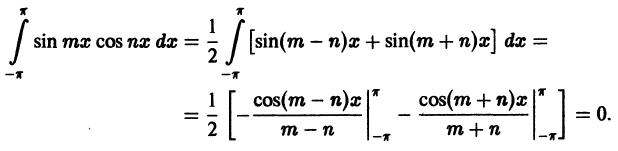
При m = n имеем
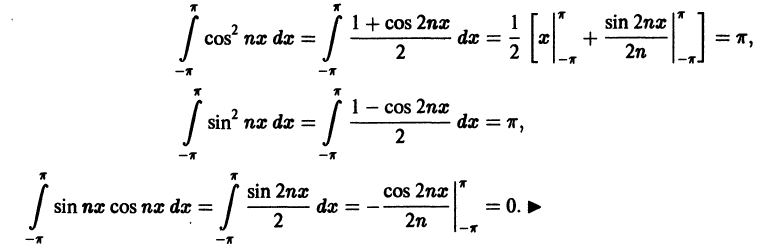
Тригонометрический ряд Фурье
Поставим себе задачей вычислить коэффициенты 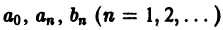 тригонометрического ряда (1), зная функцию f(х).
тригонометрического ряда (1), зная функцию f(х).
Теорема:
Пусть равенство
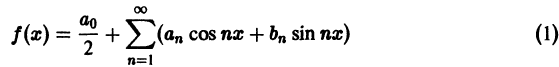
имеет место для всех значений х, причем ряд в правой части равенства сходится равномерно на отрезке 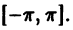 Тогда справедливы формулы
Тогда справедливы формулы
Из равномерной сходимости ряда (1) вытекает непрерывность, а значит, и интегрируемость функции fх). Поэтому равенства (2) имеют смысл. Более того, ряд (1) можно почленно интегрировать. Имеем
откуда и следует первая из формул (2) для n = 0.
Умножим теперь обе части равенства (1) на функцию cos mх, где m — произвольное натуральное число:
Ряд (3), как и ряд (1), сходится равномерно. Поэтому его можно интегрировать почленно,
Все интегралы в правой части, кроме одного, который получается при n = m, равны нулю в силу ортогональности тригонометрической системы. Поэтому
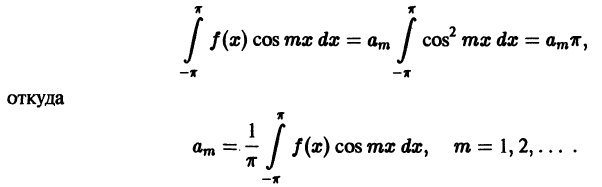
Аналогично, умножая обе части равенства (1) на sin mx; и интегрируя от 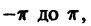 получим
получим
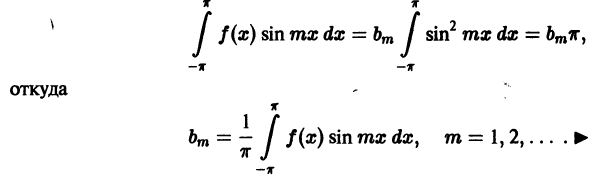
Пусть дана произвольная периодическая функция f(x) периода 2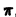 , интегрируемая на отрезке [
, интегрируемая на отрезке [ 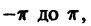 ]. Можно ли ее представить в виде суммы некоторого сходящегося тригонометрического ряда, заранее неизвестно. Однако по формулам (2) можно вычислить постоянные
]. Можно ли ее представить в виде суммы некоторого сходящегося тригонометрического ряда, заранее неизвестно. Однако по формулам (2) можно вычислить постоянные 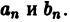
Определение:
Тригонометрический ряд

коэффициенты 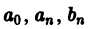 которого определяются через функцию f(x) по формулам
которого определяются через функцию f(x) по формулам
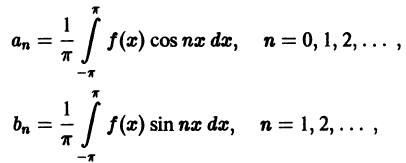
называется тригонометрическим рядом Фурье функции f(x), а коэффициенты 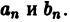 определяемые по этим формулам, называются коэффициентами Фурье функции f(x).
определяемые по этим формулам, называются коэффициентами Фурье функции f(x).
Каждой интегрируемой на отрезке 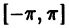 функции f(х) можно поставить в соответствие ее ряд Фурье
функции f(х) можно поставить в соответствие ее ряд Фурье
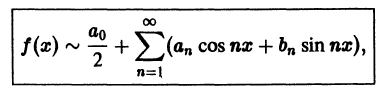
т.е. тригонометрический ряд, коэффициенты которого определяются по формулам (2). Однако если от функции f(х) не требовать ничего, кроме интегрируемости на отрезке 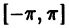 , то знак соответствия в последнем соотношении, вообще говоря, нельзя заменить знаком равенства.
, то знак соответствия в последнем соотношении, вообще говоря, нельзя заменить знаком равенства.
Замечание:
Часто требуется разложить в тригонометрический ряд функцию f(x), определенную только на отрезке 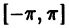 и, следовательно, не являющуюся периодической. Так как в формулах (2) для коэффициентов Фурье интегралы вычисляются по отрезку
и, следовательно, не являющуюся периодической. Так как в формулах (2) для коэффициентов Фурье интегралы вычисляются по отрезку 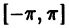 , то для такой функции тоже можно написать тригонометрический ряд Фурье. Вместе с тем, если продолжить функцию f(x) периодически на всю ось Ох, то получим функцию F(x), периодическую с периодом 2
, то для такой функции тоже можно написать тригонометрический ряд Фурье. Вместе с тем, если продолжить функцию f(x) периодически на всю ось Ох, то получим функцию F(x), периодическую с периодом 2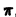 , совпадающую с f(x) на интервале
, совпадающую с f(x) на интервале 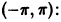
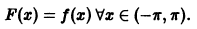
Эту функцию F(x) называют периодическим продолжением функции f(x). При этом функция F(x) не имеет однозначного определения в точках 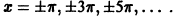
Ряд Фурье для функции F(x) тождествен ряду Фурье для функции f(х). К тому же, если ряд Фурье для функции f(x) сходится к ней, то его сумма, являясь периодической функцией, дает периодическое продолжение функции f(x) с отрезка 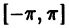 на всю ось Ох. В этом смысле говорить о ряде Фурье для функции f(x), определенной на отрезке
на всю ось Ох. В этом смысле говорить о ряде Фурье для функции f(x), определенной на отрезке 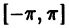 , равносильно тому, что говорить о ряде Фурье для функции F(x), являющейся периодическим продолжением функции f(х) на всю ось Ох. Отсюда следует, что признаки сходимости рядов Фурье достаточно сформулировать для периодических функций.
, равносильно тому, что говорить о ряде Фурье для функции F(x), являющейся периодическим продолжением функции f(х) на всю ось Ох. Отсюда следует, что признаки сходимости рядов Фурье достаточно сформулировать для периодических функций.
Достаточные условия разложимости функции в ряд Фурье
Приведем достаточный признак сходимости ряда Фурье, т. е. сформулируем условия на заданную функцию, при выполнении которых построенный по ней ряд Фурье сходится, и выясним, как при этом ведет себя сумма этого ряда. Важно подчеркнуть, что хотя приведенный ниже класс кусочно-монотонных функций и является достаточно широким, функции, ряд Фурье для которых сходится, им не исчерпываются.
Определение:
Функция f(x) называется кусочно-монотонной на отрезке [a, b], если этот отрезок можно разбить конечным числом точек 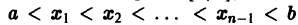 на интервалы
на интервалы 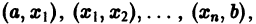 на каждом из которых f(х) монотонна, т. е. либо не убывает, либо не возрастает (см. рис. 1).
на каждом из которых f(х) монотонна, т. е. либо не убывает, либо не возрастает (см. рис. 1).
Пример:
Функция
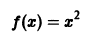
является кусочно-монотонной на интервале 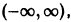 так как этот интервал можно разбить на два интервала
так как этот интервал можно разбить на два интервала 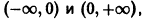 на первом из которых она убывает (и значит, не возрастает), а на втором возрастает (и значит, не убывает).
на первом из которых она убывает (и значит, не возрастает), а на втором возрастает (и значит, не убывает).
Пример:
Функция
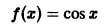
кусочно-монотонна на отрезке 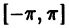 , так как этот отрезок можно разбить на два интервала
, так как этот отрезок можно разбить на два интервала 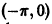 и
и 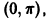 на первом из которых cos x возрастает от -1 до +1, а на втором убывает от +1 до -1.
на первом из которых cos x возрастает от -1 до +1, а на втором убывает от +1 до -1.
Теорема:
Функция f(x), кусочно-монотонная и ограниченная на отрезке [a, b], может иметь на нем только точки разрыва первого рода.
Пусть, например, 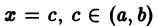 — точка разрыва функции f(x). Тогда в силу ограниченности функции f(x) и монотонности по обе стороны от точки с существуют конечные односторонние пределы
— точка разрыва функции f(x). Тогда в силу ограниченности функции f(x) и монотонности по обе стороны от точки с существуют конечные односторонние пределы
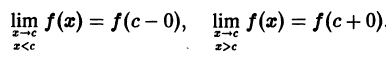
Это означает, что точка с есть точка разрыва первого рода (рис. 2).
Теорема:
Если периодическая функция f(x) с периодом 2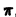 кусочно-монотонна и ограничена на отрезке
кусочно-монотонна и ограничена на отрезке 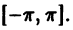 , то ее ряд Фурье сходится в каждой точке х этого отрезка, причем для суммы
, то ее ряд Фурье сходится в каждой точке х этого отрезка, причем для суммы
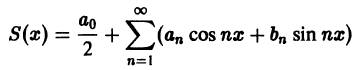
этого ряда выполняются равенства:
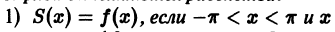 является точкой непрерывности f(x)
является точкой непрерывности f(x)
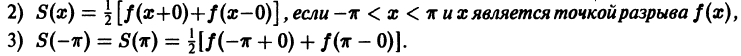
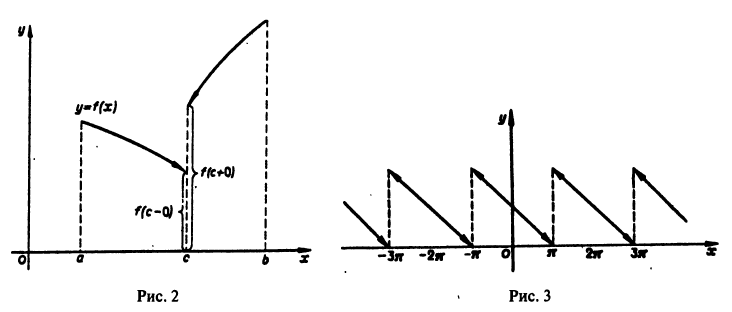
Пример:
Функция f(х) периода 2 , определяемая на интервале
, определяемая на интервале  равенством
равенством
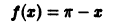
(рис. 3), удовлетворяет условиям теоремы. Поэтому ее можно разложить в ряд Фурье. Находим для нее коэффициенты Фурье:
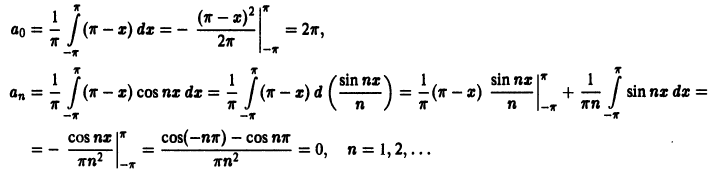
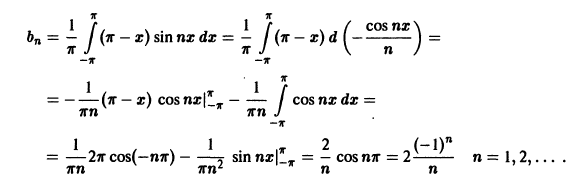
Ряд Фурье для данной функции имеет вид
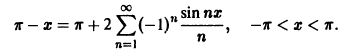
Пример:
Разложить функцию в ряд Фурье (рис. 4) на интервале 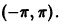
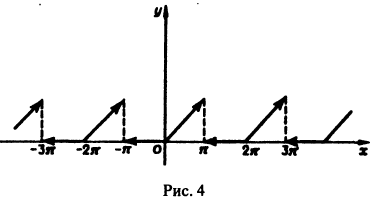
Данная функция удовлетворяет условиям теоремы. Найдем коэффициенты Фурье. Используя свойство аддитивности определенного интеграла, будем иметь
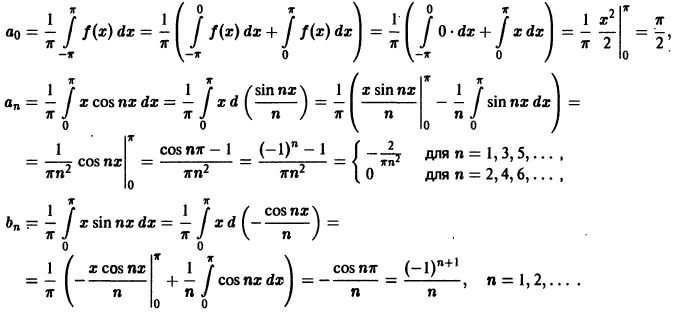
Следовательно, ряд Фурье имеет следующий вид:
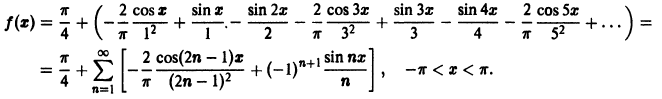
На концах отрезка 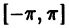 , т.е. в точках
, т.е. в точках 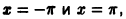 которые являются точками разрыва первого рода, будем иметь
которые являются точками разрыва первого рода, будем иметь
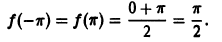
Замечание:
Если в найденном ряде Фурье положить х = 0, то получим
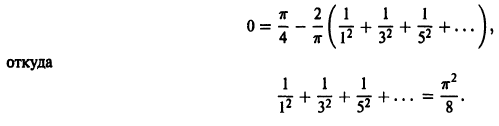
Разложение в ряд Фурье четных и нечетных функций
Функция f(x), определенная на отрезке [-l, l], где l > 0, называется четной, если
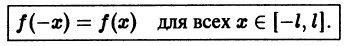
График четной функции симметричен относительно оси ординат.
Функция f(x), определенная на отрезке l), где l > 0, называется нечетной, если
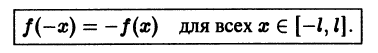
График нечетной функции симметричен относительно начала координат.
Пример:
а) Функция
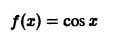
является четной на отрезке 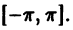 . так как
. так как
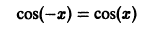
для всех 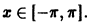
б) Функция
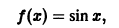
где 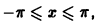 является нечетной, так как
является нечетной, так как
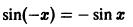
для всех 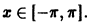
в) Функция
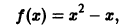
где 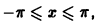 не принадлежит ни к четным, ни к нечетным функциям, так как
не принадлежит ни к четным, ни к нечетным функциям, так как
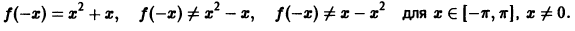
Пусть функция f(х), удовлетворяющая условиям теоремы 1, является четной на отрезке 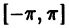 . Тогда
. Тогда
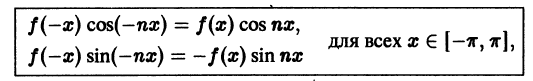
т. е. f(x) cos nх является четной функцией, а f(x) sin nх — нечетной. Поэтому коэффициенты Фурье четной функции f(х) будут равны
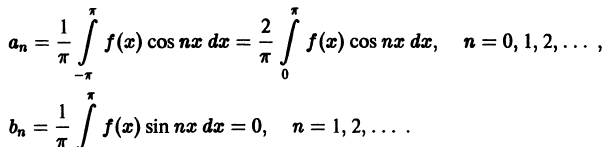
Следовательно, ряд Фурье четной функции имеет вид
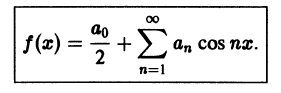
Если f(x) — нечетная функция на отрезке  , то произведение f(x) cos nх будет нечетной функцией, а произведение f(x) sin nх — четной функцией. Поэтому будем иметь
, то произведение f(x) cos nх будет нечетной функцией, а произведение f(x) sin nх — четной функцией. Поэтому будем иметь
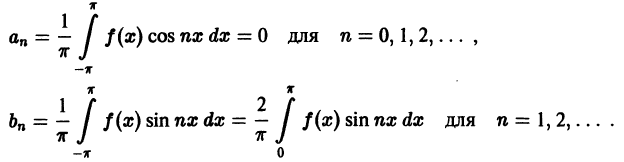
Таким образом, ряд Фурье нечетной функции имеет вид
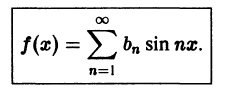
Пример:
Разложить в ряд Фурье на отрезке 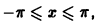 функцию
функцию
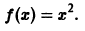
Так как эта функция четная и удовлетворяет условиям теоремы 1, то ее ряд Фурье имеет вид
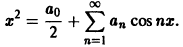
Находим коэффициенты Фурье. Имеем
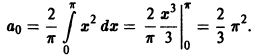
Применяя дважды интегрирование по частям, получим, что
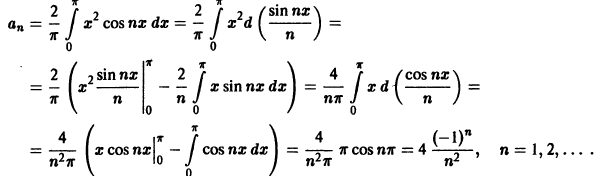
Значит, ряд Фурье данной функции выглядит так:
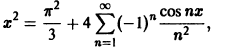
или, в развернутом виде,
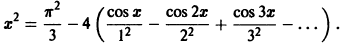
Это равенство справедливо для любого 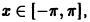 так как в точках
так как в точках 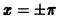 сумма ряда совпадает со значениями функции
сумма ряда совпадает со значениями функции 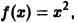 поскольку
поскольку
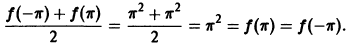
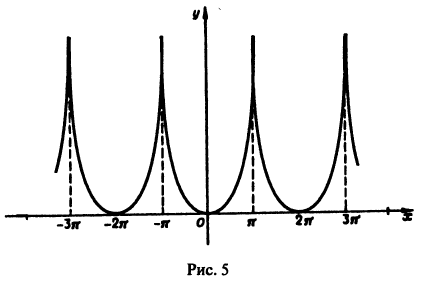
Графики функции 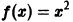 и суммы полученного ряда даны на рис. 5.
и суммы полученного ряда даны на рис. 5.
Замечание:
Этот ряд Фурье позволяет найти сумму одного из сходящихся числовых рядов, а именно, при х = 0 получаем, что
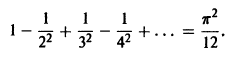
Пример 2. Разложить в ряд Фурье на интервале 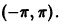 функцию f(x) = x.
функцию f(x) = x.
Функция f(x) удовлетворяет условиям теоремы 1, следовательно ее можно разложить в ряд Фурье, который в силу нечетности этой функции будет иметь вид
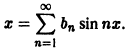
Интегрируя по частям, находим коэффициенты Фурье
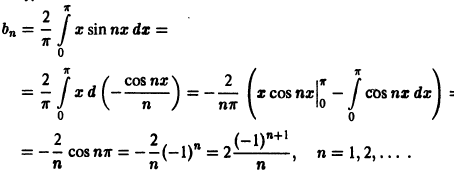
Следовательно, ряд Фурье данной функции имеет вид
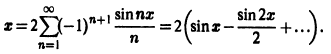
Это равенство имеет место для всех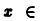
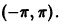 В точках
В точках 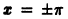 сумма ряда Фурье не совпадает со значениями функции f(х) = х, так как она равна
сумма ряда Фурье не совпадает со значениями функции f(х) = х, так как она равна
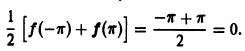
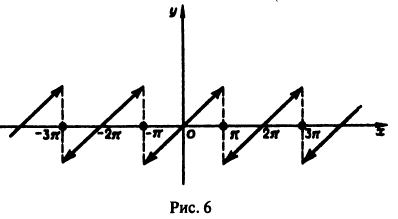
Вне отрезка 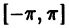 сумма ряда является периодическим продолжением функции f(х) = x; ее график изображен на рис. 6.
сумма ряда является периодическим продолжением функции f(х) = x; ее график изображен на рис. 6.
Разложение функции, заданной на отрезке, в ряд по синусам или по косинусам
Пусть ограниченная кусочно-монотонная функция f(х) задана на отрезке 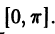 Значения этой функции на отрезке
Значения этой функции на отрезке 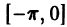 можно доопределить различным образом. Например, можно определить функцию f(х) на отрезке
можно доопределить различным образом. Например, можно определить функцию f(х) на отрезке 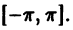 так, чтобы f(х) = f(-х). В этом случае говорят, что f(х) «продолжена на отрезок
так, чтобы f(х) = f(-х). В этом случае говорят, что f(х) «продолжена на отрезок 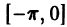 четным образом»; ее ряд Фурье будет содержать только косинусы. Если же функцию f(х) определить на отрезке
четным образом»; ее ряд Фурье будет содержать только косинусы. Если же функцию f(х) определить на отрезке 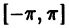 так, чтобы f(х) = — f(-х), то получится нечетная функция, и тогда говорят, что f(x) «продолжена на отрезок
так, чтобы f(х) = — f(-х), то получится нечетная функция, и тогда говорят, что f(x) «продолжена на отрезок 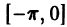 нечетным образом»; в этом случае ее ряд Фурье будет содержать только синусы.
нечетным образом»; в этом случае ее ряд Фурье будет содержать только синусы.
Итак, каждую ограниченную кусочно-монотонную функцию /(х), определенную на отрезке 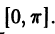 можно разложить в ряд Фурье и по синусам, и по косинусам.
можно разложить в ряд Фурье и по синусам, и по косинусам.
Пример:
Функцию
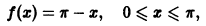
разложить в ряд Фурье: а) по косинусам; б) по синусам.
Данная функция при ее четном и нечетном продолжениях в отрезок 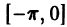 будет ограниченной и кусочно-монотонной
будет ограниченной и кусочно-монотонной
а) Продолжим f(x) в отрезок 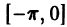 четным образом (рис. 7), тогда ее ряд будет иметь вид
четным образом (рис. 7), тогда ее ряд будет иметь вид
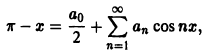
где коэффициенты Фурье равны соответственно
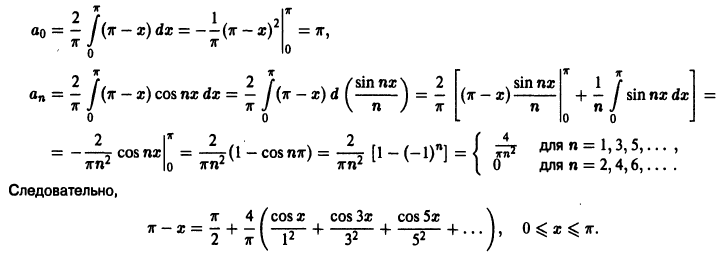
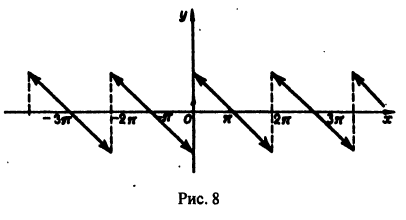
б) Продолжим f{x) в отрезок 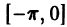 нечетным образом (рис. 8). Тогда ее ряд Фурье
нечетным образом (рис. 8). Тогда ее ряд Фурье
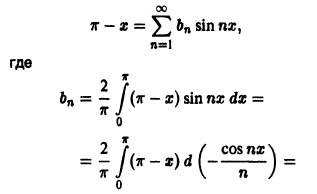
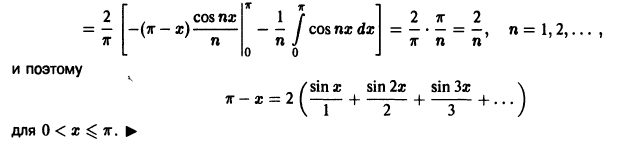
Ряд Фурье для функции с произвольным периодом
Пусть функция f(x) является периодической с периодом 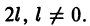 Для разложения ее в ряд Фурье на отрезке
Для разложения ее в ряд Фурье на отрезке 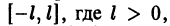 сделаем замену переменной, положив
сделаем замену переменной, положив 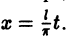 Тогда функция
Тогда функция 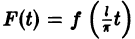 будет периодической функцией аргумента t с периодом
будет периодической функцией аргумента t с периодом 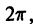 т. к.
т. к.
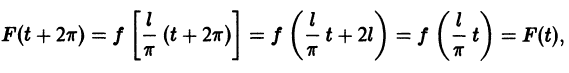
и ее можно разложить на отрезке 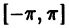 в ряд Фурье
в ряд Фурье
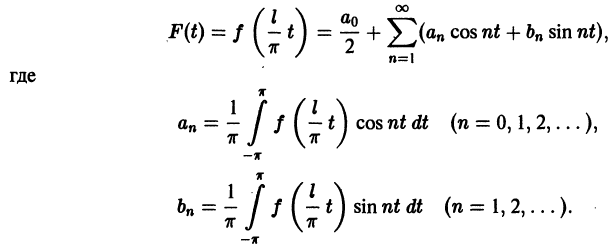
Возвращаясь к переменной х, т. е. положив 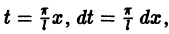 получим
получим
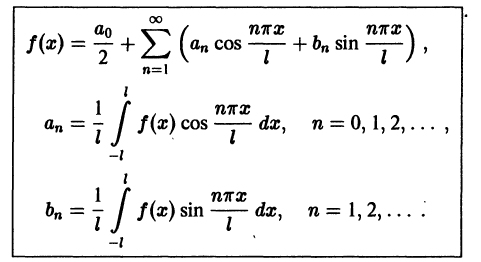
Все теоремы, справедливые для рядов Фурье периодических функций с периодом 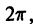 остаются в силе и для периодических функций с произвольным периодом 2 l. В частности, сохраняет свою силу и достаточный признак разложимости функции в ряд Фурье.
остаются в силе и для периодических функций с произвольным периодом 2 l. В частности, сохраняет свою силу и достаточный признак разложимости функции в ряд Фурье.
Пример:
Разложить в ряд Фурье периодическую функцию с периодом 2 l, заданную на отрезке 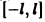 формулой
формулой
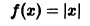
Так как данная функция четная, то ее ряд Фурье имеет вид
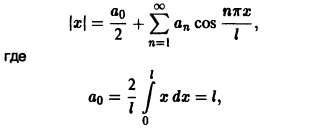
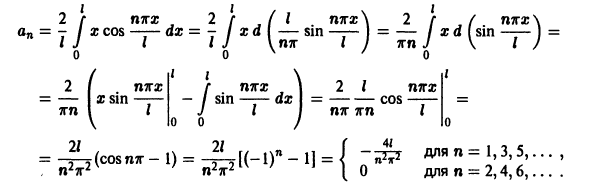
Подставляя в ряд Фурье найденные значения коэффициентов Фурье, получим
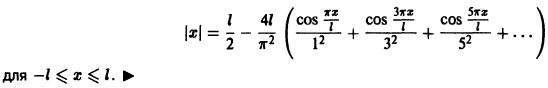
Отметим одно важное свойство периодических функций.
Теорема:
Если функция f(x) имеет период Т и интегрируема, то для любого числа а выполняется равенство
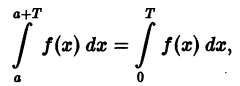
т. е. интеграл no отрезку, длина которого равна периоду Т, имеет одно и то же значение независимо от положения этого отрезка на числовой оси.
В самом деле,
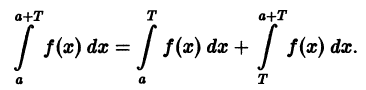
Делаем замену переменной во втором интеграле, полагая х = t + T, dx = dt. Это дает
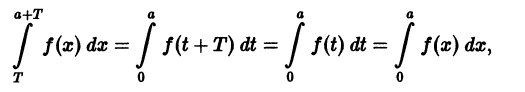
и следовательно,
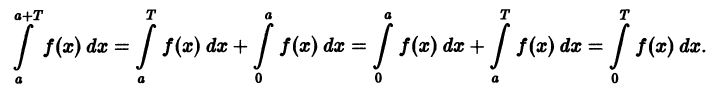
Геометрически это свойство означает, что в случае  площади заштрихованных на рис. 10 областей равны между собой.
площади заштрихованных на рис. 10 областей равны между собой.
В частности, для функции f(x) с периодом Т =  получим при
получим при 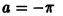
Пример:
Функция
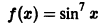
является периодической с периодом Т = 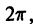 В силу нечетности данной функции без вычисления интегралов можно утверждать, что при любом а
В силу нечетности данной функции без вычисления интегралов можно утверждать, что при любом а
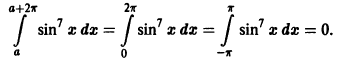
Доказанное свойство, в частности, показывает, что коэффициенты Фурье периодической функции f(x) с периодом 2 l можно вычислять по формулам
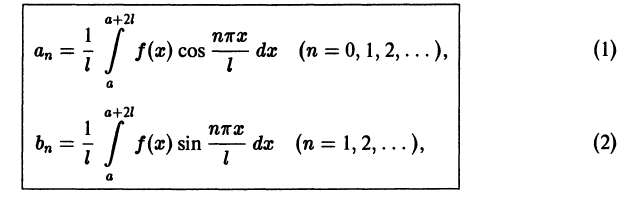
где a — произвольное действительное число (отметим, что функции  имеют период 2 l).
имеют период 2 l).
Пример:
Разложить в ряд Фурье заданную на интервале 0 < х <  функцию
функцию

с периодом 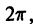 (рис. 11).
(рис. 11).
Найдем коэффициенты Фурье данной функции. Положив в формулах (1) и (2) а = 0, 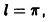 найдем, что
найдем, что
Следовательно, ряд Фурье будет выглядеть так:
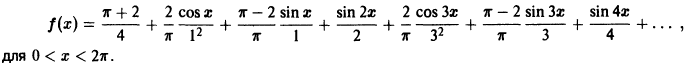
В точке х = 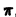 (точка разрыва первого рода) имеем
(точка разрыва первого рода) имеем
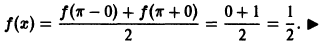
Комплексная запись ряда Фурье
В этом параграфе используются некоторые элементы комплексного анализа (см. главу XXX, где все, производимые здесь действия с комплексными выражениями, строго обоснованы).
Пусть функция f(x) удовлетворяет достаточным условиям разложимости в ряд Фурье. Тогда на отрезке  ее можно представить рядом вида
ее можно представить рядом вида
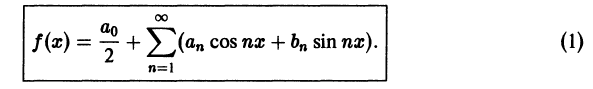
Используя формулы Эйлера (см. ***)
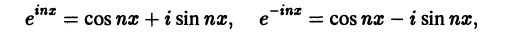
найдем, что
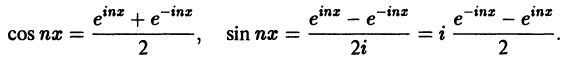
Подставляя эти выражения в ряд (1) вместо cos nх и sin nх, будем иметь
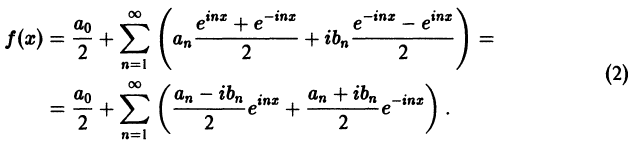
Введем следующие обозначения
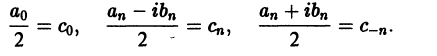
Тогда ряд (2) примет вид
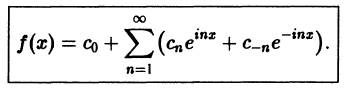
Преобразуем правую часть этого равенства следующим образом
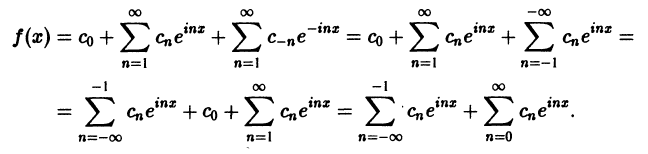
Последнее равенство можно записать так:
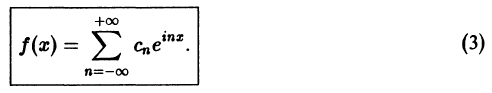
Таким образом, ряд Фурье (1) представлен в комплексной форме (3).
Найдем выражения коэффициентов 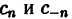 через интегралы. Имеем
через интегралы. Имеем
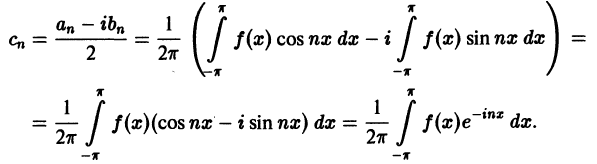
Аналогично находим
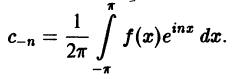
Окончательно формулы для 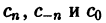 можно записать так:
можно записать так:
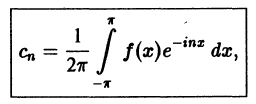
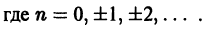
Коэффициенты Cn называются комплексными коэффициентами Фурье функции f(x).
Для периодической функции f(x) с периодом 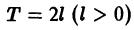 комплексная форма ряда Фурье примет вид
комплексная форма ряда Фурье примет вид

где коэффициенты Cn вычисляются по формулам
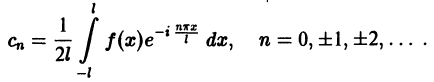
Сходимость рядов (3) и (4) понимается так: ряды (3) и (4) называются сходящимися для данного значения х, если существуют пределы
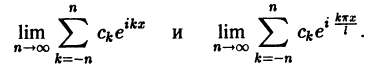
Пример:
Разложить в комплексный ряд Фурье функцию периода 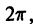
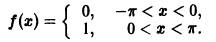
Данная функция удовлетворяет достаточным условиям разложимости в ряд Фурье. Пусть
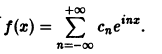
Найдем комплексные коэффициенты Фурье этой функции. Имеем
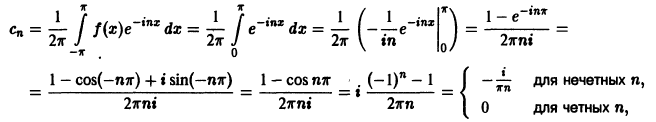
или, короче,
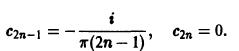
Подставляя значения Сn в ряд (3), окончательно получим
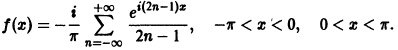
Заметим, что этот ряд можно записать и так:
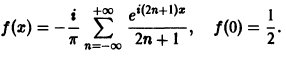
Ряды Фурье по общим ортогональным системам функций
Ортогональные системы функций
Обозначим через 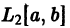 множество всех (действительных) функций, определенных и интегрируемых на отрезке [а, b] с квадратом, т. е. таких, для которых существует интеграл
множество всех (действительных) функций, определенных и интегрируемых на отрезке [а, b] с квадратом, т. е. таких, для которых существует интеграл
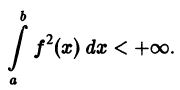
В частности, все функции f(х), непрерывные на отрезке 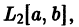 и значения их интегралов Лебега совпадают со значениями интегралов Римана.
и значения их интегралов Лебега совпадают со значениями интегралов Римана.
Определение:
Система функций 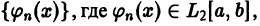 называется ортогональной на отрезке [а,b], если
называется ортогональной на отрезке [а,b], если
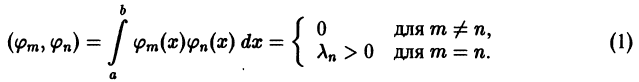
Условие (1) предполагает, в частности, что ни одна из функций 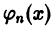 не равна тождественно нулю.
не равна тождественно нулю.
Введем обозначение
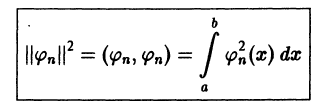
и назовем величину 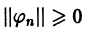 нормой функции
нормой функции 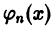 .
.
Если в ортогональной системе 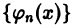 для всякого n имеем
для всякого n имеем 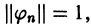 то система функций
то система функций 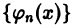 называется ортонормированной.
называется ортонормированной.
Если система 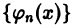 ортогональна, то система
ортогональна, то система 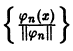 ортонормирована.
ортонормирована.
Пример:
Тригонометрическая система
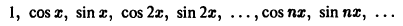
ортогональна на отрезке 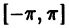 . Система функций
. Система функций
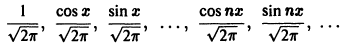
является ортонормированной системой функций на  .
.
Пример:
Косинус-система
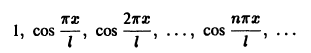
и синус-система
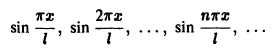
являются ортогональными на отрезке [0, l] , но не ортонормированными 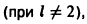 так как их нормы
так как их нормы
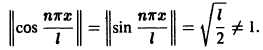
Пример:
Многочлены, определяемые равенством

(n = 0, 1, 2, …), называются многочленами (полиномами) Лежандра. При n = 0 имеем
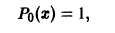
при n = 1 получаем
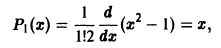
при n = 2 имеем
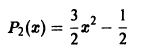
и т.д.
Можно доказать, что функции
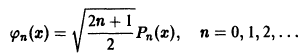
образуют ортонормированную систему функций на отрезке [-1, 1].
Покажем, например, ортогональность полиномов Лежандра. Пусть m>n. В этом случае, интегрируя n раз по частям, находим
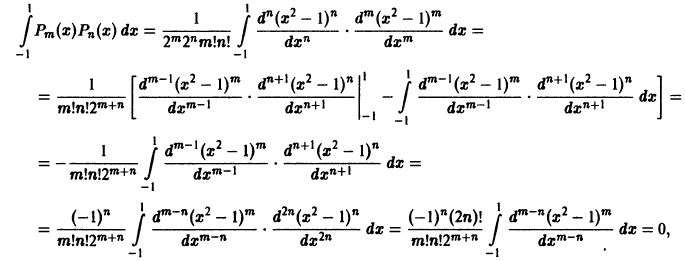
поскольку для функции  все производные до порядка m — 1 включительно обращаются в нуль на концах отрезка [-1, 1].
все производные до порядка m — 1 включительно обращаются в нуль на концах отрезка [-1, 1].
Определение:
Система функций 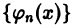 называется ортогональной на интервале (а,b) с весом р(х), если:
называется ортогональной на интервале (а,b) с весом р(х), если:
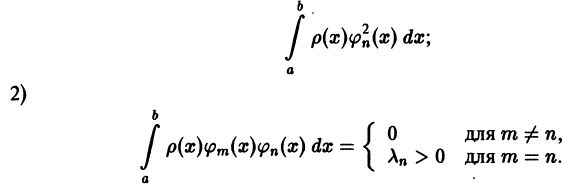
Здесь предполагается, что весовая функция р(х) определена и положительна всюду на интервале (а, b) за возможным исключением конечного числа точек, где р(х) может обращаться в нуль.
Пример:
Система функций Бесселя 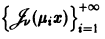 ортогональна на интервале (0,1) с весом р(х) = х, т.е.
ортогональна на интервале (0,1) с весом р(х) = х, т.е.
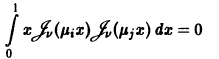
для 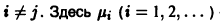 — нули функции Бесселя
— нули функции Бесселя 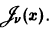
Пример:
Рассмотрим многочлены Чебышева—Эрмита, которые могут быть определены при помощи равенства
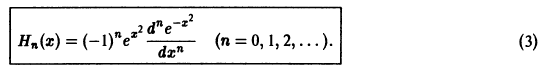
Выполнив дифференцирование в формуле (3), находим
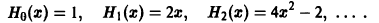
Можно показать, что многочлены Чебышева — Эрмита ортогональны на интервале 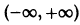 с весом
с весом 
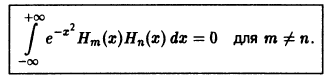
Пусть  — ортогональная система функций в интервале (а, b) и пусть ряд
— ортогональная система функций в интервале (а, b) и пусть ряд
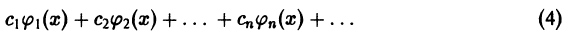
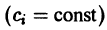 сходится на этом интервале к функции f(x):
сходится на этом интервале к функции f(x):
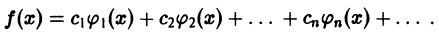
Умножая обе части последнего равенства на 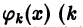 — фиксировано) и интегрируя по х от а до b, в силу ортогональности системы
— фиксировано) и интегрируя по х от а до b, в силу ортогональности системы 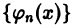 получим, что
получим, что
Эта операция имеет, вообще говоря, чисто формальный характер. Тем не менее, в некоторых случаях, например, когда ряд (4) сходится равномерно, все функции 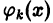 непрерывны и интервал (а, b) конечен, эта операция законна. Но для нас сейчас важна именно формальная трактовка. Итак, пусть задана функция
непрерывны и интервал (а, b) конечен, эта операция законна. Но для нас сейчас важна именно формальная трактовка. Итак, пусть задана функция 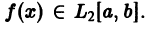 Образуем числа
Образуем числа 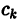 по формуле (5) и напишем
по формуле (5) и напишем
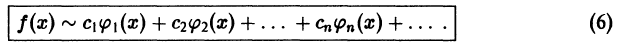
Ряд, стоящий в правой части, называется рядом Фурье функции f(x) относительно системы 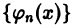 . Числа Cn называются коэффициентами Фурье функции f(x) по этой системе. Знак ~ в формуле (6) означает лишь, что числа Сn связаны с функцией f(x) формулой (5) (при этом не предполагается, что ряд справа вообще сходится, затем более сходится к функции f(x)). Поэтому естественно возникает вопрос: каковы свойства этого ряда? В каком смысле он «представляет» функцию f(x)?
. Числа Cn называются коэффициентами Фурье функции f(x) по этой системе. Знак ~ в формуле (6) означает лишь, что числа Сn связаны с функцией f(x) формулой (5) (при этом не предполагается, что ряд справа вообще сходится, затем более сходится к функции f(x)). Поэтому естественно возникает вопрос: каковы свойства этого ряда? В каком смысле он «представляет» функцию f(x)?
Сходимость в среднем
Определение:
Последовательность 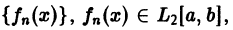 сходится к элементу
сходится к элементу 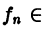
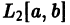 в среднем, если
в среднем, если
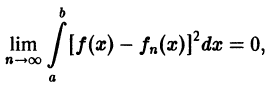
или, что то же, 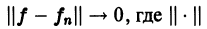 — норма в пространстве
— норма в пространстве 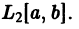
Теорема:
Если последовательность 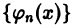 сходится равномерно, то она сходится и в среднем.
сходится равномерно, то она сходится и в среднем.
Пусть последовательность 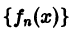 сходится равномерно на отрезке [а, b] к функции f(x). Это означает, что для всякого
сходится равномерно на отрезке [а, b] к функции f(x). Это означает, что для всякого 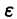 > 0 при всех достаточно больших n имеем
> 0 при всех достаточно больших n имеем
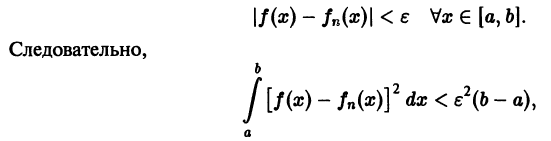
откуда вытекает наше утверждение.
Обратное утверждение неверно: последовательность  может сходиться в среднем к f(x), но не быть равномерно сходящейся.
может сходиться в среднем к f(x), но не быть равномерно сходящейся.
Пример:
Рассмотрим последовательность
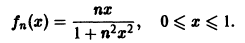
Легко видеть, что
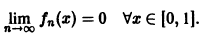
Но эта сходимость не равномерна: существует 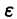 , например,
, например, 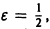 такое, что сколь бы большим ни было n, на отрезке [0,1] найдется точка, именно, точка
такое, что сколь бы большим ни было n, на отрезке [0,1] найдется точка, именно, точка 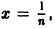 в которой значение функции fn(x) равно
в которой значение функции fn(x) равно 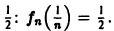
Таким образом, за счет увеличения n сделать неравенство 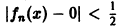 справедливым сразу для всех значений х от 0 до 1 никак нельзя. Иными словами, уже для
справедливым сразу для всех значений х от 0 до 1 никак нельзя. Иными словами, уже для 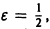 не существует номера N, который годился бы для всех
не существует номера N, который годился бы для всех 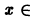 [0, 1] одновременно (здесь характерен горб высоты
[0, 1] одновременно (здесь характерен горб высоты 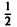 (рис. 12), «передвигающийся» справа налево с возрастанием n). С другой стороны,
(рис. 12), «передвигающийся» справа налево с возрастанием n). С другой стороны,
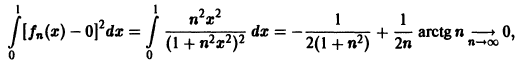
так что последовательность 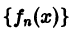 сходится в среднем к функции f(х) = 0.
сходится в среднем к функции f(х) = 0.
Минимальное свойство коэффициентов Фурье. Неравенство Бесселя. Равенство Парсеваля
Пусть 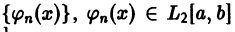 — ортонормированная система функций на отрезке [а,b],
— ортонормированная система функций на отрезке [а,b],
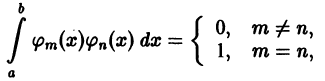
и пусть 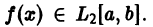 Обозначим через
Обозначим через 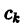 коэффициенты Фурье функции f(x) по ортонормированной системе
коэффициенты Фурье функции f(x) по ортонормированной системе 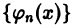 :
:
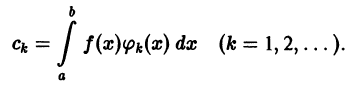
Рассмотрим линейную комбинацию
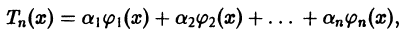
где 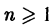 — фиксированное целое число, и найдем значения постоянных
— фиксированное целое число, и найдем значения постоянных 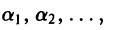 аn, при которых интеграл
аn, при которых интеграл

принимает минимальное значение. Запишем его подробнее
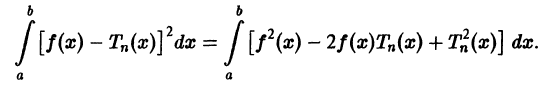
Интегрируя почленно, в силу ортонормированности системы 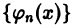 получим
получим
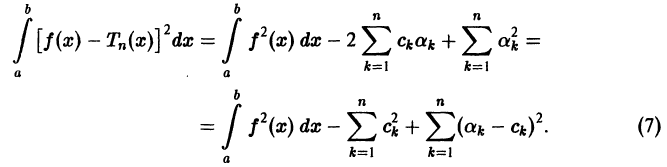
Первые два слагаемых в правой части равенства (7) не зависят от 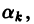 а третье слагаемое неотрицательно. Поэтому интеграл (*) принимает минимальное значение при
а третье слагаемое неотрицательно. Поэтому интеграл (*) принимает минимальное значение при 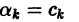 (к = 1, 2,…). Интеграл
(к = 1, 2,…). Интеграл
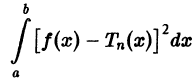
называют средним квадратичным приближением функции f(x) линейной комбинацией Тn(х). Таким образом, среднее квадратичное приближение функции 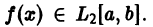 принимает минимальное значение, когда
принимает минимальное значение, когда 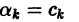 (к = 1,2,…), т. е. когда Тn(х) есть n-я частичная сумма ряда Фурье функции f(x) по системе
(к = 1,2,…), т. е. когда Тn(х) есть n-я частичная сумма ряда Фурье функции f(x) по системе 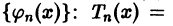 Sn(x). Полагая
Sn(x). Полагая 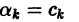 , из (7) получаем
, из (7) получаем
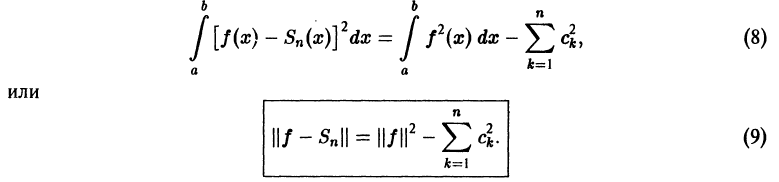
Равенство (9) называется тождеством Бесселя. Так как его левая часть неотрицательна, то из него следует неравенство Бесселя
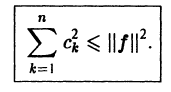
Поскольку n здесь произвольно, то неравенство Бесселя можно представить в усиленной форме

т. е. для всякой функции 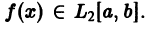 ряд из квадратов коэффициентов Фурье этой функции по ортонормированной системе
ряд из квадратов коэффициентов Фурье этой функции по ортонормированной системе 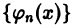 сходится. Так как система
сходится. Так как система
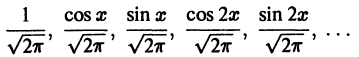
ортонормирована на отрезке 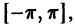 то неравенство (10) в переводе на привычную запись тригонометрического ряда Фурье дает соотношение
то неравенство (10) в переводе на привычную запись тригонометрического ряда Фурье дает соотношение
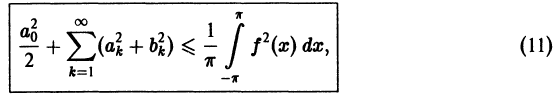
справедливое для любой функции f(x) с интегрируемым квадратом.
Если 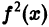 интегрируема, то в силу необходимого условия сходимости ряда в левой части неравенства (11) получаем, что
интегрируема, то в силу необходимого условия сходимости ряда в левой части неравенства (11) получаем, что 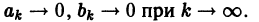
Равенство Парсеваля
Для некоторых систем 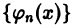 знак неравенства в формуле (10) может быть заменен (для всех функций
знак неравенства в формуле (10) может быть заменен (для всех функций 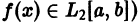 знаком равенства. Получаемое равенство
знаком равенства. Получаемое равенство

называется равенством Парсеваля—Стеклова {условием полноты).
Тождество Бесселя (9) позволяет записать условие (12) в равносильной форме
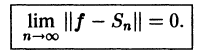
Тем самым выполнение условия полноты означает, что частичные суммы Sn(х) ряда Фурье функции f(x) сходятся к функции f(x) в среднем, т. е. по норме пространства 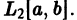
Определение:
Ортонормированная система 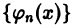 называется полной в
называется полной в 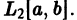 если всякую функцию
если всякую функцию
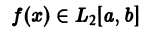
можно с любой точностью приблизить в среднем линейной комбинацией вида
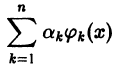
с достаточно большим числом слагаемых, т. е. если для всякой функции 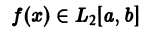 и для любого
и для любого 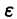 > 0 найдется натуральное число N0 и числа
> 0 найдется натуральное число N0 и числа 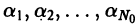 такие, что
такие, что
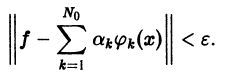
Из приведенных рассуждений следует
Теорема:
Если ортонормированная система 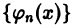 полна в пространстве
полна в пространстве 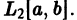 , то ряд Фурье всякой функции
, то ряд Фурье всякой функции 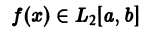 по этой системе сходится к f(x) в среднем, т. е. по норме
по этой системе сходится к f(x) в среднем, т. е. по норме 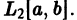
Можно показать, что тригонометрическая система
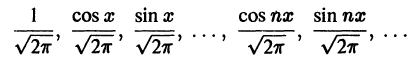
полна в пространстве 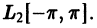 Отсюда следует утверждение.
Отсюда следует утверждение.
Теорема:
Если функция 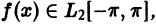 то ее тригонометрический ряд Фурье сходится к ней в среднем.
то ее тригонометрический ряд Фурье сходится к ней в среднем.
Замкнутые системы. Полнота и замкнутость систем
Определение. Ортонормированная система функций 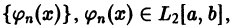 называется замкнутой, если в пространстве
называется замкнутой, если в пространстве 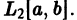 не существует отличной от нуля функции, ортогональной ко всем функциям
не существует отличной от нуля функции, ортогональной ко всем функциям 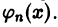
В пространстве 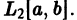 понятия полноты и замкнутости ортонормированных систем совпадают.
понятия полноты и замкнутости ортонормированных систем совпадают.
Ряды Фурье основные определения и свойства с подробным объяснением и теорией
При изучении разнообразных периодических процессов, т. е. процессов, которые через определенный промежуток времени повторяются (встречаются в радиотехнике, электронике, теории упругости, теории и практике автоматического регулирования и т. д.), целесообразнее разлагать периодические функции, описывающие эти процессы, не в степенной ряд, а в так называемый тригонометрический ряд.
Напомним, что функция у = f(x), определенная на множестве D, называется периодической (см. п. 14.3) с периодом Т > 0, если при каждом х € D значение 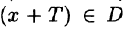 и выполняется равенство
и выполняется равенство 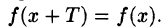
Для построения графика периодической функции периода Т достаточно построить его на любом отрезке длины Т и периодически продолжить его во всю область определения.
Отметим основные свойства периодической функции.
- Алгебраическая сумма периодических функций, имеющих один и тот же период Т, есть периодическая функция с периодом Т.
- Если функция f(x) имеет период Т , то функция f(ax) имеет период действительно,
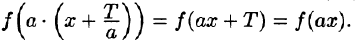
- Если функция f(х) имеет период T и интегрируема на отрезке
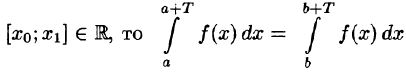
при любых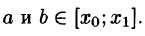
Пусть, например, 0 < а < b < Т, тогда
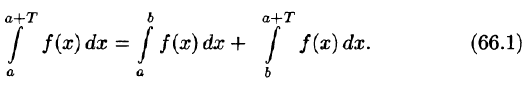
С другой стороны,
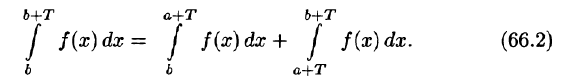
Но
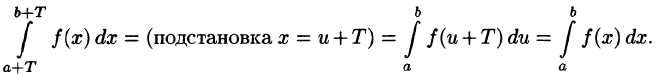
Подставляем полученный результат в (66.2) и, сравнивая с (66.1), имеем
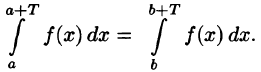
В частности,
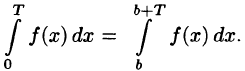
Простейшими периодическими функциями являются тригонометрические функции sinх и cosх. Период этих функций равен 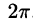 , т.е.
, т.е. 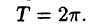
Простейшим периодическим процессом (движением) является простое гармоническое колебание (движение), описываемое функцией

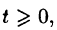 где А — амплитуда колебания,
где А — амплитуда колебания, 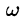 — частота,
— частота, 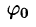 — начальная фаза.
— начальная фаза.
Функцию такого вида (и ее график) называют простой гармоникой. Основным периодом функции (66.3) является 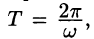 т. е. одно полное колебание совершается за промежуток времени
т. е. одно полное колебание совершается за промежуток времени 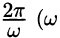 показывает, сколько колебаний совершает точка в течение
показывает, сколько колебаний совершает точка в течение 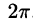 : единиц времени).
: единиц времени).
Проведем преобразование функции (66.3):
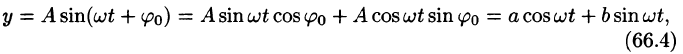
где 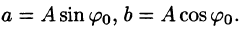 Отсюда видно, что простое гармоническое колебание описывается периодическими функциями
Отсюда видно, что простое гармоническое колебание описывается периодическими функциями 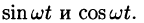
Сложное гармоническое колебание, возникающее в результате наложения конечного (или бесконечного) числа простых гармоник, также описывается функциями вида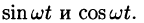 Так, функция
Так, функция
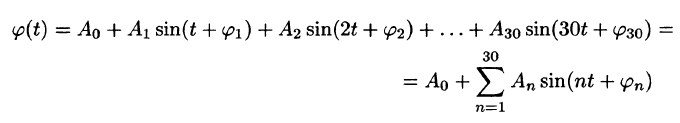
или, что равносильно, функция
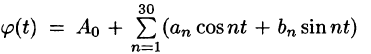
задает сложное гармоническое колебание. Так как период первой гармоники есть
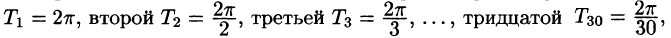
период функции 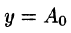 («нулевая гармоника») есть любое число, то функция
(«нулевая гармоника») есть любое число, то функция 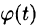 имеет период, равный
имеет период, равный 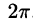 , т. е.
, т. е. 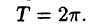
Понятно, что при наложении простых гармоник получаем периодическую функцию, описывающую сложное периодическое колебание (периодический процесс).
Возникает вопрос: всякую ли периодическую функцию, описывающую периодический процесс, можно представить в виде суммы простых гармоник вида (66.3) или (66.4)? Если да, то как найти неизвестные параметры (коэффициенты) каждой из этих гармоник? Ответим сначала на второй вопрос, а потом и на первый.
Тригонометрический ряд Фурье
С помощью так называемого тригонометрического ряда любую (практически) периодическую функцию можно представить в виде ряда, членами которого являются простые гармоники.
Тригонометрическим рядом называется функциональный ряд вида
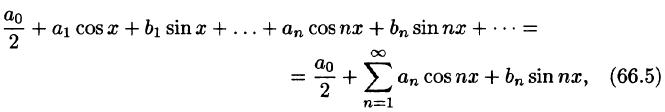
где действительные числа 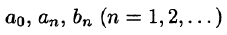 называются коэффициентами ряда.
называются коэффициентами ряда.
Ряд (66.5) можно записать в виде
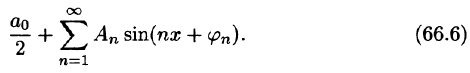
Действительно, положив 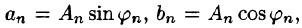 получим:
получим: 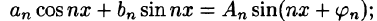 ряд (66.5) принимает вид (66.6), при этом
ряд (66.5) принимает вид (66.6), при этом 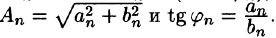
Свободный член ряда записан в виде 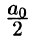 для единообразия получающихся в дальнейшем формул.
для единообразия получающихся в дальнейшем формул.
Приведем формулы, которые понадобятся нам в дальнейшем. Считая m и n целыми положительными, находим:
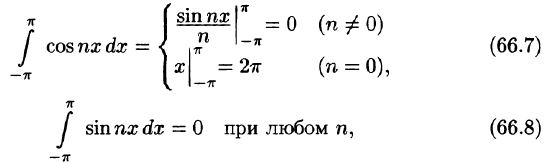
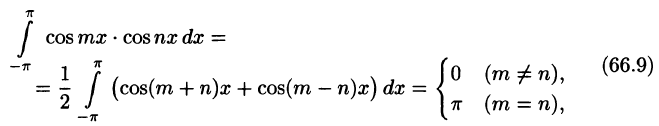
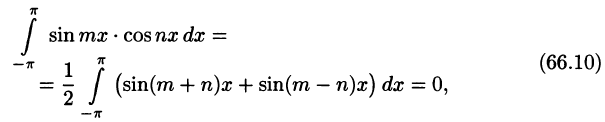
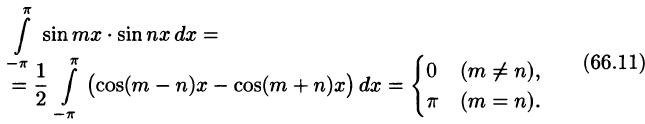
Замечанья.
1. Формулы (66.7)-(66.11) показывают, что семейство функций
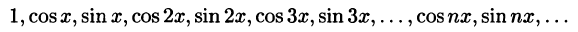
обладает свойством ортогональности: интеграл от произведения любых двух функций этого семейства на интервале, имеющем длину  равен нулю.
равен нулю.
2.Формулы (66.7)-(66.11) справедливы и в случае, когда область интегрирования есть отрезок  (см. свойство 3 периодических функций, п. 66.1).
(см. свойство 3 периодических функций, п. 66.1).
Пусть f(х) — произвольная периодическая функция с периодом 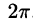 Предположим, что функция f(х) разлагается в тригонометрический ряд, т. е. f(х) является суммой ряда (66.5):
Предположим, что функция f(х) разлагается в тригонометрический ряд, т. е. f(х) является суммой ряда (66.5):
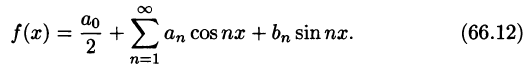
Так как функция f(х) (и сумма ряда) имеет период 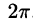 , то ее можно рассматривать в любом промежутке длины
, то ее можно рассматривать в любом промежутке длины 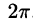 . В качестве основного промежутка возьмем отрезок
. В качестве основного промежутка возьмем отрезок 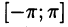 (также удобно взять отрезок
(также удобно взять отрезок 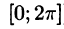 ) и предположим, что ряд (66.12) на этом отрезке можно почленно интегрировать. Вычислим коэффициенты
) и предположим, что ряд (66.12) на этом отрезке можно почленно интегрировать. Вычислим коэффициенты  . Для этого проинтегрируем обе части равенства (66.12) в пределах от
. Для этого проинтегрируем обе части равенства (66.12) в пределах от 
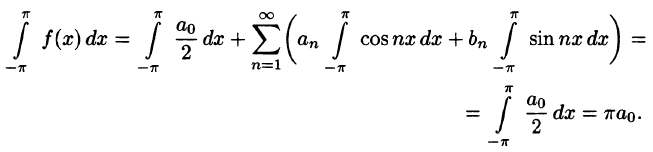
Интегралы от всех, кроме нулевого, членов ряда равны нулю в силу формул (66.7) и (66.8). Отсюда
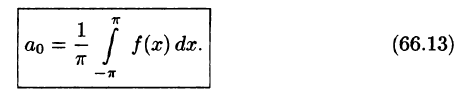
Умножив обе части равенства (66.12) на cos mar и проинтегрировав полученный ряд в пределах от  , получим:
, получим:
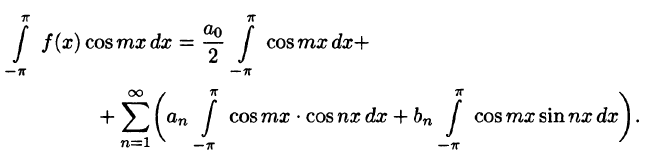
В силу формул (66.7), (66.9) и (66.10) из последнего равенства при m = п получаем:
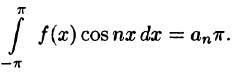
Отсюда
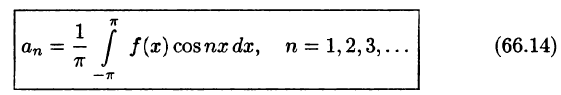
Аналогично, умножив равенство (66.12) на sinmx и проинтегрировав почленно на отрезке 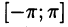 , найдем:
, найдем:
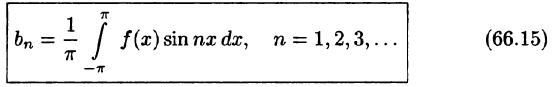
Числа 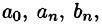 определяемые по формулам (66.13)-(66.15), называются коэффициентами Фурье функции f(x), а тригонометрический ряд (66.5) с такими коэффициентами — рядом Фурье функции f(x).
определяемые по формулам (66.13)-(66.15), называются коэффициентами Фурье функции f(x), а тригонометрический ряд (66.5) с такими коэффициентами — рядом Фурье функции f(x).
Для интегрируемой на отрезке 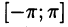 функции f(x) записывают
функции f(x) записывают
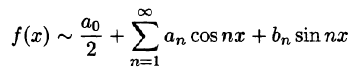
и говорят: функции f(x) соответствует (поставлен в соответствие) ее ряд Фурье. Если ряд Фурье сходится, то его сумму обозначим S(x).
Разложение в ряд Фурье периодических функций
Разложение в ряд Фурье периодических функций
периодических функций
Теорема Дирихле
Выясним условия, при которых знак соответствия (~) можно заменить знаком равенства (=), т. е. условия, при которых ряд Фурье функции f(х) сходится и имеет своей суммой как раз функцию f(х).
Будем рассматривать функции f(x), имеющие период 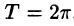 Такие функции называют
Такие функции называют 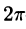 —периодическими.
—периодическими.
Сформулируем теорему, представляющую достаточное условие разложимости функции в ряд Фурье.
Теорема Дирихле:
Пусть 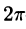 -периодическая функция f(x) на отрезке
-периодическая функция f(x) на отрезке 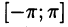 удовлетворяет двум условиям:
удовлетворяет двум условиям:
- f(х) кусочно-непрерывна, т. е. непрерывна или имеет конечное число точек разрыва I рода;
- f(x) кусочно-монотонна, т. е. монотонна на всем отрезке, либо этот отрезок можно разбить на конечное число интервалов так, что на каждом из них функция монотонна.
Тогда соответствующий функции f(х) ряд Фурье сходится на этом отрезке и при этом:
- В точках непрерывности функции сумма ряда S(x) совпадает с самой функцией: S(x) = f(x);
- В каждой точке
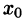 разрыва функции сумма ряда равна
разрыва функции сумма ряда равна 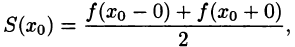 т. е. равна среднему арифметическому пределов функции /(х) справа и слева;
т. е. равна среднему арифметическому пределов функции /(х) справа и слева; - В точках
 (на концах отрезка) сумма ряда равна
(на концах отрезка) сумма ряда равна 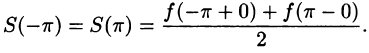
Таким образом, если функция f(х) удовлетворяет условиям 1 и 2 теоремы (условия Дирихле), то на отрезке 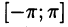 имеет место разложение (66.12):
имеет место разложение (66.12):
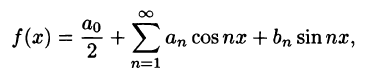
причем коэффициенты вычисляются по формулам (66.13)-(66.15). Это равенство может нарушиться только в точках разрыва функции f(х) и на концах отрезка 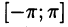 .
.
В силу периодичности исходной функции и суммы ряда Фурье может быть получено указанное разложение во всей области определения функции.
Замечания:
1.Если функция f(x) с периодом 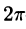 на отрезке
на отрезке 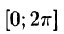 удовлетворяет условиям Дирихле, то для нее имеет место разложение (66.12), где коэффициенты вычисляются по формулам
удовлетворяет условиям Дирихле, то для нее имеет место разложение (66.12), где коэффициенты вычисляются по формулам
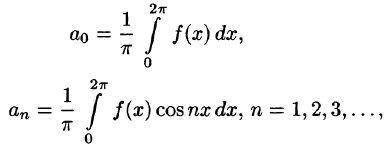
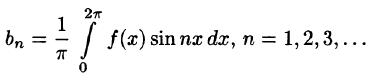
(Интегралы 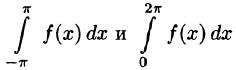 равны в силу свойства 3 периодической функции — см. п. 66.1.)
равны в силу свойства 3 периодической функции — см. п. 66.1.)
2.Условиям Дирихле удовлетворяют большинство функций, которые встречаются в математике и ее приложениях. Существуют функции, не удовлетворяющие условиям Дирихле, но при этом разложимые в ряд Фурье, т. е. теорема Дирихле дает лишь достаточное условие разложимости, но не необходимое.
Пример:
Разложить в ряд Фурье функцию f(x) периода 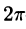 , заданную на отрезке
, заданную на отрезке 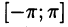 формулой
формулой
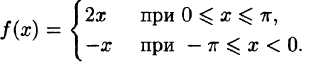
Решение:
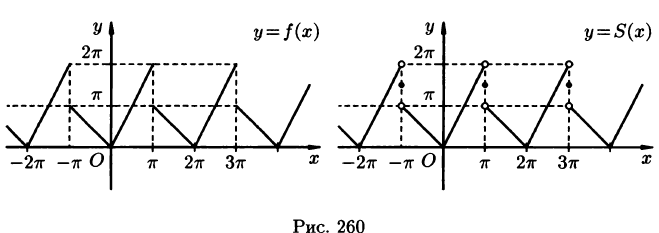
На рисунке 260 изображен график функции f(х). Эта функция удовлетворяет условиям Дирихле, значит, она разложима в ряд Фурье. Находим коэффициенты ряда:
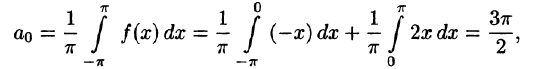
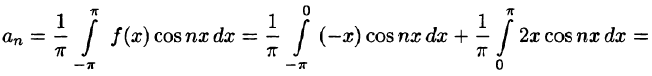
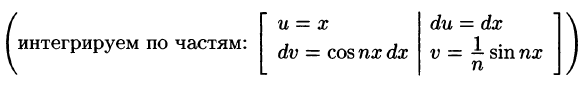
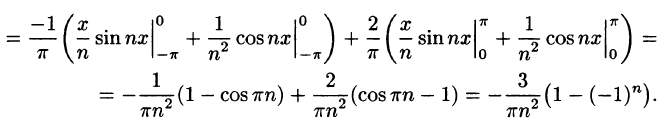
Аналогично находим
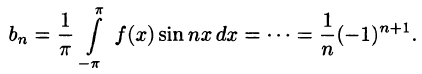
Исходной функции f(x) соответствует ряд Фурье
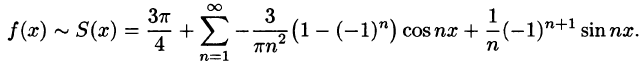
Функция f(х) непрерывна во всех внутренних точкой отрезка 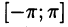 , поэтому, согласно теореме Дирихле, для всех этих точек имеем равенство f(х) = S(х), т. е.
, поэтому, согласно теореме Дирихле, для всех этих точек имеем равенство f(х) = S(х), т. е.
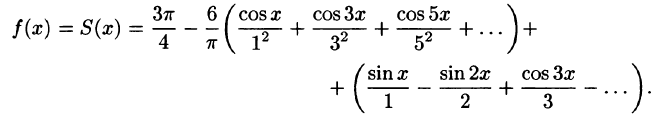
В точках 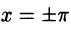 сумма S(x) ряда равна
сумма S(x) ряда равна
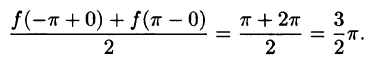
Графики функций f(х) и S(х) показаны на рис. 260.
Разложение в ряд Фурье четных и нечетных функций
Если разлагаемая на отрезке 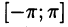 в ряд Фурье функция f(х) является четной или нечетной, то это отражается на формулах коэффициентов Фурье (вычисление их упрощается) и на виде самого ряда (он становится так называемым неполным).
в ряд Фурье функция f(х) является четной или нечетной, то это отражается на формулах коэффициентов Фурье (вычисление их упрощается) и на виде самого ряда (он становится так называемым неполным).
Если функция f(x) четная, то ее ряд Фурье имеет вид
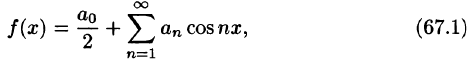
где
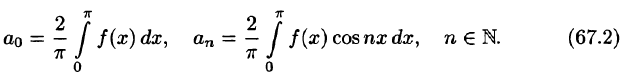
Если функция f(x) нечетная, то ее ряд Фурье имеет вид

где
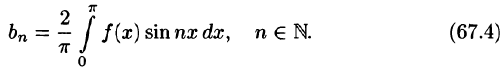
Как известно (см. п. 39.4), если функция f(x) интегрируема на симметричном отрезке [—а; а], то
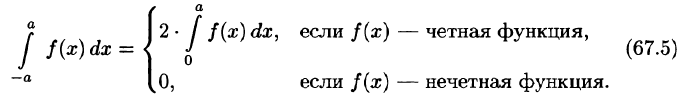
Если функция f(x) — четная, то f(х) cos nx — четная функция 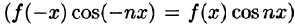 , a f(x) sin nx — нечетная функция
, a f(x) sin nx — нечетная функция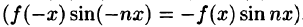 .
.
Если же f(х) — нечетная функция, то, очевидно, функция f(х) cosnx — нечетная, a f(x) sinnx — четная.
С учетом формулы (67.5) из формул (66.13)-(66.15) получаем формулы (67.1)-(67.4).
Ряды (67.1) и (67.3) называются неполными тригонометрическими рядами, или рядами по косинусам и по синусам соответственно.
Пример:
Разложить в ряд Фурье функцию
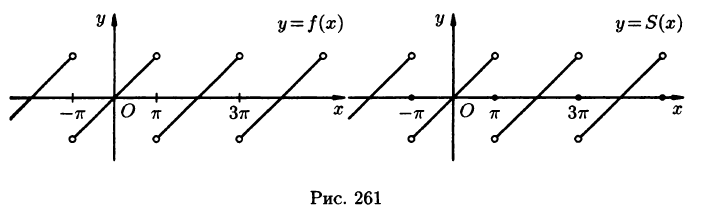
Решение:
На рисунке 261 изображен график заданной функции. Условиям Дирихле функция у = х удовлетворяет. Эта функция — нечетная. Следовательно, 
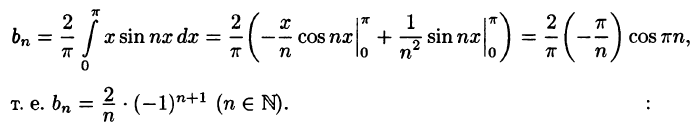
Ряд Фурье содержит только синусы:
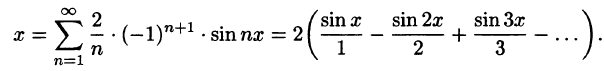
При этом
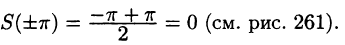
Разложение в ряд Фурье функций произвольного периода
Разлагать в ряд Фурье можно и периодические функции с периодом, отличным от  .
.
Пусть функция f(x), определенная на отрезке [-l; l], имеет период  где l — произвольное положительное число) и удовлетворяет на этом отрезке условиям Дирихле.
где l — произвольное положительное число) и удовлетворяет на этом отрезке условиям Дирихле.
Сделав подстановку 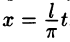 , данную функцию f(х) преобразуем в функцию
, данную функцию f(х) преобразуем в функцию 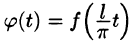 , которая определена на отрезке
, которая определена на отрезке 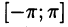 и имеет период
и имеет период 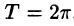 .
.
Действительно, если 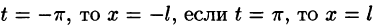 и при
и при 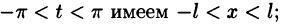
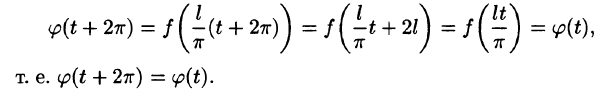
Разложение функции  в ряд Фурье на отрезке
в ряд Фурье на отрезке  имеет вид
имеет вид
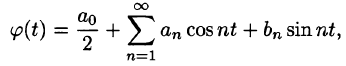
где
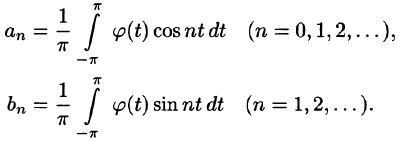
Возвращаясь к переменной х и заметив, что 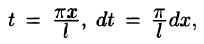 получим
получим
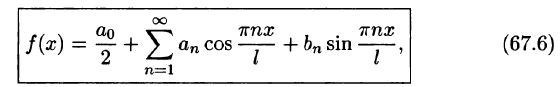
где
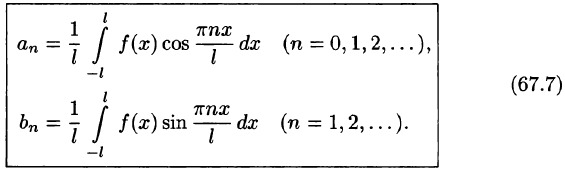
Ряд (67.6) с коэффициентами, вычисляемыми по формулам (67.7), называется рядом Фурье для функции f(x) с периодом Т = 2l.
Замечание:
Все теоремы, имеющие место для рядов Фурье  -периодических функций, остаются в силе и для рядов Фурье функций, период которых Т = 2l. В частности, если f(х) на отрезке [—l; l] четная, то ее ряд Фурье имеет вид
-периодических функций, остаются в силе и для рядов Фурье функций, период которых Т = 2l. В частности, если f(х) на отрезке [—l; l] четная, то ее ряд Фурье имеет вид
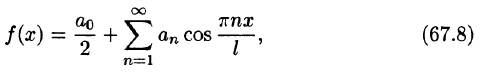
где
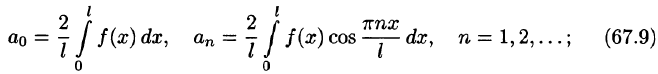
если f(x) — нечетная функция, то
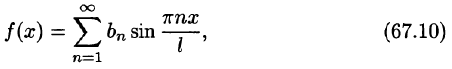
где
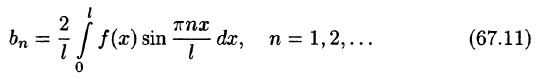
Пример:
Разложить функцию f(x) = х на интервале (—4; 4) в ряд Фурье.
Решение:
Данная функция нечетная, удовлетворяет условиям Дирихле. По формулам (67.10) и (67.11), при l = 4, имеем:
где
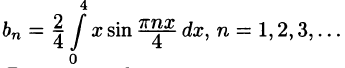
Вычисляем 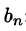 :
:
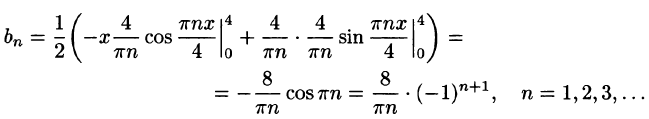
Таким образом,
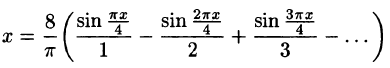
для -4 < x < 4.
Представление непериодической функции рядом Фурье
Пусть у = f(х) — непериодическая функция, заданная на всей числовой оси 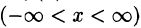 .
.
Такая функция не может быть разложена в ряд Фурье, т. к. сумма ряда Фурье есть функция периодическая и, следовательно, не может быть равна f(x) для всех x.
Однако непериодическая функция f(x) может быть представлена в виде ряда Фурье на любом конечном промежутке [a; b], на котором она удовлетворяет условиям Дирихле. Для этого можно поместить начало координат в середину отрезка [a; b] и построить функцию 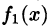 периода Т = 21 = |b — а| такую, что
периода Т = 21 = |b — а| такую, что 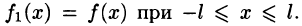 На рисунке 262 приведена иллюстрация построения функции
На рисунке 262 приведена иллюстрация построения функции 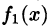 .
.
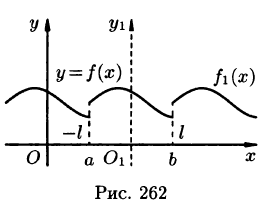
Разлагаем функцию в ряд Фурье. Сумма этого ряда во всех точках отрезка [а; b] (кроме точек разрыва) совпадает с заданной функцией f(x). Вне этого промежутка сумма ряда и f(x) являются совершенно различными функциями.
в ряд Фурье. Сумма этого ряда во всех точках отрезка [а; b] (кроме точек разрыва) совпадает с заданной функцией f(x). Вне этого промежутка сумма ряда и f(x) являются совершенно различными функциями.
Пусть теперь непериодическую функцию f(х) требуется разложить в ряд Фурье на отрезке [0; l]. (Это частный случай: начало координат перенесено в точку х = а отрезка [а; b]; область определения функции f(x) будет иметь вид [0; l], где l = |b- а|.)
Такую функцию можно произвольным образом доопределить на отрезке [-l;0], а затем осуществить ее периодическое продолжение с периодом Т = 2l. Разложив в ряд Фурье на отрезке [—l,l] полученную таким образом периодическую функцию  , получим искомый ряд для функции f(x) при
, получим искомый ряд для функции f(x) при 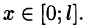
В частности, функцию f(x) можно доопределить на отрезке [—l; 0] четным образом (т. е. чтобы при 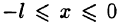 было f(x) = f(—x)) — см. рис. 263. В этом случае функция f(x) разлагается в ряд Фурье, который содержит только косинусы (см. формулы (67.8) и (67.9)).
было f(x) = f(—x)) — см. рис. 263. В этом случае функция f(x) разлагается в ряд Фурье, который содержит только косинусы (см. формулы (67.8) и (67.9)).
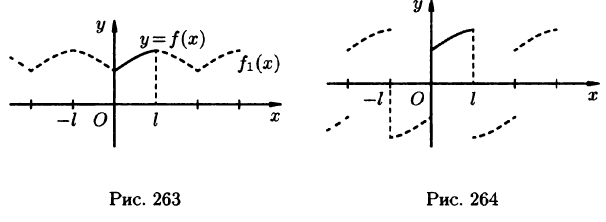
Если же функцию f(x) продолжить на отрезок [-l; 0] нечетным образом (см. рис. 264), то она разлагается в ряд, состоящий только из синусов (см. формулы (67.10) и (67.11)).
Ряд косинусов и ряд синусов для функции f(x), заданной на отрезке [0; l], имеют одну и ту же сумму. Если 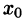 — точка разрыва функции f(x), то сумма как одного, так и другого ряда равна одному и тому же числу:
— точка разрыва функции f(x), то сумма как одного, так и другого ряда равна одному и тому же числу:
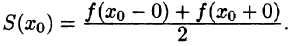
Замечание:
Все, что было сказано о разложении в ряд Фурье функции f(x) на отрезке [0;l], переносится практически без изменения на случай, когда функция задана на отрезке 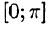 ; такую функцию .можно разложить как в ряд косинусов, так и в ряд синусов (формулы (67.1) и (67.3)).
; такую функцию .можно разложить как в ряд косинусов, так и в ряд синусов (формулы (67.1) и (67.3)).
Пример:
Разложить в ряд косинусов функцию
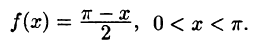
Решение:
Продолжим функцию f(x) на отрезок 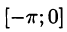 четным образом (см. рис. 265). Разлагаем в ряд функцию
четным образом (см. рис. 265). Разлагаем в ряд функцию
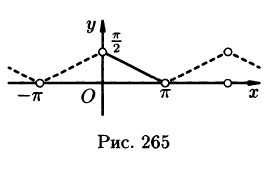
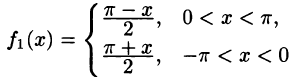
с периодом  . Условиям теоремы Дирихле функция
. Условиям теоремы Дирихле функция 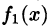 удовлетворяет. Используя формулы (67.1) и (67.2), находим:
удовлетворяет. Используя формулы (67.1) и (67.2), находим:
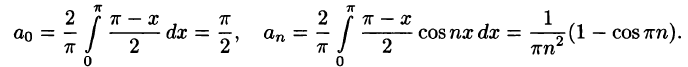
Таким образом,
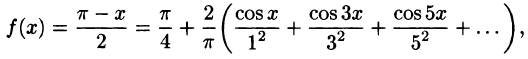
где
Комплексная форма ряда Фурье
Ряды Фурье часто применяются в комплексной форме записи. Преобразуем ряд (66.12) и его коэффициенты (66.13)-(66.15) к комплексной форме. Для этого используем формулы Эйлера, выражающие косинус и синус через показательную функцию:
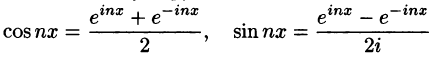
(из формулы Эйлера 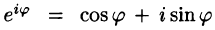 и вытекающего из нее равенства
и вытекающего из нее равенства 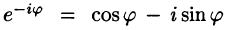 находим, что
находим, что 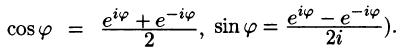 Подставив эти выражения в ряд (66.12), находим:
Подставив эти выражения в ряд (66.12), находим:
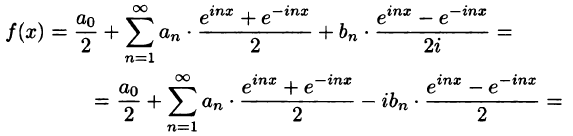
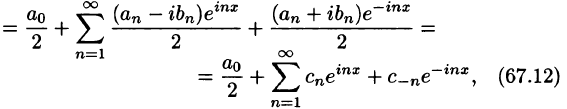
где обозначено
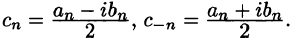
Найдем выражения для комплексных коэффициентов  Используя выражения для
Используя выражения для  (формулы (66.14) и (66.15)), получим:
(формулы (66.14) и (66.15)), получим:
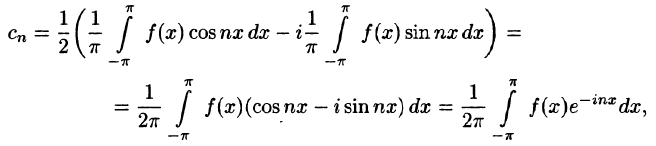
т. е.
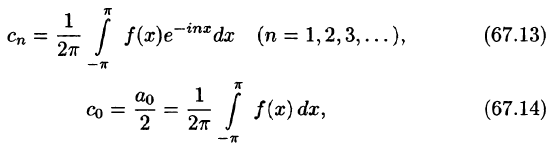
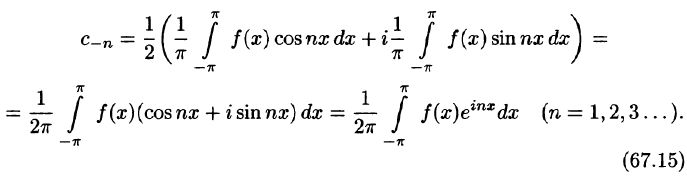
Таким образом, формулу (67.12) можно записать в виде
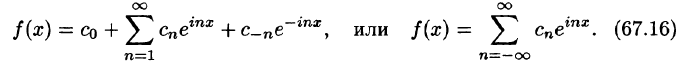
Коэффициенты этого ряда, согласно формулам (67.13)-(67.15), можно записать в виде
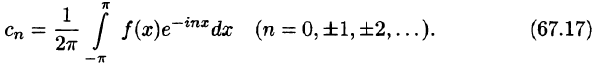
Равенство (67.16) называется комплексной формой ряда Фурье функции f(x), а числа 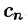 , найденные по формуле (67.17), — комплексными коэффициентами ряда Фурье.
, найденные по формуле (67.17), — комплексными коэффициентами ряда Фурье.
Если функция f(x) задается на отрезке [—l; l], то комплексная форма ее ряда Фурье имеет вид
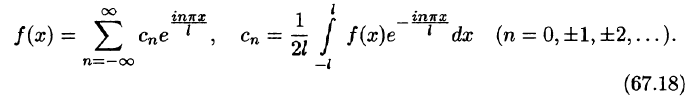
Как видим, комплексная форма ряда Фурье (и коэффициентов) более компактна, чем обыкновенный ряд Фурье.
В электротехнике и радиотехнике члены ряда 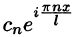 называются гармониками, коэффициенты
называются гармониками, коэффициенты 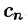 — комплексными амплитудами гармоник, а числа
— комплексными амплитудами гармоник, а числа 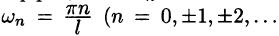 — волновыми числами
— волновыми числами 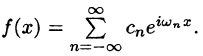
Совокупность величин  называется амплитудными спектром.
называется амплитудными спектром.
Графически амплитудный спектр изображается в виде вертикальных отрезков длиной 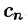 , расположенных в точках
, расположенных в точках 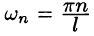 числовой оси.
числовой оси.
Пример:
Построить ряд Фурье в комплексной форме для 2-периодической функции
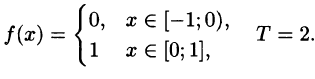
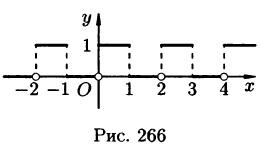
Решение:
На рисунке 266 изображен график функции f(х). По формулам (67.18) находим (l = 1):
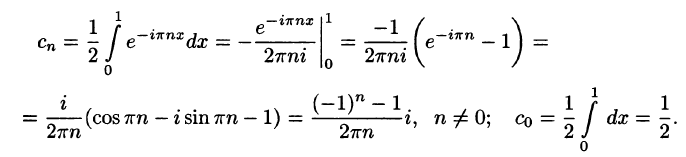
Следовательно, для всех точек непрерывности функции f(х) справедливо равенство
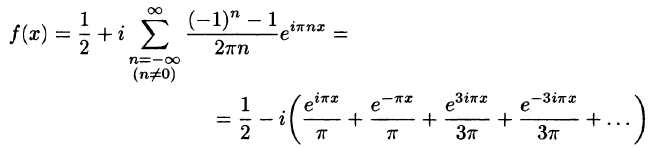
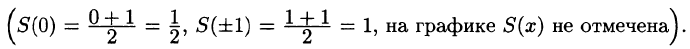
Интеграл Фурье
Как известно, всякую (периодическую или непериодическую) функцию f(х), удовлетворяющую на отрезке [—l; l] условиям теоремы Дирихле, можно разложить в ряд Фурье
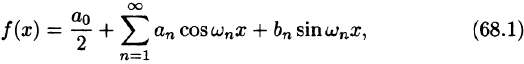
где 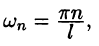
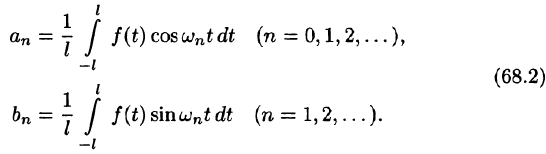
Это разложение будет справедливым на всей числовой оси Ох в том случае, когда f(x) — периодическая функция с периодом Т = 2l.
Рассмотрим случай, когда f(x) — непериодическая функция, заданная на бесконечном промежутке 
Будем предполагать, что на любом конечном промежутке [—l; l] функция f(x) удовлетворяет условиям теоремы Дирихле и что сходится следующий несобственный интеграл:
Говорят: f(х) абсолютно интегрируема на всей числовой оси.
Подставляя в ряд (68.1) значения коэффициентов  (68.2), получим:
(68.2), получим:
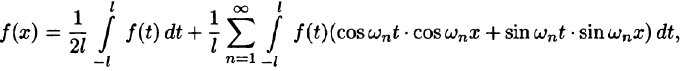
т. e.
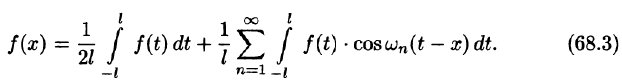
Будем теперь неограниченно увеличивать l. Первое слагаемое в правой части равенства (68.3) при  стремится к нулю, т. к.
стремится к нулю, т. к.
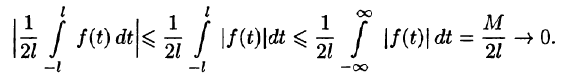
Рассмотрим второе слагаемое в равенстве (68.3). Величина 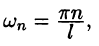 принимает значения
принимает значения 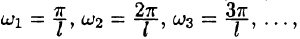 образующие бесконечную арифметическую прогрессию с разностью
образующие бесконечную арифметическую прогрессию с разностью 
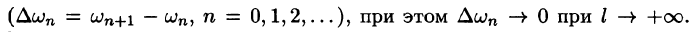
Итак,
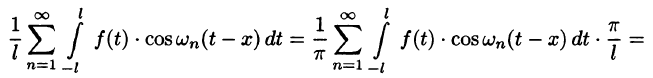
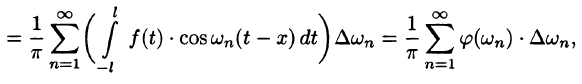
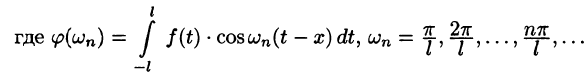
Полученная сумма напоминает интегральную сумму для функции
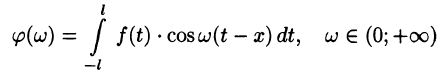
(доказывается, что так оно и есть), поэтому, переходя в равенстве (68.3) к пределу при  получаем
получаем
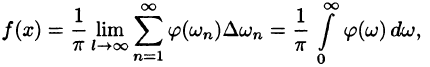
или
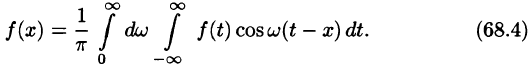
Формула (68.4) называется формулой Фурье, а интеграл в правой части формулы — интегралом Фурье для функции f(x). Формула Фурье имеет место в точках непрерывности функции f(х); в точках разрыва данной функции интеграл Фурье равен среднему арифметическому ее односторонних пределов:
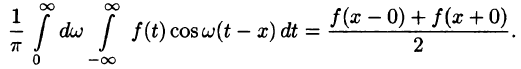
Формулу (68.4) можно переписать в другом виде (в виде однократного интеграла):
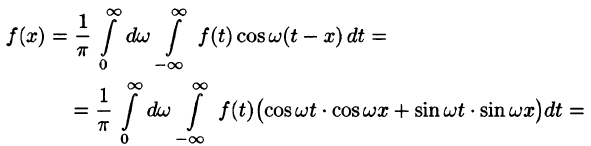
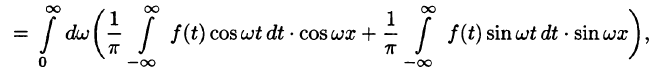
т. е.
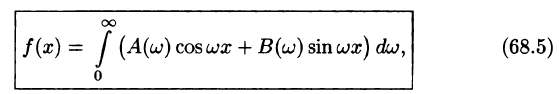
где
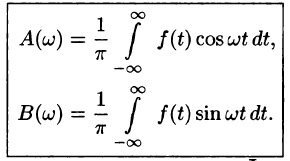
Как видно, есть аналогия между рядом Фурье и интегралом Фурье: в обоих случаях функция f(x) раскладывается на сумму гармонических составляющих. Однако, ряд Фурье суммируется по индексу п, принимающему дискретные значения п = 1,2,3,…, в интеграле Фурье производится интегрирование по непрерывной переменной  .
.
Некоторые сведения, связанные с интегралом Фурье, изложим в виде замечаний.
Замечания:
1.Если функция f(x) — четная, то формула Фурье (68.5) принимает вид
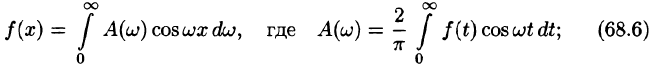
в случае нечетной функции —
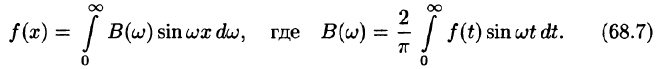
2.Если функция f(x) задана лишь на промежутке  , то ее можно продолжить на промежуток
, то ее можно продолжить на промежуток  разными способами, в частности — четным или нечетным образом: в первом случав она будет представлена формулой (68.6), во втором — формулой (68.7).
разными способами, в частности — четным или нечетным образом: в первом случав она будет представлена формулой (68.6), во втором — формулой (68.7).
3.Формулу Фурье (68.5) можно представить в симметричной форме записи, если положить в формулах (68.6) и (68.7)
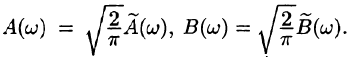
В случае четной функции
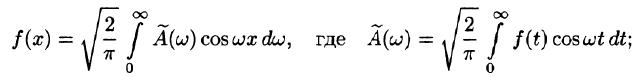
в случае нечетной функции
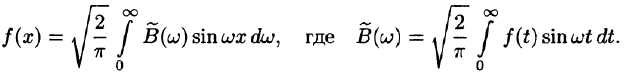
Функции  называются соответственно косинус-пре-образованием и синус-преобразованием Фурье для функции f(x).
называются соответственно косинус-пре-образованием и синус-преобразованием Фурье для функции f(x).
4.Интеграл Фурье (68.4) в комплексной форме имеет вид
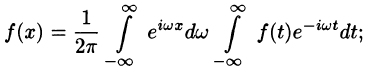
интеграл Фурье (68.5) имеет вид
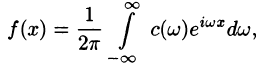
где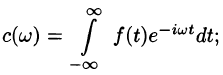 или в симметричной форме записи
или в симметричной форме записи
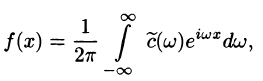
где
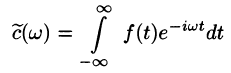
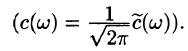
Пример:
Представить интегралом Фурье функцию
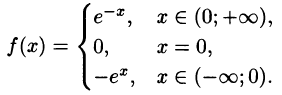
Решение:
Функция удовлетворяет условиям представимости интегралом Фурье, абсолютно интегрируема на промежутке 
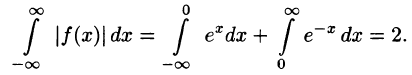
Функция нечетная, применим формулу (68.7):
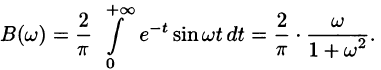
Следовательно,
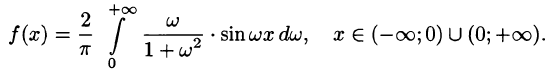
Замечание. Интересно отметить, что если х = 1, то
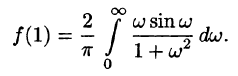
С другой стороны, 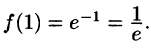 Таким образом,
Таким образом,
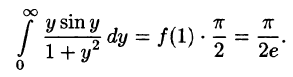
Иными словами, при помощи представления функций интегралом Фурье иногда можно вычислить величины несобственных интегралов.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

