Разложение многочленов на множители в математике с примерами решения и образцами выполнения

Понятие о разложении на множители:

Часто, особенно при преобразованиях дробных алгебраических выражений, бывает нужно представить данный многочлен в виде произведения двух или более многочленов. При этом требуется, чтобы оба множителя содержали одну букву. Преобразование многочлена к виду произведения многочленов называется разложением многочлена на множители.

Например, равенство 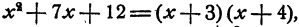которое легко проверяется перемножением многочленов x + З и х + 4 дает разложение многочлена 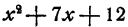на множители х + 3 и х + 4 .

Конечно, разложение на множители возможно далеко не всегда.

Например, многочлен x + 2 нельзя представить, в виде произведения двух многочленов, содержащих букву х, так как старший член произведения двух таких многочленов содержит х по крайней мере во второй степени, а может быть и в более высокой, в то время как многочлен х + 2 таких степеней буквы х не содержит. Многочленов, не допускающих разложения на множители, существует сколько угодно.

Многочлен, который не может быть представлен в виде произведения двух многочленов или в виде произведения многочлена на одночлен, содержащий хотя бы одну букву, называется неприводимым или неразложимым на множители многочленом. Так, многочлен x + 2 неприводим. Наоборот, если многочлен может быть разложен на множители, то он называется приводимым.

Задача о разложении многочлена на множители имеет сходство с задачей о разложении целых чисел на множители. Здесь неприводимые многочлены играют такую роль, какую там играют простые числа, а приводимые многочлены — такую же, как составные числа. Задача о разложении целого числа на множители считается решенной до конца, когда число разложено, на простые множители и дальнейшее разложение невозможно. Таким же образом задача о разложении многочлена на множители может считаться решенной до конца, если все множители, получающиеся в результате разложения, оказываются неприводимыми. Однако так поставленная задача в общем виде очень трудна. В частности, часто бывает трудно ответить на вопрос, приводим заданный многочлен или не приводим? Полное решение этой задачи недоступно по своей трудности для учащихся средней школы.

Однако существует целый ряд простых приемов для разложения многочленов на множители, и искусное владение этими приемами дает возможность почти всегда найти разложение, если только оно вообще возможно.

Заметим еще, что ставить задачу о разложении на множители имеет смысл для многочленов, содержащих более одного члена. Для одночленов, задача решена сама собой, так как одночлен есть произведение степеней букв, а степень тоже есть произведение, но только равных множителей. Преобразование, подобное

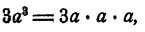
нельзя рассматривать как разложение на множители. Это просто переход от сокращенной записи 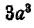к развернутой За • а • а. Даже в арифметике при разложении целых чисел на простые множители принято пользоваться записью с применением степеней. Например,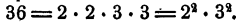

Вынесение за скобку

Пример:

Разложить на множители многочлен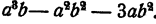

Решение:

Здесь можно заметить, что все три члена многочлена имеют общий множитель ab. Действительно,

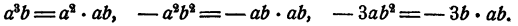
На основании распределительного закона данный многочлен можно записать в виде произведения суммы первых множителей его членов на одночлен ab. Итак,

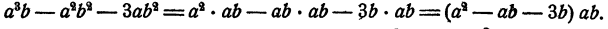
Ответ :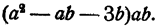

Прием, примененный в рассмотренном примере, называется вынесением за скобку. Этот прием тесно связан с правилом умножения многочлена на одночлен. Так же как правило умножения многочлена на одночлен, вынесение за скобку основывается на распределительном законе. При умножении многочлена на одночлен распределительный закон применяется для того, чтобы представить в виде суммы произведение суммы на число. При вынесении за скобку, наоборот, сумма нескольких слагаемых, имеющих общий множитель, преобразовывается в произведение некоторой суммы на этот множитель.

При вынесении за скобку следует руководствоваться следующим правилом:

Правило. .Если все члены многочлена содержат некоторую букву в каких-либо степенях, то можно вынести за скобку степень этой буквы с наименьшим из показателей, с которыми буква входит в отдельные члены многочлена. Если таких букв имеется несколько, то выносится за скобку произведение степеней этих букв с надлежащими показателями.

Точно так же можно выносить за скобку числовой коэффициент. Вообще говоря, этот коэффициент может быть взят каким угодно. Например,

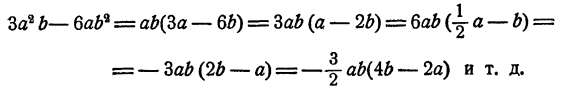
Однако наиболее удобно так выбирать коэффициент, чтобы многочлен, остающийся в скобке, имел целые коэффициенты, не имеющие общего целого множителя, например,

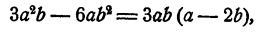
или

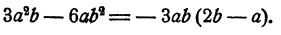
При преобразовании алгебраических выражений вынесение за скобку играет вспомогательную роль. Поэтому выбор знака коэффициента, а иногда и его величины, должен производиться в соответствии с целью, для достижения которой делается вынесение за скобку. В частности, часто бывает нужно вынести за скобку численный множитель, например,

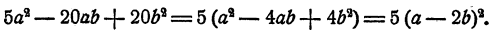
Отметим, наконец, что вынесение за скобку возможно во всяком алгебраическом выражении, представляющем собой сумму нескольких слагаемых, имеющих общий множитель, например,

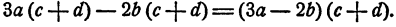
Иногда при этом наличие общего множителя становится очевидным только после некоторых преобразований.

Пример:

Разложить на множители многочлен

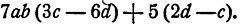
Решение:

Здесь мы видим, что если из выражения,
находящегося в первой скобке, вынести число 3, то в скобке останется двучлен, члены которого только знаками отличаются от членов второй скобки. Поэтому преобразование нужно вести так:

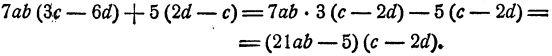
Применение вынесения за скобку к расположению многочлена по степеням одной буквы

Многочлены, содержащие одну букву, целесообразно записывать в порядке убывания степеней. Это оказалось полезным при умножении многочленов, это полезно при разложении на множители и при делении многочлена на многочлен.

Такая запись часто оказывается удобной и для многочленов, содержащих несколько букв. При этом из всех букв нужно выбрать одну, главную букву и записывать, одночлены в порядке убывания степеней этой буквы.

Например, многочлен расположен в порядке убывания степеней буквы х. Если бы мы в этом многочлене в качестве главной буквы взяли вместо х другую букву, например b, мы должны были бы записать его члены в другом порядке, именно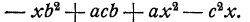

При таком расположении часто оказывается, что имеется несколько, членов, содержащих главную букву в одной и той же степени. В нашем примере имеется два члена, содержащих х в первой степени. Для того чтобы еще более подчеркнуть, что за главную букву принимается х, целесообразно рассматривать члены, содержащие х в одной и той же степени, как подобные, и соединять их вместе посредством вынесения буквы х в надлежащей степени за скобку из алгебраической суммы таких членов. Так,

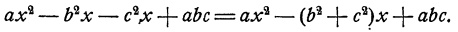
В такой записи многочлен выглядит как многочлен, зависящий только от одной буквы х, но с буквенными коэффициентами и с буквенным свободным членом. Так, коэффициентами в многочлене 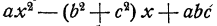являются 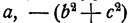и свободным членом является abc.

Естественно поставить вопрос о том, какую букву нужно выбрать за главную, если мы хотим расположить по степеням одной буквы многочлен, зависящий от нескольких букв.

Если многочлен рассматривается без связи с какой-либо задачей, то выбор главной буквы совершенно безразличен. Если же многочлен получается при решении задачи, часто условие задачи подсказывает, какую букву следует считать главной.

Рассмотрим один пример этого рода.

Задача:

Коробка имеет длину а см, ширину b см. Требуется найти высоту, при которой площадь поверхности коробки равняется s см.

Решение:

Обозначим высоту буквой х. Поверхность коробки составлена из шести прямоугольников. Два из этих прямоугольников (дно и крышка) имеют площадь аb 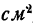другие два (левая и правая стенки) имеют площадь bх 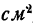, и последние два (передняя и задняя стенки) имеют площадь ах 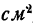. Следовательно, между четырьмя буквами a, b, s и х имеется следующая зависимость:

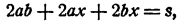
или, что то- же самое,

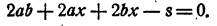
Мы получили уравнение, в левой части которого находится многочлен, зависящий от букв a, b, x и s Какую же из этих .четырех букв следует принять за главную букву? Конечно, х, так как х играет особую роль в задаче. Числа а, b и s — это числа известные данные. Число х — неизвестное. Поэтому полученное нами уравнение следует записать так:

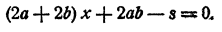
А теперь его легко решить.

Сумма чисел 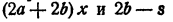равна нулю. Следовательно, это противоположные числа:

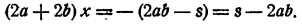
Произведение числа х на число 2а + 2b равно s — 2аb. Следовательно,

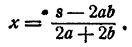
Задача решена.

Способ группировки

Рассмотрим следующий пример на умножение многочленов:

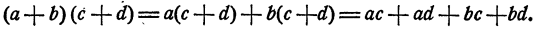
Мы воспользовались правилом 1 умножения многочлена на многочлен (гл. III, § 9).

Представим теперь себе, что у нас поставлена обратная задача. Дан многочлен 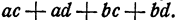Требуется разложить его на множители. Очевидно, что для этого нужно провести те же вычисления, но в обратном порядке:

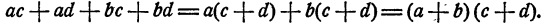
Мы объединяем первое слагаемое со вторым и выносим из их суммы а за скобку, одновременно объединяем третье и четвертое слагаемые и из их суммы выносим за скобку b: В обеих скобках получается одно и то же выражение с + d, и его снова выносим за скобку.

Рассмотрим теперь еще один пример, в котором разложение на множители заранее неизвестно.

Пример:

Разложить на множители многочлен

Решение:

Мы видим, что если объединить первое и второе слагаемые, то из их суммы можно вынести за скобку За, а из суммы третьего слагаемого с четвертым можно вынести за скобку — 2b. В обоих случаях в скобке остается одно и то же выражение c + d, так что многочлен преобразуется в сумму двух слагаемых, имеющих общий множитель с + d. После этого можно вынести за скобку c + d.

Наметив такой план преобразований, переходим к его осуществлению:

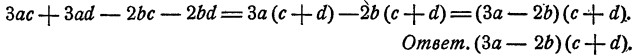
Примененный в рассмотренном примере способ называется способом группировки. В общем виде способ группировки состоит в том, что слагаемые, из которых составлен многочлен, объединяются в группы с таким расчетом, чтобы после вынесения в каждой группе некоторых одночленов за скобку в скобках оказались бы одинаковые многочлены.

Конечно, совсем не обязательно объединять слагаемые, находящиеся рядом, как это было сделано в рассмотренных примерах. В многочлене 3ac+3ad-2bc-2bd мы могли с тем же успехом объединить первое слагаемое С третьим, а второе с четвертым. Действительно,

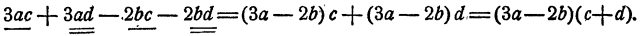
А в многочлене а*—АЬс— аЪ — 4ас группировка соседних слагаемых ничего не дает. Здесь нужно объединить первое слагаемое с третьим, второе с четвертым пли первое с четвертым, второе с третьим:

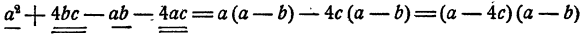
или

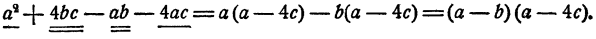
Разложение отдельных членов многочлена на подобные слагаемые

Часто бывает, что при умножении многочлена на многочлен после того как скобки раскрыта можно сделать приведение подобных членов. Поэтому при разложении многочлена на множители часто бывает полезно прежде чем совершать группировку разбить некоторые одночлены на подобные слагаемые с тем, чтобы эти слагаемые разнести потом в разные группы.

Пример:

Разложить на множители многочлен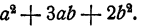

Решение:

В этом многочлене группировка его членов бесполезна для разложения на множители. Однако, если предварительно разбить одночлен 3аb на сумму двух членов аb и 2ab и разнести их в разные группы, то разложение удастся. Действительно,

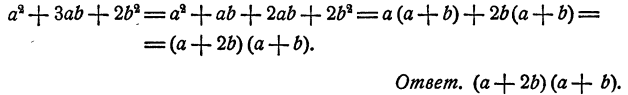
Более того, при умножении многочленов возможно, что некоторые слагаемые, получившиеся в результате раскрытия скобок, при приведений подобных членов взаимно уничтожаются. Поэтому иногда при разложении многочлена на множители перед группировкой слагаемых нужно вставить новый одночлен, взяв его два раза с противоположными знаками.

Пример:

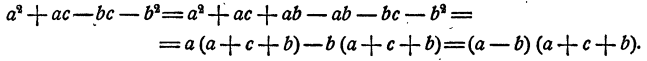
Применение формул сокращенного умножения

Формулы сокращенного умножения часто значительно облегчают разложение на множители, позволяя избежать разложения одночленов на подобные слагаемые и обойтись без вставки новых одночленов .

Пример:

Разложить на множители

Решение:

Мы видим, что исследуемый многочлен есть разность квадратов чисел х и 2. Следовательно, его можно записать в виде произведения суммы этих чисел на их разность

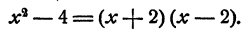
Пример:

Разложить на множители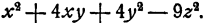

Решение:

Мы видим, что сумма первых трех слагаемых есть квадрат суммы чисел х и 2у. Действительно, квадрат первого числа равен 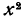, удвоенное произведение первого на второе равно 4ху, квадрат второго равен 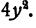Итак,

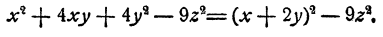
Теперь наш многочлен приведен к виду разности квадратов чисел (х + 2у) и 3z. Следовательно, его можно представить в виде произведения суммы этих чисел на их разность

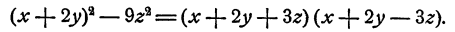
Пример:

Разложить на множители многочлен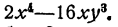

Решение:

Прежде всего надо вынести за скобку 2х

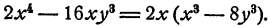
Теперь мы видим, что многочлен, находящийся в скобке, есть разность кубов чисел х и 2у. По сокращенной формуле мы знаем, что разность кубов двух чисел равна произведению разности этих чисел на «неполный квадрат их суммы». Итак,

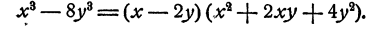
Окончательно получаем

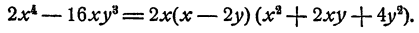
Мы прерывали запись действий рассуждениями. Конечно, при решении такого рода примеров рассуждения надлежит производить без записи—вслух или про себя, и запись должна выглядеть так:

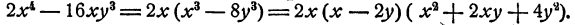
Более сложные примеры с решением

Мы разобрали несколько приемов разложения многочлена на множители— вынесение за скобку, способ группировки, разложение одночленов на подобные слагаемые, использование формул сокращенного умножения. Не существует никаких общих правил для того, какими из этих приемов и в каких сочетаниях их друг с другом надлежит пользоваться для достижения цели в каждом частном
случае. (Конечно, если это возможно, следует раньше всего сделать вынесение за скобку. Это никогда не ведет к усложнению, но часто упрощает задачу.) Поэтому, прежде чем приступить к выкладке, необходимо вдуматься в строение разлагаемого многочлена и
составить план действий. Для того чтобы показать, как составлять этот план, рассмотрим несколько более сложных примеров.

Пример:

Разложить на множители многочлен

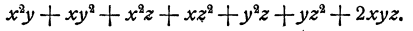
Решение:

Мы видим, что если из суммы первых двух слагаемых вынести х у, в скобке останется х + у. Попробуем сгруппировать остальные слагаемые так, чтобы х + у входило множителем в сумму слагаемых каждой группы. Мы видим, что «хорошей» в этом
смысле группой является сумма 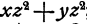при вынесении из нее за скобку 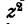в скобке останется х + у. Остается группа слагаемых 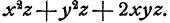Если в этой группе вынести за скобку z, то в скобке oстанется 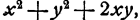т. е. квадрат суммы (х + у). Итак,

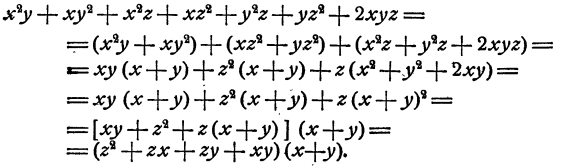
Первый множитель можно разложить дальше, воспользовавшись способом группировки:

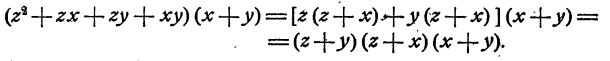
Пример:

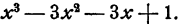
Решение:

Здесь прежде всего бросается в глаза, сходство с кубом суммы или разности чисел , х и 1. Однако это сходство обманчиво— знаки не те! Поэтому следует искать другой прием. Например, хорошо сгруппировать вместе крайние члены 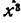и 1 и средние — 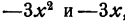, ибо 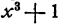содержит , множитель x + l по формуле суммы кубов, и тот же множитель х + 1 обнаруживается в 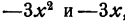; посредством вынесения за скобку. Итак,

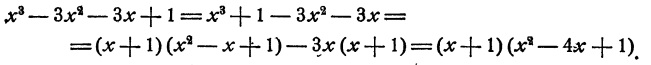
Пример:

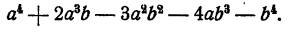
Решение:

Здесь целесообразно член 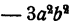разбить на сумму двух членов 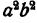и 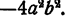Действительно, тогда сумма первых трех членов, а также взятая с обратным знаком сумма последних трех представится в виде квадратов, и после этого останется применить формулу для разложения разности квадратов. Осуществим этот план:

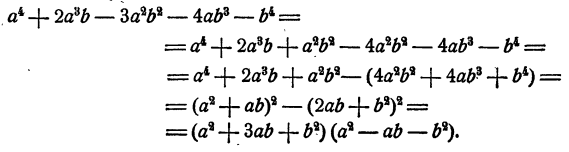
Пример:

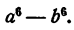
Решение:

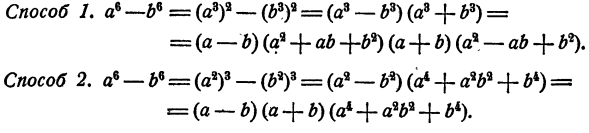
Сравнивая результаты, мы видим, что 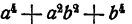разлагается на два множителя: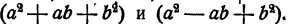. В этом можно убедиться и непосредственно:

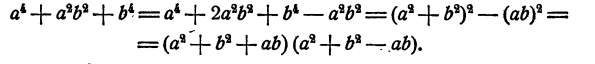
Пример:

Разложить на множители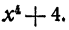

Решение:

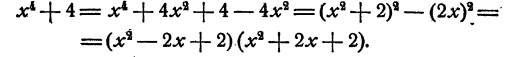
Пример:

Разложить на множители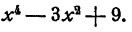

Решение:

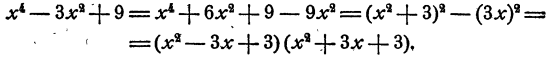
В последних двух примерах разложение удается посредством преобразования в разность квадратов. Этот прием часто ведет к цели при разложении так называемого биквадратного трехчлена, т. е. трехчлена, составленного из четвертой и второй степеней Одной буквы с некоторыми коэффициентами и свободного члена.

Разложение квадратного трехчлена на множители

Квадратным трехчленом называется многочлен второй степени, содержащий одну букву, например,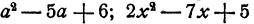 и т. д.

В частности, член, содержащий первую степень буквы, или свободный член могут отсутствовать. Такого^ рода выражения называются неполными квадратными трехчленами, хотя на самом деле они состоят только из двух слагаемых. Например,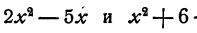 неполные трехчлены.

Для разложения квадратного трехчлена на множители можно рекомендовать два способа, которые мы рассмотрим на решении одного примера.

Пример:

Разложить на множители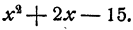

Решение:

Способ 1. Рассмотрим тождество

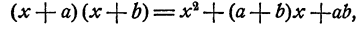
которое легко проверяется. Действительно,

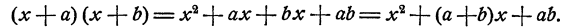
Из этого тождества следует, что если мы сумеем разложить коэффициент при х на сумму двух слагаемых а и b так, чтобы произведение ab этих слагаемых равнялось свободному члену, то нам удастся найти разложение трехчлена на множители.

В нашем примере 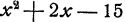в качестве таких слагаемых можно взять 5 и —3. Тогда

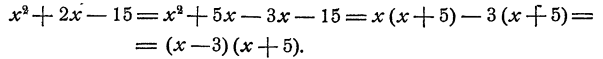
Способ 2. В данном трехчлене 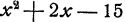выделим полный квадрат суммы посредством следующего рассуждения. Заметим, что 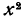есть квадрат числа х. Примем х за первое слагаемое. Рассмотрим затем следующий член 2х как удвоенное произведение первого слагаемого х на второе. Очевидно, что за второе слагаемое s нужно принять 1. Затем добавляем квадрат этого второго слагаемого и, чтобы равенство не нарушилось, сразу его отнимаем. Получим

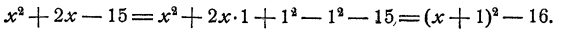
Дальнейшее ясно: 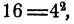и следовательно,

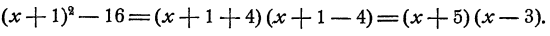
Во втором способе, в отличие от первого, мы не прибегаем к подбору. Мы собираем все члены, содержащие х, в выражение, имеющее вид полного квадрата, и затем, если это возможно, пользуемся
формулой для разложения разности квадратов.

Пример:

Разложить на множители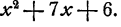

Решение:

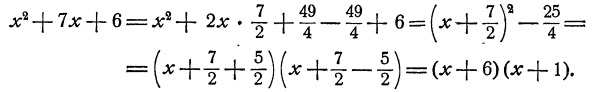
Если коэффициент при 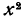отличен от 1, следует предварительно вынести его за скобку.

Пример:

Разложить на множители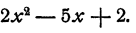

Решение:

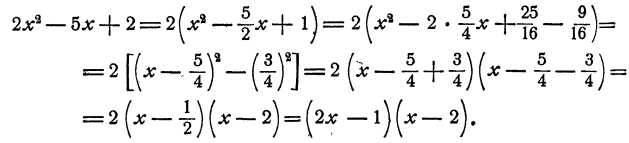
Второй способ, кроме этого, дает возможность выяснить вопрос о том, разлагается квадратный трехчлен на множители или нет. Именно, если число, остающееся после выделения полного квадрата суммы или разности из квадратного трехчлена, не является квадратом со знаком минус, то трехчлен не может быть разложен на множители.

Пример:

Разложить на множители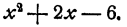

Решение:

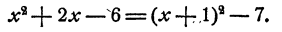
Этот трехчлен на множители не разлагается.

Пример:

Разложить на множители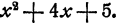

Решение:

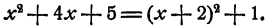
Разложение на множители тоже невозможно.

Оба приема разложения можно применять к трехчленам, содержащим, кроме выбранной главной буквы, также и другие буквы.

Пример:

Разложить на множители

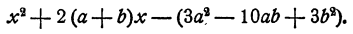
Решение:

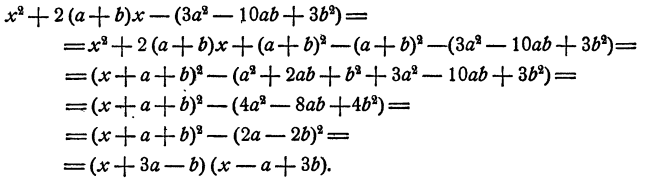
Дополнение к разложению многочленов на множители

Смотрите также:

Предмет математический анализ

Формальная теория комплексных чисел.	Наибольший общий делитель многочленов.
Некоторые понятия анализа в области комплексных чисел.	Разложение правильных рациональных дробей на элементарные.

Решение заданий и задач по предметам:

• Математика
• Высшая математика
• Математический анализ
• Линейная алгебра

Дополнительные лекции по высшей математике:

1. Тождественные преобразования алгебраических выражений
2. Функции и графики
3. Преобразования графиков функций
4. Квадратная функция и её графики
5. Алгебраические неравенства
6. Неравенства
7. Неравенства с переменными
8. Прогрессии в математике
9. Арифметическая прогрессия
10. Геометрическая прогрессия
11. Показатели в математике
12. Логарифмы в математике
13. Исследование уравнений
14. Уравнения высших степеней
15. Уравнения высших степеней с одним неизвестным
16. Комплексные числа
17. Непрерывная дробь (цепная дробь)
18. Алгебраические уравнения
19. Неопределенные уравнения
20. Соединения
21. Бином Ньютона
22. Число е
23. Непрерывные дроби
24. Функция
25. Исследование функций
26. Предел
27. Интеграл
28. Двойной интеграл
29. Тройной интеграл
30. Интегрирование
31. Неопределённый интеграл
32. Определенный интеграл
33. Криволинейные интегралы
34. Поверхностные интегралы
35. Несобственные интегралы
36. Кратные интегралы
37. Интегралы, зависящие от параметра
38. Квадратный трехчлен
39. Производная
40. Применение производной к исследованию функций
41. Приложения производной
42. Дифференциал функции
43. Дифференцирование в математике
44. Формулы и правила дифференцирования
45. Дифференциальное исчисление
46. Дифференциальные уравнения
47. Дифференциальные уравнения первого порядка
48. Дифференциальные уравнения высших порядков
49. Дифференциальные уравнения в частных производных
50. Тригонометрические функции
51. Тригонометрические уравнения и неравенства
52. Показательная функция
53. Показательные уравнения
54. Обобщенная степень
55. Взаимно обратные функции
56. Логарифмическая функция
57. Уравнения и неравенства
58. Положительные и отрицательные числа
59. Алгебраические выражения
60. Иррациональные алгебраические выражения
61. Преобразование алгебраических выражений
62. Преобразование дробных алгебраических выражений
63. Многочлены от одного переменного
64. Алгебраические дроби
65. Пропорции
66. Уравнения
67. Системы уравнений
68. Системы уравнений высших степеней
69. Системы алгебраических уравнений
70. Системы линейных уравнений
71. Системы дифференциальных уравнений
72. Арифметический квадратный корень
73. Квадратные и кубические корни
74. Извлечение квадратного корня
75. Рациональные числа
76. Иррациональные числа
77. Арифметический корень
78. Квадратные уравнения
79. Иррациональные уравнения
80. Последовательность
81. Ряды сходящиеся и расходящиеся
82. Тригонометрические функции произвольного угла
83. Тригонометрические формулы
84. Обратные тригонометрические функции
85. Теорема Безу
86. Математическая индукция
87. Показатель степени
88. Показательные функции и логарифмы
89. Множество
90. Множество действительных чисел
91. Числовые множества
92. Преобразование рациональных выражений
93. Преобразование иррациональных выражений
94. Геометрия
95. Действительные числа
96. Степени и корни
97. Степень с рациональным показателем
98. Тригонометрические функции угла
99. Тригонометрические функции числового аргумента
100. Тригонометрические выражения и их преобразования
101. Преобразование тригонометрических выражений
102. Комбинаторика
103. Вычислительная математика
104. Прямая линия на плоскости и ее уравнения
105. Прямая и плоскость
106. Линии и уравнения
107. Прямая линия
108. Уравнения прямой и плоскости в пространстве
109. Кривые второго порядка
110. Кривые и поверхности второго порядка
111. Числовые ряды
112. Степенные ряды
113. Ряды Фурье
114. Преобразование Фурье
115. Функциональные ряды
116. Функции многих переменных
117. Метод координат
118. Гармонический анализ
119. Вещественные числа
120. Предел последовательности
121. Аналитическая геометрия
122. Аналитическая геометрия на плоскости
123. Аналитическая геометрия в пространстве
124. Функции одной переменной
125. Высшая алгебра
126. Векторная алгебра
127. Векторный анализ
128. Векторы
129. Скалярное произведение векторов
130. Векторное произведение векторов
131. Смешанное произведение векторов
132. Операции над векторами
133. Непрерывность функций
134. Предел и непрерывность функций нескольких переменных
135. Предел и непрерывность функции одной переменной
136. Производные и дифференциалы функции одной переменной
137. Частные производные и дифференцируемость функций нескольких переменных
138. Дифференциальное исчисление функции одной переменной
139. Матрицы
140. Линейные и евклидовы пространства
141. Линейные отображения
142. Дифференциальные теоремы о среднем
143. Теория устойчивости дифференциальных уравнений
144. Функции комплексного переменного
145. Преобразование Лапласа
146. Теории поля
147. Операционное исчисление
148. Системы координат
149. Рациональная функция
150. Интегральное исчисление
151. Интегральное исчисление функций одной переменной
152. Дифференциальное исчисление функций нескольких переменных
153. Отношение в математике
154. Математическая логика
155. Графы в математике
156. Линейные пространства
157. Первообразная и неопределенный интеграл
158. Линейная функция
159. Выпуклые множества точек
160. Система координат