Рациональные числа в математике их свойства с примерами решения и образцами выполнения

Оглавление:

Вообразим, что мы не знаем никаких других чисел, кроме натуральных, т. е. кроме целых положительных. Тогда действия сложение и умножение окажутся выполнимыми всегда, а действие, скажем, деление — не всегда.

Например, деление числа 20 на 4 будет выполнимым, так как результат этого деления — число 5 — содержится во множестве натуральных чисел.

Деление же числа 20 на 7 уже будет невыполнимым, так как во множестве натуральных чисел нет числа 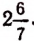Рациональные числа .

Если же мы расширим множество натуральных чисел введением дробных положительных чисел, то придем к тому, что в этой расширенной области станут выполнимыми не только сложение и умножение, но и деление.

Однако в этой расширенной области, так же как и в области натуральных чисел, не всегда будет выполнимым действие вычитание. Например, вычитание из числа 5 числа 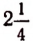Рациональные числа будет выполнимым, а вычитание из числа 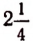числа 5 уже будет невыполнимым, так как во множестве положительных чисел нет числа — .

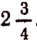Если же мы расширим множество целых и дробных положительных чисел введением еще и отрицательных чисел, то в этой дважды расширенной числовой области уже станут выполнимыми все первые четыре действия.

Обратим внимание на то, что для выполнения прямых действий (сложения и умножения) не требовалось расширения понятия натурального числа, между тем как для выполнения обратных действий (деления и вычитания) такое расширение оказалось уже необходимым.

Понятие натурального числа и дальнейшие расширения понятия числа происходили и происходят под влиянием и для удовлетворения практических потребностей людей (включая и потребности математической практики).

Если рассматривать указанные выше расширения как необходимость, вытекающую только из внутренних потребностей самой математики, то, как мы видели, «повод» к такому расширению давали обратные действия: деление и вычитание.

Однако следует заметить, что причиной введения дробных чисел служила не только невыполнимость деления, но, пожалуй, в большей степени, задача измерения величины в случае, когда единица измерения не укладывалась в измеряемой величине целое число раз.

Рациональная числовая область

В результате указанных выше двух расширений понятия числа мы пришли к такой числовой области, в которой содержатся все целые и дробные (положительные и отрицательные) числа. Такую числовую область с присоединенным к ней нулем называют рациональной числовой областью.

Определение:

Все целые и дробные числа (положительные и отрицательные), включая нуль, называются числами рациональными.

В рациональной числовой области все четыре действия, за исключением деления на нуль, всегда выполнимы.

Конечные и бесконечные десятичные дроби

Всякая десятичная дробь, которая изображается конечным числом цифр, называется конечной десятичной дробью. Например, 5,23; 0,4711; 2,14159 суть конечные десятичные дроби.

Всякая десятичная дробь, в которой после запятой следует бесконечное множество цифр, называется бесконечной десятичной дробью. Например, 5,12112111211112… есть бесконечная десятичная дробь. Здесь цифры после запятой идут без конца по следующему закону: единица, два; два раза единица, два; три раза единица,1 два и т. д. без конца.

Если в бесконечной десятичной дроби, начиная с некоторого места после запятой, одна и та же группа цифр повторяется без конца, непосредственно следуя одна за другой, то такая дробь называется бесконечной периодической десятичной дробью.

Примеры:

суть бесконечные периодические десятичные дроби. Из них первые три — чистые периодические, а две последние — смешанные периодические.

Всякая конечная десятичная дробь есть число рациональное. Например, 2,69 есть рациональное число 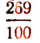Рациональные числа .

Всякая бесконечная периодическая десятичная дробь есть также рациональное число. Например, как известно из арифметики,

2,444 … есть рациональное число — 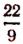Рациональные числа ,

2,2555 … есть рациональное число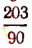 Рациональные числа

О возможности изображения всякого рационального числа в виде бесконечной десятичной дроби

Как известно из арифметики, всякое рациональное число можно изобразить в виде бесконечной десятичной дроби. Действительно,

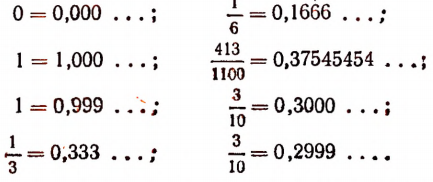
Итак, всякое рациональное число может быть изображено в форме, бесконечной десятичной дроби, которая обязательно будет периодической.

§ 5. ОСНОВНАЯ ТЕОРЕМА О РАЦИОНАЛЬНЫХ ЧИСЛАХ

Теорема:

Между любыми двумя различными рациональными числами заключено бесконечно много (бесконечное множество) других рациональных чисел.

Доказательство. Пусть 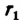и 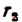любые рациональные числа и пусть, например, 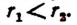Тогда

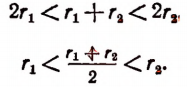
Число 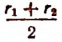Рациональные числа обозначим для краткости через 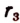. Очевидно, что 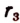есть рациональное число, заключенное между 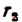и .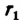

Теперь рассмотрим числа 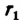Рациональные числа и 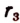. По доказанному выше найдется рациональное число 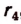, заключенное между 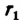и 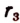, а следовательно, заключенное между 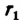и .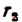

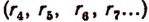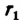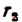Такие рассуждения можно повторять сколько угодно раз и получить еще сколько угодно рациональных чисел Рациональные числа , лежащих между числами и . Теорема доказана.

Пример:

Между числами 1 и 1,1 заключено бесконечное множество таких чисел, как, например, 1,01; 1,011; 1,0111; 1,01111; 1,011111;… Кроме этого множества чисел, можно указать сколько угодно других бесконечных множеств рациональных чисел, также заключенных между 1 и 1,1. Например, 1,07; 1,007; 1,0007;…

Рациональные точки числовой оси

Множеству рациональных чисел соответствует определенное множество точек числовой оси (см. стр. 44). Для нескольких произвольно взятых рациональных чисел это соответствие указано на рисунке 65.

Точки числовой оси, соответствующее рациональным числам, называются рациональными точками числовой оси. Рациональные точки числовой оси для образности будем называть «черными».

Было доказано, что между двумя любыми различными рациональными числами заключено бесконечное множество других рациональных чисел. Образно это мы можем сформулировать так: между двумя любыми «черными» точками числовой оси заключено бесконечное множество других «черных» точек.

В следующей главе мы обнаружим, что рациональные т. е. «черные») точки далеко не заполняют собой всю числовую ось, т. е. что на числовой оси, кроме этих рациональных («черных») точек, имеется бесконечное множество еще и других точек, которые все мы будем образно называть «красными».

Термины «черные» и «красные» точки здесь введены условно и временно лишь с тем, чтобы в изложение темы ввести элемент наглядности. Эти термины не следует понимать в буквальном смысле слова, так как точка не имеет измерений, а поэтому бессмысленно говорить и о ее цвете.

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике: