Оглавление:
Прогрессия — это последовательность величин, каждая последующая из них находится в некоторой, общей для всей прогрессии, зависимости от предыдущей.
Арифметическая прогрессия
Задача:
Рабочему поручили выкопать колодец и условились платить ему за первый метр глубины 3 руб., за второй 5 руб. ит. д., увеличивая плату за каждый следующий метр на 2 руб. Сколько уплатили рабочему, если колодец был вырыт им в 10 м глубины?
Для решения задачи надо найти сумму таких чисел:
3+5+7+9+11+ 13+15+17+19+21.
Сумму эту мы можем найти проще, чем обыкновенным сложением. Обозначив её буквой s, напишем две такие строки:
s = 3+ 5+ 7+ 9+11 + 13 + 15+17 + 19 + 21,
s=21+19+17+15+13+11+ 9+ 7 + 5+ 3.
Вторую строку мы написали, переставив слагаемые первой строки в обратном порядке, от чего, конечно, сумма не изменилась. Сложим теперь все числа, стоящие друг под другом.
2s=24 + 24 + 24 + 24 + 24 + 24 + 24 + 24 + 24 + 24,
т. е.
2s=24 ∙ 10 = 240,
и, следовательно,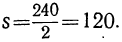
Таким образом, за всю работу уплатили 120 рублей.
В этой задаче нам пришлось иметь дело с рядом чисел, последовательно возрастающих на одно и то же число. Подобные ряды носят название арифметических прогрессий.
Определение:
Арифметической, или разностной, прогрессией называется такой ряд чисел, в котором каждое число, начиная со второго, равняется предыдущему, сложенному с одним и тем же постоянным для этого ряда числом (положительным или отрицательным).
Так, два ряда чисел: 10, 14, 18, 22, 26, 30, 34, 38, 42, 46 и 6, 4, 2, 0, —2, —4, —6 составляют арифметические прогрессии, так как в них каждое число, начиная со второго, равно предыдущему числу, сложенному в первом ряду с положительным числом 4, а во втором—с отрицательным числом —2.
Числа, составляющие прогрессию, называются её членами. Положительное или отрицательное число, которое надо прибавить к предыдущему члену, чтобы получить последующий, называется разностью прогрессии.
Прогрессия называется возрастающей или убывающей, смотря по тому, увеличиваются ли её члены по мере удаления от начала ряда или уменьшаются; разность возрастающей прогрессии есть число положительное, а убывающей — отрицательное.
Для обозначения того, что ряд чисел представляет собой арифметическую прогрессию, иногда ставят в начале ряда знак ÷.
Обыкновенно принято обозначать: первый члена, а последний l, разность d, число всех членов n и сумму их s.
Формула любого члена арифметической прогрессии
Пусть имеем прогрессию: ÷ 10, 14, 18, … (разность 4).
Тогда 2-й член = 10+4 = 14;
3-й „ =10+4+4=10+4∙2=18;
4-й „ =10+4+4+4 = 10+4∙3 = 22 и т. д.
Значит:
10-й член= 10+4∙9=46;
20-й „ =10+4∙19=86 и т. д.
Подобно этому, если имеем прогрессию: ÷ 6, 4, 2,… (разность—2), то
2-й член=6+(—2)=4;
3-й „ =6+(-2)+(-2)=6+(-2)∙2=2 и т. д.
Например:
10-й член=6+(—2) ∙ 9= —12.
Вообще, если прогрессия будет такая: ÷ α, b, с,… (разность d), то
2-й член=а+d;
3-й „ = α+d+d=a+ 2d;
4-й „ =a+2d+d=a+3d и т. д.
Значит, 10-й член окажется a+9d. 15-й член будет a + 14d, вообще m-й член будет a+d(m -1). Таким образом:
Всякий член арифметической прогрессии равен первому её члену, сложенному с произведением разности прогрессии на число членов, предшествующих определяемому.
В частности, последний член равен первому члену, сложенному с произведением разности на число всех членов, уменьшенное на 1, т. е.:
l=a+d(n-1). (1)
Примеры:
1) Найти 10-й член прогрессии: ÷60, 75, 90,…
Так как разность этой прогрессии равна 15, то 10-й член будет
60 + 15 ∙ 9 = 195.
2) Найти 12-й член прогрессии: ÷40, 37, 34,…
Так как разность равна —3, то 12-й член должен быть
40+(-3) ∙ 11=40-33 = 7.
3) Каким будет n-е число в последовательном ряду нечётных чисел: 1, 3, 5, .. .?
Такое число будет
l+2(n-1) = l+2n-2 — 2n-l.
Следствие. Арифметическую прогрессию, у которой первый член есть а, разность d и число членов п, можно изобразить так:
α, α+b, α+2d, a+3d, …, a+d(n-1).
Формула суммы членов арифметической прогрессии
Предварительно убедимся в следующем свойстве:
Сумма двух членов арифметической прогрессии, равноотстоящих от концов, равна сумме крайних членов.
Например, в прогрессии: ÷ 3, 7, 11, 15, 19, 23 находим:
3+23=26; 7+19=26; 11 + 15=26.
Понятно, почему это так: первые слагаемые этих сумм (т. е. 3, 7, 11) идут, возрастая на 4, а вторые слагаемые (23, 19, 15) идут, убывая на 4; поэтому сумма каждой пары остаётся та же.
Возьмём ещё пример убывающей прогрессии: ÷ 8, 6, 4, 2, 0, —2, —4. В ней
8+(-4) = 4, 6 + (-2) = 4, 4+0=4.
Член 2, отстоящий одинаково от начала и от конца, должен быть сложен сам с собой: 2+2=4. И здесь объяснение то же самое: слагаемые 8, 6, 4, 2 идут, уменьшаясь на 2, а слагаемые —4, —2, 0 и 2 идут, увеличиваясь на 2; от этого сумма каждой пары остаётся без изменения.
Теперь выведем формулу для суммы членов любой арифметической прогрессии. Для этого применим тот способ, посредством которого мы нашли сумму членов арифметической прогрессии в задаче, а именно: сложим почленно два таких равенства:
s=a+b+c+.. ∙+i+k+l
s =l+k+i+.. .+c+b+α
2s=(a+l)+(b+k)+(c+i) + … + (i+c) + (k+b)+(l+α).
Но
α+l = b+k=c+i = …=l+a;
следовательно:
2s = (α+l)n, откуда 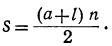 (2)
(2)
Сумма всех членов арифметической прогрессии равна половине произведения суммы крайних членов на число членов.
Таким образом, в задачедля суммы s по этой формуле найдём то число, которое мы нашли ранее другим путём:
s= [(3+21) ∙ 10]: 2=120.
Пример:
Найти сумму натуральных чисел от 1 до n включительно.
Ряд: 1, 2, 3, …, n есть арифметическая прогрессия, у которой первый член 1, разность 1, число членов n и последний член тоже и; поэтому:
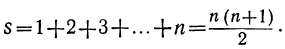
Так: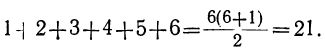
Пример:
Найти сумму первых n нечётных чисел.
Как мы видели, n-е нечётное число равно 2n—1; поэтому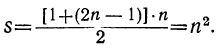
Так:
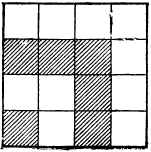
1 + 3=4=2²; l+3+5=9=3²; 1+3+5+7 = 16=4² и т. д.
Это свойство сумм нечётных чисел наглядно изображается чертежом 25, который составлен так: к квадрату (внизу слева) приставлены 3 таких же квадрата (1 сверху, 1 сбоку и 1 в верхнем углу); к этим квадратам приставлены ещё 5 квадратов (2 сверху, 2 сбоку и 1 в верхнем правом углу). К ним, далее, приложены 7 квадратов, потом 9 квадратов и т. д. Тогда очевидно, что
1 + 3=2² , 1+3+5=3² ,
1 + 3+5 +7 = 4² и т. д.
Пример:
Найти сумму 10 членов прогрессии: ÷3, 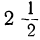 , 2,…
, 2,…
Здесь α=3, 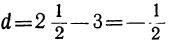 , поэтому 10-й член прогрессии будет
, поэтому 10-й член прогрессии будет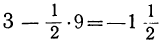 , и потому искомая сумма равна:
, и потому искомая сумма равна: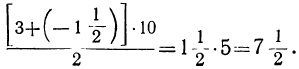
Проверка: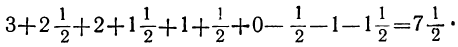
77. Замечание. Так как для пяти чисел a, l, d, n и s мы имеем два уравнения: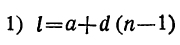 и
и 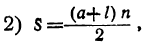
то по данным трём из этих чисел можем находить остальные два. Для примера решим следующую задачу:
Найти число членов прогрессии, у которой первый член 7, разность—2 и сумма всех членов 12.
В этой задаче даны: a=7, d=-2 и s=12; остаются неизвестными l и n. Подставив в формулы (1) и (2) заданные числа, находим:
l =7-2(n-l)=9-2n; 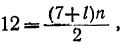
откуда: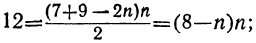
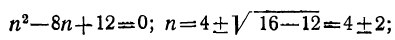
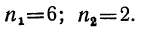
Получаются два ответа: число членов или 6, или 2. И действительно, две прогрессии: 7, 5, 3, 1, —1, —3 и 7, 5 имеют одну и ту же сумму 12.
Формула суммы квадратов чисел натурального ряда
Выведем формулу, определяющую сумму квадратов первых n чисел натурального ряда. Для вывода этой формулы рассмотрим n следующих тождеств:
2³=(1+ 1)³=1³∙1²∙1+3∙1∙1²+1³;
3³=(2+1)³ =2³ +3∙2² ∙ 1+3∙2∙ 1²+1³;
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
(n+1)³ =n³ +3n² ∙1+3n∙1²+1³ .
Сложив эти тождества и сократив одинаковые члены в правой и левой частях полученного тождества, будем иметь:
(n+l)³ =1+3(1²+2²+3²+…+n² )+3(1+2+3+…+n)+n.
Но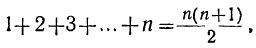
следовательно: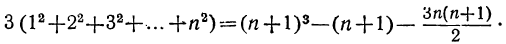
Упростим правую часть этого равенства: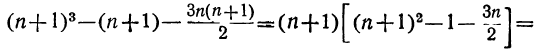
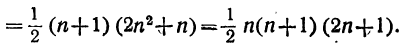
Итак,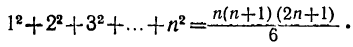
Геометрическая прогрессия
Задача:
По преданию, индийский принц Сирам предложил изобретателю шахматной игры просить у него награду, какую он захочет. Тот попросил, чтобы ему дали за первый квадрат шахматной доски 1 пшеничное зерно, за второй квадрат 2 зерна, за третий 4 и т. д., увеличивая вдвое за каждый из следующих квадратов. Принц согласился. Но когда подсчитали количество зёрен пшеницы, которое следует выдать за все 64 квадрата шахматной доски, то. оказалось, что награда в этом размере не может быть выдана по недостатку пшеницы. Сколько же зёрен пришлось бы выдать изобретателю?
Количество зёрен, которое надлежало бы выдать за все 64 квадрата, равно сумме S следующего ряда чисел:
s = 1+2+2² +2³ +… + 2⁶²+2⁶³.
Мы можем найти эту сумму, не вычисляя отдельно слагаемых, так: умножим обе части написанного равенства на 2:
2s=2+2²+ 2³+2⁴ + …+ 2⁶³+2⁶⁴.
Теперь вычтем из этого равенства предыдущее; тогда в левой части получим s, а в правой 2⁶⁴—1 (числа 2, 2², 2³, …, 2⁶³ все сократятся):
s= 2⁶⁴-1.
Значит, придётся вычислить степень 2⁶⁴, что можно сделать или последовательным умножением на 2 по формуле:
2⁶⁴ =2∙2∙2∙2… (64 множителя),
или по формуле:
2⁶⁴= [(2¹⁶)² ]² =(65 536² )² .
Окончательное число зёрен будет:
s= 2⁶⁴ -l = 118 446 744 073 709 551 615.
Можно вычислить, что если бы такое число зёрен рассыпать равномерно по всей земной суше, то образовался бы слой пшеницы толщиной около 9 мм.
В этой задаче мы имели дело с рядом чисел, из которых каждое начиная со второго равно предыдущему числу, умноженному на одно и то же число. Такие ряды чисел называются геометрическими прогрессиями.
Определение:
Геометрической, или кратной, прогрессией называется такой ряд чисел, в котором каждое число начиная со второго равняется предшествующему, умноженному на одно и то же число, постоянное для этого ряда. Так, три ряда:
2, 4, 8, 16, 32, 64, 128, … ;
8, -16, 32, -64, 128, -256, 512, . . . ;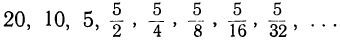
составляют геометрические прогрессии, потому что в этих рядах каждое число, начиная со второго, получается из предшествующего умножением в первом ряду на 2, во втором на —2 и в третьем на 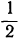 .
.
Для обозначения того, что данный ряд есть геометрическая прогрессия, иногда ставят в начале его знак ÷÷.
Как и в арифметической прогрессии, числа, составляющие геометрическую прогрессию, называются её членами; число, на которое надо умножить предыдущий член, чтобы получить последующий, называется знаменателем прогрессии.
Прогрессия называется возрастающей или убывающей, смотря по тому, увеличивается или уменьшается абсолютная величина членов прогрессии по мере удаления от начала ряда; так, из трёх указанных выше прогрессий первая и вторая — возрастающие, а третья — убывающая. В возрастающей прогрессии абсолютная величина знаменателя больше 1, в убывающей она меньше 1.
Обыкновенно знаменатель прогрессии обозначают буквой q, а члены, число их и сумму обозначают также, как это принято для арифметической прогрессии, т. е. a, b, с, … , l (последний член), n (число членов) и s (сумма).
Сравнение геометрической прогрессии с арифметической прогрессией
Разность двух рядом стоящих членов арифметической прогрессии остаётся одна и та же, вследствие чего члены её возрастают (или убывают) равномерно (черт. 26, левый). Посмотрим, какова разность двух соседних членов в геометрической прогрессии:
∺ а, b, с, … (знаменатель q).
Из определения прогрессии следует: b=aq, c=bq, d=cq и т. д.; следовательно,
b — a=aq — a=a (q — 1); с — b=bq — b=b(q — 1) и т. д.
Если прогрессия возрастающая и члены её положительные, то тогда a < b < с < … и т. д.; поэтому и
a(q-1)<b (q-1) <c( q-1 )<…,
т. е.
b — a < c — b < d — c < … и т. д.
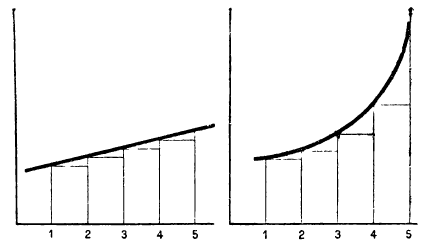
Значит, в возрастающей геометрической прогрессии с положительными членами разность двух соседних членов увеличивается номере удаления их от начала ряда; вследствие этого члены такой прогрессии по мере их удаления от начала ряда возрастают всё быстрее и быстрее, что наглядно изображено на чертеже 26 (правый). Например:
÷ 2, 4, 6, 8, 10, 12, …
∺ 2, 4, 8, 16, 32, 64, …
Формула любого члена геометрической прогрессии
Пусть мы имеем такую геометрическую прогрессию:
∺ 3, 6, 12, 24, … (знаменатель 2).
Тогда:
2-й член=3∙2=6;
3-й „ =3∙2∙2=3∙2² =12;
4-й „ =3∙2∙2∙2=3∙2³ =24 и т. д.
Например: 10-й член=3-2⁹=3∙512=1536.
Подобно этому, если мы имеем прогрессию: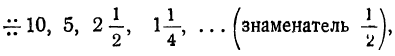
то
2-й член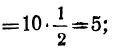
3-й 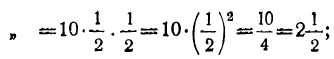
4-й 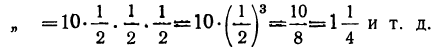
Вообще, если имеем прогрессию в буквенном виде:
∺ а, b, с, … (знаменатель q),
то в ней
2-й член=аq=aq¹;
3-й „ =aq∙q=aq²;
4-й „ = aq² ∙q = aq³ и т. д.
Таким образом, 10-й член=аq⁹, вообще m-й член=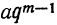 . Значит:
. Значит:
Всякий член геометрической прогрессии, начиная со второго, равен первому члену, умноженному на знаменатель прогрессии в степени, показатель которой равен числу членов, предшествующих определяемому.
В частности, последний член l, которому предшествует n — 1 членов, выразится формулой: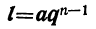
Пример:
Найти 6-й член прогрессии: ∺ 3, 12, …
Знаменатель такой прогрессии есть 12:3=4; поэтому 6-й член= 3∙45 =3072.
Пример:
Найти 10-й член прогрессии: ∺ 20, 10, …
Так как знаменатель этой прогрессии равен 10 : 20=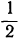 то 10-й член равен:
то 10-й член равен: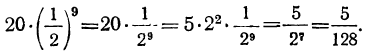
Следствие. Геометрическую прогрессию, у которой первый член есть а, знаменатель q и число всех членов n, можно изобразить так:
∺ α, aq, aq², aq³ , …, aqⁿ⁻¹.
Формула суммы членов геометрической прогрессии
Применим тот приём, которым мы раньше нашли сумму l+2+2² +… +2⁶³. Умножим обе части равенства
s=α+b+c+…+k+l (1)
на знаменатель q, тогда получим:
sq=aq+bq+cq+…+kq+lq.
Но
aq=b, bq=c, cq = d, … , kq=l,
следовательно,
sq = b+c+d+…+l+lq. (2)
Вычтя почленно из равенства (2) равенство (1), найдём:
sq — s=lq- а, т. е. (q — 1)s=lq — а,
откуда: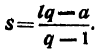
Сумма членов геометрической прогрессии равна дроби, у которой числитель есть разность между произведением последнего члена на знаменатель прогрессии и первым членом её, а знаменатель есть разность между знаменателем прогрессии и единицей.
Замечания. 1. Так как для убывающей геометрической прогрессии — 1 < q < 1, то для такой прогрессии лучше придать формуле суммы иной вид, умножив числитель и знаменатель дроби на — 1: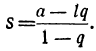
2. Если вместо члена l подставим равное ему выражение aqⁿ⁻¹, то формула для суммы примет такой вид: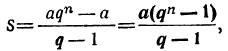 или
или 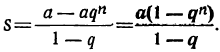
Пример:
Найти сумму восьми членов прогрессии, у которой а=1
и 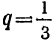 . Тогда:
. Тогда: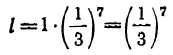
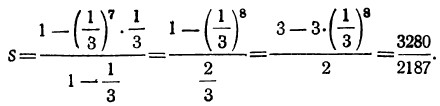
Пример на геометрическую прогрессию
Найти первый член а и последний l, если q=3, n=5 и s=242.
Сначала находим l по формуле l=aqⁿ⁻¹=α∙3⁴ и затем эту величину и данные числа подставим в формулу для суммы: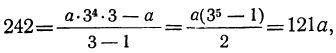
откуда:
α = 242 : 121=2.
Теперь находим:
α =2∙3⁴ =162.
Проверка: 2+6+18+54+162=242.
Бесконечные прогрессии
Некоторые свойства бесконечных прогрессий:
Если ряд чисел, составляющих прогрессию, продолжается неограниченно, то прогрессия называется бесконечной. Рассмотрим некоторые свойства таких прогрессий.
а) Возьмём бесконечно возрастающую арифметическую прогрессию, у которой разность очень мала; например, такую:
∺1; 1,01; 1,02; 1,03; 1,04; …
Несмотря на то, что члены этой прогрессии при удалении от начала ряда растут очень медленно, они, однако, при достаточном удалении превзойдут любое данное число, как бы велико оно ни было; например, они сделаются больше 1 000000. Действительно, для того чтобы (n+ 1)-й член такой прогрессии, равной сумме 1+0,01 n, сделался больше 1 000 000, достаточно для n взять такое большое число, которое удовлетворяло бы неравенству: 1+0,01n> 1 000000.
Из него находим: 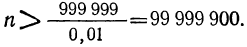
Так как в бесконечной прогрессии число п может быть как угодно большим, то его можно взять большим 99999 900; тогда 14-0,01 n сделается больше 1 000 000.
Рассуждение это можно повторить о всякой арифметической возрастающей бесконечной прогрессии; поэтому мы можем высказать такое общее заключение:
Члены бесконечно возрастающей арифметической прогрессии при достаточном удалении их от начала ряда превосходят любое данное число, как бы оно велико ни было.
Возьмём бесконечно убывающую арифметическую прогрессию, например: ÷ 1900, 998, 996,… (разность—2). Как бы ни был велик начальный член, начиная с некоторого места, члены прогрессии становятся отрицательными, и при достаточном удалении от начала ряда абсолютная величина их превосходит любое данное число, как бы велико оно ни было.
б) Возьмём теперь бесконечно возрастающую геометрическую прогрессию с положительными членами, например такую:
∺1; 1,01; 1,01²=1,0201; 1,01³ = 1,030301; .. . (знаменатель 1,01), и сравним её с бесконечной арифметической прогрессией:
-:-1; 1,01; 1,02; 1,03,… (разность 0,01),
у которой первые два члена одинаковы со взятой нами геометрической прогрессией.
Как мы видели раньше, члены геометрической прогрессии возрастают быстрее, чем члены арифметической прогрессии.
Но члены возрастающей арифметической прогрессии при достаточном удалении их от начала ряда превосходят любое число; значит, члены нашей геометрической прогрессии и подавно могут сделаться больше всякого данного числа. Таким образом:
Члены бесконечно возрастающей геометрической прогрессии (с положительными членами) при достаточном удалении от начала ряда превосходят любое данное число, как бы оно велико ни было.
Свойство это применимо и к такой возрастающей геометрической прогрессии, у которой члены, все или некоторые, — отрицательные числа (например, —5, —10, —20,… или 5, — 10, 20, —40,…); тогда надо только говорить не о самих членах, а об их абсолютной величине.
в) Возьмём теперь какой-нибудь пример бесконечно убывающей геометрической прогрессии с положительными членами, например такой: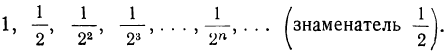
Члены такой прогрессии при удалении их от начала ряда, конечно, уменьшаются, но могут ли они при этом сделаться меньше всякого данного положительного числа, например меньше 0,000001, это сразу не видно. Чтобы обнаружить это, возьмём вспомогательную прогрессию, члены которой обратны членам взятой нами прогрессии:
1, 2, 2², 2³,…, 2ⁿ,… (знаменатель 2).
Прогрессия эта возрастающая, и потому, как мы сейчас видели, члены её при достаточном удалении от начала ряда превосходят любое данное число; значит, они превосходят и 1000 000. Если же окажется, что
2ⁿ > 1 000 000,
то тогда, очевидно: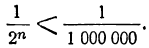
Применим это рассуждение к какой угодно бесконечно убывающей геометрической прогрессии (с положительными членами):
∺ a, b, c,… (знаменатель q < l).
Чтобы показать, что члены этой прогрессии при достаточном удалении от начала ряда делаются меньше любого данного положительного числа а (как бы мало это число ни было), возьмём вспомогательную геометрическую прогрессию: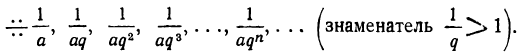
Прогрессия эта возрастающая, так как её знаменатель больше 1. Но члены возрастающей геометрической прогрессии могут превзойти всякое данное число; следовательно, они превзойдут и число 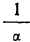 .
.
Поэтому при достаточно большом n будет удовлетворено неравенство: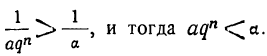
Таким образом:
Члены бесконечно убывающей геометрической прогрессии с положительными членами при достаточном удалении от начала ряда делаются меньше любого данного положительного числа.
Если в бесконечно убывающей геометрической прогрессии все или некоторые члены отрицательны, то указанное свойство применимо и к этой прогрессии, только надо будет говорить не о самих членах, а об их абсолютных величинах.
Понятие о пределе
Положим, что в бесконечно убывающей геометрической прогрессии: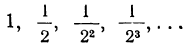
мы взяли 10 членов от начала; тогда последний (10-й) член будет 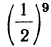 , а сумма этих 10 членов (которую обозначим s₁₀) будет:
, а сумма этих 10 членов (которую обозначим s₁₀) будет: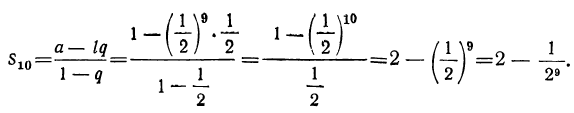
Подобно этому найдём: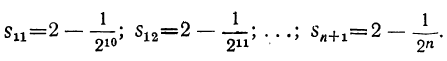
Мы видим, что по мере увеличения числа членов сумма их приближается всё более и более к 2. Так, сумма 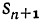 меньше 2 на дробь
меньше 2 на дробь 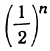 , а эта дробь, как мы видели, при достаточно большом n делается меньше любого данного положительного числа.
, а эта дробь, как мы видели, при достаточно большом n делается меньше любого данного положительного числа.
Если какая-нибудь переменная величина (в нашем примере — сумма членов прогрессии), изменяясь, приближается всё более и более к некоторому постоянному числу (в нашем примере — к числу 2) так, что абсолютная величина разности между этим числом и переменной делается и остаётся меньше любого данного положительного числа, как бы мало оно ни было, то это постоянное число называется пределом переменной величины.
Заметив это, мы можем сказать, что переменная сумма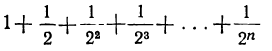
при неограниченном возрастании п стремится к пределу 2, что записывают так: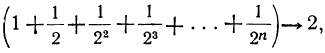 если n→∞
если n→∞
( n→∞ читается: „n стремится к бесконечности»), или пишут так: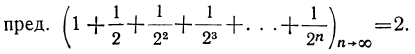
Здесь „пред.» есть сокращённое слово „предел», а добавление внизу скобки: n→∞ заменяет собой фразу: „когда n неограниченно увеличивается» (когда n стоемится к ∞).
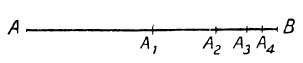
Можно наглядно показать (черт. 27), что рассматриваемая сумма приближается неограниченно близко к 2. Пусть отрезок AA₁ =1 и АВ=2. Тогда 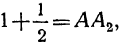 ,
, 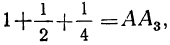
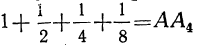
и т.д.; ясно, что при увеличении числа членов прогрессии мы неограниченно приближаемся к точке В, и значит, сумма 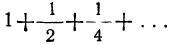 стремится к отрезку АВ=2.
стремится к отрезку АВ=2.
Формула суммы бесконечно убывающей геометрической прогрессии
Если в бесконечно убывающей геометрической прогрессии:
a, aq, aq², aq³,… (— 1< q < 1)
возьмём п членов от начала, то n-й член будет aq aqⁿ⁻¹ и сумма n членов будет: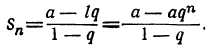
Формулу эту можно представить так (подписав знаменатель под каждым членом числителя):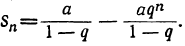
Предположим, что n неограниченно увеличивается. Тогда число 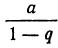 остаётся неизменным, а дробь
остаётся неизменным, а дробь 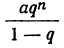 по абсолютной величине уменьшается и притом неограниченно, так как числитель её по абсолютной величине делается меньше любого данного положительного числа, а знаменатель остаётся неизменным. Значит:
по абсолютной величине уменьшается и притом неограниченно, так как числитель её по абсолютной величине делается меньше любого данного положительного числа, а знаменатель остаётся неизменным. Значит: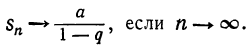
Этот предел 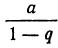 и называется суммой бесконечно убывающей геометрической прогрессий, т. е. сумма членов бесконечно убывающей геометрической прогрессии равна частному от деления первого члена прогрессии на разность единицы и знаменателя прогрессии.
и называется суммой бесконечно убывающей геометрической прогрессий, т. е. сумма членов бесконечно убывающей геометрической прогрессии равна частному от деления первого члена прогрессии на разность единицы и знаменателя прогрессии.
Например, сумма членов геометрической прогрессии: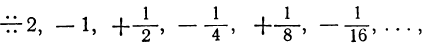
у которой 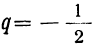 и α=2, равна
и α=2, равна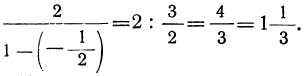
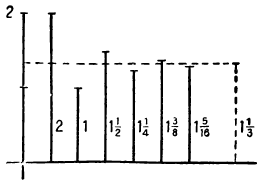
На прилагаемом чертеже изображён ряд ординат, наглядно изображающих сравнительную величину одного, суммы двух, трёх, четырёх и т. д. членов данной прогрессии. Ординаты эти поочерёдно становятся то больше 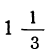 , то меньше
, то меньше 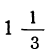 , приближаясь всё более к этому числу (черт. 28).
, приближаясь всё более к этому числу (черт. 28).
Применение геометрической прогрессии к десятичным периодическим дробям
Возьмём следующие два примера десятичных чистых периодических дробей (т. е. таких, у которых период начинается тотчас после запятой): 1) 0,999… и 2) 0,232323…
Дроби эти представляют собой суммы: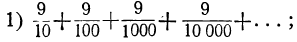
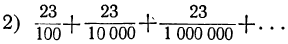
Слагаемые этих сумм — члены бесконечно убывающих геометрических прогрессий, у которых знаменатели прогрессии: у первой 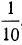 , у второй
, у второй 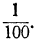 Суммы эти равны:
Суммы эти равны: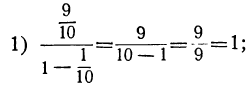
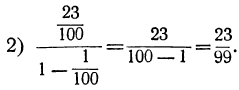
Из этих примеров видно, что
чистая периодическая дробь равна такой обыкновенной дроби, у которой числитель есть период, а знаменатель — число, изображаемое цифрой 9, повторённой столько раз, сколько цифр в периоде.
Возьмём теперь два примера смешанных периодических дробей (т. е. таких, у которых период начинается не тотчас после запятой):
3) 0,2888… и 4) 0,3545454…
Дроби эти можно представить в виде сумм: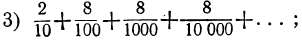
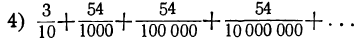
Слагаемые этих сумм, начиная со второго, суть члены бесконечных убывающих геометрических прогрессий; в третьей сумме знаменателем служит дробь 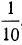 , в четвёртой сумме — дробь
, в четвёртой сумме — дробь 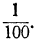 Поэтому эти суммы равны:
Поэтому эти суммы равны: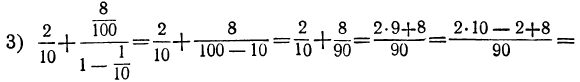
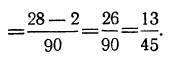
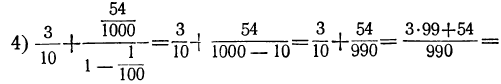
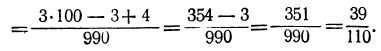
Из этих примеров видно, что:
Смешанная периодическая дробь равна такой обыкновенной дроби, у которой числитель есть число, стоящее до второго периода, без числа, стоящего до первого периода, а знаменатель есть число, изображаемое цифрой 9, повторённой столько раз, сколько цифр в периоде, со столькими нулями на конце, сколько цифр между запятой и первым периодом.
Дополнительный материал по прогрессиям

Смотрите также:
| О единственности положительного решения уравнения n-й степени. | Усреднение. |
| Расчет единичного «голого» права собственности. | Суммирование степеней целых чисел. |
Числовые последовательности
Поставим в соответствие каждому натуральному числу квадрат этого числа:
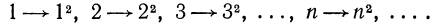
Рассмотренное соответствие является функцией. Обозначим эту функцию буквой 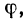 тогда:
тогда:
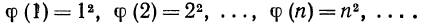
Областью определения этой функции 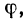 служит множество N натуральных чисел:
служит множество N натуральных чисел: 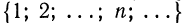 множеством ее значений— множество
множеством ее значений— множество 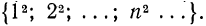
Функция, заданная на множестве натуральных чисел, называется бесконечной последовательностью. Функция, заданная на множестве первых п натуральных чисел, называется конечной последовательностью.
Значения функции 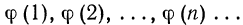 называются членами последовательности. Члены последовательности обозначаются также символами
называются членами последовательности. Члены последовательности обозначаются также символами  где
где 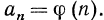 Это равенство называют также формулой общего члена. Последовательность
Это равенство называют также формулой общего члена. Последовательность 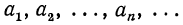 обозначается так:
обозначается так: 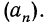
Так как последовательность—это частный вид функции, то способы задания функции применимы и для задания последовательности. Графический и табличный способы могут быть использованы для задания конечных последовательностей. Для бесконечных же последовательностей особенно важны два следующих способа задания, которые мы сейчас рассмотрим.
Последовательность может быть задана аналитически, т. е. с помощью формулы общего (n-го) члена 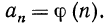
Например:
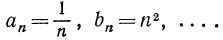
Давая аргументу «значения 1, 2, 3, …, будем получать соответствующие значения последовательности. Так, последовательность 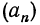 имеет вид
имеет вид 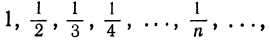 а последовательность
а последовательность 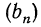 имеет вид
имеет вид 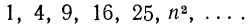
2.Любой член последовательности, начиная с некоторого, часто выражают через предшествующие (один или несколько). Например, последовательность 1; 2; 3; 5; 8; 11; … может быть задана следующим образом:
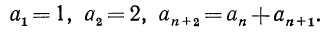
Действительно,
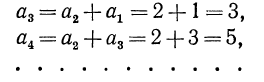
Такой способ задания последовательности называется рекуррентным. При рекуррентном способе задания последовательности обычно указывают: а) первый член последовательности (или несколько первых членов); б) формулу, позволяющую определить любой член последовательности по известным предшествующим членам.
Примеры:
1. Выписать несколько первых членов последовательности, если известно, что 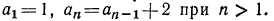
Решение:
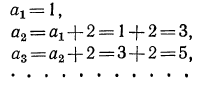
Итак, получаем последовательность 1, 3, 5, 7, 9…..
2.Выписать несколько членов последовательности, если известно, что 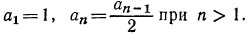
Решение:
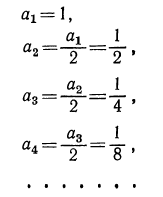
Итак, получаем последовательность 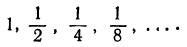
Последовательность называется возрастающей, если каждый последующий ее член больше предыдущего, т. е. 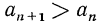 для любого n. Например, возрастающими являются такие последовательности:
для любого n. Например, возрастающими являются такие последовательности:
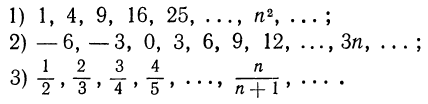
Последовательность называется убывающей, если каждый последующий ее член меньше предыдущего, т. е. 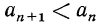 Для любого n. Например, убывающими являются такие последовательности:
Для любого n. Например, убывающими являются такие последовательности:
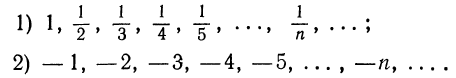
Последовательность называется монотонной, если она возрастающая или убывающая.
Арифметическая прогрессия
Основные понятия: Числовая последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом d, называется арифметической прогрессией. Число d — называется разностью арифметической прогрессии. Таким образом, арифметическая прогрессия определяется условиями: 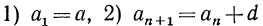 для любого
для любого 
Например, если 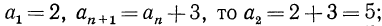
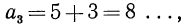 т. е. получаем последовательность 2, 5, 8, И, 14, 17…..
т. е. получаем последовательность 2, 5, 8, И, 14, 17…..
Очевидно, что при 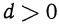 арифметическая прогрессия является возрастающей последовательностью, а если
арифметическая прогрессия является возрастающей последовательностью, а если 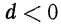 — убывающей; если
— убывающей; если 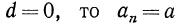 —постоянная последовательность.
—постоянная последовательность.
Например, прогрессии:
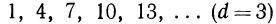 возрастающая,
возрастающая,
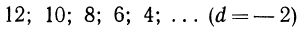 — убывающая,
— убывающая,
 — постоянная.
— постоянная.
Задание арифметической прогрессии, указанное выше, является по сути дела рекуррентным заданием последовательности. Такое задание во многих случаях неудобно. Действительно, для того чтобы найти какой-нибудь член арифметической прогрессии с достаточно большим номером (например, 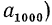 при рекуррентном задании необходимо знать все предшествующие ему члены (в данном случае число их равно 999). Эту вычислительную работу можно сократить, получив из рекуррентного соотношения
при рекуррентном задании необходимо знать все предшествующие ему члены (в данном случае число их равно 999). Эту вычислительную работу можно сократить, получив из рекуррентного соотношения 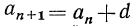 формулу n-го (или общего) члена арифметической прогрессии.
формулу n-го (или общего) члена арифметической прогрессии.
Имеем:
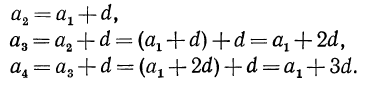
Легко сообразить, что
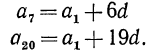
Вообще
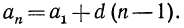
Зная 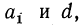 по формуле общего члена можно непосредственно (без вычисления предыдущих членов) вычислить любой член арифметической прогрессии.
по формуле общего члена можно непосредственно (без вычисления предыдущих членов) вычислить любой член арифметической прогрессии.
Например, если 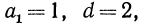 то по формуле общего члена имеем
то по формуле общего члена имеем 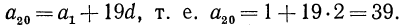
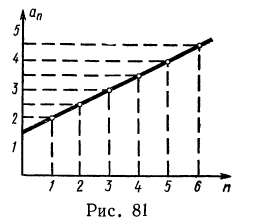
Характеристическое свойство
Арифметическая прогрессия обладает следующим характеристическим свойством: любой член ее, начиная со второго, является средним арифметическим предшествующего и последующего членов.
Доказательство. Пусть 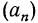 —арифметическая прогрессия. По определению
—арифметическая прогрессия. По определению 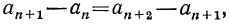 откуда
откуда
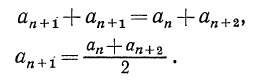
Справедливо и обратное: если некоторая последовательность такова, что любой ее член, начиная со второго, является средним арифметическим предшествующего и последующего членов, то эта последовательность—арифметическая прогрессия.
Действительно, пусть для любых трех соседних членов некоторой последовательности 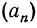 справедливо соотношение6
справедливо соотношение6
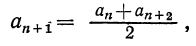
тогда 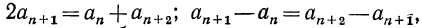 т. е. разность между любым членом последовательности и ему предшествующим равна одному и тому же числу. Значит
т. е. разность между любым членом последовательности и ему предшествующим равна одному и тому же числу. Значит 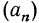 арифметическая прогрессия. Таким образом, рассматриваемое свойство присуще арифметической прогрессии и только ей.
арифметическая прогрессия. Таким образом, рассматриваемое свойство присуще арифметической прогрессии и только ей.
Связь с линейной функцией
На рис. 81 построен график арифметической прогрессии, у которой 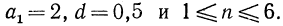 и Рассматривая рисунок, замечаем, что точки графика лежат на одной прямой. Покажем, что это не случайно. Запишем формулу общего члена рассматриваемой арифметической прогрессии
и Рассматривая рисунок, замечаем, что точки графика лежат на одной прямой. Покажем, что это не случайно. Запишем формулу общего члена рассматриваемой арифметической прогрессии  Мы получили формулу вида
Мы получили формулу вида 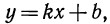 а такой формулой, как известно, задается линейная функция.
а такой формулой, как известно, задается линейная функция.
Таким образом, арифметическая прогрессия является линейной функцией, заданной на множестве натуральных чисел.
Справедливо и обратное: линейная функция, областью определения которой служит множество натуральных чисел, является арифметической прогрессией.
Пример:
Последовательность 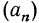 задана формулой ее n-го члена
задана формулой ее n-го члена 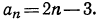 Доказать, что последовательность есть арифметическая прогрессия и найти ее первый член и разность.
Доказать, что последовательность есть арифметическая прогрессия и найти ее первый член и разность.
Решение:
Запишем формулу общего члена для члена с номером  Имеем
Имеем 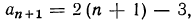 тогда
тогда 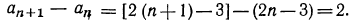 Таким образом, разность между последующим и предшествующим членами этой последовательности есть величина постоянная. Следовательно, это арифметическая прогрессия, у которой
Таким образом, разность между последующим и предшествующим членами этой последовательности есть величина постоянная. Следовательно, это арифметическая прогрессия, у которой 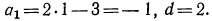 Сама прогрессия имеет такой вид:
Сама прогрессия имеет такой вид:
-1; 1; 3; 5; ….
Формула суммы n первых членов
Рассмотрим какую-нибудь конечную арифметическую прогрессию, например
3; 6; 9; 12; 15; 18
и сравним суммы членов, равноудаленных от конца, 3+18; 6+15; 9+12. Легко видеть, что эти суммы равны. Это не случайно, так как можно доказать, что в конечной арифметической прогрессии 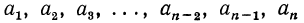 сумма членов, равноудаленных от конца равна сумме первого и последнего членов, т. е.
сумма членов, равноудаленных от конца равна сумме первого и последнего членов, т. е.
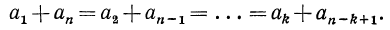
Например, докажем, что 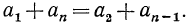 По формуле общего члена арифметической прогрессии имеем
По формуле общего члена арифметической прогрессии имеем
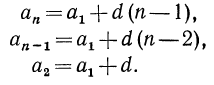
Подставляя в проверяемое равенство 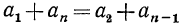 найденные значения для
найденные значения для 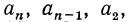 получим
получим 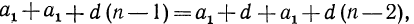 т.е.
т.е. 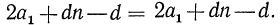 Мы получили верное равенство, что и доказывает сформулированное выше утверждение.
Мы получили верное равенство, что и доказывает сформулированное выше утверждение.
Воспользуемся этим фактом для вывода формулы суммы n первых членов арифметической прогрессии. Обозначим эту сумму через 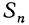 и выпишем эту сумму дважды, поменяв во втором случае порядок слагаемых на обратный:
и выпишем эту сумму дважды, поменяв во втором случае порядок слагаемых на обратный:
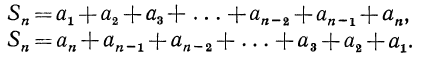
Сложим почленно эти равенства: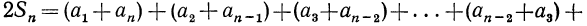
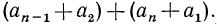 Сумма каждой пары в правой части равенства равна
Сумма каждой пары в правой части равенства равна 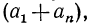 а число таких пар равно n, поэтому
а число таких пар равно n, поэтому
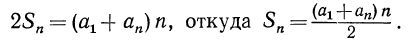
Примеры:
1. Найти сумму первых 10 членов арифметической прогрессии 2, 5, 8, 11…..
Решение:
Из условия задачи 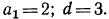 По формуле общего члена
По формуле общего члена 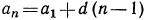 найдем
найдем 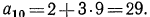
По формуле суммы n членов 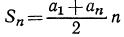 имеем
имеем
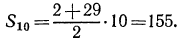
Замечание. Формулу суммы n членов арифметической прогрессии можно записать в другом виде, если вместо 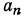 подставить его значение
подставить его значение 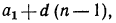 тогда
тогда
Дана конечная арифметическая прогрессия 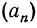 Зная три пяти:
Зная три пяти: 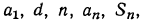 найти остальные два:
найти остальные два:
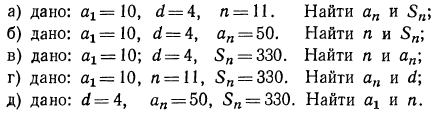
Решение:
а) По формуле n-го члена 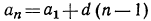 найдем
найдем 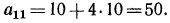 Затем по формуле
Затем по формуле 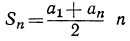 найдем
найдем 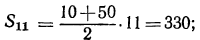
б) из формулы 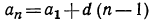 получим
получим
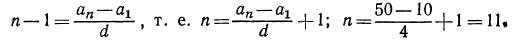
Далее, имеем 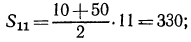
в) воспользуемся формулой 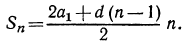 Подставляя данные значения, получаем
Подставляя данные значения, получаем 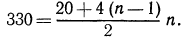 Таким образом, мы получили квадратное уравнение относительно n; решим его:
Таким образом, мы получили квадратное уравнение относительно n; решим его:
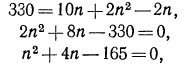
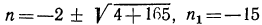 (не подходит по условию задачи);
(не подходит по условию задачи); 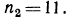 Зная n, найдем
Зная n, найдем 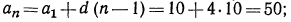
г) из формулы 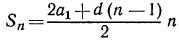 найдем d:
найдем d:
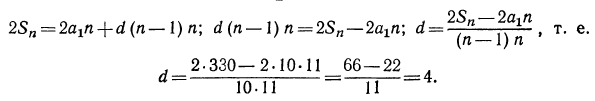
Теперь можно найти 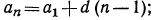
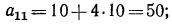
д) из формулы 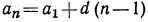 найдем
найдем 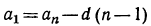 и подставим найденное значение
и подставим найденное значение 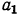 в формулу
в формулу 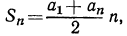 тогда
тогда
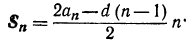 Теперь найдем n:
Теперь найдем n:
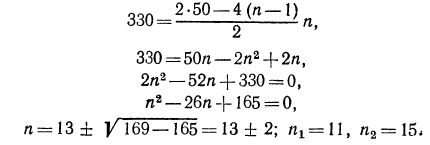
Если 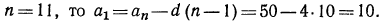
Если 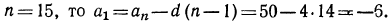
Выпишем обе прогрессии:

Легко видеть, что в обоих случаях сумма членов равна 330.
Геометрическая прогрессия
Основные понятия:
Определение:
Числовая последовательность, первый член которой отличен от нуля, а каоюдый член, начиная со второго, равен предшествующему члену, умноженному на одно и то же, не равное нулю число q, называется геометрической прогрессией. Число q называется знаменателем прогрессии.
Таким образом, геометрическая прогрессия определяется условиями:
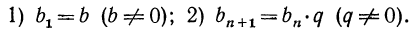
Например, если 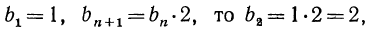
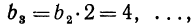 т. е. получаем последовательность 1, 2, 4, 8, 16…..
т. е. получаем последовательность 1, 2, 4, 8, 16…..
Очевидно, что при 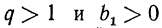 геометрическая прогрессия является возрастающей последовательностью, а если
геометрическая прогрессия является возрастающей последовательностью, а если 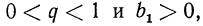 то убывающей, если же
то убывающей, если же 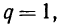 то
то 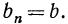 При
При 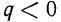 геометрическая прогрессия не является монотонной. Примеры прогрессий:
геометрическая прогрессия не является монотонной. Примеры прогрессий:
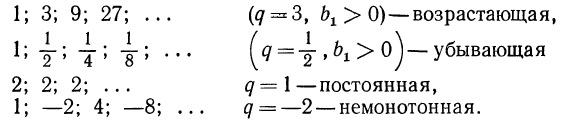
Задание геометрической прогрессии, указанное выше, является рекуррентным заданием последовательности. Такое задание во многих случаях неудобно. Действительно, для того чтобы найти какой-нибудь член геометрической прогрессии с достаточно большим номером, при рекуррентном задании необходимо знать все предшествующие ему члены. Эту вычислительную работу можно сократить, получив из рекуррентного соотношения 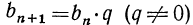 формулу n-то или общего члена геометрической прогрессии. Имеем:
формулу n-то или общего члена геометрической прогрессии. Имеем:
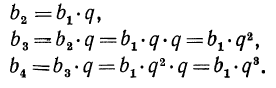
Легко сообразить, что
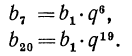
Вообще
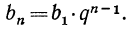
Зная 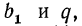 по формуле общего члена можно непосредственно (без вычисления предыдущих членов) вычислить любой член геометрической прогрессии. Так, если
по формуле общего члена можно непосредственно (без вычисления предыдущих членов) вычислить любой член геометрической прогрессии. Так, если 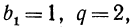 то по формуле общего члена имеем, например,
то по формуле общего члена имеем, например, 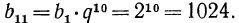
Характеристическое свойство
Геометрическая прогрессия, все члены которой положительные числа, обладает следующим характеристическим свойством.
Любой член геометрической прогрессии, начиная со второго, является средним геометрическим предшествующего и последующего членов.
Доказательство. Пусть 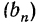 — геометрическая прогрессия. Тогда по определению имеем:
— геометрическая прогрессия. Тогда по определению имеем:
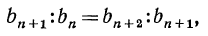
откуда
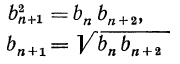
Справедливо и обратное: если некоторая последовательность положительных чисел такова, что любой ее член, начиная со второго, является средним геометрическим предшествующего и последующего членов, то эта последовательность — геометрическая прогрессия.
Действительно, пусть для любых трех соседних членов некоторой последовательности 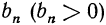 справедливо соотношение
справедливо соотношение 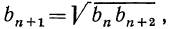 тогда
тогда
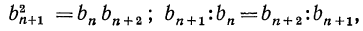
а это и означает, что 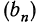 —геометрическая прогрессия.
—геометрическая прогрессия.
Формула суммы n первых членов
В заключение выведем формулу суммы n первых членов геометрической прогрессии. Обозначим эту сумму через 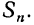 Можно записать, что
Можно записать, что
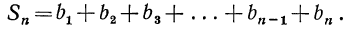
Умножим обе части равенства (1) на q
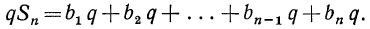
Но 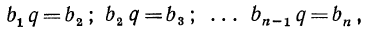 поэтому
поэтому
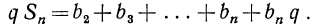
Вычтем почленно из равенства (2) равенство (1):
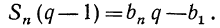
Если положить 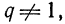 то
то
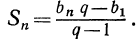
Если 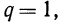 то прогрессия имеет вид
то прогрессия имеет вид 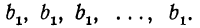 В этом случае
В этом случае 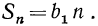
Для примера найдем сумму пяти первых членов геометрической прогрессии 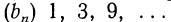
По условию задачи 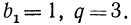 Найдем пятый член прогрессии по формуле
Найдем пятый член прогрессии по формуле 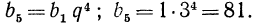
Теперь по формуле суммы n первых членов прогрессии найдем 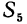
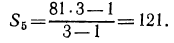
Замечания 1. Формулу суммы n членов геометрической прогрессии можно записать в другом виде, если вместо 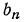 подставить его значение
подставить его значение 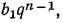 тогда
тогда
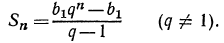
2.В каждой конечной геометрической прогрессии произведение крайних членов прогрессии равно произведению двух членов, одинаково отстоящих от крайних, т. е. в прогрессии 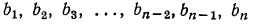 справедливы равенства
справедливы равенства
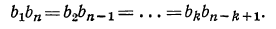
Например, докажем, что 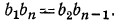 По формуле общего члена геометрической прогрессии имеем:
По формуле общего члена геометрической прогрессии имеем:
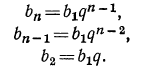
Подставляя в предполагаемое равенство 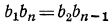 найденные значения для
найденные значения для 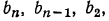 получаем:
получаем:
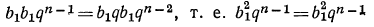
— вернее равенство, что и доказывает сформулированное выше утверждение.
Сводная таблица, иллюстрирующая свойства арифметической и геометрической прогрессий, приведена на стр. 187.
Примеры:
1. Восьмой член геометрической прогрессии равен 256, знаменатель прогрессии 4. Найти первый член этой прогрессии.
Решение:
По условию 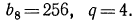 По формуле общего члена имеем
По формуле общего члена имеем 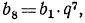 откуда
откуда
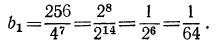
Определить знаменатель и сумму n членов геометрической прогрессии, в которой 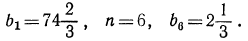

Решение:
По формуле общего члена имеем 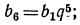 значит,
значит, 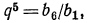 или
или
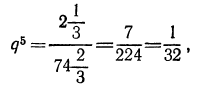
т. е. 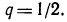 Далее, по формуле
Далее, по формуле 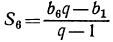 имеем
имеем
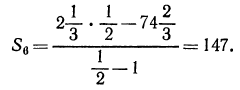
3.Определить первый и последний члены геометрической прогрессии, в которой 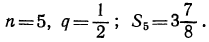
Решение:
Воспользуемся формулой 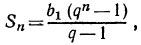 из которой найдем
из которой найдем 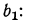
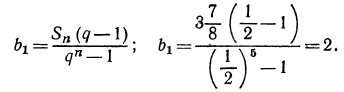
Теперь по формуле 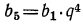 найдем последний член прогрессии:
найдем последний член прогрессии: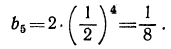
4.Определить число членов геометрической прогрессии, в которой 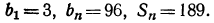
Решение:
Прежде всего из формулы 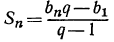 найдем q. Имеем:
найдем q. Имеем:
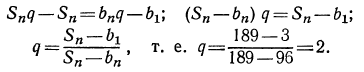
Затем воспользуемся формулой n-го члена 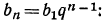
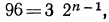 откуда
откуда 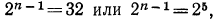
т. е. 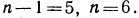
Определить первый член, знаменатель и число членов геометрической прогрессии, в которой 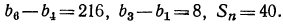
Решение:
Воспользуемся формулой общего члена геометрической прогрессии: 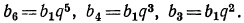 Тогда первые два данных уравнения примут вид:
Тогда первые два данных уравнения примут вид:
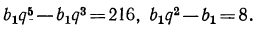
Разделим почленно одно уравнение на другое:
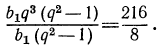
Так как 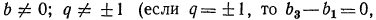 что противоречит условию), то, сократив левую часть уравнения на
что противоречит условию), то, сократив левую часть уравнения на 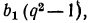 получим
получим 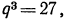 откуда
откуда 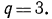
Теперь из уравнения 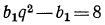 найдем
найдем 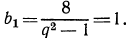
Для определения n воспользуемся формулой 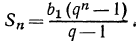 Подставляя в это выражение найденные и данные значения, получим:
Подставляя в это выражение найденные и данные значения, получим:
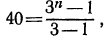 откуда
откуда 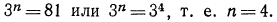
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

