Оглавление:







Примеры построения линий пересечения поверхностей с плоскостью
- Пример построения линии поверхности для плоской поверхности I. Давайте рассмотрим пример создания пересечения между плоскостью, плоскостью вращения и линейчатой плоскостью. Пример I. Нарисуйте линию пересечения между вращающейся плоскостью и конкретной плоскостью, чтобы определить естественную форму поперечного сечения.
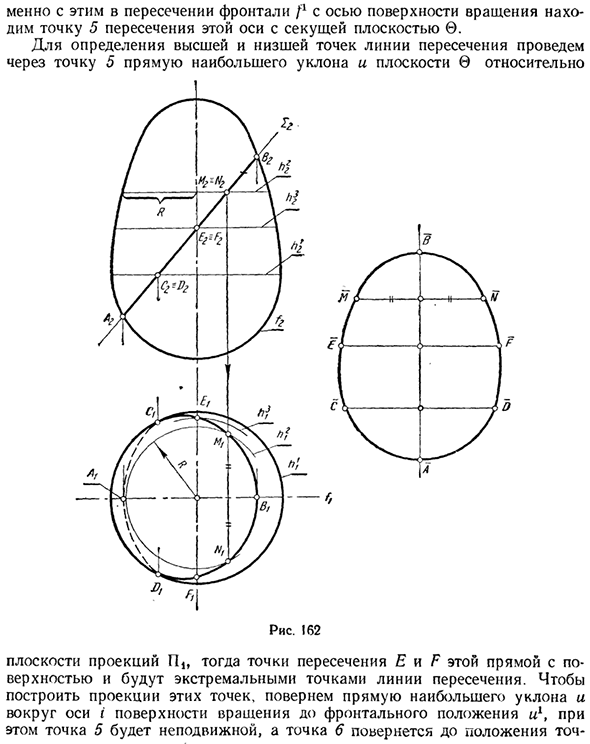
- Рассмотрим случай, когда секущей плоскостью является плоскость проекции, например плоскость проекции 12 спереди (фиг. 162). Отметьте самую низкую точку A и самую высокую точку B на главном меридиане / удельной поверхности. Отметьте точки С и D на экваторе гл. Это видимые точки на плоскости проекции II, которые делят горизонтальную проекцию желаемой линии пересечения на видимые и невидимые части.
Построить опорные точки заранее. Людмила Фирмаль
Чтобы построить случайные точки на плоскости вращения, нарисуйте графически простую линию, которая является параллельной линией, и отметьте их как точки, которые принадлежат секущей 2. На рисунке 162 изображена параллельная окружность ft2 радиуса R, на которой отмечены точки M и N, принадлежащие плоскости 2.
Точки E и F, обнаруженные с помощью параллели L3, являются видимыми точками на плоскости проекции Г13. Это потому, что они находятся на поверхности меридианов. Построение естественного типа сечения легче всего выполнить путем непосредственного измерения высоты и широты точек сечения. В то же время высота точки должна измеряться в поле P2.
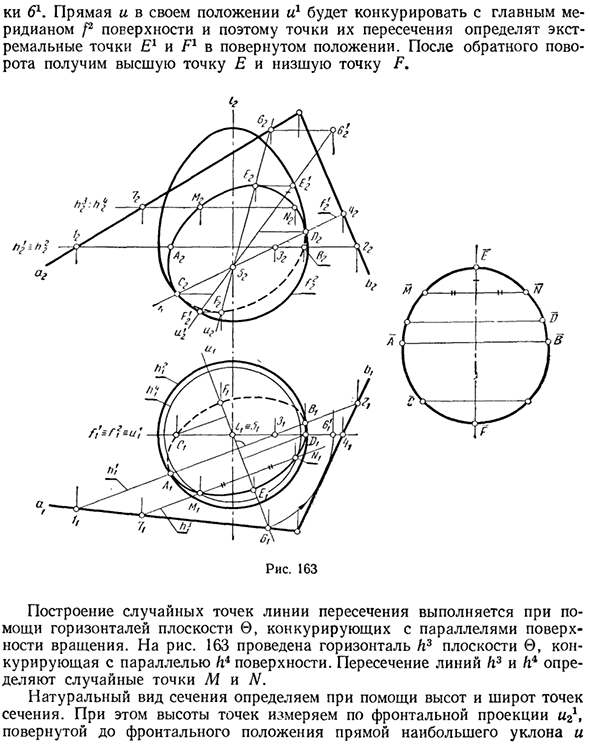
Это связано с тем, что точка находится впереди и поэтому не искажается в поле P2, поэтому широта в поле P2 находится на прямой (горизонтальной), выступающей вперед, поэтому она не искажается в поле nt. Далее рассмотрим случай, когда плоскость вращения пересекает плоскость в общем положении 0 (a X b) (рис. 163). Сначала создайте опорную точку.
Найдите видимые точки A и B плоскости проекции Pf на пересечении горизонтальной плоскости hl, которая конкурирует с экватором I2 этой плоскости. Видимые точки C и D в плоскости проекции Г12 определяются на пересечении передней / плоской плоскости 0 и конкурируют с основным меридианом f2 поверхности.
В то же время * 1 В этом и следующих примерах секущая плоскость считается прозрачной, чтобы не вносить ненужную сложность. Это находит пересечение 5 этой оси и секущей плоскости 0 на пересечении фронта f1 и оси вращения. Нарисуйте, чтобы определить самую высокую и самую низкую точки линии пересечения.
В случае проекционной плоскости P4 пересечение E и F между этой линией и поверхностью является крайним значением линии пересечения. Чтобы создать проекцию этих точек, поверните прямую линию с максимальным наклоном вокруг оси I плоскости вращения в переднее положение u1, зафиксируйте точку 5 и поверните точку 6 в положение точки. Ци б1.
Поскольку прямая линия и ее положение u1 конкурируют с основным меридианом f2 поверхности, их пересечение определяет крайние точки E1 и F1 повернутой позиции. После обратного вращения получите самую высокую точку E и самую низкую точку F. Рис. 163 Построение случайных точек пересекающейся линии выполняется с использованием горизонтальной линии плоскости 0, которая конкурирует с параллельными линиями плоскости вращения.
Рисунок 163 содержит горизонтальную плоскость L3 0 и конкурирует с параллельной поверхностью h4. Пересечение линий / i3 и / i4 определяется случайными точками M и N. Естественная форма сечения определяется с использованием высоты и широты точек сечения. В этом случае высота точки измеряется от передней проекции и поворачивается на 2 ° в прямую переднюю позицию с максимальным углом наклона.
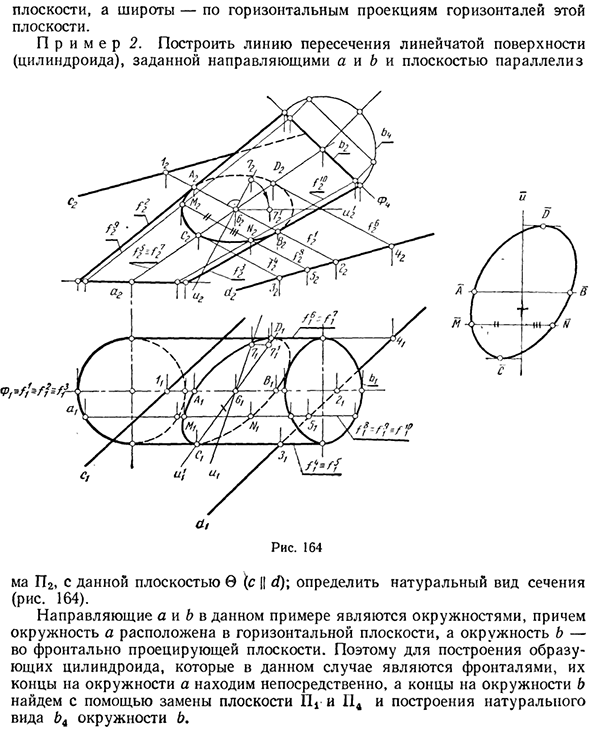
Плоскость, а широта — на горизонтальной проекции контура этой плоскости. Пример 2. Нарисуйте линию пересечения между линейчатой поверхностью (цилиндрической поверхностью), определяемой направляющими А и В, и параллельной плоскостью. ma P2 с плоскостью, заданной в (c || d), определить естественное сечение (рис. 164).
В этом примере направляющие a и b — это круги, круг a — в горизонтальной плоскости, а круг b — в плоскости, спроецированной вперед. Таким образом, чтобы построить цилиндрический генератор (в данном случае фронт), найдите край круга a и замените плоскости 11d и 114, чтобы построить естественную форму b-го круга b. Найди конец.
Чтобы создать точку пересечения цилиндра на определенной плоскости 0, вы должны нарисовать переднюю грань на плоскости резки, которая конкурирует с генератором цилиндров. На рис. 164 показана плоскость 8 спереди / А, конкурирующая с двумя генераторами р и / 3 цилиндров. Получите точку An, которая является видимой точкой плоскости проекции Г12 на пересечении генераторов f2 и f3.
Аналогичным образом найдите видимые точки C и D плоскости проекции П, которые конкурируют с генераторами цилиндров f6 и r, используя фронт плоскости 0/4 и f * соответственно. На пересечении фронта плоскости 0 соревнуйтесь с генераторами / 9 и / 10, чтобы найти случайную точку M w N искомой линии пересечения.
Естественная форма сечения определяется с использованием высоты и широты точек сечения. В этом случае высота точки измеряется горизонтальной проекцией. Вдоль фронтальной проекции фронта этой плоскости мы вернулись в горизонтальное положение прямой с максимальным наклоном и плоскостью 0 относительно плоскости проекции P2 и широтой точки.
Если проецируется вторая плоскость, построение точек сечения несколько упрощается. Это потому, что нет необходимости строить линию на плоскости, которая конфликтует с генератором линейчатой поверхности. 2. Рассмотренный пример дает представление об общем способе построения пересечения вращающейся плоскости, линейчатой плоскости и произвольной плоскости.
Однако часто форма кривой, возникающей в результате поперечного сечения поверхности лицом, известна заранее. В этом случае вы можете создать линии пересечения, используя основные элементы, которые определяют эту кривую. Поэтому сфера всегда пересекает круговую плоскость. Вращающийся цилиндр обычно пересекает плоскость вдоль эллипса.
Если секущая плоскость параллельна или перпендикулярна оси цилиндра, вы получите пару прямых или окружностей, которые параллельны поперечному сечению, соответственно (рис. 165). В сечении вращающегося конуса получены все виды квадратичных кривых (коническое сечение на рис. 166). Когда секущий не параллелен Пришло время рассказать Рис. 165
Гиперболический паро прямой поробо / овальный круг Не один из генераторов конуса. То есть он пересекается со всеми генераторами. Эллипс получается в разрезе (рис. 166). В частности, если секущая плоскость перпендикулярна оси конуса, получается окружность. Если секущая плоскость параллельна только одной образующей конуса, в поперечном сечении получается парабола.
Если секущая плоскость параллельна двум генераторам, вы получите гиперболу в поперечном сечении, особенно если плоскость проходит через вершину конуса, вы получите набор линий, которые пересекаются на вершине. Конечно это Если линия пересечения плоской поверхности представляет собой круг или эллипс и если она разбита на пару линий, избегайте кропотливого построения линии пересечения по точкам и построения этих линий по их основным элементам Можно нарисовать.
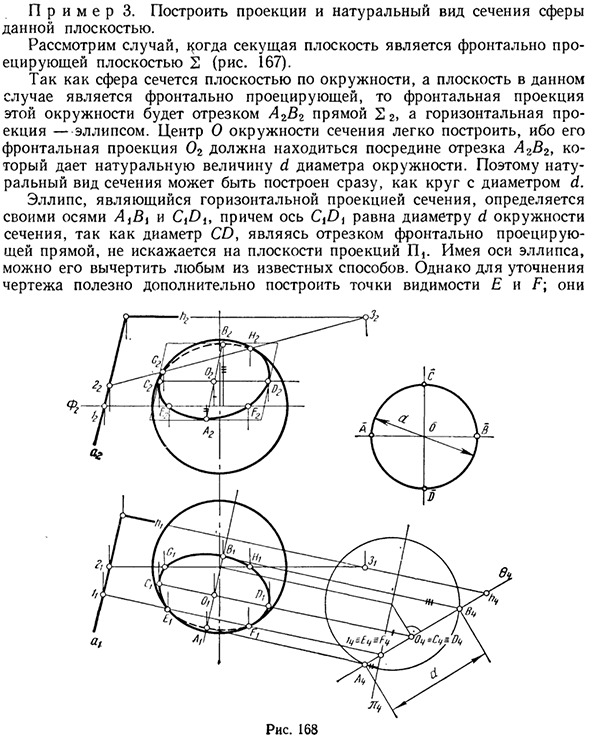
В общем, проекции окружностей и эллипсов являются эллипсами, поэтому состав этих проекций определяет центр эллипса и его ось или диаметр сопряженного элемента. Покажем пример структуры такого раздела. Пример 3. Построить естественный вид с проекцией сечения сферы на заданную плоскость. Рассмотрим случай, когда секущей плоскостью является поверхность 2, выступающая вперед (рис. 167).
Поскольку сфера разрезается плоскостью по окружности, в этом случае плоскость является передней проекцией, передняя проекция этого круга является отрезком прямой линии A2B2 22>, а горизонтальная проекция является эллипсом. Центр окружности сечения легко построить, поскольку передний выступ 02 должен находиться в центре сегмента AgB2, давая естественный размер d диаметра круга.
Следовательно, вы можете быстро создать естественный разрез, например, круг диаметром d. Эллипс, который является горизонтальной проекцией поперечного сечения, определяется его осью и CtDit, а ось Cj £> равна диаметру окружности d поперечного сечения. Это связано с тем, что диаметр CD, представляющий собой отрезок спроецированной спереди линии, не искажается на плоскости проекции P.
Если у вас есть ось эллипса, вы можете нарисовать ее любым из известных способов. Однако видны точки E и F \ для наглядности рисунка Рисунок 168 Его можно легко разместить на пересечении сечения 2 и экватора h сферы. Если вы создаете эллипс с помощью случайных точек, определенных на пересечении сферы и секущей плоскости, а не создаете эллипс вдоль оси, вы должны построить базовую структуру для уточнения эллипса. мы рекомендуем.
Рассмотрим пересечение сферы (рис. 168) и плоскости в общем положении 0 (axL). Этот случай можно свести к предыдущему случаю путем замены проективной плоскости P2 плоскостью P4, перпендикулярной горизонтальной плоскости h секущей плоскости 0. Затем плоскость проецируется на систему плоскостей (P, GZ), поэтому вы можете точно построить горизонтальную проекцию и естественную форму поперечного сечения, как на рисунке. 167.
Чтобы создать эллипс, который является фронтальной проекцией поперечного сечения, необходимо создать фронтальную проекцию с диаметрами AB и CO, которые перпендикулярны окружности поперечного сечения. Это легко сделать из условия, при котором высота точки сохраняется при замене плоскости G12 на P4. Эти выступы диаметра A2B2 и C2D2 являются сопряженным диаметром эллипса.
Это связано с тем, что взаимно перпендикулярные диаметры окружностей имеют свойства сопряжения (каждый диаметр сопряжения делит колонну пополам параллельно другому диаметру). Это свойство сохраняется при параллельной проекции круга внутри эллипса. Вы можете рисовать известным способом (используя описанный параллелограмм), используя сопряженный диаметр эллипса.
Кроме того, на передней проекции U и H определяются видимые точки. Они построены с использованием 2-3 граней 0 спереди. Конкурировать с главным меридианом сферы. Пример 4. Создание проекции конуса и естественного сечения Ca вращение определенной плоскости.
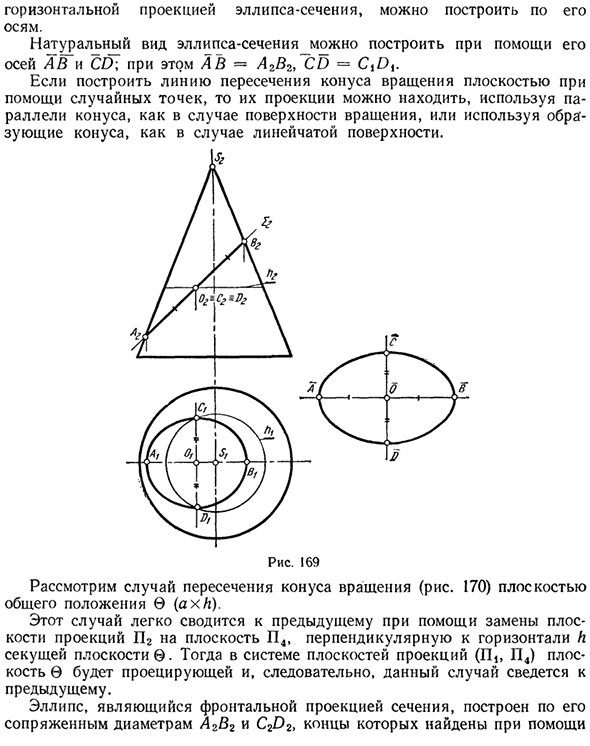
Сначала рассмотрим случай, когда секущая плоскость выступает вперед (рис. 169). В этом случае плоскость 2, спроецированная на фронт, пересекает все генераторы конуса, что приводит к эллипсу в поперечном сечении. Передняя проекция эллипса — это отрезок A2B2 линии 22, а горизонтальная проекция — эллипс. Это связано с тем, что ортографическая проекция эллипса также является эллипсом в общих случаях.
Поскольку главная ось AB эллиптического сечения является передней, она не будет искажаться в плоскости проекции P2. Короткая ось QD — это линия, спроецированная спереди. Таким образом, она проецируется в точку 02 = C2 = D2 в плоскости A2, разделяя сегмент ArBr пополам (точка O является центром эллипса), и проецируется в плоскость II без искажений.
- Чтобы создать горизонтальные проекции C и D, которые являются короткими осями, достаточно провести коническую параллель h на уровне точек C и D. C и D — круговые хорды, которые являются горизонтальными проекциями этих параллельных линий. эллипс Для горизонтальной проекции эллиптических секций вы можете строить вдоль этой оси.
Естественный вид эллиптического сечения может быть построен с использованием его осей AB и CD. Где A B = A2B3 CD = C, D, При использовании случайных точек для построения линий пересечения между вращающимися конусами и плоскостями их проекции используют параллельные конические линии, как во вращающихся плоскостях, или конусы, как на линейчатых поверхностях.
Можно найти с помощью генератора. Рис. 169 Людмила Фирмаль
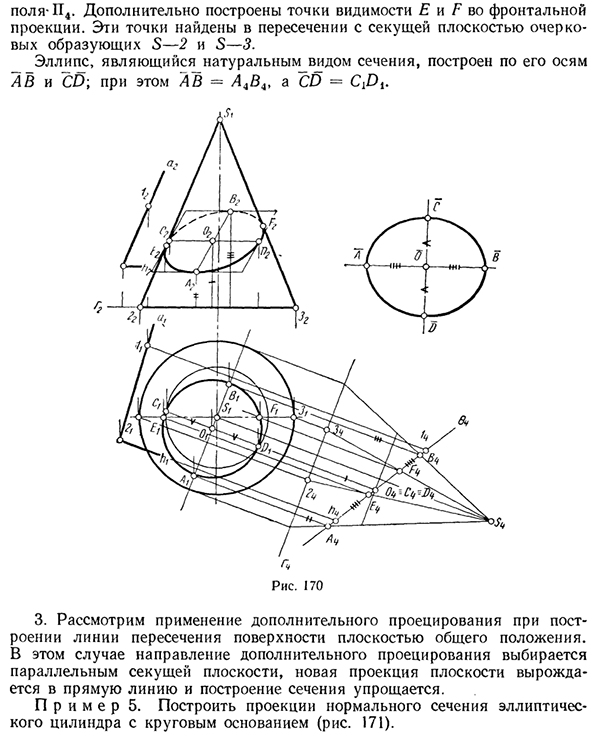
Рассмотрим пересечение вращающегося конуса (рис. 170) с плоскостью в общем положении 0 (axI). В этом случае плоскость P2 проекции можно легко уменьшить до предыдущего случая, заменив ее плоскостью P4, перпендикулярной горизонтальному направлению h плоскости резки ©. В системе проекционных плоскостей (III, P4) этот случай сводится к предыдущему случаю, потому что проецируется плоскость 6.
Эллипс, который является передней проекцией сечения, построен в соответствии с его сопряженными диаметрами A2B2 и C2D2. Поле -II4. Кроме того, поля зрения E и F были построены для фронтальной проекции. Эти точки были найдены на пересечениях с секущими плоскостями генераторов контуров S-2 и S-3.
Эллипс, естественный тип сечения, построен вдоль его осей AB и CO. Где A B = A4B4, CD = CtDt. 3. Рассмотрите возможность использования дополнительных проекций при построении пересечений между поверхностью и плоскостью в общем месте. В этом случае направление дополнительной проекции выбирается параллельно секущей плоскости, новая проекция на плоскости уменьшается до прямой линии, а структура поперечного сечения упрощается.
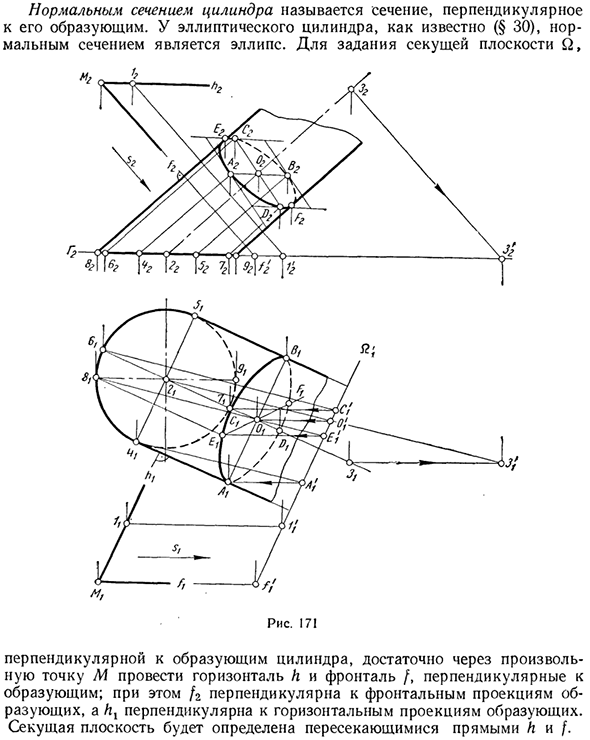
Пример 5. Создайте проекцию нормальной части эллиптического цилиндра с круглым дном (рис. 171). Нормальный участок цилиндра — это участок, перпендикулярный генератору. Как известно (§30) в эллиптическом цилиндре, эллипс является нормальным поперечным сечением. Чтобы определить секущую плоскость Q:
Достаточно провести горизонталь h и фронт / вертикаль к генератору через любую точку М, перпендикулярную генератору цилиндра. В этом случае / 2 перпендикулярна фронтальной проекции генератора, а hx перпендикулярна горизонтальной проекции генератора. Секущая плоскость определяется пересекающейся линией Ли /. Используйте дополнительные проекции для создания секционных проекций.
Для направления s проекции выберите направление передней талии / второй плоскости и спроецируйте вторую плоскость и этот цилиндр в этом направлении на плоскость Г в нижней части цилиндра. Затем плоскость Q проецируется на линию Q, а генератор цилиндров проецируется на линию, параллельную линии 2 — «?». Является ли дополнительная проекция оси цилиндра. Теперь вы можете найти случайную точку на нужной линии пересечения.
Так, например, чтобы найти точку A генератора, конечной точкой которого является точка 4, нарисуйте дополнительную проекцию этого генератора в точке 4Y, параллельной линии 2. 3 \, на пересечении плоскости резания с дополнительной проекцией, проекцией точки А / точки А. Найдите основную проекцию A по обратной проекции и найдите Ar в точке A.
Однако, поскольку интересующий участок представляет собой эллипс, его проекция также может быть построена из сопряженного диаметра. Центр эллипса О определяется обратной проекцией пересечения пересечения О / дополнительной проекцией секущей плоскости и дополнительной проекцией оси цилиндра 2t — 3 .
Если на нижней части цилиндра нарисованы два взаимно перпендикулярных диаметра 4-5 и 6-7, то эллиптическое поперечное сечение можно рассматривать как ортогональную проекцию нижнего круга на секущую плоскость Q, поэтому эти диаметры равны 2 Целевой эллипс проецируется на плоскость Q с двумя сопряженными диаметрами AB и CD.
На рисунке 171 показаны структуры этих диаметров концов A и C с использованием обратной проекции. Вторые концы этих диаметров B и D получены из условий AO = OB и CO-OD. Диаметр сопряженной части эллиптического сечения и I проецируется на плоскость Hi проекции по оси эллипса, которая является горизонтальной проекцией сечения. Кроме того, поля зрения E и F были построены для фронтальной проекции.
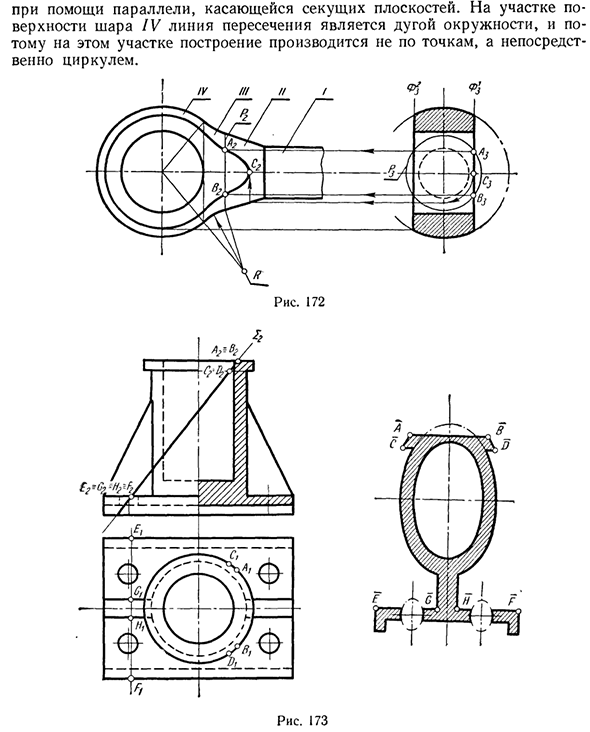
Точка находится на пересечении с секущей плоскостью генератора контура, где точки — это точки 8 и 9. 4. Рассмотрите возможность создания раздела для двух технических частей. Пример 6. Нарисуйте линию разреза головки рычага с двумя передними плоскостями F1 и Ф * (Рисунок 172). Эта головка представляет собой специфическое вращающееся тело, окруженное поверхностями цилиндра /, конуса //, тора /// и шара IV.
После резки головы в передних плоскостях F1 и F2, вы получите переднюю и заднюю части линии пересечения (фронтальные проекции совпадают). Точка линии пересечения может быть легко построена с использованием параллельных линий вращающейся поверхности, окружающей эту головку. На этом рисунке показана конфигурация точек A и B с использованием параллельного p.
Это круг в плоскости профиля и не искажается в поле P3. На чертеже также показана композиция точки С. Это вершина гиперболы, где коническая поверхность // пересекается. Точка С построена Касаясь секущей плоскости параллельно. Для площади поверхности шара IV линия пересечения представляет собой дугу, поэтому построение на этом участке выполняется непосредственно компасом, а не точкой. Рис. 172 Рис. 173
Пример 7. Построить естественный вид разреза этой части из плоскости проекции 2 (рис. 173). Нет необходимости строить горизонтальную проекцию сечения, поскольку высота и широта точек линий, которые ограничивают сечение, определяются непосредственно чертежом для создания желаемого естественного внешнего вида. Фактически, высота точки P2 не искажена, а широта точки находится на линии, которая выступает вперед, поэтому она не искажается в поле П |.
На этом рисунке показана конфигурация естественных типов точек A, B, C, D, £, Ft G и H в поперечном сечении. Эти точки построены с использованием высоты и широты. Эллипс, полученный в сечении цилиндра, нанесен вдоль его оси. Малая ось каждого эллипса равна диаметру соответствующего цилиндра, а большой эллипс представляет собой 2 2 выступающий сегмент, заключенный между выступами генератора контура цилиндра.
Смотрите также:
Решение задач по начертательной геометрии
| Циклические и топографические поверхности | Пересечение поверхностей с прямой |
| Пересечение поверхностей с плоскостью | Плоскости, касательные к поверхностям |

