Применение производной к исследованию функций с примерами решения и образцами выполнения

Оглавление:

Как уже неоднократно замечалось, в окружающем нас мире, во всей деятельности человека, науке, технике, да и в обыденной жизни, встречаются функциональные зависимости. Понятие производной является основным при их изучении.

Возрастание и убывание функции

Определение:

Функция f(х) называется возрастающей на отрезке

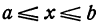
Применение производной к исследованию функций

если для любых значений независимого переменного хх и х2, взятых на этом отрезке, всегда из условия х1 и х2 вытекает, что f(х1) < (x2).

Таким образом, функция называется возрастающей, если большему значению независимого переменного соответствует большее значение функции. Ясно, что для возрастающей функции меньшему значению независимого переменного соответствует и меньшее значение функции (рис. 51).

Пример:

Рассмотрим функцию 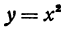Применение производной к исследованию функций . Чем больше положительное х, тем больше и его квадрат, т. е. если

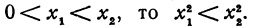
Следовательно, функция 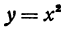Применение производной к исследованию функций возрастает на любом отрезке, лежащем правее начала координат.

Определение:

Функция f(х) называется убывающей на отрезке 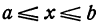Применение производной к исследованию функций , если для любых значений х1 и х2 независимого перемернного, взятых на этом отрезке, всегда из условия х1< х2 вытекает, что f(x1) > f(x2), т. е. функция называется убывающей, если большему значению независимого переменного соответствует меньшее значение функции. Ясно, что для убывающей функции меньшему значению независимого переменного соответствует большее значение функции (рис. 52).

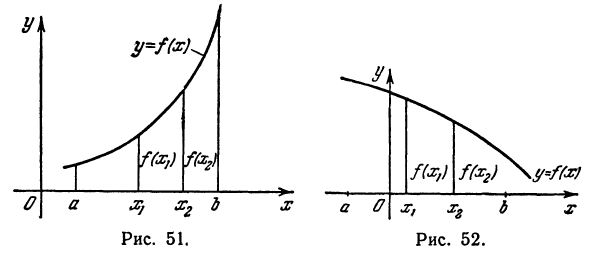
Возрастающая функция имеет график, идущий слева направо вверх. Убывающая функция имеет график, идущий слева направо вниз.

Пример:

Рассмотрим снова функцию 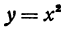Применение производной к исследованию функций . Так как с увеличением абсолютной величины отрицательное число уменьшается, то функция 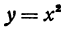является убывающей на любом отрезке, расположенном слева от начала координат.

Если функция f(х), имеющая производную для каждого значения х(а <х < b) , возрастает, то ее производная положительна, но может обращаться в нуль в отдельных точках. В самом деле, пусть 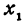Применение производной к исследованию функций — произвольное значение, взятое на отрезке а < х < b. Дадим 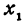приращение h > 0 и найдем соответствующее приращение функции, оно равно

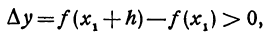
так как функция возрастающая.

Если же дадим 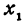Применение производной к исследованию функций отрицательное приращение h < 0, то приращение функции

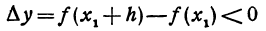
т. е. будет отрицательно, в силу возрастания функции.

Таким образом, для возрастающей функции приращение независимого переменного и приращение функции имеют

всегда одинаковые знаки. Следовательно, дробь

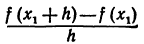
всегда положительна, а поэтому ее предел, который является значением производной при х = 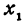Применение производной к исследованию функций , или положителен, или равен нулю.

Если функция f(х) убывает на отрезке 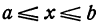Применение производной к исследованию функций и имеет для каждого значения х производную, то ее производная при каждом значении х или отрицательна, или равна нулю. Это вытекает из того, что для убывающей функции знаки приращения функции и приращения независимого переменного всегда противоположны, поэтому дробь 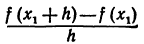Применение производной к исследованию функций всегда имеет знак минус, а следовательно, ее предел отрицателен или равен нулю.

Теперь выясним, что можно сказать о функции, если известен знак ее производной. Напомним, что производная 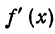Применение производной к исследованию функций есть предел дроби 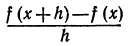при условии, что 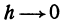. Поэтому, если производная не равна нулю, то ее знак при достаточно малых n совпадает со знаком 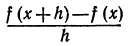Применение производной к исследованию функций . (см. гл. VI, § 4, свойство 5).

Таким образом, если 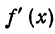Применение производной к исследованию функций > 0, то 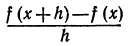> 0

т. е. f(х + h) — f(х) и h одного знака. Функция в этом случае возрастает.

Если 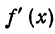Применение производной к исследованию функций < 0, то 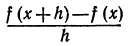< 0 , т. е. знаки

f(х + h) — f(х) и h различны. Функция в этом случае убывает. Эти два последних предложения имеют большое значение для дальнейшего курса.

Определение:

Значение независимого переменного, при котором производная 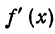Применение производной к исследованию функций равна нулю или не существует, называется критическим значением.

Пример:

Найдем критические значения для функции

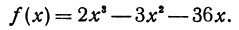
Ее производная

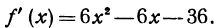
Приравняв производную нулю, получим

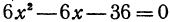
откуда

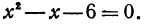
Решая это уравнение, находим:

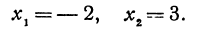
Пример:

Найдем критические значения функции

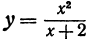
Так как

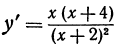
то те значения» при которых производная равна нулю, найдутся из уравнения х ( х + 4) = 0. Они равны х = — 4, х = 0. Производная не существует при тех значениях х, при которых знаменатель обращается в нуль, т. е. 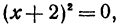Применение производной к исследованию функций откуда находим х = — 2. Итак, рассматриваемая функция имеет следующие критические значения:

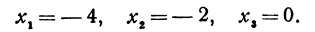
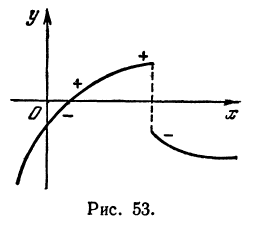
В дальнейшем придется часто пользоваться следующим важным свойством: изменение знака любой величины может произойти либо когда она проходит через нуль, либо когда она претерпевает разрыв (рис. 53)

Так, например, функция у = 3х—6 при х = 1 имеет значение 3 х 1 — 6 = — 3, а при х = 3 значение 3 х 3 — 6 = 3, т. е. эта функция меняет знак. В силу указанного свойства она должна пройти через нуль (так как она непрерывна). Действительно, при х = 2 она равна нулю.

Функция 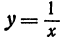Применение производной к исследованию функций при значении х = —1 равна —1, а при х = 4 принимает значение 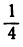. На основании указанного свойства можно утверждать, что между —1 и 4 функция или обращается в нуль, или терпит разрыв. Действительно, при х = 0 она терпит разрыв.

Значит, производная может сменить знак только при переходе через критические значения.

Исследование функций на возрастание и убывание

Изложенное позволяет производить исследование функций на возрастание и убывание. Приведем примеры.

Пример:

Рассмотрим функцию

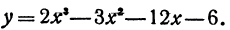
Для того чтобы выяснить, где эта функция возрастает и где убывает, нужно определить, где ее производная положительна и где отрицательна. Так как смена знаков возможна только при переходе через критические значения, то надо прежде всего найти эти значения. Находим производную:

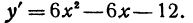
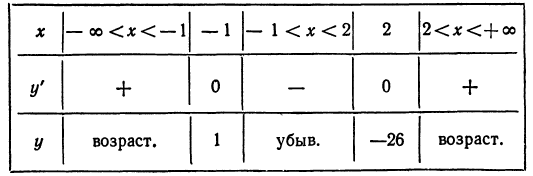
Критическими значениями будут те, в которых производная обращается в нуль. Приравнивая производную нулю и решая полученное уравнение, находим критические значения: х1 = —1, х2 = 2. Других критических значений нет, потому что производная существует всюду. Таким образом, производная может изменить знак только при переходе независимого переменного через х1 = — 1 и х2 = 2. Эти значения разбивают ось х на три участка:

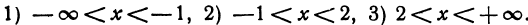
При изменении независимого переменного на каждом из этих участков производная сохраняет знак (в противном случае она должна была бы обратиться в нуль еще раз, а этого нет). Для того чтобы узнать, какой знак имеет производная на рассматриваемом участке, возьмем произвольное значение х, принадлежащее этому участку, и найдем знак производной при этом значении х. Так, например, на участке — < х < —1 возьмем х = —10, получим

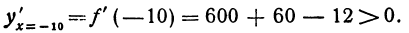
Для участка —1 < х < + 2 возьмем число х = 0, получим

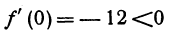
и, наконец, для участка 2 < х < + Применение производной к исследованию функций возьмем число х = 10, получим

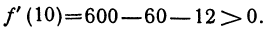
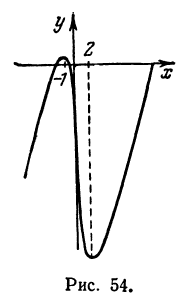
Итак, при изменении х от — Применение производной к исследованию функций до —1 производная положительна, поэтому (см. § 1 этой главы) Рис. 54. функция возрастает. При изменении х от —1 до 2 производная отрицательна, следовательно, функция убывает. И наконец, при изменении х от 2 до Применение производной к исследованию функций производная положительна, значит, функция возрастает (рис. 54).

Результаты исследования сводим в таблицу:

Пример:

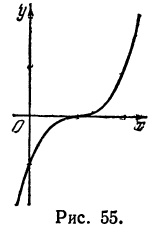
Рассмотрим функцию 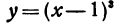Применение производной к исследованию функций . Ее производная

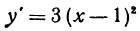
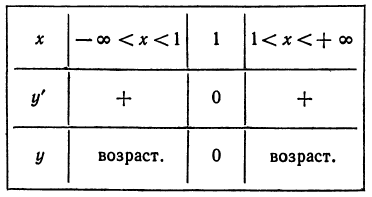
обращается в нуль только при х = 1 и все время положительна, т. е. у’ не меняет знака. Таким образом, функция у всегда возрастает (рис. 55).

Приведем таблицу, отражающую исследование:

Исследование функций на возрастание и убывание позволяет часто решать задачи о нахождении максимальных и минимальных значений, которыми мы и займемся в следующем параграфе.

Максимальные и минимальные значения функции

Значение функции f(с) назовем максимальным или максимумом, если оно больше всех значений функции f(x) при х, достаточно мало отличающихся от с. Иначе говоря, можно найти отрезок, содержащий с в качестве внутренней точки и такой, что при любом х, взятом на этом отрезке Применение производной к исследованию функций , будет иметь место неравенство f(c) > f(x).

Значение функции j(с) называется минимальным или минимумом, если оно меньше всех значений функции f(х) при х, достаточно мало отличающихся от с, т. е. можно найти отрезок, содержащий с в качестве внутренней точки и такой, что при любом x, взятом на этом отрезке Применение производной к исследованию функций , будет выполнено неравенство f(c) < f(x) .

Максимальные и минимальные значения называются экстремальными значениями функции.

Пример:

Рассмотрим функцию

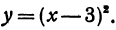
Эта функция равна нулю при х = 3, а при всех остальных значениях х она положительна. Следовательно, при х = 3 она имеет минимум, равный нулю.

Пример:

Для функции f(x) = sin х значение 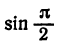Применение производной к исследованию функций = 1, является максимальным, так как 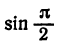> sin х для всех х,

отличающихся от 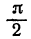Применение производной к исследованию функций меньше чем на 2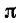т. е. в этом случае «достаточно мало» означает меньше, чем 2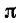. Конечно, функция sin x имеет не один максимум.

Пример:

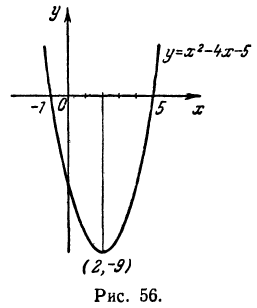
Докажем, что функция

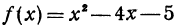
имеет минимум при х = 2. Для этого покажем, что f(2) < f(x) или f(x) — f(2) > 0. В самом деле,

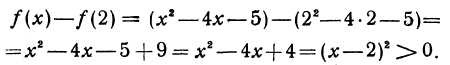
Здесь нам удалось доказать, что неравенство f(2) < f(x) справедливо для всех значений х, а не только достаточно близких к числу 2. Можно сказать, что в данном случае «Достаточно близко» означает на всей оси Ох (рис. 56).

Вообще же доказать существование, а тем более найти экстремальные значения является трудной задачей. При решении этой задачи помогают следующие теоремы.

Теорема:

Необходимые условия существования экстремума. Если функция f(х) имеет экстремум при х = с, то ее производная при х = с или равна нулю, или вовсе не существует.

Доказательство этой теоремы проведем только для случая максимума (для случая минимума доказательство повторяется, только знаки неравенств меняются на обратные).

Итак, пусть функция f(х) при х = с имеет максимум, т. е. для всех х, достаточно близких к с, выполнено неравенство f(c) > f(x) . Это неравенство перепишем, положив x = с + h , где h достаточно мало по абсолютной величине и любое по знаку. Тогда f(c) > f( с + h ) или f( с + h ) — f(c) < 0. Если h >0, то

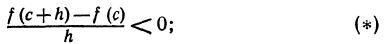
если h < 0 , то

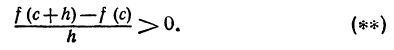
Функция f(х) при х = с: 1) или не имеет производной, 2) или имеет производную. В случае 1) теорема доказана. Если же имеет место случай 2), то, по определению производной, она является определенным числом, равным

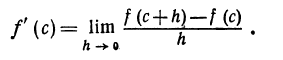
В силу (*) производная f’ (с) не может быть положительным числом. Она или отрицательна, или равна нулю. А в силу (**) производная не может быть отрицательной, она или положительна, или равна нулю.

Так как при отыскании производной h должно принимать как положительные, так и отрицательные значения, то для того, чтобы не получить противоречия, производная необходимо должна быть равна нулю. Теорема доказана.

Доказанная теорема дает необходимые условия для существования экстремума. Это значит, что если экстремум существует, то одно из указанных условий наверное выполнено. Однако может случиться, что одно из этих условий выполнено, а экстремум не существует. Приведем пример.

Пример:

Рассмотрим функцию

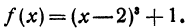
Ее производная 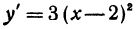Применение производной к исследованию функций обращается в нуль при х = 2. Вычислим

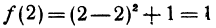
но при х < 2 f(х) имеет числовые значения, меньшие единицы, а при х > 2 ее числовые значения больше, чем единица. Таким образом, нельзя указать отрезка, содержащего внутри себя х = 2 и такого, чтобы на нем было всегда f(2) > f(х) или f(2) < f(х) , т. е. f(2) не является экстремальным значением.

Значит, доказанная теорема позволяет найти те значения независимого переменного, при которых возможны экстремумы, но утверждать наличие экстремумов на основании этой теоремы нельзя. Для отыскания экстремумов служит теорема, дающая достаточные условия существования экстремумов.

Предварительно условимся об употреблении некоторых выражений. Если функция задана на отрезке, содержащем х = с, и если при функция имеет отрицательные значения, а при х > с положительные значения, то будем говорить, что «при переходе через х = с функция меняет знак минус на плюс» (причем при х = с функция может и не существовать).

После этого разъяснения смысл фразы «при переходе через х = с функция меняет знак плюс на минус» становится также ясным. При употреблении этих выражений мы не обращаем внимания на существование функции при х = с.

Теорема:

Достаточные условия существования экстремума. Если функция f(х) определена и непрерывна на отрезке, содержащем х = с, и если производная f'(х) этой функции при переходе через х=с меняет знак плюс на минус, то функция при х = с имеет максимум; если же производная при переходе через х = с меняет знак минус на плюс, то функция при х = с имеет минимум.

Рассмотрим случай изменения знака плюс на минус. По условию при всех значениях х, меньших с, производная положительна; это значит, что функция возрастает, т. е. при х < с имеем f(х) < f(с). При х, больших с, производная отрицательна, поэтому функция убывает, т. е. при x > с имеем f(с )> f(х). Значит, всегда на отрезке имеем f(с) > f(x), а это и значит, что f(с) — максимальное значение функции.

Случай изменения знака минус на плюс рассматривается аналогично.

Пример:

Найдем экстремальные значения функции

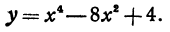
Ее производная равна 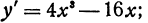Применение производной к исследованию функций она, как известно, непрерывна; поэтому критические значения найдем, приравнивая производную нулю и решая полученное уравнение:

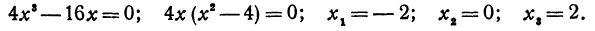
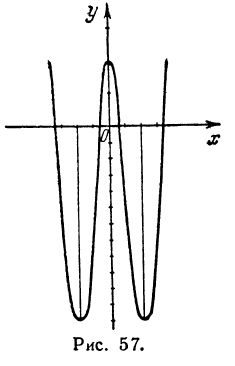
В результате получены три критических значения (рис. 57).

Исследуем знаки производной так, как это было показано раньше, и сведем результаты в таблицу:

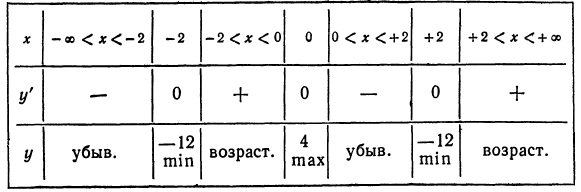
Отсюда видно, что при переходе через x = — 2 производная меняет знак минус на плюс, значит, при x = — 2 функция имеет минимум. При переходе через x = 0 производная меняет знак плюс на минус, поэтому при x = 0 функция имеет максимум. При переходе через x = + 2 производная меняет знак минус на плюс, поэтому при x = 2 функция имеет минимум. Минимум при х = — 2 равен —12, максимум при x = 0 равен 4, и минимум при х = 2 равен—12.

Пример:

Найдем экстремумы функции у = 3 sin 2х + 1, рассматриваемой на отрезке 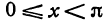Применение производной к исследованию функций . Производная у’=6 cos 2х обращается в нуль при

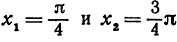
(учитываем только значения, лежащие на отрезке 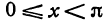Применение производной к исследованию функций ).

Исследуем знаки производной и результаты сведем в таблицу:

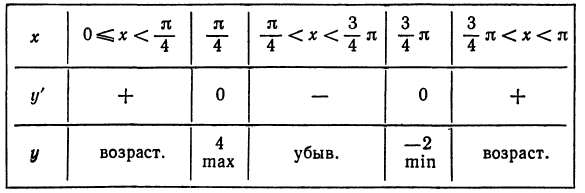
Из таблицы видно, что функция у = 3 sin 2х + 1 при 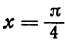Применение производной к исследованию функций , имеет максимум, равный 4, а при 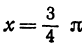минимум, равный —2.

Пример:

Найдем экстремумы функции 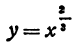Применение производной к исследованию функций .

Ее производная, равная ,

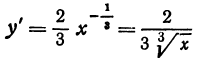
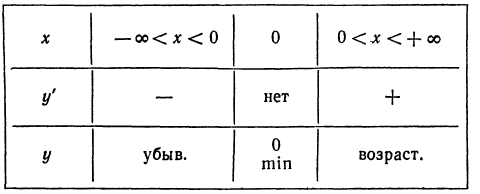
нигде не обращается в нуль, но при x = 0 она не существует, так как знаменатель при этом обращается в нуль. Поэтому единственное критическое значение равно нулю. Исследуем, меняет ли производная при переходе через нуль свой знак. Если х < 0, то производная имеет знак минус; если же x >0, то производная имеет знак плюс, так что при переходе через нуль производная меняет знак — на +. Следовательно, функция при x = 0 имеет минимум, равный нулю (ем. таблицу и рис. 58).

Пример:

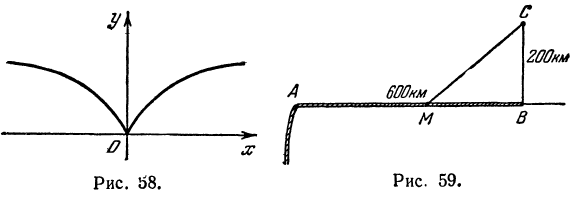
Железная дорога проложена по берегу моря (рис. 59). На траверзе пункта В находится остров С (на траверзе — это значит на перпендикуляре, проведенном из точки В к линии берега). Остров С снабжается продуктами через город A, расположенный на расстоянии 600 км по железной дороге от пункта В. Расстояние BС = 200 км. Грузы из А на остров можно отправлять прямо морем или комбинированным путем, сначала по железной дороге, а затем морем. Скорость перевозки по железной дороге равна 50 км/час, а по морю 30 км\час. Стоимость перевозки единицы груза на 1 км по железной дороге в два раза выше, чем по морю.

Нужно определить место перевалочного пункта М с железнодорожного транспорта на морской так, чтобы перевозка из А на остров С происходила в кратчайшее время. Кроме того, надо определить положение другого перевалочного пункта, который обеспечил бы самую дешевую перевозку. Погрузочные работы в расчет не принимаются.

Обозначим через х расстояние AM. Тогда МВ = 600—х, и из прямоугольного треугольника МВС находим:

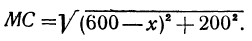
Время, необходимое для перевозки по железной дороге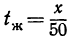 Применение производной к исследованию функций .

Время, затраченное на перевозку морем, обозначим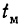 Применение производной к исследованию функций , оно равно

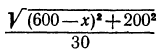
Следовательно, время, затраченное на всю перевозку из А на остров С, равно

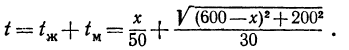
Надо определить минимум этой функции в зависимости от положения х перевалочного пункта М. Находим производную:

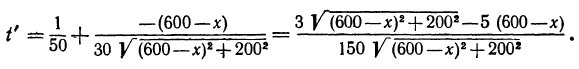
Приравнивая производную нулю, будем иметь

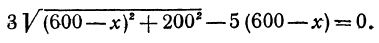
Решая это уравнение, получаем:

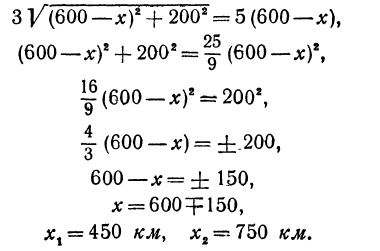
Найдены два критических значения. Однако по смыслу задачи надо взять только 450 км. Этим первая часть задачи решена.

Вторая часть не требует никаких дополнительных вычислений. В самом деле, путь АС короче всякого ломаного пути AMC и проходит по морю, поэтому это будет самый дешевый путь. Итак, самая дешевая перевозка осуществится, если перевалочный пункт сделать в городе А.

В заключение параграфа рассмотрим задачу, имеющую важное физическое значение. Если в некоторой однородной среде (например, воздухе, воде, стекле и т. д.) прямолинейно и равномерно движется точка М со скоростью v, то путь s, пройденный точкой М за промежуток времени t равен s = vt. Теперь сформулируем задачу.

Задача:

Две различные однородные среды соприкасаются по прямой линии (рис. 60).

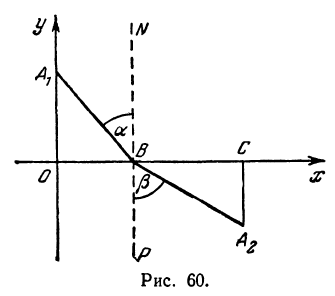
Точка М в каждой из сред может двигаться прямолинейно и равномерно: в первой среде со скоростью v1 во второй — со скоростью v2 . Точка А1 лежит в первой среде, а точка А2 — во второй. Требуется в кратчайшее время перевести точку М из А1 в A2, а также определить вид ломаной линии, по которой при этом должна двигаться точка М.

Решение:

Выберем оси координат так, чтобы ось Ох совпала с прямой, являющейся границей сред, а ось Oy проведем через точку А1 перпендикулярно оси Ох. В этой системе координат абсцисса точки А1 равна нулю, а ордината— некоторому числу y1 так что A1(0, у1). Координаты точки А2 в этой же системе координат обозначим х2 , y2 так что А2(х2, у2).

Пусть точка М, выйдя из A1 приходит в точку В(х, 0), лежащую на границе сред. Тогда путь s1 пройденный в первой среде, можно найти как расстояние между точками А1 и B, т. е.

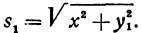
Путь s2 от точки В до А2, пройденный во второй среде, выразится так:

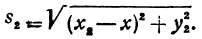
Время движений в первой среде

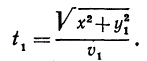
Время движения во второй среде

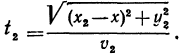
Следовательно, время t, затраченное на прохождение всего пути из А1 в А2, равно

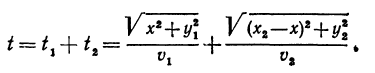
Меняя положение точки В(х, 0) на оси Ох, мы будем менять время t, Таким образом, в задаче требуется определить минимум функции Для этого найдем ее производную:

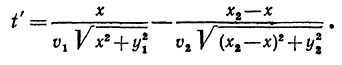
Приравнивая производную нулю, получим

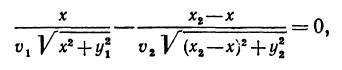
откуда

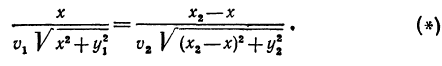
Но

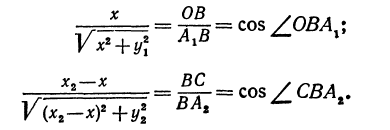
Поэтому равенство (*) можно переписать так:

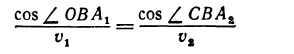
или

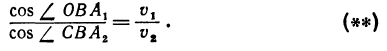
Проведем через точку В прямую РN, перпендикулярную оси Ох, и обозначим

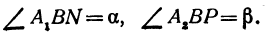
Так как

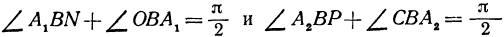
то

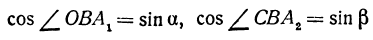
и равенство (**) примет вид

Если угол а назовем углом падения, а угол 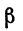Применение производной к исследованию функций — углом преломления, то равенство (***) даст известный из физики закон преломления света. Здесь, как говорят, осуществляется «минимальный принцип».

Выпуклость и вогнутость линии. Точка перегиба

Возьмем произвольную точку Р на кривой, заданной уравнением у=f(х), и проведем через точку Р касательную к этой кривой. Тогда могут представиться три случая (рис. 61)

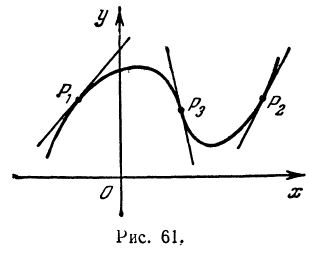
1) вблизи точки Р кривая расположена ниже касательной (точка Р1), 2) вблизи точки Р кривая расположена выше касательной (точка Р2), 3) кривая пересекает касательную в точке Р (точка Р3). В первом случае будем говорить, что кривая выпукла вблизи точки Р , во втором, — что кривая вогнута вблизи точки Р , и в третьем, — что кривая имеет точку перегиба Р . Таким образом, точки перегиба — это точки, в которых выпуклость сменяется вогнутостью или наоборот.

Чтобы иметь возможность судить по уравнению у=f(х) о выпуклости, вогнутости и наличии точек перегиба, рассмотрим вторую производную f«( х).

Предположим, что вторая производная f«( х) отрицательна, т. е. f«( х) < 0. Так как вторая производная по определению есть производная от производной f( х) , то, применяя результат § 1, заключаем, что если f«( х) < 0, то производная f'(х) убывает. А это значит, что с возрастанием абсциссы угол наклона касательной к оси Ох уменьшается.

На рис. 62 изображена кривая, у которой угол наклона касательной убывает с возрастанием абсциссы точки касания. Значит, для нее f«(х) < 0 . Как видно из рис. 62, этот случай соответствует выпуклой кривой.

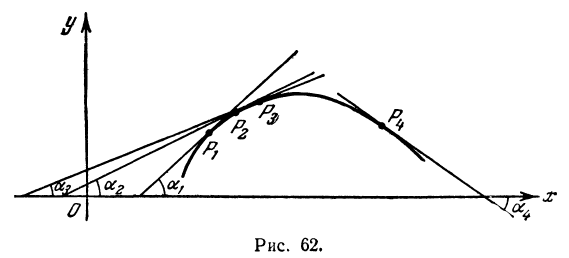
Если вторая производная положительна, т. е. f«(х) > 0 то производная f'(х) возрастает. Это значит, что с увеличением абсциссы угол наклона касательной к оси Ох увеличивается. Из рис. 63 видно, что в этом случае кривая вогнута.

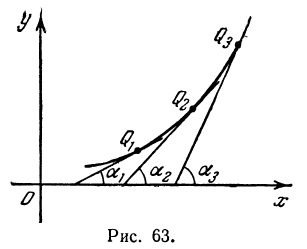
Таким образом случай выпуклости соответствует неравенству f«(х) < 0 , случай вогнутости соответствует неравенству f«(х) > 0 .

В тех точках, в которых выпуклость сменяется вогнутостью, т. е. В тючках перегиба, f»(x) = 0.

Пример:

Рассмотрим кривую, заданную уравнением

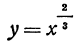
(см. пр. 7 § 3). Производная равна

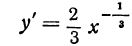
вторая производная равна

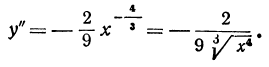
Вторая производная всегда отрицательна, поэтому кривая выпукла, а так как при x = 0 производная не существует, то график имеет вид, представленный на рис. 58.

Значения независимого переменного, при которых вторая производная или равна нулю, или не существует, называются критическими значениями для второй производной. Вторая производная может сменить знак только при переходе через критические значения (ср. § 1). Значит, точки перегиба могут быть только при критических значениях независимого переменного (ср. необходимые условия существования экстремума).

Исследование выпуклости и вогнутости кривой производится по плану, похожему на план исследования экстремумов, Покажем на примере, как это делается.

Пример:

Исследуем на выпуклость и вогнутость кривую, заданную уравнением

Сначала найдем первую производную от функции (*)

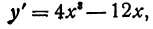
а затем вторую производную:

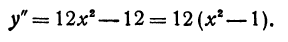
Находим критические значения для второй производной. Так как она существует всюду, то критические значения найдем из уравнения

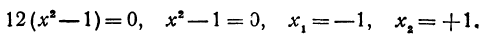
Найдены два критических значения. Эти значения разбивают ось х на три участка:

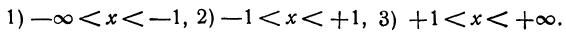
На первом участке вторая производная имеет знак плюс, на втором знак минус и на третьем знак плюс.

Значит, при переходе через х = —1 вторая производная меняет знак плюс на минус, т. е. при х = —1 имеется точка перегиба. При переходе через х =+1 вторая производная меняет знак минус на плюс, значит, и здесь имеется точка перегиба.

Результаты проведенных рассуждений сведем в таблицу:

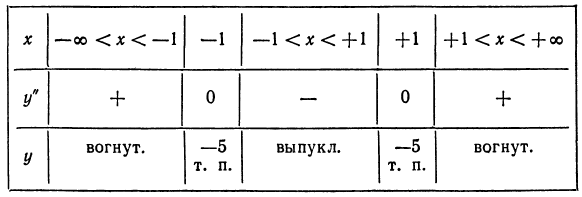
Общий план исследования функций и построения графиков

Изложенное в предыдущих параграфах позволяет провести качественное исследование функции и построить ее график. Под качественным исследованием понимают такое исследование, которое позволяет выяснить существенные свойства функции, но не претендует, например, на нахождение точных значений функции. Приведем примеры такого исследования.

Пример:

Построим график функции

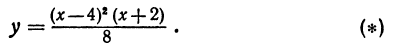
1.Так как все действия, указанные в правой части равенства (*), выполнимы при любых значениях независимого переменного х, то функция существует всюду, т. е. ее область существования

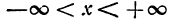
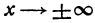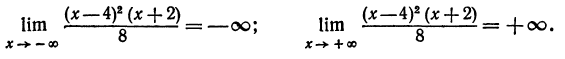
2.Предельные значения при Применение производной к исследованию функций :

3.Вычисляем первую и вторую производные:

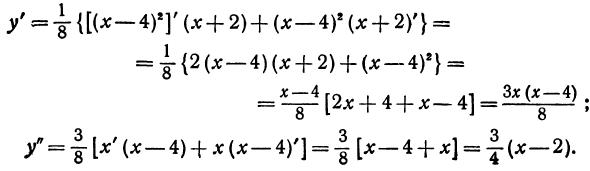
4.Находим критические значения для у’ и у»:

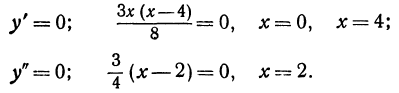
5. Нумеруем критические значения в порядке возрастания:

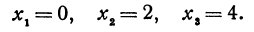
6.Составляем таблицу:

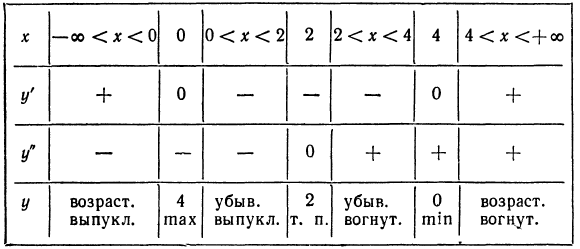
7.Строим график (рис. 64).

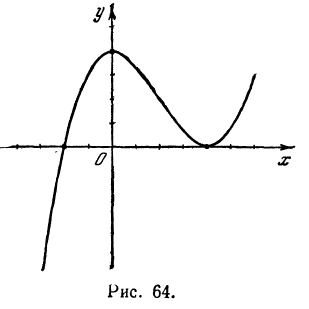
Пример:

Исследовать и построить график функции

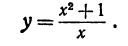
1. Находим область существования функции. Так как деление на нуль не имеет смысла, то область существования не содержит x = 0, т. е. область существования состоит из двух кусков:

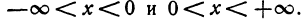
Значит, и график функции состоит также из двух кусков.

2.Исследуем поведение функции в удаленных частях плоскости и при приближении к границе области существования.

Так как степень числителя больше степени знаменателя (см. гл. VI, пр. 8), то

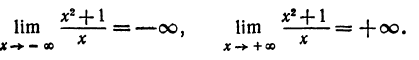
Если х приближается к нулю слева, т. е. остается отрицательным, то знаменатель дроби отрицательный, в то время как числитель приближается к +1, поэтому вся дробь отрицательна и неограниченно увеличивается по абсолютной величине. Это значит, что

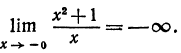
Если х приближается к нулю справа, т. е. остается положительным, то знаменатель дроби будет положительным, в то время как числитель приближается к +1, поэтому вся дробь положительна и неограниченно возрастает. Это значит, что

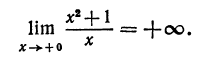
3. Находим первую и вторую производные

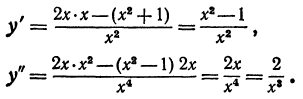
4.Находим критические значения для первой и второй производных:

а) 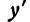Применение производной к исследованию функций не существует при х = 0;

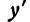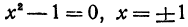
б) Применение производной к исследованию функций = 0;

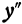в) Применение производной к исследованию функций не существует при x = 0;

г) у» не может быть равна нулю ни при каких значениях x.

5.Нумеруем критические значения для первой и второй производных в порядке их возрастания:

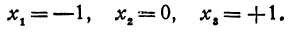
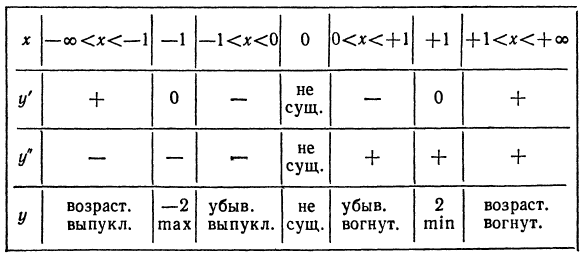
6.Составляя таблицу, отмечаем в ней знаки производных, тем самым мы исследуем функцию на возрастание и убывание, выпуклость и вогнутость, находим экстремумы и точки перегиба:

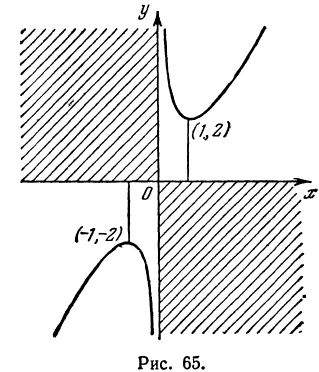
7.Строим график (рис. 65).

Пример:

Исследовать и построить график функции (*)

1.Область существования. Так как все действия, указанные в правой части равенства (*), выполнимы при любом значении независимого переменного х, то областью существования является вся ось Ох; это записываем так:

Значит, график функции (*)состоит из одного куска.

2.Поведение функции в удаленных частях плоскости. Найдем предел функции при неограниченном возрастании независимого переменного:

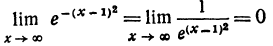
(см. гл. VI, конец § 3 и конец § 5).

Найдем предел функции при неограниченном убывании независимого переменного:

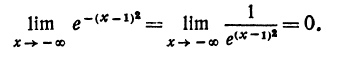
3.Находим первую и вторую производные:

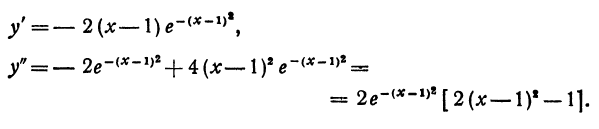
4.Находим критические значения для первой и второй производных:

а) первая производная существует всюду;

б) из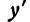 Применение производной к исследованию функций = 0 находим

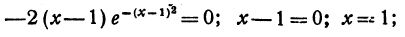
в) вторая производная существует всюду;

г) полагаем 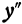Применение производной к исследованию функций = 0 и решаем полученное уравнение

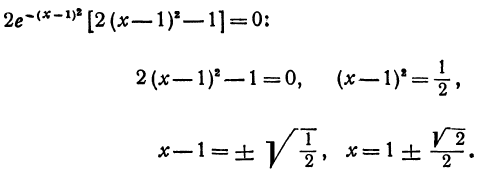
5.Пронумеруем критические значения для первой и второй производных в порядке их возрастания:

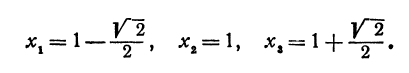
6.Составляем таблицу, в которой отмечаем знаки производных и тем самым исследуем функцию на возрастание и убывание, выпуклость и вогнутость и наличие экстремумов.

7.Строим график (см. таблицу и рис. 66 на стр. 132).

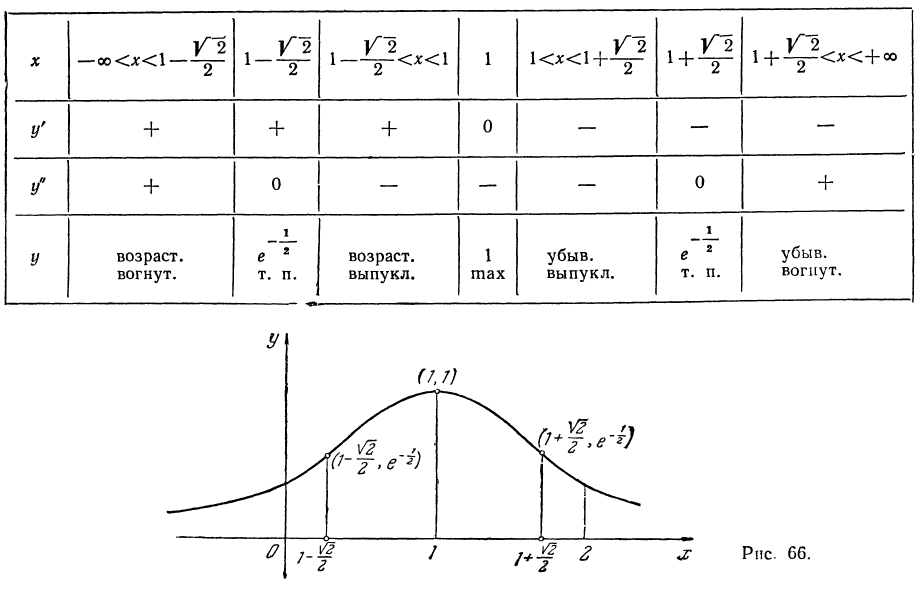
Связь между графиком функции и графиком ее производной

Пусть задана функция f(x), имеющая производную 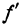Применение производной к исследованию функций (х). Рассмотрим, во-первых, кривую, определяемую уравнением у = f(х) , и, во-вторых, кривую, определяемую уравнением у = f'(х). Например, если дана функция 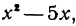Применение производной к исследованию функций ее производная 2х—5, то будем рассматривать, во-первых, параболу, определяемую уравнением

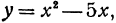
и, во-вторых, прямую, уравнение которой у = 2х—5.

Если функция f(х) при 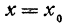Применение производной к исследованию функций имеет экстремум, то ее производная при этом значении 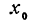или равна нулю, или вовсе не существует; поэтому график функции у = f'(х) при 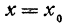Применение производной к исследованию функций или пересекает ось Ох, или терпит разрыв.

Если график функции у = f(х) при 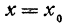Применение производной к исследованию функций имеет точку перегиба, т. е. если в этом месте выпуклость сменяется вогнутостью (или наоборот), и если существует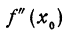, то график у = f'(х) имеет при 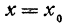Применение производной к исследованию функций экстремум, так как 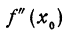= 0.

Дальше в этом параграфе все рассуждения и заключения будут основываться на графиках, поэтому они не будут претендовать на абсолютную точность. Иными словами, здесь будут проводиться только качественные исследования.

Итак, пусть функция f(х) определена графиком, изображенным на рис. 67, а. Под графиком функции у = f(х) будем строить график функции у = f'(х) . На обоих чертежах (а и б) точки, имеющие одинаковые абсциссы, будут расположены на одной прямой, параллельной оси Оу.

На участке АВ функция f(х) возрастает, поэтому ее производная положительна, но так как функция на этом участке выпукла, то производная убывает. Следовательно, график функции у = f'(х) на соответствующем участке аb будет определять положительную убывающую кривую. Максимуму функции f(х) (точке В) на рис. 67, б будет соответствовать точка пересечения с осью Ох (точка b). На участке ВС (рис. 67,а) кривая убывает, поэтому соответствующий участок кривой у = f'(х) располагается ниже оси Ох и убывает. Точке перегиба С на рис. 67,а соответствует минимум на рис. 67, б . Минимуму на рис. 67,а (точке D) соответствует точка пересечения с осью Ох (точка d). Разрыву функции у = f(х) соответствует и разрыв производной. В результате получаем график производной, изображенный на рис. 67,6. В § 5 (пр. 1) был построен график функции

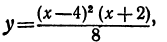
а в § 3 гл III была построена парабола

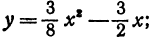
легко увидеть, что функция

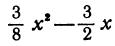
является производной от функции

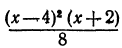
Если соединить графики этих функций, то получим изображенное на рис. 68.

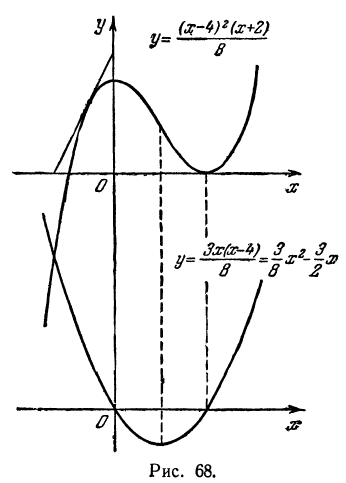
Этот чертеж подтверждает сказанное выше.

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике: