Оглавление:
Самое главное приложение производной состоит в том, что производные позволяют понять, каковы максимальные и минимальные значений исследуемой функции на каком-либо участке (конечном или бесконечном). Однако есть и другие приложения производной: производные позволяют сравнивать степень роста (или убывания) двух или нескольких функций, определять направления их выпуклости, вычислять кривизну и так далее.
Возрастание и убывание функции
Пусть нам дана функция у = f(х), графически представленная на рис. 87. Проследим за ходом изменения величины ординат точек изображенной кривой при возрастании их абсцисс.
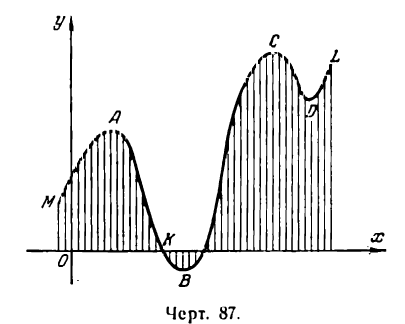
Мы видим, что при возрастании аргумента х ординаты соответствующих точек на участке МА кривой растут, на участке АК убывают. При дальнейшем возрастании аргумента ординаты, принимая отрицательные значения, продолжают убывать *) во всех точках дуги КВ, ординаты же точек дуги ВС возрастают и т. д.
*) Известно, что то отрицательное число меньше, у которого абсолютная величина больше, и наоборот.
Данную функцию для участков МА, ВС и DL называют возрастающей, а для участков АВ и СD — убывающей.
Определение:
Функция у = f(х) называется возрастающей в данном промежутке значений х, если при увеличении аргумента х в этом промежутке соответствующие значения у возрастают, и убывающей, если при увеличении х значения у убывают.
В дальнейшем изложении данной главы изменения аргумента будут рассматриваться только возрастающие, а функция и ее первая и вторая производные — только непрерывные при всех рассматриваемых значениях аргумента.
Признаки возрастания и убывания функции
Теорема:
Если производная функции у = f(х) в данном промежутке значений х положительна, то функция возрастает в этом промежутке, а если производная отрицательна, то функция убывает.
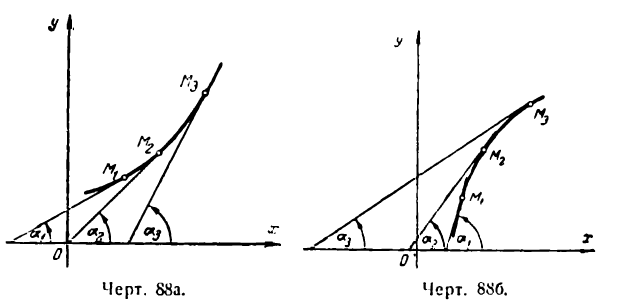
Не доказывая этой теоремы, поясним ее геометрически.
I. Пусть в данном промежутке значений х
Приняв во внимание геометрический смысл производной, можно утверждать, что угловой коэффициент касательных, проведенных к графику функции у = f(х), в рассматриваемом промежутке положителен. Иначе говоря, касательные образуют с положительным направлением оси Ох острый угол (рис. 88а и 88б), а это наблюдается в том случае когда график в данном промежутке поднимается т.е. функция возрастает.
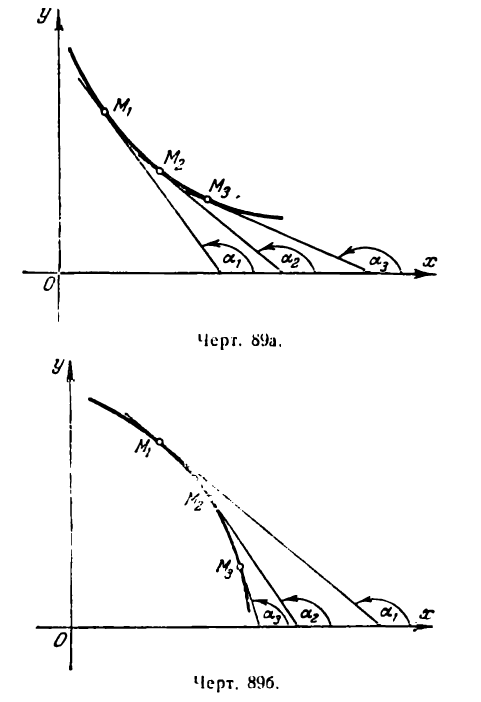
II. Положим, что в данном промежутке значений х
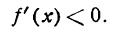
Это значит, что угловой коэффициент касательных, проведенных к графику функции у = f(х), отрицателен. Иначе говоря, касательные образуют тупой угол с положительным направлением оси Ох (рис. 89а и 89б), а это бывает в случае, когда график в рассматриваемом промежутке опускается, т. е. функция убывает.
Пример:
Определить промежутки возрастания и убывания функции
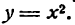
Решение:
Найдем производную данной функции
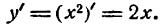
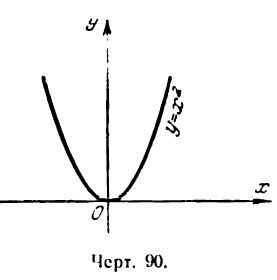
Величина 2х имеет положительное значение при всяком положительном х и отрицательное — при любом отрицательном его значении.
Отсюда следует, что данная функция убывающая при х < 0 и возрастающая при х > 0 (рис. 90).
Максимум и минимум функции
Рассматривая ход изменения функции на рис. 87, мы можем отметить, что ординаты точек на участках МА и ВС возрастают, достигая в точках А и С кривой наибольшей величины сравнительно со значениями ординат ближайших к ним точек, и убывают на участках АВ и СD до наименьшей величины в точках В и D сравнительно со значениями ординат соседних к ним точек.
Те значения аргумента, при которых функция имеет наибольшую или наименьшую величину, называются соответственно точками максимума или минимума функции, а значение функции при этих значениях аргумента — максимумом или минимумом ее.
Как видно, точка максимума служит границей перехода от возрастания функции к ее убыванию, а точка минимума— границей перехода от убывания функции к ее возрастанию.
Определение:
Функция у = f(х) имеет максимум при х — а, если при всех х, достаточно близких к а, выполняется неравенство
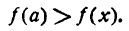
Определение:
Функция у = f(х) имеет минимум при если при всех х, достаточно близких к а выполняется неравенство
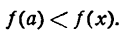
Признаки максимума и минимума функции
I. Пусть точке А графика функции у = f(х) соответствует максимум при х = а (рис. 91). Как видно из рисежа, во всех точках, расположенных левее А, касательные образуют с положительным направлением оси Ох острые углы. Поэтому
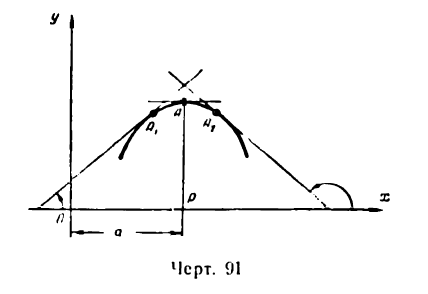
тангенс этих углов, а согласно геометрическому смыслу производной и 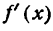 в указанных точках имеет положительное значение.
в указанных точках имеет положительное значение.
В точках же, лежащих правее А, касательные образуют с положительным направлением оси Ох тупые углы, а потому тангенс этих углов, а также первая производная имеет отрицательное значение.
Так как производная функции непрерывна, то ее значение должно меняться без скачков, и, следовательно, при переходе от положительных значений к отрицательным пройдет при х = а через нуль, т. е. в точке А
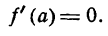
Если функция у = f(x) при х = а имеет максимум, то
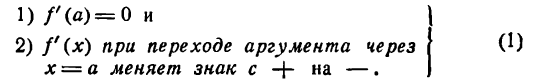
II. Положим, что точке В графика функции у = f(х) соответствует минимум при х = а (рис. 92). Рассуждая так же, придем к выводу, что в этом случае первая производная
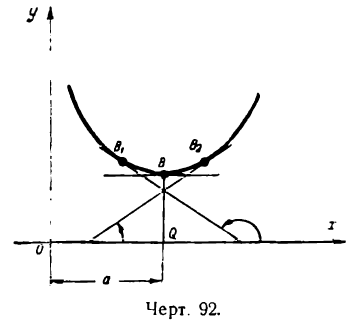
при возрастании х меняет отрицательные значения на положительные и, будучи непрерывной, обращается при х = а в нуль, т. е. в точке В
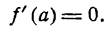
Таким образом, если функция у = f(x) при х = а имеет минимум, то
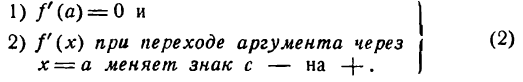
Справедливы обратные утверждения. Функция y = f(x) при х = а имеет максимум, если
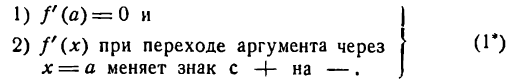
Функция у = f(х) при х = а имеет минимум, если

Признаки (1 * ) и (2*) являются достаточными признаками максимума и минимума функции, т. е. такими признаками, наличие которых влечет за собой или максимум или минимум функции.
*) Бывают случаи, когда в точках кривой, соответствующих максимуму или минимуму функции, касательная параллельна не оси Ох, а оси Оу. Такие функции исключаются нами из рассмотрения.
Как видно из равенства  , касательная, проведенная в точках А и В графиков, параллельна оси Ох*).
, касательная, проведенная в точках А и В графиков, параллельна оси Ох*).
III. Может, однако, случиться, что первая производная функции, обращаясь в нуль при х = а, не меняет знака при переходе аргумента через х = а. В этом случае функция не имеет ни максимума ни минимума. На рис. 93 показано, что касательная в точке А кривой у = f(х) параллельна оси Ох, т. е.  , но
, но 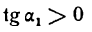 и
и 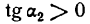
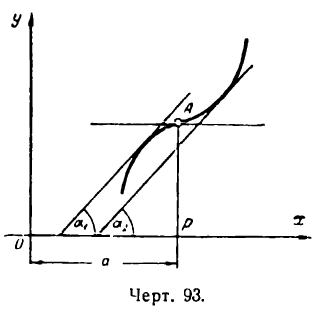
Следовательно, первая производная функции у = f(х) при переходе аргумента через х = а не меняет знака. Функция, как показывает рисеж, не имеет при х = а ни максимума ни минимума.
Значения аргумента, обращающие первую производную в нуль, будем называть критическими значениями аргумента.
Правило нахождения максимума и минимума функции
Пусть дана функция у = f(х). Для исследования ее на максимум и минимум прежде всего нужно решить уравнение 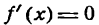 для нахождения критических значений аргумента. Пусть действительными корнями этого уравнения будут х1, х2, х3 и т. д. **).
для нахождения критических значений аргумента. Пусть действительными корнями этого уравнения будут х1, х2, х3 и т. д. **).
**) Этих корней будет ограниченное число, если мы исключим из рассмотрения бесконечно колеблющиеся функции.
Затем нужно исследовать знак f'(x) для найденных критических значений х, начиная с х1 (наименьшего); с этой целью определяют знак производной сначала для 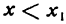 подставляя какое-либо число, меньшее
подставляя какое-либо число, меньшее 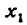 (производная при всех значениях
(производная при всех значениях 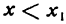 не обращается в нуль, а потому ее знак в силу непрерывности сохраняется неизменным при
не обращается в нуль, а потому ее знак в силу непрерывности сохраняется неизменным при 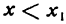 как это следует из выводов).
как это следует из выводов).
После этого определяют знак производной при каком-либо значении х в промежутке между х1 и х2 (в промежутке между x1 и х2 производная сохраняет один и тот же знак по тому же свойству непрерывной функции).
Найдя таким образом знаки производной для значений х, сначала меньшего, а потом большего чем x1, устанавливают, существует ли при этом значении х= х1 максимум или минимум функции или нет ни того ни другого.
Точно так же исследуют знак f'(x) для остальных критических значений х.
Первое правило. Таким образом, для исследования функции y = f(x) на максимум и минимум нужно:
I. Найти производную функции у’ = f'(x).
П. Приравняв ее нулю, найти действительные корни полученного уравнения) пусть они будут х1, x2, х3 и т. д.
III. Расположив значения x1, х2, х3, … в порядке их возрастания, подставить в производную сначала какое-либо число, меньшее х1, затем подставить число, заключенное в промежутке между х1 и х2;
если при этом знак производной меняется с + на —, то при х = x1| имеет место максимум;
если с — на + , то при х—х1 имеет место минимум;
если же знак производной не меняется, функция при х = х1 не имеет ни максимума ни минимума;
таким же образом определить знак производной до х2 и после х2 и т. д.
IV. Найти максимальные и минимальные значения функции, т. е. вычислить f(x1), f(x2), f(x3) и т. д.
Четвертый пункт этого правила нужен только в том случае, если есть необходимость знать положение точек на кривой, соответствующих максимуму и минимуму функции.
Рассмотрим несколько примеров.
Пример:
Исследовать на максимум и минимум функцию
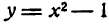
Решение:
Находим производную функции:
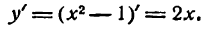
II. Приравниваем ее нулю:
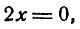
откуда
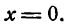
III. Определяем знак производной для значения x < 0, например для х = —1:
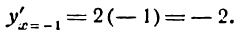
Теперь находим знак производной для х > 0, например для х — 1:
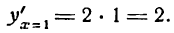
Изменение знака производной с минуса на плюс показывает, что данная функция при x = 0 имеет минимум.
IV. Находим минимальное значение функции, т. е. f(0):
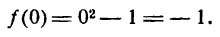
Теперь мы можем представить на рисеже положение найденной точки A(0; — 1) и вид кривой вблизи нее (рис. 94).
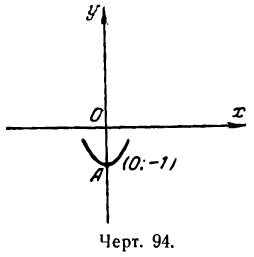
Пример:
Исследовать на максимум и минимум функцию
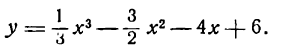
Решение:
Согласно правилу имеем:
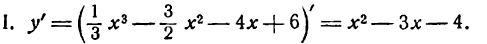
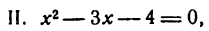
откуда
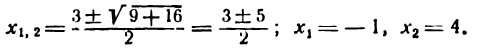
III. 1) Исследуем критическое значение х1 = —1. Берем значение х < — 1, например х = — 2; тогда
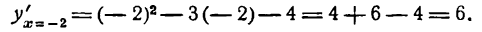
Возьмем значение х > — 1, например х = 0; тогда
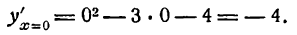
Перемена знака производной с плюса на минус показывает, что функция при х = —1 имеет максимум.
2) Исследуем критическое значение x2 = 4. Беря для x < 4 значение x = 0, а для х > 4 значение х = 5, имеем:
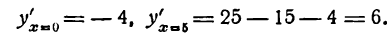
Следовательно, при х = 4 функция имеет минимум.
IV. Максимальное и минимальное значения функции будут:
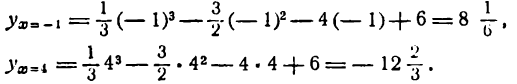
Результат вычисления запишем в таблицу:
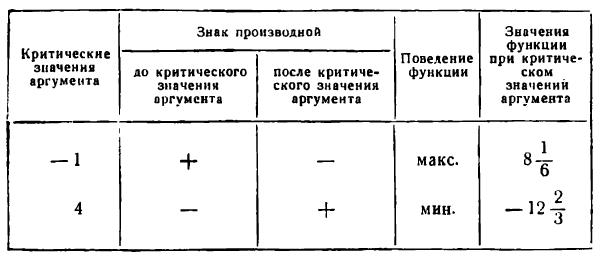
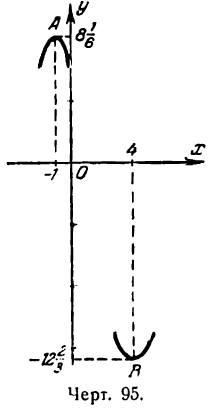
Обозначив точки графика функции, соответствующие максимуму и минимуму ее через А и В, напишем:
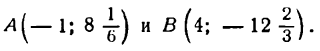
Положение точек A и В и вид кривой вблизи них представлены на рис. 95.
Пример:
Исследовать на максимум и минимум функцию
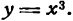
Решение:
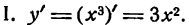
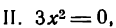
откуда 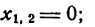
III. Для х < 0, например для х = -1
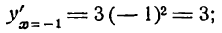
для х > 0, например для x = 1,
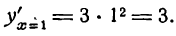
Знаки производной оказались одинаковыми при переходе через критическое значение х = 0; следовательно, данная функция при х = 0 не имеет ни максимума ни минимума (рис. 71).
Выпуклость и вогнутость кривой
Рассмотрим кривую, изображенную на рис. 96. Проведя касательную, например АВ, мы видим, что точки кривой, смежные с точкой касания А и лежащие по обе стороны от нее, располагаются ниже касательной. В таком случае говорят, что кривая выпукла вверх в точке А; если часть кривой между точками М и N удовлетворяет этому условию, то эту часть кривой называют выпуклой вверх или просто выпуклой.
Возьмем кривую, изображенную на рис. 97.
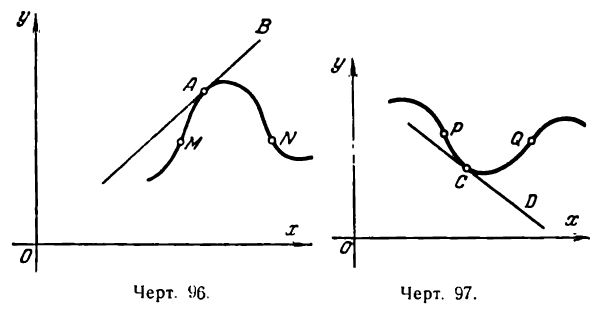
Здесь мы наблюдаем другое явление, а именно: точки кривой, близкие к точке касания С и расположенные по разным сторонам от нее, лежат выше касательной СD. В этом случае говорят, что кривая в точке С вогнута вверх и часть кривой между точками Р и Q, удовлетворяющей этому условию, называют вогнутой вверх или просто вогнутой.
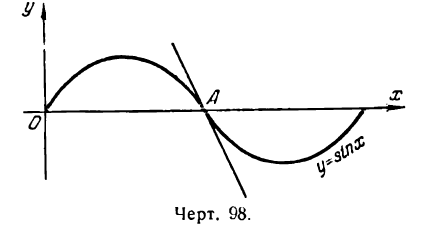
Бывают случаи, когда кривая в одной своей части выпукла, а в другой вогнута; так, например, синусоида (рис. 98) имеет и выпуклость (выше оси Ох) и вогнутость (ниже оси Ох), причем точка А служит границей между ними. Касательная, проведенная к кривой в этой точке, является общей для выпуклой и вогнутой части ее; эта касательная в то же время пересекает кривую в точке касания; поэтому синусоида в точке А ни выпукла ни вогнута. Эта точка носит название тонки перегиба.
Признаки выпуклости и вогнутости кривой
Теорема:
Если вторая производная функции у = f(x) в данном промежутке значений х положительна, то кривая вогнута в этом промежутке, а если отрицательна, — то выпукла.
Поясним эту теорему геометрически.
I. Пусть в данном промежутке значений х

Так как f»(x) является производной функции f'(x), то, применяя признак возрастания и убывания к функции f'(x) , скажем, что при условии (1) f'(x) возрастает с возрастанием х в данном промежутке. Но тогда согласно геометрическому смыслу первой производной возрастает и угловой коэффициент касательных, проведенных к графику функции y = f(x) в точках данного промежутка, т. е. растет тангенс угла наклона этих касательных, а следовательно, и угол их наклона к положительному направлению оси Ох.
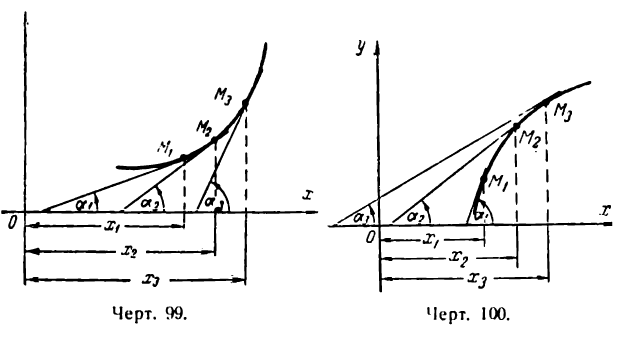
Итак, при условии (1) с возрастанием х угол, образованный касательными к кривой y — f(х) с положительным направлением оси Ох, растет, а это наблюдается только в случае, когда касательные проведены в точках, лежащих на вогнутом участке кривой (рис. 99).
II. Пусть в данном промежутке значений х

При этом условии с возрастанием х функция f'(x) убывает, а потому убывает и угловой коэффициент касательных, проведенных к графику функции у = f(x) в точках данного промежутка, т. е. убывает тангенс угла наклона этих касательных, а следовательно, и угол их наклона к положительному направлению оси Ох.
Таким образом, при условии (2) с возрастанием х угол между касательными к кривой у=f(х) и положительным направлением оси Ох убывает, а это имеет место только в случае, когда касательные проведены на выпуклом участке кривой (рис. 100).
Пример:
Узнать, выпукла или вогнута кривая  в точке, абсцисса которой равна —2.
в точке, абсцисса которой равна —2.
Решение:
Находим вторую производную данной функции и определяем ее знак при х = — 2:
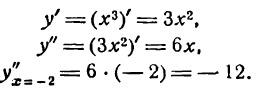
Вторая производная отрицательна; следовательно, кривая 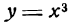 в данной точке выпукла (рис. 71).
в данной точке выпукла (рис. 71).
Нахождение точки перегиба
Определение:
Точкой перегиба кривой называется точка, которая отделяет выпуклую часть кривой от вогнутой.
Если график функции у=f(х) меняет выпуклость на вогнутость или наоборот, то при этом вторая производная данной функции должна менять свой знак, обращаясь в нуль в точке перегиба.
Легко показать, что справедливо и обратное утверждение: если при данном х вторая производная функции у = f(х) равна нулю и при переходе аргумента через данное значение х меняет знак, то при этом график функции имеет точку перегиба.
Это является достаточным признаком точки перегиба. Отсюда имеем следующее правило.
Чтобы найти точку перегиба кривой у =f(х), нужно:
I.Отыскать вторую производную функции у = f(х).
II. Приравняв ее нулю, решить полученное уравнение; пусть действительными корнями его будут х1, х2, х3 и т. д. *).
*) Предполагается, что уравнение имеет ограниченное число корней.
III. Расположив значения х1, х2, х3, … в порядке их возрастания, подставить во вторую производную сначала любое число, меньшее х1, затем — любое число, заключенное между х1 и х2\ если в обоих случаях получатся разные знаки, то при х = х1 имеется точка перегиба, если же одинаковые, то точки перегиба нет; таким же образом определить знак второй производной до и после х2 и т. д.
IV. Найти ординаты точек перегиба, т. е. вычислить функцию для тех значений аргумента, для которых имеет место перегиб.
Пример:
Найти точку перегиба кривой 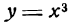 .
.
Решение:
Согласно правилу находим;
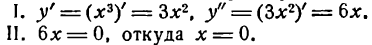
III. Определяем знак:
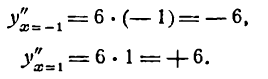
Как видно, при х = 0 имеет место точка перегиба.
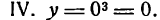
Кривая 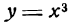 имеет точку перегиба в начале координат и здесь меняет выпуклость на вогнутость, как это видно из чередования знаков второй производной (рис. 71).
имеет точку перегиба в начале координат и здесь меняет выпуклость на вогнутость, как это видно из чередования знаков второй производной (рис. 71).
Второе правило нахождения максимума и минимума функции
Теорема:
Если для некоторой функции у=f(х)
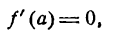
то данная функция при х = а имеет
максимум, если f» (а) < 0 и минимум, если f» (а) > 0
Покажем справедливость теоремы следующими соображениями.
При условии f’ (а) = 0 функция у = f(x) имеет максимум или минимум или точку перегиба. Но согласно теореме 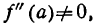 поэтому точка перегиба исключается.
поэтому точка перегиба исключается.
При f»(а) < 0 точка с абсциссой х = а лежит на выпуклой части графика функции, а при f»(а) >0 — на вогнутой его части. Следовательно, в первом случае имеет место максимум, во втором — минимум, что и требовалось показать.
Может однако случиться, что при f'(а) = 0 также и f»(а ) = 0, тогда при помощи второй производной нельзя установить, что имеет функция: максимум или минимум. В этом случае для решения вопроса нужно прибегнуть к первому правилу.
Таким образом, имеем второе правило для нахождения максимума и минимума функции:
Найти вторую производную функции и подставить в нее каждое из критических значений аргумента; если в результате подстановки одного из них вторая производная будет отрицательной, то при этом значении аргумента функция имеет максимум, если положительной,— то минимум, а если же вторая производная обращается в нуль, то для решения вопроса нужно обратиться к первому правилу.
Рассмотрим несколько примеров.
Пример:
Исследовать на максимум и минимум функцию
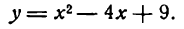
Решение:
Согласно правилу имеем:
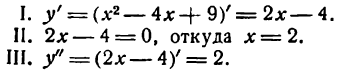
Вторая производная оказалась положительной; следовательно, при х = 2 имеет место минимум.
Пример:
Исследовать на максимум и минимум функцию
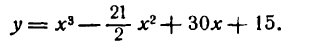
Решение:
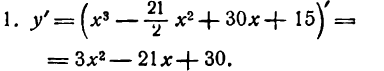
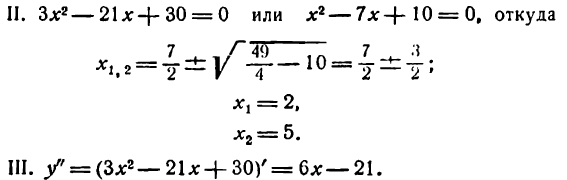
Подставим во вторую производную вместо х поочередно значения 2 и 5:
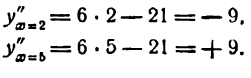
Как видно, при х =2 функция имеет максимум, при х = 5 — минимум.
Пример:
Исследовать на максимум и минимум функцию
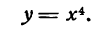
Решение:
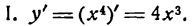
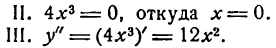
Подставив значение x = 0, получим:
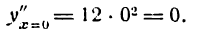
Вторая производная оказалась равной нулю, поэтому указанным способом установить максимум и минимум нельзя. Обратившись к первому правилу, будем иметь:
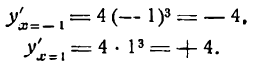
Перемена знака первой производной показывает, что при x = 0 функция имеет минимум.
Задачи на максимум и минимум функции
Теория максимума и минимума функции имеет большое применение как в самой математике, так и в технических дисциплинах. Решим несколько задач.
Задача:
Разбить число 20 на два слагаемых, произведение которых имело бы наибольшее значение.
Решение:
Будем искать эти слагаемые. Обозначим одно из них буквой х; тогда другое слагаемое выразится в виде 20 — х. Произведение этих слагаемых есть переменная величина, меняющаяся с изменением слагаемого х. Обозначая произведение буквой у, запишем:
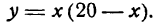
Мы получили функцию, выражающую зависимость произведения у от величины слагаемого х. В задаче требуется найти такое х, при котором у принимает наибольшее значение, т. е. задача свелась к нахождению максимума функции.
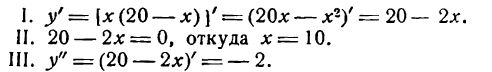
Следовательно, при x = 10 функция имеет максимум.
Число 20 нужно разбить на два равных слагаемых, тогда их произведение будет наибольшим.
Задача:
Найти высоту конуса наибольшего объема, который можно вписать в шар радиуса, равного R.
Решение:
Обозначив радиус основания, высоту и объем конуса соответственно буквами r, h и v, запишем:
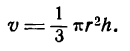
Это равенство выражает зависимость v от двух переменных r и h исключим одну из этих величин, а именно r. Для этого из прямоугольного треугольника АВО (рис. 101)
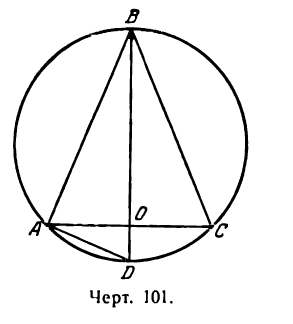
выводим (по теореме о квадрате перпендикуляра, опущенного из вершины прямого угла на гипотенузу):
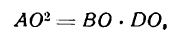
или
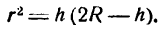
Подставив значение 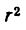 в формулу объема конуса, получим:
в формулу объема конуса, получим:
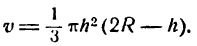
Мы видим, что объем v конуса, вписанного в шар радиуса R, есть функция от высоты этого конуса h. Найти высоту, при которой вписанный конус имеет наибольший объем, это значит найти такое h , при котором функция v имеет максимум.
Ищем максимум функции v:
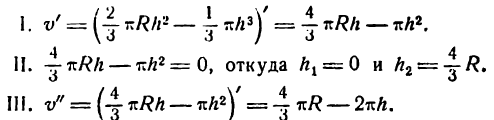
Подставив вместо h сначала h1 = 0, а потом 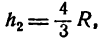 получим:
получим:
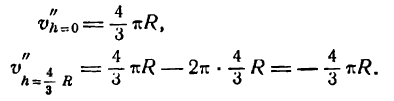
В первом случае имеем минимум, во втором — искомый
максимум.
Следовательно, при 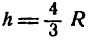 конус, вписанный в шар радиуса /?, имеет наибольший объем.
конус, вписанный в шар радиуса /?, имеет наибольший объем.
Задача:
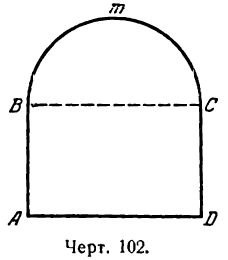
Окно имеет форму прямоугольника, завершенного полукругом; периметр фигуры окна равен 6 м. Каковы должны быть его размеры, чтобы оно пропускало максимум света (рис. 102).
Решение:
Как известно, количество света, проходящего через окно, тем больше, чем больше площадь окна. Обозначим:
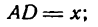
тогда длина полуокружности В m С будет равна 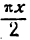 , а высота окна
, а высота окна
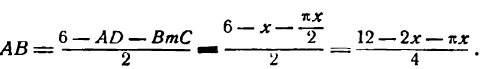
Площадь всего окна состоит из площадей прямоугольника АВСD и полукруга ВmС, По соответствующим формулам найдем:
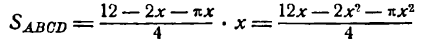
Обозначив площадь окна буквой у, получим:
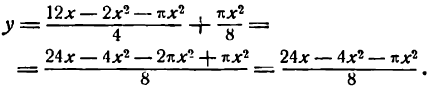
Мы видим, что площадь окна у в условиях нашей задачи является функцией его основания х, и задача свелась к нахождению максимума функции у.
Исследуем полученную функцию на максимум:
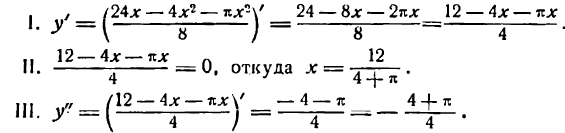
Вторая производная оказалась отрицательной, значит, при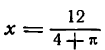 площадь окна наибольшая.
площадь окна наибольшая.
Для прохождения наибольшего количества света через окно с контуром в 6 м нужно, чтобы ширина его была равна
Графики функций
В настоящей главе мы познакомились с тем, как изучаются свойства функции с помощью ее производных. Знание этих свойств позволяет нам получить представление о функции, а также построить ее график.
Пример:
Построить график функции
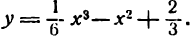
Решение:
Исследуем данную функцию на максимум и минимум.
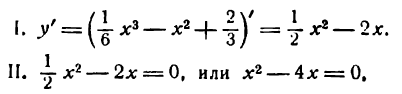
откуда x1 = 0 и х2 = 4.
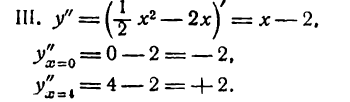
При x = 0 функция имеет максимум, при x = 4 — минимум.
IV. Найдем ординаты точек, соответствующих максимуму и минимуму функции:
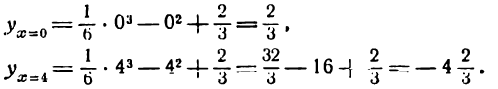
Координаты искомых точек суть 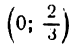 и
и 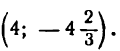
Исследуем теперь данную функцию на точку перегиба; для этого найденную вторую производную приравняем нулю:
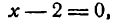
откуда
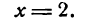
Чтобы убедиться, что при х = 2 имеет место перегиб, определим знаки второй производной для х < 2 и для х > 2; в результате получим:
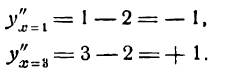
Смена знаков второй производной показывает, что аргументу х = 2 соответствует точка перегиба. Найдя ее ординату, будем иметь:
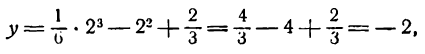
и координаты точки перегиба (2; — 2).
Чтобы яснее представить график данной функции, вычислим координаты еще нескольких точек *).
*) Часто бывает полезно найти точки пересечения кривой с осями координат, однако это нередко связано с большими трудностями при решении уравнений высших степеней.
Положив, например, х = — 2 и х = 6, получим:
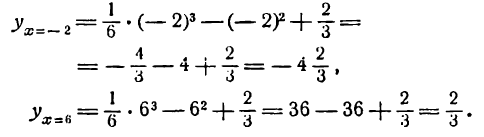
Координаты дополнительных точек суть 
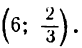
Составим таблицу найденных значений координат точек:
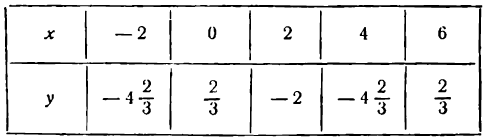
Построим все эти точки и проведем через них плавную линию (рис.103).
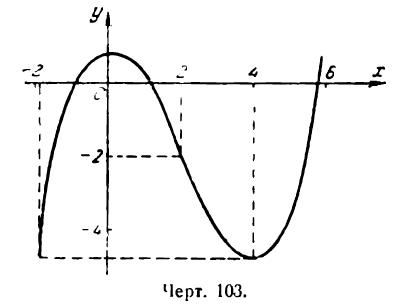
Для построения графика функции следует придерживаться такой схемы.
- Найти значения х, при которых данная функция имеет максимум или минимум.
- Найти значения х, при которых график функции имеет точки перегиба.
- Вычислить значения ординат точек, соответствующие найденным значениям абсцисс; присоединив к этим точкам еще несколько дополнительных, записать найденные значения х и у в таблицу.
- Построить найденные точки и провести через них плавную линию.
Приложение производных к исследованию функций
Использование производных позволяет прояснить многие особенности в поведении функций. Наиболее важными особенностями функций являются интервалы монотонности и точки экстремумов функций. Кроме того, для приложений нужно уметь находить полиномы, значения которых вместе с производными совпадают со значениями функции в известной точке. Такие полиномы называют приближающими. Если функция относится к классу монотонных функций, то ее производная сохраняет знак на интервале монотонности, причем возрастающая функция имеет положительную производную, а убывающая — отрицательную. Действительно, если 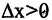 и так как
и так как
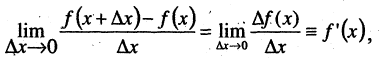
то знак производной совпадает со знаком приращения функции. Для возрастающих функций 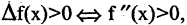 для убывающих функций
для убывающих функций 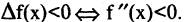
Функция имеет локальный максимум (минимум) в точке 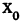 , если она определена как в точке
, если она определена как в точке 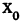 , так и в окрестности этой точки и значение функции в точке
, так и в окрестности этой точки и значение функции в точке 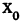 больше (меньше), чем ее
больше (меньше), чем ее
значения во всех соседних точках: т. е. 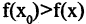 в точках максимума и
в точках максимума и 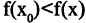 в точках минимума для всех х из окрестности точки
в точках минимума для всех х из окрестности точки 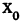 .
.
Функция имеет локальный максимум (минимум) в точке 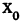 , если она определена как в точке
, если она определена как в точке 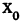 , так и в окрестности этой точки и значение функции в точке
, так и в окрестности этой точки и значение функции в точке 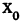 больше (меньше), чем ее значения во всех соседних точках: т. е.
больше (меньше), чем ее значения во всех соседних точках: т. е. 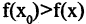 в точках максимума и
в точках максимума и 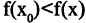 в точках минимума для всех х из окрестности точки
в точках минимума для всех х из окрестности точки 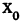 .
.
Минимумы и максимумы функции объединены единым понятием — экстремумы. До точки максимума функция возрастает, следовательно, ее производная положительна 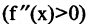 , после точки максимума — убывает, производная отрицательна
, после точки максимума — убывает, производная отрицательна 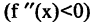 . Для точки минимума первоначально функция убывает
. Для точки минимума первоначально функция убывает 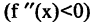 , а потом возрастает
, а потом возрастает 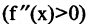 . В самих точках экстремумов производная или равна нулю (обычный экстремум) или не существует (острый экстремум). На рис. 3.6 функция имеет экстремумы в точках
. В самих точках экстремумов производная или равна нулю (обычный экстремум) или не существует (острый экстремум). На рис. 3.6 функция имеет экстремумы в точках 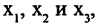 причем в точке
причем в точке 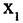 — острый максимум, а в точках
— острый максимум, а в точках 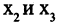 — обычный минимум и максимум. Тем самым в точках экстремумов функции производная равна нулю или не существует (необходимое условие экстремума) и меняет знак с «+» на «-» в точках максимумов и с «-» на «+» в точках минимумов (достаточные условия экстремума).
— обычный минимум и максимум. Тем самым в точках экстремумов функции производная равна нулю или не существует (необходимое условие экстремума) и меняет знак с «+» на «-» в точках максимумов и с «-» на «+» в точках минимумов (достаточные условия экстремума).
Замечание:
Не надо путать наибольшее и наименьшее значение и экстремум. Экстремум достигается всегда внутри промежутка, а наибольшее и наименьшее значения могут достигаться и в точках экстремумов, и на границах промежутка, и в точках разрыва. На рис. 3.6 точка х3 является точкой максимума и в ней достигается наибольшее значение, наименьшее значение достигается в точке а, т.е. на границе промежутка.
Формула Тейлора
Пусть функция 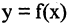 в интервале (а,b) имеет производные до
в интервале (а,b) имеет производные до 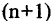 -го порядка включительно. Приближающий полином п-ой степени, значение которого и его производных до порядка п включительно совпадают со значением функции и ее производных в точке
-го порядка включительно. Приближающий полином п-ой степени, значение которого и его производных до порядка п включительно совпадают со значением функции и ее производных в точке 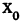 , имеет вид
, имеет вид
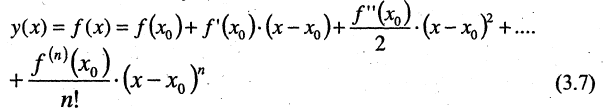
В окрестности точки 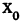 замена функции полиномом дает некоторую ошибку. Формула Тейлора обеспечивает возможность точной замены данной функции полиномом
замена функции полиномом дает некоторую ошибку. Формула Тейлора обеспечивает возможность точной замены данной функции полиномом
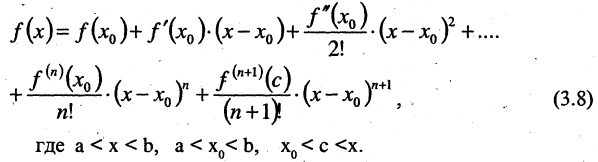
Выражение
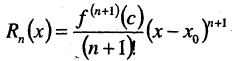
называется остаточным членом формулы Тейлора в форме Лагранжа. Величина 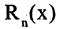 определяет погрешность, возникающую при замене функции полиномом степени п. Форма Лагранжа позволяет при вычислениях найти оценку сверху для
определяет погрешность, возникающую при замене функции полиномом степени п. Форма Лагранжа позволяет при вычислениях найти оценку сверху для 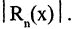
Если учесть, что 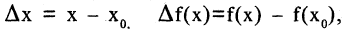 а
а 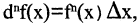 то получим дифференциальную форму формулы Тейлора
то получим дифференциальную форму формулы Тейлора
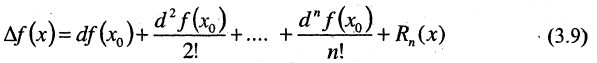
Формула Маклорена — частный случай формулы Тейлора, когда 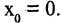
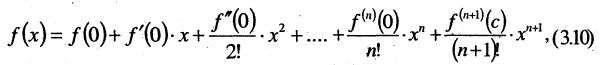
Пример:
Вычислить значение числа е.
Решение. Построим формулу Тейлора для функции 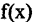
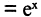 в окрестности точки
в окрестности точки 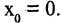 Прежде всего вычислим производные:
Прежде всего вычислим производные:
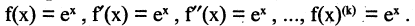
Отсюда 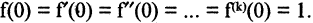
Из (4.16) для 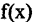
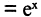 имеем
имеем
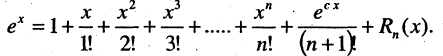
Эта формула получена для 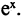 Если в правой части положить
Если в правой части положить 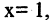 то
то
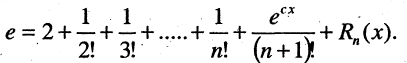
В зависимости от требований задачи эта формула позволяет получить сколь угодно точные значения величины е. Так
для 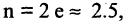 ошибка не превышает величины 0.23,
ошибка не превышает величины 0.23,
для 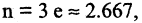 ошибка не превышает величины 0.052,
ошибка не превышает величины 0.052,
для 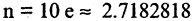 и ошибка не более, чем
и ошибка не более, чем 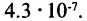
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

