Преобразование Лапласа с примерами решения и образцами выполнения

Оглавление:

Ранее мы рассмотрели интегральное преобразование Фурье

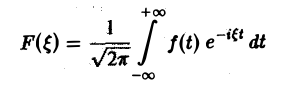
с ядром K(t, ξ) = 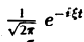Преобразование Лапласа .

Преобразование Фурье неудобно тем, что должно быть выполнено условие абсолютной интегрируемости функции f(t) на всей оси t,

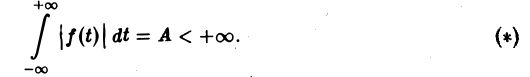
Преобразование Лапласа позволяет освободиться от этого ограничения.

Определение:

Функцией-оригиналом будем называть всякую комплекснозначную функцию f(t) действительного аргумента t, удовлетворяющую следующим условиям:

f(t) непрерывна на всей оси t, кроме отдельных точек, в которых f(t) имеет разрыв 1-го рода, причем на каждом конечном интервале оси t таких точек может быть лишь конечное число;
функция f(t) равна нулю при отрицательных значениях t, f(t) = 0 при t < 0;
при возрастании t модуль f(t) возрастает не быстрее показательной функции, т. е. существуют числа М > 0 и з такие, что для всех t

Ясно, что если неравенство (1) выполняется при некотором s = s1, то оно будет выполнятся при всяком s2 > s1.

Точная нижняя грань sо всех чисел s, so = infs, для которых выполняется неравенство (1), называется показателем роста функции f(t).

Замечание:

В общем случае неравенство

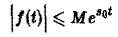
не имеет места, но справедлива оценка

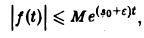
где ε > 0 — любое. Так, функция f(t) = t, t ≥ 0, имеет показатель роста so =0. Для нее неравенство |t| ≤ М ∀t ≥ 0 не выполняется, но ∀ε > О, ∀t > 0 верно неравенство 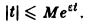Преобразование Лапласа

Условие (1) гораздо менее ограничительное, чем условие (*).

Пример:

Функция

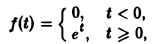
не удовлетворяет условию (*), но условие (1) выполнено при любом s ≥ 1 и М ≥ 1; показатель роста so = 1. Так что f(t) является функцией-оригиналом. С другой стороны, функция

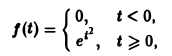
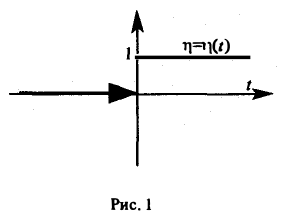
не является функцией-оригиналом: она имеет бесконечный порядок роста, sо = +∞. Простейшей функцией-оригиналом является
так называемая единичная функция

Если некоторая функция φ(t) удовлетворяет условиям 1 и 3 определения 1, но не удовлетворяет условию 2, то произведение f(t) = φ(t) η(t) уже является функцией-оригиналом.

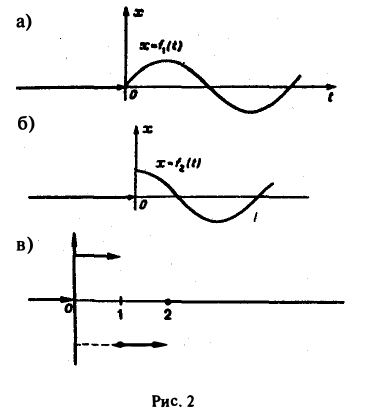
Для простоты записи мы будем, как правило, множитель η(t) опускать, условившись, что все функции, которые мы будем рассматривать, равны нулю для отрицательных t, так что если речь идет о какой-то функции f(t) например, о sin t, cos t, e^t и т. д., то всегда подразумеваются следующие функции (рис. 2):

Определение:

Пусть f(t) есть функция-оригинал. Изображением функции f(t) по Лапласу называется функция F(p) комплексного переменного р = s + iσ, определяемая формулой

где интеграл берется по положительной полуоси t. Функцию F(p) называют также преобразованием Лапласа функции f(t); ядро преобразования K(t, р) = e^-pt.
Тот факт, что функция f(x) имеет своим изображением F(p), будем записывать так:

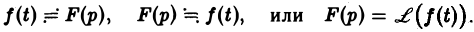
Пример:

Найти изображение единичной функции η(t).

Функция 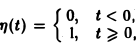Преобразование Лапласа является функцией-оригиналом с показателем роста s0 = 0. В силу формулы (2) изображением функции η(t) будет функция

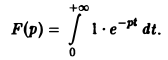
Если р = s + iσ, то при s > 0 интеграл в правой части последнего равенства будет сходящимся, и мы получим

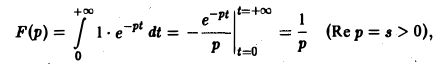
так что изображением функции η(t) будет функция 1/p. Как мы условились, будем писать, что η(t) = 1, и тогда полученный результат запишется так:

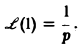
Теорема:

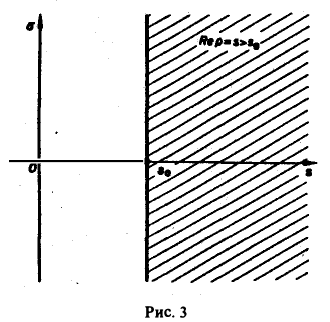
Для всякой функции-оригинала f(t) с показателем роста sо изображение F(p) определено в полуплоскости Re p = s > So и является в этой полуплоскости аналитической функцией (рис. 3).

Пусть

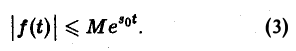
Для доказательства существования изображения F(p) в указанной полуплоскости достаточно установить, что несобственный интеграл (2) абсолютно сходится при s > so. Используя (3), получаем

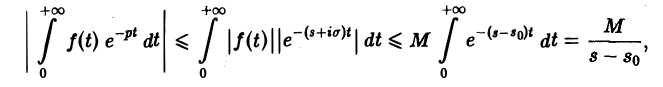
что и доказывает абсолютную сходимость интеграла (2). Одновременно мы получили оценку преобразования Лапласа F(p) в полуплоскости сходимости Re р = s > so

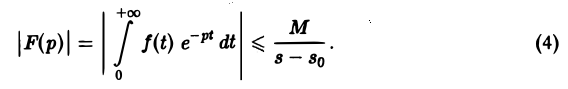
Дифференцируя выражение (2) формально под знаком интеграла по р, находим

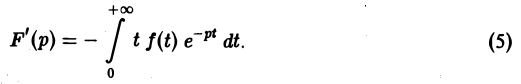
Существование интеграла (5) устанавливается так же, как было установлено существование интеграла (2).

Применяя для F'(p) интегрирование по частям, получаем оценку

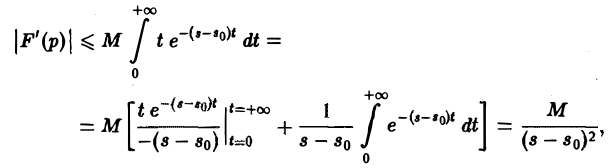
откуда следует абсолютная сходимость интеграла (5). (Внеинтегральное слагаемое Преобразование Лапласа — при t → + ∞ имеет предел, равный нулю). В любой полуплоскости Re р ≥ S1 > So интеграл (5) сходится равномерно относительно р, поскольку он мажорируется сходящимся интегралом

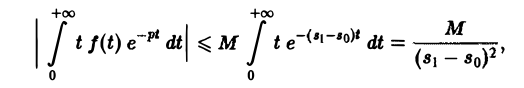
не зависящим от р. Следовательно, дифференцированиепо р законно и равенство (5) справедливо.

Поскольку производная F'(p) существует, преобразование Лапласа F(p) всюду в полуплоскости Re p = s > sо является аналитической функцией.

Из неравенства (4) вытекает

Следствие:

Если точка р стремится к бесконечности так, что Re р = s неограниченно возрастает, то

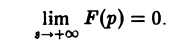
Пример:

Найдем еще изображение функции f(t) =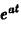 Преобразование Лапласа , где а = а + iβ — любое комплексное число.

Показатель роста sо функции f(t) равен а.

Считая Rep = s> а, получим

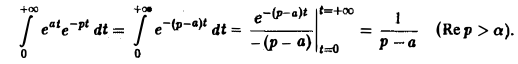
Таким образом,

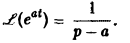
При а = 0 вновь получаем формулу

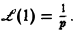
Обратим внимание на то, что изображение функции 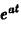Преобразование Лапласа является аналитической функцией аргумента р не только в полуплоскости Re p > а, но и во всех точках р, кроме точки р = а, где это изображение имеет простой полюс. В дальнейшем мы не раз встретимся с подобной ситуацией, когда изображение F(p) будет аналитической функцией во всей плоскости комплексного переменного р, за исключением изолированных особых точек. Противоречия с теоремой 1 нет. Последняя утверждает лишь, что в полуплоскости Re p > So функция F(p) не имеет особых точек: все они оказываются лежащими или левее прямой Re p = So, или на самой этой прямой.

Замечание:

В операционном исчислении иногда пользуются изображением функции f(t) по Хевисайду, определяемым равенством

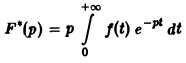
и отличаюикмся от шоСражения по Лапласу множителем р.

Свойства преобразования Лапласа

В дальнейшем через f(t), φ(t), … будем обозначать функции-оригиналы, а через F(p), Ф(р), … — их изображения по Лапласу,

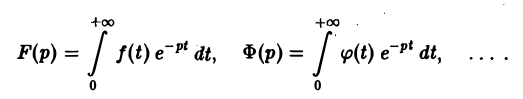
Из определения изображения следует, что если f(t) = 9 ∀t, то F(p) = 0.

Теорема единственности:

Если две непрерывные функции f(t) и φ{t) имеют одно и тоже изображение F(p), то они тождественно равны.

Теорема:

Линейность преобразования Лапласа. Если f{t) и φ{t) — функции-оригиналы, то для любых комплексных постоянных а и β

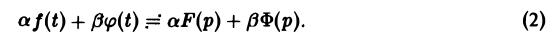
Справедливость утверждения вытекает из свойства линейности интеграла, определяющего изображение:

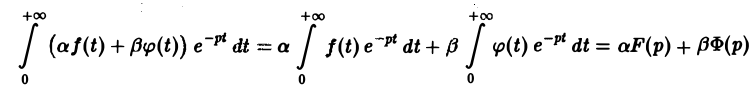
Преобразование Лапласа — показатели роста функций f(t) и φ(t) соответственно).

На основании этого свойства получаем

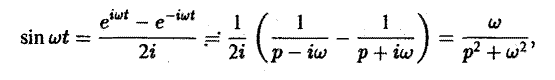
т. е. (3)

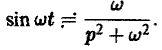
Аналогично находим, что
(4)

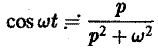
и, далее,
(5) (6)

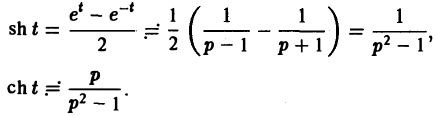
Теорема подобия:

Если f(t) — функция-оригинал и F(p) — ее изображение по Лапласу, то для любого постоянного а > 0

Полагая at = т, имеем

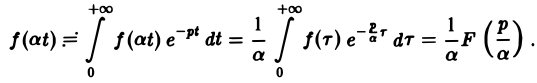
Пользуясь этой теоремой, из формул (5) и (6) получаем

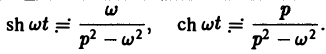
Теорема:

О дифференцировании оригинала. Пусть f(t) является функцией-оригиналом с изображением F(p) и пусть 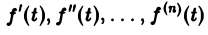Преобразование Лапласа — также функции-оригиналы, — показатель роста функции 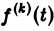(k = 0, 1,…, п). Тогда

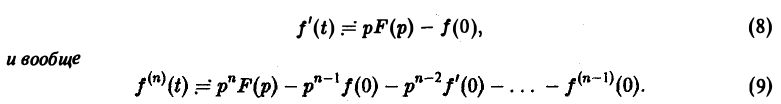
Здесь под fk(0) (k = 0,1,… , п — 1) понимается правое предельное значение 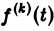Преобразование Лапласа .

Пусть f(t) = F(p). Найдем изображение f'(t). Имеем

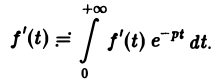
Интегрируя по частям, получаем

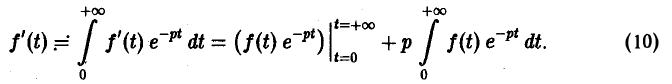
Внеинтегральное слагаемое в правой части (10) обращается в нуль при t → + ∞, т. к. при Re р = s > Преобразование Лапласа имеем

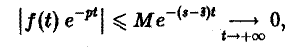
подстановка t = 0 дает -f(0).

Второе слагаемое справа в (10) равно pF(p). Таким образом, соотношение (10) принимаетвид

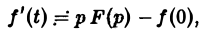
и формула (8) доказана. В частности, если f(0) = 0, то f'(t) = pF(p). Для отыскания изображения 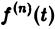Преобразование Лапласа запишем

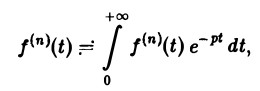
откуда, интегрируя п раз по частям, получим

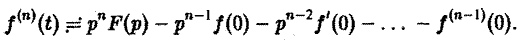
Пример:

Пользуясь теоремой о дифференцировании оригинала, найти изображение функции f(t) = sin²t.

Пусть f(t) = F(p). Тогда

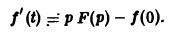
Но f(0) = О, а f'(0) = 2 sin t cos t = sin 2t = 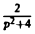Преобразование Лапласа . Следовательно, 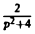= pF(p), откуда F(p) =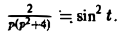

Теорема 5 устанавливает замечательное свойство интегрального преобразования Лапласа: оно (как и преобразование Фурье) переводит операцию дифференцирования в алгебраическую операцию умножения на р.

Формула включения. Если f(t) и f'(t) являются функциями-оригиналами, то (11)

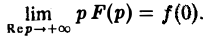
В самом деле, f'(<) = р F(p) — f(0). В силу следствия из теоремы 1, всякое изображение стремится к нулю при Rе р = s → + ∞. Значит, 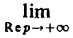Преобразование Лапласа [pF(p) — f(0)] = 0, откуда вытекает формула включения (11).

Теорема:

О дифференцировании изображения. Дифференцирование изображения сводится к умножению на (—t) оригинала,

Так как функция F(p) в полуплоскости Rep = s > so является аналитической, то ее можно дифференцировать по р. Имеем

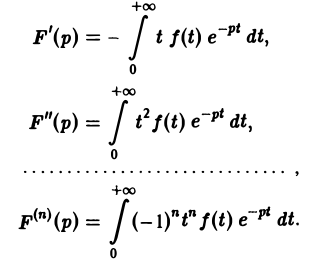
Последнее как раз и означает, что 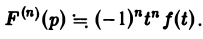Преобразование Лапласа

Пример:

Пользуясь теоремой 6, найти изображение функции 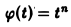Преобразование Лапласа .

Как известно, 1 = 1/p. Здесь f(t) = 1, F(p) = 1/p. Отсюда (1/p)’= (-t) • 1, или 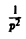Преобразование Лапласа = t. Вновь применяя теорему 6, найдем

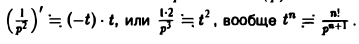
Теорема:

Интегрирование оригинала. Интегрирование оригинала сводится к делению изображения на р: если f(t) = F(p), то

Положим

Нетрудно проверить, что если f(t) есть функция-оригинал, то и φ(t) будет функцией-оригиналом, причем φ(0) = 0. Пусть φ(t) = Ф(р). В силу (14)

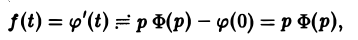
С другой стороны, f(t) =’ F(p), откуда F(p) = рФ(р), т.е. Ф(р) =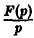 Преобразование Лапласа .

Последнее равносильно доказываемому соотношению (13).

Пример:

Найти изображение функции

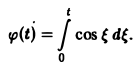
В данном случае f(t) = cos t, так что F(p) = 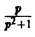Преобразование Лапласа . Поэтому

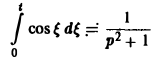
Теорема:

Интегрирование изображения. Если f(t) = F(p) и интеграл 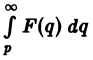Преобразование Лапласа сходится, то он служит изображением функции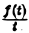

Действительно,

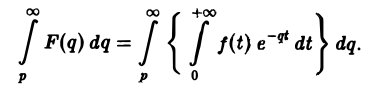
Предполагая, что путь интегрирования (р, ∞) лежит в полуплоскости Re p ≥ а> so, мы можем изменить порядок интегрирования (t > 0):

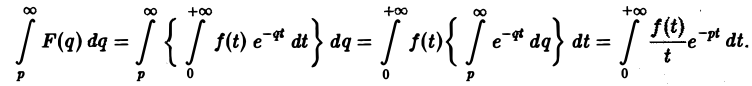
Последнее равенство означает, что 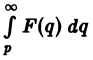Преобразование Лапласа является изображением функции .

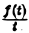Пример:

Найти изображение функции 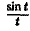Преобразование Лапласа .

Как известно, sin t = 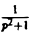Преобразование Лапласа .

Поэтому

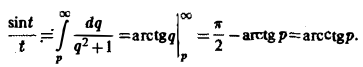
Теорема запаздывания:

Если f{t) = F(p), то для любого положительного τ («запаздывания»)

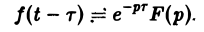
Так как

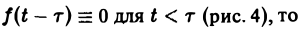
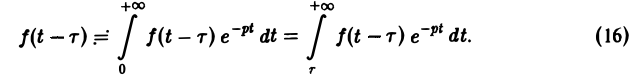
Положим ξ = t- τ. Тогда dt = d ξ. При t = τ получаем ξ = 0, при t = + ∞ имеем ξ = + ∞.

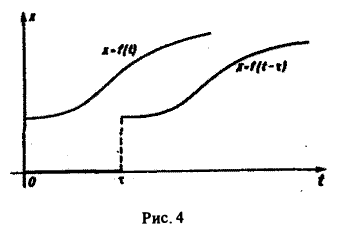
Поэтому соотношение (16) принимает вид

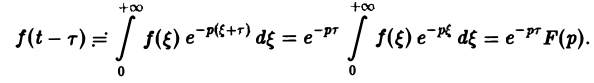
Пример:

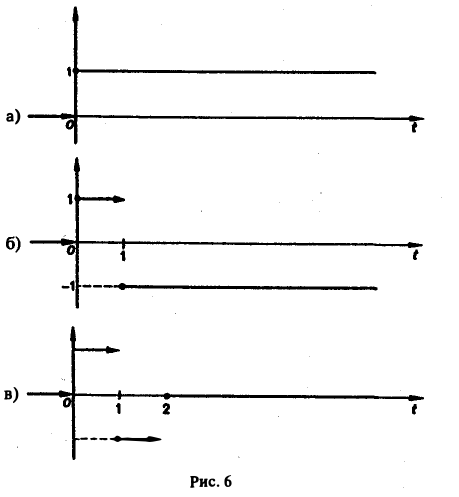
Найти изображение функции f(t), заданной графически (рис. 5).

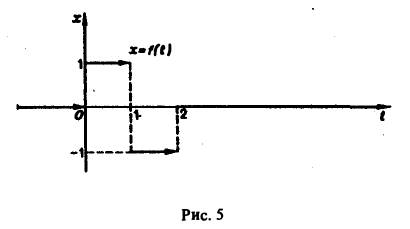
Запишем выражение для функции f(t) в следующем виде:

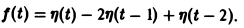
Это выражение можно получить так. Рассмотрим функцию f1(t) = η(t) для t ≥ 0 (рис. 6 а) и вычтем из нее функцию

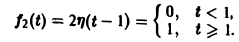
Разность f(t) — h(t) будет равна единице для t ∈ [0,1) и -1 для t ≥ 1 (рис. 6 b). К полученной разности прибавим функцию

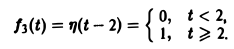
В результате получим функцию f(t) (рис. 6 в), так что

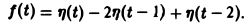
Отсюда, пользуясь теоремой запаздывания, найдем

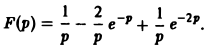
Теорема смещения:

Если f{t) = F(p) для любого комплексного числа ро

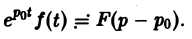
В самом деле,

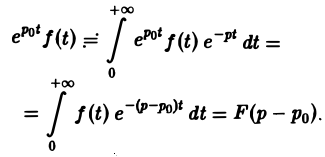
Теорема позволяет по известным изображениям функций находить изображения тех же функций, умноженных на показательную функцию 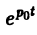Преобразование Лапласа , например,

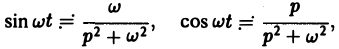
так что

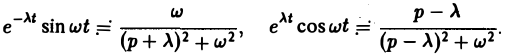
Свертка функций. Теорема умножения

Пусть функции f(t) и φ(t) определены и непрерывны для всех t. Сверткой (f *φ)(t) этих функций называется новая функция от t, определяемая равенством

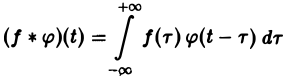
(если этот интеграл существует).

Для функций-оригиналов f(t) и φ(t) операция свертки всегда выполнима, причем
(17)

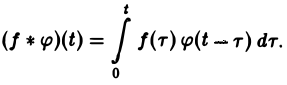
В самом деле, произведение функций-оригиналов f( τ ) φ(t — τ), как функция от τ, является финитной функцией, т.е. обращается в нуль вне некоторого конечного промежутка (в данном случае вне отрезка 0 ≤ τ ≤ t). Для финитных непрерывных функций операция свертки выполнима, и мы получаем формулу (17).

Нетрудно проверить, что операциясвертки коммутативна,

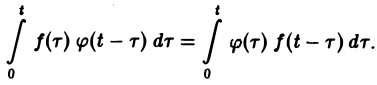
Теорема умножения:

Если f(t) = F(p), <p(t) =’Ф(р), то свертка (f * φ)(t) имеет изображение F(p) • Ф(р),

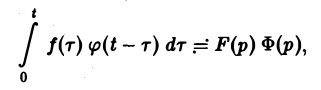
или

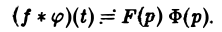
Нетрудно проверить, что свертка (f * φ)(t) функций-оригиналов есть функция-оригинал с показателем роста s* = mах{s1, s2}, где s1, s2 ~ показатели роста функций f(t) и φ(t) соответственно. Найдем изображение свертки,

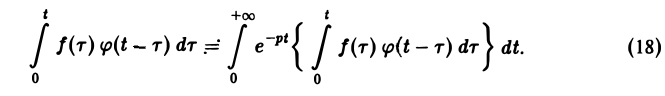
Воспользовавшись тем, что

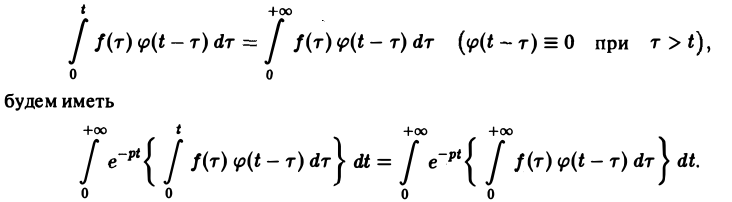
Меняя порядок интегрирования в интеграле справа (при Re р = s > s* такая операция законна) и применяя теорему запаздывания, получим

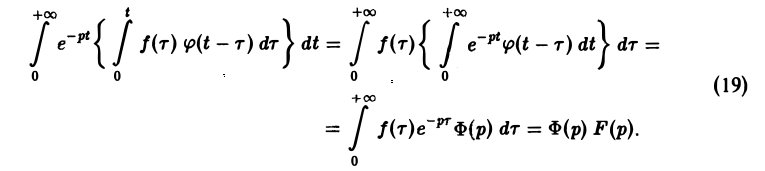
Таким образом, из (18) и (19) находим

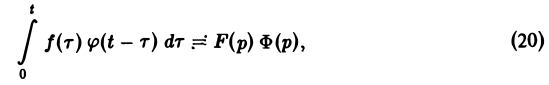
— умножению изображений отвечает свертывание оригиналов,

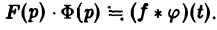
Пример:

Найти изображение функции

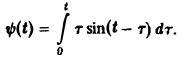
Функция ψ(t) есть свертка функций f(y) = t и φ(t) = sin t. В силу теоремы умножения

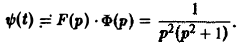
Задача:

Пусть функция f(t), периодическая с периодом Т, есть функция-оригинал. Показать, что ее изображение по Лапласу F[p) дается формулой

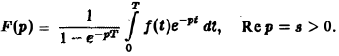
Отыскание оригинала по изображению

Задача ставится так: дана функция F(p), надо найти функцию f(t). изображением которой является F(p).

Сформулируем условия, достаточные для того, чтобы функция F(p) комплексного переменного р служила изображением.

Теорема:

Если аналитическая в полуплоскости Rep = s > so функция F(p)

1) стремится к нулю при |р| —» + ∞ в любой полуплоскости Re р = а > So равномерно относительно arg р;

2) интеграл

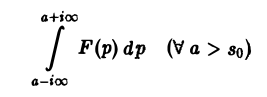
сходится абсолютно, то F(p) является изображением некоторой функции-оригинала f{t).

Задача:

Может ли функция F(p) = 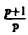Преобразование Лапласа служить изображением некоторой функции-оригинала? Укажем некоторые способы отыскания оригинала по изображению.

Отыскание оригинала с помощью таблиц изображений

Прежде всего стоит привести функцию F(p) к более простому, «табличному» виду. Например, в случае, когда F(p) — дробно-рациональная функция аргумента р,ее разлагают на элементарные дроби и пользуются подходящими свойствами преобразования Лапласа.

Пример:

Найти оригинал для

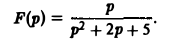
Запишем функцию F(p) в виде:

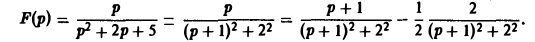
Пользуясь теоремой смещения и свойством линейности преобразования Лапласа, получаем

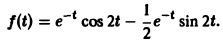
Пример:

Найти оригинал для функции

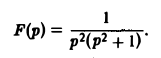
Запишем F(p) в виде

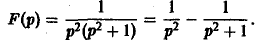
Отсюда f(t) = t — sin t.

Использование теоремы обращения и следствий из нее

Теорема обращения:

Если функция f(t) есть функция-оригинал с показателем роста so и F{p) — ее изображение, то в любой точке непрерывности функции f(t) выполняется соотношение

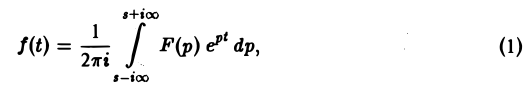
где интеграл берется вдоль любой прямой Re p = s > So и понимается в смысле главного значения, т. е. как

Формула (1) называется формулой обращения преобразования Лапласа, или формулой Меллина. В самом деле, пусть, например, f(t) — кусочно-гладкая на каждом конечном отрезке [0, а] функция-оригинал-с показателем роста so. Рассмотрим функцию φ(t) = 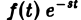Преобразование Лапласа , где s>so — любое.

Функция φ(t) удовлетворяет условиям применимости интегральной формулы Фурье, и, следовательно, справедлива формула обращения преобразования Фурье,

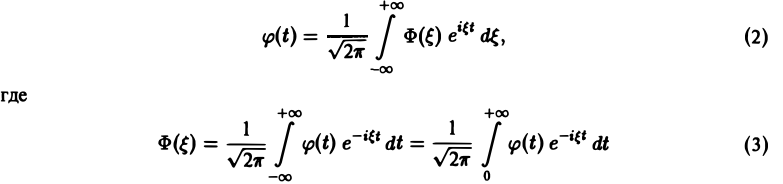
(φ(t) ≡ 0 при t < 0). Подставляя в (3) выражение φ(t) = f(t)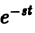 Преобразование Лапласа , найдем

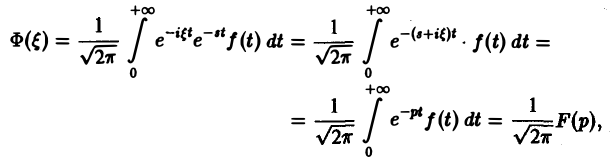
где F{p) — преобразование Лапласа функции f(t) при р = s + iξ. Формулу (2) можно переписать в виде

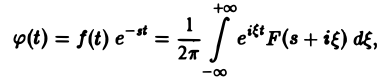
откуда получаем формулу обращения преобразования Лапласа

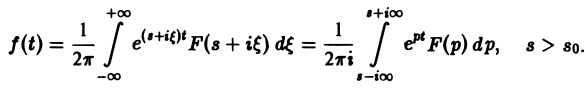
Как следствие из теоремы обращения получаем теорему единственности.

Теорема:

Две непрерывные функции f(t) и φ(t), имеющие одно и то же изображение F(p), тождественны.
Непосредственное вычисление интеграла обращения (1) обычно затруднительно. Отыскание оригинала по изображению упрощается при некоторых дополнительных ограничениях на F(p).

Теорема:

Пусть изображение F(p) — дробно-рациональная функция с полюсами р1, p2….pп. Тогда оригиналом для F(p) будет функция f(t) η(t), где

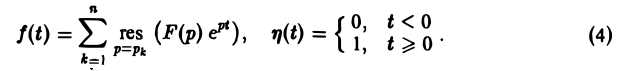
Пусть изображение F(p) — дробно-рациональная функция, F(p) = 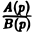Преобразование Лапласа , где А(р), В(р) — многочлены относительно р (взаимно простые), причем степень числителя А(р) меньше степени знаменателя В(р), т. к. для всякого изображения должно выполняться предельное соотношение

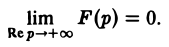
Пусть корни знаменателя В(р), являющиеся полюсами изображения F(p), суть р1, р2, …, рп, а их кратности равны r1, r2, …, rп соответственно.

Если число s, фигурирующее в формуле (1), взять большим всех Re pk (k = 1,2,…, п), то по формуле обращения, которая в этих условиях применима, получим

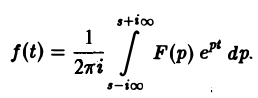
Рассмотрим замкнутый контур ГR (рис.7), состоящий из дуги CR окружности радиуса R с центром в начале координат и стягивающей ее хорды АВ (отрезка прямой Re р = s), и проходимый в положительном направлении, причем радиус R настолько велик, что все полюсы F(p) лежат внутри ГR.

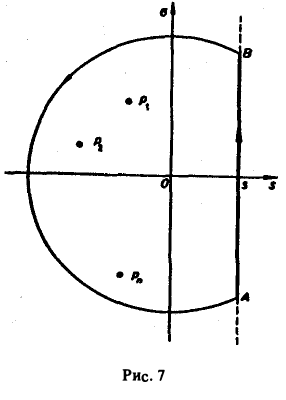
По теореме Коши о вычетах при любом R, удовлетворяющем указанному условию, будем иметь

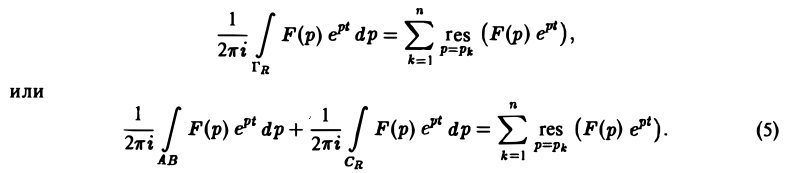
Второе слагаемое слева в равенстве (5) стремится к нулю при R → ∞. Это следует из леммы Жордана, если в ней заменить р на iz и учесть, что F(p) → 0 при Re p → + ∞. Переходя в равенстве (5) к пределу при R → ∞, мы получим слева

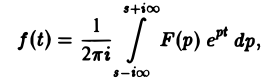
а справа — сумму вычетов по всем полюсам функции F(p)

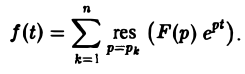
Замечание:

Воспользовавшись формулой для вычисления вычетов, найдем, что

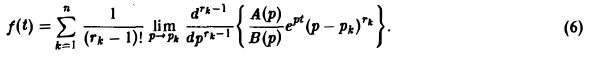
Если все полюсы p1, р2,…, рn — простые, то

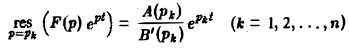
и формула (6) принимает вид

Пример:

Найти оригинал для функции

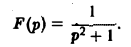
Функция F(p) имеет простые полюсы р1 = i. p2 = -i. Пользуясь формулой (7), находим

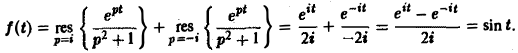
Теорема:

Пусть изображение F(p) является аналитической функцией в бесконечно удаленной точке р = ∞, причем ее разложение в окрестности |р| > R бесконечно удаленной точки имеет вид

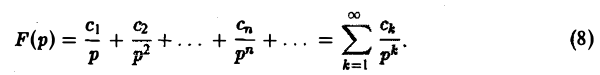
Тогда оригиналом для F(p) будет функция f(t) η{t), где

Пример:

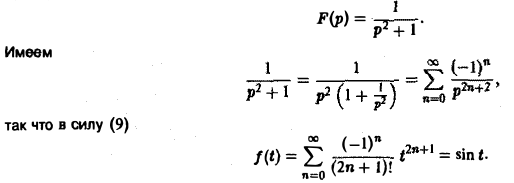
Приложения преобразования Лапласа (операционного исчисления)

Решение линейных дифференциальных уравнений с постоянными коэффициентами

Дано линейное дифференциальное уравнение второго порядка с постоянными коэффициентами
(1)

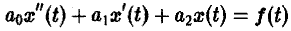
(ао, а1, а2 — действительные числа) и требуется найти решение уравнения (1) для t > 0, удовлетворяющее начальным условиям

Будем считать, что f(t) есть функция-оригинал. Тогда x(t) — также функция-оригинал. Пусть

f(t) = F(p), x(t) = X(p).

По теореме о дифференцировании оригинала имеем

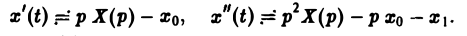
Перейдем в уравнении (1) от оригиналов к изображениям. Имеем

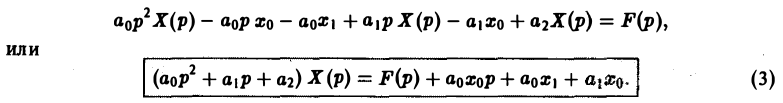
Это уже не дифференциальное, а алгебраическое уравнение относительно изображения Х(р) искомой функции. Его называют операторным уравнением. Решая его, найдем операторное решение задачи (1)-(2) —

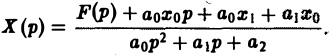
Оригинал для Х(р) будет искомым решением х(t) задачи (1)-(2).

Общий случай линейного дифференциального уравнения n-го порядка (n ≥ 1) с постоянными коэффициентами от случая п = 2 принципиально ничем не отличается.

Приведем общую схему решения задачи Коши

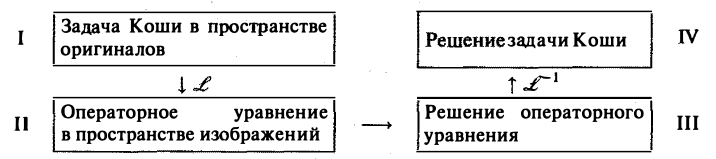
Здесь 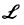означает применение к 1 преобразование Лапласа, 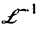— применение к III обратного преобразования Лапласа.

Пример:

Решить задачу Коши

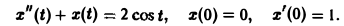
Здесь

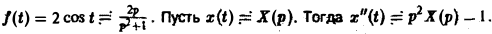
Операторное уравнение

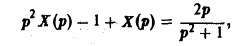
Откуда

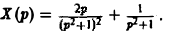
По теореме о дифференцировании изображения

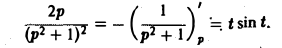
Поэтому

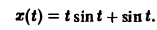
Формула Дюамеля

В приложениях операционного исчисления к решению дифференциальных уравнений часто пользуются следствием из теоремы умножения, известным под названием формулы Дюамеля.

Пусть f(t) и φt) — функции-оригиналы, причем функция f(t) непрерывна на [0, + ∞), a φ(t) — непрерывно дифференцируема на [0,+ ∞). Тогда если f(t) = F(p), φ{t) = Ф(р),то по теореме умножения получаем, что

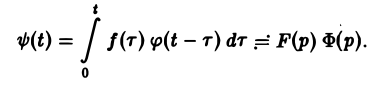
Нетрудно проверить, что функция ψ(t) непрерывно дифференцируема на [0, + ∞), причем

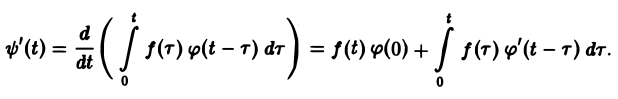
Отсюда, в силу правила дифференцирования оригиналов, учитывая, что ψ(0) = 0, получаем формулу Дюамеля
(4)

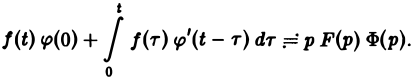
Покажем применение этой формулы.

Пусть требуется решить линейное дифференциальное уравнение n-го порядка (n ≥ 1) с постоянными коэффициентами

при нулевых начальных условиях

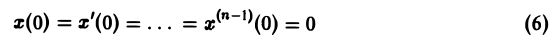
(последнее ограничение несущественно: задачу с ненулевыми начальными условиями можно свести к задаче с нулевыми условиями заменой искомой функции).

Если известно решение x(t) дифференциального уравнения с той же левой частью и правой частью, равной единице,

L[x(t)] = l (7)

при нулевых начальных условиях

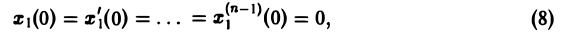
то формула Дюамеля (4) позволяет сразу получить решение исходной задачи (5)-(6).

В самом деле, операторные уравнения, отвечающие задачам (5)-(6) и (7)-(8), имеют соответственно вид

где F(p) — изображение функции f(t). Из (9) и (10) легко находи

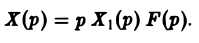
Отсюда по формуле Дюамеля

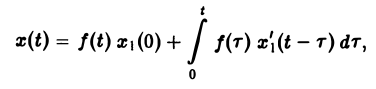
или, поскольку x1(0) = 0, (11)

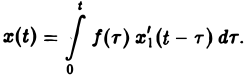
Пример:

Решить задачу Коши

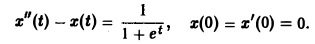
Рассмотрим вспомогательную задачу

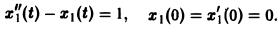
Применяя операционный метод, находим

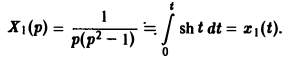
По формуле (11) получаем решение x(t) исходной задачи:

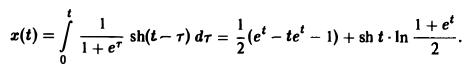
Интегрирование систем линейных дифференциальных уравнений с постоянными коэффициентами

Интегрирование систем осуществляется так же, как и решение одного линейного дифференциального уравнения — путем перехода от системы дифференциальных уравнений к системе операторных уравнений. Решая последнюю как систему линейных алгебраических уравнений относительно изображений искомых функций, получаем операторное решение системы. Оригинал для негобудетрешением исходной системы дифференциальных уравнений.

Пример:

Найти решение линейной системы

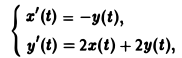
удовлетворяющее начальным условиям х(0) = у(0) = I.

Пусть х(<) = Х(р), y(t) = Y(p). Пользуясь свойством линейности преобразования Лапласа и теоремой о дифференцировании оригиналов, сводим исходную задачу Коши к операторной системе

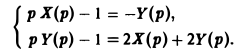
Решая последнюю относительно Х(р) и У(р), получаем

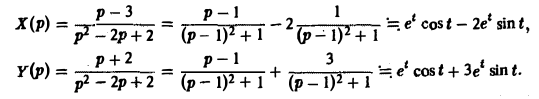
Решение исходной задачи Коши

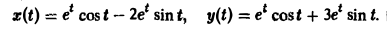
Решение интегральных уравнений

Напомним, что интегральным уравнением называют уравнение, в котором неизвестная функция входит под знак интеграла. Мы рассмотрим лишь уравнение вида (12)

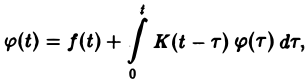
называемое линейным интегральным уравнением Вольтерра второго рода с ядром K(t — т), зависящим от разности аргументов (уравнение типа свертки). Здесь φ(t) — искомая функция, f(t) и K(t) — заданные функции.

Пусть f(t) и K(t) есть функции-оригиналы, f(t) =’ F(p), K(t) =’ K(p).

Применяя к обеим частям (12) преобразование Лапласа и, пользуясь теоремой умножения, получим
(13)

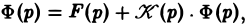
где Ф(р) = φ(t). Из (13)

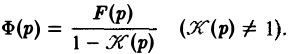
Оригинал для Ф(р) будет решением интегрального уравнения (12).

Пример:

Решить интегральное уравнение

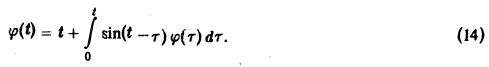
Применяя преобразование Лапласа к обеим частям (14), получим

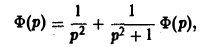
откуда

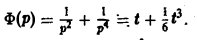
Функция 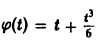Преобразование Лапласа является решением уравнения (14) (подстановка 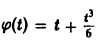в уравнение (14) обращает последнее в тождество по t).

Замечание:

Преобразование Лапласа может быть использовано также при решении некоторых задач для уравнений математической физики.

Таблица преобразования Лапласа

Дополнение к преобразованию Лапласа

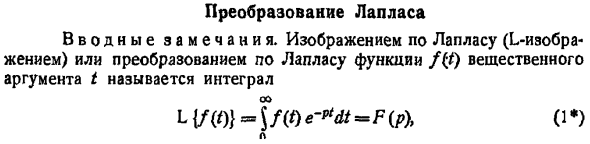
Смотрите также:

Устойчивость движения при наличии гироскопических сил	Основные свойства преобразования Лапласа
Второй метод Ляпунова	Нахождение оригиналов для дробно-рациональных изображений

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике: