Построение проекции точек, лежащих на поверхности пирамиды
На рис. 4.63 показан пример построения горизонтальных и профильных проекций точек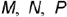 
и 
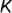. лежащих на поверхности пирамиды и заданных фронтальными проекциям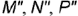и 
и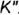 
.
1 Построение горизонтальных проекций точек, лежащих на поверхности пирамиды:
горизонтальная проекция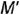 
точки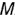 
, лежащей на ребре пирамиды 
, определяется на горизонтальной проекции 
этого ребра;
- горизонтальные проекции точек
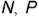и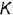 
построены на вспомогательных прямых, проведенных через их заданные фронтальные проекци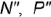и 
и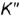 
параллельно основанию пирамиды.
Для построения горизонтальных проекций точек, лежащих на гранях пирамиды (на примере заданной точки Р(Р»)), рассмотрим графический алгоритм, действия которого определяются теоремами о принадлежности точки и прямой плоскости.
1-е действие. Провести через точку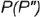 
на поверхности пирамиды вспомогательную линию 
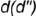, параллельную основанию пирамиды, которая пересекает ребро 
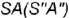по вспомогательной точке 
.
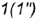2-е действие. Построить горизонтальную проекцию точки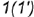 
по ее принадлежности ребру
3-е действие. Через построенную точку 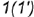провести горизонтальную проекцию 
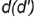вспомогательной линии параллельно стороне 
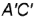основания пирамиды.
4-е действие. Построить по линии связи горизонтальную проекцию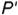 
точки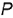 
по ее принадлежности вспомогательной линии .
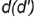Повторить действия графического алгоритма и построить аналогично горизонтальные проекци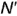и 
и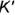 
точек 
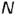и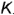 
.
Проекции точек на поверхности пирамиды можно строить также с помощью вспомогательных прямых, проходящих через се вершину (смотри пост-роение проекции точки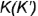 
с помощью вспомогательной прямой 
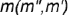(см. рис. 4.63)).
2 Построение профильных проекции точек, лежащих на поверхности пирамиды:
- профильные проекции заданных точек
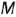и 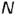построены по их принадлежности ребрам пирамиды: 
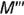— по принадлежности ребру 
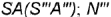— по принадлежности ребру 
;
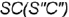профильные проекции точек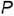 
и 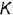построены по координатам 
определяется координатой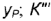 
— координатой 
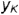(на профильной проекции 
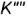невидима, так как лежит на невидимой грани 
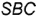(взята в скобки).
!!! Запомните характерные признаки очерков пирамиды на чертеже два треугольника и многоугольник основания. Для усечённой пирамиды — две трапеции и многоугольник основания!
Построение проекций призмы и пирамиды со срезами плоскостями частного положения
Любая плоскость пересекает поверхность призмы и пирамиды по замкнутым ломаным линиям, вершины которых лежат в точках пересечения ребер, граней и основании многогранника с плоскостями срезов. Следовательно, построение срезов на проекциях гранных поверхностей сводится к построению проекций точек, лежащих на поверхности призмы или пирамиды.
Построение проекций призмы со срезами плоскостями частного положения
На рис. 4.64 показан пример построения проекций прямой правильной треугольной призмы высотой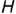 
со срезами, выполненными плоскостями частного положения — фронтально-проецирующей плоскостью 
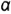и профильной плоскостью 
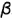. Для упрощения графических описаний взята призма без срезов из предыдущего примера (см. рис 4.62), горизонтальная, фронтальная и профильная проекции которой уже построены
Для построения проекций призмы со срезами следует выполнить предлагаемый графический алгоритм, определяющий порядок действий при решении всех подобных задач:
1-е действие. Построить тонкими линиями на поле чертежа горизонтальную, фронтальную и профильную проекции заданной прямой правильной треугольной призмы без срезов, а затем выполнить на ее фронтальной проекции срезы плоскостями частного положения по заданному условию: фронтально-проецирующей плоскостью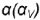 
и профильной плоскостью 
.
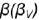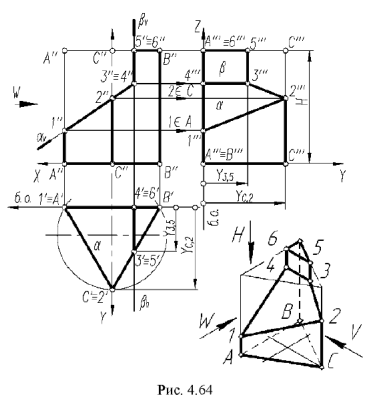
2-е действие. Обозначить на фронтальной проекции точки пересечения плоскостей срезов ребрами, гранями и основанием призмы:
- точки
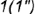и 
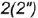лежат на ребрах призмы 
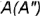и 
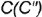; - совпадающие точк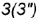и
и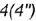 
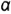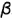— лежат на гранях призмы и определяют вырожденную в точку проекцию фронтально-проецирующей линии пересечения плоскостей срезов и : - совпадающие точк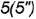и
и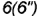 
— лежат на верхнем основании призмы и определяют вырожденную в точку проекцию фронтально-проецирующей линии пересечения плоскости 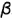с верхним основанием призмы.
3-е действие. Достроить горизонтальную проекцию призмы со срезами, построив проекции плоскостей срезов по горизонтальным проекциям обозначенных точек, и определить видимость плоскостей срезов:
- Плоскость среза 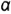определяет четырехугольник
- точка
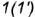лежит на ребре 
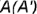; - точка
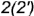лежит на ребре 
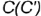: - совпадающие точк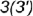и
и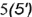 
лежат на передней грани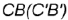 
- совпадающие точк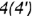и
и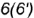 
лежат на задней грани 
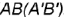. Четырехугольник 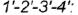— искаженная по величине видимая горизонтальная проекция фронтально-проецирующей плоскости среза .
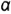- Плоскость среза 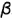определяют совпадающие проекции отрезков
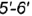и 
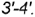. -отрезок 
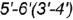— горизонтальная, вырожденная в линию, видимая проекция профильной плоскости среза 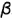(проекция прямоугольника).
4-е действие. Выполнить графический анализ построенной горизонтальной проекции призмы для определения ее очерка и внутреннего контура:
Горизонтальный очерк определяет треугольник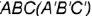 
. 2. Внутренний контур определяет видимый отрезок .
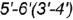5-е действие. Достроить профильную проекцию призмы, построив проекции плоскостей срезов по профильным проекциям обозначенных точек, и определить видимость плоскостей срезов:
1. Плоскость среза 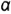определяет видимый и искаженный по величине четырехугольник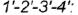
- точка
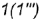лежит на ребре 
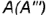; - точка
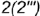лежит на ребре 
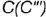; - точка
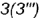построена по координате 
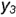; - точка
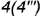лежит на задней грани 
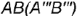которая спроецировалась в прямую;
- Плоскость среза
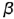определяет видимая натуральная проекция прямоугольника 
:
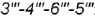- точк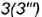и
и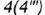 
уже построены, так как линия пересечения плоскостей среза 3-4 принадлежит плоскостям 
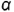и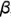 
; - точка
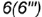лежит на задней грани 
, - точка
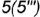построена по координате 
.
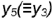6-е действие. Выполнить графический анализ построенной профильной проекции призмы для определения ее очерка и внутреннего контура:
- Профильный очерк определяют:
слева — профильная проекция ребра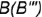 
, совпадающая с проекцией грани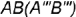 
справа участок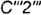 
ребра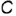 
и ломаная линия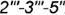 
-снизу — отрезок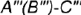 
нижнего основания призмы;
- сверху — отрезок
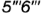— линия пересечения плоскости 
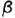с верхним основанием призмы (участок основания).
- Внутренний контур определяют видимые отрезк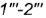и
и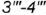 
.
7-е действие. Оформить чертеж призмы, обведя сплошными толстыми линиями очерки и видимые линии внутреннего контура каждой ее проекции (оставить на чертеже тонкими сплошными линиями очерки проекции призмы без срезов и линии построения ).
Эта теория взята со страницы задач по начертательной геометрии:
Возможно эти страницы вам будут полезны:
