Оглавление:
Простейшее показательное уравнение — это уравнение вида 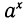 = b. Пусть основание а>0 и отлично от 1. Так как функция у = строго монотонна, то каждое свое значение она принимает ровно один раз. Это означает, что уравнение
= b. Пусть основание а>0 и отлично от 1. Так как функция у = строго монотонна, то каждое свое значение она принимает ровно один раз. Это означает, что уравнение 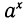 = b при b>0 имеет одно решение, которое по определению логарифма равно log0 b. Если 0, то уравнение
= b при b>0 имеет одно решение, которое по определению логарифма равно log0 b. Если 0, то уравнение 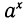 = b корней не имеет, так как
= b корней не имеет, так как 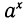 всегда больше нуля. Если число b записано в виде ас, т. е. если уравнение представлено в виде
всегда больше нуля. Если число b записано в виде ас, т. е. если уравнение представлено в виде 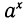 = ас, то оно имеет один корень х = с.
= ас, то оно имеет один корень х = с.
Сформулируем общий результат о решении простейшего показательного уравнения (схема XI).
Теорема:
Пусть а > 0 и а ≠ 1. Уравнение 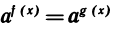 равносильно уравнению f (x) = g (х).
равносильно уравнению f (x) = g (х).
Доказательство:
Докажем, что если 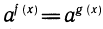 то f(x) = g(x). Действительно, так как показательная функция строго монотонна, то из равенства ее значений ac = ad следует равенство показателей c = d. Обратно: если f(x) = g(x), то
то f(x) = g(x). Действительно, так как показательная функция строго монотонна, то из равенства ее значений ac = ad следует равенство показателей c = d. Обратно: если f(x) = g(x), то 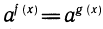 .
.
Примеры:
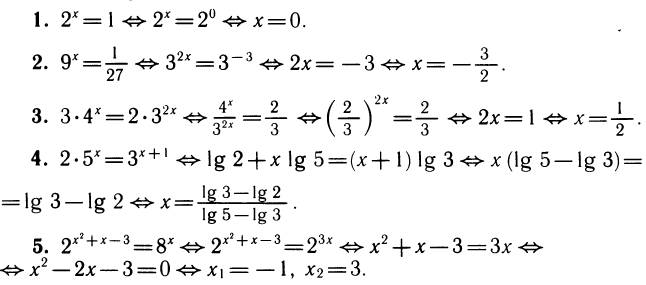
Простейшее логарифмическое уравнение — это уравнение вида logax=b. Оно имеет единственное решение х — а при любом b.
Сформулируем общий результат о решении простейшего логарифмического уравнения (схема XI).
Теорема:
Уравнение ioga f (х) = loga g (х) равносильно уравнению f(x)=g(x) при ограничениях f (х)> 0, g(x)>0.
Доказательство:
Пусть х — решение уравнения 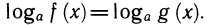
Тогда определены логарифмы чисел f (х) и g (х), т. е. эти числа должны быть больше нуля. Потенцируя равенство 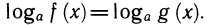 получаем равенство f(x) = g (x). Обратно, пусть х — решение уравнения f (х) = g (х), причем g(x)>0 и f (х)> 0. Тогда равенство f{x) = g(x) можно прологарифмировать, И МЫ получим
получаем равенство f(x) = g (x). Обратно, пусть х — решение уравнения f (х) = g (х), причем g(x)>0 и f (х)> 0. Тогда равенство f{x) = g(x) можно прологарифмировать, И МЫ получим 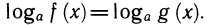 .
.
Примеры:
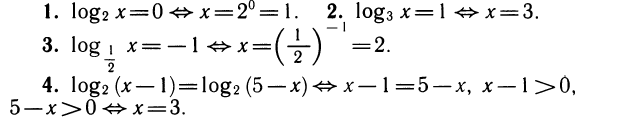
Мы решили уравнение х— 1 = 5 — х, а затем проверили, удовлетворяет ли решение условиям х— 1 >0 и 5 — х>0. Заметим, что если f (x) = g (х) и f (х)>0, то тогда и g (x)>0, т. е. из двух неравенств достаточно проверить только одно.
Показательные уравнения справочные сведения
Показательная функция 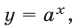 где
где 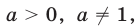 определена на
определена на 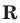 , а множество ее значений — множество всех положительных чисел.
, а множество ее значений — множество всех положительных чисел.
2.Для любых 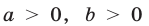 и при любых значениях
и при любых значениях 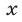 и
и 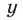 ну верны равенства (основные свойства степени):
ну верны равенства (основные свойства степени):
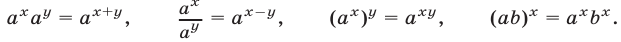
3. Простейшее показательное уравнение
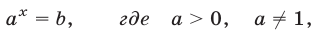
не имеет корней при 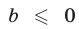 и имеет единственный корень
и имеет единственный корень 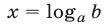 при
при 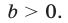
В частности, уравнение 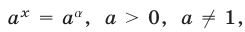 имеет единственный корень
имеет единственный корень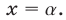
4.Уравнение
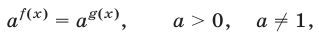
равносильно уравнению
5.Уравнение
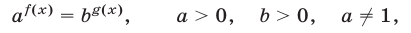
равносильно каждому из уравнений
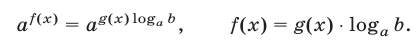
Примеры с решениями
Пример:
Решить уравнение 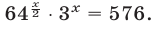
Решение:
Данное уравнение равносильно каждому из уравнений 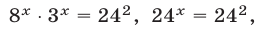 откуда
откуда 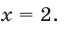
Ответ. 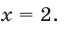
Пример:
Решить уравнение 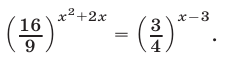
Решение:
Это уравнение равносильно каждому из уравнений: 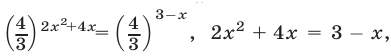
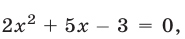
откуда находим 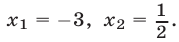
Ответ. 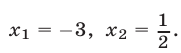
Пример:
Решить уравнение
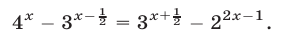
Решение:
Пусть 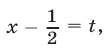 тогда уравнение примет вид
тогда уравнение примет вид
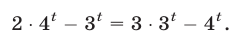
Это уравнение равносильно каждому из уравнений: 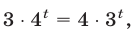
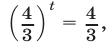 откуда
откуда 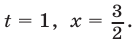
Ответ.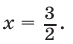
Пример:
Решить уравнение
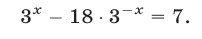
Решение:
Полагая 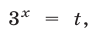 получаем уравнение
получаем уравнение 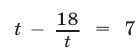 или
или 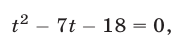 откуда находим
откуда находим 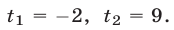
Следовательно, исходное уравнение равносильно совокупности уравнений 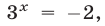
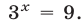 Первое из них не имеет корней, второе имеет единственный корень
Первое из них не имеет корней, второе имеет единственный корень 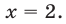
Ответ. 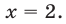
Пример:
Решить уравнение
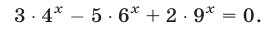
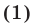
Решение:
Запишем данное уравнение в виде
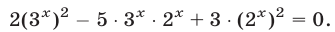
и заметим, что левая часть уравнения (2) — однородный многочлен степени  от
от 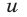 и
и 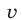 где
где 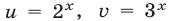 (сумма степеней
(сумма степеней 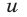 и
и 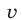 в каждом члене этого многочлена равна двум).
в каждом члене этого многочлена равна двум).
Разделив обе части уравнения (2) на 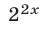 и полагая
и полагая 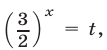 получим уравнение
получим уравнение 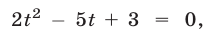 имеющее корни
имеющее корни 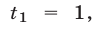
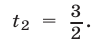 Исходное уравнение (1) равносильно совокупности уравнений
Исходное уравнение (1) равносильно совокупности уравнений 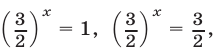 откуда находим
откуда находим 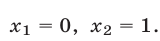
Ответ. 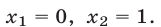
Пример:
Решить уравнение
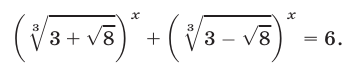
Решение:
Воспользуемся равенством 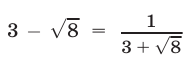 и положим
и положим 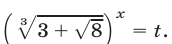 Тогда уравнение примет вид
Тогда уравнение примет вид 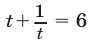 или
или 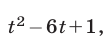 откуда
откуда 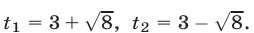 Исходное уравнение равносильно совокупности уравнении
Исходное уравнение равносильно совокупности уравнении
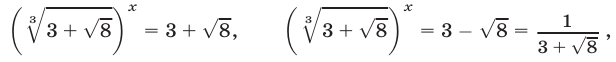
откуда 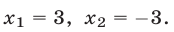
Ответ, 
Пример:
Решить уравнение
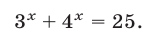
Решение:
Число 2 является корнем этого уравнения. Докажем, что уравнение не имеет других корней. Так как каждая из функций 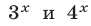 является возрастающей, то и
является возрастающей, то и 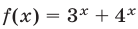 — также возрастающая функция. Поэтому
— также возрастающая функция. Поэтому 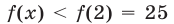 при
при 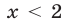 и
и 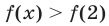 при
при 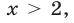 т. е. функция не принимает значение, равное 25, при
т. е. функция не принимает значение, равное 25, при 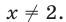 Это означает, что
Это означает, что 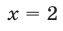 — единственный корень уравнения.
— единственный корень уравнения.
Показательные неравенства
Простейшее показательное неравенство — это неравенство вида 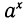 >b или
>b или 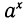 < b (или
< b (или 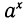 ≥ b, или
≥ b, или 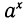 ≤ b). Решение такого неравенства нетрудно представить себе графически, построив график показательной функции у =
≤ b). Решение такого неравенства нетрудно представить себе графически, построив график показательной функции у = 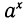 и проведя прямую у=b (схема XI). Рассмотрим для примера два из 16 возможных вариантов.
и проведя прямую у=b (схема XI). Рассмотрим для примера два из 16 возможных вариантов.
Пусть а> 1 и b >0. Решением неравенства 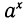 ≥ b является промежуток
≥ b является промежуток 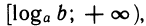 , т. е. все числа
, т. е. все числа 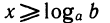 (схема XI).
(схема XI).
Пусть а>1 и b ≤ 0. Решением неравенства 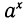 ≥ b является множество всех вещественных чисел R.
≥ b является множество всех вещественных чисел R.
Примеры:
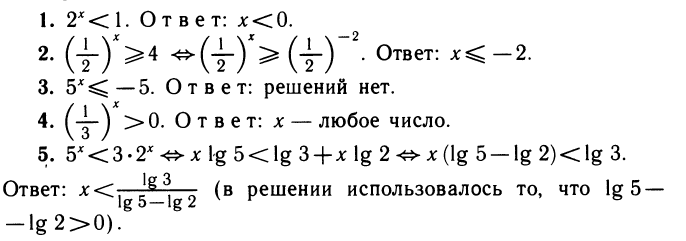
Можно сказать, что неравенство типа 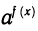 >b мы решаем логарифмированием. При логарифмировании неравенств надо помнить два правила: 1) в обеих частях неравенства должны стоять положительные числа; 2) при логарифмировании по основанию а>1 знак неравенства сохраняется, если же 0<а<1, то знак неравенства меняется на противоположный.
>b мы решаем логарифмированием. При логарифмировании неравенств надо помнить два правила: 1) в обеих частях неравенства должны стоять положительные числа; 2) при логарифмировании по основанию а>1 знак неравенства сохраняется, если же 0<а<1, то знак неравенства меняется на противоположный.
Простейшее логарифмическое неравенство — это неравенство вида 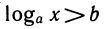 (вместо знака > может стоять ≤ , ≥ . Аналогично показательному неравенству здесь также возможно много вариантов (схема XI). Логарифмическое неравенство решают потенцированием. При этом надо помнить два правила: 1) при переходе от выражения loga f (х) к выражению f (х) надо добавлять условие f (х)>0; 2) если а>1, то при потенцировании знак неравенства сохраняется; если же 0<а<1, то знак неравенства меняется на противоположный.
(вместо знака > может стоять ≤ , ≥ . Аналогично показательному неравенству здесь также возможно много вариантов (схема XI). Логарифмическое неравенство решают потенцированием. При этом надо помнить два правила: 1) при переходе от выражения loga f (х) к выражению f (х) надо добавлять условие f (х)>0; 2) если а>1, то при потенцировании знак неравенства сохраняется; если же 0<а<1, то знак неравенства меняется на противоположный.
Примеры:
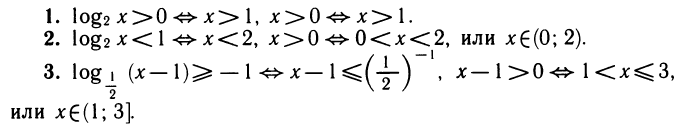
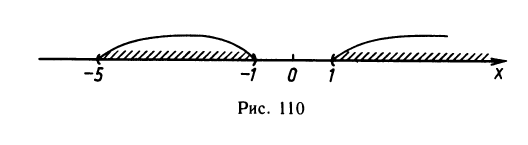
4. 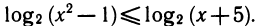 Сначала учтем условия x2 — 1>0 и x + 5>0. Решение этой системы неравенств изображено на рисунке 110. Затем потенцируем: x2 — 1 ≤ x+5 ⇔ x2 — х — 6 ≤ 0 ⇔ -2 ≤ x ≤ 3. Соединяя решения вместе, получим ответ: -2 ≤ х<-1 и 1< x ≤ З, или [—2; —1)U(1;3].
Сначала учтем условия x2 — 1>0 и x + 5>0. Решение этой системы неравенств изображено на рисунке 110. Затем потенцируем: x2 — 1 ≤ x+5 ⇔ x2 — х — 6 ≤ 0 ⇔ -2 ≤ x ≤ 3. Соединяя решения вместе, получим ответ: -2 ≤ х<-1 и 1< x ≤ З, или [—2; —1)U(1;3].
Введение новой неизвестной
Основной прием, с помощью которого решают показательные и логарифмические уравнения и неравенства,— это введение новой неизвестной. Поясним этот прием на ряде примеров.
1) Выражение показательных функций друг через друга.
Рассмотрим выражения 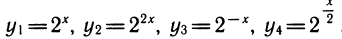 . Все они могут быть алгебраически выражены друг через друга. Например,
. Все они могут быть алгебраически выражены друг через друга. Например, 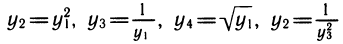 и т. д. Алгебраическая связь между различными степенями может быть осложнена добавлением в показателе степени постоянных слагаемых:
и т. д. Алгебраическая связь между различными степенями может быть осложнена добавлением в показателе степени постоянных слагаемых: 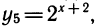
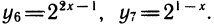 Однако и сейчас несложно выразить эти выражения, например, через у1. Получим
Однако и сейчас несложно выразить эти выражения, например, через у1. Получим 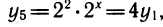
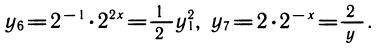
К этому полезно напомнить связь между различными основаниями. Например, 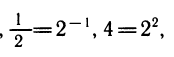
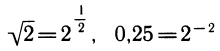 и т. п. Поэтому выражения
и т. п. Поэтому выражения 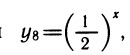
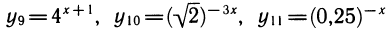
также нетрудно выразить через у1:
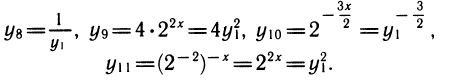
Если в уравнении или неравенстве встречается несколько показательных функций, то надо все их выразить через одну. Обычно после этого показательное уравнение или неравенство превращается в алгебраическое.
Примеры:
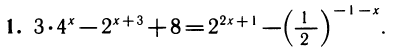
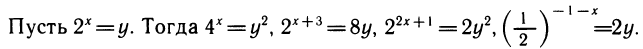
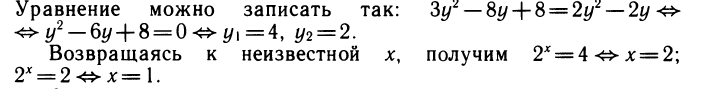
Ответ: xi = 2, x2 = 1.
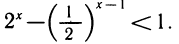
Делаем замену 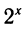 =у. Неравенство перепишем таким образом:
=у. Неравенство перепишем таким образом:
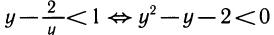
(мы умножили неравенство на у, что можно, так как

Так как 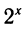 > — 1 верно при всех х, то остается решить неравенство
> — 1 верно при всех х, то остается решить неравенство 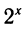 < 2 ⇔ x<1.
< 2 ⇔ x<1.
Ответ: х<1. (Иначе ответ можно записать так: (— ∞ ; 1).)
2) Выражение логарифмических функций друг через друга.
Рассмотрим выражения 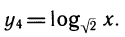
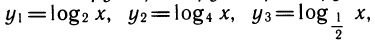
Используя модуль перехода, легко связать эти выражения между собой:
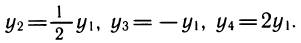
Свойства логарифмов позволяют по-разному записать связи между выражениями. Например,
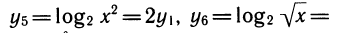
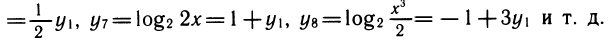
Если в уравнении или неравенстве встречается несколько логарифмических функций, то надо (если не удается избавиться от логарифмов потенцированием) выразить их через одну и свести логарифмическое уравнение или неравенство к алгебраическому.
Примеры:
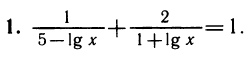
Делаем замену lg х = у. Получаем уравнение относительно у:
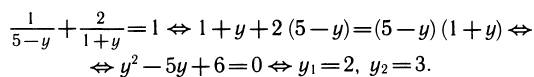
Возвращаясь к неизвестной х, получим lg х = 2, х=100; lgx = 3, х= 1000.
Ответ, x1 = 100, x2 =1000.
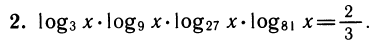
Перейдем к основанию 3. Получим 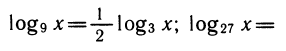
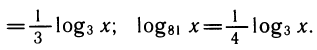
заменив log3x на у, получим
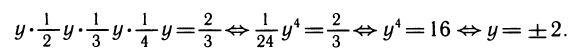
Возвpащаясь к неизвестной х, получим log3x = 2, x = 9; log3x =—2, 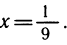
Ответ: 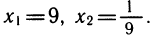
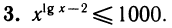
Логарифмируя, получим равносильное данному неравенство (lg x —2) 1g x ≤ 3.
Положим lg х = у. Получим неравенство (у — 2)y ≤ З ⇔ 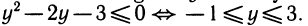
Возвращаясь к неизвестной х, получим — l ≤ lg x ≤ 3 ⇔ 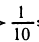 x 1000
x 1000
Ответ: 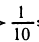 ≤ x ≤ 1000, или в другой записи [
≤ x ≤ 1000, или в другой записи [ 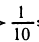 ; 1 ООО].
; 1 ООО].
Использование свойства монотонности функций при решении показательных уравнений
Монотонность функций часто позволяет определить число корней уравнения, а иногда и найти их значения. Рассмотрим примеры решения уравнений.
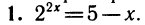
В левой части уравнения имеем возрастающую функцию, а в правой — убывающую. Следовательно, уравнение не может иметь более одного корня (рис. 111). Один корень можно угадать: х=1. Это число и является окончательным ответом.
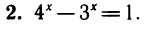
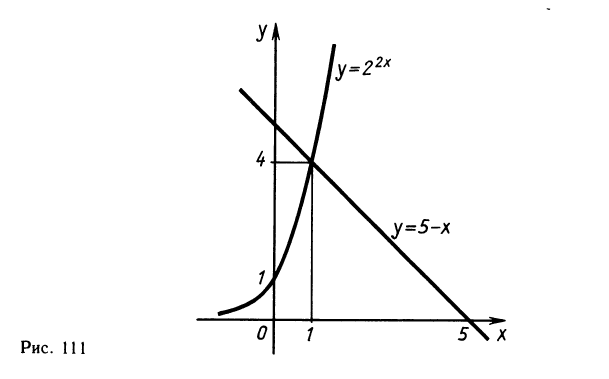
Одно решение х=1 легко найти подбором. Докажем, что других корней нет. Перепишем уравнение так: 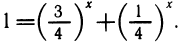
В правой части последнего уравнения сумма убывающих функций т. е. значение у = 1 эта сумма может принять только один раз.
Ответ: х = 1.
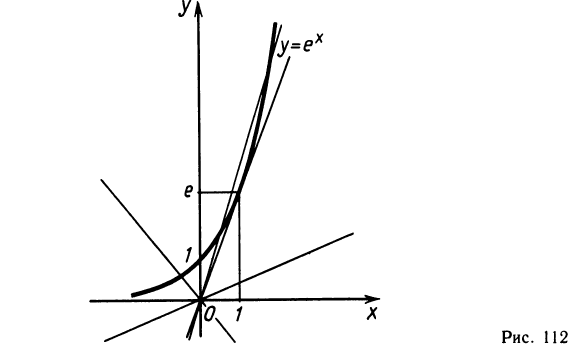
3. Сколько корней имеет уравнение 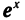 = ах?
= ах?
Изобразим схематически графики функций у = 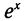 и у = ах (рис. 112). При а<0 графики имеют одну точку пересечения. При а>0 графики могут не пересекаться, касаться друг друга или пересекаться в двух точках. Граничным значением параметра а, при котором происходит разделение основных случаев — две точки пересечения или ни одной, является значение а, при котором прямая у = ах является касательной к графику функции у =
и у = ах (рис. 112). При а<0 графики имеют одну точку пересечения. При а>0 графики могут не пересекаться, касаться друг друга или пересекаться в двух точках. Граничным значением параметра а, при котором происходит разделение основных случаев — две точки пересечения или ни одной, является значение а, при котором прямая у = ах является касательной к графику функции у = 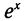 некоторой точке. Найдем это значение а. Пусть касание произошло в точке хо, тогда производная функция у =
некоторой точке. Найдем это значение а. Пусть касание произошло в точке хо, тогда производная функция у = 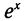 в этой точке равна а. Поэтому получаем уравнение
в этой точке равна а. Поэтому получаем уравнение 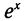 = а, т. е. x0 = ln а. Точка с абсциссой х0 = ln а должна лежать как на графике функции у=
= а, т. е. x0 = ln а. Точка с абсциссой х0 = ln а должна лежать как на графике функции у=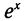 , так и на прямой у = ах. Получаем
, так и на прямой у = ах. Получаем 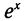 ° = ах, т. е. а = а ln а, так как а ≠ 0, то ln а= 1 и а = е.
° = ах, т. е. а = а ln а, так как а ≠ 0, то ln а= 1 и а = е.
Ответ: при 0 ≤ а<0 один корень, при а>е два корня, при а = е один корень, при корней нет.
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:
| Рациональные уравнения примеры с решением |
| Иррациональные уравнения примеры с решением |
| Логарифмические уравнения примеры с решением |
| Простейшие тригонометрические уравнения примеры с решением |
Показательные уравнения и примеры решения
Определение. Уравнение называется показательным, если неизвестная входит в показатель степени.
Рассмотрим простейшие приемы решения показательных уравнений на отдельных примерах.
1. Решить уравнение
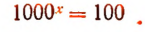
Представим левую и правую части уравнения в виде степеней, имеющих одинаковые основания:
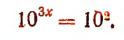
Отсюда 3х = 2, или 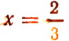 .
.
Мы здесь воспользовались следующей теоремой:
Если степени равны и основания равны, положительны и отличны от единицы, то равны и их показатели степеней.
Докажем эту теорему.
Пусть а > 1 и 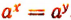 . Докажем, что в этом случае
. Докажем, что в этом случае
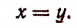
Допустим противное тому, что требуется доказать, т. е. допустим, что х > у или что х < у. Тогда получим по свойству показательной функции, что либо 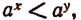 либо
либо 
Оба эти результата противоречат условию теоремы. Следовательно, х=у, что и требовалось доказать.
Также доказывается теорема и для случая, когда 0<а<1.
Замечание. Из равенства  не обязательно следует, что
не обязательно следует, что
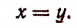
Из равенства  также не обязательно вытекает равенство х=у.
также не обязательно вытекает равенство х=у.
2. Решить уравнение 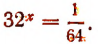
Преобразуя левую и правую части уравнения, получим:

3. Решить уравнение
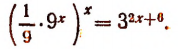
Преобразуя левую часть уравнения, получим:
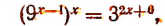
или

или
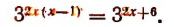
Отсюда
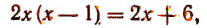
или
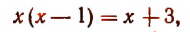
или
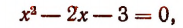
Отсюда
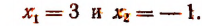
Значит, данное показательное уравнение имеет два корня:
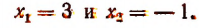
4. Решить уравнение
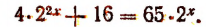
Примем за новую неизвестную выражение 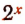 и обозначим это выражение буквой у. Тогда получим:
и обозначим это выражение буквой у. Тогда получим:
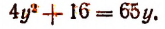
Отсюда
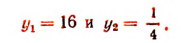
Следовательно,
либо 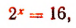 , либо
, либо 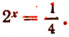
Из уравнения  имеем х = 4.
имеем х = 4.
Из уравнения  имеем х = —2.
имеем х = —2.
Итак, данное показательное уравнение имеет два корня: 4 и — 2.
5. Решить уравнение 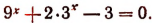
Снова, обозначая 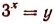 и решая полученное квадратное уравнение, находим:
и решая полученное квадратное уравнение, находим:
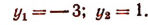
Таким образом, получим:
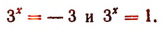
Как было указано при исследовании показательной функции, степень 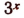 ни при каком х не может быть отрицательной, следовательно, первое из полученных уравнений не имеет корней. Из второго уравнения находим х = 0. Значит, первоначальное уравнение имеет лишь один корень, равный нулю.
ни при каком х не может быть отрицательной, следовательно, первое из полученных уравнений не имеет корней. Из второго уравнения находим х = 0. Значит, первоначальное уравнение имеет лишь один корень, равный нулю.
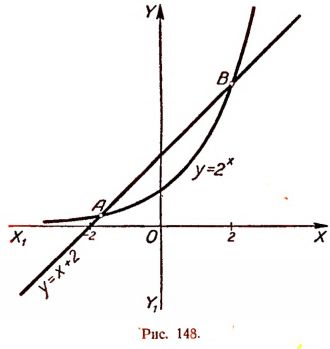
6. Решить уравнение
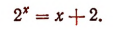
Для решения этого уравнения применим графический метод. Построим на одной координатной плоскости (рис. 148) графики функций:
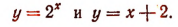
Тогда абсциссы точек пересечения этих линий, т. е. абсциссы точек А и В, будут корнями данного уравнения. Абсцисса точки В, равная числу 2, будет точным корнем данного уравнения, а абсцисса точки А, равная приближенно —1,7, будет его приближенным корнем. Других корней данное уравнение не имеет.
Сведения, изложенные в этой главе, окажутся полезными при изучении логарифмов, которым посвящена следующая глава.
Примем к сведению без доказательства еще следующую теорему:
Если а есть положительной число, отличное от единицы, а N — любое положительное число, то уравнение 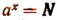 с неизвестным х имеет один и только один действительный корень (рациональный или иррациональный).
с неизвестным х имеет один и только один действительный корень (рациональный или иррациональный).
Примеры. Уравнение  имеет единственный действительный корень, равный рациональному числу 5.
имеет единственный действительный корень, равный рациональному числу 5.
Уравнение 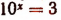 имеет единственный действительный иррациональный корень, приближенное значение которого с точностью до 0,00001 равно 0,47712.
имеет единственный действительный иррациональный корень, приближенное значение которого с точностью до 0,00001 равно 0,47712.
Итак, мы можем сделать следующие заключения:
- Выражение
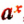 , где а>0, имеет при каждом действительном значении х одно и только одно действительное значение.
, где а>0, имеет при каждом действительном значении х одно и только одно действительное значение. - Действия над выражениями вида
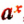 , в которых х является любым действительным числом, можно выполнять по тем же правилам, по которым они выполняются над степенями с целым положительным показателем. Поэтому выражение
, в которых х является любым действительным числом, можно выполнять по тем же правилам, по которым они выполняются над степенями с целым положительным показателем. Поэтому выражение 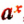 при всяком действительном значении х также называется степенью (обобщенной).
при всяком действительном значении х также называется степенью (обобщенной).
Примеры зависимостей, выражающихся с помощью показательных функций.
1.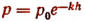 (барометрическая формула):
(барометрическая формула): 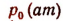 —давление на уровне моря;
—давление на уровне моря;
k —некоторая известная постоянная;
е —2,718;
h(м) —высота над уровнем моря;
р(ат) —давление на высоте А над уровнем моря.
Здесь h есть независимая переменная, или аргумент, а р есть зависимая переменная, или функция.
По этой формуле можно определять давление р по заданному значению h.
2. Если температура воздуха равна 20° С и тело в течение 20 минут охлаждается от 100 до 60°, то зависимость температуры Т охлаждающегося тела от времени t минут (в течение которого будет происходить охлаждение) выразится формулой
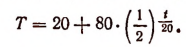
Здесь t есть аргумент, а Т—функция.
Пользуясь этой формулой, можно узнать, например, что через один час температура тела понизится до 30°.
Приведенные формулы выводятся в курсах высшей математики.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

