Оглавление:
Некоторые наиболее часто встречающиеся виды трансцендентных функций, прежде всего показательные, открывают доступ ко многим исследованиям. Л.Эйлер
Свойства показательной функции и её график
В курсе алгебры рассматривалась степень с действительным показателем. Напомним основные свойства степени. Пусть a>0, b>0, х,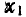 и
и 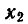 — любые действительные числа. Тогда
— любые действительные числа. Тогда
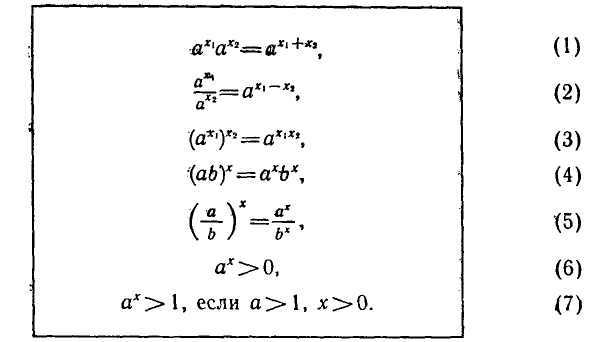
Эйлер Леонард (1707—1783) — математик, механик, физик и астроном, академик Петербургской Академии Наук. Научные труды Л. Эйлера относились ко всем областям естествознания, к которым можно применить математические методы.
Кроме того, в курсе алгебры рассматривались функции 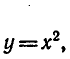
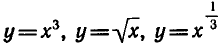 и т. д., т. е. степенные функции
и т. д., т. е. степенные функции 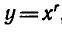 , где r — заданное число, а х — переменная.
, где r — заданное число, а х — переменная.
В практике используются также функции 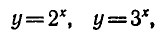
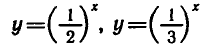 т. е. Функция вида
т. е. Функция вида 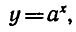
где а — заданное число, а х — переменная. Такие функции называют показательными. Это название объясняется тем, что аргументом показательной функции является показатель степени, а основание степени — заданное число.
Показательной функцией называется функция 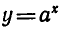 , где а — заданное число,
, где а — заданное число, 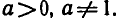
Показательная функция обладает следующими свойствами:
1) Область определения показательной функции — множество R всех действительных чисел.
Это свойство следует из того, что степень 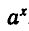 , где а > 0, определена для всех
, где а > 0, определена для всех 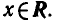
2) Множество значений показательной функции — множество всех положительных чисел.
Чтобы убедиться в этом, нужно показать, что уравнение 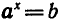 , где
, где
а > 0, 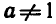 , не имеет корней, если
, не имеет корней, если 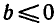 , и имеет корень при любом b > 0. По свойству степени (6) это уравнение не имеет корней, если
, и имеет корень при любом b > 0. По свойству степени (6) это уравнение не имеет корней, если 
То, что это уравнение имеет корень при любом b > 0, доказывается в курсе высшей математики. Это означает, что любая прямая у = b, где
b > 0, пересекается с графиком показательной функции.
3) Показательная функция 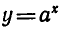 является возрастающей на множестве всех действительных чисел, если а> 1, и убывающей, если 0<а<1.
является возрастающей на множестве всех действительных чисел, если а> 1, и убывающей, если 0<а<1.
Пусть а> 1 и  . Покажем, что
. Покажем, что  , т. е.
, т. е. 
Так как  , то
, то 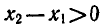 и по свойству степени (7) имеем
и по свойству степени (7) имеем 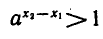 т. е.
т. е. 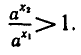
Отсюда, учитывая, что 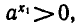 получаем
получаем 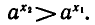
Пусть 0<а<1 и  Покажем, что
Покажем, что 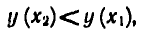 , т. е.
, т. е. 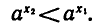
Так как 0<а<1, то 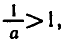 и поэтому
и поэтому 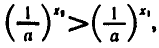
т. е.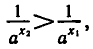 откуда
откуда 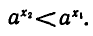
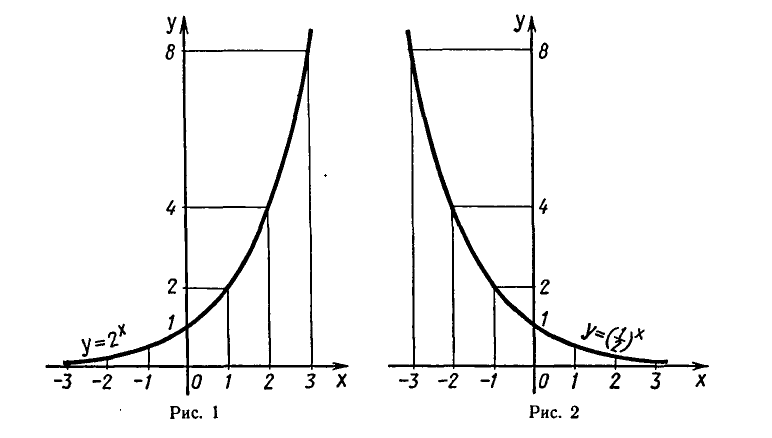
Построим графики функций 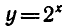 и
и 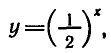 используя
используя
рассмотренные свойства, по нескольким точкам, принадлежащим
графику (рис. 1 и 2 ).
Отметим, что график функции 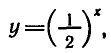 проходит через точку
проходит через точку
(0; 1) и расположен выше оси Ох. Если х < 0 и убывает, то график быстро приближается к оси Ох (но не пересекает ее); если х > 0
и возрастает, то график быстро поднимается вверх. Такой же
вид имеет график любой функции 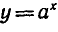 , если а > 1 (рис. 3).
, если а > 1 (рис. 3).
График функции 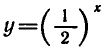 также проходит через точку (0; 1)
также проходит через точку (0; 1)
и расположен выше оси Ох. Если x > 0 и возрастает, то график
быстро приближается к оси Ох (не пересекая ее); если х < 0 и
убывает, то график быстро поднимается вверх. Такой же вид
имеет график любой функции 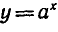 , если 0 < а < 1
, если 0 < а < 1
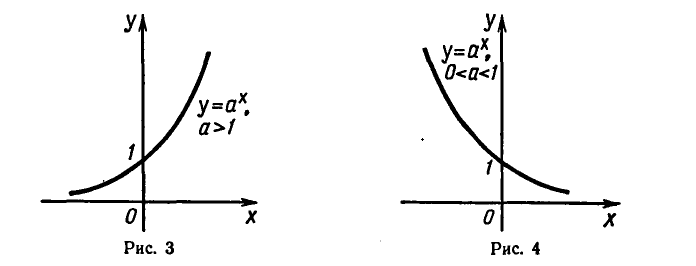
Показательная функции часто используется при описании
различных физических процессов. Как радиоактивный распад
вписывается формулой
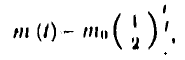
где m (t) и 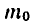 — масса радиоактивного вещества соответственно в момент момент времени t и в начальный момент t=0. T —
— масса радиоактивного вещества соответственно в момент момент времени t и в начальный момент t=0. T —
период полураспада (промежуток примени, за который первоначальное количество вещества уменьшается вдвое).
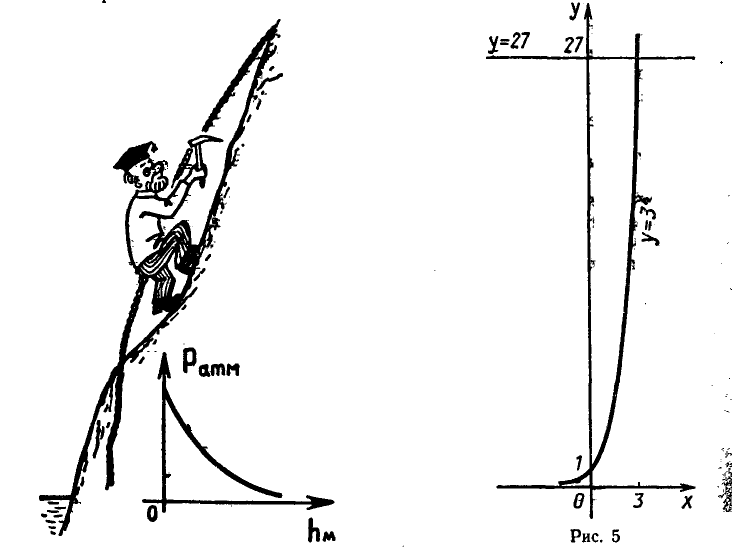
С помощью показательной функции выражается давление
воздуха в зависимости от высоты подъема, ток самоиндукции
в катушке после включения постоянного напряжения и т. д.
Задача:
Решить уравнение 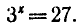
По свойству показательной функции данное уравнение
имеет корень, так как 27 > 0 . Одним из корней является число
х = 3, так как 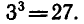
Других корней нет, так как функция 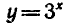 возрастает на всей числовой прямой, и поэтому
возрастает на всей числовой прямой, и поэтому 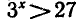 при х > 3 и
при х > 3 и 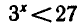 при
при
х < 3 и (рис. 5). ▲
Задача:
Период полураспада плутония равен 140 суткам.
Сколько плутония останется через 10 лет, если его начальная
масса равна 8 г?
Воспользуемся формулой (8). В данной задаче t = 10*365
(считаем, что в году 365 дней), T = 140. 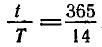
Вычисления проведем на микрокалькуляторе МК-54 по программе

Ответ. Через 10 лет плутония останется примерно 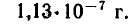
Показательные уравнения и неравенства
Рассмотрим несколько примеров показательных уравнений
и неравенств, т. е. уравнений и неравенств, в которых неизвестное содержится в показателе степени.
- Уравнения
Решение показательных уравнений часто сводится к решению
уравнения
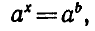
где 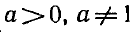 , х — неизвестное. Это уравнение имеет единственный корень х = b, так как справедлива следующая теорема:
, х — неизвестное. Это уравнение имеет единственный корень х = b, так как справедлива следующая теорема:
Теорема. Если а > 0 , 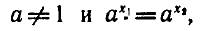 то
то 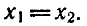
О Предположим, что равенство 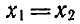 не выполняется, т. е.
не выполняется, т. е.
 или
или 
Пусть, например,  . Тогда если а > 1, то показательная функция
. Тогда если а > 1, то показательная функция 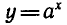 возрастает и поэтому должно выполняться неравенство
возрастает и поэтому должно выполняться неравенство  если 0 < а < 1, то функция убывает и должно выполняться неравенство
если 0 < а < 1, то функция убывает и должно выполняться неравенство 
В обоих случаях получилось противоречие с условием 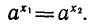
Задача:
Решить уравнение 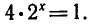
Запишем уравнение в виде 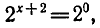 откуда x+2 = 0.
откуда x+2 = 0.
Ответ. x = — 2.
Задача:
Решить уравнение 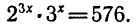
Так как 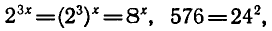 то уравнение можно записать в виде
то уравнение можно записать в виде 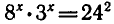 или в виде
или в виде 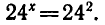 Отсюда х = 2.
Отсюда х = 2.
Ответ. х = 2.
Задача:
Решить уравнение 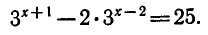
Вынося в левой части за скобки общий множитель 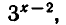
получаем 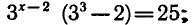
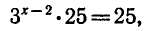 откуда
откуда 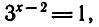
х — 2 = 0, х=2.
Ответ. х = 2.
Задача:
Решить уравнение 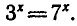
Так как 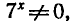 то уравнение можно записать в виде
то уравнение можно записать в виде 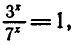 откуда
откуда 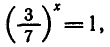 х = 0.
х = 0.
Ответ. x = 0.
Задача:
Решить уравнение 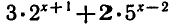
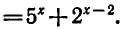
Запишем уравнение в виде 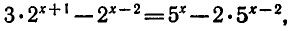
откуда 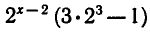
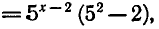
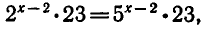
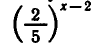
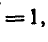
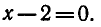
Ответ. х = 2.
Задача:
Решить уравнение 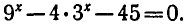
Заменой 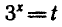 данное уравнение сводится к квадратному
данное уравнение сводится к квадратному
уравнению 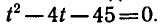
Решая это уравнение, находим его корни: 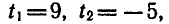 откуда
откуда 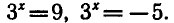
Уравнение 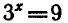 имеет корень х = 2, а уравнение
имеет корень х = 2, а уравнение 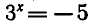 не имеет корней, так как показательная функция не может принимать отрицательные значения.
не имеет корней, так как показательная функция не может принимать отрицательные значения.
О т в е т. х = 2
Неравенства
Решение показательных неравенств часто сводится к решению
неравенств 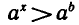 или
или  . Эти неравенства решаются с
. Эти неравенства решаются с
помощью свойства возрастания или убывания показательной
функции.
Задача:
Решить неравенство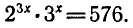
Запишем неравенство в виде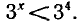 Так как 3 > 1 , то
Так как 3 > 1 , то
функция 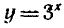 является возрастающей. Следовательно, при x>4 выполняется неравенство
является возрастающей. Следовательно, при x>4 выполняется неравенство 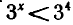 , а при
, а при  выполняется неравенство
выполняется неравенство 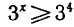 . Таким образом, при х < 4 неравенство
. Таким образом, при х < 4 неравенство  является верным, а при
является верным, а при  — неверным, т. е.
— неверным, т. е.
неравенство 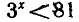 выполняется тогда и только тогда, когда
выполняется тогда и только тогда, когда
х < 4 .
Ответ. х < 4
Задача:
Решить неравенство 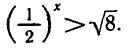
Запишем неравенство в виде 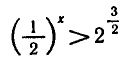 или
или 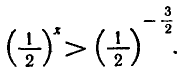
Так как 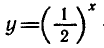 — убывающая функция, то
— убывающая функция, то 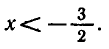
Ответ.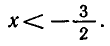
Задача:
Решить неравенство 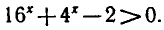
Обозначим 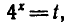 тогда получим квадратное неравенство
тогда получим квадратное неравенство 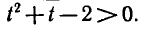 Это неравенство выполняется при t < — 2 и при
Это неравенство выполняется при t < — 2 и при
t > 1 . Так как 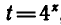 , то получим два неравенства
, то получим два неравенства 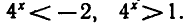
Первое неравенство не имеет решений, так как 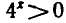 при всех
при всех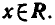
Второе неравенство можно записать в виде 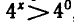 , откуда x >0.
, откуда x >0.
Ответ. x > 0.
Задача:
Решить графически уравнение 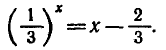
Построим графики функций 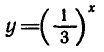 и
и 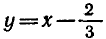 (рис- 6 )
(рис- 6 )
Из рисунка видно, что графики этих функций пересекаются в точке с абсциссой 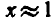 . Проверка показывает, что x = 1 — корень данного уравнения:
. Проверка показывает, что x = 1 — корень данного уравнения:
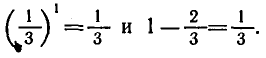
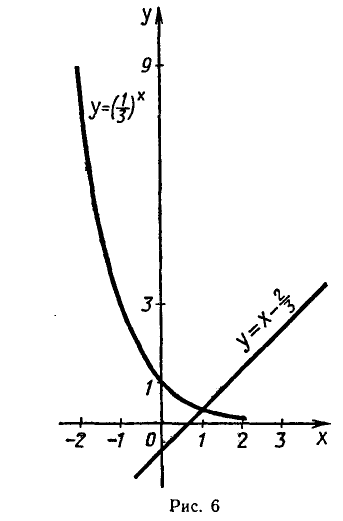
Покажем, что других корней нет. Функция 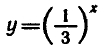
убывающая, а функция 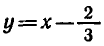 — возрастающая. Следовательно, при х > 1 значения первой функции меньше
— возрастающая. Следовательно, при х > 1 значения первой функции меньше 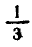 , а второй — больше
, а второй — больше 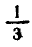 ; при x < 1, наоборот, значения первой функции больше
; при x < 1, наоборот, значения первой функции больше 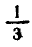 , а второй — меньше
, а второй — меньше 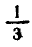 . Геометрически
. Геометрически
(рис. 6) это означает, что графики этих функций при x > 1 и x < 1 «расходятся» и потому не могут иметь точек пересечения при 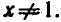
Заметим, что из решения этой задачи, в частности, следует, что неравенство 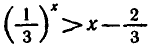 выполняется при х < 1, а неравенство
выполняется при х < 1, а неравенство 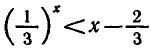 при х > 1.
при х > 1.
Системы уравнений
Задача:
Решить систему уравнений
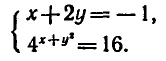
Решим эту систему способом подстановки:
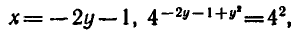
откуда 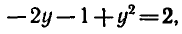
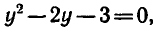
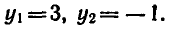
Найдем значения х:
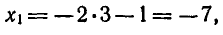
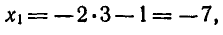
Ответ. ( — 7 ; 3), (1; — 1 ) .
Задача:
Решить систему уравнений
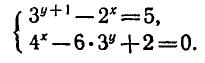
Обозначим 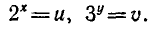
Тогда система запишется так:
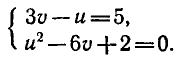
Решим эту систему способом подстановки
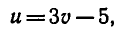
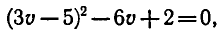
Найдем значения u: 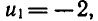
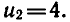
Возвратимся к принятым обозначениям:
1) 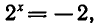
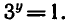 Так как первое из этих уравнений корней не имеет, то решений системы в этом случае нет.
Так как первое из этих уравнений корней не имеет, то решений системы в этом случае нет.
2) 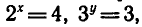 откуда х = 2, у = 1.
откуда х = 2, у = 1.
О т в е т. (2; 1 ).
Показательная функция
Показательной функцией называется функция, заданная формулой y=a x , где a > 0 и a ≠ 1
Порядок роста и убывания функции
Функция — это основной математический инструмент для изучения связей, зависимостей между различными величинами. Чем большим запасом функций мы располагаем, тем шире и богаче наши возможности математического описания окружающего мира.
Вслед за линейными мы подробно изучали квадратичные зависимости. Так, путь при равноускоренном движении квадратично зависит от времени; энергия падающего тела квадратично зависит от его скорости; количество теплоты, выделяемой током, текущим по проводнику, квадратично зависит от силы тока и т. п.
Степенные зависимости более высокого порядка также встречаются на практике. Например, по закону Стефана — Больц-мана излучательная способность абсолютно черного тела пропорциональна четвертой степени его температуры. Масса шара является кубической функцией его радиуса.
Если мы изобразим на одном чертеже (схема IX) графики степенных функций вида 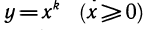 при положительных значениях k, то увидим, что, чем больше k, тем быстрее при больших значениях х растут эти функции. Степенные функции образуют естественную шкалу, позволяющую сравнивать рост различных функций со стандартными, степенными функциями.
при положительных значениях k, то увидим, что, чем больше k, тем быстрее при больших значениях х растут эти функции. Степенные функции образуют естественную шкалу, позволяющую сравнивать рост различных функций со стандартными, степенными функциями.
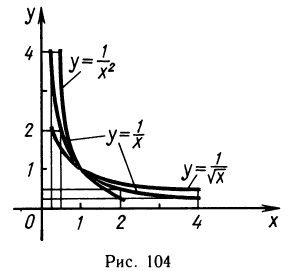
Аналогичная картина наблюдается и с убывающими функциями. Простейшая убывающая функция задается обратно пропорциональной зависимостью 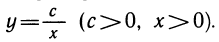 Изображая на одном чертеже (рис. 104) графики функций
Изображая на одном чертеже (рис. 104) графики функций 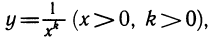 видим, что, чем больше k, тем быстрее убывают эти функции при больших значениях х.
видим, что, чем больше k, тем быстрее убывают эти функции при больших значениях х.

Гильберт Давид (1862—1943) —
немецкий математик, основатель Геттин-генской математической школы. Гильберт завершил начатое Евклидом. Ему принадлежит глубокое обобщение евклидовой геометрии (гильбертовы пространства), он получил важнейшие результаты в математической логике.
«Арифметические знаки — это записанные геометрические фигуры, а геометрические фигуры — это нарисованные формулы».
Д. Гильберт
В естествознании и технике встречаются процессы, рост или затухание которых происходит быстрее, чем у любой степенной функции. С примерами быстро растущих функций человек столкнулся очень давно. В древней легенде об изобретателе шахмат говорится, что он потребовал за первую клетку шахматной доски одно пшеничное зерно, а за каждую следующую — вдвое больше, чем за предыдущую. Человеку трудно представить себе порядок величины 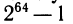 (общее число зерен, плату за изобретение шахмат). Если грубо заменить
(общее число зерен, плату за изобретение шахмат). Если грубо заменить 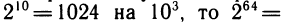
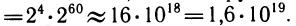
Достаточно сказать, что расстояние от Земли до Солнца в миллиметрах приблизительно равно 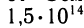 , так что, считая диаметр зерна за 1 мм, можно этим зерном 100 тысяч раз уложить путь до Солнца.
, так что, считая диаметр зерна за 1 мм, можно этим зерном 100 тысяч раз уложить путь до Солнца.
Поразительное явление быстрого роста членов геометрической прогрессии, т. е. чисел вида cqn, отражено во многих старинных задачах. Однако лишь с конца XVII в. стали систематически рассматриваться зависимости типа y = cqx, в которых переменная х принимает не только целые значения. Такие функции называются показательными.
Показательные функции, к изучению которых мы переходим в этой главе, обладают замечательным свойством: скорость их роста пропорциональна значению самой функции. Они как костер, который, чем больше разгорается, тем больше в него надо подкладывать дров.
Мы знаем, что скорость роста линейной функции постоянна, квадратичной функции линейна и вообще производная степенной функции, являясь меньшей степенью, растет медленнее, чем сама функция. Необходимость изучения функций, у которых производная пропорциональна самой функции, возникла с обнаружением различных законов естествознания, таких, как законы размножения, законы радиоактивного излучения, законы движения в тормозящей среде и т. д. Как эти законы связаны с показательными функциями, мы обсудим в главе, посвященной интегралу.
Определение степени с произвольным показателем
В основе определения показательной функции лежит понятие степени. Как надо понимать выражение 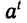 ? Его определение строится постепенно. Сначала надо вспомнить, что такое степень с натуральным показателем, т. е. рассмотреть случай, когда t — натуральное число. Запись
? Его определение строится постепенно. Сначала надо вспомнить, что такое степень с натуральным показателем, т. е. рассмотреть случай, когда t — натуральное число. Запись 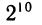 мы понимаем как произведение 10 одинаковых множителей, каждый из которых равен 2. В общем виде если t = n — натуральное число, то запись
мы понимаем как произведение 10 одинаковых множителей, каждый из которых равен 2. В общем виде если t = n — натуральное число, то запись 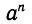 означает произведение п множителей, каждый из которых равен а.
означает произведение п множителей, каждый из которых равен а.
Если t — отрицательное целое число, то его можно записать в виде t= — n, где n — натуральное число. Тогда 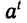 определяется так:
определяется так: 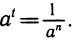 Например,
Например, 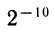 по определению равно
по определению равно 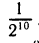 .
.
Если t=0, то 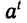 принимается равным единице, т. е. а°=1. Заметим, что
принимается равным единице, т. е. а°=1. Заметим, что 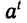 при t ≤ 0 не определено при а—0. Тем самым мы определили степень с произвольным целым показателем. Дальнейшее обобщение понятия степени требует положительности основания а. Рассмотрим случай, когда t — рациональное число. Его можно записать в виде дроби
при t ≤ 0 не определено при а—0. Тем самым мы определили степень с произвольным целым показателем. Дальнейшее обобщение понятия степени требует положительности основания а. Рассмотрим случай, когда t — рациональное число. Его можно записать в виде дроби 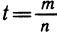 , где m — целое число, n — натуральное число. По определению
, где m — целое число, n — натуральное число. По определению 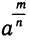 =
=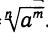 В частности,
В частности,
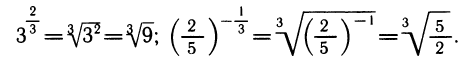
Степень с произвольным вещественным показателем t определяется следующим образом. Для числа t выбирается последовательность рациональных чисел t1, t2…, tn,…. задающая приближение числа t с любой степенью точности. Строится последовательность степеней с рациональными показателями 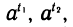
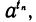 …, . Оказывается, что эта последовательность задает приближение некоторого числа с с любой степенью точности. Это число и называется степенью
…, . Оказывается, что эта последовательность задает приближение некоторого числа с с любой степенью точности. Это число и называется степенью 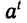 .
.
Таким образом, мы определили степень 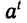 для положительного основания а и любого показателя t. Замечания.
для положительного основания а и любого показателя t. Замечания.
- Степень числа с натуральным показателем имеет смысл не только для положительного, но и для любого основания, так как эта степень определяется с помощью операции умножения, а умножать можно любые числа. Поэтому имеют смысл равенства
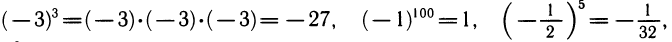
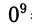 = 0 и т. п. Степень с целым отрицательным показателем может быть определена для любого числа, кроме нуля, так как ее вычисление сводится к операциям умножения и деления. Определение же степени с рациональным показателем требует операции извлечения корня, которая выполнима, как правило, только для положительных чисел. Поэтому мы с самого начала считаем основание степени положительным числом.
= 0 и т. п. Степень с целым отрицательным показателем может быть определена для любого числа, кроме нуля, так как ее вычисление сводится к операциям умножения и деления. Определение же степени с рациональным показателем требует операции извлечения корня, которая выполнима, как правило, только для положительных чисел. Поэтому мы с самого начала считаем основание степени положительным числом.
2. Степень с иррациональным показателем вычисляется приближенно. Сначала мы задаем приближения к числу t с помощью рациональных чисел, затем вычисляем степени с рациональным показателем. У нас остался невыясненным вопрос: как, зная погрешность приближения числа t с помощью рационального числа tn, оценить погрешность приближения 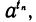 к числу
к числу 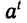 ?
?
Свойства степени
Операция возведения в натуральную степень имеет хорошо известные свойства. Перечислим их.
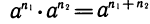 , т. е. при умножении степеней с одинаковым основаниями показатели складываются.
, т. е. при умножении степеней с одинаковым основаниями показатели складываются.
2. 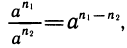 т. е. при делении степеней с одинаковыми основаниями показатели вычитаются.
т. е. при делении степеней с одинаковыми основаниями показатели вычитаются.
3. 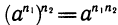 т. е. при возведении степени в степень показатели перемножаются.
т. е. при возведении степени в степень показатели перемножаются.
Для натуральных показателей эти свойства выводятся из определения степени и свойств умножения. Аналогичные свойства сохраняются для степеней с произвольными вещественными показателями:
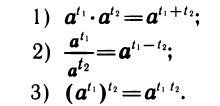
Доказательство свойств степени с произвольным вещественным показателем проводится, начиная со случая натурального показателя и переходя последовательно к целым, рациональным и любым показателям.
В приведенных выше свойствах основание степени было одним и тем же, а менялись показатели степени. Можно сформулировать свойства степеней с одинаковыми показателями, но разными основаниями:
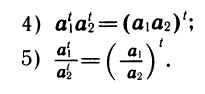
Исследование показательной функции
Определение:
Показательной функцией называется функция вида у = 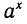 , где а — фиксированное положительное число.
, где а — фиксированное положительное число.
При исследовании показательной функции будем считать, что основание а ≠ 1, так как при а= 1 функция получается постоянной.
Перечислим основные свойства показательной функции.
- Область определения: множество всех вещественных чисел R.
- Монотонность: при а>1 функция у =
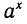 строго возрастает, при 0<а<1 функция у =
строго возрастает, при 0<а<1 функция у = 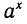 строго убывает (схема X).
строго убывает (схема X). - Положительность: значения функции у =
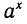 положительны (при любом основании а>0) .
положительны (при любом основании а>0) . - Область значений: множество всех положительных чисел, т. е. промежуток (0; + ∞).
Свойство 1 подчеркивает, что степень 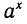 определена при любом вещественном показателе х. Доказательство свойств 2 и 3 показательной функции проводится так: эти свойства проверяются последовательно для натуральных, целых, рациональных показателей, а затем уже переносятся на произвольные вещественные показатели.
определена при любом вещественном показателе х. Доказательство свойств 2 и 3 показательной функции проводится так: эти свойства проверяются последовательно для натуральных, целых, рациональных показателей, а затем уже переносятся на произвольные вещественные показатели.
Свойства показательной функции позволяют построить ее график. Графики показательных функций при различных основаниях показаны на рисунке 105.
Рассмотрим показательную функцию у = 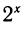 . С ростом х значения этой функции возрастают очень быстро. Так,
. С ростом х значения этой функции возрастают очень быстро. Так, 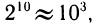
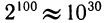 и т. д. Если же брать отрицательные значения х, то
и т. д. Если же брать отрицательные значения х, то 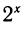 будет быстро приближаться к нулю:
будет быстро приближаться к нулю: 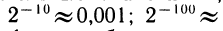
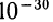 и т. д. Это свойство показательной функции быстро увеличиваться, с одной стороны, и быстро приближаться к нулю, с другой, хорошо видно на графике.
и т. д. Это свойство показательной функции быстро увеличиваться, с одной стороны, и быстро приближаться к нулю, с другой, хорошо видно на графике.
Вместе с функцией у = 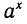 показательной функцией считают и функцию вида у = с
показательной функцией считают и функцию вида у = с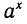 , где с — постоянная. К такому виду можно привести, например, функцию у=
, где с — постоянная. К такому виду можно привести, например, функцию у=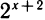 , сделав преобразование:
, сделав преобразование:
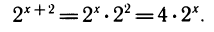
Производная показательной функции
Вычислим среднюю скорость роста показательной функции у=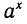 на отрезке [х; х+ ∆х]:
на отрезке [х; х+ ∆х]:
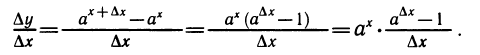
Мы видим, что средняя скорость роста показательной функции на отрезке [х; x + ∆х] равна значению этой функции в точке х, умноженному на число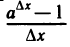 . Исследуем, как ведет себя это число при маленьких значениях ∆х. Так как а°=1, то значение
. Исследуем, как ведет себя это число при маленьких значениях ∆х. Так как а°=1, то значение 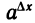 при маленьких значениях ∆х близко к 1. Если на графике функции проведем секущую, проходящую через точки (0; 1) и ( ∆х;
при маленьких значениях ∆х близко к 1. Если на графике функции проведем секущую, проходящую через точки (0; 1) и ( ∆х; 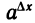 ), то ее угловой коэффициент будет равен числу
), то ее угловой коэффициент будет равен числу 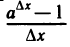 =tg a (рис. 106).
=tg a (рис. 106).
При 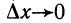 секущая будет приближаться к касательной к
секущая будет приближаться к касательной к
графику функции в точке (0; 1). Это означает, что 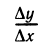 будет
будет
приближаться к произведению 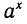 на значение производной при х=0. Итак, для нахождения производной функции у=
на значение производной при х=0. Итак, для нахождения производной функции у=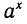 надо знать только значение этой производной в нуле. Если мы его обозначим через k, то получим формулу
надо знать только значение этой производной в нуле. Если мы его обозначим через k, то получим формулу
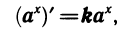
т. е. производная показательной функции пропорциональна самой функции.
Как же найти коэффициент пропорциональности k? Мы знаем, что он равен угловому коэффициенту касательной, проведенной в точке (0; 1). Можно приближенно по графику вычислить этот коэффициент. Так, известно, что для а=10 значение k ≈2,3, поэтому 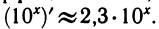
С помощью знака предела коэффициент k можно записать так:
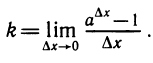
3. Число е
Посмотрим на графики показательных функций при различных а (рис. 105). Все они проходят через точку М (0; 1). Проведем в этой точке касательные к графикам. Мы видим, что, чем больше основание а, тем «круче» касательная. Так, при а = 2 угловой коэффициент касательной равен 0,693, а при а=10 угловой коэффициент касательной равен 2,303. Ясно, что при непрерывном изменении а от 2 до 10 угловой коэффициент касательной в точке М будет непрерывно меняться и найдется такое значение а, для которого этот коэффициент будет равен единице. Такое основание а обозначается буквой е. Число е иррационально. Его приближенное значение таково: е ≈ 2,718.
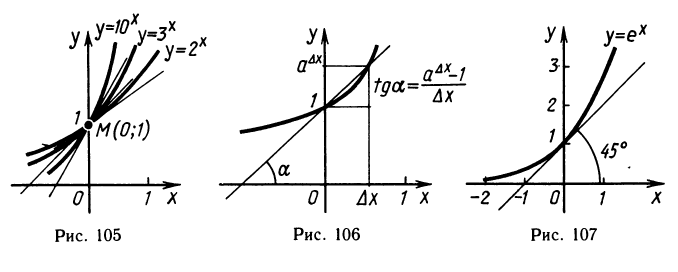
Итак, е — это такое число, что угловой коэффициент касательной к графику функции у=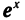 в точке х = 0 равен единице, т. е. касательная в этой точке образует с осью абсцисс угол 45° (рис. 107).
в точке х = 0 равен единице, т. е. касательная в этой точке образует с осью абсцисс угол 45° (рис. 107).
Можно сказать иначе. Мы уже знаем, что производная любой показательной функции пропорциональна самой этой функции. Число е — это основание, для которого коэффициент пропорциональности равен единице, т. е. е — это такое число, что производная функции у = 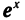 равна самой этой функции:
равна самой этой функции:
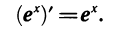
Функцию у = 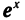 часто обозначают у = ехр х (читается: «Эксп от х») и называют экспонентой. Экспонентами называют и функции более общего вида: у =
часто обозначают у = ехр х (читается: «Эксп от х») и называют экспонентой. Экспонентами называют и функции более общего вида: у = 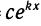 . Подумайте, понятен ли вам смысл таких распространенных выражений: «Численность бактерий растет по экспоненте», «Сила тока затухает по экспоненте», «Его успехи растут по экспоненте».
. Подумайте, понятен ли вам смысл таких распространенных выражений: «Численность бактерий растет по экспоненте», «Сила тока затухает по экспоненте», «Его успехи растут по экспоненте».
Аксиоматическое определение показательной функции
Показательная функция y = f(x), где f(x) = 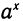 , обладает замечательным свойством:
, обладает замечательным свойством:
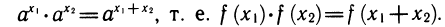
Это свойство может быть положено в основу определения показательной функции.
Пусть функция f задана на всей числовой оси R и для любых чисел x1,x2 удовлетворяет соотношению
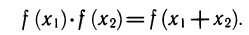
Написанное соотношение называют функциональным уравнением. Вопрос можно поставить так: каковы функции f с областью определения R, удовлетворяющие функциональному уравнению
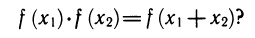
Прежде всего функция f {х) = 0 удовлетворяет этому уравнению. Будем считать, что f не является тождественным нулем. Из функционального уравнения следует цепочка свойств функции /, которые мы перечислим в виде серии нетрудных задач с указаниями на то, как их надо решать.
1)f(0)=1 (рассмотреть f(x+O), где х — какое-либо число, для которого f(x) ≠ 0).
2) f(х) ≠ 0 для любого х (рассмотреть f (x + ( — x))).
3) f(x)>0 для любых х (рассмотреть 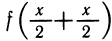 )
)
4) 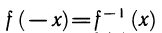 (рассмотреть f (x + ( —x))).
(рассмотреть f (x + ( —x))).
Обозначим f(1) через а.
5) 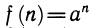 где n ∈ N (рассмотреть f (1 + 1+ …-+-1)).
где n ∈ N (рассмотреть f (1 + 1+ …-+-1)).
6) 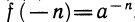 , где n ∈ N (воспользоваться 4) и 5)).
, где n ∈ N (воспользоваться 4) и 5)).
7) 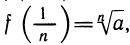 где n ∈ N (рассмотреть
где n ∈ N (рассмотреть 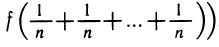 .
.
8) f(r) = ar, где r — рациональное число.
Таким образом, мы видим, что значения всякой, не равной тождественно нулю функции, определенной на всей числовой оси и удовлетворяющей функциональному уравнению f( x1)-f( x2) = f(x1+x2), для рациональных значений аргумента г совпадают со значениями а’ при некотором а. Для того чтобы сделать вывод о том, что f (х) совпадает с 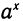 при любом вещественном х, одного функционального уравнения мало. Надо добавить еще какое-либо свойство — монотонность или непрерывность. Вот почему, стараясь избежать трудоемкого описания значений показательной функции с помощью рациональных приближений, часто дают следующее определение показательной функции:
при любом вещественном х, одного функционального уравнения мало. Надо добавить еще какое-либо свойство — монотонность или непрерывность. Вот почему, стараясь избежать трудоемкого описания значений показательной функции с помощью рациональных приближений, часто дают следующее определение показательной функции:
Показательная функция y = f (х) — это строго монотонная функция, определенная на всей числовой оси и удовлетворяющая функциональному уравнению
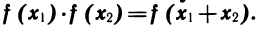
В одном мгновеньи видеть вечность, Огромный мир — в зерне песка, В единой горсти — бесконечность И небо — в чашечке цветка.
У. Блейк, пер. С. Маршака
Дополнение к показательной функции

Смотрите также:
| Исследование функции у = ах1 + Ьх + с | Логарифмическая функция |
| Тригонометрические функции. Радианная мера угла | Некоторые простые неявные функции |
Показательная функция
Определение:
Показательной функцией называется функция вида 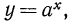 где основание а—произвольное положительное число, отличное от единицы. От отрицательных значений а отказываются по той причине, что при этом для некоторых значений переменной х значения степени
где основание а—произвольное положительное число, отличное от единицы. От отрицательных значений а отказываются по той причине, что при этом для некоторых значений переменной х значения степени 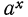 не существуют. Например, при
не существуют. Например, при 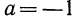 и при
и при 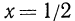 значение
значение 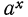 не определено. Легко сообразить, что значение
не определено. Легко сообразить, что значение 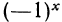 не определено и при
не определено и при 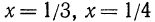 в соответствии с определением степени с рациональным показателем.
в соответствии с определением степени с рациональным показателем.
В случае 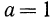 значение степени
значение степени 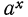 при любом х равно единице. Случай
при любом х равно единице. Случай 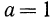 не рассматривают потому, что он не интересен.
не рассматривают потому, что он не интересен.
Данное выше определение показательной функции позволяет находить значение у для всякого значения х.
Рассмотрим в качестве примера показательную функцию 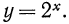 Эта функция определена на множестве всех целых значений х. Действительно,
Эта функция определена на множестве всех целых значений х. Действительно,
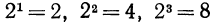
и, вообще,
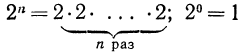 (по определению).
(по определению).
При отрицательных целых значениях х имеем
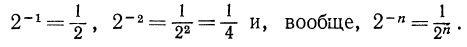
Эта функция определена также при любом рациональном х, например:

Наконец, функция определена и при любом иррациональном х (здесь мы этот случай не рассматриваем).
Итак, показательная функция определена на всем множестве действительных чисел.
Найденные значения показательной функции 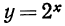 запишем в виде таблицы
запишем в виде таблицы
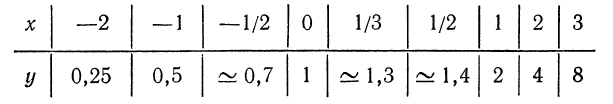
Предлагаем читателю убедиться самостоятельно в том, что функция 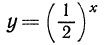 принимает следующие значения:
принимает следующие значения:
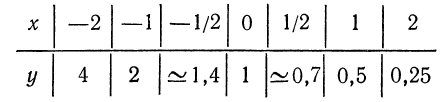
Свойства показательной функции
Рассмотрим приведенные в п. 1 таблицы. Мы замечаем следующие свойства:
1.Показательные функции 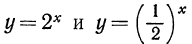 принимают только положительные значения, это вытекает из свойства степени с рациональным показателем. Любая показательная функция обладает этим свойством.
принимают только положительные значения, это вытекает из свойства степени с рациональным показателем. Любая показательная функция обладает этим свойством.
2. Показательная функция 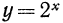 является монотонно возрастающей.
является монотонно возрастающей.
Докажем, что показательная функция 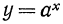 при любом
при любом  является монотонно возрастающей. Действительно, выберем два произвольных значения
является монотонно возрастающей. Действительно, выберем два произвольных значения 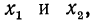 причем пусть
причем пусть 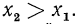 Составим для них разность соответствующих значений показательной функции
Составим для них разность соответствующих значений показательной функции 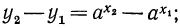 вынесем
вынесем 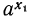 за скобку:
за скобку:
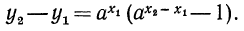
Заметим, что число  положительно, тогда
положительно, тогда 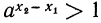 (положительная степень числа, большего единицы, сама больше единицы). Следовательно, разность
(положительная степень числа, большего единицы, сама больше единицы). Следовательно, разность 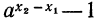 положительна и, так как
положительна и, так как 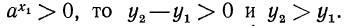
Тем самым можно считать доказанным тот факт, что показательная функция 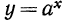 при
при 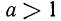 является монотонно возрастающей.
является монотонно возрастающей.
3.Показательная функция 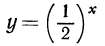 является монотонно убывающей.
является монотонно убывающей.
Предоставляем читателю доказать, что показательная функция 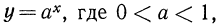 всегда является монотонно убывающей.
всегда является монотонно убывающей.
График показательной функции
Воспользовавшись составленными в п. 1 таблицами, построим в координатной
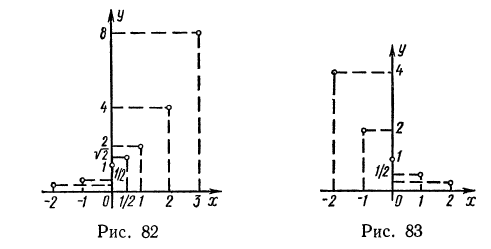
плоскости точки с соответствующими координатами для функции 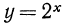 на рис. 82 и для функции
на рис. 82 и для функции 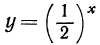 на рис. 83. Эти точки намечают в каждом случае некоторую линию, расположенную выше оси абсцисс. Уменьшая шаг таблицы, можно доказать, что мы будем получать точки, попадающие на те же линии. Соединяя эти точки плавной кривой, получим графики функций
на рис. 83. Эти точки намечают в каждом случае некоторую линию, расположенную выше оси абсцисс. Уменьшая шаг таблицы, можно доказать, что мы будем получать точки, попадающие на те же линии. Соединяя эти точки плавной кривой, получим графики функций 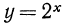 и
и 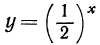
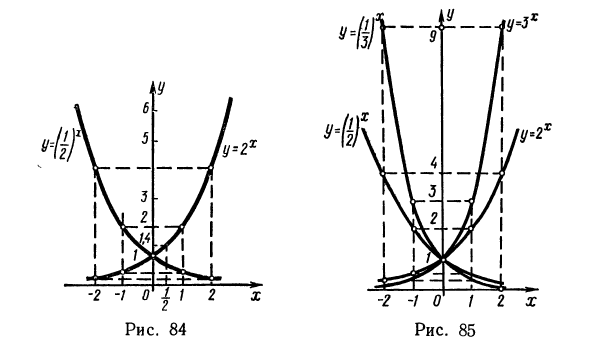
На рис. 85 изображены графики показательной функции 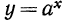 при различных основаниях
при различных основаниях 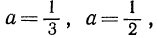
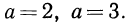
Рассматривая эти графики, мы видим, что показательная функция при а > 1 растет тем быстрее, чем больше а, а при основании 0 < а < 1 убывает тем быстрее, чем меньше а.
В заключение еще раз перечислим основные свойства показательной функции (в справедливости этих свойств советуем читателю убедиться, рассматривая рис. 85).
1°. Областью определения показательной функции является множество всех действительных чисел.
2°. Показательная функция принимает только положительные значения, т. е. областью ее значений является множество положительных чисел.
3°. Если а> 1, то при 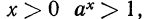 а при
а при 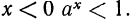 Если же
Если же 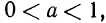 то, наоборот, при
то, наоборот, при 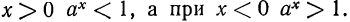
4°. Если 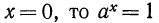 (график показательной функции пересекает ось ординат в точке у= 1).
(график показательной функции пересекает ось ординат в точке у= 1).
5°. При а> 1 показательная функция 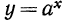 является монотонно возрастающей, а при
является монотонно возрастающей, а при 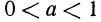 —монотонно убывающей.
—монотонно убывающей.
Из этого свойства показательной функции вытекает важное следствие. Если две степени одного и того же положительного числа, отличного от единицы, равны, то равны и их показатели, т. е. если 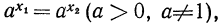 то
то 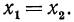
Другими словами: показательная функция принимает каждое свое значение один раз.
6°. Если а> 1, то при неограниченном возрастании 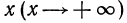 значения функции
значения функции 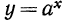 также неограниченно растут
также неограниченно растут 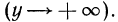 При неограниченном убывании аргумента
При неограниченном убывании аргумента 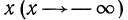 значения этой функции стремятся к нулю, оставаясь при этом положительными
значения этой функции стремятся к нулю, оставаясь при этом положительными 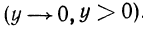 Если 0<а<1, то при неограниченном возрастании аргумента
Если 0<а<1, то при неограниченном возрастании аргумента 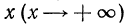 значения функции
значения функции 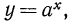 стремятся к нулю, оставаясь при этом положительными
стремятся к нулю, оставаясь при этом положительными 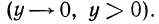 При неограниченном убывании аргумента
При неограниченном убывании аргумента 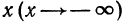 значения этой функции неограниченно растут
значения этой функции неограниченно растут 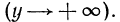
Примеры:
1. При помощи графика функции 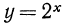 найти: а) значение у, соответствующее значению х = 0,5; б) при каком значении х значение у равно 4.
найти: а) значение у, соответствующее значению х = 0,5; б) при каком значении х значение у равно 4.
Решение:
а) Через точку 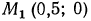 проведем прямую, параллельную оси ординат до пересечения с графиком функции
проведем прямую, параллельную оси ординат до пересечения с графиком функции 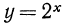 (рис. 86). Эта прямая пересечет график функции в точке
(рис. 86). Эта прямая пересечет график функции в точке 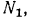 ордината которой
ордината которой 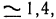 откуда
откуда 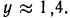
б) Через точку 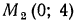 проведем прямую, параллельную оси абсцисс. Эта прямая пересечет график функции
проведем прямую, параллельную оси абсцисс. Эта прямая пересечет график функции 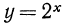 в точке абсцисса которой 2, откуда х = 2 (см. рис. 86).
в точке абсцисса которой 2, откуда х = 2 (см. рис. 86).
Рис. 86 2. Сравнить значения выражений:
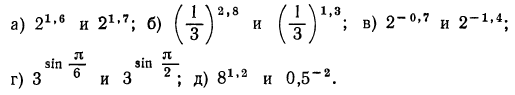
Решение:
Как известно, при а > 1 показательная функция 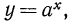 является монотонно возрастающей, а при 0 <а< 1—монотонно убывающей. На этом и основано сравнение значений выше приведенных выражений:
является монотонно возрастающей, а при 0 <а< 1—монотонно убывающей. На этом и основано сравнение значений выше приведенных выражений:
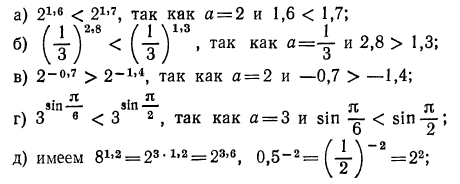
но 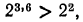 поэтому
поэтому 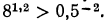
Рекомендуем читателю убедиться в справедливости выше перечисленных неравенств, рассматривая графики функций 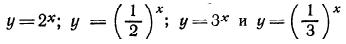 (см- Рис- 85)
(см- Рис- 85)
3.Решить уравнения и неравенства 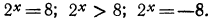
Решение:
Уравнение 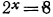 можно переписать в виде
можно переписать в виде  (уравняв основания). Так как показательная функция
(уравняв основания). Так как показательная функция 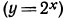 принимает каждое свое значение один раз (в силу монотонности), то х = 3.
принимает каждое свое значение один раз (в силу монотонности), то х = 3.
Переписав неравенство 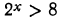 в виде
в виде 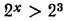 и учитывая, что показательная функция
и учитывая, что показательная функция 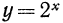 является монотонно возрастающей, получим x > 3.
является монотонно возрастающей, получим x > 3.
Уравнение 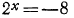 не имеет корней, так как показательная функция может принимать только положительные значения. 4. Решить следующие уравнения и неравенства:
не имеет корней, так как показательная функция может принимать только положительные значения. 4. Решить следующие уравнения и неравенства:

Решение:
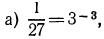 поэтому уравнение примет вид:
поэтому уравнение примет вид: 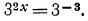 Используя свойство монотонности показательной функции, получаем уравнение
Используя свойство монотонности показательной функции, получаем уравнение 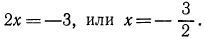
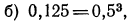 поэтому уравнение примет вид:
поэтому уравнение примет вид: 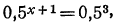 откуда
откуда 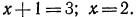
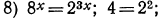 уравнение примет вид:
уравнение примет вид: 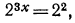 откуда
откуда 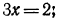
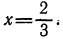
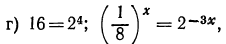 уравнение примет вид
уравнение примет вид 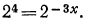 Значит,
Значит, 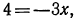 откуда
откуда 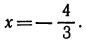
д) Показательная фуннция с основанием а= 13 является монотонно возрастающей, поэтому 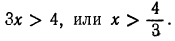
е) Показательная функция с основанием 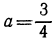 является монотонно убывающей, поэтому
является монотонно убывающей, поэтому 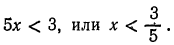
Целая и дробная части числа
Целой частью числа х называется наибольшее целое число, не превосходящее х. Целая часть числа х обозначается символом 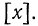 Для любого х имеем
Для любого х имеем
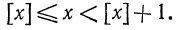
Пример:

Дробной частью числа х называется разность между х и его целой частью. Дробная часть числа х обозначается символом 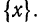 Значит,
Значит, 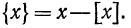
Так как 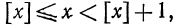 то можно записать, что
то можно записать, что 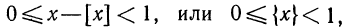 т. е. дробная часть числа — это неотрицательное число, меньшее единицы.
т. е. дробная часть числа — это неотрицательное число, меньшее единицы.
Например:
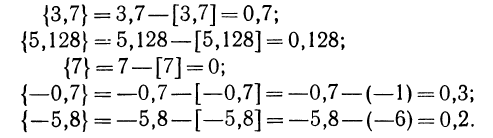
Из равенства 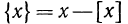 следует, что
следует, что 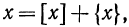 т. е. любое число х можно записать в виде суммы его целой и дробной части. Например,
т. е. любое число х можно записать в виде суммы его целой и дробной части. Например,
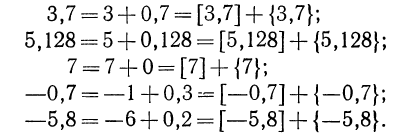
Функция 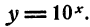
В практике вычислений особую роль играет функция 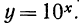 Покажем, что, зная значения выражения
Покажем, что, зная значения выражения 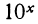 для
для 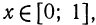 легко вычислить значения этого выражения для любого х.
легко вычислить значения этого выражения для любого х.
Пусть нужно найти приближенное значение выражения 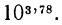 Представим показатель степени 3,78 в виде суммы целой и дробной части:
Представим показатель степени 3,78 в виде суммы целой и дробной части: 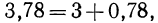 тогда
тогда
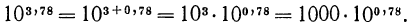
Таким образом, для отыскания приближенного значения осталось найти значение выражения 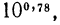 где
где 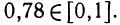
Рассмотрим еще один пример —найти приближенное значение выражения 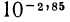 Представим показатель степени —2,85 в виде суммы целой и дробной части:
Представим показатель степени —2,85 в виде суммы целой и дробной части: 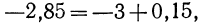 тогда
тогда
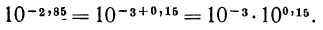
Для решения задачи осталось найти значение выражения 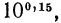 где
где 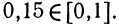
Итак, зная значения выражения 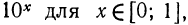 легко вычислить значения этого выражения для любого x. Значения выражения
легко вычислить значения этого выражения для любого x. Значения выражения 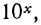 где
где 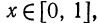 можно приближенно найти, построив график функции
можно приближенно найти, построив график функции 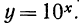 на отрезке [0; 1]. Для этого составим таблицу ее значений с шагом 1/8:
на отрезке [0; 1]. Для этого составим таблицу ее значений с шагом 1/8:
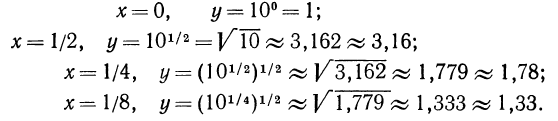
(Все вычисления выполнены по таблицам В. М. Брадиса «Четырехзначные математические таблицы», М., «Просвещение», 1969, таблица IV и затем округлены до сотых).
Далее имеем:
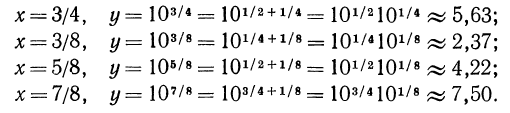
Найденные значения выражения 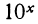 занесем в таблицу
занесем в таблицу

Построим в координатной плоскости точки, координаты которых указаны в таблице (причем по оси абсцисс в качестве единицы масштаба возьмем 10 см, а по оси ординат—1 см), и соединим эти точки плавной кривой (рис. 87).
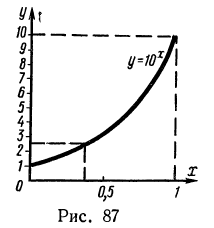
Построенный график позволяет находить приближенные значения функции 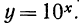 для любого х. По- ^ кажем на примерах, как находить приближенные значения функции
для любого х. По- ^ кажем на примерах, как находить приближенные значения функции 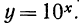
Примеры. 1. Пусть х = 3,56, тогда 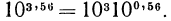 По графику находим
По графику находим 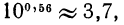 откуда
откуда 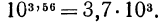
Пусть х =-1,3, тогда 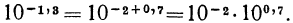 По графику находим
По графику находим 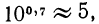 откуда
откуда 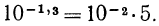
Если требуется большая степень точности для вычисления значений выражения 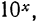 пользуются таблицами, например четырехзначными математическими таблицами В. М. Брадиса.
пользуются таблицами, например четырехзначными математическими таблицами В. М. Брадиса.
Приведенная ниже таблица содержит значения функции 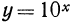 для значений переменной х от 0,0000 до 0,9999. Рассмотрим начало этой таблицы.
для значений переменной х от 0,0000 до 0,9999. Рассмотрим начало этой таблицы.
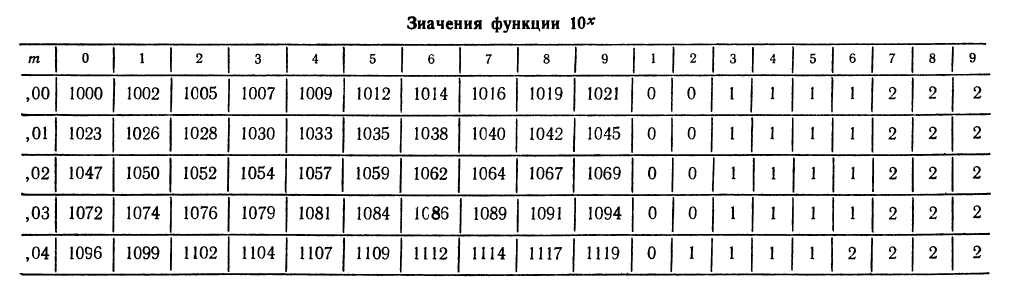
Найдем, например, значение выражения 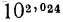 Прежде всего преобразуем это выражение
Прежде всего преобразуем это выражение 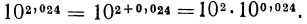 Для решения задачи надо найти значение функции
Для решения задачи надо найти значение функции 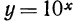 при х =0,024. Возьмем строку «02» и столбец «4». В их пересечении стоит число 1057. Чтобы найти значение выражения
при х =0,024. Возьмем строку «02» и столбец «4». В их пересечении стоит число 1057. Чтобы найти значение выражения 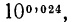 заметим, что
заметим, что 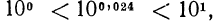 т. е.
т. е. 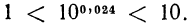 Значит,
Значит, 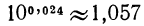 и окончательно
и окончательно 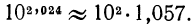
Если бы требовалось найти значение 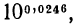 то к найденному в таблице числу 1057 нужно было бы прибавить 1 —поправку, помещенную в таблице справа на пересечении строки 02 и столбца «6». Таким образом,
то к найденному в таблице числу 1057 нужно было бы прибавить 1 —поправку, помещенную в таблице справа на пересечении строки 02 и столбца «6». Таким образом, 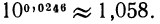 Аналогично можно найти
Аналогично можно найти 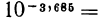
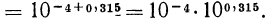 Значение выражения
Значение выражения 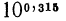 находим по таблице
находим по таблице 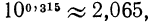 откуда
откуда 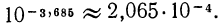
С помощью таблицы значений функции 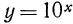 можно представить в виде степени с основанием 10 любое положительное число. Возьмем для примера число 11,09. Найдем это число в таблице. Оно находится на пересечении строки «04» и столбца «5», т. е.
можно представить в виде степени с основанием 10 любое положительное число. Возьмем для примера число 11,09. Найдем это число в таблице. Оно находится на пересечении строки «04» и столбца «5», т. е. 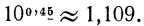 Значит,
Значит, 
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

