Оглавление:





Пересечение поверхностей с прямой
- До H EL 1 и прямой поверхности в ЕС 1. Чтобы построить пересечение прямой и любой поверхности, вам нужно провести вспомогательную секущу через эту линию. Затем найдите пересечение плоскости построения и указанной поверхности и, наконец, определите пересечение результирующей линии и этой линии.
- Эти точки являются желаемым пересечением линии и поверхности. Плоскость проекции, которая проходит через определенную прямую линию. Это связано с тем, что линию пересечения между поверхностью и плоскостью проекции, как правило, легче построить, чем плоскостью в общем месте.
Обычно выбирается в качестве вспомогательной плоскости. Людмила Фирмаль
Однако в особых случаях выгодно выбирать плоскость, которая находится в общем месте, которое пересекает конкретную поверхность вдоль простой графической линии в качестве вспомогательной плоскости. Эти случаи описаны ниже.
Поскольку эта линия и линия пересечения плоской поверхности, проведенная через эту линию, являются конкурирующими линиями, общий метод построения пересечения линия-поверхность может быть сформулирован следующим образом: Чтобы создать пересечение линии с поверхностью, необходимо создать вспомогательную линию на поверхности, которая конфликтует с этой линией, и найти пересечение линии с линией.
В то же время при создании выносных линий необходимо определять отдельные точки, используя простые графические линии поверхности. Таким образом, для вращающейся поверхности такая простая линия параллельна (круг), а для доминирующей поверхности — генератор (линия).
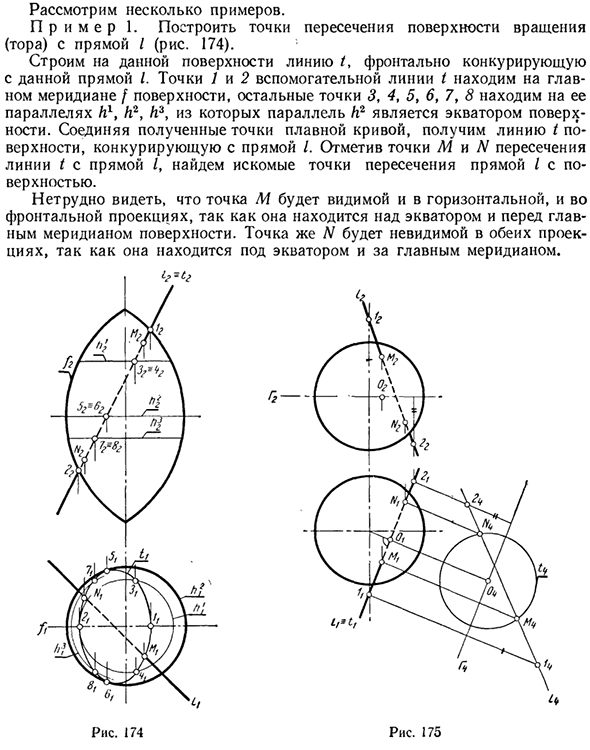
Давайте посмотрим на некоторые примеры. Пример 1. Создайте пересечение вращающейся поверхности (тора) и линии / (рис. 174). Постройте линию / на этой поверхности. Это будет конкурировать с этой линией / с фронта. Найдите точки вспомогательных линий 1 и 2 на главном меридиане поверхности и найдите оставшиеся точки 3, 4, 5, 6, 7 и 8 на их параллельных линиях Л1, Л2 и Л3.
Соедините точки полученной гладкой кривой, чтобы получить линию / поверхность, которая конкурирует с линией /. После разметки точки пересечения M w N линии t и линии / найдите нужное пересечение линии I и поверхности. Поскольку точка M находится выше экватора и перед основным меридианом поверхности, легко увидеть, что она видна как в горизонтальной, так и в передней проекциях.
Точка N скрыта обеими проекциями, потому что она находится за главным меридианом ниже экватора. Рис. 175 Рис. 174 Пример 2. Создайте пересечение сферы и линии / (рисунок 175). Создайте прямую линию / горизонтальную линию на поверхности сферы. Поскольку все плоские кривые на сфере являются кружками, линия t также является окружностью.
- Чтобы избежать создания эллипса, который является передней проекцией этого круга, замените плоскость проекции P2 плоскостью P4, которая параллельна линии nt и перпендикулярна плоскости nt. На плоскости проекции P4 линия t рисуется окружностью t4. Построив проекцию прямой // 4 и определив пересечения M4 и N4 проекций / 4 и / 4, мы можем найти основные проекции Mif Nt и M2, N2 искомого пересечения прямой I и сферы. 2.
Особые случаи При построении пересечения прямой линии и криволинейной поверхности, когда проецируется прямая линия или криволинейная поверхность, ее необходимо преобразовать в точечную или кривую линию, используя соответствующее уменьшение проекции. Рассмотрим это на примере. Пример 3.
Создайте пересечение поверхности конуса и линии проекции профиля i (рисунок 176). Людмила Фирмаль
Рисунок 17g Требуемые проекции профиля точки M3 и N3 соответствуют проекции профиля этой линии. Фронтальная проекция этих точек может быть легко определена. М2 — с использованием шины S — коническая, N2 — фронтальная проекция нижней части конуса. Пример 4. Создайте пересечение поверхности цилиндра и линии I (рис. 177).
Поскольку этот цилиндрический поверхностный генератор расположен спереди, вы можете преобразовать его в плоскость проекции, заменив плоскость проекции один раз. Для этого достаточно заменить самолет Г! * В плоскости П4 перпендикулярно генератору Данная поверхность. Далее в плоскости проекции «» цилиндрическая поверхность рисуется по кругу.
Проекция U линии / также строится, и когда точки пересечения Mi и N4 проекции U и проекции данной поверхности определены, цель Найти основные проекции точек M2, Nz и / N Nx легко. При общем решении этого примера легко видеть, что эллипс, который конкурирует с прямой линией, должен быть построен на определенной поверхности. Это решение является более сложным и менее точным.
Кроме вышеупомянутых решений. 3. При построении пересечения прямой и цилиндрической или конической поверхности линии этих граней, которые конфликтуют с прямой, обычно не являются графически простыми линиями. В качестве помощи можно избежать трудоемкого строительства этих линий Плоскость, которая использует плоскость вместо плоскости проекции, которая проходит через данную линию.
Кость в общем положении, выбранная для пересечения определенной цилиндрической или конической поверхности графически простой линией. Для цилиндрических граней вспомогательная плоскость проведена через эту прямую линию, параллельную образующей цилиндрической грани, а для конических граней она проведена через эту прямую и верхнюю часть конической грани.
В обоих случаях пересечение происходит вдоль шинной (прямой) поверхности. Чтобы построить эти генераторы, вам нужно найти вспомогательную плоскую трассировку на дне цилиндра или конуса и пометить пересечение этой трассы с нижней частью цилиндра или конуса. Эти точки определяют генератор, который вам нужен. Эти структуры могут интерпретироваться по-разному, используя дополнительные проекции.
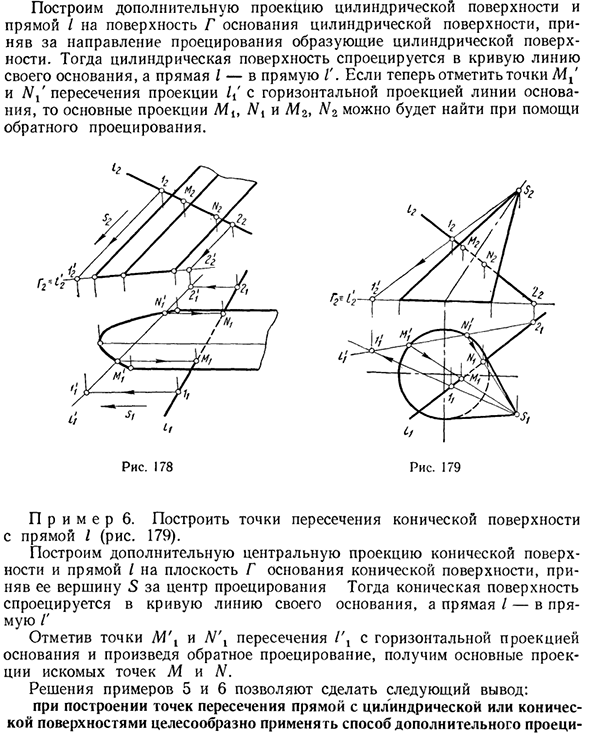
Пример 5. Создайте пересечение цилиндрической поверхности и прямой линии / (рис. 178). Создайте дополнительную проекцию цилиндрической поверхности и прямой линии / на поверхность Г нижней поверхности цилиндрической поверхности с генератором цилиндрической поверхности в качестве направления проекции. Затем цилиндрическая грань проецируется на ее базовую кривую, а линия / проецируется на линию /.
Теперь, если вы отметите точки M / и Nx на пересечении «Проекция 1X» и базовой горизонтальной проекции, вы можете использовать обратную проекцию, чтобы найти основные проекции Mt, N {и M2, N2. Пример 6. Создайте пересечение конической поверхности и линии / (рис. 179).
Используя вершину 5 в качестве центра проекции, создайте дополнительную центральную проекцию конической поверхности и линии / на нижнюю плоскость Г конической поверхности, спроецируйте коническую поверхность на нижнюю кривую и спроецируйте линию / на линию Г. Отметьте точки M \ и N \ на пересечении 1 \ как базовую горизонтальную проекцию и выполните обратную проекцию, чтобы получить основную проекцию в нужной точке MiN.
Решения в Примерах 5 и 6 могут привести к следующим выводам: Рекомендуется использовать дополнительную проекцию при построении пересечения прямой линии с цилиндрической или конической поверхностью. Параллельно цилиндрической поверхности и в центре конуса, поверхность преобразуется в выступ, и решение значительно упрощается.
Смотрите также:
Решение задач по начертательной геометрии

