Парабола в математике

Парабола

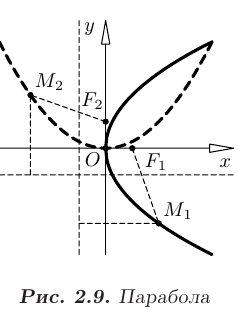
Параболой называется геометрическое место точек плоскости 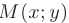, для которых расстояние до некоторой фиксированной точки , называемой фокусом параболы, равно расстоянию до некоторой фиксированной прямой, называемой директрисой параболы. Расстояние от фокуса до директрисы параболы равно 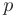и называется параметром параболы.

Если фокус параболы 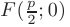расположен на оси 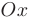, а директриса параболы перпендикулярна к этой оси 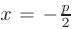то парабола будет симметрична относительна оси 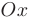(см. сплошную линию на рис. 2.9) и ее уравнение имеет канонический вид

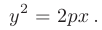
Если фокус параболы 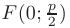расположен на оси 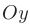, а директриса параболы перпендикулярна к этой оси 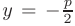то парабола будет симметрична относительна оси (см. штриховую линию на рис. 2.9) и ее уравнение также имеет канонический вид

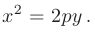
В рассмотренных случаях, вершина параболы, расположенная в середине перпендикуляра, опущенного из ее фокуса на директрису, совпадает с началом координат .

Если параметр параболы положителен: 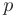> 0, то направление ветвей параболы совпадает с положительным направлением оси симметрии; если параметр параболы отрицателен: 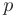< 0, то направление ветвей параболы совпадает с отрицательным направлением оси симметрии.

Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:

Помощь по математике

Возможно эти страницы вам будут полезны:

Эллипс в математике

Гипербола в математике

Предел последовательности в математике

Функция одной переменной в математике