Оглавление:
Подмножество прямого произведения 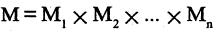 называется
называется 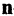 — местным отношением R на множестве М, т. е.
— местным отношением R на множестве М, т. е. 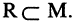 Это означает, что рассматриваются некоторые
Это означает, что рассматриваются некоторые 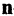 -ки элементов из одного и того же множества М и эти элементы находятся между собой в отношении R. Отношение может быть задано на множестве элементов любой природы.
-ки элементов из одного и того же множества М и эти элементы находятся между собой в отношении R. Отношение может быть задано на множестве элементов любой природы.
Если 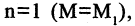 то отношение называется унарным. Установить на М унарное отношение означает приписать некоторым его элементам признак R. По существу, одноместное отношение есть подмножество М. Примеры унарных отношений: «быть целым числом» на множестве вещественных чисел, «быть открытым слогом» на множестве слогов и т.п.
то отношение называется унарным. Установить на М унарное отношение означает приписать некоторым его элементам признак R. По существу, одноместное отношение есть подмножество М. Примеры унарных отношений: «быть целым числом» на множестве вещественных чисел, «быть открытым слогом» на множестве слогов и т.п.
Если 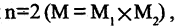 то отношение называется бинарным. Эти отношения обычно записывают как
то отношение называется бинарным. Эти отношения обычно записывают как 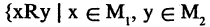 (или
(или 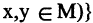 и говорят, что элементы
и говорят, что элементы 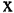 и
и 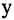 из множества М находятся между собой в отношении R. Например, «продукт
из множества М находятся между собой в отношении R. Например, «продукт 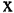 чаще покупают, чем
чаще покупают, чем 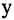 ».Существуют также тернарные
».Существуют также тернарные 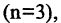 тетрарные
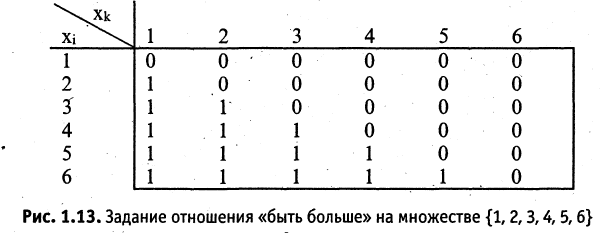
тетрарные 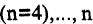 — арные отношения. Для задания бинарных отношений на конечных множествах удобно использовать списки пар или таблицы (матрицы). В этом случае, если элементы и у находятся между собой в отношении R, то в матрице на соответствующем месте пишут 1, в противном случае пишут ноль. Например, отношение «быть больше» на множестве чисел
— арные отношения. Для задания бинарных отношений на конечных множествах удобно использовать списки пар или таблицы (матрицы). В этом случае, если элементы и у находятся между собой в отношении R, то в матрице на соответствующем месте пишут 1, в противном случае пишут ноль. Например, отношение «быть больше» на множестве чисел 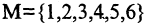 можно задать так:
можно задать так:
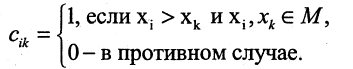
Таблица этого отношения имеет вид, представленный на рис. 1.13.
Бинарные отношения удобно задавать с помощью ориентированных графов (см. главу 1.6). Отношение называется полным, если 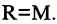 Это означает, что все элементы множества М находятся в отношении R. Например, отношение «учиться в одной учебной группе» на множестве студентов данной учебной группы является полным, но отношение «быть сыном» не является полным на множестве всех людей. Если
Это означает, что все элементы множества М находятся в отношении R. Например, отношение «учиться в одной учебной группе» на множестве студентов данной учебной группы является полным, но отношение «быть сыном» не является полным на множестве всех людей. Если 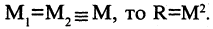 Например, множество М — отрезок числовой оси, тогда полное отношение
Например, множество М — отрезок числовой оси, тогда полное отношение 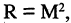 заданное на отрезке числовой оси, геометрически соответствует квадрату со стороной М (см. рис. 1.14).
заданное на отрезке числовой оси, геометрически соответствует квадрату со стороной М (см. рис. 1.14).
Отношение называется тождественным, если оно равносильно отношению 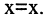 Тождественное отношение обычно обозначают буквой Е. Таблица такого отношения представляет собой единичную матрицу. Примером тождественного отношения
Тождественное отношение обычно обозначают буквой Е. Таблица такого отношения представляет собой единичную матрицу. Примером тождественного отношения
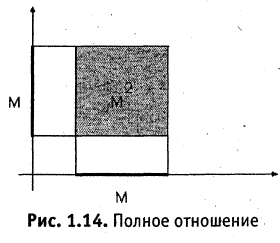
является отношение равенства на множестве вещественных чисел.
Так как отношения — это множества, то для них справедливы все теоретико-множественные операции, но существуют операции специфические для отношений.
Для отношения R определена операция обращения. Отношение 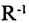 обратно к R, если
обратно к R, если 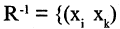
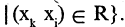 Переход от R к
Переход от R к 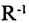 осуществляется взаимной перестановкой компонент каждой упорядоченной пары. Пример обратных отношений: «
осуществляется взаимной перестановкой компонент каждой упорядоченной пары. Пример обратных отношений: «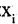 старше
старше 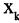 » и «
» и «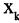 старше
старше 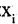 ». Композицией двух отношений R и Р, заданных на множестве М, называется отношение
». Композицией двух отношений R и Р, заданных на множестве М, называется отношение 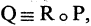 такое, что для любых
такое, что для любых 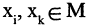 существует хотя бы один элемент
существует хотя бы один элемент 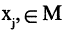 такой, что если
такой, что если 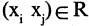 и
и 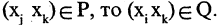 Можно доказать важное свойство композиции:
Можно доказать важное свойство композиции: 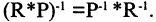
Пример. Пусть заданы отношения в виде таблиц.
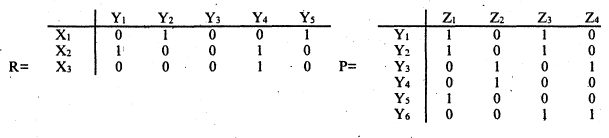
Отношения удобно представить в виде списков пар: для R это пары 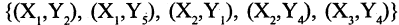 , соответственно для Р это пары
, соответственно для Р это пары 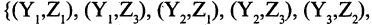
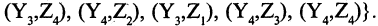 Композицией двух отношений R и Р будет отношение
Композицией двух отношений R и Р будет отношение 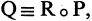 состоящее из следующих пар:
состоящее из следующих пар: 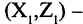 так как существует элемент
так как существует элемент 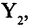 такой, что он входит в пары
такой, что он входит в пары 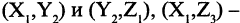 так как существует элемент
так как существует элемент 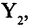 такой, что он входит в пары
такой, что он входит в пары 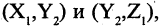 (таким же свойством обладает и элемент
(таким же свойством обладает и элемент 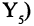 и так далее.
и так далее.
Таблица, соответствующая композиции 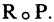
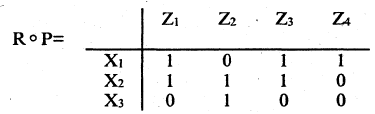
Свойства отношений
Рефлексивность. Отношение R, заданное на множестве М называется рефлексивным, если для любого 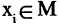 имеет место
имеет место 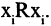 Формально рефлексивность можно задать так:
Формально рефлексивность можно задать так: 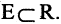 Рефлексивное отношение всегда выполняется между объектом и им самим. Наиболее яркими примерами рефлексивных отношений являются самообслуживание и равенство.
Рефлексивное отношение всегда выполняется между объектом и им самим. Наиболее яркими примерами рефлексивных отношений являются самообслуживание и равенство.
Антирефлексивность. Отношение R, заданное на множестве М, антирефлексивно, если 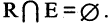 В антирефлексивных отношениях из условия
В антирефлексивных отношениях из условия 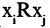 следует, что
следует, что 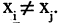 Примеры антирефлексивных отношений: быть старше, быть меньше и др.
Примеры антирефлексивных отношений: быть старше, быть меньше и др.
Симметричность. Отношение R, заданное на множестве М, называется симметричным, если при выполнении соотношения 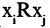 одновременно выполняется и соотношение
одновременно выполняется и соотношение 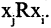 Формально соотношение симметрично, если
Формально соотношение симметрично, если 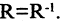 Например, отношения «стоять рядом на полке» на множестве книг или « быть родственниками» на множестве людей симметричны.
Например, отношения «стоять рядом на полке» на множестве книг или « быть родственниками» на множестве людей симметричны.
Асимметричность. Отношение R, заданное на множестве М, называется асимметричным, если 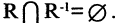 В асимметричных отношениях из двух соотношений
В асимметричных отношениях из двух соотношений 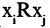 и
и 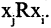 может выполняться не более одного (одно или не одного). Пример асимметричного отношения: «быть отцом» (если
может выполняться не более одного (одно или не одного). Пример асимметричного отношения: «быть отцом» (если 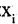 — отец
— отец 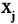 , то
, то 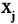 не может быть отцом
не может быть отцом 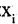 ).
).
Антисимметричность. Отношение R, заданное на множестве М, обладает свойством антисимметричности, если 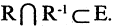 Это означает, что если для
Это означает, что если для 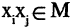 одновременно выполняются соотношения
одновременно выполняются соотношения 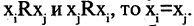 Антисимметричны все отношения нестрогого порядка: «быть не больше», «быть не выше» и т.п.
Антисимметричны все отношения нестрогого порядка: «быть не больше», «быть не выше» и т.п.
Транзитивность. Отношение R, заданное на множестве М, транзитивно, если для любых 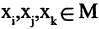 из выполнимости со-
из выполнимости со-
отношений 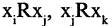 следует
следует 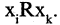 Формально это можно записать так:
Формально это можно записать так: 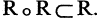 Про отношение, не обладающее таким свойством говорят, что оно нетранзитивно. Например, отношение «стоять рядом на полке» нетранзитивно. Действительно, пусть тома некоторой энциклопедии стоят в порядке возрастания номеров томов. Тогда, если первый том стоит рядом со вторым, а второй — рядом с третьим, то, очевидно, что первый не стоит рядом с третьим.
Про отношение, не обладающее таким свойством говорят, что оно нетранзитивно. Например, отношение «стоять рядом на полке» нетранзитивно. Действительно, пусть тома некоторой энциклопедии стоят в порядке возрастания номеров томов. Тогда, если первый том стоит рядом со вторым, а второй — рядом с третьим, то, очевидно, что первый не стоит рядом с третьим.
Все общие свойства отношений можно разбить на три группы: рефлексивности (каждое отношение рефлексивно или ан-тирефлексивно), симметричности (отношение всегда или симметрично, или асимметрично, или антисимметрично), транзитивности (каждое отношение транзитивно или не транзитив-но). Отношениям, обладающим определенным набором свойств, присвоены специальные названия.
Отношение эквивалентности
Отношение R, обладающее свойствами рефлексивности, симметричности и транзитивности называется отношением эквивалентности. Для эквивалентных отношений вместо записи 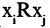 обычно пишут
обычно пишут 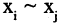 (читается: «
(читается: «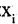 эквивалентно
эквивалентно 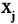 »). Эквивалентными отношениями являются: «быть конгруэнтными» на множестве плоских треугольников, «быть одного размера» на множестве образцов обуви, «быть родственниками» на множестве людей и т.п.
»). Эквивалентными отношениями являются: «быть конгруэнтными» на множестве плоских треугольников, «быть одного размера» на множестве образцов обуви, «быть родственниками» на множестве людей и т.п.
Введение отношения эквивалентности R на множестве М определяет разбиение всех элементов этого множества на классы эквивалентности 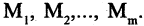 Множество всех классов эквивалентности
Множество всех классов эквивалентности 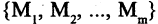 образует фактор множество множества М и обозначается M/R. При этом каждый элемент данного класса является полномочным представителем этого класса. Совокупность по одному и только по одному представителю каждого класса называется системой представителей соответствующего отношения эквивалентности. Примером введения отношения эквивалентности и образования системы представителей может служить формирование представительного органа власти на основе выборов.
образует фактор множество множества М и обозначается M/R. При этом каждый элемент данного класса является полномочным представителем этого класса. Совокупность по одному и только по одному представителю каждого класса называется системой представителей соответствующего отношения эквивалентности. Примером введения отношения эквивалентности и образования системы представителей может служить формирование представительного органа власти на основе выборов.
Отношение толерантности
Отношение 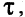 заданное на множестве М, называется отношением толерантности, если оно рефлексивно, симметрично и нетранзитивно. Обозначение:
заданное на множестве М, называется отношением толерантности, если оно рефлексивно, симметрично и нетранзитивно. Обозначение: 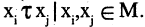 Если потребовать транзитивность всех пар элементов из М, то получим эквивалентное отношение. Следовательно, толерантность может рассматриваться как расширение эквивалентности. Эквивалентность — в смысле равенства, толерантность — в смысле сходства, похожести. Содержательно толерантность означает следующее: объект находится в данном отношении сам с собой (рефлексивность), сходство двух объектов не зависит от порядка сравнения (симметричность), но если первый объект сходен со вторым, а второй сходен с третьим, то не обязательно, что первый был сходен с третьим. Толерантность позволяет третьим, то не обязательно, что первый был сходен с третьим. Толерантность позволяет формализовать интуитивные представление о сходстве объектов, их похожести в чем-то. Например, отношение
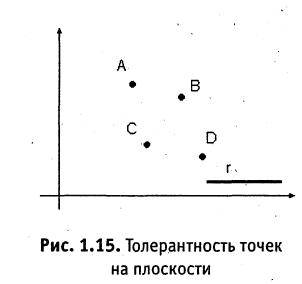
Если потребовать транзитивность всех пар элементов из М, то получим эквивалентное отношение. Следовательно, толерантность может рассматриваться как расширение эквивалентности. Эквивалентность — в смысле равенства, толерантность — в смысле сходства, похожести. Содержательно толерантность означает следующее: объект находится в данном отношении сам с собой (рефлексивность), сходство двух объектов не зависит от порядка сравнения (симметричность), но если первый объект сходен со вторым, а второй сходен с третьим, то не обязательно, что первый был сходен с третьим. Толерантность позволяет третьим, то не обязательно, что первый был сходен с третьим. Толерантность позволяет формализовать интуитивные представление о сходстве объектов, их похожести в чем-то. Например, отношение  «быть на расстоянии не более r», заданное на множестве точек на плоскости. Рис. 1.15 иллюстрирует этот пример. Точка А отстоит от В и С не более чем на r, так же как точка В от Д и С в то время как А находится от Д на расстоянии, значительно большем, чем r.
«быть на расстоянии не более r», заданное на множестве точек на плоскости. Рис. 1.15 иллюстрирует этот пример. Точка А отстоит от В и С не более чем на r, так же как точка В от Д и С в то время как А находится от Д на расстоянии, значительно большем, чем r.
Отношение порядка
Отношение R, обладающее свойствами рефлексивности, антисимметричности и транзитивности, называется отношением порядка. Если на данном множестве введено отношение порядка, то это множество называется упорядоченным. В этом случае вместо 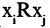 пишут
пишут 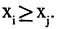 Множество совершенно упорядочено, если для любых двух элементов
Множество совершенно упорядочено, если для любых двух элементов 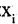 и
и 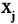 из множества М
из множества М
имеет место либо 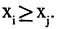 , либо
, либо 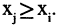 В противном случае говорят, что множество частично упорядочено. Например, отношение «быть выше» на множестве деревьев — совершенно упорядочено, а отношение «быть делителем» на множестве целых чисел — частично упорядочено.
В противном случае говорят, что множество частично упорядочено. Например, отношение «быть выше» на множестве деревьев — совершенно упорядочено, а отношение «быть делителем» на множестве целых чисел — частично упорядочено.
Пусть каждому элементу 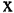 из множества М по некоторому правилу f поставлено в соответствие вещественное число
из множества М по некоторому правилу f поставлено в соответствие вещественное число 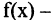 вес элемента
вес элемента 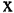 . Введение веса для каждого элемента позволяет упорядочить их по мере возрастания (убывания) весов, а затем сравнивать элементы в соответствии с присвоенным весом. Примерами упорядочения посредством введения весов являются: присвоению каждому товару его цены, каждому станку его надежности, каждому телу его веса, объема и т.п. Взвешивание вариантов решений посредством формирования комплексного показателя качества является одним из самых распространенных способов решения проблемы выбора на множестве разнокачественных признаков.
. Введение веса для каждого элемента позволяет упорядочить их по мере возрастания (убывания) весов, а затем сравнивать элементы в соответствии с присвоенным весом. Примерами упорядочения посредством введения весов являются: присвоению каждому товару его цены, каждому станку его надежности, каждому телу его веса, объема и т.п. Взвешивание вариантов решений посредством формирования комплексного показателя качества является одним из самых распространенных способов решения проблемы выбора на множестве разнокачественных признаков.
Если отношение обладает свойствами антирефлексивности, асимметричности и транзитивности, то оно называется отношением строгого порядка (обозначается 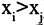 ). Примером отношения строгого порядка является порядок букв в фиксированном алфавите. Упорядочение букв в алфавите позволяет, в свою очередь, упорядочить слова в словарях (лексикографическое упорядочение слов).
). Примером отношения строгого порядка является порядок букв в фиксированном алфавите. Упорядочение букв в алфавите позволяет, в свою очередь, упорядочить слова в словарях (лексикографическое упорядочение слов).
Группы. Кольца. Пространства
Множество 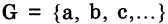 называется группой, если определена бинарная операция, которая каждой паре элементов а, b множества G ставит в соответствие объект
называется группой, если определена бинарная операция, которая каждой паре элементов а, b множества G ставит в соответствие объект  так, что
так, что
1) объект  является элементом множества G (замкнутость по отношению к операции);
является элементом множества G (замкнутость по отношению к операции);
2) 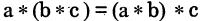 (справедлив ассоциативный закон);
(справедлив ассоциативный закон);
3) множество G содержит такой элемент Е, что
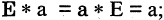
4) для каждого элемента а существует обратный 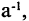 такой что
такой что
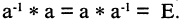
Если для всех элементов группы 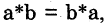 то бинарная операция называется коммутативной, а группа — Абелевой группой.
то бинарная операция называется коммутативной, а группа — Абелевой группой.
Множество G называется кольцом, если на нем определены две бинарные операции, которые обычно называются умножением и сложением, и, кроме того:
1.G есть коммутативная группа по сложению, т. е. G замкнуто по отношению к операции сложения и справедливо, что
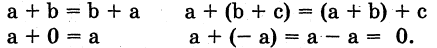
Здесь «0» — нулевой элемент, а « -а» — обратный.
2.G замкнуто по отношению к умножению, т. е. аb принадлежит множеству G, причем

3.Выполняются дистрибутивные законы

Если кольцо содержит такой элемент Е, что а Е = Е а = а, то кольцо называют кольцом с единицей. Элементы кольца называют скалярами. Множество R с элементами 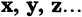 называется линейным векторным пространством над кольцом G , а элементы
называется линейным векторным пространством над кольцом G , а элементы 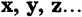 векторами, если определены две бинарные операции векторное сложение и умножение вектора на скаляр, причем
векторами, если определены две бинарные операции векторное сложение и умножение вектора на скаляр, причем
1.R есть коммутативная группа по векторному сложению, т. е. R замкнуто по отношению к операции сложения и справедливо, что
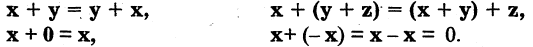
2.Если 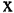 вектор из R и а есть скаляр из G, то R замкнуто по отношению к умножению вектора на скаляр.
вектор из R и а есть скаляр из G, то R замкнуто по отношению к умножению вектора на скаляр.
3.При умножении вектора на скаляр справедливы ассоциативный и дистрибутивный законы:
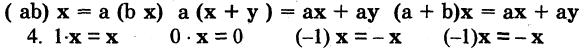
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

