Оглавление:
Группы основных тригонометрических формул:
Формулы сложения (четвертая группа)
Основными формулами сложения являются следующие:
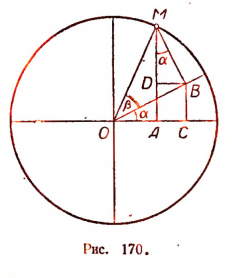
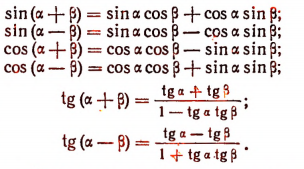
Первая из этих формул читается так: синус, суммы двух чисел равен синусу первого числа, умноженному на косинус второго, плюс косинус первого на синус второго.
Аналогично читаются и остальные формулы.
Теперь перейдем к выводам и доказательствам.
Вывод формул синуса суммы и косинуса суммы (при ограниченных условиях). Пусть 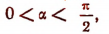
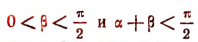 (рис. 170). Проведем
(рис. 170). Проведем 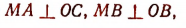
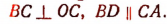
Тогда
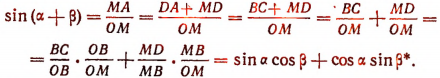
* Углы BMD и ВОС равны между собой как углы с взаимно перпендикулярными сторонами.
Аналогично
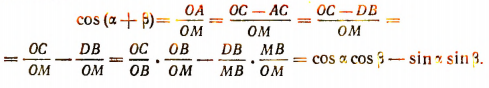
Доказательство общности. Пусть требуется доказать общность каждой из двух выведенных формул:
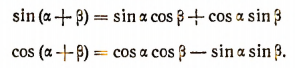
Это значит требуется доказать, что каждая из них справедлива при любых значениях 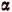 и
и 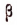 , а не только при значениях, удовлетворяющих неравенствам:
, а не только при значениях, удовлетворяющих неравенствам: 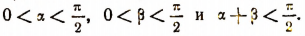
Требующееся доказательство мы расчленим на пять последовательных этапов:
1. Пусть 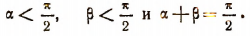
Тогда 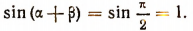
Наряду с этим
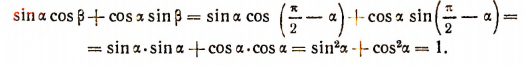
Следовательно, при 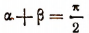 формула
формула 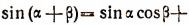
 остается в силе, так как ее левая и правая части обращаются в единицу, как это было показано выше.
остается в силе, так как ее левая и правая части обращаются в единицу, как это было показано выше.
Подобным же образом можно доказать, что при 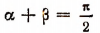 остается в силе и формула
остается в силе и формула 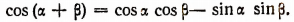
2. Пусть 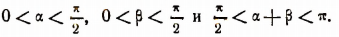
Примем 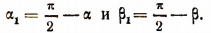
Тогда 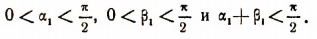
Для 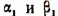 , как это уже доказано, будет справедливой формула
, как это уже доказано, будет справедливой формула 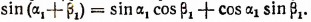
Заменяя теперь 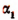 и
и 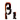 их выражениями через
их выражениями через 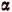 и
и 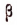 , получим:
, получим:
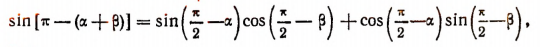
или
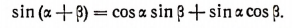
Это свидетельствует о справедливости формулы при
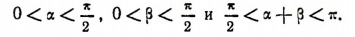
То же самое можно доказать и по отношению к формуле
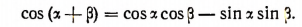
3. На третьем этапе мы докажем следующее положение. Если формулы

справедливы для каких-нибудь значений 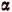 и
и 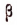 , то они будут справедливы и в том случае, если одно из значений
, то они будут справедливы и в том случае, если одно из значений 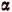 и
и 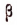 мы увеличим на
мы увеличим на 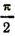 .
.
Рассмотрим выражение 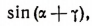 в котором
в котором 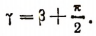
Легко видеть, что
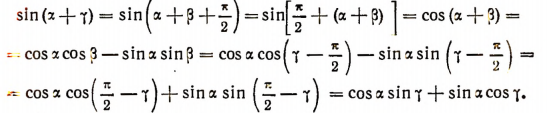
Итак, оказалось, что
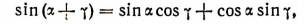
т. е. наша формула осталась в силе.
То же самое можно доказать и по отношению к формуле
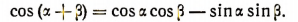
4. На четвертом этапе докажем, что рассматриваемые нами две формулы справедливы для любых положительных значений 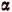 и
и 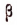 .
.
Пусть 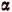 и
и 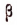 —любые положительные числа. Тогда найдутся такие целые числа m и n, что
—любые положительные числа. Тогда найдутся такие целые числа m и n, что 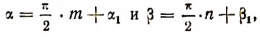 где будет
где будет 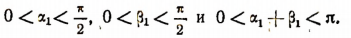
По доказанному ранее наши формулы справедливы для 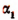 и
и 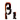 . По доказанному же в предыдущем этапе они будут оставаться справедливыми, если к
. По доказанному же в предыдущем этапе они будут оставаться справедливыми, если к 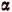 прибавим последовательно m раз, а к
прибавим последовательно m раз, а к 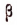 n раз по
n раз по 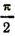 . Следовательно, наши формулы останутся в силе и для произвольных положительных чисел
. Следовательно, наши формулы останутся в силе и для произвольных положительных чисел 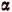 и
и 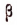 .
.
5. Наконец, докажем, что наши формулы справедливы и для любых отрицательных чисел 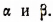
Пусть 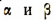 — любые отрицательные числа. Тогда найдутся такие целые числа m и n, что суммы
— любые отрицательные числа. Тогда найдутся такие целые числа m и n, что суммы 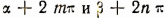 окажутся числами положительными, которые обозначим соответственно через
окажутся числами положительными, которые обозначим соответственно через 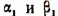 .
.
Для положительных чисел 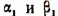 по уже доказанному наши формулы
по уже доказанному наши формулы
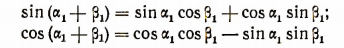
справедливы.
В эти формулы подставим 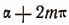 вместо
вместо 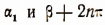 вместо
вместо 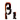 . Тогда получим:
. Тогда получим:
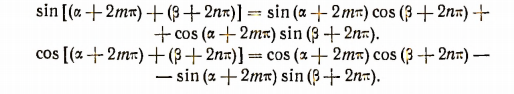
Отсюда вследствие периодичности тригонометрических функцгй получим:
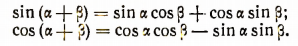
Таким образом, справедливость формул доказана и для отрицательных значений 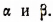
В тех случаях, когда 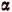 или
или 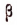 равны
равны 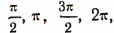 справедливость наших формул можно доказать непосредственной проверкой.
справедливость наших формул можно доказать непосредственной проверкой.
Итак, доказано, что наши две формулы справедливы при любых значениях 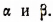 Этим и доказана общность каждой из этих формул.
Этим и доказана общность каждой из этих формул.
Вывод остальных формул сложения. Опираясь на то, что формулы
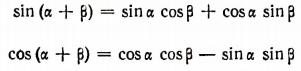
верны при любых значениях 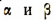 , можно все остальные формулы сложения вывести очень кратким путем.
, можно все остальные формулы сложения вывести очень кратким путем.
Действительно, рассматривая разность  как сумму
как сумму 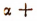
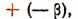 получим:
получим:
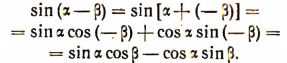
Далее,
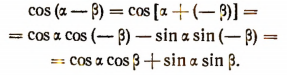
Наконец,
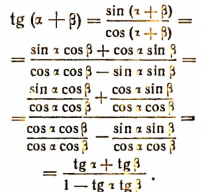
Аналогично получим, что
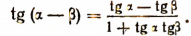
Формулы сложения позволяют находить тригонометрическую функцию суммы или разности двух углов через тригонометрические функции самих этих углов.
Например,
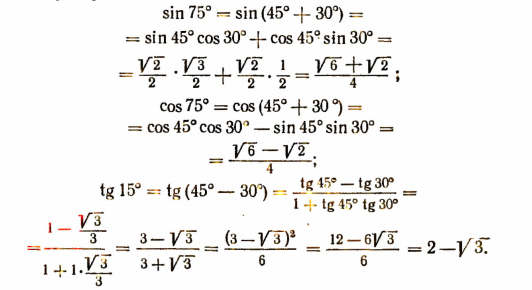
Примеры:
1. Доказать тождество
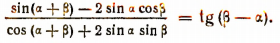
Доказательство:
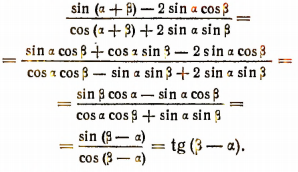
2. Доказать тождество
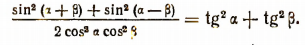
Доказательство:
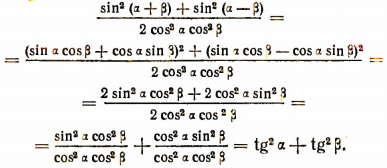
3. Доказать тождество
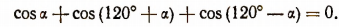
Доказательство:
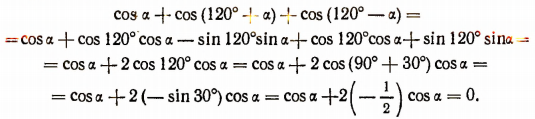
Формулы умножения (пятая группа)
Основными формулами умножения являются следующие:
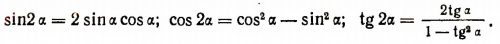
Первая из этих формул читается так: синус двойного угла равен удвоенному синусу данного угла, умноженному на косинус того же угла.
Полезно эту формулу читать и так: синус любого угла равен удвоенному синусу половины этого угла, умноженному на косинус также половины этого угла.
Например,
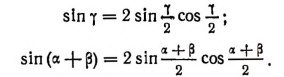
Соответствующим образом читаются и формулы:
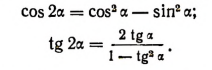
Вывод основных формул умножения.
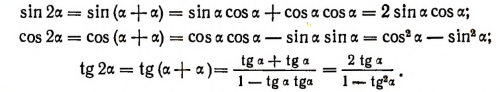
Из основных формул умножения вытекают и такие формулы:
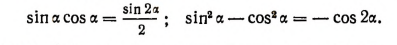
Основные формулы умножения позволяют находить значения тригонометрических функций удвоенного угла по данному значению какой-либо тригонометрической функции самого угла.
Например, если 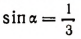
и
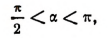
то
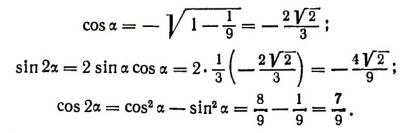
Последовательное применение формул сложения позволяет выражать тригонометрические функции углов Зх, 4х, 5х и т. д. через тригонометрические функции угла х.
Примеры:
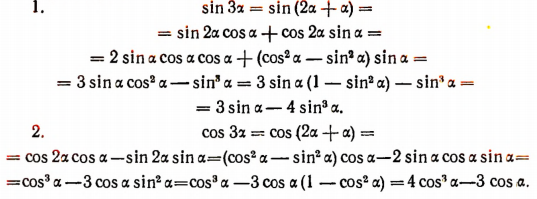
По значениям тригонометрических функций, например 1°, можно при помощи формул сложения найти значения тригонометрических функций углов, содержащих любое целое число градусов.
3. Доказать тождество
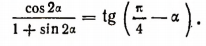
Доказательство:
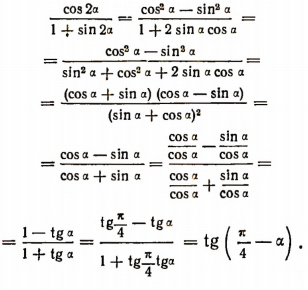
Формулы деления (шестая группа)
Основными формулами деления являются следующие:
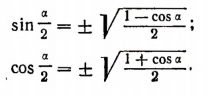
Складывая и вычитая, получим соответственно:
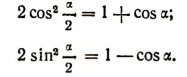
Отсюда легко получаются написанные выше две формулы деления.
Формулы деления позволяют находить значение тригонометрической функции половинного угла по данному значению функции самого угла.
Например, если 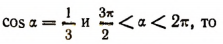
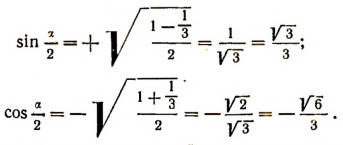
Выведем еще формулы и для 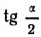 :
:
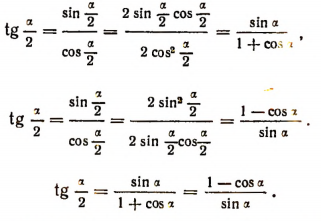
Полезно знать формулы для 1+ cos a и 1—cos a. Складывая и вычитая почленно равенства
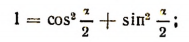
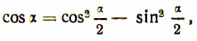
получим соответственно:
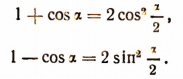
Полезность этих двух последних формул заключается, в частности, в том, что они преобразовывают выражения 1 + cos а и 1 — cos а к виду, удобному для логарифмирования. Этими формулами приходится очень часто пользоваться.
Формулы понижения степени для 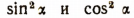 позволяют вторые степени sin а и cos а выражать через первую степень cos 2а.
позволяют вторые степени sin а и cos а выражать через первую степень cos 2а.
Действительно, складывая и вычитая почленно равенства
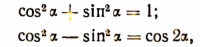
получим соответственно:
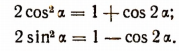
Отсюда
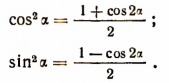
Формулы, выражающие тригонометрические функции угла через тангенс половинного угла (седьмая группа)
Легко понять следующие последовательные преобразования
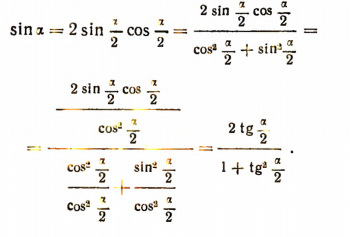
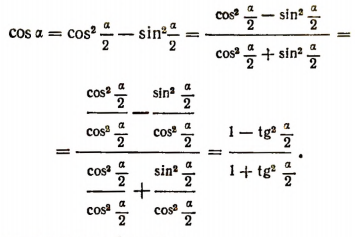
Итак, мы получили две формулы:
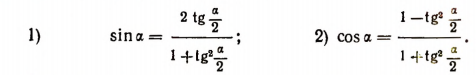
Отсюда сразу вытекает еще и следующая формула:
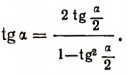
Рассматривая эти формулы, легко заметить, что все тригонометрические функции угла я выражаются через 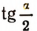 рационально, т. е. с помощью только одних четырех действий. (Вспомним, что, например, sin a выражается через tg а иррационально:
рационально, т. е. с помощью только одних четырех действий. (Вспомним, что, например, sin a выражается через tg а иррационально:
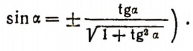
Формулы преобразования суммы или разности тригонометрических функций в произведение (восьмая группа)
Основными формулами преобразования суммы и разности тригонометрических функций являются следующие:
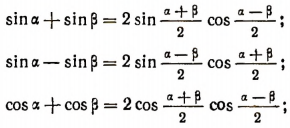
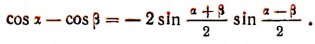
Первая из этих формул читается так: сумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус их полуразности.
Соответствующим образом читаются и остальные формулы.
Вывод этих формул.
Складывая и вычитая почленно известные нам равенства
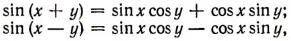
получим соответственно:
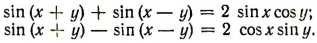
Положим, 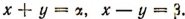
Тогда 
При этих обозначениях получим:
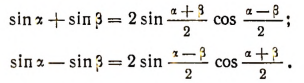
Складывая и вычитая почленно равенства
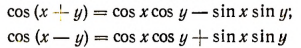
и изменяя обозначения, получим:
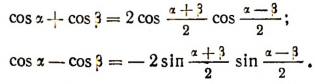
Выведенные формулы справедливы при любых значениях 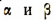 , так как, каковы бы ни были числа
, так как, каковы бы ни были числа 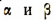 , можно подобрать такие х и у, чтобы соблюдались соотношения
, можно подобрать такие х и у, чтобы соблюдались соотношения
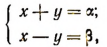
в чем легко убедиться, разрешив эту систему относительно х и у.
Сумма и разность тангенсов
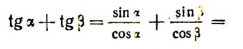
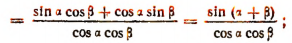
Аналогично
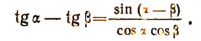
Формулы преобразования произведений тригонометрических функций (девятая группа)
Такими формулами являются:
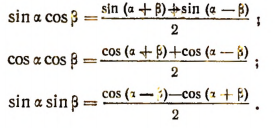
Вывод. Складывая почленно равенства
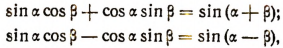
получим:
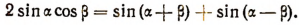
Отсюда
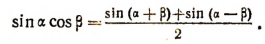
Складывая и вычитая почленно равенства
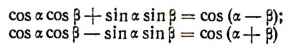
и деля полученные результаты на 2, получим соответственно
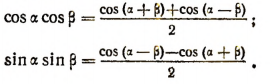
Примеры:
1. Зная, что 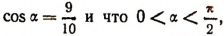 найти
найти 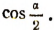
Пользуясь формулой 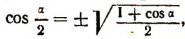 получим:
получим:
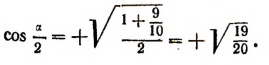
2. Зная, что 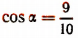 и что
и что 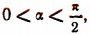 найти
найти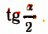
Пользуясь формулой 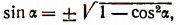 найдем, что
найдем, что
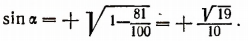
Пользуясь формулой 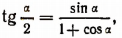 найдем, что
найдем, что
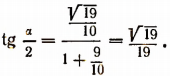
3. Преобразовать к виду, удобному для логарифмирования, выражение 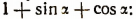
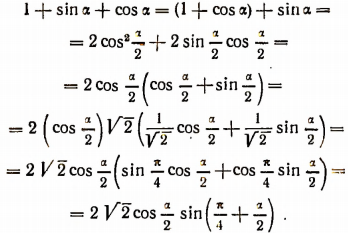
4. Преобразовать к виду, удобному для логарифмирования, выражение
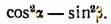
Применяя формулы понижения степени, получим:
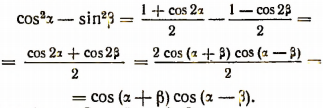
5. Зная, что tg a = 3, найти sin 2a.
Полагая в формуле 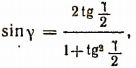 что
что 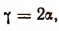 получим:
получим:
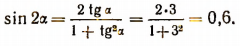
6. Доказать тождество 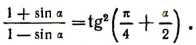
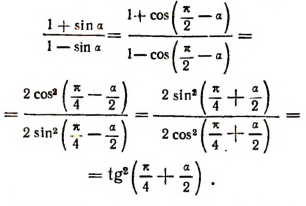
7. Разность 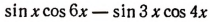 преобразовать в произведение.
преобразовать в произведение.
Пользуясь формулой 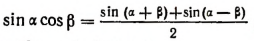 , получим:
, получим:
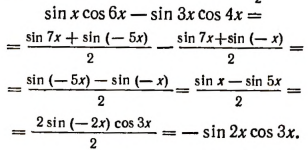
Примеры на доказательство условных тождеств.
1. Доказать, что если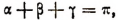 то
то 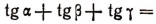
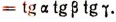
Доказательство:
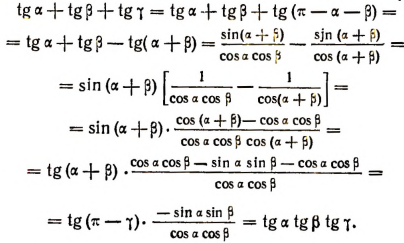
Другой способ доказательства.
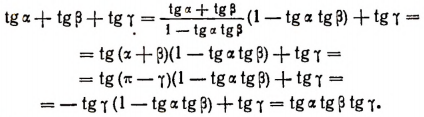
2. Доказать, что если 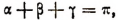 то
то
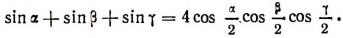
Доказательство:
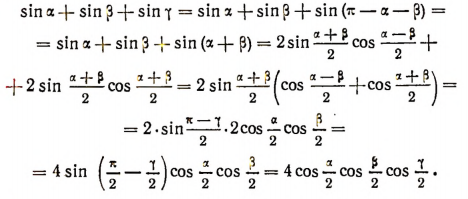
Примеры на преобразование выражений к виду, удобному для логарифмирования, путем введения вспомогательного угла.
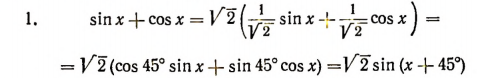
(здесь вспомогательным углом служит угол 45°).
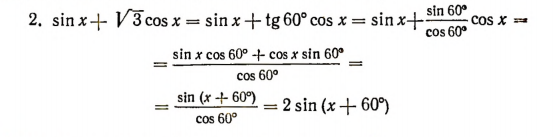
(здесь вспомогательным углом служит угол 60°).
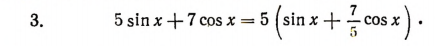
Найдем такой вспомогательный угол 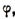 чтобы
чтобы 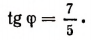
Теперь получим:
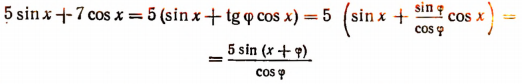
(вспомогательный угол 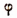 равен приближенно 54°30′).
равен приближенно 54°30′).
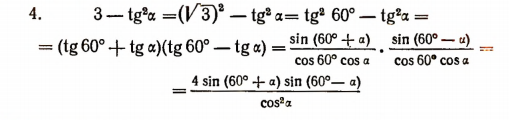
(здесь вспомогательным углом служит угол 60°).
6. Доказать тождество 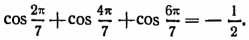
Доказательство:
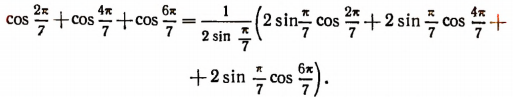
Воспользуемся формулой 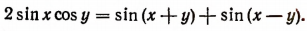
Теперь получим:
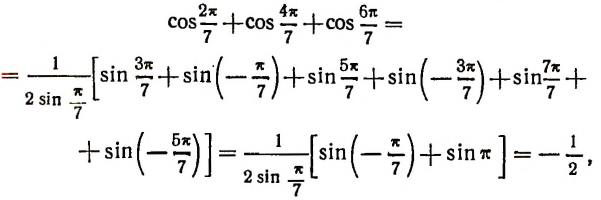
что и требовалось доказать.
6. Доказать тождество 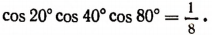
Доказательство:
Воспользуемся дважды формулой 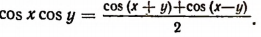 Тогда
Тогда
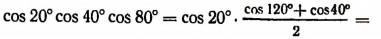
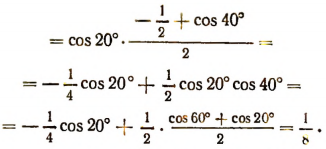
7. Доказать тождество 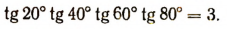
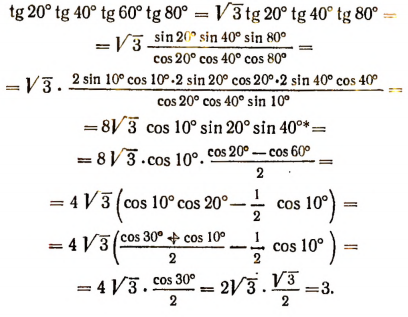
Периодичность тригонометрических функций и их графики
Периодичность тригонометрических функций
Мы знаем, что при всяком значении х
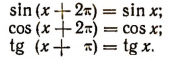
Это свойство тригонометрических функций характеризует их периодичность.
Дадим общее определение понятию периодичности функции.
Определение:
Функция называется периодической, если существует число, отличное от нуля, прибавление которого к произвольному значению ее аргумента не меняет значения функции. Наименьшее положительное число, прибавление которого к любому значению аргумента не меняет значения функции, называется периодом функции.
Теорема:
Период функций sin х и cos x равен 2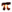 , а период функций tg х равен
, а период функций tg х равен 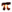 .
.
Доказательство:
Нам известно, что 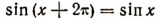 при всяком значении х.
при всяком значении х.
Пусть h есть какое угодно положительное число, меньшее, чем 2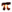 . Посмотрим, возможно ли равенство
. Посмотрим, возможно ли равенство 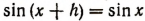 при всяком значении x.
при всяком значении x.
Чтобы равенство
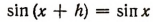
было справедливо при x = 0, h должно равняться только числу 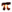 , так как по условию 0 < h < 2
, так как по условию 0 < h < 2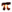 . Но если взять h =
. Но если взять h = 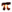 , то равенство
, то равенство
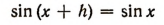
уже будет неверным (например, при 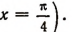
Следовательно, никакое положительное число, меньшее 2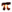 , не может быть периодом функции sin x. Значит, периодом функции x является именно число 2
, не может быть периодом функции sin x. Значит, периодом функции x является именно число 2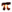 .
.
Таким же методом можно доказать, что периодом cos x является 2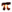 , а периодом tg x является число
, а периодом tg x является число 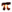 .
.
Графики тригонометрических функций
А. График функции y = sin х.
При возрастании х от 0 до 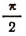 у возрастает от 0 до 1.
у возрастает от 0 до 1.
При возрастании х от 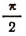 до
до 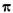 у убывает от 1 до 0.
у убывает от 1 до 0.
При возрастании у от 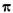 до
до 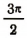 у убывает от 0 до — 1.
у убывает от 0 до — 1.
При возрастании х от 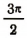 до 2
до 2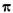 у возрастает от — 1 до 0.
у возрастает от — 1 до 0.
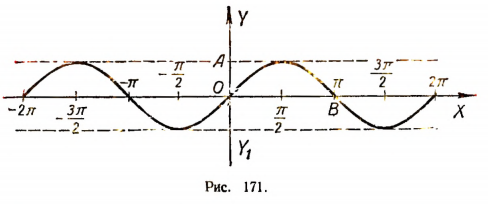
График имеет вид, изображенный на рисунке 171. Одна волна кривой, построенная на участке от 0 до 2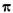 будет вследствие периодичности функции sin х повторяться бесконечное множество раз как слева, так и справа.
будет вследствие периодичности функции sin х повторяться бесконечное множество раз как слева, так и справа.
Отрезок OA принят за единицу длины. Отрезок ОВ равен 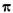 единицам длины.
единицам длины.
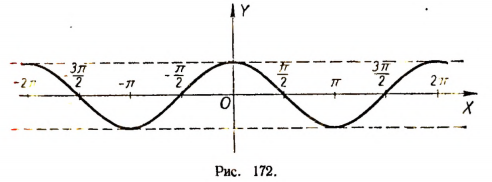
Б. График функции у = cos x (рис. 172).
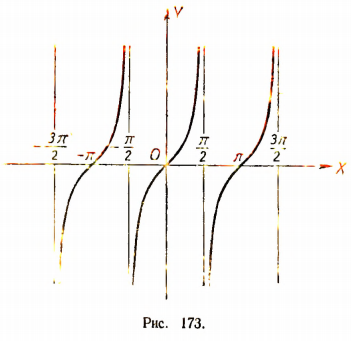
В. График функции 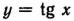 (рис. 173).
(рис. 173).
Этот график состоит из бесконечного множества одинаковых отдельных бесконечных ветвей, расположенных, как указано на рисунке 173.
Тригонометрические уравнения
Основные определения и понятия:
Определение:
Тригонометрическим уравнением называется уравнение, содержащее неизвестную величину только под знаком тригонометрических функций. Например, уравнения
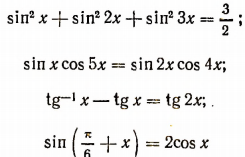
суть тригонометрические.
Уравнение же, например, х — sin х — cos х = 0,2 не является чисто тригонометрическим, так как неизвестное х содержится в этом уравнении не только под знаками тригонометрических функций. Такие уравнения будем называть смешанными тригонометрическими.
Корнем или решением тригонометрического уравнения (так же, как и всякого другого уравнения) называется такое значение неизвестного, которое удовлетворяет уравнению.
Например, числа 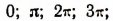 и т. д. или
и т. д. или 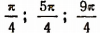 и т. д. являются корнями или решениями уравнения
и т. д. являются корнями или решениями уравнения 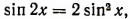 а число, скажем,
а число, скажем, 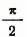 корнем этого уравнения не будет.
корнем этого уравнения не будет.
Решить тригонометрическое уравнение — значит найти все его корни или убедиться в отсутствии таковых.
Обычно тригонометрическое уравнение имеет бесконечное множество корней. (В противоположность этому алгебраическое уравнение с одним неизвестным может иметь лишь конечное число корней.) Но встречаются и такие уравнения, которые не имеют ни одного действительного корня.
Уравнение sin 2х = 1 имеет бесконечное множество корней, а именно: 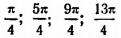 и т. д., а уравнение sin 2х = 2 не имеет ни одного действительного корня.
и т. д., а уравнение sin 2х = 2 не имеет ни одного действительного корня.
Простейшие тригонометрические уравнения и их общие решения
Простейшими тригонометрическими уравнениями называются следующие:
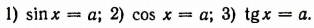
А. Решение уравнения sin х = а
Если 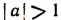 , то уравнение sin х = а не имеет ни одного действительного решения, так как синус никакого действительного числа не может оказаться числом, абсолютная величина которого больше единицы (sin х изменяется лишь в границах от — 1 до +1). Пусть
, то уравнение sin х = а не имеет ни одного действительного решения, так как синус никакого действительного числа не может оказаться числом, абсолютная величина которого больше единицы (sin х изменяется лишь в границах от — 1 до +1). Пусть 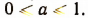
Возьмем тригонометрический круг с радиусом, равным 1 (рис. 174). Отложим на ОВ от точки 0 отрезок OQ, равный а, и через точку Q проведем прямую, параллельную 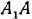 , до пересечения с окружностью в точках
, до пересечения с окружностью в точках 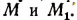
Пусть острый положительный угол 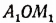 содержит
содержит 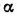 радианов. . Тогда тупой угол
радианов. . Тогда тупой угол 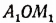 будет содержать
будет содержать  радианов.
радианов.
Числа 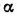 и
и  будут корнями уравнения sin х = а. Но корнями уравнения sin х = а будут в силу периодичности не только числа
будут корнями уравнения sin х = а. Но корнями уравнения sin х = а будут в силу периодичности не только числа 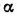 и
и  , но и все числа, определяемые формулами:
, но и все числа, определяемые формулами:
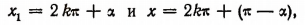
где k — любое целое число.
Перепишем эти две формулы так:
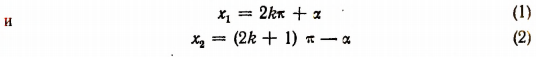
и назовем 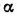 главным решением уравнения sin х = а. Тогда первую формулу можно прочитать так: произведение числа
главным решением уравнения sin х = а. Тогда первую формулу можно прочитать так: произведение числа 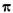 на любое четное число плюс главное решение
на любое четное число плюс главное решение 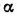 будет решением уравнения
будет решением уравнения
sin х = а.
Вторую же формулу можно прочитать так: произведение числа 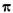 на любое нечетное число минус главное решение
на любое нечетное число минус главное решение 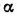 будет решением уравнения sin х = а.
будет решением уравнения sin х = а.
Вместо этих двух формул можно написать одну:
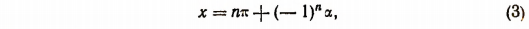
где n — целое число.
Эта одна последняя формула содержит в себе как все ранения, содержащиеся в формуле 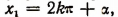 так и все решения, содержащиеся в формуле
так и все решения, содержащиеся в формуле 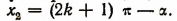
Из формулы (3) при четных значениях n получается формула (1), а при нечетных — формула (2). Выражение 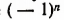 при четном значении n дает единицу, а при нечетном — минус единицу.
при четном значении n дает единицу, а при нечетном — минус единицу.
Формула (3) называется общим решением уравнения sin x = а.
Давая в этой формуле букве n произвольные целые значения, можно получить сколько угодно частных решений уравнения sin x = а.
Формула (3) остается в силе и в том случае, когда а удовлетворяет условию — 1 < а < 0. Только в этом случае главное решение будет отрицательным числом в границах от 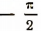 до 0. Убедиться в этом можно с помощью таких же рассуждений, которые были изложены для случая 0 < а < 1.
до 0. Убедиться в этом можно с помощью таких же рассуждений, которые были изложены для случая 0 < а < 1.
Б. Решение уравнения cos x = а
Пусть 0 < а < 1. Возьмем тригонометрический круг с радиусом 1 и отложим на OA от точки О отрезок ОР, равный а (рис. 175).
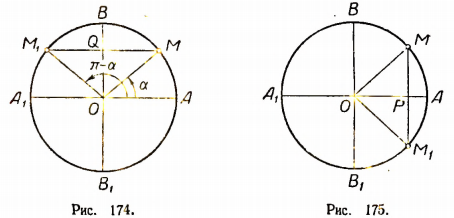
Через точку Р проведем прямую, параллельную 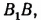 до пересечения с окружностью в точках
до пересечения с окружностью в точках 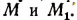 . Пусть положительный острый угол АОМ содержит х радианов. Тогда угол
. Пусть положительный острый угол АОМ содержит х радианов. Тогда угол 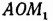 будет содержать —
будет содержать — 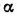 радианов.
радианов.
Общим решением уравнения cos x = а будет 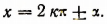
Если — 1 < а < 0, то 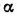 будет числом радианов, содержащихся в угле, оканчивающимся в четверти II.
будет числом радианов, содержащихся в угле, оканчивающимся в четверти II.
В. Решение уравнения tg x = a
Уравнение tg x = a имеет решения при всяком значении а. Проведя рассуждения, аналогичные предыдущим, получим общее решение
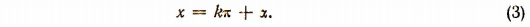
Если а>0, то за 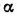 мoжно брать число радианов соответствующего угла, оканчивающегося в четверти I, а если a < 0, то угла, оканчивающегося в четверти IV.
мoжно брать число радианов соответствующего угла, оканчивающегося в четверти I, а если a < 0, то угла, оканчивающегося в четверти IV.
Примеры:
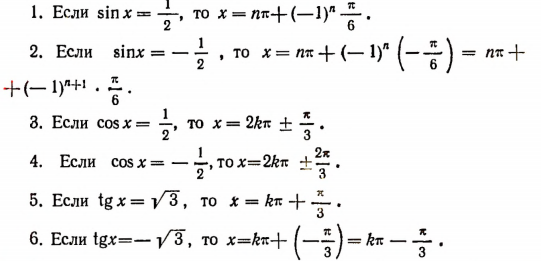
3. Решение уравнений вида 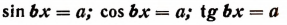
1. Решить уравнение 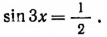
Обозначив 3x буквой u, получим:
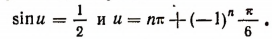
Отсюда
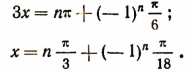
2. Решить уравнение 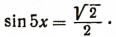
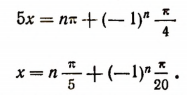
В градусном измерении ответ запишется так:
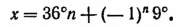
3. Решить уравнение 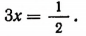
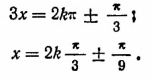
4. Решить уравнение tg 5x = 1.
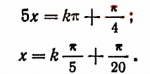
Более сложные тригонометрические уравнения
Уравнение 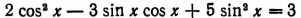 содержит различные тригонометрические функции от одной и той же неизвестной величины х.
содержит различные тригонометрические функции от одной и той же неизвестной величины х.
В уравнение 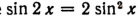 дважды входит одна и та же функция синус, но величины, стоящие под знаками синусов, различны.
дважды входит одна и та же функция синус, но величины, стоящие под знаками синусов, различны.
В уравнение же 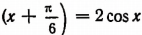 входят и различные функции, и различные выражения, стоящие под их знаками.
входят и различные функции, и различные выражения, стоящие под их знаками.
Решение более или менее сложных тригонометрических уравнений, подобных приведенным выше, сводится обычно к нахождению значения одной какой-нибудь тригонометрической функции от выражения, содержащего неизвестное.
Ознакомимся с приемами решения тригонометрических уравнений на примерах.
Пусть дано уравнение 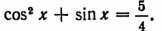
Заменив 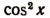 выражением
выражением 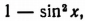 мы приходим к квадратному уравнению относительно sin x:
мы приходим к квадратному уравнению относительно sin x:
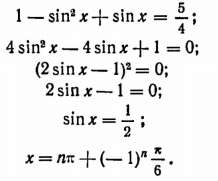
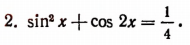
Заменив 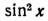 выражением
выражением 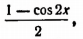 мы приходим к уравнению первой степени относительно cos 2x:
мы приходим к уравнению первой степени относительно cos 2x:
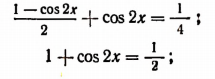
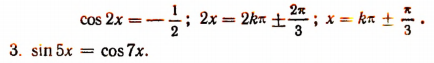
Заменяя cos 7x выражением 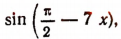 мы преобразовываем данное уравнение к такому уравнению, в котором правая часть есть нуль, а левая — произведение выражений, содержащих неизвестную величину x:
мы преобразовываем данное уравнение к такому уравнению, в котором правая часть есть нуль, а левая — произведение выражений, содержащих неизвестную величину x:
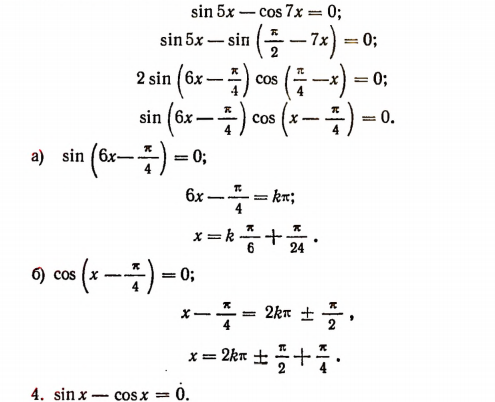
Это уравнение является однородным первого измерения относительно sin x и cos x. В силу этого уравнения 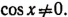 Если бы cos x = 0, то оказалось бы, что sin x = 0. Но sin x и cos x не могут быть нулями одновременно.
Если бы cos x = 0, то оказалось бы, что sin x = 0. Но sin x и cos x не могут быть нулями одновременно.
Поэтому мы можем все члены уравнения разделить на cos x:
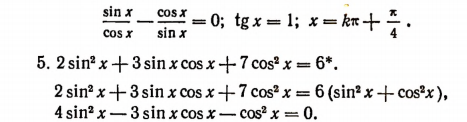
В силу этого уравнения 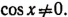 Поэтому мы можем все члены уравнения разделить на
Поэтому мы можем все члены уравнения разделить на 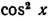
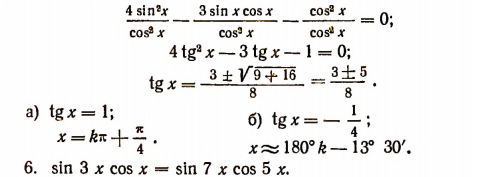
Воспользуемся формулой
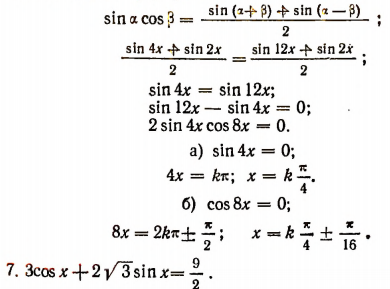
Воспользуемся формулами, выражающими sin x и cos x через 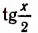 (см. § 4). Благодаря этому задача сведется к решению квадратного уравнения относительно
(см. § 4). Благодаря этому задача сведется к решению квадратного уравнения относительно 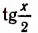 :
:
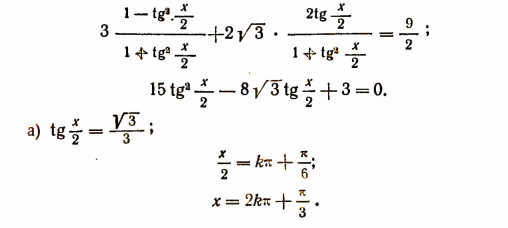
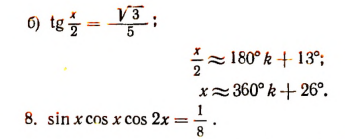
Воспользуемся формулой 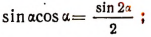
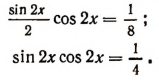
Еще раз обратившись к формуле 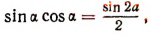 получим:
получим:
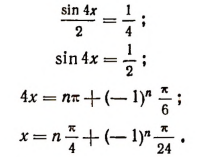
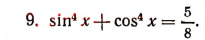 К левой части уравнения прибавим два взаимно уничтожающихся члена
К левой части уравнения прибавим два взаимно уничтожающихся члена 
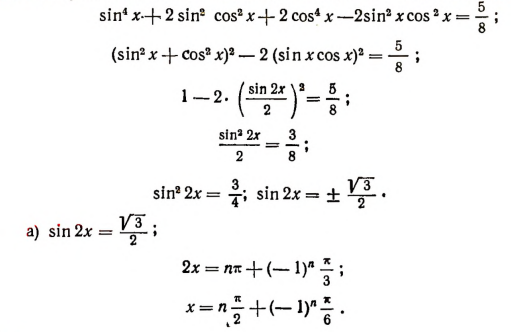
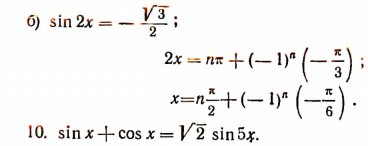
Разделим левую и правую части уравнения на 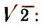
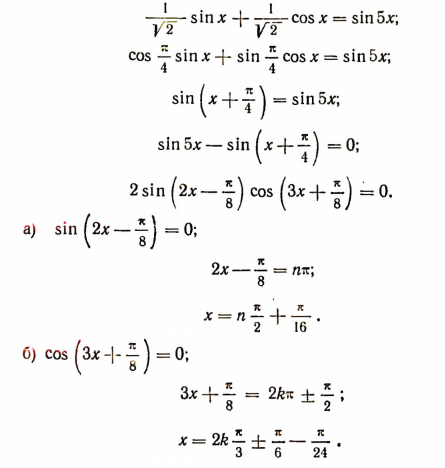
Условия равенства одноименных тригонометрических функций
А. Условия равенства синусов
Синусы двух чисел х и у равны друг другу (sin х = sin у) тогда и только тогда, когда либо разность х — у равна произведению числа 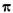 на четное число, либо когда сумма х + у равна произведению числа
на четное число, либо когда сумма х + у равна произведению числа 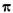 на нечетное число.
на нечетное число.
Доказательство:
Равенства
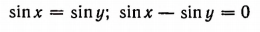
и

равносильны. Но последнее равенство справедливо
либо при 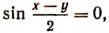 либо при
либо при 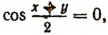 т. е. либо при
т. е. либо при 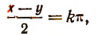 либо при
либо при 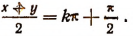
Отсюда следует, что равенство sin х = sin у будет справедливо тогда и только тогда, когда, либо 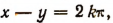 либо х + у =
либо х + у = 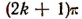 , где k — любое целое число.
, где k — любое целое число.
Б. Условия равенства косинусов
Косинусы двух чисел х и у равны между собой (cos х = cos у) тогда и только тогда, когда либо сумма х + у, либо разность х— у равна произведению числа я на четное число.
Доказательство:
Равенства
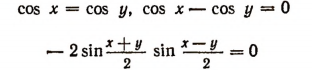
равносильны.
Но последнее равенство справедливо либо при 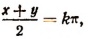 либо при
либо при 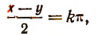 т. е. либо при
т. е. либо при 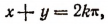 либо при
либо при 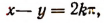 где k-любое целое число.
где k-любое целое число.
В. Условие равенства тангенсов
Тангенсы двух чисел х и у равны друг другу (tg х = tg у) тогда и только тогда, когда разность x — у равна произведению числа 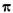 на любое целое число, т. е. когда разность х— у кратна числу
на любое целое число, т. е. когда разность х— у кратна числу 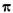 . (Мы здесь исключаем такие значения х и у, при которых tg х и tg у не существуют.)
. (Мы здесь исключаем такие значения х и у, при которых tg х и tg у не существуют.)
Доказательство:
Равенства tg x = tg у,
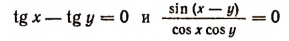
равносильны. Но последнее равенство справедливо лишь тогда, когда sin (x — у) = 0, т. е. лишь тогда, когда 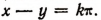
Выведенные условия равенства одноименных тригонометрических функций запоминать нет необходимости. Лучше запомнить способ их вывода.
Применение выведенных условий к решению тригонометрических уравнений
1. Решить уравнение sin ах = sin bх.
Решение:
По условиям равенства синусов
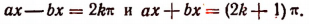
Следовательно, решениями данного уравнения будут:
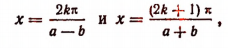
где k—любое целое число.
2. Решить уравнение 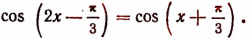
Решение:
По условиям равенства косинусов
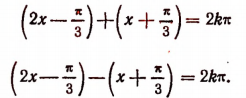
Следовательно, решениями данного уравнения будут:
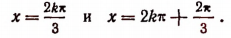
3. Решить уравнение tg ax = tg bx.
Решение:
По условию равенства тангенсов 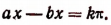 Отсюда
Отсюда
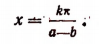
4. Решить уравнение sin 3x = cos 2х.
Решение:
Преобразуем уравнение так, чтобы получить равенство одноименных функций:
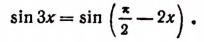
По условиям равенства синусов
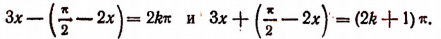
Отсюда
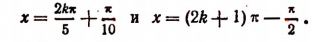
5. Решить уравнение 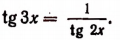
Решение:
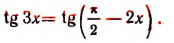
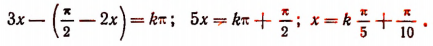
Смешанные тригонометрические уравнения
Смешанными тригонометрическими уравнениями мы называем такие уравнения, в которых неизвестное входит одновременно и под знаком и не под знаком тригонометрической функции. Например, уравнения 5 cos х = х; tg х = х; cos 2 х = 0,4 х; х sin х = 1; х + 2 sin х = 1 суть смешанные тригонометрические уравнения. Корни таких уравнений можно находить, как правило, лишь приближенно. Поясним, как это делается.
Сначала с помощью графического метода можно определить число корней и их первые грубые приближения. Затем, пользуясь таблицей значений тригонометрических функций числового аргумента, можно каждое из найденных грубых приближений путем испытаний уточнять.
Примеры:
1. Решить уравнение cos 2х = 0,4х.
Построим на миллиметровой бумаге графики функций у= cos 2х и
у = 0,4х (рис. 176). Эти графики пересекаются в трех точках 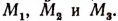 Поэтому уравнение cos 2х = 0,4х имеет три различных корня. Этими корнями будут абсциссы точек
Поэтому уравнение cos 2х = 0,4х имеет три различных корня. Этими корнями будут абсциссы точек 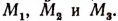
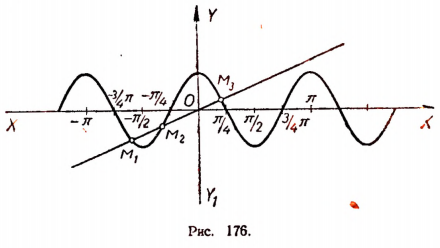
Эти абсциссы, как видно на рисунке 176, близки к числам 0,6; — 0.9 и — 1,9. Последние и являются первыми грубыми приближенными значениями корней.
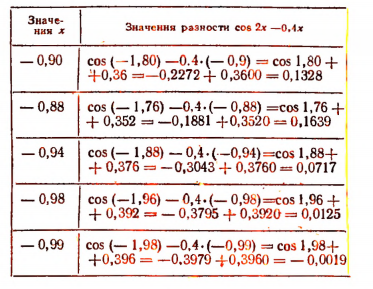
Чтобы уточнить первый корень, найдем значения разности
cos 2х — 0,4х при х = 0,6 и при других значениях, близких к 0,6, пользуясь таблицами.
Уточнение первого корня

Из этой таблицы видно, что значения cos 2х и 0,4х становятся довольно близкими друг другу при х = 0,65.
Число 0,65 мы можем считать уже лучшим приближенным значением первого корня, чем значение 0,6.
Уточнение второго корня
За более точное значение второго корня можно взять число —0,99.
За уточненный третий корень после надлежащих испытаний можем принять число — 1,92.
Если бы нам было необходимо получить корни с еще большей точностью, то мы воспользовались бы более точными таблицами значений тригонометрических функций числового аргумента и совершили бы терпеливо все необходимые испытания.
2. Пусть требуется решить уравнение cos х = х.
Построим графики функций у = cos х и у = х (рис. 177). Эти графики пересекаются лишь в одной точке М. Поэтому уравнение cos х = х имеет лишь один корень. Этим корнем является абсцисса точки М, т. е. длина отрезка ОР. Эта абсцисса, как видно из рисунка, близка к числу 0,7.
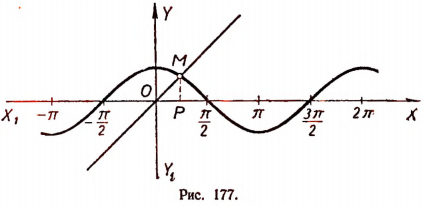
Уточним этот корень путем испытаний.
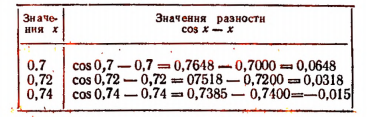
За уточненный корень можно принять число 0,74.
3. Решить уравнение tg х = х.
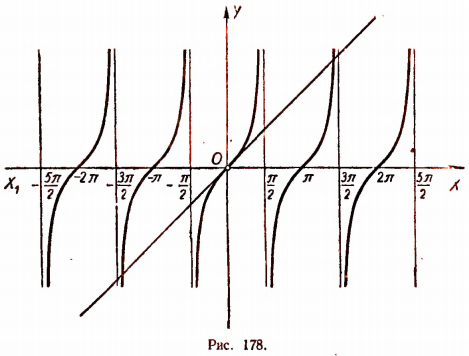
Построим графики функций у = tg x и у = х (рис. 178).
График функции у = tg х состоит из бесконечного множества отдельных бесконечных ветвей. Поэтому прямая у = х. Имеет бесчисленное множество точек пересечения с графиком у = tg х.
Следовательно, уравнение tg х = х имеет бесконечное множество различных корней.
Число нуль является точным корнем этого уравнения, так как tg 0 = 0. Кроме этого нулевого корня, уравнение tg х = х, как это уже было выяснено, имеет бесконечное множество положительных корней и бесконечное множество отрицательных корней. Ограничимся задачей найти только наименьший положительный корень. Из рисунка 178 видно, что этот корень близок к числу 4,5.
Для уточнения этого корня проведем испытания.

За уточненный наименьший положительный корень уравнения
tg х = х можно принять число 4,49.
4. Решить уравнение х sin х — 0,5 = 0.
Перепишем это уравнение в виде 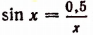 построим графики функций
построим графики функций
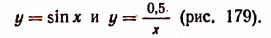
Эти графики пересекаются в бесконечном множестве точек. Поэтому данное уравнение имеет бесконечное множество корней
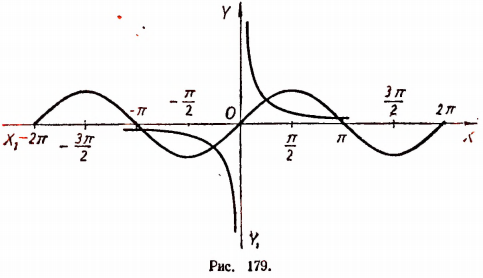
(положительных и отрицательных). Из рисунка 179 видно, что наименьший положительный корень близок к числу 0,7. Путем испытаний можем получить уточненное значение этого корня, равное 0,74.
О косекансе, секансе и котангенсе
В курсах тригонометрии, кроме sin х, cos х и tg х, рассматриваются еще три тригонометрические функции с scs (косеканс х), sec (секанс x), ctg (котангенс x).
Изучать функции csc x, sec x и ctg x нет необходимости. Эти функции являются величинами, обратными sin x, cos x, tg x, а именно:
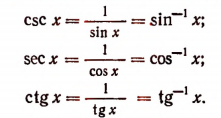
Задачи, в которых фигурируют csc x, sec x, ctg x, можно решать путем замены этих функций их выражениями через sin x, cos x, tg x. Поясним это на примерах.
1. Упростить выражение
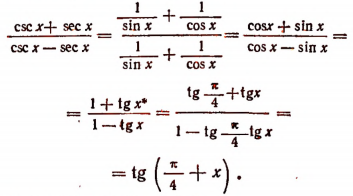
Мы здесь воспользовались формулой
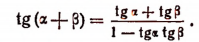
2. Доказать тождество
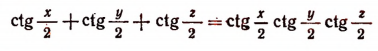
при условии, что
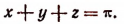
Доказательство:
Из условия  следует, что
следует, что
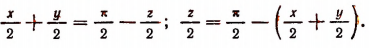
Из того, что
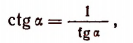
следует, что
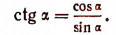
Поэтому

Простое гармоническое колебание
Пусть точка М (рис. 180) движется с постоянной угловой скоростью ч> радианов в секунду по окружности. Тогда проекция точки М на вертикальный диаметр, т. е. точка Р, будет совершать колебательные движения вдоль вертикального диаметра вверх и вниз между точками В и Bv Такое движение точки Р и называется простым гармоническим колебанием.
Чтобы вывести формулу простого гармонического колебания, примем следующие обозначения:
t — время в секундах;
R — радиус окружности; — положение движущейся по окружности точки в начальный момент, т. е. при t = 0 (рис. 181);
— положение движущейся по окружности точки в начальный момент, т. е. при t = 0 (рис. 181);
М — положение движущейся по окружности точки через t секунд;
у — ордината точки Р (у изменяется в границах от — R до + R);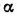 — угол АО
— угол АО в радианах.
в радианах.
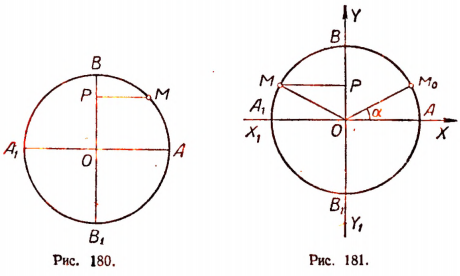
Тогда поворот радиуса-вектора из положения  до положения
до положения 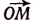 будет равен wt радианам. Поворот же из положения
будет равен wt радианам. Поворот же из положения 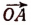 до положения
до положения 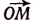 будет равен wt +
будет равен wt + 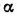 радианам.
радианам.
По определению синуса
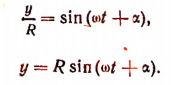
Последнее уравнение и выражает закон простого гармонического колебания. В этом уравнении постоянная R называется амплитудой колебания; постоянная 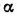 называется начальной фазой колебания, а переменная wt +
называется начальной фазой колебания, а переменная wt + 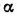 — фазой колеблющейся точки.
— фазой колеблющейся точки.
Время Т, в течение которого точка М совершит один полный оборот по окружности, а точка Р — одно полное колебание, называется периодом гармонического колебания.
Легко понять, что
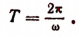
Из данного определения следует, что 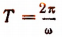 есть период функции
есть период функции
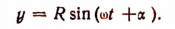
В этом можно убедиться и непосредственно. Действительно,
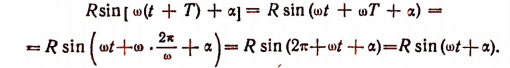
Величина, обратная периоду колебания, т. е.
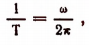
называется частотой колебания.
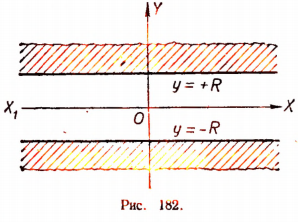
Она показывает, сколько полных колебаний совершает точка Р в единицу времени (в 1 сек.)
В природе протекает много разнообразных процессов колебательного характера, близких к гармоническому колебанию. Однако простое гармоническое колебание обладает еще одной весьма ценной особенностью. Как правило, можно как угодно сложные колебательные движения представлять с любой степенью точности в виде суммы различных простых гармонических колебаний, т. е. сводить анализ сложных процессов движения к анализу простейших.
Разложение сложных колебательных процессов на сумму простых гармонических колебаний является мощным средством исследования разнообразных физических явлений. Подробные сведения обо всем этом излагаются в курсах математического анализа.
График функции 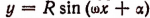 называется синусоидальной кривой. Весь график этой функции располагается в полосе, образованной прямыми
называется синусоидальной кривой. Весь график этой функции располагается в полосе, образованной прямыми 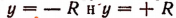 (рис. 182).
(рис. 182).
Чтобы составить представление о графике функции 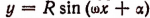 рекомендуется построить последовательно графики следующих более простых функций:
рекомендуется построить последовательно графики следующих более простых функций:

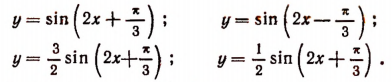
График функции 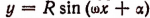 пересекает ось
пересекает ось 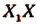 при тех значениях х, при которых
при тех значениях х, при которых 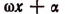 равно
равно 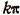 , где k — любое целое число, т. е. при значениях х, определяемых формулой
, где k — любое целое число, т. е. при значениях х, определяемых формулой
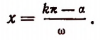
Таким образом, абсциссами точек пересечения с осью 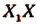 будут числа:
будут числа:
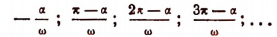
Наибольшее значение R функция 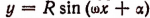 принимает при тех значениях х, при которых
принимает при тех значениях х, при которых
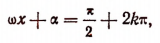
где k — любое целое число, т. е. в тех точках, для которых
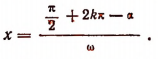
Наименьшее значение R эта функция принимает при таких значениях х, при которых
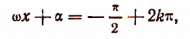
т. е. при
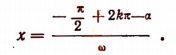
На рисунке 183 изображен сплошной линией график функции 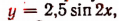 а пунктиром — график функции
а пунктиром — график функции 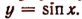
Охарактеризуем функцию у = 2,5 sin 2х и ее график. Период функции равен 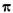 . График этой функции пересекает ось
. График этой функции пересекает ось 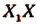 в точках, в которых
в точках, в которых  или
или 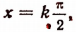 т. е. в точках
т. е. в точках 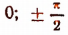
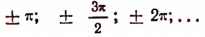
Наибольшее значение 2,5 функция имеет в точках, в которых 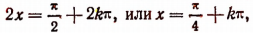 т. е. в точках
т. е. в точках 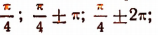
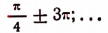
Наименьшее значение, равное —2,5, она имеет в точках, в которых 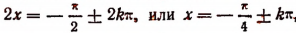 т. е. в точках
т. е. в точках 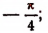
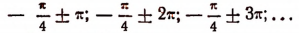
Весь график располагается в полосе, образованной прямыми у = 2,5 и
у = — 2,5. Амплитуда колебания равна 2,5, а начальная фаза равна нулю. На рисунке 184 изображен график функции 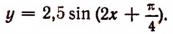
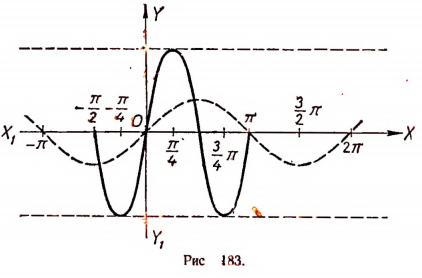
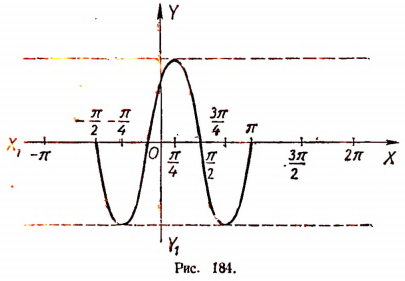
Период функции равен 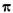 . График пересекает ось
. График пересекает ось 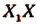 в точках, в которых
в точках, в которых 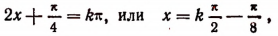
т. е. в точках 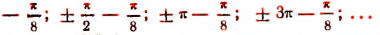
Наибольшее значение 2,5 функция имеет в точках, в которых 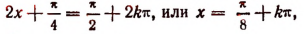 т. е. в точках
т. е. в точках 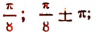
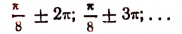
Наименьшее значение, равное —2,5, функция имеет в точках, в которых 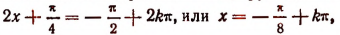
т. е. в точках 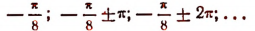
Весь график располагается в полосе, образованной прямыми у = 2,5 и
у = — 2,5.
Амплитуда колебания равна 2,5, а начальная фаза у.
График функции 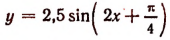 есть не что иное, как график функции у = 2,5 sin 2x, смещенный влево на
есть не что иное, как график функции у = 2,5 sin 2x, смещенный влево на 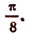
Основные тригонометрические формулы
I группа формул
Соотношения между тригонометрическими функциями одного и того же аргумента.
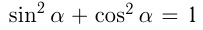 (основное тригонометрическое тождество).
(основное тригонометрическое тождество).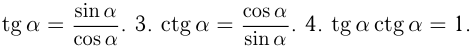
II группа. Формулы сложения
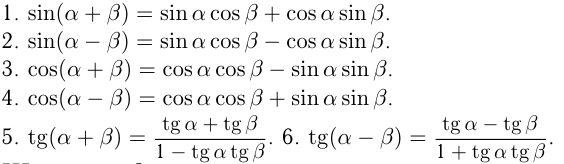
III группа. Формулы кратных аргументов
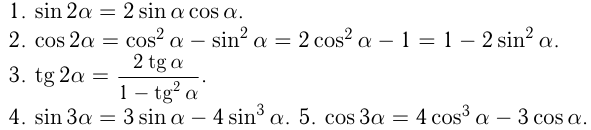
IV группа. Формулы преобразования сумм и разностей
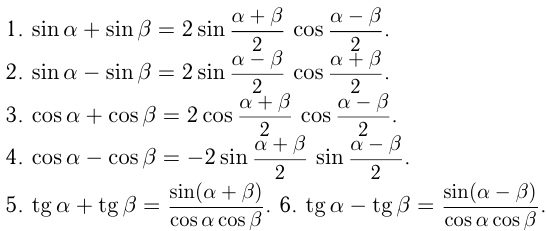
V группа. Формулы преобразования произведений в суммы и разности
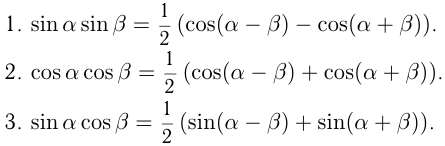
VI группа. Формулы понижения степени
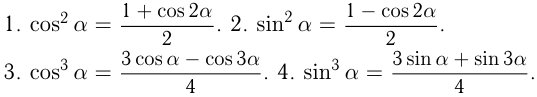
VII группа. Формулы половинного аргумента
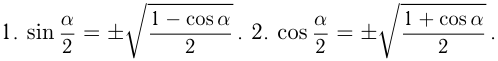
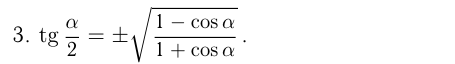
В этих формулах знак выбирается в зависимости от того,в какой четверти находится угол 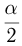 .
.
VIII группа. Выражение тригонометрических функций через тангенс половинного угла
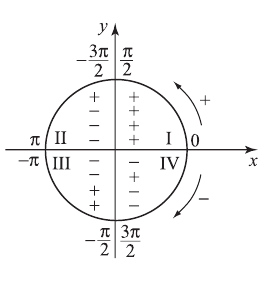
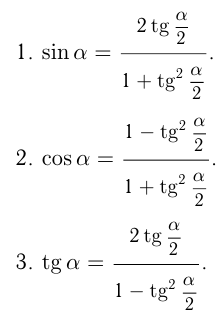
IX группа. Формулы приведения тригонометрических функций для углов
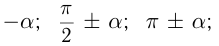
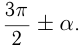
Эти формулы определяются следующими простыми правилами: для 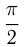 и
и 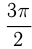 функция меняется на кофункцию, т.е. синус на косинус, котангенс на тангенс и т.д., для
функция меняется на кофункцию, т.е. синус на косинус, котангенс на тангенс и т.д., для 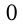 и
и 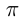 функция не меняется. Знак перед новой функцией ставится в зависимости от того, какой знак имела первая функция в той четверти, куда попадает угол
функция не меняется. Знак перед новой функцией ставится в зависимости от того, какой знак имела первая функция в той четверти, куда попадает угол 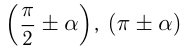 и т.п., если
и т.п., если 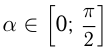 .
.
Например, 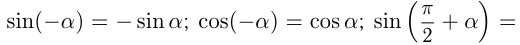
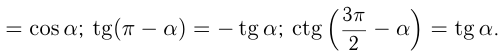
Переход от градусной меры угла к радианной осуществляется по формуле: 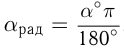
Если 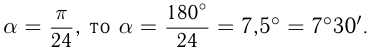
Значения тригонометрических функций основных углов:
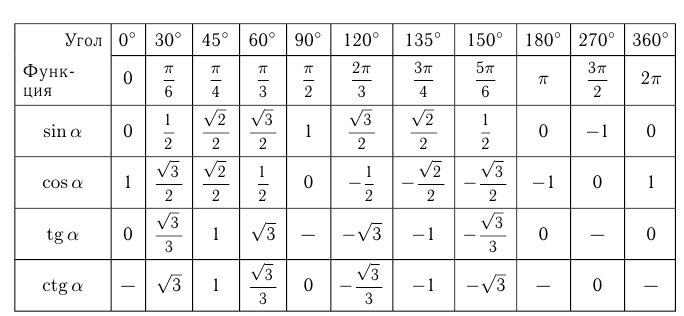
Возможно вам будут полезны эти страницы:
| Доказать рациональность числа задачи с решением |
| Тригонометрия: определение и пример |
| Вычисление значений тригонометрических выражений задачи с решением |
| Что такое уравнение и как его решать |
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

