Оглавление:
Под операциями над векторами понимают операции сложения и вычитания векторов, а также умножение вектора на число.
1). Сложение векторов
Пусть  и
и 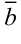 — два произвольных вектора.
— два произвольных вектора.
Сумму векторов можно найти по следующим правилам:
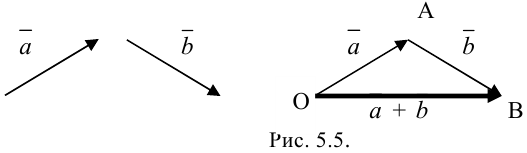
- Правило треугольника
Выберем произвольную точку 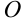 и построим вектор
и построим вектор 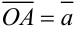 . От точки
. От точки  отложим вектор
отложим вектор 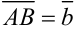 . Вектор
. Вектор 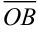 , соединяющий начало первого вектора с концом второго, называется суммой векторов
, соединяющий начало первого вектора с концом второго, называется суммой векторов  и
и 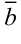 :
: 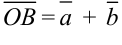 (рис. 5.5).
(рис. 5.5).
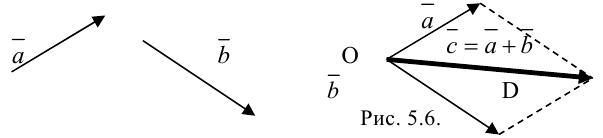
- Правило параллелограмма
Выберем произвольную точку 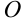 и отложим от нее векторы
и отложим от нее векторы 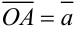 и
и 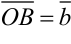 . Достроим фигуру до параллелограмма. Тогда вектор
. Достроим фигуру до параллелограмма. Тогда вектор 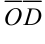 , исходящий из вершины
, исходящий из вершины 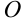 в противоположную вершину
в противоположную вершину 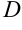 , является суммой векторов
, является суммой векторов  и
и 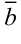 :
: 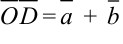 (рис. 5.6.).
(рис. 5.6.).
- Правило многоугольника:
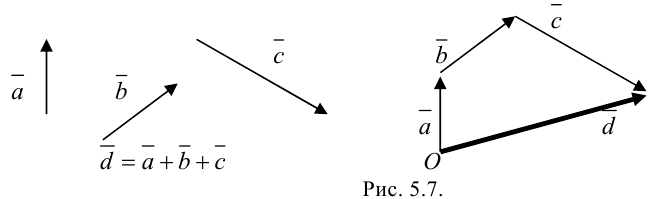
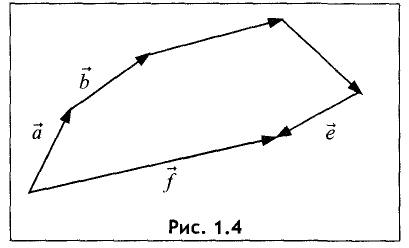
Для нахождения суммы трех и более векторов используют правило многоугольника. Выберем произвольную точку  и построим вектор
и построим вектор 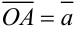 . От конца первого вектора откладываем второй вектор, от конца второго — третий и т.д. Суммой нескольких векторов называется вектор, начало которого совпадает с началом первого вектора, а конец — с концом последнего. Например, на рисунке 5.7. построена сумма трех векторов:
. От конца первого вектора откладываем второй вектор, от конца второго — третий и т.д. Суммой нескольких векторов называется вектор, начало которого совпадает с началом первого вектора, а конец — с концом последнего. Например, на рисунке 5.7. построена сумма трех векторов:
2). Вычитание векторов.
Под разностью векторов  и
и 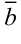 понимается вектор
понимается вектор 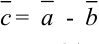 , равный сумме вектора
, равный сумме вектора  и вектора, противоположного вектору
и вектора, противоположного вектору 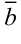 :
: 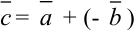 (рис. 5.8.).
(рис. 5.8.).
Отметим, что в параллелограмме, построенном на векторах  и
и 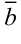 , одна направленная диагональ является суммой векторов
, одна направленная диагональ является суммой векторов  и
и  , а другая — разностью (рис. 5.9.).
, а другая — разностью (рис. 5.9.).

3). Умножение вектора на число.
Произведением вектора  на число
на число  называется вектор
называется вектор 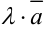 (или
(или 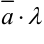 ), который имеет длину
), который имеет длину 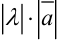 , коллинеарен вектору
, коллинеарен вектору  , имеет направление вектора
, имеет направление вектора  , если
, если 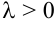 и противоположное направление, если
и противоположное направление, если 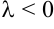 .
.
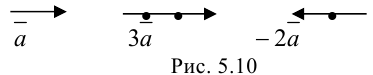
Например, если дан вектор  , то векторы
, то векторы 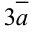 и
и 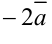 будут иметь вид (рис. 5.10):
будут иметь вид (рис. 5.10):
Линейные операции над векторами обладает следующими свойствами:
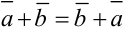 — свойство коммутативности,
— свойство коммутативности,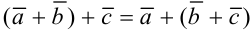 — свойство ассоциативности,
— свойство ассоциативности,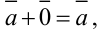
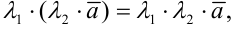
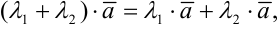
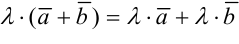 .
.
Эти свойства позволяют проводить преобразования в линейных операциях с вектором так, как это делается в обычной алгебре: слагаемые менять местами, вводить скобки, группировать выносить за скобки как скалярные, так и векторные общие множители.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Критерий Кронеккера-Капелли совместности систем линейных уравнений. |
| Понятие вектора. Виды векторов. |
| Скалярное произведение векторов. |
| Координаты вектора на плоскости и в пространстве. |
Глава I
Операции над векторами
Величины, значения которых могут быть выражены действительными числами, называются скалярами.
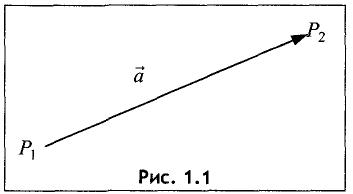
Вектором называется величина, определяемая числовым значением и направлением в пространстве (рис. 1.1).
Обозначается вектор различными способами: 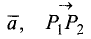 и т.д.
и т.д.
Длина вектора называется его модулем и обозначается 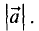
Единичным вектором называется вектор, длина которого
равна единице.
Нулевым вектором называется вектор, модуль которого равен
нулю, а направление не определено.
Два вектора называются равными, если равны их модули и
совпадают направления.
Свободные векторы получаются из данного вектора 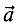 путем
путем
параллельного переноса.
Скользящие векторы получаются из данного вектора 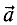 путем
путем
переноса вдоль прямой, на которой лежит вектор 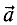 .
.
Связанные векторы — это векторы, которые нельзя переносить,
например, по физическим причинам.
Умножение вектора на скаляр
Если 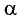 — действительное число и
— действительное число и 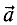 — вектор, то произведение
— вектор, то произведение
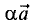 также является вектором с длиной
также является вектором с длиной 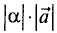 и направлением, совпадающим с направлением вектора
и направлением, совпадающим с направлением вектора 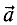 при
при 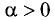 и противоположным при
и противоположным при 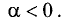 При
При 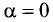 произведение
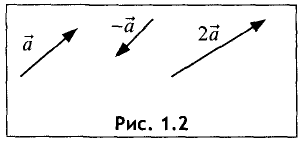
произведение 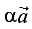 является нулевым вектором. На рис. 1.2 показаны векторы, полученные умножением вектора
является нулевым вектором. На рис. 1.2 показаны векторы, полученные умножением вектора 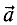 на -1 и 2.
на -1 и 2.
Сложение векторов
Сумма 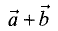 двух векторов
двух векторов 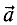 и
и 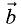 является третьим вектором,
является третьим вектором,
получающимся при параллельном переносе вектора 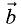 так, что его
так, что его
начало совпадает с концом вектора 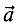 , начало суммарного вектора
, начало суммарного вектора
совпадает с началом вектора 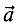 , а конец суммарного вектора
, а конец суммарного вектора
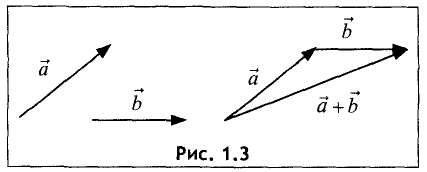
совпадает с концом вектора 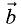 (правило треугольника). На рис. 1.3
(правило треугольника). На рис. 1.3
приведен пример сложения двух векторов.
Сумма нескольких векторов 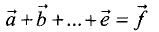 является некоторым
является некоторым
вектором 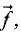 который замыкает ломаную, состоящую из
который замыкает ломаную, состоящую из 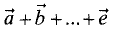 (рис. 1.4).
(рис. 1.4).
Разность векторов 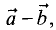 представленная на рис. 1.5 рассматривается как сумма векторов
представленная на рис. 1.5 рассматривается как сумма векторов 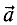 и
и 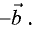
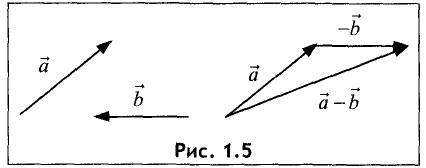
Справедливы равенства:
1. 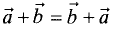 — переместительный закон.
— переместительный закон.
2.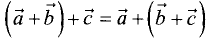 — сочетательный закон.
— сочетательный закон.
3.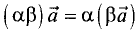 — сочетательный закон.
— сочетательный закон.
4.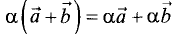 — первый распределительный закон.
— первый распределительный закон.
5.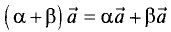 — второй распределительный закон.
— второй распределительный закон.
6.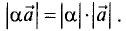
Линейная комбинация векторов
Линейной комбинацией векторов 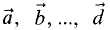 с действительными
с действительными
коэффициентами 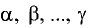 называют вектор
называют вектор 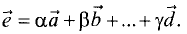
Коллинеарными называют два вектора 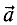 и
и 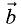 , линейная
, линейная
комбинация которых с некоторыми действительными числами 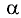 и
и 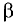 принимает вид
принимает вид 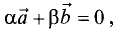 причем
причем  и
и  не равны одновременно нулю. Геометрический смысл: векторы
не равны одновременно нулю. Геометрический смысл: векторы  и
и 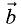 параллельны одной прямой.
параллельны одной прямой.
Компланарными называют три вектора 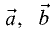 и
и 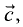 линейная
линейная
комбинация которых с некоторыми действительными числами 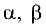 и
и 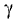 принимает вид
принимает вид 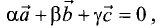 причем
причем 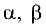 и
и 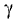 не равны
не равны
одновременно нулю. Геометрический смысл: векторы 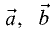 и
и 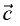
параллельны одной плоскости.
Линейно независимыми векторами на плоскости называются два
вектора, если они не коллинеарные, а в трехмерном пространстве —
три вектора, если они не компланарные.
Два или три ортогональных (перпендикулярных) вектора являются линейно независимыми и образуют двойку или тройку
линейно независимых векторов.
Если три единичных взаимно перпендикулярных вектора
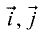 и
и 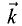 образуют правую тройку векторов, то эти векторы
образуют правую тройку векторов, то эти векторы
являются базой прямоугольной декартовой системы координат
(рис. 1.6).
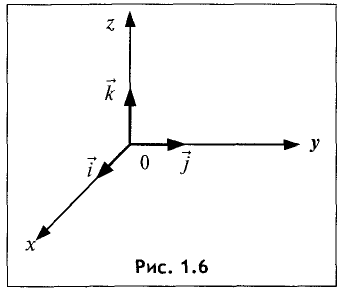
Такие векторы называются ортами координат.
Система координат называется правой потому, что векторы
 и
и  имеют такую же ориентацию, как соответственно
имеют такую же ориентацию, как соответственно
большой, указательный и средний пальцы правой руки. Для
определения правого направления системы координат может быть
использовано правило правого винта: если винт вкручивается в ось Oz со стороны нуля, то отвертка вращается от х к у.
Вектор 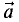 в прямоугольной декартовой системе координат
в прямоугольной декартовой системе координат
записывается в виде
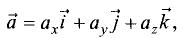
где 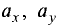 и
и 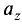 —- прямоугольные декартовы координаты вектора
—- прямоугольные декартовы координаты вектора 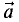
или проекции этого вектора на соответствующие оси.
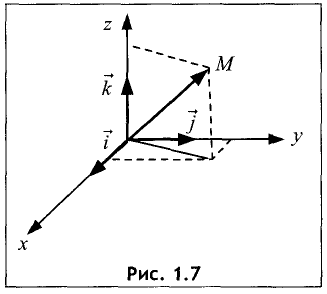
Координаты точки
Дана прямоугольная декартова система координат (рис. 1.7). В этой системе координат каждой точке М однозначно соответствует вектор 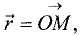 который называется радиусом-вектором точки
который называется радиусом-вектором точки
М. Декартовы координаты вектора 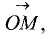 отнесенные к
отнесенные к  и
и  ,
,
называются декартовыми координатами точки М.
Умножение векторов
Скалярное произведение векторов 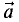 и
и 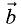 , обозначаемое
, обозначаемое 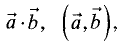
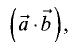 есть скаляр
есть скаляр 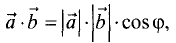 где
где 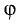 — угол между векторами
— угол между векторами 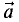 и
и 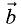 .
.
Пример:
Определить скалярное произведение векторов 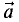 и
и 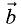
при 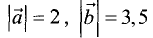 и
и 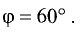
Решение:
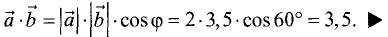
Пример:
Определить скалярное произведение между каждой
из орт  и
и  прямоугольной декартовой системы координат.
прямоугольной декартовой системы координат.
Решение:
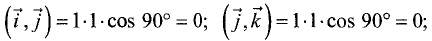
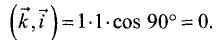 Таким образом, скалярное произведение между каждой из орт
Таким образом, скалярное произведение между каждой из орт 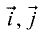 и
и 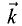 прямоугольной декартовой системы
прямоугольной декартовой системы
координат равно нулю. ►
Пример:
Определить скалярное произведение любой из орт
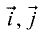 и
и 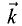 между собой прямоугольной декартовой системы координат.
между собой прямоугольной декартовой системы координат.
Решение:
Для примера рассмотрим орту 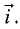 Для остальных орт
Для остальных орт
результат аналогичен. 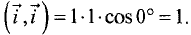 ►
►
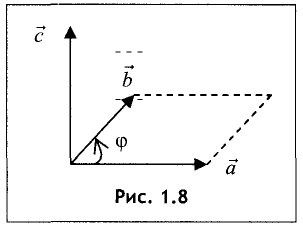
Векторное произведение векторов 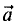 и
и 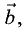 обозначаемое
обозначаемое 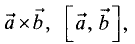
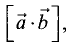 есть вектор
есть вектор 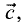 имеющий длину
имеющий длину 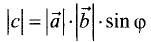 (площадь параллелограмма, построенного на
(площадь параллелограмма, построенного на 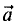 и
и 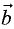 как на сторонах) и направленный перпендикулярно к
как на сторонах) и направленный перпендикулярно к 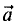 и
и 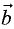 , причем так, что векторы
, причем так, что векторы 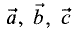 образуют правую тройку
образуют правую тройку
векторов (рис. 1.8).
Пример:
Определить векторное произведение между каждой
из орт 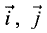 и
и 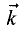 прямоугольной декартовой системы координат.
прямоугольной декартовой системы координат.
Решение:
Для примера рассмотрим векторное произведение
между векторами 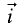 и
и 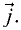 Для остальных сочетаний орт результат
Для остальных сочетаний орт результат
аналогичен, 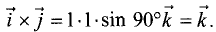 ►
►
Произведения векторов обладают следующими свойствами:
1.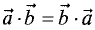 —коммутативность;
—коммутативность;
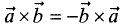 — антикоммутативность.
— антикоммутативность.
2.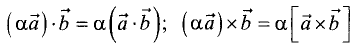 —ассоциативность.
—ассоциативность.
3.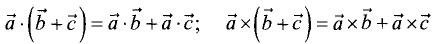 — дистрибутивность.
— дистрибутивность.
4.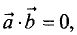 если
если 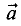 и
и 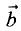 ортогональные;
ортогональные; 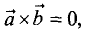 если
если 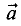 и
и 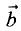
коллинеарные.
5. 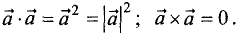
6.В общем случае 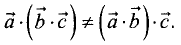
Смешанное произведение 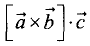 — это скаляр, равный объему
— это скаляр, равный объему
параллелепипеда, построенного на векторах 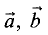 и
и 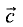 как на ребрах.
как на ребрах.
Пример:
Упростить выражения 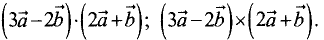
Решение:
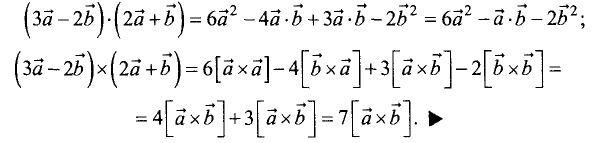
Выражения произведений векторов в прямоугольной декартовой системе координат
Пусть даны векторы:
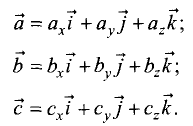
Используя правила умножения векторов, можно показать
справедливость следующих формул:
■ для скалярного произведения
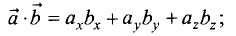
■ для векторного произведения
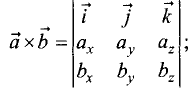
■ для смешанного произведения
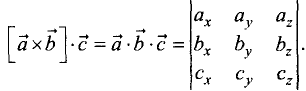
Для векторного и смешанного произведений результаты
представлены в виде определителей.
Определителем (детерминантом) n-го порядка называется число D,
образованное из 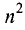 чисел
чисел 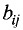 (элементов), расположенных в квадратной таблице из n строк и n столбцов следующим образом:
(элементов), расположенных в квадратной таблице из n строк и n столбцов следующим образом:
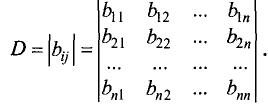
При вычислении определителя 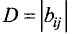 n-го порядка его можно
n-го порядка его можно
разложить на сумму произведений всех элементов какой-либо
строки (или столбца), умноженных на соответствующие им
алгебраические дополнения, по формуле
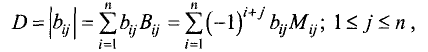
где 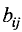 — элемент i-й строки (столбца) j-го столбца (строки);
— элемент i-й строки (столбца) j-го столбца (строки);
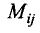 — минор порядка n-1, получающийся из D вычеркиванием i-й строки (столбца) и j-го столбца (строки);
— минор порядка n-1, получающийся из D вычеркиванием i-й строки (столбца) и j-го столбца (строки);
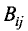 — алгебраическое дополнение.
— алгебраическое дополнение.
Таким образом, определитель 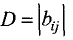 n-го порядка сводится к определителю (n-1)-го порядка, затем к определителю (n-2)-го порядка и т.д.
n-го порядка сводится к определителю (n-1)-го порядка, затем к определителю (n-2)-го порядка и т.д.
Определитель второго порядка вычисляется по формуле
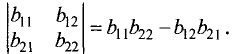
Пример:
Найти скалярное и векторное произведения векторов:
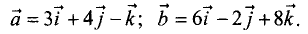
Решение:
Скалярное произведение векторов
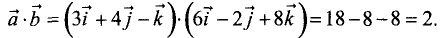
Векторное произведение векторов находим по формуле
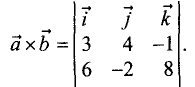
Разложим данный определитель по первой строке и найдем
векторное произведение:
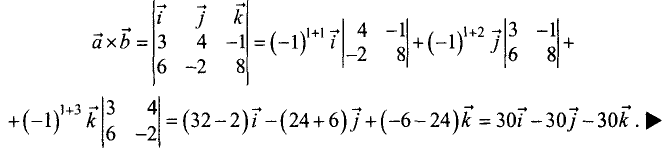
Пример:
Найти смешанное произведение векторов:
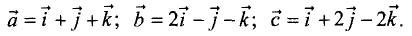
Решение:
Смешанное произведение находим по формуле
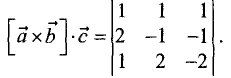
Разложим данный определитель по первой строке и найдем
векторное произведение:
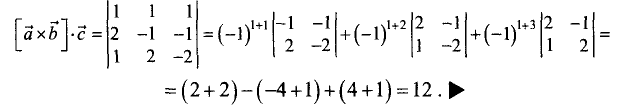
В n-мерной системе координат вектор может быть представлен в виде
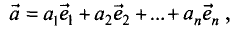
где 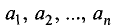 — проекции вектора
— проекции вектора 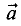 на первую координатную
на первую координатную
ось, вторую и т.д.;
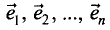 — орты первой координатной оси, второй и т.д.
— орты первой координатной оси, второй и т.д.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

