Оглавление:
Операционное исчисление играет важную роль при решении прикладных задач, особенно в современной автоматике и телемеханике.
Операционное исчисление — один из методов математического анализа, позволяющий в ряде случаев сводить исследование дифференциальных и некоторых типов интегральных операторов и решение уравнений, содержащих эти операторы, к рассмотрению более простых алгебраических задач.
Методы операционного исчисления предполагают реализацию следующей условной схемы решения задачи.
- От искомых функций переходят к некоторым другим функциям — их изображениям.
- Над изображениями производят операции, соответствующие заданным операциям над самими функциями.
- Получив некоторый результат при действиях над изображениями, возвращаются к самим функциям.
В качестве преобразования, позволяющего перейти от функции к их изображениям, будем применять так называемое преобразование Лапласа.
Преобразование Лапласа
Оригиналы и их изображения:
Основными первоначальными понятиями операционного исчисления являются понятия функции-оригинала и функции-изображения.
Пусть f(t) — действительная функция действительного переменного t (под t будем понимать время или координату).
Функция f(t) называется оригиналом, если она удовлетворяет следующим условиям:
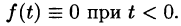
- f(t) — кусочно-непрерывная при
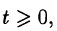 т. е. она непрерывна или имеет точки разрыва I рода, причем на каждом конечном промежутке оси t таких точек лишь конечное число.
т. е. она непрерывна или имеет точки разрыва I рода, причем на каждом конечном промежутке оси t таких точек лишь конечное число. - Существуют такие числа
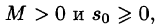 что для всех t выполняется неравенство
что для всех t выполняется неравенство 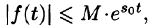 , т. е. при возрастании t функция f(t) может возрастать не быстрее некоторой показательной функции. Число
, т. е. при возрастании t функция f(t) может возрастать не быстрее некоторой показательной функции. Число 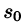 называется показателем роста f(t).
называется показателем роста f(t).
Условия 1-3 выполняются для большинства функций, описывающих различные физические процессы.
Первое условие означает, что процесс начинается с некоторого момента времени; удобнее считать, что в момент t = 0. Третьему условию удовлетворяют ограниченные функции (для них можно положить 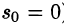 ), степенные
), степенные 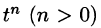 и другие (для функций вида
и другие (для функций вида 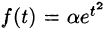 ( условие 3 не выполняется). Не является оригиналом, например, функция
( условие 3 не выполняется). Не является оригиналом, например, функция 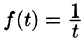 (не удовлетворяет второму условию).
(не удовлетворяет второму условию).
Замечание:
Функция f(t) может быть и комплексной функцией действительно переменного, т. е. иметь вид 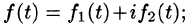 она считается оригиналом, если действительные функции
она считается оригиналом, если действительные функции 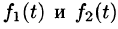 являются оригиналами.
являются оригиналами.
Изображением оригинала f(t) называется функция F(p) комплексного переменного 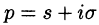 , определяемая интегралом
, определяемая интегралом
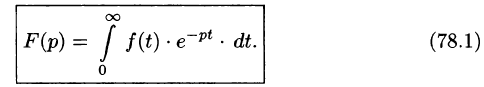
Операцию перехода от оригинала f(t) к изображению F(p) называют преобразованием Лапласа. Соответствие между оригиналом f(t) и изображением F(p) записывается в виде 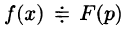 или
или 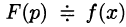 (принято оригиналы обозначать малыми буквами, а их изображения — соответствующими большими буквами).
(принято оригиналы обозначать малыми буквами, а их изображения — соответствующими большими буквами).
Теорема:
Существование изображения. Для всякого оригинала f(t) изображение F(p) существует (определено) в полуплоскости 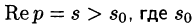 — показатель роста функции f(t) , причем функция F(p) является аналитической в этой полуплоскости
— показатель роста функции f(t) , причем функция F(p) является аналитической в этой полуплоскости 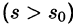 .
.
Докажем первую часть теоремы. Пусть  произвольная точка полуплоскости
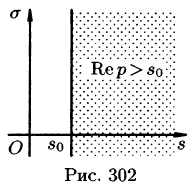
произвольная точка полуплоскости  (см. рис. 302).
(см. рис. 302).
Учитывая, что 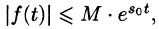 находим:
находим:
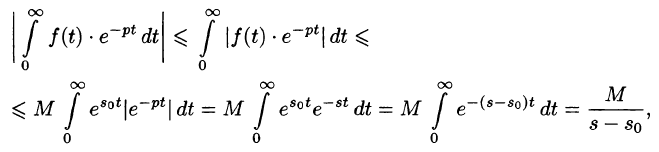
так как
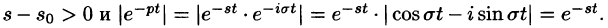
Таким образом,
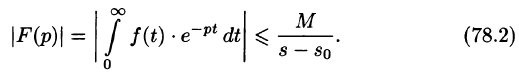
Отсюда вытекает абсолютная сходимость интеграла (78.1), т. е. изображение F(p) существует и однозначно в полуплоскости 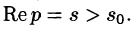
Следствие:
Необходимый признак существования изображения. Если функция F(p) является изображением функции f(t) , то
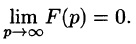
Это утверждение непосредственно вытекает из неравенства (78.2), когда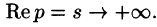
Так как F(p) — аналитическая функция в полуплоскости
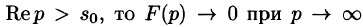
по любому направлению. Отсюда, в частности, следует, что функции 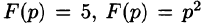 не могут быть изображениями.
не могут быть изображениями.
Отметим, что из аналитичности функции F(p) следует, что все ее особые точки должны лежать левее прямой 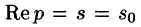 или на самой этой прямой. Функция F(p) , не удовлетворяющая этому условию, не является изображением функции f(t). Не является изображением, например, функция
или на самой этой прямой. Функция F(p) , не удовлетворяющая этому условию, не является изображением функции f(t). Не является изображением, например, функция 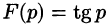 (ее особые точки расположены на всей оси s).
(ее особые точки расположены на всей оси s).
Теорема:
О единственности оригинала. Если функция F(p) служит изображением двух оригиналов 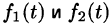 , то эти оригиналы совпадают друг с другом во всех точках, в которых они непрерывны.
, то эти оригиналы совпадают друг с другом во всех точках, в которых они непрерывны.
(Примем без доказательства.)
Пример:
Найти изображение единичной функции Хевисайда
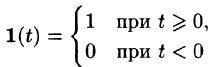
(см. рис. 303).
Решение:
По формуле (78.1) при 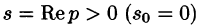 находим:
находим:
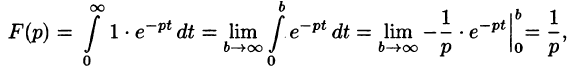
т. e. 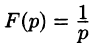 , или, в символической записи,
, или, в символической записи, 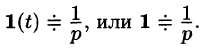
Замечание:
В дальнейшем функцию-оригинал будем кратко записывать в виде f(t) , подразумевал, что
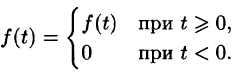
Пример:
Найти изображение функции 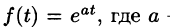 — любое число.
— любое число.
Решение:
Данная функция является оригиналом. По формуле (78.1) имеем
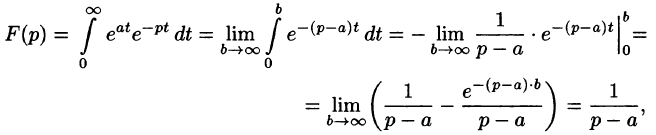
если Re(p — a) > 0. Таким образом,
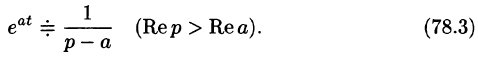
Пример:
Найти изображение функции f(t) = t.
Решение:
В этом случае преобразование Лапласа имеет вид
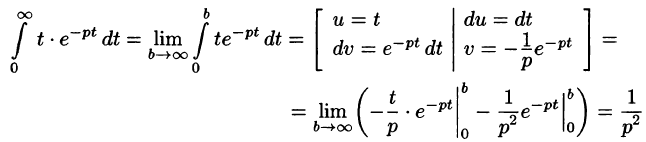
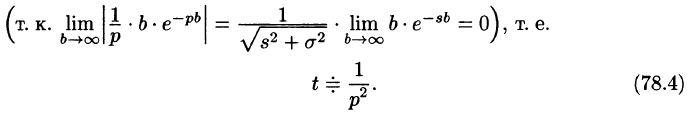
Замечание:
Функция 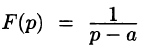 является аналитической не только в полуплоскости Rep > Re а, где интеграл (78.1) сходится, а на всей комплексной плоскости р, кроме точки р = а. Такая особенность наблюдается и для многих других изображений. Далее для нас будет более важным, как правило, само изображение функции, а не область, в которой оно выражается интегралом (78.1).
является аналитической не только в полуплоскости Rep > Re а, где интеграл (78.1) сходится, а на всей комплексной плоскости р, кроме точки р = а. Такая особенность наблюдается и для многих других изображений. Далее для нас будет более важным, как правило, само изображение функции, а не область, в которой оно выражается интегралом (78.1).
Свойства преобразования Лапласа
Находить изображения, пользуясь только определением изображения, не всегда просто и удобно. Свойства преобразования Лапласа существенно облегчают задачу нахождения изображений для большого числа разнообразных функций, а также задачу отыскания оригиналов по их изображениям.
Линейность
Линейной комбинации оригиналов соответствует такая же линейная комбинация изображений, т. е. если
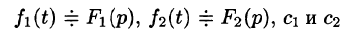
— постоянные числа, то
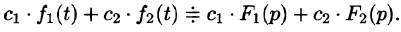
Используя свойства интеграла, находим
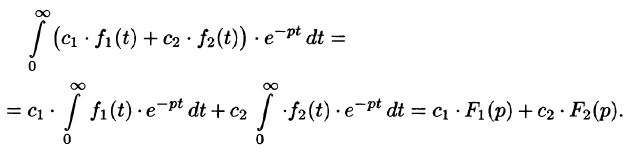
Пример:
Найти изображения функций 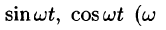 — любое число), с (const),
— любое число), с (const), 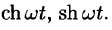
Решение:
Пользуясь свойством линейности, формулой (78.3), находим:
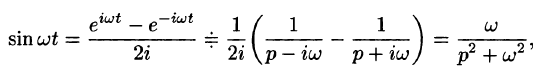
т. е.

Аналогично получаем формулу

Далее, 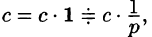 т. е.
т. е.
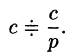
Наконец,
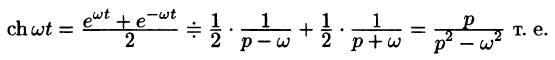

Аналогично получаем формулу

Подобие
Если
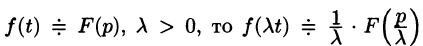
т.е. умножение аргумента оригинала на положительное число 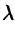 приводит к делению изображения и его аргумента на это число.
приводит к делению изображения и его аргумента на это число.
По формуле (78.1) имеем
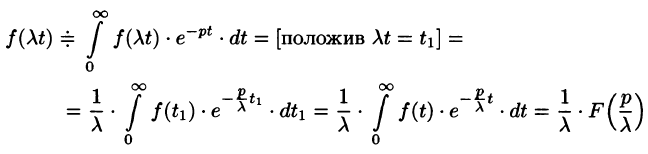
(так как безразлично, какой буквой обозначена переменная интегрирования).
Например, пусть 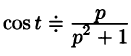 . Тогда
. Тогда
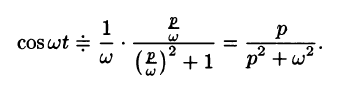
Смещение (затухание)
Если
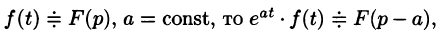
т. е. умножение оригинала на функцию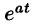 влечет за собой смещение переменной р.
влечет за собой смещение переменной р.
В силу формулы (78.1) имеем
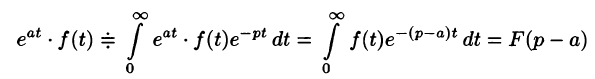
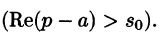
Благодаря этому свойству можно расширить таблицу соответствия между оригиналами и их изображениями:
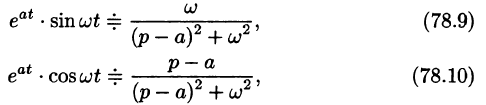
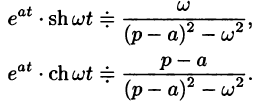
Пример:
Найти оригинал по его изображению
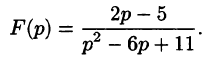
Решение:
Преобразуем данную дробь так, чтобы можно было воспользоваться свойством смещения:
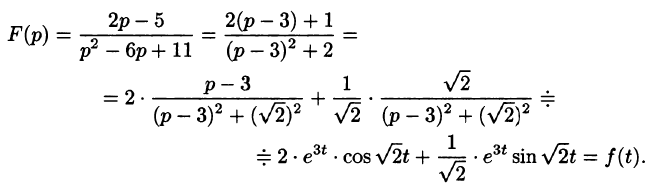
(См. формулы (78.9), (78.10) и свойство линейности.)
Запаздывание
Если
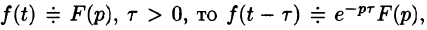
т. е. запаздывание оригинала на положительную величину 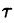 приводит к умножению изображения оригинала без запаздывания на
приводит к умножению изображения оригинала без запаздывания на 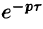 .
.
Положив 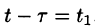 , получим
, получим
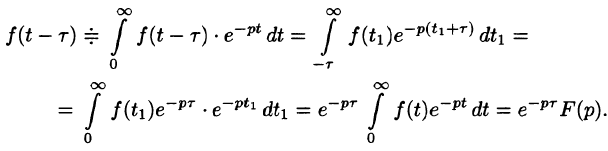
Поясним термин «запаздывание». Графики функции f(t) и 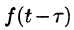 имеют одинаковый вид, но график функции
имеют одинаковый вид, но график функции 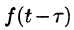 сдвинут на
сдвинут на 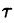 единиц
единиц
Рис. 304
Рис. 305
вправо (см. рис. 304). Следовательно, функции f(t) и 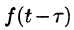 описывают один и тот же процесс, но процесс, описываемый функцией
описывают один и тот же процесс, но процесс, описываемый функцией 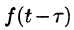 , начинается с опозданием на время
, начинается с опозданием на время 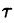 .
.
Свойство запаздывания удобно применять при отыскании изображения функций, которые на разных участках задаются различными аналитическими выражениями; функций, описывающих импульсные процессы.
Функция
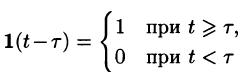
называется обобщенной единично ной функцией (см. рис 305).
Так как
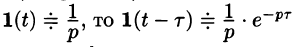
Запаздывающую функцию
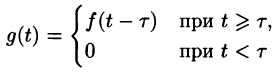
можно записать так:
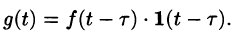
Пример:
Найти изображение f(t) = t — 1.
Решение:
Для того чтобы быть оригиналом, функция f(t) должна удовлетворять условиям 1-3 (см. п. 78.1). В этом смысле исходную задачу можно понимать двояко.
Если понимать функцию f(t) как
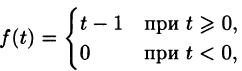
т. е. 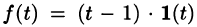 (см. рис. 306, а), то, зная, что
(см. рис. 306, а), то, зная, что 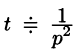 (см. формулу (78.4)),
(см. формулу (78.4)), 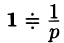 и, используя свойство линейности, находим
и, используя свойство линейности, находим
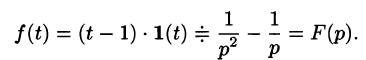
Если же понимать функцию f(t) как
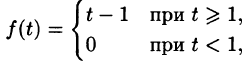
т. е. 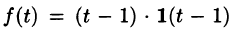 (см. рис. 306, б), то, используя свойство запаздывания, находим
(см. рис. 306, б), то, используя свойство запаздывания, находим
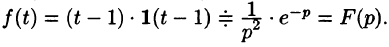
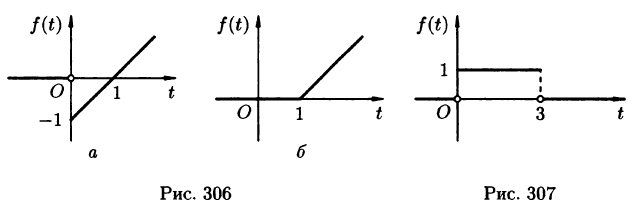
Пример:
Найти изображение функции
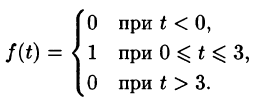
Решение:
Данная функция описывает единичный импульс (см. рис. 307), который можно рассматривать как разность двух оригиналов: единичной функции 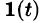 и обобщенной единичной функции
и обобщенной единичной функции 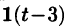 . Поэтому
. Поэтому
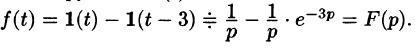
Пример:
Найти изображение функции

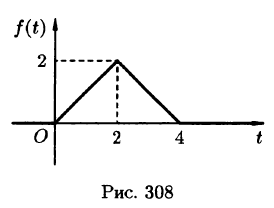
Решение:
Функция-оригинал изображена на рис. 308. Запишем ее одним аналитическим выражением, используя функции Хевисайда 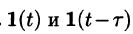 :
:
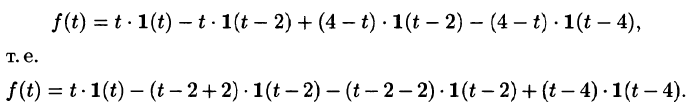
Раскроем скобки и приведем подобные слагаемые:
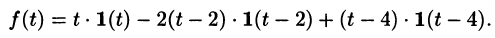
Изображение функции f(t) будет равно
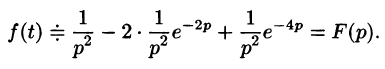
Замечания:
1.Изображение периодического оригинала с периодом, равным Т,
есть 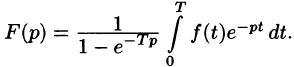
2.Свойство опережения
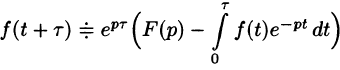
применяется значительно реже.
Дифференцирование оригинала
Если 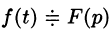 и функции
и функции 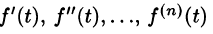 являются оригиналами, то
являются оригиналами, то

По определению изображения находим
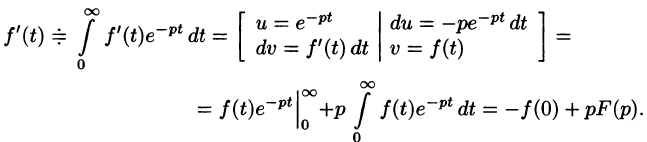
Итак,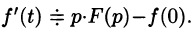 Пользуясь полученным результатом, найдем изображение второй производной f»(t):
Пользуясь полученным результатом, найдем изображение второй производной f»(t):
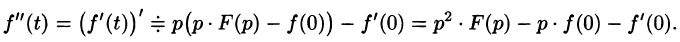
Аналогично найдем изображение третьей производной f»‘(t):
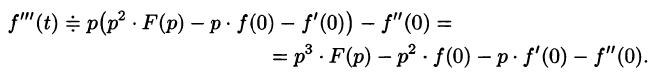
Применяя формулу (78.11) (п — 1) раз, получим формулу (78.14).
Замечание. Формулы (78.11)-(78.14) просто выглядят при нулевых начальных условиях: если
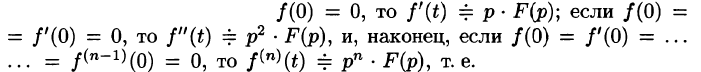
т. е. дифференцированию оригинала соответствует умножение его изображения на р.
Рассмотренное свойство дифференцирования оригинала вместе со свойством линейности широко используется при решении линейных дифференциальных уравнений.
Пример:
Найти изображение выражения
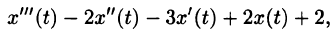
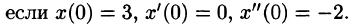
Решение:
Пусть 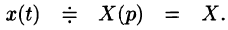 Тогда, согласно формулам (78.11)—(78.13), имеем
Тогда, согласно формулам (78.11)—(78.13), имеем
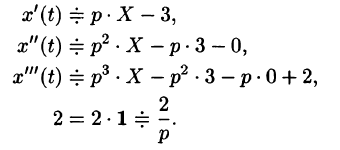
Следовательно,
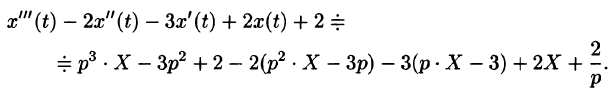
Дифференцирование изображения
Если 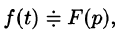 то
то
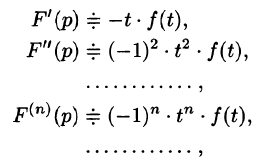
т. е. дифференцированию изображения соответствует умножение его оригинала на (-t).
Согласно теореме 78.1 существования изображения, F(p) является аналитической функцией в полуплоскости 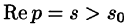 Следовательно, у нее существует производная любого порядка. Дифференцируя интеграл (78.1) по параметру р (обоснование законности этой операции опустим), получим
Следовательно, у нее существует производная любого порядка. Дифференцируя интеграл (78.1) по параметру р (обоснование законности этой операции опустим), получим
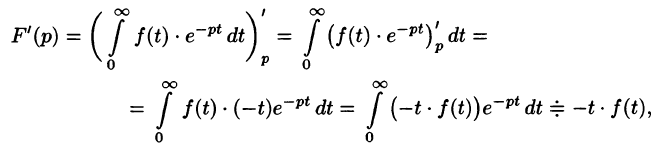
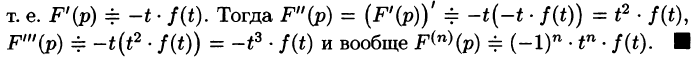
Пример:
Найти изображения функций 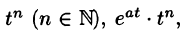
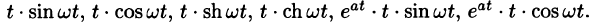
Решение:
Так как 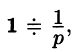 , то, в силу свойства дифференцирования изображения, имеем
, то, в силу свойства дифференцирования изображения, имеем 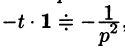 т. е.
т. е.
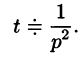
Далее находим
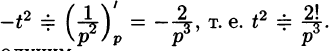
Продолжая дифференцирование, получим
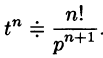
С учетом свойства смещения получаем
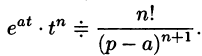
Согласно формуле (78.5), 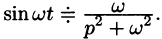 Следовательно,
Следовательно,
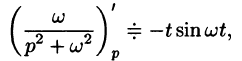
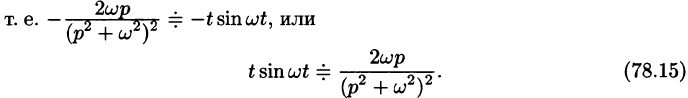
Аналогично, используя формулы (78.6), (78.7) и (78.8), находим
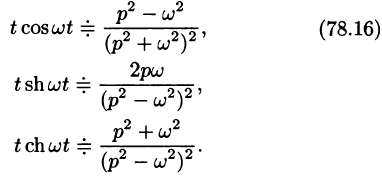
С учетом свойства смещения и формул (78.15) и (78.16), получаем
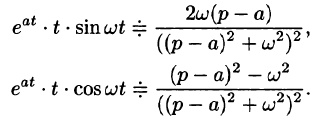
Интегрирование оригинала
Если
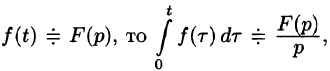
т. е. интегрированию оригинала от 0 до t соответствует деление его изображения на р.
Функция 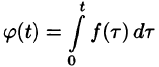 является оригиналом (можно проверить).
является оригиналом (можно проверить).
Пусть 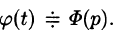 Тогда по свойству дифференцирования оригинала имеем
Тогда по свойству дифференцирования оригинала имеем
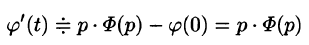
(так как 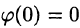 ). А так как
). А так как
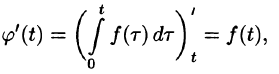
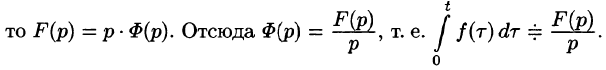
Интегрирование изображения
Если 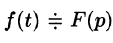 и интеграл
и интеграл 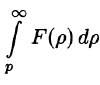 сходится, то
сходится, то 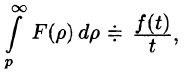 т. е. интегрированию изображения от p до
т. е. интегрированию изображения от p до 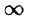 соответствует деление его оригинала на t.
соответствует деление его оригинала на t.
Используя формулу (78.1) и изменяя порядок интегрирования (обоснование законности этой операции опускаем), получаем
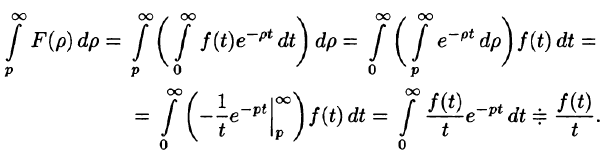
Пример:
Найти изображение функции 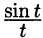 найти изображение интегрального синуса
найти изображение интегрального синуса 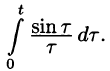
Решение:
Так как
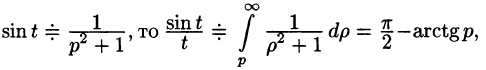
т. е. 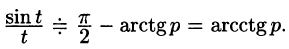 Применяя свойство интегрирования t оригинала, получаем
Применяя свойство интегрирования t оригинала, получаем
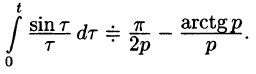
Умножение изображений
Если 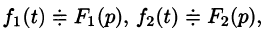 то
то
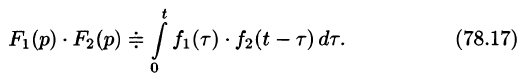
Можно показать, что функция 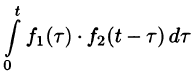 является оригиналом.
является оригиналом.
Используя преобразование Лапласа (78.1), можно записать
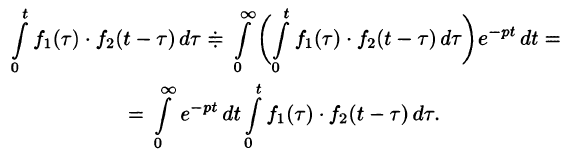
Область D интегрирования полученного двукратного интеграла определяется условиями 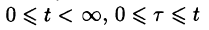 (см. рис. 309).
(см. рис. 309).
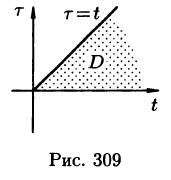
Изменяя порядок интегрирования и полагая 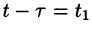 , получим
, получим
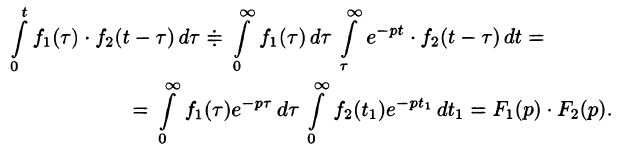
Интеграл в правой части формулы (78.17) называется сверткой функции 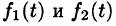 и обозначается символом
и обозначается символом 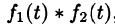 , т. е.
, т. е.
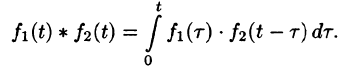
Можно убедиться (положив 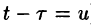 ), что свертывание обладает свойством переместительности, т. е.
), что свертывание обладает свойством переместительности, т. е. 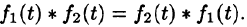
Умножение изображений соответствует свертыванию их оригиналов, т. е.
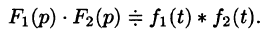
Пример:
Найти оригинал функций
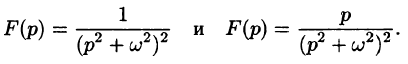
Решение:
Так как
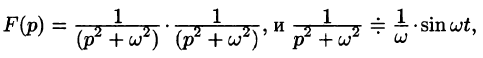
то
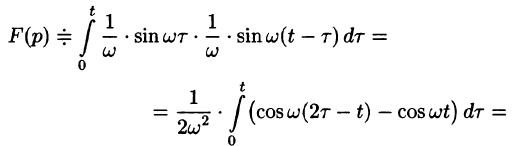
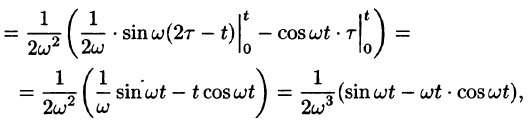
т. e.
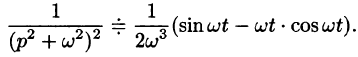
Аналогично получаем
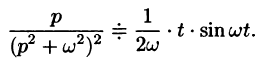
Следствие:
Если 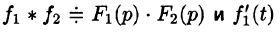 также является оригиналом, то
также является оригиналом, то
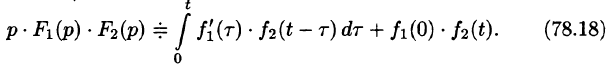
Запишем произведение 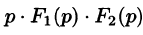 в виде
в виде
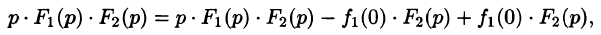
или
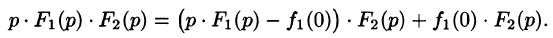
Первое слагаемое в правой части есть произведение изображений, соответствующих оригиналам 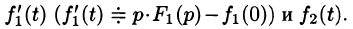 Поэтому на основании свойства умножения изображений и линейности можно записать
Поэтому на основании свойства умножения изображений и линейности можно записать 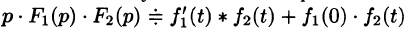 или
или
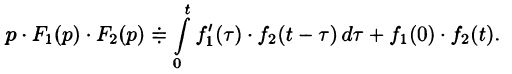
Формула (78.18) называется формулой Дюамеля. На основании свойства переместительности свертки формулу Дюамеля можно записать в виде
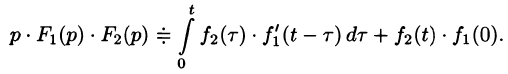
Формулу Дюамеля можно применять для определения оригиналов по известным изображениям.
Пример:
Найти оригинал, соответствующий изображению
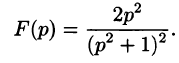
Решение:
Так как
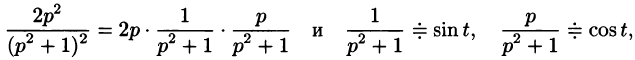
то на основании формулы Дюамеля (78.18) имеем
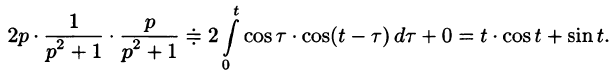
Умножение оригиналов
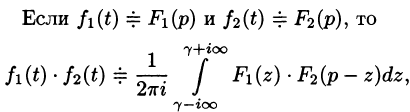
где путь интегрирования — вертикальная прямая 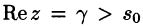 (см. рис. 310) (примем без доказательства).
(см. рис. 310) (примем без доказательства).
Резюме
Рассмотренные свойства преобразования Лапласа представляют собой основные правила (аппарат) операционного исчисления. Для удобства пользования перечислим эти свойства.
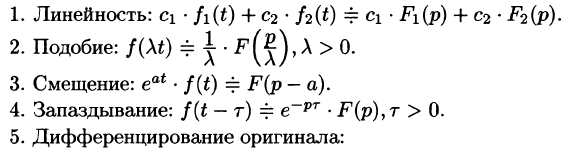
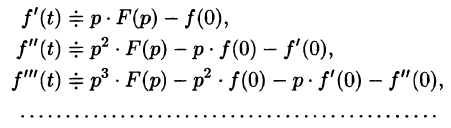
6. Дифференцирование изображения
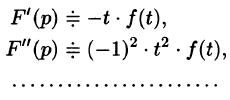
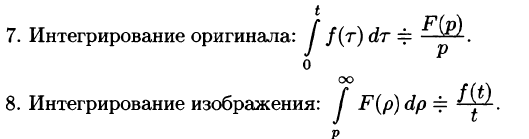
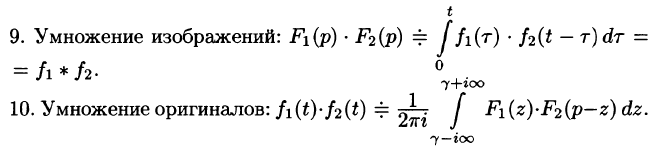
Таблица оригиналов и изображений
Составим краткую таблицу, устанавливающую соответствие между некоторыми оригиналами (часто встречающимися на практике) и их изображениями. Достаточно полная таблица оригиналов и изображений, позволяющая по заданному оригиналу находить изображение и наоборот, есть, в частности, в книге «Справочник по операционному исчислению» (авторы В. А. Диткин и П. И. Кузнецов).



Обратное преобразование Лапласа
Теоремы разложения:
Рассмотрим две теоремы, называемые теоремами разложения, позволяющие по заданному изображению F(p) находить соответствующий ему оригинал f(t).
Теорема:
Если функция F(p) в окрестности точки 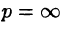 может быть представлена в виде ряда Лорана
может быть представлена в виде ряда Лорана
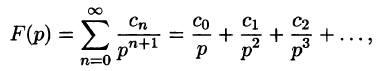
то функция
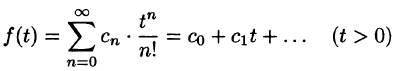
является оригиналом, имеющим изображение F(p), т. е.
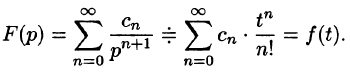
Примем эту теорему без доказательства.
Пример:
Найти оригинал f(t), если
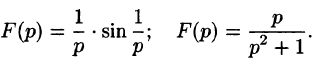
Решение:
Имеем
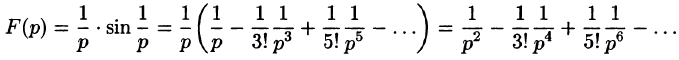
Следовательно, на основании теоремы 79.1
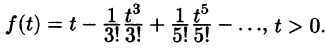
Запишем лорановское разложение функции 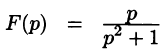 в окрестности точки
в окрестности точки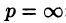 :
:
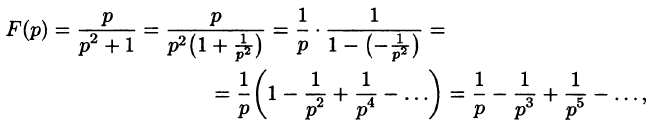
где 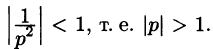 Следовательно,
Следовательно,
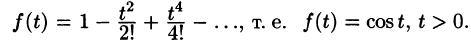
Теорема:
Если 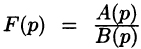 правильная рациональная дробь, знаменатель которой В(р) имеет лишь простые корни (нули)
правильная рациональная дробь, знаменатель которой В(р) имеет лишь простые корни (нули)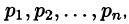 то функция
то функция
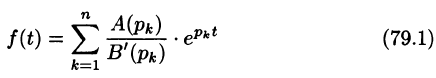
является оригиналом, имеющим изображение F(p).
Отметим, что дробь 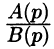 должна быть правильной (степень многочлена А(р) ниже степени многочлена В(р)) в противном случае не выполняется необходимый признак существования изображения
должна быть правильной (степень многочлена А(р) ниже степени многочлена В(р)) в противном случае не выполняется необходимый признак существования изображения
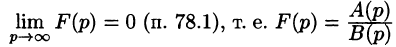
не может быть изображением.
Разложим правильную рациональную дробь 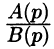 на простейшие:
на простейшие:
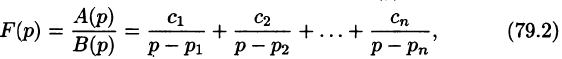
где 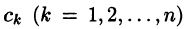 — неопределенные коэффициенты. Для определения коэффициента
— неопределенные коэффициенты. Для определения коэффициента 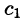 этого разложения умножим обе части этого равенства почленно на
этого разложения умножим обе части этого равенства почленно на 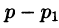 :
:
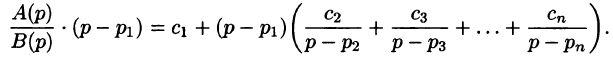
Переходя в этом равенстве к пределу при 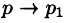 , получаем
, получаем
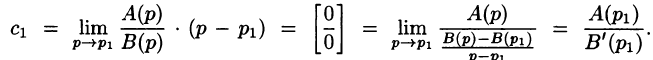
Итак, 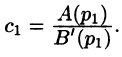 Аналогичным путем (умножая обе части равенства (79.2) на
Аналогичным путем (умножая обе части равенства (79.2) на 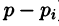 найдем
найдем 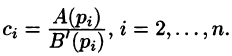
Подставляя найденные значения 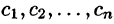 в равенство (79.2), получим
в равенство (79.2), получим
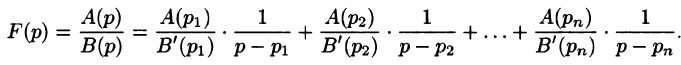
Так как по формуле (78.3)
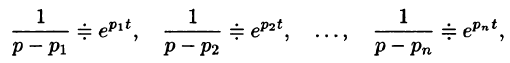
то на основании свойства линейности имеем
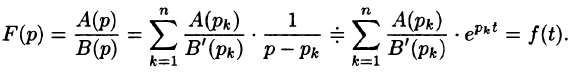
Замечание:
Легко заметить, что коэффициенты 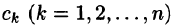 определяются как вычеты комплексной функции F(p) в простых полюсах (формула (77.4)):
определяются как вычеты комплексной функции F(p) в простых полюсах (формула (77.4)):
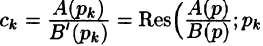
Можно показать, что если 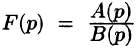 правильная дробь, но корни (нули)
правильная дробь, но корни (нули)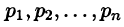 знаменателя В(р) имеют кратности
знаменателя В(р) имеют кратности 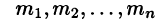 соответственно, то в этом случае оригинал изображения F(p) определяется формулой
соответственно, то в этом случае оригинал изображения F(p) определяется формулой
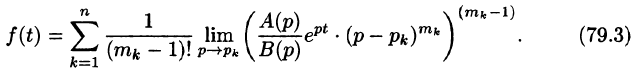
Теорему 79.2 можно сформулировать следующим образом:
Теорема:
Если изображение 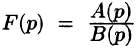 является дробно-рациональной функцией от
является дробно-рациональной функцией от 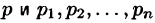 — простые или кратные полюсы этой функции, то оригинал f(t), соответствующий изображению F(p), определяется формулой
— простые или кратные полюсы этой функции, то оригинал f(t), соответствующий изображению F(p), определяется формулой
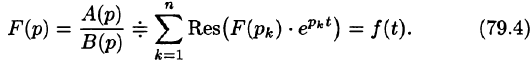
Формула Римана-Меллина
Общий способ определения оригинала по изображению дает обратное преобразование Лапласа (формула обращения Римана-Меллина), имеющее вид
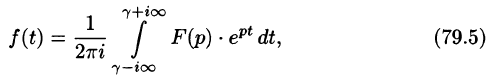
где интеграл берется вдоль любой прямой 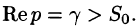 .
.
При определенных условиях интеграл (79.5) вычисляется по формуле
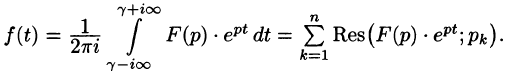
Замечание:
На практике отыскание функции-оригинала обычно проводят по следующему плану: прежде всего следует по таблице оригиналов и изображений попытаться отыскать для заданного изображения F(p) соответствующий ему оригинал; второй путь состоит в том, что функцию F(p) стараются представить в виде суммы простейших рациональных дробей, а затем, пользуясь свойством линейности, найти оригинал; наконец, использовать теоремы разложения, свойство умножения изображений, формулу обращения и т.д.
Пример:
Найти оригинал по его изображению
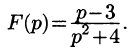
Решение:
Проще всего поступить так:
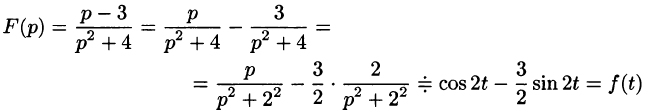
(использовали свойство линейности и формулы (78.5) и (78.6)).
Если же использовать теорему 79.2 разложения, то будем иметь:
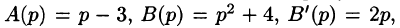
корни знаменателя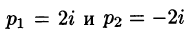 и, согласно формуле (79.1),
и, согласно формуле (79.1),
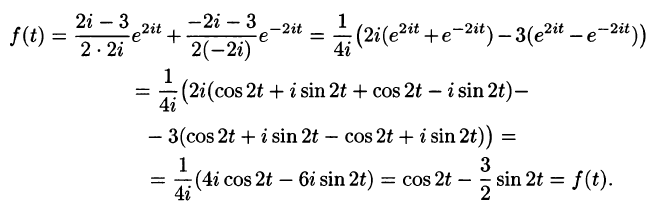
Пример:
Найти функцию-оригинал, если ее изображение
задано как 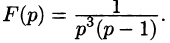
Решение:
Здесь
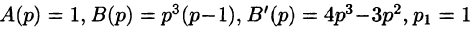
— простой корень знаменателя, 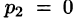 — 3-кратный корень (m = 3). Используя формулы (79.1) и (79.3), имеем:
— 3-кратный корень (m = 3). Используя формулы (79.1) и (79.3), имеем:
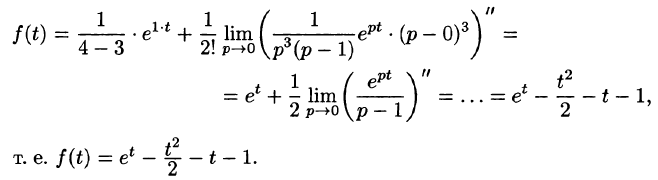
Приведем другой способ нахождения f(t). Разобьем дробь 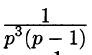
на сумму простейших дробей:
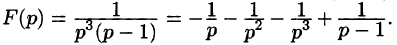
Следовательно,
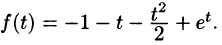
Приведем третий способ нахождения f(t). Представим F(p) как
произведение 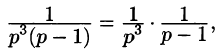 и так как
и так как 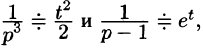 пользуясь свойством умножения изображений, имеем:
пользуясь свойством умножения изображений, имеем:
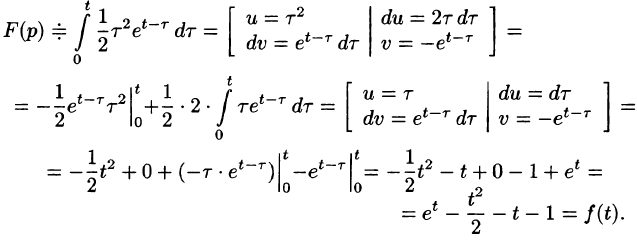
Операционный метод решения линейных дифференциальных уравнений и их систем
Пусть требуется найти частное решение линейного дифференциального уравнения с постоянными коэффициентами
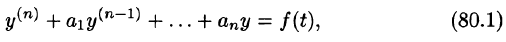
удовлетворяющее начальным условиям
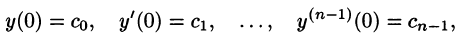
где  — заданные числа.
— заданные числа.
Будем считать, что искомая функция y(t) вместе с ее рассматриваемыми производными и функция f(t) являются оригиналами.
Пусть 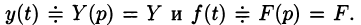 Пользуясь свойствами дифференцирования оригинала и линейности, перейдем в уравнении(80.1) от оригиналов к изображениям:
Пользуясь свойствами дифференцирования оригинала и линейности, перейдем в уравнении(80.1) от оригиналов к изображениям:
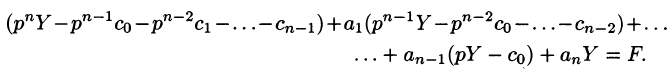
Полученное уравнение называют операторным (или уравнением в изображениях). Разрешим его относительно Y:
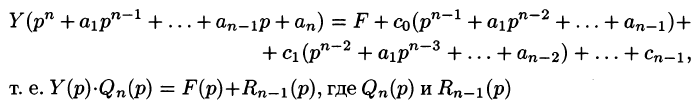
— алгебраические многочлены от p степени п и п-1 соответственно. Из последнего уравнения находим
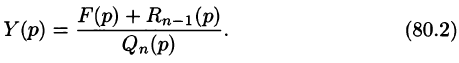
Полученное равенство называют операторным решением дифференциального уравнения (80.1). Оно имеет более простой вид, если все начальные условия равны нулю, т. е.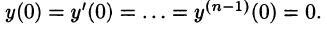
В этом случае 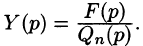
Находя оригинал y(t), соответствующий найденному изображению (80.2), получаем, в силу теоремы единственности, частное решение дифференциального уравнения (80.1).
Замечание:
Полученное решение y(t) во многих случаях оказывается справедливым при всех значениях t (а не только при 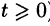 ).
).
Пример:
Решить операционным методом дифференциальное уравнение 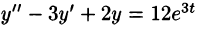 при условиях
при условиях 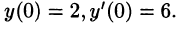
Решение:
Пусть 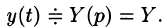 Тогда
Тогда
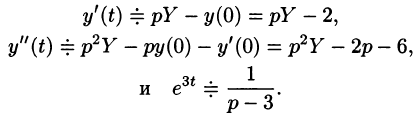
Подставляя эти выражения в дифференциальное уравнение, получаем операторное уравнение:
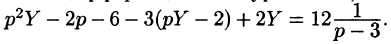
Отсюда 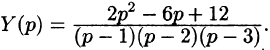 Находим y(t). Можно разбить дробь на сумму простейших
Находим y(t). Можно разбить дробь на сумму простейших 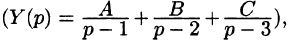 но так как корни знаменателя
но так как корни знаменателя 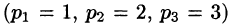 простые, то удобно воспользоваться второй теоремой разложения (формула (79.1)), в которой
простые, то удобно воспользоваться второй теоремой разложения (формула (79.1)), в которой
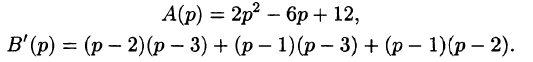
Получаем:
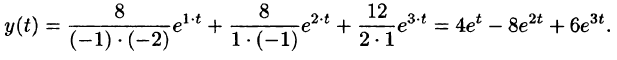
Пример:
Найти решение уравнения
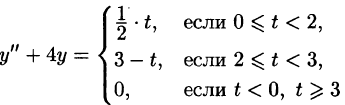
при условии 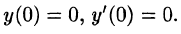
Решение:
График данной функции имеет вид, изображенный на рисунке 311.
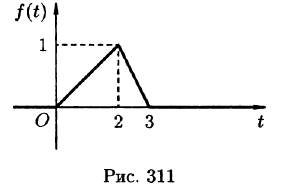
С помощью единичной функции правую часть данного дифференциального уравнения можно записать одним аналитическим выражением:
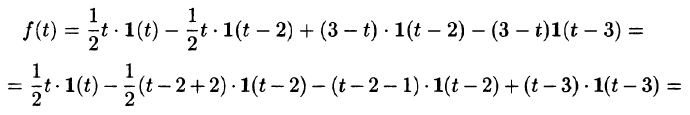
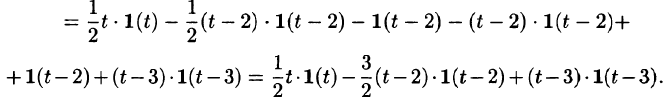
Таким образом, имеем
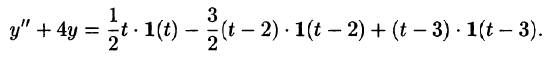
Операторное уравнение, при нулевых начальных условиях имеет вид
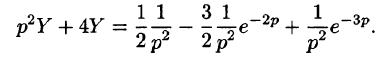
Отсюда
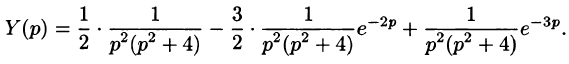
Так как
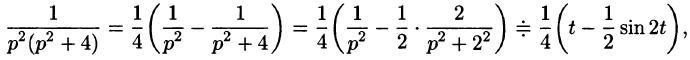
то по теореме запаздывания находим:
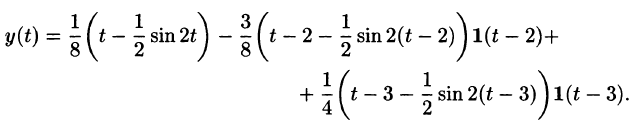
Аналогично применяется операционный метод для решения систем линейных дифференциальных уравнений с постоянными коэффициентами.
Покажем это на конкретном примере.
Пример:
Решить систему дифференциальных уравнений
Решение:
Пусть
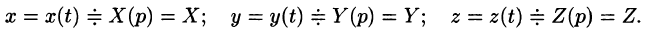
Находим, что
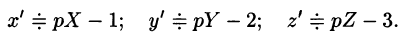
Система операторных уравнений принимает вид
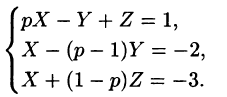
Решая эту систему алгебраических уравнений, находим:
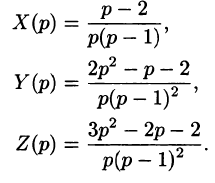
Переходя от изображений к оригиналам, получаем искомые решения:
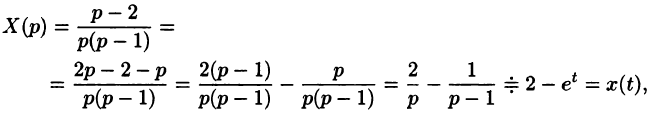
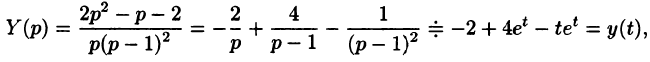
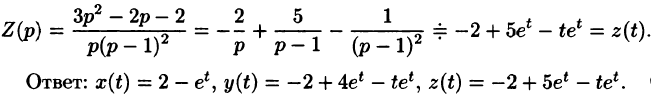
С помощью операционного исчисления можно также находить решения линейных дифференциальных уравнений с переменными коэффициентами, уравнений в частных производных, уравнений в конечных разностях (разностных уравнений); производить суммирование рядов; вычислять интегралы. При этом решение этих и других задач значительно упрощается.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

