Взаимно обратные функции с примерами и образцами решения

Оглавление:

Показательная и логарифмическая функции являются взаимно обратными функциями. Подробное ознакомление с этим понятием начнем с простых примеров.

Напишем формулу для вычисления площади круга по его радиусу: S =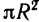 Взаимно обратные функции . Эта формула задает площадь круга S как функцию его радиуса R, т. е. для каждого (положительного) числа R по этой формуле вычисляется площадь круга S. Представим себе, что надо решить обратную задачу: по данной площади круга S

вычислить его радиус. Для этого выразим R через S так: 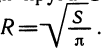Взаимно обратные функции

Новая формула задает радиус круга R как функцию его площади S. Полученные две функции S=S(R) и R =R(S) являются примерами взаимно обратных функций.

Приведем еще примеры взаимно обратных функций:

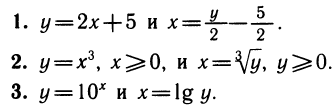
В каждом из указанных примеров соответствие между переменными величинами, задаваемое взаимно обратными функциями, одно и то же. В самом деле, зависимость между радиусом и площадью круга остается одной и той же: записывается ли она в виде S = 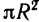Взаимно обратные функции или же в виде 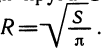Точно так же функции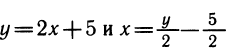

выражают одну и ту же зависимость между переменными х и у.

Определение. Две функции fug называются взаимно обратными, если формулы y=f (х) и x=g(y) выражают одну и ту же зависимость между переменными х и у, т. е. если равенство y=f (х) верно тогда и только тогда, когда верно равенство x = g (y).

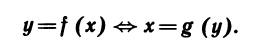
Если две функции f и g взаимно обратны, то g называют обратной функцией для f и, наоборот, f — обратной для g.

Как ответить на вопрос, что такое обратная функция для функции f? Это можно сделать следующим образом: обратная функция для функции f — это такая функция g, что f и g образуют пару взаимно обратных функций.

Как мы уже отметили, зависимость y = 2x+ 5 и 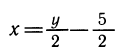Взаимно обратные функции

между переменными x и у одна и та же. Эту же зависимость можно записать и так: 2х —y + 5 = 0. Из последней формулы можно выразить у как функцию от х, а можно и, наоборот, выразить х как функцию от у. Эти две функции будут взаимно обратны.

Таким образом, исходным понятием является понятие зависимости. Если есть некоторая зависимость между переменными хну, которая позволяет выразить у как функцию от х и х как функцию от у, то эти две функции и являются взаимно обратными.

Графики взаимно обратных функций

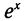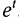При построении графиков взаимно обратных функций необходимо внимательно следить за обозначениями переменных. Рассмотрим функцию f. Аргумент этой функции и ее значения можно обозначить произвольными буквами. Так, в формулах у= Взаимно обратные функции , s = , N = 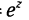переменные обозначены различными буквами, однако каждая из этих формул определяет одну и ту же показательную функцию, экспоненту.

Определение взаимно обратных функций сформулировано на языке зависимостей. Чтобы определить, являются ли эти две функции f и g (заметьте, здесь пока нет обозначений для переменных) взаимно обратными, надо взять две переменные, например х и у, составить две формулы y = f{x) и x = g(y) и затем определить, задают эти две формулы одну и ту же зависимость между переменными хну или нет.

Различия в обозначениях переменных сказываются при построении графиков функций. Пусть у нас есть две переменные х и у, значения которых откладываются на выбранных координатных осях, которые мы обозначаем этими же буквами х и у. Рассмотрим зависимости между х и у.

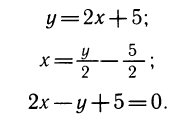
Ясно, что это разные записи одной и той же зависимости между переменными х и у.

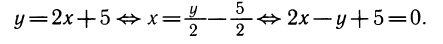
Поэтому график каждой из этих зависимостей один и тот же — он состоит из всех точек Р (х; у), координаты которых связаны соотношением у = 2х+5, справедливым тогда и только тогда, когда 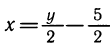Взаимно обратные функции или 2ч —у + 5 = 0 (рис. 113). Точно так же график зависимостей у = 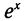и х = ln у в системе координат (х; у) один и тот же (и зависимость между х и у на самом деле одна и та же; рис. 113).

Посмотрим на зависимость 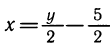Взаимно обратные функции . Она выражает х как некоторую функцию от у. Аргумент этой функции обозначен буквой у, а значения — буквой х. Поменяем местами х и у, т. е. рассмотрим зависимость 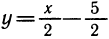Взаимно обратные функции . Функция осталась одной и той же, но теперь ее аргумент обозначен, как обычно, буквой х, а значения — буквой у. Построим график функции 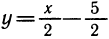(например, по двум точкам на рисунке 113). 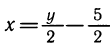Мы видим, что этот график отличен от графика зависимости Взаимно обратные функции .

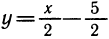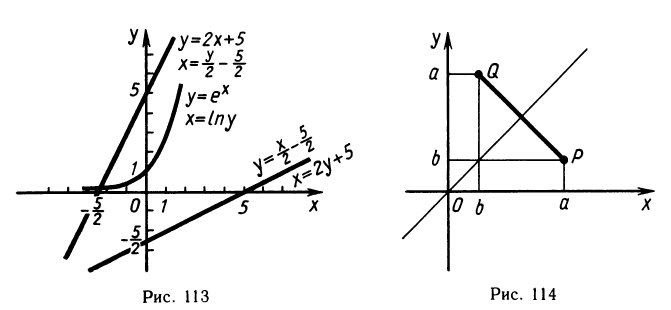
Как связаны между собой графики функций у = 2х+5 и Взаимно обратные функции ?

Возьмем какую-либо точку на графике первой функции, например Р(0; 5). Поменяем местами координаты, т. е. рассмотрим точку Q (5; 0). Эта точка лежит на графике второй функции 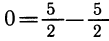Взаимно обратные функции ,

Точки Р (0; 5) и Q (5; 0) симметричны друг другу относительно биссектрисы угла хОу, т. е. прямой у — х. Из рисунка 114 видно, что при любых а и b точки Р (а; b) и Q (b а) симметричны друг другу относительно прямой у=х.

Теорема:

Пусть f и g — взаимно обратные функции. Графики функций y — f(x) и y = g(x) симметричны друг другу относительно биссектрисы угла хОу.

Доказательство

По определению взаимно обратных функций формулы y = f(x) и х = g(y) выражают одну и ту же зависимость между переменными х и у, а значит, эта зависимость изображается одним и тем же графиком — некоторой кривой С (схема XII). Кривая С является графиком функции y = f(x). Возьмем произвольную точку Р (а; b) ∈ С. Это означает, что b = f(a) и одновременно a = g(b). Построим точку Q, симметричную точке Р относительно биссектрисы угла хОу. Как мы заметили раньше, точка Q будет иметь координаты (b; а). Так как a = g (b), то точка Q принадлежит графику функции y = g(x): действительно, при х = b значение у = а равно g (х). Таким образом, все точки, симметричные точкам кривой С относительно указанной прямой, лежат на графике функции у = g (х). Они исчерпывают этот график целиком, так как аналогично показывается, что всякая точка функции y — g(x) при указанной симметрии попадает на график функции y = f(x). Теорема доказана.

На рисунке 115 изображены графики пар взаимно обратных функций:

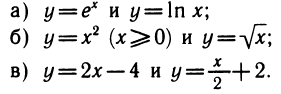
Условие существования обратной функции

Дана функция y = f(x). Поставим следующий вопрос: при каком условии существует функция, обратная к функции f? По определению обратная функция к функции f строится так: из соотношения y=f(x) надо х выразить как функцию от у.

Таким образом, самым простым ответом на поставленный вопрос будет такой: функция f имеет обратную, если из соотношения y = f(x) переменную x можно однозначно выразить через у. Мы уже знакомы с примерами функций, для которых это можно сделать. Приведем примеры таких функций, для которых нельзя однозначно выразить аргумент через заданное значение функции.

у=\х. Для данного положительного числа у найдутся два значения аргумента х, такие, что |х|=у. Например, если у = 2, то х = 2 или х= — 2. Значит, выразить однозначно х через у нельзя.
у = 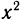. Ситуация здесь такая же, как в предыдущем примере: Х = 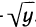или х=—.
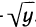y = sinx. При заданном значении у (где |y| ≤ l) найдется не по два, как в предыдущих примерах, а даже бесконечно много таких значений х, что y = sin х. Здесь также х нельзя однозначно выразить через у.

Сравним графически эти примеры с примерами, приведенными ранее. Возьмем число у0 из области значений функции f и проведем прямую у = уо, параллельную оси абсцисс. В ранее рассмотренных случаях эта прямая пересекает график в одной точке, т. е. можно по заданному значению у однозначно найти значение х. В последних трех примерах при некоторых у прямая пересекает график более чем в одной точке: для этих значений у мы не можем однозначно найти х, значит, эти функции не имеют обратных.

Дадим геометрическую трактовку условия того, что функция имеет обратную.

Функция y = f(x) имеет обратную, если всякая прямая у = уо пересекает график функции у = {х) не более чем в одной точке (она может совсем не пересекать график, если уо не принадлежит области значений функции f).

Это же условие можно сформулировать иначе: уравнение f(x)=yo при каждом уо имеет не более одного решения.

Условие того, что функция имеет обратную, заведомо выполняется, если функция строго возрастает или строго убывает. Действительно, если f, например, строго возрастает, то при двух различных значениях аргумента она принимает различные значения, так как большему значению аргумента соответствует большее значение функции. Следовательно, уравнение f(x) = y для строго монотонной функции имеет не более одного решения.

Показательная функция у = 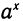Взаимно обратные функции строго монотонна, поэтому она имеет обратную — логарифмическую функцию y = loga x. Строго говоря, определение логарифма числа у требовало возможности однозначно определить показатель х, такой, что 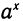Взаимно обратные функции =у, т. е. чтобы из соотношения 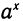=у можно было однозначно выразить х через у.

Мы знаем, что многие функции не имеют обратных. Если при некотором b уравнение f(x) = b имеет более одного решения, то функция y =f(x) обратной не имеет. На графике это означает, что прямая у = b пересекает график функции более чем в одной точке.

Многие изучавшиеся ранее функции не имеют обратных, например у = 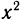Взаимно обратные функции , y = sin x, y = tg x и т. п. С неоднозначностью решения уравнения f(x)=b можно справиться следующим образом: уменьшить область определения функции f так, чтобы ее область значений не изменилась, но чтобы каждое свое значение она принимала ровно один раз.

Примеры:

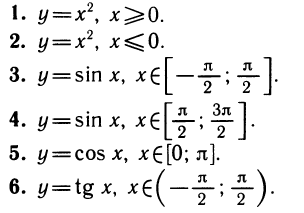
В каждом из приведенных примеров функция сохранила область значений: для у = 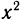Взаимно обратные функции это промежуток [0; + ∞]. Для синуса и косинуса это отрезок [—1; 1], для тангенса это вся числовая ось. В то же время, уменьшив область определения, мы добились монотонности функции, а значит, и единственности решения уравнения f(x)=b.

Каждая из выписанных выше функций имеет обратную. Для обратных операций из примеров 1, 3, 5, 6 нами раньше введены специальные обозначения:

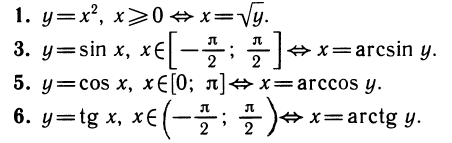
С помощью этих обозначений можно ввести функции, обратные к тем, которые были перечислены выше:

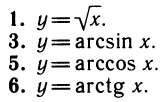
Функции в пропущенных примерах 2 и 4 можно выразить через уже введенные:

2. у=—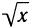 Взаимно обратные функции является обратной функцией для функции у = 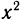, х ≤ О.

4. у = π — arcsin x является обратной функцией для функции у=sin, 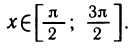Взаимно обратные функции

Проверим последнее утверждение:

а) Вычислим sin у:

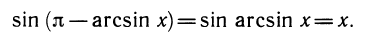
б) Проверим, что π —arcsin х имеет областью значений отрезок

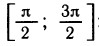
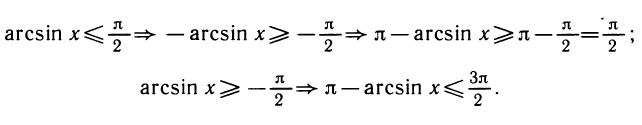
Взаимно обратные функции

Свойства взаимно обратных функций

1) Тождества. Пусть f и g — взаимно обратные функции. Это означает, что равенства y = f(х) и x=g(y) равносильны. Подставим одно из этих равенств в другое. Получим два тождества:

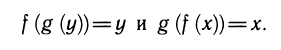
Примеры:

Пусть f — показательная, g — логарифмическая функция. Получаем знакомые тождества:

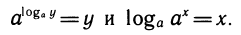
2. Функции у = Взаимно обратные функции , х ≥ 0 и у = 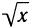взаимно обратны. Имеем два тождества:

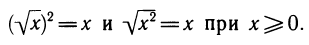
2) Область определения. Пусть f и g — взаимно обратные функции. Область определения функции f совпадает с областью значений функции g, и, наоборот, область значений функции f совпадает с областью определения функции g. Действительно, обратная функция к функции y = f(x) определена для всякого числа у, которое является значением функции f для некоторого числа х: мы берем равенство y = f(x) и из него выражаем л: как функцию от у. Это свойство наглядно проявляется на графике: график функции y = f(x) совпадает с графиком обратной функции x = g(y), только аргумент функции g откладывается по оси у. Ясно, что аргументы функции g — это значения функции f и наоборот.

Пример. Область определения показательной функции — вся числовая ось R, а ее область значений — множество всех положительных чисел. У логарифмической функции наоборот: область определения — множество всех положительных чисел, а область значений — все множество R.

3) Монотонность.

Теорема:

Если одна из взаимно обратных функций строго возрастает, то и другая строго возрастает.

Действительно, пусть f и g— взаимно обратные функции, причем f строго возрастает. Докажем, что тогда и g строго возрастает. Пусть x₁ и x₂ — два числа, лежащие в области определения функции g, причем x₁ < x₂. Надо доказать, что g ( x₁ )<g{ x₂ ). Обозначим g(x1) = y1, g( x₂)=y2. Надо доказать, что g (х)<g (х2). Обозначим g( x₁ ) = yi, g( x₂ ) = y2. Числа у1 и у2 лежат в области определения функции f, так как они являются значениями функции g. Предположим, что у1 ≥ у2. В силу монотонности функции f имеем f {у1) ≥ {у2). Но f (y1) = f{g ( x₁ )) = x₁ и f (у2)= x₂ , т. е. x₁ ≥ x₂ , что противоречит условию x₁ < x₂ . Следовательно, у1<у2, что и требовалось доказать.

Выведем общую формулу производной обратной функции аналогично тому, как мы выводили формулу производной логарифмической функции. Пусть f и g — взаимно обратные функции. Как найти производную функции g, зная производную функции f?

Графики функций y = f(x) и y=g(x) симметричны друг другу относительно биссектрисы I угла хОу (рис. 116,а).

Возьмем какую-нибудь точку х = а и вычислим значение одной из функций в этой точке: f (a)=b. Тогда по определению обратной функции g (b)—a.

Точки (а;f (а)) = (а; b) и (b; g (b))=(b; а) симметричны относительно указанной прямой l. Так как кривые симметричны, то и касательные к ним симметричны относительно прямой l.

Из симметрии ясно, что угол одной из этих прямых с осью х равен углу другой прямой с осью у. Если первая прямая образует с осью х угол а, то ее угловой коэффициент равен k1 =tg а; тогда вторая прямая имеет угловой коэффициент 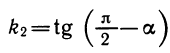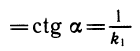Взаимно обратные функции (рис. 116,). Таким образом, угловые коэффициенты прямых, симметричных относительно прямой l, взаимно обратны, т. е.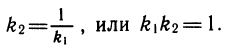

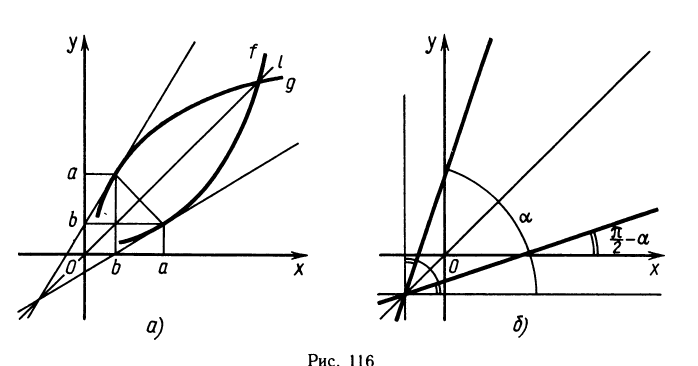
Переходя к производным и учитывая, что угловой коэффициент касательной является значением производной в точке касания, делаем вывод:

Значения производных взаимно обратных функций в соответствующих точках взаимно обратны, т. е.

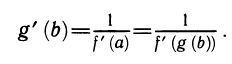
Напомним еще, что b = f{a) и a = g{b).

Замечание:

В приведенных выше рассуждениях предполагалось, что k1 ≠ 0 т. е. касательные к кривым не параллельны осям координат.

Приведем примеры нахождения производной обратной функции.

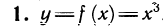
Обратной функцией будет функция y = g(x) = 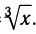Взаимно обратные функции Найдем производную функции g:

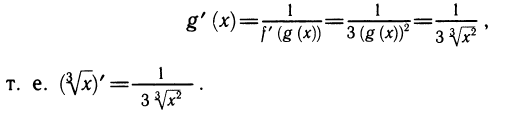
Обратной функцией будет y = g (x) = arcsin x. Найдем производную арксинуса:

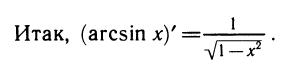
Аналогично вычисляется производная арктангенса:

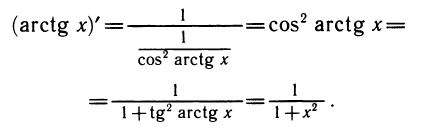
Дополнение к обратным функциям

Смотрите также:

Предмет математический анализ

Ограниченность непрерывных функций.	Равномерная непрерывность.
Промежуточные значения непрерывных функций.	Многочлены и рациональные функции.

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике: