Оглавление:
Дифференциальное исчисление — это раздел высшей математики, в котором изучаются понятия производной и дифференциала и способы их применения к исследованию функций. Формирование дифференциального исчисления связано с именами Исаака Ньютона и Готфрида Лейбница. Именно они чётко сформировали основные положения и указали на взаимообратный характер дифференцирования и интегрирования. Создание дифференциального исчисления (вместе с интегральным) открыло новую эпоху в развитии математики. С этим связаны такие дисциплины как теория рядов, теория дифференциальных уравнений и многие другие. Методы математического анализа нашли применение во всех разделах математики. Очень распространилась область применения математики в естественных науках и технике.
Что такое дифференциальное исчисление и как его решать
Производная функции
Ниже через D будет обозначаться промежуток на числовой оси 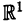 , т. е. D — это множество вида
, т. е. D — это множество вида 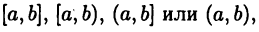 причем промежуток может быть и бесконечным.
причем промежуток может быть и бесконечным.
Пусть функция 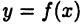 определена в некотором промежутке D и точка
определена в некотором промежутке D и точка 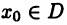 такова, что при каждом малом (по модулю) приращении
такова, что при каждом малом (по модулю) приращении 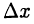 выполнено включение
выполнено включение 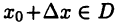 (другими словами,
(другими словами, 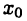 является внутренней точкой промежутка D). Тогда наряду со значением
является внутренней точкой промежутка D). Тогда наряду со значением 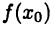 функции
функции 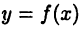 определено и значение
определено и значение 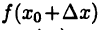 и, следовательно, функция получит приращение
и, следовательно, функция получит приращение 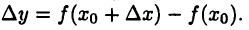
Производной функции 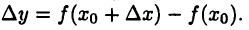 в точке
в точке 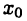 называется предел
называется предел
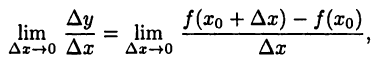
если, конечно, он существует. Если функция 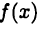 в точке
в точке 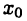 имеет производную, то говорят, что она дифференцируема в этой точке. Вычисление производной функции называют ее дифференцированием.
имеет производную, то говорят, что она дифференцируема в этой точке. Вычисление производной функции называют ее дифференцированием.
Производим функции 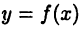 в точке х обозначается одним из символов:
в точке х обозначается одним из символов:
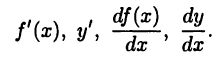
Таким образом,
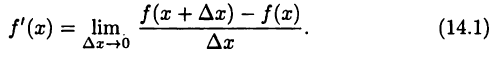
Пример:
Найти производную функции 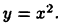 Так как
Так как
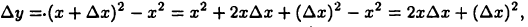
то
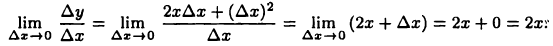
Следовательно 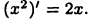
Пример:
Найти производную функции 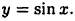 Имеем
Имеем
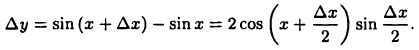
Отсюда получим
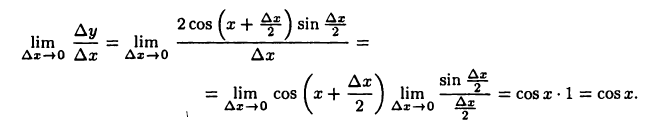
Следовательно, 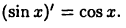
Вычисление производных и изучение их свойств составляют главный предмет дифференциального исчисления.
Геометрический и физический смысл производной
Задача о касательной к кривой
Пусть дана непрерывная функция 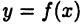 , график которой представляет собой кривую К (см. рис. 17).
, график которой представляет собой кривую К (см. рис. 17).
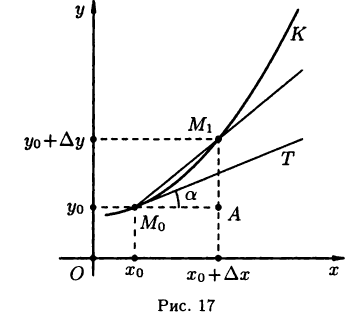
Требуется построить касательную к кривой К в некоторой точке 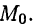 Выбрав на К еще одну точку
Выбрав на К еще одну точку 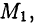 проведем секущую
проведем секущую 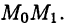 Если точку
Если точку 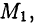 перемещать по кривой К, то секущая будет вращаться вокруг точки
перемещать по кривой К, то секущая будет вращаться вокруг точки 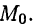 Касательной к кривой К в точке
Касательной к кривой К в точке 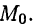 естественно назвать предельное положение
естественно назвать предельное положение 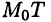 секущей, когда точка
секущей, когда точка 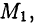 стремится вдоль кривой к точке
стремится вдоль кривой к точке 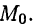
Найдем угловой коэффициент касательной 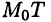 , т. е. число
, т. е. число 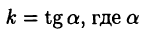 — угол между касательной
— угол между касательной 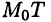 и положительным направлением оси х. Из прямоугольного треугольника
и положительным направлением оси х. Из прямоугольного треугольника 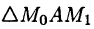 имеем
имеем
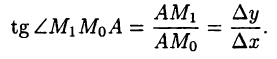
Для получения углового коэффициента k перейдем к пределу при
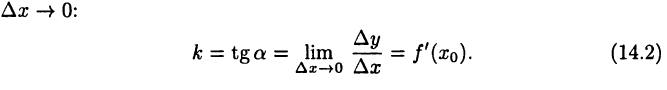
Следовательно, производная функции с геометрической точки зрения равна угловому коэффициенту касательной к графику функции в данной точке.
Задача о вычислении скорости
Рассмотрим прямолинейное движение материальной точки, положение которой определяется расстоянием S, отсчитываемым от некоторой начальной точки О (см. рис. 18).
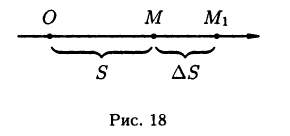
Пусть движение точки описывается функцией S(t), которая при каждом значении времени t определяет пройденное точкой расстояние S = S(t). Требуется определить скорость 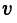 ; точки в момент времени t.
; точки в момент времени t.
Пусть в момент времени t точка занимает положение M. Для определения скорости 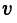 придадим t приращение
придадим t приращение 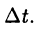 Тогда пройденный точкой путь получит приращение
Тогда пройденный точкой путь получит приращение 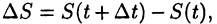 и точка окажется в новом положении
и точка окажется в новом положении 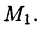 Отношение
Отношение 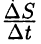 равно средней скорости движения точки за промежуток
равно средней скорости движения точки за промежуток 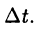 Скорость точки в момент времени t, очевидно, определится предельным переходом
Скорость точки в момент времени t, очевидно, определится предельным переходом
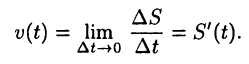
Таким образом, производная функции с физической точки зрения равна скорости движения точки в данный момент времени.
Непрерывность дифференцируемой функции
Укажем связь между понятиями непрерывности и дифференцируемости функции.
Теорема:
Если функция 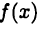 дифференцируема в точке х, то она непрерывна в этой точке.
дифференцируема в точке х, то она непрерывна в этой точке.
► Для доказательства непрерывности функции 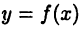 в точке х достаточно показать, что
в точке х достаточно показать, что 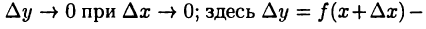
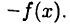
Имеем
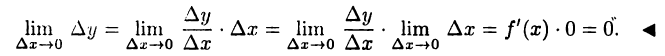
Обратное к теореме 14.1 утверждение не верно: функция может быть непрерывной в данной точке, однако не быть дифференцируемой. Простым примером является функция у = |х|, график которой изображен на рис. 8 а (с. 45); она всюду непрерывна, однако при х = 0 не дифференцируема (покажите это!).
Правила дифференцирования
Простейшие правила:
Теорема:
Если функции 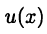 и
и 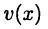 дифференцируемые точке х, то их сумма, разность, произведение и частное (последнее при условии, что
дифференцируемые точке х, то их сумма, разность, произведение и частное (последнее при условии, что 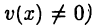 также дифференцируемы в этой точке и имеют место равенства:
также дифференцируемы в этой точке и имеют место равенства:
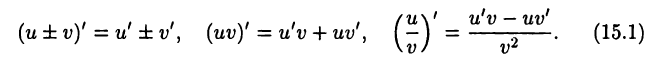
► Ограничимся доказательством второй из формул (15.1). Предварительно отметим, что в силу теоремы 14.1 функции 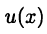 и
и 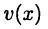 непрерывны. Поэтому
непрерывны. Поэтому
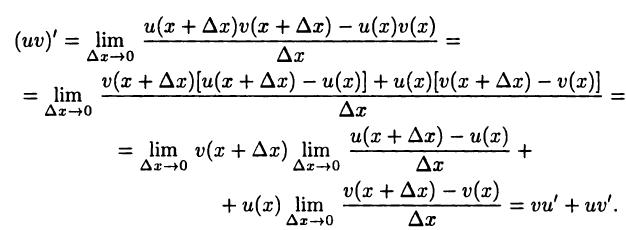
Дифференцирование сложной функции
Теорема:
Пусть дана сложная функция 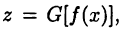 причем функция
причем функция 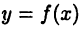 дифференцируема в точке
дифференцируема в точке 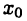 , а функция G(y) — в точке
, а функция G(y) — в точке 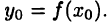
Тогда функция 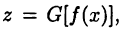 дифференцируема в точке
дифференцируема в точке 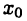 и при
и при 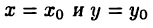 имеет место равенство
имеет место равенство
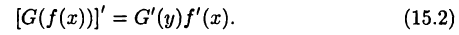
Имеем 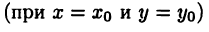
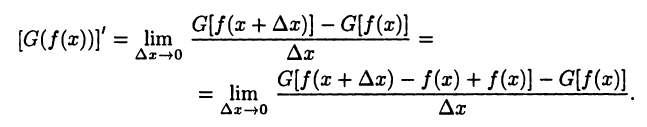
Полагая 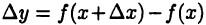 и учитывая, что в силу непрерывности функции
и учитывая, что в силу непрерывности функции 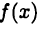 имеем
имеем 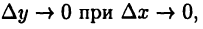 получим
получим
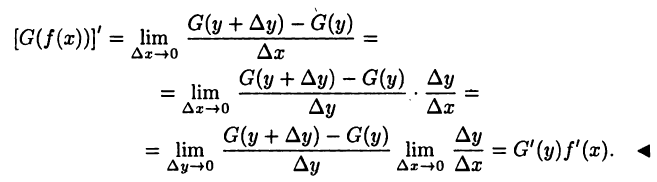
Пример:
Найти производную функции 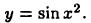 Рассматриваемая функция является суперпозицией функций
Рассматриваемая функция является суперпозицией функций 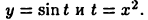 Поэтому из формулы (15.2) получим (см. также примеры 14.2 и 14.1)
Поэтому из формулы (15.2) получим (см. также примеры 14.2 и 14.1)
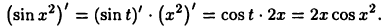
Дифференцирование обратной функции
Теорема:
Пусть дана функция 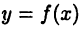 имеющая обратную функцию
имеющая обратную функцию 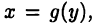 и пусть функция
и пусть функция 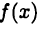 дифференцируема в точке
дифференцируема в точке 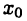 , причем
, причем 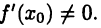 Тогда обратная функция
Тогда обратная функция 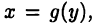 дифференцируема в соответствующей точке
дифференцируема в соответствующей точке 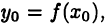 причем при
причем при 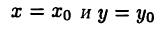 имеет место равенство
имеет место равенство

Докажите эту теорему, предварительно установив, что если придать значению 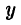 ненулевое приращение
ненулевое приращение 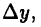 то функция
то функция 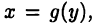 получит ненулевое приращение
получит ненулевое приращение 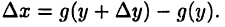
Пример:
Найдем производную функции 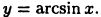 Так как эта функция является обратной к функции
Так как эта функция является обратной к функции 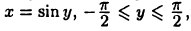 то в силу теоремы 15.3 получим (см. также пример 14.2)
то в силу теоремы 15.3 получим (см. также пример 14.2)
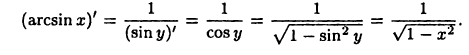
Дифференцирование функций, заданных параметрически
Пусть функция 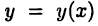 задана параметрически уравнениями
задана параметрически уравнениями 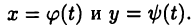
Теорема:
Пусть функции 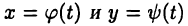 дифференцируемы при некотором
дифференцируемы при некотором 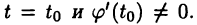 Тогда функция
Тогда функция 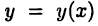 дифференцируема в точке
дифференцируема в точке 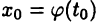 имеет место равенство
имеет место равенство

Докажите эту теорему. Указание: по определению параметрически заданных функций функция 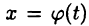 имеет обратную
имеет обратную 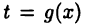 и
и 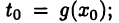 поэтому функция
поэтому функция 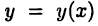 определяется равенством У = Ф\9(х)]- Далее следует воспользоваться теоремами 15.2 и 15.3.
определяется равенством У = Ф\9(х)]- Далее следует воспользоваться теоремами 15.2 и 15.3.
Производные основных элементарных функций
Выше в примерах 14.2-15.2 были найдены производные некоторых элементарных функций. Аналогично можно вычислить производные и других основных элементарных функций. В таблице 3 приведены некоторые из них.

Пользуясь таблицей 3 и основными правилами дифференцирования, приведенными в теоремах 15.1-15.4, можно вычислять производные широкого класса функций.
Односторонние производные
В определении производной предполагалось, что предел (14.1) не зависит от знака приращения 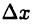 при стремлении
при стремлении 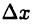 к 0. Если же в указанном определении потребовать, чтобы
к 0. Если же в указанном определении потребовать, чтобы 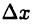 было только одного знака, то придем к понятию односторонней производной.
было только одного знака, то придем к понятию односторонней производной.
Правой производной функции 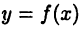 в точке
в точке 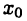 называется предел
называется предел
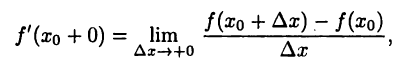
если, конечно, он существует. Аналогично определяется левая производная 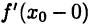 функции. Правая и левая производные функции называются ее односторонними производными.
функции. Правая и левая производные функции называются ее односторонними производными.
Ясно, что если функция 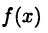 имеет в точке
имеет в точке 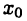 обычную производную, то она имеет и обе односторонние производные и все они совпадают. В то же время функция может иметь односторонние производные и не иметь производной
обычную производную, то она имеет и обе односторонние производные и все они совпадают. В то же время функция может иметь односторонние производные и не иметь производной 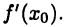 Например, функция
Например, функция 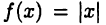 (см. рис. 8 а (с. 45)) в точке х = 0 имеет односторонние производные
(см. рис. 8 а (с. 45)) в точке х = 0 имеет односторонние производные 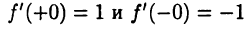 и не имеет производной
и не имеет производной 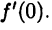 Справедлива очевидная
Справедлива очевидная
Теорема:
Для существования производной 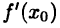 необходимо и достаточно существования и равенства ее односторонних производных
необходимо и достаточно существования и равенства ее односторонних производных 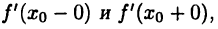 при этом
при этом
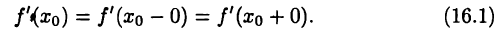
Бесконечные производные
В определении производной предполагалось, что предел (14.1) должен быть конечным. Если же выполнено равенство
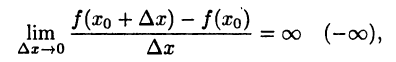
то говорят, что функция 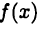 в точке
в точке 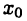 имеет бесконечную производную и пишут
имеет бесконечную производную и пишут 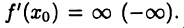 Геометрически этот факт означает, что касательная к кривой
Геометрически этот факт означает, что касательная к кривой 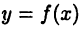 в точке
в точке 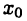 параллельна оси у.
параллельна оси у.
Пример:
Покажем, что функция 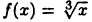 в точке х = 0 имеет бесконечную производную
в точке х = 0 имеет бесконечную производную 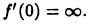 Действительно, имеем
Действительно, имеем
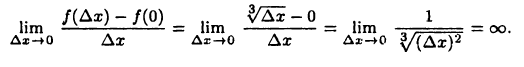
Производные высших порядков
Пусть функция 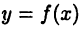 имеет конечную производную
имеет конечную производную 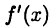 в каждой точке х некоторого множества D. Тогда ее производную
в каждой точке х некоторого множества D. Тогда ее производную 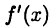 можно рассматривать как функцию, определенную на множестве D. В свою очередь функция
можно рассматривать как функцию, определенную на множестве D. В свою очередь функция 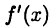 может в некоторых точках множества D иметь производную. В этом случае говорят о производной
может в некоторых точках множества D иметь производную. В этом случае говорят о производной 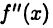 второго порядка (в отличие от производной
второго порядка (в отличие от производной 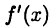 называемой также производной первого порядка). Таким образом,
называемой также производной первого порядка). Таким образом,
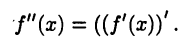
Производная второго порядка функции 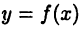 обозначается также символами
обозначается также символами
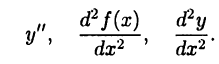
Аналогично определяются производные третьего, четвертого и т. д. порядков. При этом производная 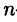 -го порядка функции
-го порядка функции 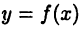 обозначается символами
обозначается символами 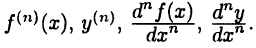
Например, для функции 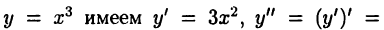
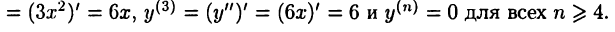
Дифференциал функции и приближенные вычисления
Формула для приращения функции
Важное значение в теории дифференцируемых функций имеет
Теорема:
Пусть функция 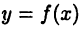 имеет производную
имеет производную 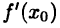 Тогда справедливо равенство
Тогда справедливо равенство
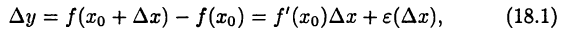
где функция 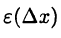 удовлетворяет соотношению:
удовлетворяет соотношению:

► Функцию 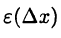 определим формулой
определим формулой 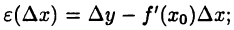 тогда равенство (18.1) очевидно. Остается убедиться в справедливости соотношения (18.2). Имеем
тогда равенство (18.1) очевидно. Остается убедиться в справедливости соотношения (18.2). Имеем
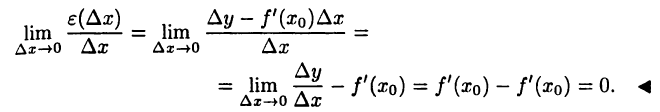
В силу равенства (18.2) функция 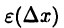 является б. м. ф. более высокого порядка, чем
является б. м. ф. более высокого порядка, чем 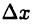 следовательно, имеет смысл говорить о приближенных равенствах (при малых
следовательно, имеет смысл говорить о приближенных равенствах (при малых 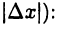
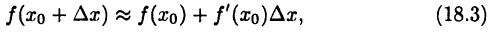
или
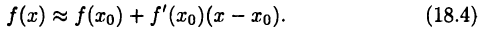
Формулы (18.3) и (18.4) важны в задачах, когда известны значения функции 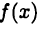 И ее производной
И ее производной 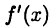 В точке
В точке 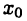 и требуется вычислить значение функции
и требуется вычислить значение функции 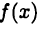 в некоторой близкой к
в некоторой близкой к 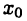 точке х.
точке х.
Пример:
Вычислить приближенно значение sin32°. Воспользуемся формулой (18.4). Для этого определим функцию 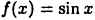 и положим
и положим 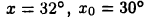 или в радианах
или в радианах 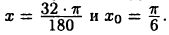 Тогда учитывая, что
Тогда учитывая, что 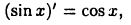
получим 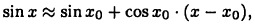 или
или
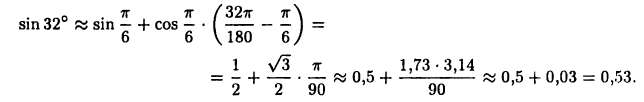
Для сравнения: имеет место равенство sin 32° = 0,5299 с четырьмя верными знаками.
Дифференциал функции
Если обозначить 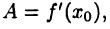 то равенство (18.1) примет вид
то равенство (18.1) примет вид

где 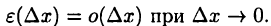
Допустим теперь, что нам неизвестно, имеет ли функция 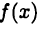 производную
производную 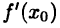 однако известно, что ее приращение
однако известно, что ее приращение 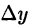 представимо в виде (18.5), где А — некоторое число. Тогда при
представимо в виде (18.5), где А — некоторое число. Тогда при 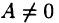 приращение
приращение 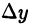 эквивалентно функции
эквивалентно функции 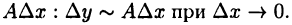 Выражение
Выражение 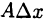 в указанном случае представляет собой главную часть приращения
в указанном случае представляет собой главную часть приращения 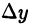 , при этом
, при этом 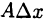 линейно (точнее пропорционально) зависит от
линейно (точнее пропорционально) зависит от 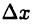 .
.
Если имеет место равенство (18.5), где А — некоторое число, то функцию 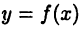 называют дифференцируемой в точке
называют дифференцируемой в точке 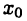 , а главную линейную часть ее приращения называют дифференциалом в точке
, а главную линейную часть ее приращения называют дифференциалом в точке 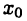 и обозначают в виде
и обозначают в виде
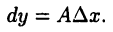
Подчеркнем, что дифференциал — это линейная функция от 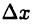 (бесконечно малая при
(бесконечно малая при 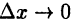 ).
).
Внимательный читатель заметил, что понятие дифференцируемо-сти функции в точке уже определялось выше как существование производной в данной точке. Наличие двух разных определений одного и того же понятия оправдывает
Теорема:
Для того чтобы функция 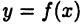 имела производную
имела производную 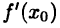 , необходимо и достаточно, чтобы функция
, необходимо и достаточно, чтобы функция 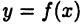 была дифференцируема в точке
была дифференцируема в точке 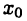 .
.
► Необходимость следует из теоремы 18.1. Докажем достаточность. Пусть выполнено равенство (18.5) при некотором А. Тогда
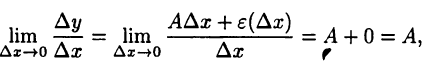
т. е. функция 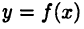 имеет производную
имеет производную 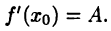
Таким образом, если функция 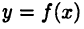 дифференцируема в точке
дифференцируема в точке 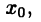 , то она имеет производную
, то она имеет производную 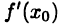 и при этом дифференциал
и при этом дифференциал 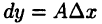 может быть записан в виде
может быть записан в виде
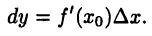
В частности, дифференциал функции 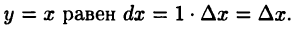
Поэтому
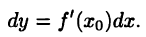
Эта формула объясняет смысл одного из обозначений производной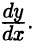
Пример:
Найти дифференциалы функций 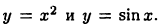 Имеем, соответственно,
Имеем, соответственно,
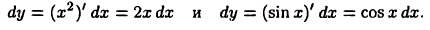
Отметим очевидные равенства
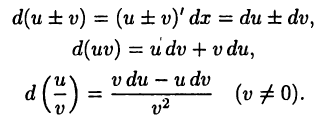
Выражение 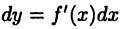 называют также дифференциалом первого порядка. При фиксированном
называют также дифференциалом первого порядка. При фиксированном 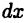 дифференциал
дифференциал 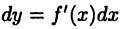 представляет собой функцию переменной х. Поэтому можно говорить о ее дифференциале, который называют дифференциалом второго порядка и обозначают в виде
представляет собой функцию переменной х. Поэтому можно говорить о ее дифференциале, который называют дифференциалом второго порядка и обозначают в виде
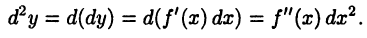
Аналогично определяются и дифференциалы более высоких порядков. При этом дифференциал 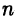 -го порядка вычисляется по формуле
-го порядка вычисляется по формуле
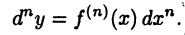
Докажите это по индукции (при этом следует помнить, что 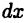 нужно рассматривать как постоянный множитель).
нужно рассматривать как постоянный множитель).
Основные свойства дифференцируемых функций
Пусть функция 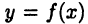 в каждой точке множества имеет D конечную производную
в каждой точке множества имеет D конечную производную 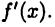 В этом случае будем говорить, что функция
В этом случае будем говорить, что функция 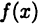 дифференцируема на множестве D.
дифференцируема на множестве D.
Выше в § 13 (с. 63) было введено понятие множества С(D) непрерывных на D функций. Аналогично через 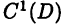 будем обозначать множество дифференцируемых на D функций. Следовательно, запись
будем обозначать множество дифференцируемых на D функций. Следовательно, запись 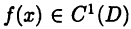 будет означать, что функция
будет означать, что функция 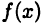 определена на множестве D и в каждой точке
определена на множестве D и в каждой точке 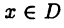 имеет производную
имеет производную 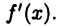 Например,
Например, 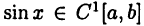 на любом отрезке
на любом отрезке 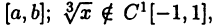 так как функция
так как функция 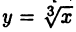 не дифференцируема при х = 0.
не дифференцируема при х = 0.
Имеет место включение

т. е. каждая дифференцируемая на D функция является и непрерывной на D. Справедливость включения (19.1) следует из теоремы 14.1.
В общем случае через 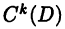 будем обозначать множество определенных на D функций и имеющих в каждой точке
будем обозначать множество определенных на D функций и имеющих в каждой точке 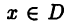 конечную производную k-го порядка.
конечную производную k-го порядка.
Теоремы о средних значениях
Были изучены некоторые свойства непрерывных на отрезке 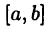 функций (например, их ограниченность и наличие наибольшего и наименьшего значений). Знание производной функции
функций (например, их ограниченность и наличие наибольшего и наименьшего значений). Знание производной функции 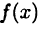 позволяет провести более детальное исследование функции. Такому исследованию посвящена основная часть этого и следующего параграфов.
позволяет провести более детальное исследование функции. Такому исследованию посвящена основная часть этого и следующего параграфов.
Приведем сначала понятия, связанные с наибольшим и наименьшим значениями функции.
Пусть функция 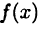 определена на отрезке
определена на отрезке 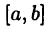 и
и 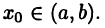 Говорят, что в точке
Говорят, что в точке 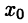 функция
функция 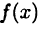 имеет локальный максимум (минимум), если
имеет локальный максимум (минимум), если 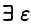 -окрестность
-окрестность 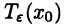 точки
точки 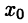 такая, что для
такая, что для 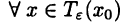 выполняется неравенство
выполняется неравенство 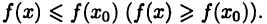 Если же для
Если же для 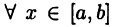 выполняется неравенство
выполняется неравенство 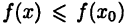
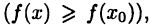 то говорят, что в точке
то говорят, что в точке 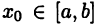 функция
функция 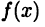 имеет глобальный максимум (минимум). Если в этих неравенствах знаки
имеет глобальный максимум (минимум). Если в этих неравенствах знаки 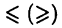 заменить на знаки
заменить на знаки 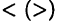 (естественно, считая, что в них
(естественно, считая, что в них 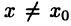 ), то говорят о строгих максимумах и минимумах. Точки минимума и максимума имеют общий термин — точки экстремума функции.
), то говорят о строгих максимумах и минимумах. Точки минимума и максимума имеют общий термин — точки экстремума функции.
Рассмотрим, например, функцию 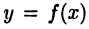 график которой изображен на рис. 19.
график которой изображен на рис. 19.
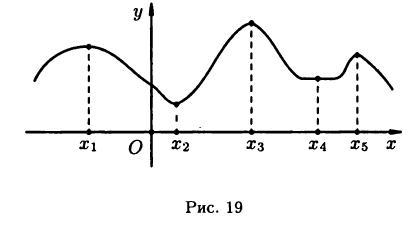
Эта функция в точках 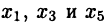 имеет локальные максимумы, а в точках
имеет локальные максимумы, а в точках 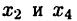 — локальные минимумы, при этом
— локальные минимумы, при этом 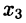 — точка глобального максимума, а
— точка глобального максимума, а 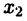 — глобального минимума. Указанные точки, за исключением
— глобального минимума. Указанные точки, за исключением 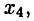 являются точками строгого экстремума.
являются точками строгого экстремума.
При отыскании экстремумов дифференцируемой функции пользуются утверждением, содержащим необходимое условие экстремума функции.
Теорема Ферма:
Пусть 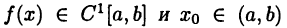 — точка экстремума этой функции. Тогда
— точка экстремума этой функции. Тогда 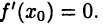
Пусть для определенности 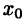 — точка локального максимума функции
— точка локального максимума функции 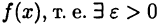 такое, что
такое, что 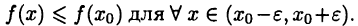
Так как функция 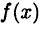 имеет производную
имеет производную 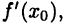 то существуют односторонние производные:
то существуют односторонние производные:
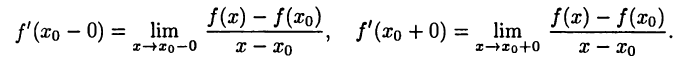
Но при 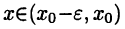 выполнено неравенство
выполнено неравенство 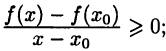 следовательно,
следовательно, 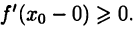 Аналогично получим
Аналогично получим 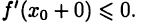 Отсюда и из (16.1) следует равенство
Отсюда и из (16.1) следует равенство 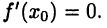
Геометрической иллюстрацией теоремы Ферма служит тот факт, что если в точке 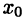 функция
функция 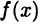 имеет экстремум, то в соответствующей точке касательная к графику кривой параллельна оси х (см, рис. 20 а).
имеет экстремум, то в соответствующей точке касательная к графику кривой параллельна оси х (см, рис. 20 а).
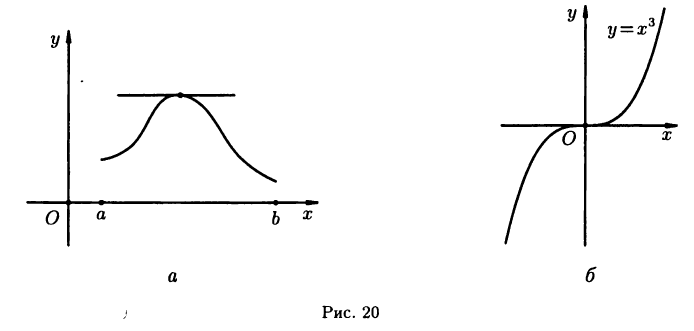
Обратное к теореме Ферма утверждение, вообще говоря, неверно. Это видно на примере функции 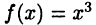 (см. рис. 20 б).
(см. рис. 20 б).
Теорема Ролля:
Пусть 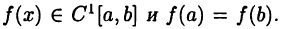 Тогда
Тогда 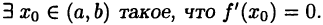
► Так как  то (см. (19.1))
то (см. (19.1)) 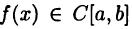 и, следовательно, по второй теореме Вейерштрасса (см. приведенную на с. 65 теорему 13.5) функция
и, следовательно, по второй теореме Вейерштрасса (см. приведенную на с. 65 теорему 13.5) функция 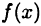 достигает на отрезке
достигает на отрезке 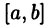 наибольшего М и наименьшего т значения. Возможны два случая: М > т или М = т.
наибольшего М и наименьшего т значения. Возможны два случая: М > т или М = т.
В первом случае в силу равенства 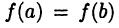 по крайней мере одно из значений М или т функция принимает внутри интервала (а, b). Пусть, например,
по крайней мере одно из значений М или т функция принимает внутри интервала (а, b). Пусть, например, 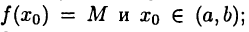 тогда по теореме Ферма получим
тогда по теореме Ферма получим 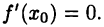
Во втором случае функция 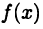 является постоянной; тогда
является постоянной; тогда 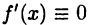 и, следовательно, в качестве
и, следовательно, в качестве 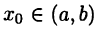 можно взять любое число из интервала (а, b)
можно взять любое число из интервала (а, b)
Важную роль во многих теоретических и практических задачах играет
Теорема Лагранжа:
Пусть 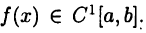 Тогда
Тогда 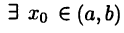 такое, что
такое, что
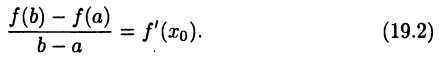
► Определим вспомогательную функцию
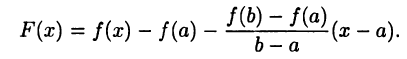
Несложно видеть, что для функции F(x) выполнены все условия теоремы Ролля. Следовательно, найдется 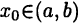 такое, что
такое, что 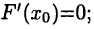 последнее равенство эквивалентно соотношению (19.2). <
последнее равенство эквивалентно соотношению (19.2). <
Геометрически теорема Лагранжа означает, что на кривой АВ найдется точка 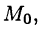 в которой касательная к кривой параллельна хорде АВ (см. рис. 21):
в которой касательная к кривой параллельна хорде АВ (см. рис. 21): 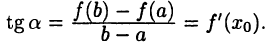
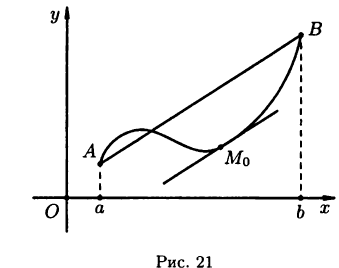
Формула (19.2) называется формулой Лагранжа или формулой конечных приращений. Ее часто записывают в виде
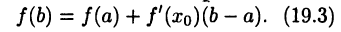
Эта формула является точной в отличие от приближенной формулы (18.4):
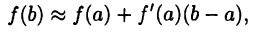
и хотя в формуле (19.3) присутствует неопределенное значение 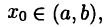 тем не менее она имеет многочисленные приложения.
тем не менее она имеет многочисленные приложения.
Теорема Лагранжа является частным случаем следующего утверждения.
Теорема Коши:
Пусть 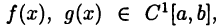 причем
причем 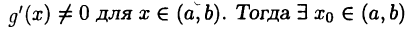 такое, что
такое, что
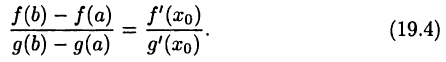
Сначала заметим, что 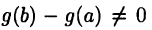 (иначе выражение в левой части равенства (19.4) не имело бы смысла); действительно, если бы
(иначе выражение в левой части равенства (19.4) не имело бы смысла); действительно, если бы 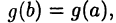 то, по теореме Ролля, нашлась бы точка
то, по теореме Ролля, нашлась бы точка 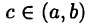 такая, что
такая, что 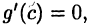 что противоречит условию теоремы. Дальнейшее доказательство теоремы почти дословно повторяет доказательство теоремы 19.3 с той лишь разницей, что рассматривается вспомогательная функция
что противоречит условию теоремы. Дальнейшее доказательство теоремы почти дословно повторяет доказательство теоремы 19.3 с той лишь разницей, что рассматривается вспомогательная функция
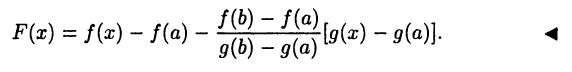
Равенство (19.4) называется формулой Коши.
Формулы Тейлора и Маклорена
Наиболее простыми из элементарных функций являются, пожалуй, степенные, т. е. функции вида 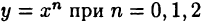 и т. д. Свойства этих функций очевидны, их несложно представлять графически, легко дифференцировать и т. п. Одним из эффективных методов исследования в математическом анализе и его приложениях является возможность представления произвольной дифференцируемой функции в виде суммы степенных функций. Разумеется, что речь, вообще говоря, идет о приближенном представлении функции.
и т. д. Свойства этих функций очевидны, их несложно представлять графически, легко дифференцировать и т. п. Одним из эффективных методов исследования в математическом анализе и его приложениях является возможность представления произвольной дифференцируемой функции в виде суммы степенных функций. Разумеется, что речь, вообще говоря, идет о приближенном представлении функции.
Формулы Тейлора и Маклорена для многочленов
Многочленом n-го порядка называется функция

где 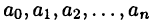 — некоторые числа, называемые коэффициентами многочлена (19.5).
— некоторые числа, называемые коэффициентами многочлена (19.5).
Многочлен (19.5) полностью определяется своими коэффициентами. Зададимся вопросом: если известны значения многочлена (19.5) и его производных до n-го порядка в точке х = 0, т. е. числа 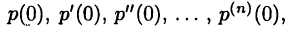 то можно ли восстановить многочлен (19.5), т. е. вычислить числа
то можно ли восстановить многочлен (19.5), т. е. вычислить числа 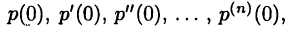 ?
?
Ответ на этот вопрос положителен. Действительно, продифференцируем многочлен (19.5) последовательно 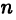 раз:
раз:
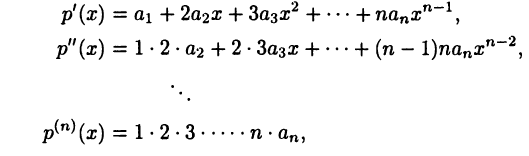
и, подставляя в эти равенства значение х = 0, найдем
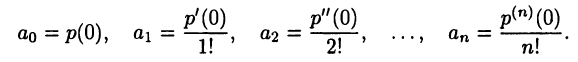
Подставляя вычисленные значения в (19.5), получим
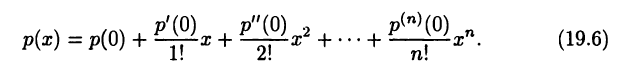
Аналогично можно рассмотреть и общий случай, когда известны числа 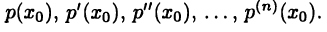 В этом случае многочлен (19.5) представляется в виде
В этом случае многочлен (19.5) представляется в виде
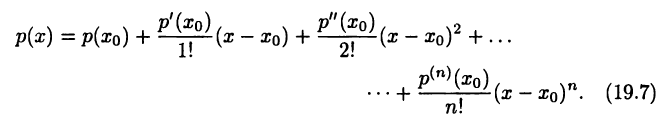
Равенства (19.6) и (19.7) называют формулами Тейлора для многочлена (19.5). Впрочем, равенство (19.6), являющееся частным случаем формулы (19.7) при 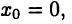 называют также формулой Маклорена.
называют также формулой Маклорена.
Формулы Тейлора и Маклорена для произвольной функции
Рассмотрим теперь произвольную функцию 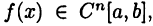 где
где  Пусть
Пусть 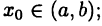 определим аналог многочлена (19.7):
определим аналог многочлена (19.7):
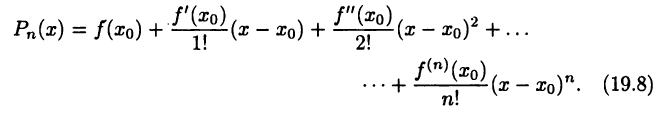
Очевидны равенства
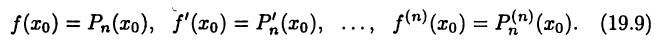
Несмотря на эти равенства, нельзя утверждать, что 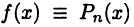 (как это было для многочленов (19.5) и (19.7)). Тем не менее факт выполнения равенств (19.9) дает основание говорить о приближенном равенстве
(как это было для многочленов (19.5) и (19.7)). Тем не менее факт выполнения равенств (19.9) дает основание говорить о приближенном равенстве 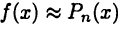 при близких к
при близких к 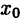 значениях х.
значениях х.
Положим

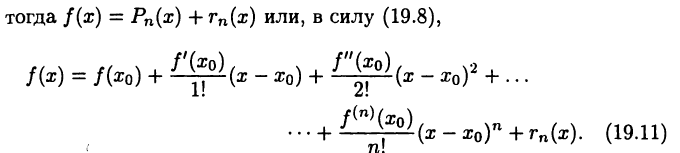
Это равенство называют формулой Тейлора для функции 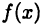 в окрестности точки
в окрестности точки 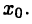 При
При 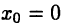 формула (19.11) принимает вид
формула (19.11) принимает вид
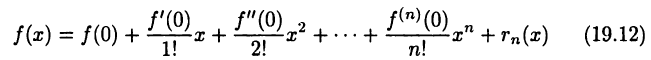
и называется формулой Маклорена для функции 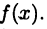
Определенная равенством (19.10) разность 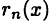 называется остаточным (дополнительным) членом в формуле Тейлора. Он указывает величину погрешности, которая возникает при замене
называется остаточным (дополнительным) членом в формуле Тейлора. Он указывает величину погрешности, которая возникает при замене 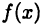 многочленом (19.8). Известны различные представления
многочленом (19.8). Известны различные представления 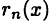 . Приведем два из них, справедливых для функций
. Приведем два из них, справедливых для функций 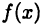 , обладающих в окрестности точки
, обладающих в окрестности точки 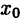 непрерывной производной
непрерывной производной 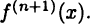
Во-первых, это дополнительный член в форме Лагранжа:
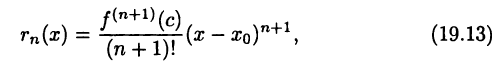
где с — некоторая точка, лежащая между х и 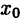 .В этой форме дополнительный член напоминает очередной член формулы Тейлора, в котором производную вычисляют не в точке
.В этой форме дополнительный член напоминает очередной член формулы Тейлора, в котором производную вычисляют не в точке 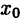 , а в некоторой точке с. Во-вторых, это дополнительный член в форме Пеано:
, а в некоторой точке с. Во-вторых, это дополнительный член в форме Пеано:
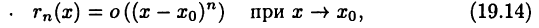
т. е.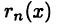 представляет собой б. м. ф. высшего порядка, чем
представляет собой б. м. ф. высшего порядка, чем 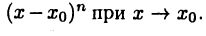
Формулы Маклорена для элементарных функции
Приведем для иллюстрации формулы Маклорена основных элементарных функций. С этой целью в формулу (19.12) вместо 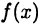 последовательно подставим функции
последовательно подставим функции 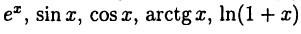 и
и 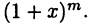 Тогда получим
Тогда получим
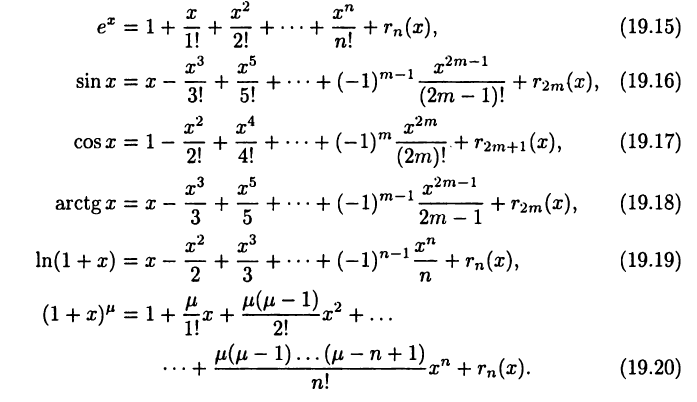
Приближенные формулы:
Формулы (19.11) и (19.12) часто используются в приближенных вычислениях. Рассмотрим для простоты формулу (19.12). Если в ней отбросить дополнительный член, то получим приближенную формулу
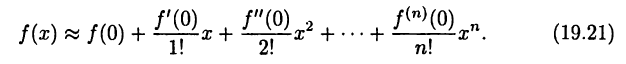
Ее точность оценивается границей погрешности 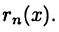
Пример:
Рассмотрим разложение (19.16) функции 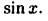 Из формулы (19.13) для дополнительного члена
Из формулы (19.13) для дополнительного члена 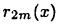 получим оценку
получим оценку
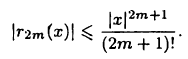
Рассмотрим формулу (19.16) сначала при т = 1, т. е. пусть 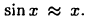 Тогда погрешность будет меньше 0,001 для чисел х, удовлетворяющие неравенству
Тогда погрешность будет меньше 0,001 для чисел х, удовлетворяющие неравенству
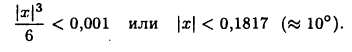
Пусть теперь m = 2, т. е. рассмотрим приближенную формулу 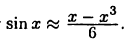 Тогда для достижения той же точности достаточно брать числа х, удовлетворяющие неравенству
Тогда для достижения той же точности достаточно брать числа х, удовлетворяющие неравенству
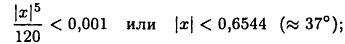
если же здесь ограничиться углами 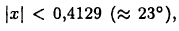 то погрешность будет меньше 0,0001.
то погрешность будет меньше 0,0001.
Правило лопиталя
Понятие производной можно использовать при раскрытии неопределенностей (см. с. 58). Ограничимся здесь рассмотрением неопределенности вида 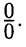 Приводимые ниже правила называют правилами Лопиталя.* В них используются обычные обозначения для односторонних пределов функций.
Приводимые ниже правила называют правилами Лопиталя.* В них используются обычные обозначения для односторонних пределов функций.
Правило:
Пусть 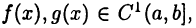 причем
причем 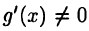 для
для 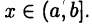 Пусть
Пусть 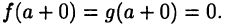 Тогда имеет место равенство
Тогда имеет место равенство
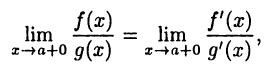
если существует (конечный или нет) второй из этих пределов.
► Доопределим функции 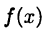 и
и 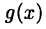 в точке х = а равенствами
в точке х = а равенствами 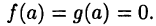 Тогда они будут непрерывны на всем отрезке [а, b], и по теореме 19.4 (Коши) для
Тогда они будут непрерывны на всем отрезке [а, b], и по теореме 19.4 (Коши) для 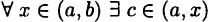 такое, что
такое, что
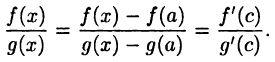
Отсюда при 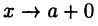 получим, во-первых,
получим, во-первых, 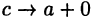 и, во-вторых,
и, во-вторых,
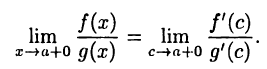
Правило L1 легко распространяется на случай, когда аргумент х стремится к бесконечности с плюсом или минусом.
Правило:
Пусть 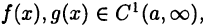 причем
причем 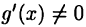 для х > а. Пусть
для х > а. Пусть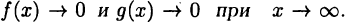 Тогда имеет место равенство
Тогда имеет место равенство
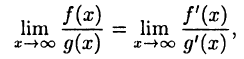
если существует (конечный или нет) второй из этих пределов.
Аналогичные правила существуют и для неопределенности вида 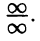
Пример:
Найти предел (замечательный предел (12.2))
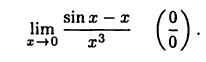
Имеем
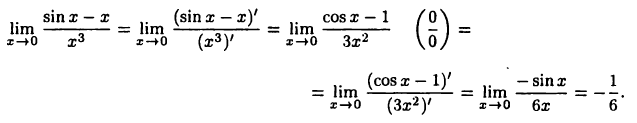
Пример:
Найти предел
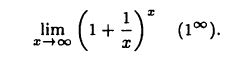
Имеем
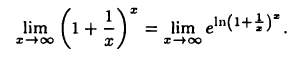
Ho
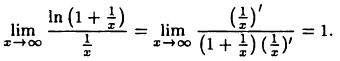
Поэтому искомый предел равен е.
Последний пример иллюстрирует тот факт, что правило Лопиталя применимо для неопределенностей разных типов; при этом необходимо предварительно преобразовать выражение к неопределенности типа 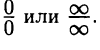
Исследование функций и построение графиков
Знание производных функции позволяет провести детальное исследование многих ее свойств: участки возрастания и убывания, наличие максимумов и минимумов, предельное поведение и т. п. Здесь обсуждаются основные вопросы, связанные с исследованием функций.
Признаки монотонности
Основной при определении интервалов возрастания и убывания функции является
Теорема:
Пусть 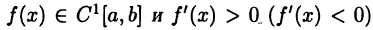 для
для 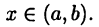 Тогда функция
Тогда функция 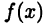 на отрезке [а, b] монотонно возрастает (убывает).
на отрезке [а, b] монотонно возрастает (убывает).
► Ограничимся рассмотрением случая 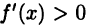 и покажем, что тогда функция
и покажем, что тогда функция 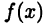 на [а, b] возрастает, т. е. для
на [а, b] возрастает, т. е. для 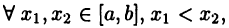 выполнено неравенство
выполнено неравенство 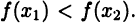 Действительно, в силу теоремы 19.3 Все
Действительно, в силу теоремы 19.3 Все 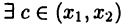 такое, что
такое, что
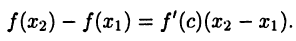
Так как 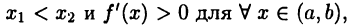 то из последнего равенства получим
то из последнего равенства получим 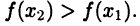
Пример:
Определить участки монотонности функции 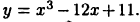 Имеем
Имеем 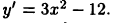 Решая последовательно неравенства
Решая последовательно неравенства 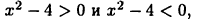 найдем, что функция возрастает при
найдем, что функция возрастает при 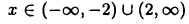 и убывает при
и убывает при 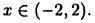
Экстремумы
Теорема 19.1 дает необходимый признак экстремума функции 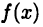 в виде
в виде 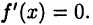 Как было отмечено, этот признак не является достаточным для существования экстремума. Поэтому точки, в которых выполняется равенство
Как было отмечено, этот признак не является достаточным для существования экстремума. Поэтому точки, в которых выполняется равенство 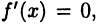 являются лишь «подозрительными» на экстремум и подлежат дополнительному исследованию. Это исследование можно проводить на основе одного из двух следующих правил.
являются лишь «подозрительными» на экстремум и подлежат дополнительному исследованию. Это исследование можно проводить на основе одного из двух следующих правил.
Правило:
Пусть 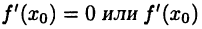 не существует, и пусть в некоторой
не существует, и пусть в некоторой 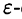 окрестности точки
окрестности точки 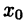 выполнено
выполнено 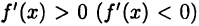 слева от
слева от 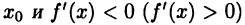 справа от
справа от 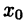 . Тогда функция
. Тогда функция 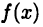 в точке
в точке 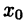 имеет максимум (минимум). Если же
имеет максимум (минимум). Если же 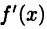 имеет один и тот же знак как слева, так и справа от
имеет один и тот же знак как слева, так и справа от 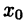 , то в этой точке функция
, то в этой точке функция 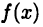 не имеет экстремума.
не имеет экстремума.
Другими словами, если производная 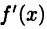 при переходе через
при переходе через 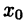 меняет знак с «+» на «-», то функция
меняет знак с «+» на «-», то функция 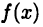 в точке
в точке 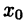 имеет максимум, и с «—» на «+» — минимум.
имеет максимум, и с «—» на «+» — минимум.
► Ограничимся рассмотрением случая, когда производная 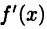 при переходе через
при переходе через 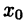 меняет знак с + на —. Пусть сначала х <
меняет знак с + на —. Пусть сначала х < 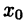 тогда
тогда
по теореме Лагранжа
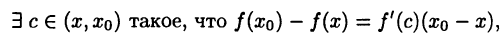
и так как 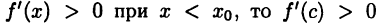 и, следовательно,
и, следовательно, 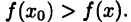 Аналогично и для
Аналогично и для 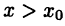 устанавливается неравенство
устанавливается неравенство 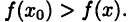
Пример:
Найти экстремумы функции 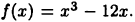 Решая уравнение
Решая уравнение 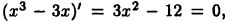 найдем «подозрительные» на экстремум точки:
найдем «подозрительные» на экстремум точки: 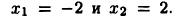 Знаки производной
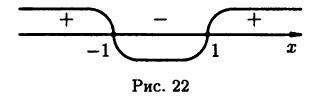
Знаки производной 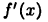 удобно изображать над числовой прямой (см. рис. 22). Приведенный рисунок показывает, что производная рассматриваемой функции меняет знак с «+» на «-» в точке х = -1 и с «—» на «+» в точке х = 1. Следовательно, рассматриваемая функция в точке х = -1 имеет максимум:
удобно изображать над числовой прямой (см. рис. 22). Приведенный рисунок показывает, что производная рассматриваемой функции меняет знак с «+» на «-» в точке х = -1 и с «—» на «+» в точке х = 1. Следовательно, рассматриваемая функция в точке х = -1 имеет максимум: 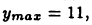 а в точке X = 1 — минимум:
а в точке X = 1 — минимум: 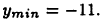
Пример:
Непрерывная функция 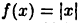 в точке х = 0 не имеет производной, при этом
в точке х = 0 не имеет производной, при этом 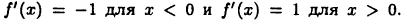 Она имеет минимум у = 0 в точке х = 0. Это, впрочем, видно и из ее графика (см. приведенный на с. 45 рис. 8 а).
Она имеет минимум у = 0 в точке х = 0. Это, впрочем, видно и из ее графика (см. приведенный на с. 45 рис. 8 а).
Правило:
Пусть 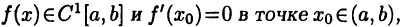 и пусть
и пусть 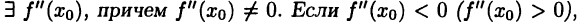 то функция
то функция 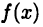 в точке
в точке 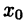 имеет максимум (минимум).
имеет максимум (минимум).
► По определению вторая производная 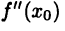 вычисляется по формуле
вычисляется по формуле
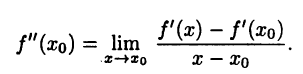
Пользуясь этим равенством, а также условием 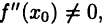 легко показать, что для функции
легко показать, что для функции 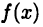 выполнены все условия правила
выполнены все условия правила
Пример:
Для рассмотренной в примере 20.2 функции 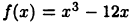 имеем
имеем 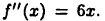 Тогда для «подозрительных» на экстремум точек
Тогда для «подозрительных» на экстремум точек 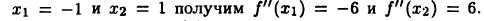 Следовательно, в точке х =-1 функция
Следовательно, в точке х =-1 функция 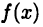 имеет максимум, а в точке х = 1 — минимум.
имеет максимум, а в точке х = 1 — минимум.
Направления выпуклости и точки перегиба
Пусть 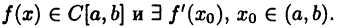
Если в некоторой 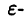 окрестности точки
окрестности точки 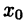 график функции
график функции 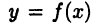 расположен не ниже (не выше) касательной к графику в точке
расположен не ниже (не выше) касательной к графику в точке 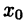 , то говорят, что график функции
, то говорят, что график функции 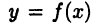 в точке
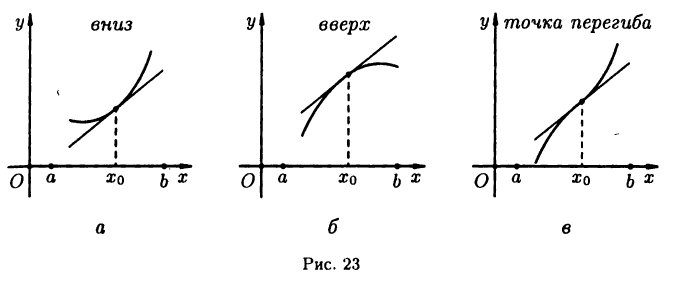
в точке 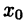 имеет выпуклость вниз (вверх) (см. рис. 23 а и б).
имеет выпуклость вниз (вверх) (см. рис. 23 а и б).
Для определения направления выпуклости графика функции можно пользоваться следующим правилом.
Теорема:
Если 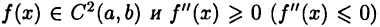 для
для 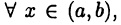 то график функции
то график функции 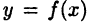 на интервале (а,b) имеет выпуклость вниз (вверх).
на интервале (а,b) имеет выпуклость вниз (вверх).
Точка 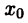 называется точкой перегиба графика функции
называется точкой перегиба графика функции 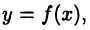 если
если 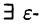 окрестность точки
окрестность точки 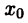 такая, что в ее левой
такая, что в ее левой 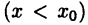 и правой
и правой 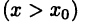 половине график функции
половине график функции 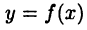 имеет разные направления выпуклости.
имеет разные направления выпуклости.
В точке перегиба касательная пересекает график функции 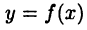 так, что с одной стороны от этой точки график расположен под касательной, а с другой — над нею (см. рис. 23 в).
так, что с одной стороны от этой точки график расположен под касательной, а с другой — над нею (см. рис. 23 в).
Из теоремы 20.2 следует необходимое условие точки перегиба.
Теорема:
Пусть график функции 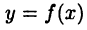 имеет точку перегиба
имеет точку перегиба 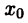 , причем существует непрерывная производная второго порядка
, причем существует непрерывная производная второго порядка 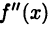 в некоторой окрестности точки
в некоторой окрестности точки 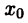 .Тогда
.Тогда 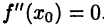
Отметим два момента. Во-первых, не всякая точка 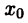 , в которой
, в которой 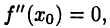 является точкой перегиба графика функции
является точкой перегиба графика функции 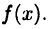 Например, для функции
Например, для функции 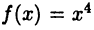 имеем
имеем 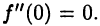 Однако в точке х = 0 график этой функции не имеет перегиба. Во-вторых, график функции может иметь перегиб в точке, в которой не существует второй производной. Например, функция
Однако в точке х = 0 график этой функции не имеет перегиба. Во-вторых, график функции может иметь перегиб в точке, в которой не существует второй производной. Например, функция 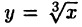 не имеет второй производной в точке х = 0,однако эта точка для нее является точкой перегиба.
не имеет второй производной в точке х = 0,однако эта точка для нее является точкой перегиба.
Поэтому если выполнено равенство 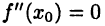 или не существует вторая производная
или не существует вторая производная 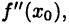 то необходимо провести дополнительное исследование о наличии перегиба в точке
то необходимо провести дополнительное исследование о наличии перегиба в точке 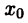 . Такое исследование может быть проведено на основе вытекающего из теоремы 20.3 следующего утверждения.
. Такое исследование может быть проведено на основе вытекающего из теоремы 20.3 следующего утверждения.
Теорема:
Пусть 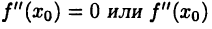 не существует. Если
не существует. Если 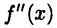 меняет знак при переходе через точку
меняет знак при переходе через точку 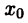 , то в указанной точке график функции имеет перегиб.
, то в указанной точке график функции имеет перегиб.
Пример:
Для рассмотренной в примере 20.2 функции 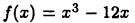 имеем
имеем 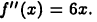 Из уравнения 6х = 0 находим единственную точку х = 0, где график функции может иметь перегиб. Так как функция
Из уравнения 6х = 0 находим единственную точку х = 0, где график функции может иметь перегиб. Так как функция 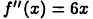 меняет знак при переходе через точку х = 0, то эта точка является точкой перегиба графика функции
меняет знак при переходе через точку х = 0, то эта точка является точкой перегиба графика функции 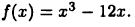
Асимптоты
Если график функции как угодно близко приближается к некоторой прямой, то такая прямая называется асимптотой функции. Существует три типа асимптот: вертикальные, горизонтальные и наклонные (см. рис. 24 а, б и в).
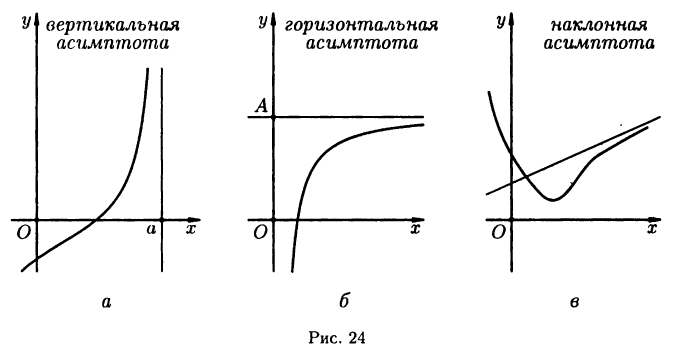
Прямая х = а называется вертикальной асимптотой функции 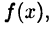 если
если
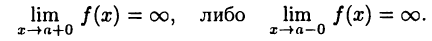
Например, функция у = tgx имеет вертикальные асимптоты 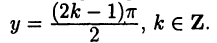
Прямая у = А называется горизонтальной асимптотой функции 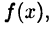 если
если
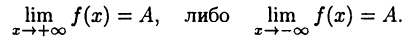
Например, функция 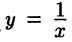 имеет как вертикальную асимптоту х = 0, так и горизонтальную асимптоту у = 0.
имеет как вертикальную асимптоту х = 0, так и горизонтальную асимптоту у = 0.
Прямая 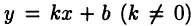 называется наклонной асимптотой функции
называется наклонной асимптотой функции 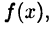 если существуют пределы
если существуют пределы
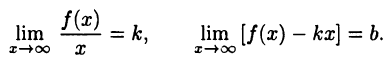
Пример:
Найти асимптоты кривой
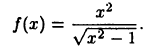
Приравнивая знаменатель к нулю, получаем две вертикальные асимптоты х=±1. Так как 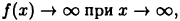 то горизонтальных асимптот нет. Для определения наклонных асимптот найдем пределы:
то горизонтальных асимптот нет. Для определения наклонных асимптот найдем пределы:
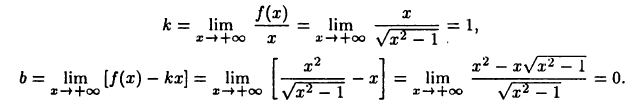
Поэтому функция при 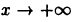 имеет наклонную асимптоту у = х. Аналогично устанавливается, что при
имеет наклонную асимптоту у = х. Аналогично устанавливается, что при 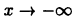 функция имеет наклонную асимптоту у = -х.
функция имеет наклонную асимптоту у = -х.
Общая схема исследования графика функции
При исследовании функции и построении ее графика рекомендуется пользоваться следующей схемой:
- найти область определения функции;
- найти точки пересечения графика функции с осями координат,
- найти точки «подозрительные на экстремум и точки перегиба»;
- с помощью анализа знака первой производной (теорема 20.1) найти интервалы возрастания и убывания функции;
- с помощью анализа знака второй производной (теорема 20.2) найти направления выпуклости графика функции;
- найти точки экстремума (правило (1) или (2)) и точки перегиба (теорема 20.4);
- найти асимптоты;
- построить график функции.
При этом в начале исследования полезно выяснить, является ли функция четной или нечетной, периодической или нет.
Основные теоремы дифференциального исчисления
Теорема:
Теорема Ферма. Пусть функция f(х) определена на интервале (а, b) и в некоторой точке 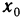 этого интервала имеет наибольшее или наименьшее значение. Тогда если в точке
этого интервала имеет наибольшее или наименьшее значение. Тогда если в точке 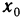 существует производная, то она равна нулю, т. е
существует производная, то она равна нулю, т. е 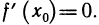
Доказательство:
Пусть для определенности Функция f(х) в точке 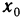 имеет наибольшее значение, т. е.
имеет наибольшее значение, т. е.  для любого
для любого 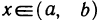 . Это значит, что
. Это значит, что 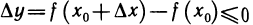 для любой точки
для любой точки 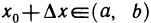 . Поэтому, если
. Поэтому, если 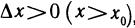 , то
, то 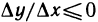 и, следовательно,
и, следовательно, 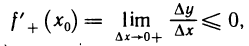
если же 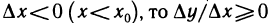 и, следовательно,
и, следовательно, 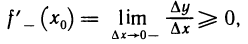
т. е. правая производная в точке 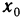 неположительная, а левая — неотрицательная. По условию,
неположительная, а левая — неотрицательная. По условию, 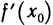 существует и, значит,
существует и, значит, 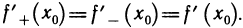 Это возможно только в случае, когда
Это возможно только в случае, когда 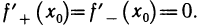 Но тогда и
Но тогда и 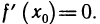
Аналогично рассматривается случай, когда в точке 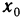 функция f(х) имеет наименьшее значение. ■
функция f(х) имеет наименьшее значение. ■
Геометрический смысл теоремы Ферма состоит в том, что если в точке 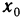 дифференцируемая функция f(х) имеет наибольшее или наименьшее значение, то в точке
дифференцируемая функция f(х) имеет наибольшее или наименьшее значение, то в точке  касательная к графику функции f(х)параллельна оси Ох (рис. 69).
касательная к графику функции f(х)параллельна оси Ох (рис. 69).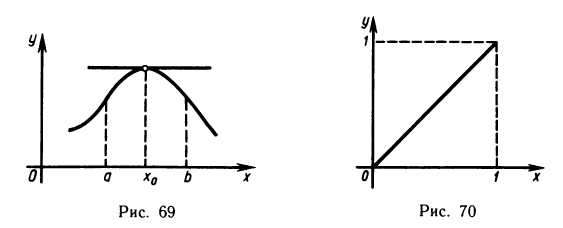
Замечание:
Теорема неверна, если функцию f(х) рассматривать на отрезке [а, b]. Так, например, функция f(x)=x на отрезке [0, 1] в точке х=0 принимает наименьшее, а в точке х=1 — наибольшее значение, однако как в той, так и в другой точке производная в нуль не обращается, а равна единице (рис. 70).
Теорема:
Теорема Ролля. Пусть на [а,b] определена функция f(х), причем: 1°) f(х) непрерывна на [а, b]; 2°) f(x) дифференцируема на (а,b); 3°) f(a) = f(b). Тогда существует точка 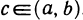 , в которой f'(с)=0
, в которой f'(с)=0
Доказательство:
Так как функция f(х) непрерывна на [а, b], то по второй теореме Вейерштрасса она имеет на этом отрезке максимальное значение М и минимальное значение m, т е. существуют такие точки 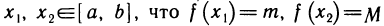 и выполняются неравенства
и выполняются неравенства 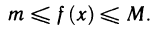
Возможны два случая: 1) М=m 2) m<М.
В первом случае 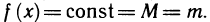 Поэтому производная f'(х) равна нулю в любой точке [а, b], и теорема доказана.
Поэтому производная f'(х) равна нулю в любой точке [а, b], и теорема доказана.
Во втором случае так как f(а)=f(b), то хотя бы одно из двух значений, m или М, не принимается на концах отрезка [а, b], т. е. существует точка 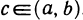 , в которой функция f(х) принимает наибольшее или наименьшее значение на интервале (а, b). В этом случае, так как f(х) дифференцируема в точке с, из теоремы Ферма следует, что f'(с) = 0.■
, в которой функция f(х) принимает наибольшее или наименьшее значение на интервале (а, b). В этом случае, так как f(х) дифференцируема в точке с, из теоремы Ферма следует, что f'(с) = 0.■
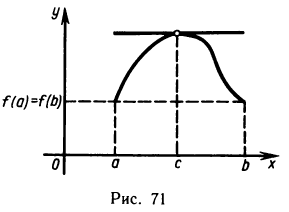
Геометрически теорема Ролля означает, что у графика непрерывной на отрезке [а, b] и дифференцируемой внутри этого отрезка функции, принимающей на его концах равные значения, существует точка (с;f(с)), в которой касательная параллельна оси Ох (рис. 71). На рис. 71 в точке с функция f(х) принимает наибольшее значение.
Следует отметить, что все три условия теоремы Ролля существенны. Чтобы убедиться в этом, достаточно привести примеры функций, для которых выполнялись бы два условия теоремы, а третье не выполнялось и производные которых не обращались бы в нуль ни в одной точке. Так, например, функция 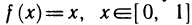 (см. рис. 70) удовлетворяет условиям 1° и 2°, но не удовлетворяет условию 3° и для нее не существует точки с такой, что f'(с) = 0. Рассмотрим еще два примера.
(см. рис. 70) удовлетворяет условиям 1° и 2°, но не удовлетворяет условию 3° и для нее не существует точки с такой, что f'(с) = 0. Рассмотрим еще два примера.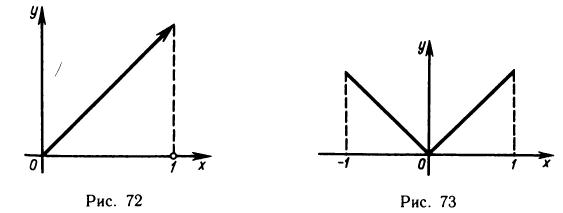
Функция f(х), равная х, если 0<х<1, и равная 0, если x=1 (рис. 72), удовлетворяет условиям 2° и 3°, но не удовлетворяет условию 1°. Функция 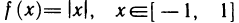 (рис. 73) удовлетворяет условиям 1° и 3°, но не удовлетворяет условию 2° Для этих функций также не существует точки, в которой их производная обращалась бы в нуль.
(рис. 73) удовлетворяет условиям 1° и 3°, но не удовлетворяет условию 2° Для этих функций также не существует точки, в которой их производная обращалась бы в нуль.
Отметим, что в математике существенность тех или иных условий доказываемых теорем проверяется построением соответствую, щих примеров, когда невыполнение того или иного условия теоремы приводит к тому, что утверждение теоремы становится неверным.
Теорема:
Теорема Лагранжа. Пусть на [а, b] определена функция f(х), причем: 1°) f (х) непрерыная на [а, b]; 2°) f(х) дифференцируема на [а, b]. Тогда существует точка 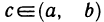 такая, что справедлива формула
такая, что справедлива формула 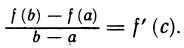
Доказательство:
Введем в рассмотрение на [a, b] вспомогательную функцию 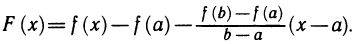
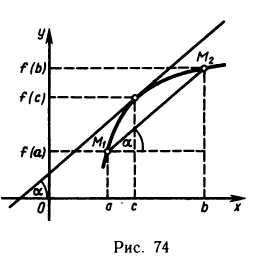
Функция F(х) удовлетворяет всем трем условиям теоремы Ролля: 1) F(х) непрерывна на [a, b] (как разность двух непрерывных функций f(х) и линейной функции 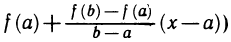 ;
;
2) F(х) дифференцируема на (a, b), т. е. внутри [a, b] имеет производную, равную 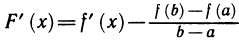
3) F(а) = 0 и F(b) = 0, т. e.F(a) = F(b).
Следовательно, по теореме Ролля существует точка 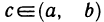 такая, что
такая, что 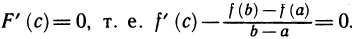 Отсюда получаем:
Отсюда получаем: 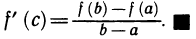
Установим геометрический смысл теоремы Лагранжа (рис. 74). Величина 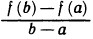 является угловым коэффициентом секущей, проходящей через точки
является угловым коэффициентом секущей, проходящей через точки 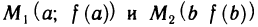 графика функции y = f(x), а f'(с) — угловой коэффициент касательной к графику в точке (с; f(c)). Из теоремы Лагранжа следует, что существует точка с такая, что касательная к графику в точке (с; f(c)) параллельна секущей
графика функции y = f(x), а f'(с) — угловой коэффициент касательной к графику в точке (с; f(c)). Из теоремы Лагранжа следует, что существует точка с такая, что касательная к графику в точке (с; f(c)) параллельна секущей 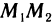 . Таких точек может быть и несколько, но, по крайней мере, одна всегда существует.
. Таких точек может быть и несколько, но, по крайней мере, одна всегда существует.
Замечание:
Равенство 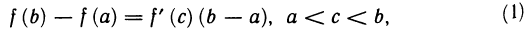
называется формулой Лагранжа или формулой конечных приращений-
Замечание:
Так как точка с лежит между 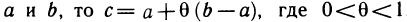 . Учитывая это, формулу Лагранжа можно записать в видe
. Учитывая это, формулу Лагранжа можно записать в видe 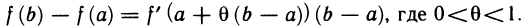
Замечание:
Если положить 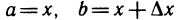 , то получим
, то получим 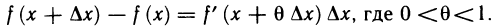
Такая запись формулы Лагранжа часто бывает удобнее, чем запись в виде (1).
Как будет показано в дальнейшем, теорема Лагранжа лежит в основе доказательства многих формул и теорем анализа.
Теорема:
Теорема Коши. Пусть функции f(х) и g(х) непрерывны на [а, b] и дифференцируемы на (а, b). Пусть, кроме того, 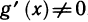 . Тогда существует точка
. Тогда существует точка 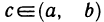 такая, что справедлива формулa
такая, что справедлива формулa 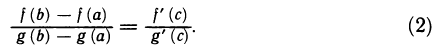
Доказательство:
Покажем сначала, что 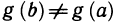 , т. е. что формула (2) имеет смысл. Действительно, если допустить, что g(b)=g(а), то по теореме Ролля для функции g(х) найдется точка
, т. е. что формула (2) имеет смысл. Действительно, если допустить, что g(b)=g(а), то по теореме Ролля для функции g(х) найдется точка 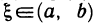 , в которой
, в которой 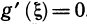 . А это противоречит условию, что
. А это противоречит условию, что 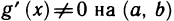 . Перейдем к доказательству формулы (2).
. Перейдем к доказательству формулы (2).
Рассмотрим на [а, b] вспомогательную функцию 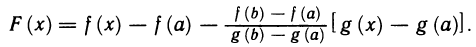
Нетрудно заметить, что F(х) на [a, b] удовлетворяет условиям теоремы Ролля. В самом деле, F(х) непрерывна на [а, b], дифференцируема на
(а, b), и, кроме того, подстановка х=a и х=b дает F(а)=0 и F(b)=0, т. е. F(a)=F(b). По теореме Ролля Для F(х) существует точка с, а<с<Ь, такая, что F'(c) = 0.
Так как 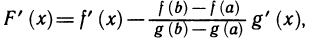 то
то 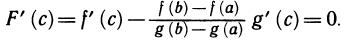
Откуда, учитывая, что 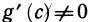 , получаем формулу (2). ■
, получаем формулу (2). ■
Замечание. Формула (2) называется формулой Коши или °бобщенной формулой конечных приращений.
Раскрытие неопределенностей и правило Лопиталя
1. Раскрытие неопределенности вида 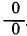 . Будем говорить, что отношение двух функций
. Будем говорить, что отношение двух функций 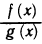 при
при  есть неопределенность вида
есть неопределенность вида 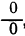 , если
, если 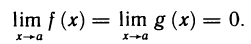
Раскрыть эту неопределенность — значит вычислить предел 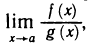 если он существует, или установить, что он не существует. Следующая теорема устанавливает правило для раскрытия неопределенности вида
если он существует, или установить, что он не существует. Следующая теорема устанавливает правило для раскрытия неопределенности вида 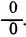
Теорема:
Теорема Лопиталя. Пусть функции f(х) и g(х) определены и дифференцируемы в некоторой окрестности точки а, за исключением, быть может, самой точки а.
Пусть, далее, 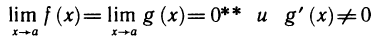 в указанной окрестности точки а. Тогда, если существует предел отношения производных
в указанной окрестности точки а. Тогда, если существует предел отношения производных 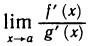 (конечный или бесконечный), то существует и предел
(конечный или бесконечный), то существует и предел 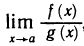 , причем справедлива формула
, причем справедлива формула 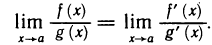
Доказательство:
Пусть 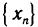 — произвольная последовательность значений аргумента, сходящаяся к точке а, причем
— произвольная последовательность значений аргумента, сходящаяся к точке а, причем 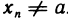 . Доопределим функции f(х) и g(х) в точке а, положив их равными нулю, т. е. f(а)=g(а)=0. Тогда, очевидно, функции f(х) и g(x) непрерывны на
. Доопределим функции f(х) и g(х) в точке а, положив их равными нулю, т. е. f(а)=g(а)=0. Тогда, очевидно, функции f(х) и g(x) непрерывны на 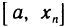 , дифференцируемы на
, дифференцируемы на 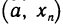 и, по условию,
и, по условию, 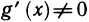 . Таким образом, для f(х) и g(х) выполнены все условия теоремы Коши на
. Таким образом, для f(х) и g(х) выполнены все условия теоремы Коши на 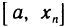 , т. е. внутри
, т. е. внутри 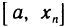 существует точка
существует точка 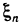 такая, что
такая, что 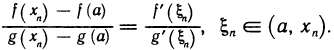
По доопределению, f(а)=g(а)=0, следовательно 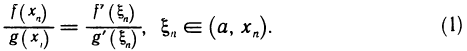
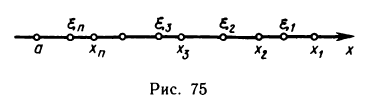
Пусть теперь в формуле (1)  Тогда, очевидно,
Тогда, очевидно,  при
при  (рис. 75). Так как
(рис. 75). Так как 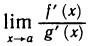 существует, то правая часть формулы (1) имеет при
существует, то правая часть формулы (1) имеет при  предел, равный
предел, равный 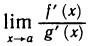 .
.
Следовательно, при  существует предел и левой части формулы (1), причем
существует предел и левой части формулы (1), причем 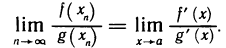
Так как 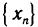 — произвольная последовательность значений аргумента, сходящаяся к а, то отсюда заключаем, что
— произвольная последовательность значений аргумента, сходящаяся к а, то отсюда заключаем, что 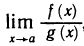 существует и
существует и 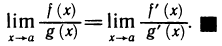
Доказанную теорему обычно называют правилом Лопиталя. Замечание 1. Если производные f'(х) и g'(х) удовлетворяют тем же требованиям, что и сами функции f(x) и g(х), то правило Лопиталя можно применить повторно. При этом получаем 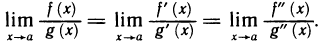
Замечание:
Теорема остается верной и в случае, когда 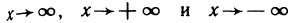 . В самом деле, пусть, например,
. В самом деле, пусть, например, 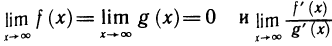 cуществует (конечный или бесконечный).
cуществует (конечный или бесконечный).
Сделаем подстановку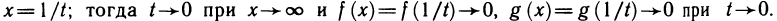 Применяя к функциям f(1/t) и g(1/t) теорему 6.5 и правило дифференцирования сложной функции, получаем
Применяя к функциям f(1/t) и g(1/t) теорему 6.5 и правило дифференцирования сложной функции, получаем 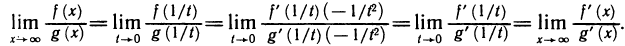
Рассмотрим примеры. 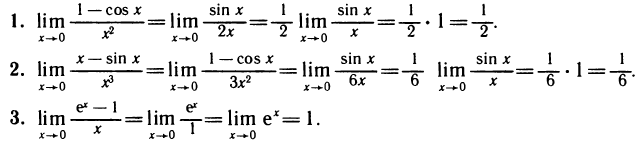
2. Раскрытие неопределенности вида 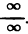 . Будем говорить, что отношение двух функции
. Будем говорить, что отношение двух функции 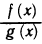 при
при  есть неопределенность вида
есть неопределенность вида 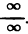 , если
, если 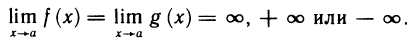
Для этой неопределенности справедливо утверждение, аналогичное теореме 6.5, а именно: если в формулировке теоремы заменить требование 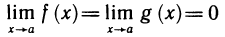 на условие
на условие 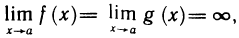 то теорема останется справедливой.
то теорема останется справедливой.
Рассмотрим примеры.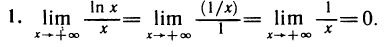
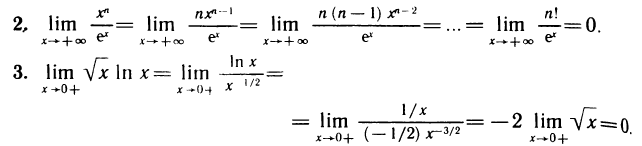
3. Другие виды неопределенностей и их раскрытие. Неопределенности вида 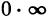 и
и 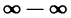 можно свести к неопределенностям
можно свести к неопределенностям 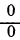 и
и 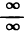 . Покажем это на примерах.
. Покажем это на примерах.
Пример:
Найти 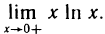
Решение:
Имеем неопределенность вида 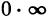 . Но
. Но 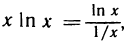 и получена неопределенность вида
и получена неопределенность вида 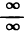 . Применяя правило Лопиталя, имеем
. Применяя правило Лопиталя, имеем 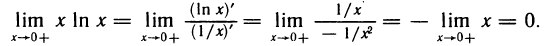
Пример:
Найти 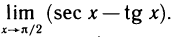
Решение:
Имеем неопределенность вида 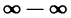 . Но
. Но 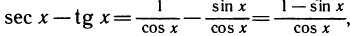 и при том же условии
и при том же условии 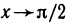 получена неопределенность вида
получена неопределенность вида 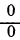 .
.
Воспользовавшись правилом Лопиталя, получим 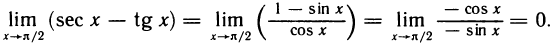
И наконец, рассмотрим неопределенности вида 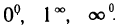 Такие неопределенности имеют место при рассмотрении функций
Такие неопределенности имеют место при рассмотрении функций 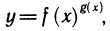 если при х->а функция f х) стремится соответственно к
если при х->а функция f х) стремится соответственно к 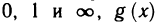 — соответственно к
— соответственно к 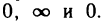 Эти неопределенности с помощью тождества
Эти неопределенности с помощью тождества 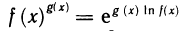
сводятся к неопределенности вида 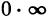 , которая уже рассмотрена.
, которая уже рассмотрена.
Пример:
Найти 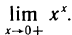
Решение:
Имеем неопределенность вида 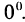 Но
Но 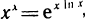 и в показателе степени получена неопределенность вида
и в показателе степени получена неопределенность вида 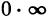 , которая нами уже рассмотрена (см. пример 1). Следовательно
, которая нами уже рассмотрена (см. пример 1). Следовательно 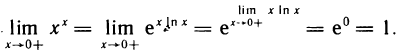
Пример:
Найти 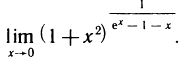
Решение:
Имеем неопределенность вида 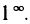 Но
Но 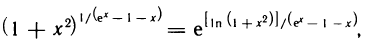
и в показателе степени получена неопределенность вида 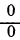 . Применяя правило Лопиталя, получаем
. Применяя правило Лопиталя, получаем 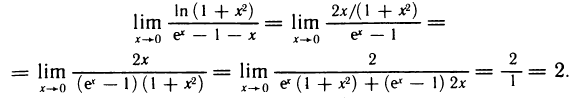
Следовательно, 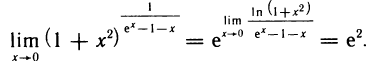
Пример:
Найти 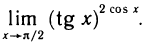
Решение:
Имеем неопределенность вида 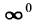 . Но
. Но 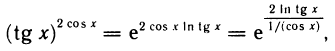
и в показателе степени получена неопределенность вида 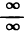 .
.
Применяя правило Лопиталя, имеем 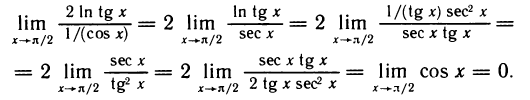 Следовательно,
Следовательно, 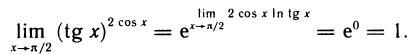
Формула Тейлора
Рассмотрим одну из главных формул математического анализа, имеющую многочисленные применения как в самом анализе, так и в смежных дисциплинах.
Теорема:
Теорема Тейлора. Пусть функция f(х) имеет в точке а и некоторой ее окрестности производные порядка 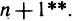 . Пусть х — любое значение аргумента из указанной окрестности,
. Пусть х — любое значение аргумента из указанной окрестности, 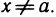 . Тогда между точками чих найдется точка
. Тогда между точками чих найдется точка 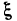 такая, что справедлива следующая формула:
такая, что справедлива следующая формула: 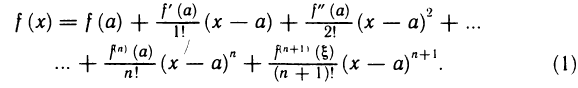
Доказательство:
Обозначим через 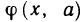 многом относительно х степени n, стоящий в правой части формулы (1) т. е. положим
многом относительно х степени n, стоящий в правой части формулы (1) т. е. положим 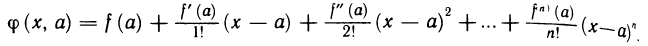
(Он называется многочленом Тейлора степени n для функции f(x)). Далее обозначим через 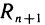 (х) разность
(х) разность 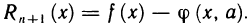
Теорема будет доказана, если установить, что 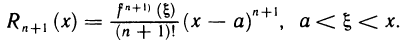
Фиксируем любое значение х из указанной окрестности. Для определенности считаем х>а. Обозначим через t переменную величину, изменяющуюся на отрезке 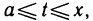 и рассмотрим на отрезке [а, х] вспомогательную функцию
и рассмотрим на отрезке [а, х] вспомогательную функцию 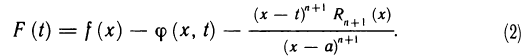
Функция F(t) удовлетворяет на [а, х] всем условиям теоремы Ролля: 1) из формулы (2) и из условий, наложенных на функцию f(х), вытекает, что F(t) непрерывна и дифференцируема на [a, x] , так как f(t) и ее производные до порядка n непрерывны и дифференцируемы на [а, x];
2) полагая в (2) t=а, имеем 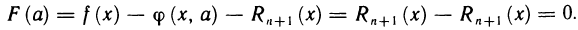
Полагая в (2) t=x, получаем 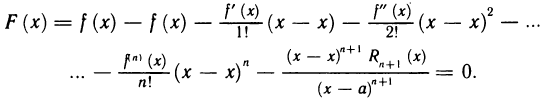
Таким образом, условие F(а)=F(х) выполнено.
На основании теоремы Ролля внутри отрезка [а, х] существует точка 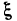 такая, что
такая, что 
Вычислим производную F'(t). Дифференцируя равенство (2) по t имеем 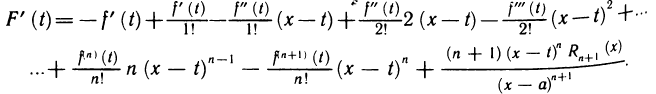
Нетрудно заметить, что все члены в правой части равенства, за исключением двух последних, взаимно уничтожаются. Таким образом 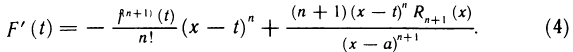
Полагая в (4) 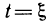 и используя равенство (3), получаем
и используя равенство (3), получаем 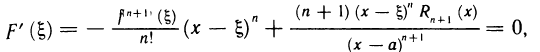
откуда 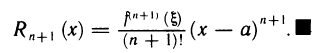
Формула (1) называется формулой Тейлора, а выражение для  — остаточным членом в форме Лагранжа. Его можно переписать в другом виде. Так как точка
— остаточным членом в форме Лагранжа. Его можно переписать в другом виде. Так как точка 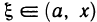 , то найдется такое число
, то найдется такое число 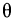 из интервала
из интервала 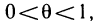 что
что 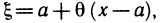 и остаточный член принимает вид
и остаточный член принимает вид 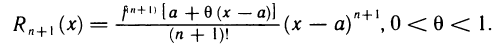
Эту форму остаточного члена наиболее часто используют в приложениях.
Другая запись формулы Тейлора и остаточного члена
Часто формулу Тейлора (1) записывают в ином виде. Положим в (1) 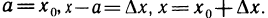 Тогда
Тогда 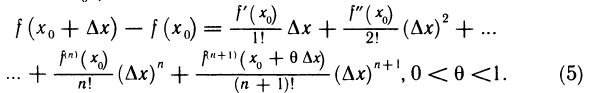
При n=0 из (5) получается формула Лагранжа 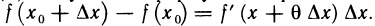
Покажем, что если функция 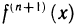 ограничена в окрестности тoчки а, то остаточный член
ограничена в окрестности тoчки а, то остаточный член 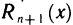 является бесконечно малой более высокого порядка, чем
является бесконечно малой более высокого порядка, чем 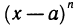 при
при 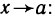
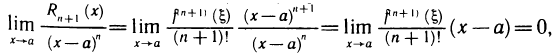
так как функция 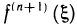 ограничена,
ограничена, 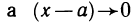 при
при 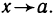
Таким образом, 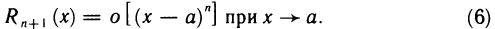
Формула (6) называется остаточным членом в форме Пеано.
Формула Маклорена
Формулой Маклорена называют формулу Тейлора (1) при а=0: 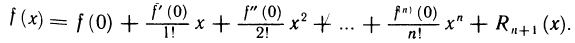
Остаточный член имеет вид: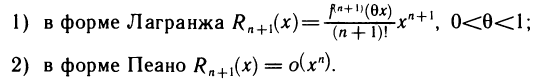
Разложение некоторых элементарных функций по формуле Маклорена

В формуле (8) остаточный член записан в виде 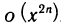 , а не в виде
, а не в виде 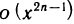 , так как следующий за последним член равен нулю [то же самое относится к формуле (9)].
, так как следующий за последним член равен нулю [то же самое относится к формуле (9)].
4) 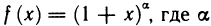 — вещественное число. Так как
— вещественное число. Так как 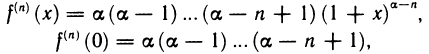
то формула Маклорена имеет вид 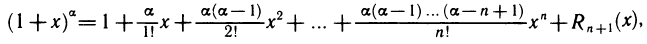
где остаточный член в форме Лагранжа равен 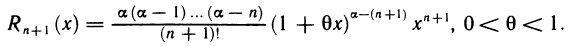
В частном случае, когда 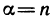 — натуральное число,
— натуральное число, 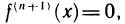 следовательно,
следовательно, 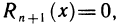 мы получаем известную из элементарной математики формулу бинома Ньютона
мы получаем известную из элементарной математики формулу бинома Ньютона 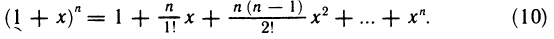
Приведенные выше разложения показывают, что с помощью формулы Маклорена функции можно с определенной степенью точности заменять многочленами, являющимися наиболее простыми элементарными функциями. Над многочленами удобно выполнять арифметические действия, нетрудно вычислить значение многочлена в любой точке и т. д. Формулы Тейлора и Маклорена позволяют приближенно заменять многочленами и более сложные функции. Кроме того, эти формулы имеют широкий круг приложений. Мы ограничимся рассмотрением двух.
Использование формулы Маклорена для вычисления пределов
Формула Тейлора является эффективным средством для вычисления пределов функций, с которыми часто приходится иметь дело при исследовании функций.
Пример:
Найти 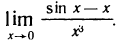
Решение:
По формуле (8) при n=2 имеем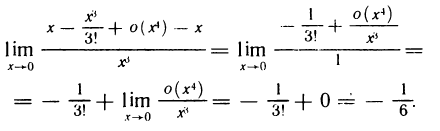
Пример:
Найти 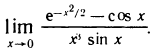
Решение:
По формулам (7), (8) и (9) имеем 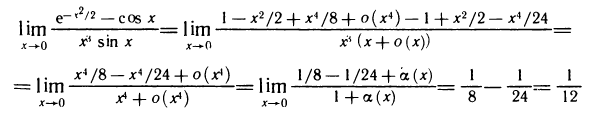
(здесь символом 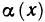 обозначена величина
обозначена величина 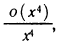 , являющаяся бесконечно малой при
, являющаяся бесконечно малой при  ).
).
Вычисление числа е
Было введено число е как предел последовательности 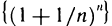 и получена грубая оценка
и получена грубая оценка 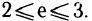
Покажем, как вычислить число е с любой необходимой точностью. Для этого запишем формулу (7) с остаточным членом в форме Лагранжа: 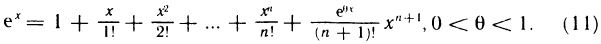
Если заменить функцию 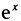 ее многочленом Тейлора степени n, то получим приближенное равенство
ее многочленом Тейлора степени n, то получим приближенное равенство 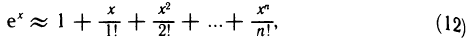
абсолютная погрешность которого 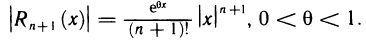
Если рассматривать функцию 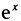 для
для 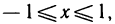 то
то 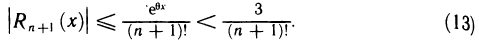
Полагая в (12) х=1, получаем приближенное значение числа е: 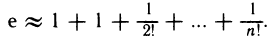
При этом абсолютная погрешность меньше 3/(n+ 1)! Если требуется вычислить значение е с точностью до 0,001, то число n определяется из неравенства 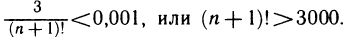 Следовательно, если взять n=6, то требуемое неравенство удовлетворяется.
Следовательно, если взять n=6, то требуемое неравенство удовлетворяется.
Таким образом, используя формулу Маклорена, можно вычислить число е с любой точностью, при этом алгоритм вычисления числа е, основанный на формулах (11) и (13), легко реализуется на ЭВМ.
Исследование поведения функций и построение графиков
Признак монотонности функции
Теорема:
Если функция f(х) дифференцируема на интервале 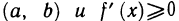
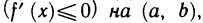 то функция f(х) не убывает (не возрастает) на
то функция f(х) не убывает (не возрастает) на
(а, b).
Доказательство:
Для определенности рассмотрим случай 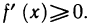 Пусть
Пусть 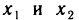 — две произвольные точки из (a, b) и
— две произвольные точки из (a, b) и 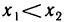 ; тогда на отрезке
; тогда на отрезке 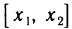 выполняются все условия теоремы Лагранжа, согласно которой имеем
выполняются все условия теоремы Лагранжа, согласно которой имеем 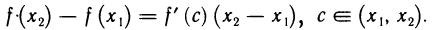
По условию, 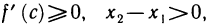 поэтому
поэтому 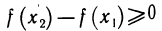 или
или 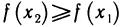 , т. е. функция f(х) не убывает на (а, b).
, т. е. функция f(х) не убывает на (а, b).
Доказательство для случая 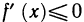 аналогично. ■
аналогично. ■
Замечание. Точно так же можно доказать, что если 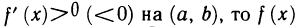 возрастает (убывает) на (а, b).
возрастает (убывает) на (а, b).
Отыскание точек локального экстремума функции
Определение:
Точка  называется точкой строгого локального максимум (минимума) функции f(х), если для всех х из некоторой
называется точкой строгого локального максимум (минимума) функции f(х), если для всех х из некоторой 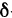 -окресности точки
-окресности точки  выполняется неравенство
выполняется неравенство 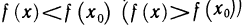 при
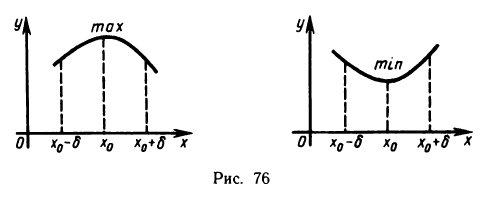
при 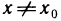 (рис. 76).
(рис. 76).
Локальный максимум (max) и локальный минимум (min) объединяются общим названием локальный, экстремум.
Из определения следует, что понятие экстремума носит локальный характер в том смысле, что неравенство 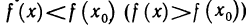 может и не выполняться для всех значений х в области определения функции, а должно выполняться лишь в некоторой окрестности точки
может и не выполняться для всех значений х в области определения функции, а должно выполняться лишь в некоторой окрестности точки  . Очевидно, функция может иметь несколько локальных максимумов и несколько локальных минимумов, причем может так случиться, что иной локальный максимум окажется меньше какого-то локального минимума.
. Очевидно, функция может иметь несколько локальных максимумов и несколько локальных минимумов, причем может так случиться, что иной локальный максимум окажется меньше какого-то локального минимума.
Теорема:
Необходимое условие локального экстремума. Если функция f(х) имеет в точке  локальный экстремум и дифференцируема в этой точке, то
локальный экстремум и дифференцируема в этой точке, то 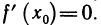
Доказательство:
Так как в точке  функция f(х) имеет локальный экстремум, то существует такой интервал
функция f(х) имеет локальный экстремум, то существует такой интервал 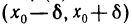 , в котором значение
, в котором значение 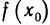 является наибольшим или наименьшим среди всех других значений этой функции. Тогда по теореме Ферма производная функции в точке
является наибольшим или наименьшим среди всех других значений этой функции. Тогда по теореме Ферма производная функции в точке  равна нулю, т. е.
равна нулю, т. е. 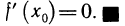
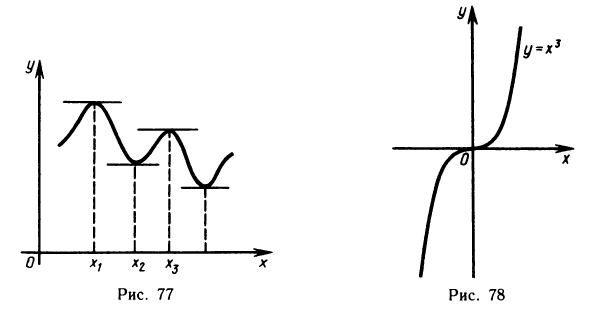
Теорема 6.8 имеет следующий геометрический смысл. Если 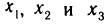 — точки локального экстремума и в соответствующих точках графика существуют касательные, то эти касательные параллельны оси Ох (рис. 77).
— точки локального экстремума и в соответствующих точках графика существуют касательные, то эти касательные параллельны оси Ох (рис. 77).
Иногда такие точки называют стационарными; мы будем называть их точками возможного экстремума. Если точка  — точка возможного экстремума, т. е.
— точка возможного экстремума, т. е. 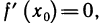 то она может и не быть точкой локального максимума или минимума. Например, если
то она может и не быть точкой локального максимума или минимума. Например, если 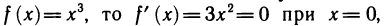 но, тем не менее, в точке х = 0 нет локального экстремума (рис. 78). Установим достаточное условие существования локального экстремума. Этому посвящается следующая теорема.
но, тем не менее, в точке х = 0 нет локального экстремума (рис. 78). Установим достаточное условие существования локального экстремума. Этому посвящается следующая теорема.
Теорема:
Достаточное условие локального экстремума. Пусть функция f(х) дифференцируема в некоторой 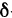 -окрестности точки
-окрестности точки  . Тогда, если
. Тогда, если 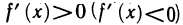 для всех х из
для всех х из 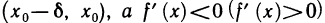 для всех х из
для всех х из 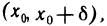 то в точке
то в точке  функция f(х) имеет локальный максимум (минимум); если же f'(х) во всей
функция f(х) имеет локальный максимум (минимум); если же f'(х) во всей 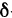 -окрестности точки
-окрестности точки  имеет один и тот же знак, то в точке
имеет один и тот же знак, то в точке  локального экстремума нет.
локального экстремума нет.
Другими словами, если f'(х) при переходе через точку  меняет знак с « + » на « —», то
меняет знак с « + » на « —», то  —точка локального максимума; если f (х) в точке
—точка локального максимума; если f (х) в точке  меняет знак с «—» на « + », то
меняет знак с «—» на « + », то  — точка локального минимума; если же f (х) в точке
— точка локального минимума; если же f (х) в точке  знака не меняет, то в точке х0 экстремума не существует.
знака не меняет, то в точке х0 экстремума не существует.
Доказательство:
Пусть f'(х) при переходе через точку  меняет знак с « + » на «—> и пусть
меняет знак с « + » на «—> и пусть 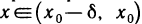 . Применим формулу Лагранжа к функции f(х) на отрезке
. Применим формулу Лагранжа к функции f(х) на отрезке 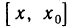 . Получаем
. Получаем 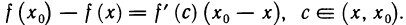
Так как 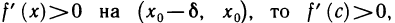 и, кроме того,
и, кроме того, 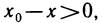 следовательно,
следовательно, 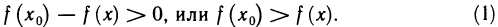
Рассмотрим теперь случай, когда 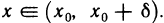 Применим формулу Лагранжа к функции f (х) на отрезке
Применим формулу Лагранжа к функции f (х) на отрезке 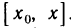 . Получаем
. Получаем 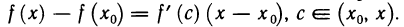
Так как 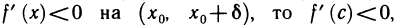 кроме того,
кроме того, 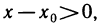 следовательно,
следовательно, 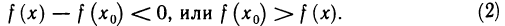
Из неравенств (1) и (2) следует, что в рассматриваемой окрестности точки  выполняется неравенство
выполняется неравенство 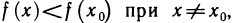 а это означает, что в точке
а это означает, что в точке  функция f(х) имеет локальный максимум.
функция f(х) имеет локальный максимум.
Аналогично рассматривается случай перемены знака f'(х) с «—» на «+».
Осталось рассмотреть случай, когда f'(х) знака не меняет. Пусть f'(х)>0 в некоторой окрестности 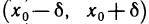 ; тогда по теореме 6.7 функция f (х) не убывает на
; тогда по теореме 6.7 функция f (х) не убывает на 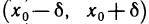 , т. е. для любых
, т. е. для любых 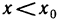 выполняется неравенство
выполняется неравенство  .
.
Замечание. Теорема 6.9 остается справедливой, если функция f(х) в самой точке  не дифференцируема, а только непрерывна. Так, например, функция
не дифференцируема, а только непрерывна. Так, например, функция 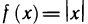 в точке x=0 непрерывна, но не дифференцируема.
в точке x=0 непрерывна, но не дифференцируема.
В качестве примера рассмотрим вопрос об отыскании точек локального экстремума функции 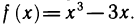 Находим производную:
Находим производную: 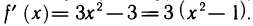 Решая уравнение
Решая уравнение 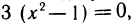 получаем две точки возможного экстремума:
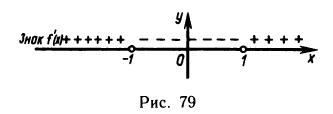
получаем две точки возможного экстремума: 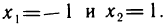 Дальнейшее исследование удобно вести, нарисовав вспомогательный чертеж (рис. 79). Отметив на нем точки
Дальнейшее исследование удобно вести, нарисовав вспомогательный чертеж (рис. 79). Отметив на нем точки 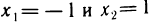 и исследовав знак f'(х) в окрестности этих точек, получаем: f(x) в точке
и исследовав знак f'(х) в окрестности этих точек, получаем: f(x) в точке 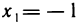 имеет локальный максимум, а в точке
имеет локальный максимум, а в точке 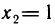 — локальный минимум. Далее находим:
— локальный минимум. Далее находим: 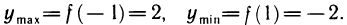
На рис. 79 видны и интервалы монотонности 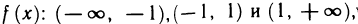 причем в первом и третьем из них функция возрастает, а во втором — убывает.
причем в первом и третьем из них функция возрастает, а во втором — убывает.
Направление выпуклости и точки перегиба графика функции
Пусть функция y=f(х) дифференцируема на интервале (а, b). Тогда существует касательная к графику функции y=f(x) в любой точке 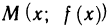 этого графика
этого графика 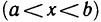 , причем касательная не параллельна оси Оу, поскольку ее угловой коэффициент, равный f'(х), конечен.
, причем касательная не параллельна оси Оу, поскольку ее угловой коэффициент, равный f'(х), конечен.
Определение:
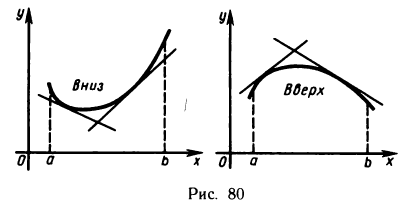
Будем говорить, что график функции y=f(x) имеет на (а, b) выпуклость, направленную вниз (вверх), если он расположен не ниже (не выше) любой касательной к графику функции на (а, b) (рис. 80).
Теорема:
Если функция y=f(x) имеет на интервале (а, b) вторую производную и 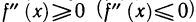 во всех точках (а, b), то график функции y=f(x) имеет на (а, b) выпуклость, направленную вниз (вверх).
во всех точках (а, b), то график функции y=f(x) имеет на (а, b) выпуклость, направленную вниз (вверх).
Доказательство:
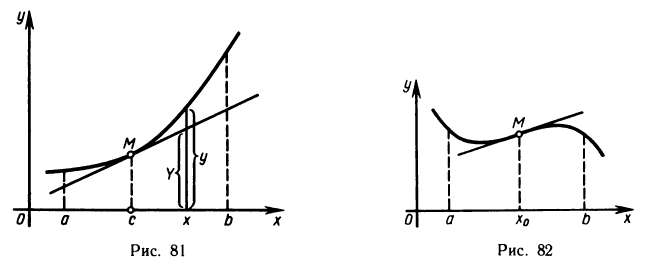
Для определенности рассмотрим случай 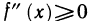 на (а, b). Обозначим через с произвольную точку (а, b) (рис. 81). Требуется доказать, что график функции y=f(x) лежит не ниже касательной, проходящей через точку М (с; f (с)).
на (а, b). Обозначим через с произвольную точку (а, b) (рис. 81). Требуется доказать, что график функции y=f(x) лежит не ниже касательной, проходящей через точку М (с; f (с)).
Запишем уравнение этой касательной, обозначая текущую ординату ее точек через 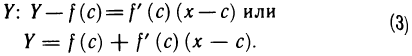
Разложим функцию f(х) в окрестности точки с по формуле Тейлора при n=1. Получим
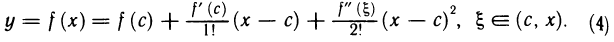
Формула (4) справедлива для любого х из (а, b). Вычитая равенство (3) из равенства (4), имеем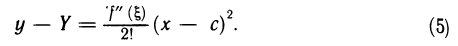
Так как, по условию, 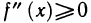 на (а, b), то правая часть равенства (5) неотрицательна, т. е.
на (а, b), то правая часть равенства (5) неотрицательна, т. е. 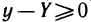 для всех х из (а, b) или
для всех х из (а, b) или 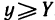 .
.
Последнее неравенство и доказывает, что график функции y=f(x) всюду в пределах (а, b) лежит не ниже касательной (3). Аналогично доказывается теорема для случая 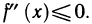 ■
■
Определение:
Точка 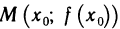 называется точкой перегиба графика функции y = f(x), если в точке М график имеет касательную, и существует такая окрестность точки
называется точкой перегиба графика функции y = f(x), если в точке М график имеет касательную, и существует такая окрестность точки  , в пределах которой график функции y=f(x) слева и справа от точки
, в пределах которой график функции y=f(x) слева и справа от точки  имеет разные направления выпуклости.
имеет разные направления выпуклости.
Очевидно, что в точке перегиба касательная пересекает график функции, так как с одной стороны от этой точки график лежит под касательной, а с другой — над нею, т. е. в окрестности точки перегиба график функции геометрически переходит с одной стороны касательной на другую и «перегибается» через нее. Отсюда и произошло название «точка перегиба» (рис. 82).
Теорема:
Необходимое условие точки перегиба. Пусть график функции y=f(x) имеет перегиб в точке 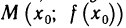 и пусть функция y = f(x) имеет в точке
и пусть функция y = f(x) имеет в точке  непрерывную вторую производную. Тогда f» (х) в точке
непрерывную вторую производную. Тогда f» (х) в точке  обращается в нуль, т. е.
обращается в нуль, т. е. 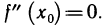
Доказательство:
Предположим обратное, т. е. допустим, что 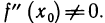 Тогда в силу непрерывности второй производной по теореме 4.8 об устойчивости знака непрерывной функции существует окрестность точки
Тогда в силу непрерывности второй производной по теореме 4.8 об устойчивости знака непрерывной функции существует окрестность точки  в которой
в которой 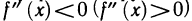 , значит, согласно теореме 6.10 график функции y=f(x) имеет определенное направление выпуклости в этой окрестности. Но это противоречит наличию перегиба в точке
, значит, согласно теореме 6.10 график функции y=f(x) имеет определенное направление выпуклости в этой окрестности. Но это противоречит наличию перегиба в точке 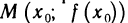 (рис. 82). Полученное противоречие доказывает теорему.
(рис. 82). Полученное противоречие доказывает теорему.
Следует заметить, что не всякая точка 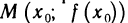 . Для которой
. Для которой 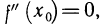 является точкой перегиба. Например, график функции
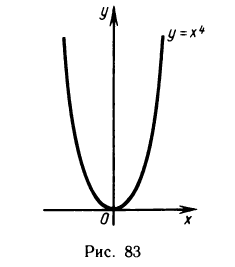
является точкой перегиба. Например, график функции 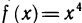 не имеет перегиба в точке (0; 0), хотя
не имеет перегиба в точке (0; 0), хотя 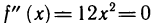 при х=0 (рис. 83). Поэтому равенство нулю второй производной является лишь необходимым условием перегиба. Точки
при х=0 (рис. 83). Поэтому равенство нулю второй производной является лишь необходимым условием перегиба. Точки 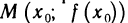 графика, для которых
графика, для которых 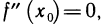 будем называть критическими. Необходимо дополнительно исследовать вопрос о наличии перегиба в каждой критической точке, для чего следует установить достаточное условие перегиба.
будем называть критическими. Необходимо дополнительно исследовать вопрос о наличии перегиба в каждой критической точке, для чего следует установить достаточное условие перегиба.
Теорема:
Достаточное условие точки перегиба. Пусть функция y=f(x) имеет вторую производную в некоторой окрестности точки  . Тогда, если в пределах указанной окрестности f»(х) имеет разные знаки слева и и справа от точки
. Тогда, если в пределах указанной окрестности f»(х) имеет разные знаки слева и и справа от точки  , то график y=f(x) имеет перегиб в точке
, то график y=f(x) имеет перегиб в точке 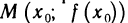 .
.
Доказательство:
Из того, что f»(х) слева и справа от точки  имеет разные знаки, на основании теоремы 6.10. заключаем, что направление выпуклости графика функции слева и справа от точки
имеет разные знаки, на основании теоремы 6.10. заключаем, что направление выпуклости графика функции слева и справа от точки  является различным. Это и означает наличие перегиба в точке
является различным. Это и означает наличие перегиба в точке 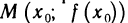 .
.
Замечание:
Теорема остается верной, если f(х) имеет вторую производную в некоторой окрестности точки 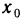 , за исключением самой точки
, за исключением самой точки 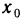 , и существует касательная к графику функции в точке М. Тогда, если в пределах указанной окрестности f»(х) имеет разные знаки слева и справа от точки
, и существует касательная к графику функции в точке М. Тогда, если в пределах указанной окрестности f»(х) имеет разные знаки слева и справа от точки 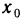 , то график функции y=f(x) имеет перегиб в точке
, то график функции y=f(x) имеет перегиб в точке 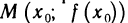 . Доказательство данного факта аналогично доказательству теоремы.
. Доказательство данного факта аналогично доказательству теоремы.
Рассмотрим пример: 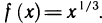 Эта функция в точке х=0 имеет бесконечную производную, а касательная к графику функции в точке О (0; 0) совпадает с осью Оу. Вторая производная в точке х=0 не существует. Однако график функции
Эта функция в точке х=0 имеет бесконечную производную, а касательная к графику функции в точке О (0; 0) совпадает с осью Оу. Вторая производная в точке х=0 не существует. Однако график функции 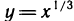 имеет перегиб в точке О (0; 0), так как вторая производная
имеет перегиб в точке О (0; 0), так как вторая производная 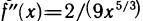 имеет слева и справа от точки х=0 разные знаки (рис. 84).
имеет слева и справа от точки х=0 разные знаки (рис. 84).
Итак, вопрос о направлении выпуклости и точках перегиба графика функции исследуется с помощью второй производной.
В качестве примера возьмем функцию 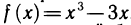 , которую начали рассматривать в п. 2. Знак второй производной будем отмечать на вспомогательном чертеже, изображенном на рис. 79. Находим вторую производную: f»(х)=6х. Из уравнения 6х=0 получаем одну критическую точку: О (0; 0). Отметив точку х=0 на вспомогательном чертеже (рис. 85) и исследовав знак f»(х) в ее окрестности, получаем: слева от точки
, которую начали рассматривать в п. 2. Знак второй производной будем отмечать на вспомогательном чертеже, изображенном на рис. 79. Находим вторую производную: f»(х)=6х. Из уравнения 6х=0 получаем одну критическую точку: О (0; 0). Отметив точку х=0 на вспомогательном чертеже (рис. 85) и исследовав знак f»(х) в ее окрестности, получаем: слева от точки 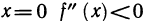 (выпуклость графика направлена вверх), а справа —
(выпуклость графика направлена вверх), а справа — 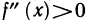 (выпуклость графика направлена вниз), т. е. точка 0 (0; 0) является точкой перегиба графика рассматриваемой функции. Этот график схематически изображен на рис. 86.
(выпуклость графика направлена вниз), т. е. точка 0 (0; 0) является точкой перегиба графика рассматриваемой функции. Этот график схематически изображен на рис. 86.
Докажем теперь, что часть эллипса 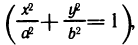 расположенная в верхней полуплоскости
расположенная в верхней полуплоскости 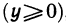 , имеет на интервале (— а, а) выпуклость, направленную вверх. В самом деле, из уравнения
, имеет на интервале (— а, а) выпуклость, направленную вверх. В самом деле, из уравнения
эллипса 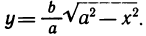 Далее находим:
Далее находим: 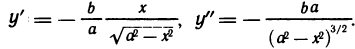
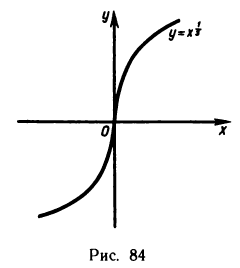
Из выражения для второй производной вытекает, что она отрицательная на интервале (—а, а). Значит, данная кривая на всем интервале ( — а, а) имеет выпуклость, направленную вверх (см. рис. 33).
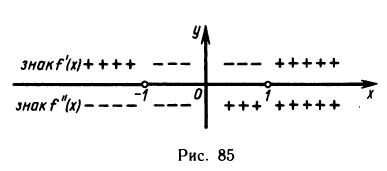
Аналогично можно показать (сделайте это самостоятельно), что часть гиперболы 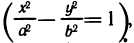 расположенная в верхней полуплоскости, на интервалах
расположенная в верхней полуплоскости, на интервалах 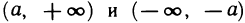 имеет выпуклость, направленную вверх.
имеет выпуклость, направленную вверх.
Асимптоты графика функции
При исследовании поведения функции на бесконечности, т. е. при 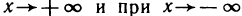 или вблизи точек разрыва 2-го рода, часто оказывается, что график функции сколь угодно близко приближается к той или иной прямой. Такие прямые называют асимптотами.
или вблизи точек разрыва 2-го рода, часто оказывается, что график функции сколь угодно близко приближается к той или иной прямой. Такие прямые называют асимптотами.
Существуют три вида асимптот: вертикальные, горизонтальные и наклонные.
Определение:
Прямая 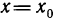 называется вертикальной асимптотой графика функции y=f(x) если хотя бы одно из предельных значений
называется вертикальной асимптотой графика функции y=f(x) если хотя бы одно из предельных значений 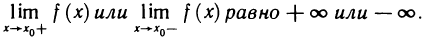
В этом случае расстояние от точки 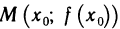 до прямой
до прямой 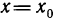 равно
равно 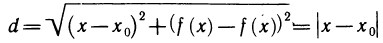 .
.
Например, график функции 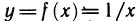 (рис. 87) имеет вертикальную асимптоту х=0, так как
(рис. 87) имеет вертикальную асимптоту х=0, так как  при
при 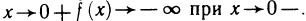
Определение:
Прямая у=А называется горизонтальной асимптотой графика функции y = f(x) при 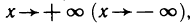 если
если 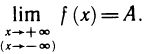
В этом случае расстояние от точки 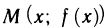 до прямой у=А равно
до прямой у=А равно 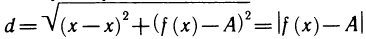 и,
и, 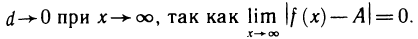
Например, график рассмотренной выше функции у=1/х имеет горизонтальную асимптоту у=0 при 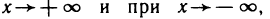 так как
так как  при
при 
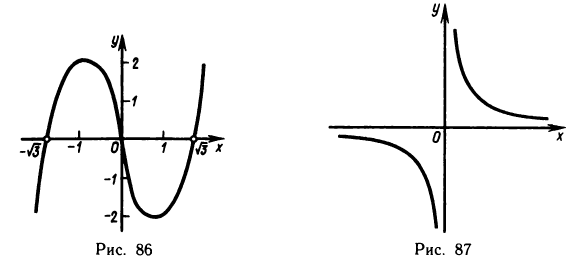
Определение:
Прямая 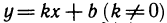 называется наклонной асимптотой графика функции y=f(x) при
называется наклонной асимптотой графика функции y=f(x) при 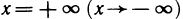 , если функцию f(х) можно представить в виде
, если функцию f(х) можно представить в виде 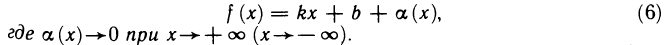
Рассмотрим геометрический смысл наклонной асимптоты. Для определенности разберем случай, когда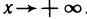 . (Случай
. (Случай 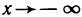 рассматривается аналогично).
рассматривается аналогично).
Пусть М (х; у) — точка графика функции y=f(x) и пусть прямая y=kx+b является наклонной асимптотой графика функции при 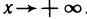 . Текущую ординату точки на асимптоте обозначим через
. Текущую ординату точки на асимптоте обозначим через 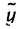 точку на асимптоте — через
точку на асимптоте — через 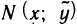 (рис. 88). Тогда
(рис. 88). Тогда 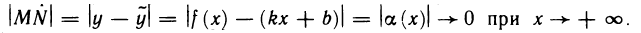 Опустим из точки М перпендикуляр MP на асимптоту. Расстояние d от точки М до асимптоты равно
Опустим из точки М перпендикуляр MP на асимптоту. Расстояние d от точки М до асимптоты равно 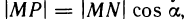 , где
, где 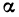 — угол между асимптотой и осью Ох, и, следовательно,
— угол между асимптотой и осью Ох, и, следовательно, 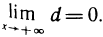
Таким образом, расстояние от точки М (х; у) графика функции до асимптоты стремится к нулю при 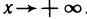 т. е. график функции неограниченно приближается к асимптоте при
т. е. график функции неограниченно приближается к асимптоте при 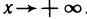 .
.
Рассмотрим способ отыскания наклонной асимптоты, т. е. способ определения чисел k и и в уравнении асимптоты. Разделив равенство (6) на х и перейдя к пределу при 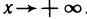 , получим
, получим
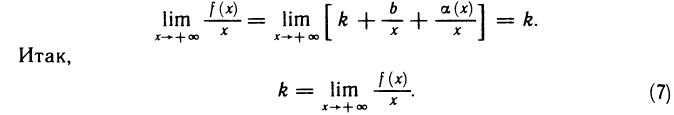
Далее, из соотношения (6) получаем: 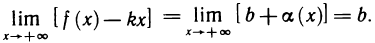
Таким образом, 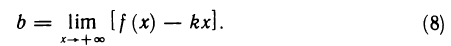
Доказано, что если прямая y=kx+b — наклонная асимптота, то числа k и b находятся по формулам (7) и (8). Обратно, если оба предела (7) и (8) существуют, причем 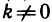 , то прямая y=kx+b является наклонной асимптотой графика функции y=f(x) при
, то прямая y=kx+b является наклонной асимптотой графика функции y=f(x) при 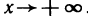 .
.
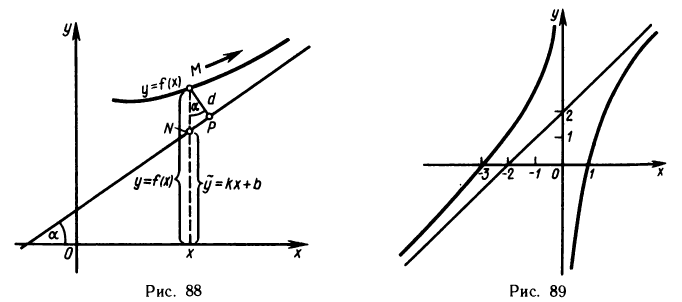
В самом деле, полагая 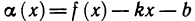 и используя равенство (8), Получаем, что
и используя равенство (8), Получаем, что 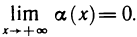 Следовательно, справедливо равенство (6):
Следовательно, справедливо равенство (6): 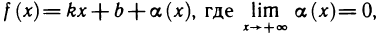 т. е. прямая
т. е. прямая 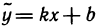 является наклонной асимптотой графика функции при
является наклонной асимптотой графика функции при 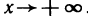
Практически целесообразно искать асимптоты в следующем порядке: 1) вертикальные асимптоты; 2) горизонтальные асимптоты; 3) наклонные асимптоты.
Пример:
Найти асимптоты графика функции 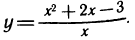
Решение:
1) Находим вертикальные асимптоты. Точка х=0 _ точка разрыва 2-го рода данной функции, причем 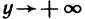 при
при 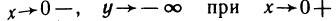 . Следовательно, ось ординат (х=0) — вертикальная асимптота.
. Следовательно, ось ординат (х=0) — вертикальная асимптота.
2) Находим горизонтальные асимптоты: 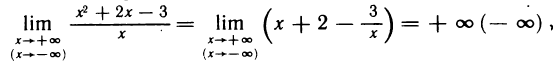 следовательно, горизонтальных асимптот нет.
следовательно, горизонтальных асимптот нет.
3) Находим наклонные асимптоты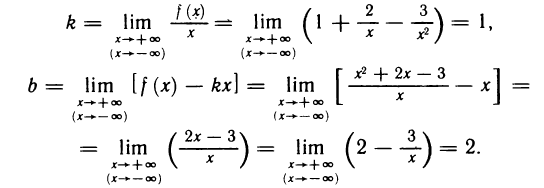
Следовательно, прямая у=х+2 является наклонной асимптотой графика данной функции как при 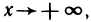 так и при
так и при 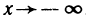 . График функции схематически изображен на рис. 89.
. График функции схематически изображен на рис. 89.
Пример:
Доказать, что гипербола 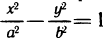 имеет своими наклонными асимптотами прямые
имеет своими наклонными асимптотами прямые 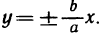
Решение:
Так как 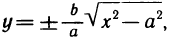 то
то 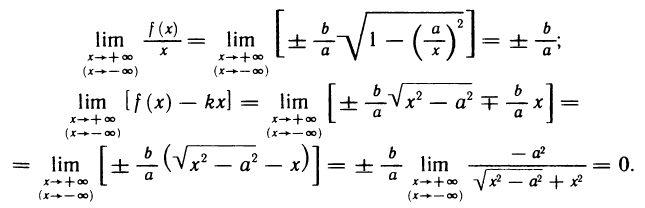
Следовательно, прямые 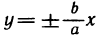 являются наклонными асимптотами данной гиперболы как при
являются наклонными асимптотами данной гиперболы как при 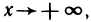 так и при
так и при 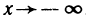 .
.
Схема исследования графика функции
Рассмотрим примерную схему, по которой целесообразно исследовать поведение Функции и строить ее график.
- Найти область определения функции.
- Найти точки пересечения графика функции с осями координат.
- Найти асимптоты.
- Найти точки возможного экстремума.
- Найти критические точки.
- С помощью вспомогательного чертежа исследовать знак пер. вой и второй производных. Определить участки возрастания и убывания функции, найти направление выпуклости графика, точки экстремума и точки перегиба.
- Построить график, учитывая исследование, проведенное в п. 1—6.
При этом в начале исследования полезно проверить, является данная функция четной или нечетной, чтобы при построении использовать симметрию графика относительно оси ординат или начала координат.
В качестве примера построим по изложенной выше схеме график функции 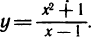
1. Областью определения функции является множество всех вещественных чисел, кроме х=1, при котором обращается в нуль знаменатель.
2. Так как уравнение 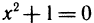 не имеет вещественных корней, то график функции не имеет точек пересечения с осью Ох, но пересекает ось Оу в точке (0; — 1).
не имеет вещественных корней, то график функции не имеет точек пересечения с осью Ох, но пересекает ось Оу в точке (0; — 1).
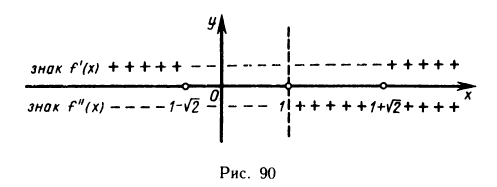
Выясним вопрос о существовании асимптот. Исследуем поведение функции вблизи точки разрыва х=1. Так как  при
при 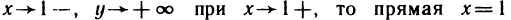 является вертикальной асимптотой графика функции.
является вертикальной асимптотой графика функции.
Если  следовательно, горизонтальной асимптоты у графика нет. Далее, из существования пределов
следовательно, горизонтальной асимптоты у графика нет. Далее, из существования пределов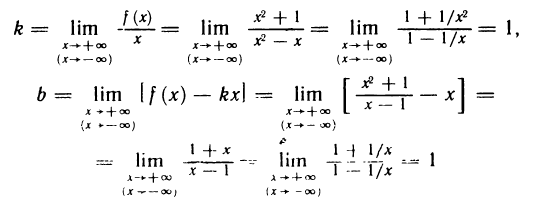
вытекает, что при 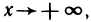 и при
и при 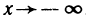 график функции имеет наклонную асимптоту у=х+1.
график функции имеет наклонную асимптоту у=х+1.
4. Для нахождения точек возможного экстремума вычислим первую производную функции: 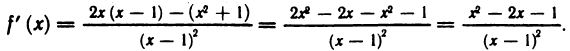
Решая уравнение 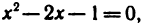 получаем две точки возможного экстремума:
получаем две точки возможного экстремума: 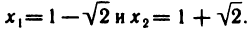
5. Для нахождения критических точек вычислим вторую производную: 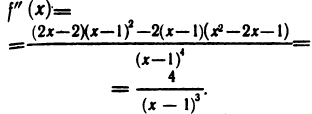
Так как f»(х) в нуль не обращается, то критических точек нет.
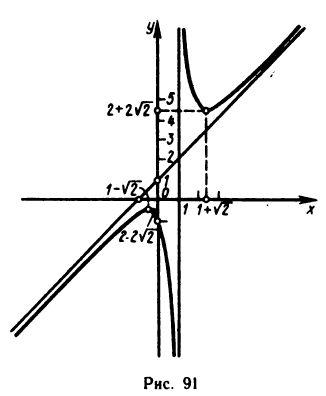
6. Нарисуем вспомогательный чертеж и исследуем знак первой и второй производных (рис.90). Получаем, что функция на 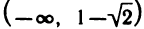 возрастает, на
возрастает, на 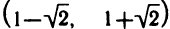 убывает, а на
убывает, а на 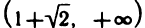 снова возрастает. Точки экстремума: 1) максимум при
снова возрастает. Точки экстремума: 1) максимум при 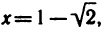 причем
причем 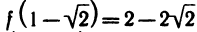 ; 2) минимум при
; 2) минимум при 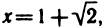 , причем
, причем 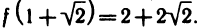 На
На 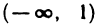 направление выпуклости графика вверх, а на
направление выпуклости графика вверх, а на 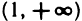 — вниз.
— вниз.
7. Используя полученные данные, строим эскиз графика (рис.91).
Интерполяция функций
Интерполяция применяется при решении многих как теоретических, так и прикладных вопросов, связанных с вычислениями.
1. Постановка задачи. Пусть на отрезке [a, b] заданы значения функции y=f (х) в точках 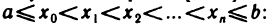
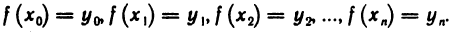
Требуется найти многочлен не выше n-й степени: 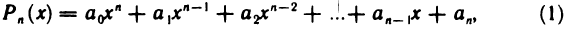
который в точках 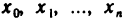 принимает те же значения, что и lанная функция, т. е. выполняются равенства
принимает те же значения, что и lанная функция, т. е. выполняются равенства 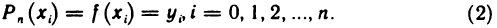
Другими словами, требуется найти такой многочлен вида (1), который на отрезке [а, b] являлся бы приближением для функции у=f(х). Поставленная задача называется задачей интерполяции многочлен (1) — интерполяционным многочленом, а точки 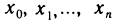 —узлами интерполяции. Решение данной задачи дает возможность находить приближенные значения функции f(х) в точках х, лежащих между узлами. Это важно, когда функция задана только в точках
—узлами интерполяции. Решение данной задачи дает возможность находить приближенные значения функции f(х) в точках х, лежащих между узлами. Это важно, когда функция задана только в точках 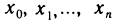 , а нужно уметь находить ее значения и в промежутках между этими точками, а также когда функция f(х) задается формулой на всем отрезке [а, b], но вычисление ее значений по этой формуле очень трудоемко.
, а нужно уметь находить ее значения и в промежутках между этими точками, а также когда функция f(х) задается формулой на всем отрезке [а, b], но вычисление ее значений по этой формуле очень трудоемко.
Покажем, что всегда существует и притом единственный интерполяционный многочлен (1), удовлетворяющий условиям (2). Для простоты ограничимся случаем n=2, т. е. случаем многочлена второй степени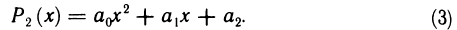
Подставляя в уравнение (3) вместо х последовательно числа 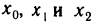 и принимая во внимание, что в этих точках многочлен принимает соответственно значения
и принимая во внимание, что в этих точках многочлен принимает соответственно значения 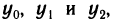 получаем систему трех уравнений первой степени с тремя неизвестными коэффициетами
получаем систему трех уравнений первой степени с тремя неизвестными коэффициетами 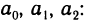
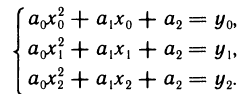
Так как числа 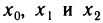 различны, то определитель этой системы отличен от нуля:
различны, то определитель этой системы отличен от нуля:
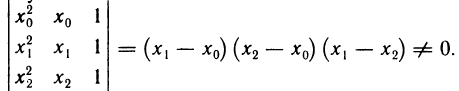
Следовательно (см. гл. 10, § 3), решение данной системы существует и оно единственно, что и доказывает утверждение. Геометрически это означает, через три точки 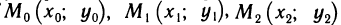 проходит единственная линия, определяемая уравнением (3). Таким образом, интерполяционный многочлен (1) всегда существует и единствен. Далее будут рассмотрены различные формы интерполяционного многочлена.
проходит единственная линия, определяемая уравнением (3). Таким образом, интерполяционный многочлен (1) всегда существует и единствен. Далее будут рассмотрены различные формы интерполяционного многочлена.
Интерполяционная формула Лагранжа
Рассмотрим вопрос об отыскании коэффициентов интерполяционного многочлена (1) Подставляя этот многочлен в систему (2), получаем систему n+1 уравнений первой степени с n-1 неизвестными коэффициентами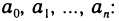
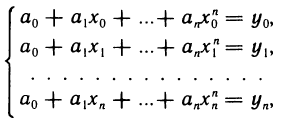
решая которую найдем значения коэффициентов 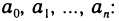
Подставляя эти значения в равенство (1), получаем искомый интер-п0.пяционный многочлен. Однако на практике, как правило, решете системы связано с громоздкими вычислениями. Поэтому интерполяционный многочлен (1) будем искать в виде 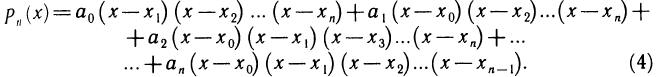
Полагая в (4) 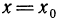 и принимая во внимание условия (2), получаем
и принимая во внимание условия (2), получаем
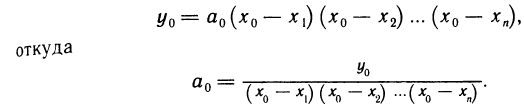
Полагая затем в (4) 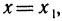 имеем
имеем
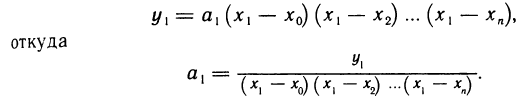
Аналогично найдем
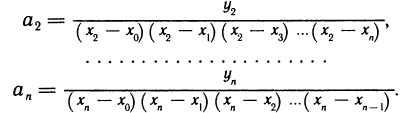
Подставляя найденные значения коэффициентов 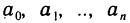 в формулу (4), получаем искомый интерполяционный многочле
в формулу (4), получаем искомый интерполяционный многочле
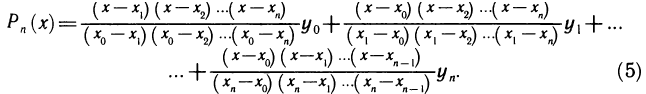
Формула (5) называется интерполяционной формулой Лагранжа.
Пример:
В результате эксперимента в точках 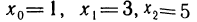 , получены значения функции f(x), соответственно равные
, получены значения функции f(x), соответственно равные 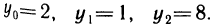 Найти многочлен второй степени
Найти многочлен второй степени 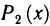 , приближенно выражающий функцию f(х).
, приближенно выражающий функцию f(х).
Решение. По формуле (5) находи
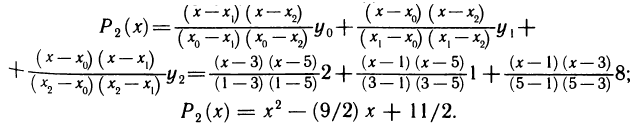
Интерполяционная формула Ньютона
Рассмотрим частный случай, когда разность h между соседними узлами интерполяции величина постоянная: 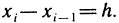 Введем следующие обозначения
Введем следующие обозначения
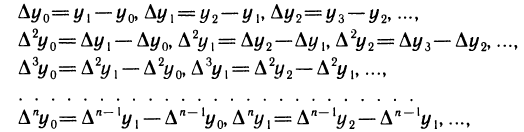
называемые разностями первого, второго, третьего, …, n-го порядков.
Найдем интерполяционный многочлен n-й степени, принимающий в точках 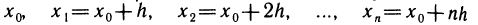 соответственно значения
соответственно значения 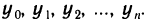 Сначала найдем многочлен первой степени, принимающий в точках
Сначала найдем многочлен первой степени, принимающий в точках 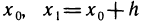 значения
значения 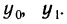 Подставляя в формулу (5) вместо х, число
Подставляя в формулу (5) вместо х, число 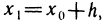 получаем
получаем 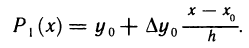
Аналогично находим:
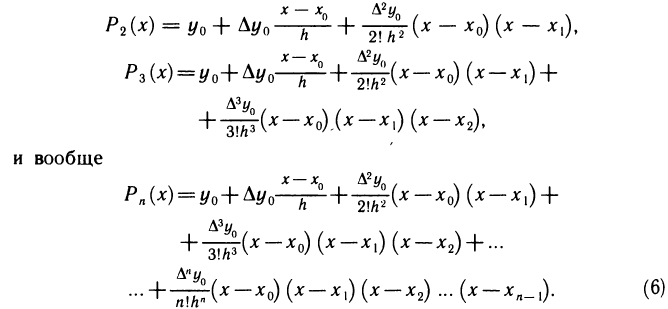
Формула (6) определяет искомый многочлен и называется интерполяционной формулой Ньютона.
Задача интерполяции имеет единственное решение, поэтому формулы Лагранжа и Ньютона для данных значений 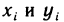 тождественны и отличаются лишь группировкой членов. На практике формула Ньютона более удобна. Особенность ее заключается в том, что в случае добавления новых узлов интерполяции в формуле Лагранжа надо пересчитывать заново все коэффициенты, а в формуле Ньютона добавятся только новые слагаемые, а старые остаются без изменения.
тождественны и отличаются лишь группировкой членов. На практике формула Ньютона более удобна. Особенность ее заключается в том, что в случае добавления новых узлов интерполяции в формуле Лагранжа надо пересчитывать заново все коэффициенты, а в формуле Ньютона добавятся только новые слагаемые, а старые остаются без изменения.
Существуют и другие формулы интерполяции, среди которых наиболее употребительна эрмитова интерполяция. Задача ставится так: заданы n узлов, n значений функции f(х) и n значений ее производной f'(х) в узлах; требуется найти многочлен степени не выше 2n—1 такой, чтобы 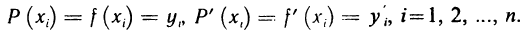
На решении этой задачи останавливаться не будем, а только заметим, что если все х, различны, то существует единственное решение, которое находится аналогично предыдущему.
Остаточный член интерполяции
Для оценки близости интерполяционного многочлена 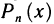 к функции f(х) необходимо исследовать разность между функцией и интерполяционным многочленом
к функции f(х) необходимо исследовать разность между функцией и интерполяционным многочленом 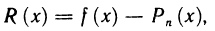 называемую остаточным членом интерполяции.
называемую остаточным членом интерполяции.
Предположим, что на отрезке [a, b] существует (n+1)-я непрерывная производная 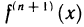 . Тогда
. Тогда 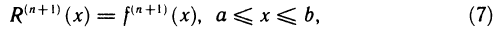
так как 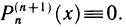 Пусть х — любое фиксированное число,
Пусть х — любое фиксированное число, 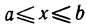 , не совпадающее с узлами интерполяции, t — переменная величина,
, не совпадающее с узлами интерполяции, t — переменная величина, 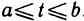 . Положим
. Положим 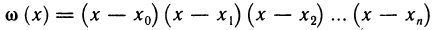
и рассмотрим на отрезке [а, b] вспомогательную функцию 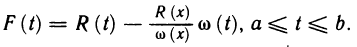
Функция F(t), очевидно, n+1 раз дифференцируема на отрезке [a, b], причем в силу (7) и того факта, что 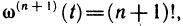 имеем
имеем 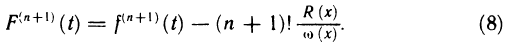
Далее, функция F(t) обращается в нуль в n+2 точках: 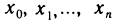 и х(х—фиксированное). Поэтому по теореме Ролля ее первая производная обращается в нуль, по крайней мере, в n+1 точке отрезка [a, b], вторая производная обращается в нуль, по крайней мере, в п точках этого отрезка и т. д. По индукции получаем, что (n+1)-я производная функции F(t) обращается, по крайней мере, один раз в нуль внутри отрезка [a, b]. Следовательно, существует точка
и х(х—фиксированное). Поэтому по теореме Ролля ее первая производная обращается в нуль, по крайней мере, в n+1 точке отрезка [a, b], вторая производная обращается в нуль, по крайней мере, в п точках этого отрезка и т. д. По индукции получаем, что (n+1)-я производная функции F(t) обращается, по крайней мере, один раз в нуль внутри отрезка [a, b]. Следовательно, существует точка 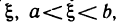 такая, что
такая, что 
Полагая в (8) 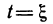 и используя (9), находим
и используя (9), находим
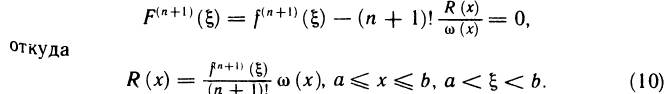
Равенство (10) определяет остаточный член интерполяции. Обозначая через k наибольшее значение функции 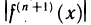 на отрезке получаем формулу оценки остаточного члена для любого
на отрезке получаем формулу оценки остаточного члена для любого 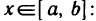
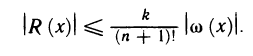
Методы приближенного вычисления корней уравнений
В этом параграфе рассмотрим вопрос о приближенном вычислении корней уравнения f(x)=0, где f (х) — некоторая непрерывная функция.
Из элементарной математики известен способ нахождения корней уравнения f(x)=0, если f (х) — линейная или квадратичная функция. Для более сложных функций обычно приходится прибегать к различным методам приближенного вычисления корней уравнения. Познакомимся с методом «вилки» и методом касательных.
Метод «вилки»
Пусть интересующий нас корень уравнения f(х)=0 является внутренней точкой отрезка [а, b] и других корней на [а, b] нет. Предположим, что функция f(х) непрерывна на [a, b] и имеет на концах этого отрезка значения разных знаков. На практике обычно грубой прикидкой находят такой отрезок. Назовем «вилкой» любой отрезок, на концах которого f(х) имеет значения разных знаков.
Для определенности будем считать, что 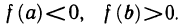 Разделим [а, b] пополам и выберем тот из полученных отрезков, на концах которого f(х) имеет разные знаки. Обозначим его
Разделим [а, b] пополам и выберем тот из полученных отрезков, на концах которого f(х) имеет разные знаки. Обозначим его 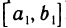 (Если бы значение f(х) в середине [а, b] равнялось нулю, то корень был бы найден.) Разделим
(Если бы значение f(х) в середине [а, b] равнялось нулю, то корень был бы найден.) Разделим 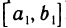 пополам и выберем тот из полученных отрезков, на концах которого f(х) имеет разные знаки, и т. д. Продолжая этот процесс неограниченно, получаем последовательность вложенных отрезков — вилок:
пополам и выберем тот из полученных отрезков, на концах которого f(х) имеет разные знаки, и т. д. Продолжая этот процесс неограниченно, получаем последовательность вложенных отрезков — вилок: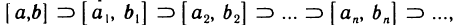
обладающих тем свойством, что для любого n 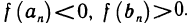
По теореме 2.13 о вложенных отрезках существует точка с, принадлежащая всем отрезкам, к которой сходится каждая из последовательностей 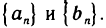
Докажем, что точка с и является искомым корнем, т. е. f (с)=0. Поскольку f(х) непрерывна в точке с, каждая из последовательностей 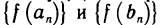 сходится к f(с). Но тогда из условий
сходится к f(с). Но тогда из условий 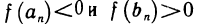 по теореме 2.10 получаем, что одновременно справедливы неравенства
по теореме 2.10 получаем, что одновременно справедливы неравенства 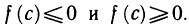 Отсюда f(с)=0, что и требовалось доказать.
Отсюда f(с)=0, что и требовалось доказать.
Теперь нетрудно понять, как вычислить приближенно корень х=с. За приближенное значение этого корня можно взять середину отрезка 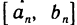 , т. е. точку
, т. е. точку 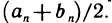 Так как длина
Так как длина 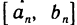 равна
равна 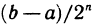 , а расстояние от корня с до точки
, а расстояние от корня с до точки 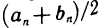 не превышает половины длины отрезка
не превышает половины длины отрезка 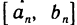 , то число
, то число 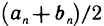 отличается от точного значения корня не более чем на
отличается от точного значения корня не более чем на 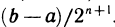 . Таким образом, описанный метод позволяет вычислить искомый корень с с любой точностью, если взять достаточно большое n. Этот метод удобен тем, что требует однотипных вычислительных операций. Поэтому его часто используют при проведении вычислений на современных быстродействующих вычислительных машинах.
. Таким образом, описанный метод позволяет вычислить искомый корень с с любой точностью, если взять достаточно большое n. Этот метод удобен тем, что требует однотипных вычислительных операций. Поэтому его часто используют при проведении вычислений на современных быстродействующих вычислительных машинах.
Метод касательных
Этот метод является одним из самых эффективных методов приближенного вычисления корней уравнения f(x)=0.
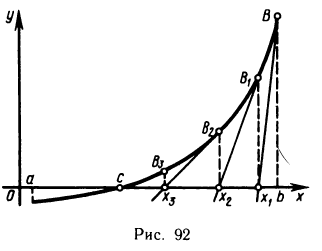
Пусть по-прежнему корень х=с является внутренней точкой [а, b]. Предположим также, что на [а, b] функция f(х) имеет непрерывные знакопостоянные производные f'(х) и f»(x), а ее значения f (а) и f(b) имеют разные знаки. Так как знак f'(х) постоянен, то функция f(х) на [а, b] либо возрастает, либо убывает, и, следовательно, в обоих случаях график функции у=f(x) пересекает ось Ох только в одной точке, т. е. х=с является единственным корнем на [а, b]. Аналогично, так как знак f»(х) постоянен, то направление выпуклости графика функции y=f(x) на этом отрезке не меняется.
Для определенности рассмотрим случай, когда 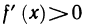 и
и 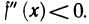 В этом случае
В этом случае 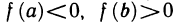 и график направлен выпуклостью вниз (рис. 92). Проведем через точку
и график направлен выпуклостью вниз (рис. 92). Проведем через точку 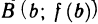 касательную к графику функции y=f(x). Ее уравнение имеет вид
касательную к графику функции y=f(x). Ее уравнение имеет вид 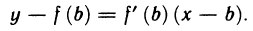
Полагая у=0, найдем абсциссу точки пересечения касательной с осью Ох: 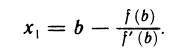
Так как 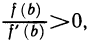 то
то  , а так как график функции y=f(x) pасположен не ниже касательной, то
, а так как график функции y=f(x) pасположен не ниже касательной, то 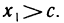 Итак,
Итак, 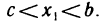 Возьмем за первое приближенное значение корня точку
Возьмем за первое приближенное значение корня точку 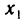 . Далее проведем касательную к графику через точку
. Далее проведем касательную к графику через точку 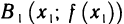 и, поступая аналогично, возьмем за второе приближенное значение корня точку
и, поступая аналогично, возьмем за второе приближенное значение корня точку 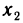 :
:
При этом 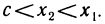 Продолжая этот процесс неограниченно для любого n получаем формулу
Продолжая этот процесс неограниченно для любого n получаем формулу
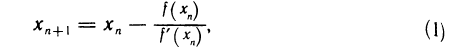
выражающую 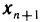 через
через 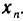 . Таким образом, имеем последовательность приближенных значений корня с, причем
. Таким образом, имеем последовательность приближенных значений корня с, причем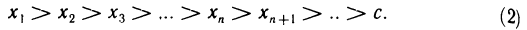
Формула (1) является основной расчетной формулой метода касательных. Он представляет собой метод последовательных приближений (итераций), который строится с помощью формулы (1).
Докажем, что последовательность 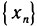 сходится к искомому корню с и оценим погрешность, т. е. отклонение приближенного значения
сходится к искомому корню с и оценим погрешность, т. е. отклонение приближенного значения 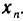 от точного значения корня с. Действительно, в силу (2), последовательность
от точного значения корня с. Действительно, в силу (2), последовательность 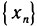 убывает и ограничена снизу числом с. Следовательно, по теореме 2.12 она имеет предел
убывает и ограничена снизу числом с. Следовательно, по теореме 2.12 она имеет предел 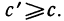 . Переходя к пределу в равенстве (1), учитывая непрерывность f(х) и f'(х), получаем
. Переходя к пределу в равенстве (1), учитывая непрерывность f(х) и f'(х), получаем 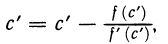
Неоткуда следует, что f(c’) = 0, т. е. с’ — корень уравнения f(x)=0. Но так как на [а, b] имеется только один корень с, то с’— с. Итак, последовательность 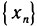 сходится к корню с.
сходится к корню с.
Оценим теперь отклонение n-го приближения 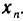 от точного значения корня с. Применяя к выражению
от точного значения корня с. Применяя к выражению 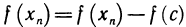 формулу Лагранжа, имеем
формулу Лагранжа, имеем 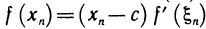 , где
, где 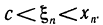 Отсюда получаем следующую оценку:
Отсюда получаем следующую оценку:
где m — наименьшее значение 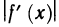 на отрезке [а, b]. Формула (3) позволяет оценить отклонение приближенного значения
на отрезке [а, b]. Формула (3) позволяет оценить отклонение приближенного значения 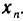 от точного значения корня с через значение модуля функции f(x) в точке
от точного значения корня с через значение модуля функции f(x) в точке 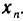 Отметим, что оценка (3) справедлива не только для метода касательных, но и вообще для любого метода приближенного вычисления корня при условии
Отметим, что оценка (3) справедлива не только для метода касательных, но и вообще для любого метода приближенного вычисления корня при условии 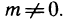
Мы рассмотрели случай, когда 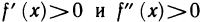 на [а, b] зависимости от комбинации знаков f'(x) и f»(х) возможны ещё три случая:
на [а, b] зависимости от комбинации знаков f'(x) и f»(х) возможны ещё три случая: 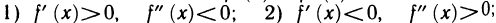
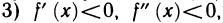 в каждом из которых обоснование метода касательных аналогично рассмотренному случаю.
в каждом из которых обоснование метода касательных аналогично рассмотренному случаю.
Пример:
Вычислить корень уравнения 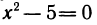 методом касательных.
методом касательных.
Решение. Рассмотрим функцию 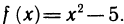 Эта функция непрерывна на всей числовой прямой. Найдем отрезок, на конца* которого функция f(х) имеет значения разных знаков. Так как f(2)= —1, f(3)=4, то таким отрезком является отрезок [2, 3].
Эта функция непрерывна на всей числовой прямой. Найдем отрезок, на конца* которого функция f(х) имеет значения разных знаков. Так как f(2)= —1, f(3)=4, то таким отрезком является отрезок [2, 3].
Внутри него находится искомый корень уравнения. Функция f(х) имеет на этом отрезке непрерывные положительные производные f'(x)=2х и f»(х)=2. Следовательно, первую касательную к графику функции y=f(x) следует проводить через точку (3; 4). Положив в формуле (1) 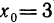 , получим первое приближение корня:
, получим первое приближение корня: 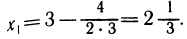 Положив теперь в формуле (1)
Положив теперь в формуле (1) 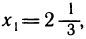 получим второе приближение корня:
получим второе приближение корня: 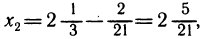 и наконец, положив
и наконец, положив 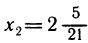 в формуле (1), получим третье приближение корня:
в формуле (1), получим третье приближение корня: 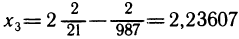 и т.д.
и т.д.
Для нахождения погрешности приближения 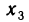 воспользуемся формулой (3). Так как производная f'(х)=2х на [2, 3] возрастает, то наименьшим ее значением на этом отрезке является f'(2)=4, т. е. m=4. Найдем
воспользуемся формулой (3). Так как производная f'(х)=2х на [2, 3] возрастает, то наименьшим ее значением на этом отрезке является f'(2)=4, т. е. m=4. Найдем 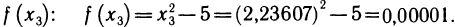 Теперь по формуле (3) имеем
Теперь по формуле (3) имеем 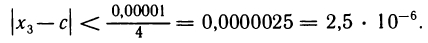
Если по условию задачи такая точность вычисления корня достаточна, то процесс построения приближений следует прекратить, в противном случае этот процесс следует продолжить.
Обозначения дифференциального исчисления


Смотрите также:
| Некоторые общие правила дифференцирования | Основные формулы |
| Производные комплексных функций | Дробно-рациональные функции |
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

