Оглавление:
Непрерывность функции:
Непрерывные функции, точки разрыва и их классификация, действия над непрерывными функциями, свойства функций, непрерывных на сегменте.
Определение:
Функция у = f(x) называется непрерывной в точке х₀, если:
- функция определена в точке x₀ и в некоторой ее окрестности, содержащей эту точку;
- функция имеет предел при х → x₀;
- предел функции при х → x₀ равен значению функции в точке x₀:
(10.1)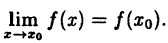
Если в точке x₀ функция непрерывна, то точка x₀ называется точкой непрерывности функции.
Пример:
Исследовать на непрерывность функцию 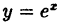 в точке х = 1.
в точке х = 1.
Решение:
Чтобы доказать, что функция 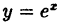 непрерывна в точке х = 1, необходимо проверить выполнение трех следующих условий (определение непрерывности):
непрерывна в точке х = 1, необходимо проверить выполнение трех следующих условий (определение непрерывности):
- функция
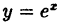 определена в точке х = 1 ⇒ f(1) = e;
определена в точке х = 1 ⇒ f(1) = e; - существует
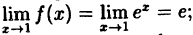 ;
; - этот предел равен значению функции в точке х = 1 :
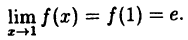
Таким образом, доказано, что функция  непрерывна в точке х = 1.
непрерывна в точке х = 1.
Замечание:
Формулу (10.1) можно записать в виде
(10.2) 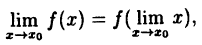
так как 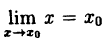 . Это значит, что при нахождении предела непрерывной функции можно переходить к пределу под знаком функции.
. Это значит, что при нахождении предела непрерывной функции можно переходить к пределу под знаком функции.
Введем понятие непрерывности функции в точке х₀ справа и слева.
Если, существует 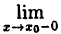 f(x) = f(x₀), то функция называется непрерывной в точке x₀ слева. Аналогично определяется непрерывность функции справа.
f(x) = f(x₀), то функция называется непрерывной в точке x₀ слева. Аналогично определяется непрерывность функции справа.
Так как ∆x = x-x₀, a ∆y = f(x)-(x₀), то условие (10.1) равносильно следующему: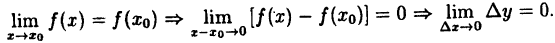
Определение:
Функция у = f(x) называется непрерывной в точке х₀, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции
(10.3) 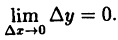
Пример:
Показать, что функция у = х³ непрерывна для любого значения аргумента х.
Решение:
Найдем приращение функции ∆y.
∆y= (x+∆x)³-x³ = x³+3x²∆x+3x∆x²+∆x³-x³ = 3x²∆x+3x∆x²+∆x³.
Используя теоремы о пределе суммы и произведения функции, получим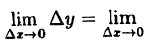 (3x²∆x 4- 3x∆x² + ∆x³) = 0.
(3x²∆x 4- 3x∆x² + ∆x³) = 0.
Следовательно, функция у = х³ непрерывна при — ∞< х < ∞.
Точки разрыва функции и их классификация
Определение:
Точка х₀ называется точкой разрыва функции у = f(x), если она принадлежит области определения функции или ее границе и не является точкой непрерывности.
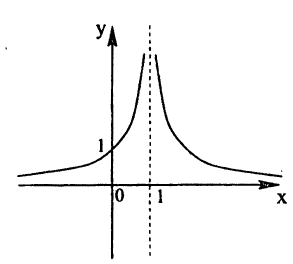
Так, например, функция 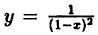 (рис. 89) терпит разрыв при х = 1. Эта функция не определена в точке х = 1, и не существует предела функции в этой точке.
(рис. 89) терпит разрыв при х = 1. Эта функция не определена в точке х = 1, и не существует предела функции в этой точке.
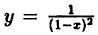
Определение:
Точка разрыва x₀ функции у = f(x) называется точкой устранимого разрыва, если существуют оба односторонних предела в точке x₀ и они равны, т. е. 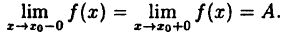
Пример:
Исследовать на непрерывность функцию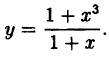
Решение:
В точке x=-1 функция не определена, так как, выполнив подстановку, получаем неопределенность 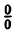 . В других точках дробь можно сократить на (1 + х), так как в них 1 + х ≠ 0. Легко видеть, что односторонние пределы слева и справа в точке х = — 1 равны между собой и их можно вычислить:
. В других точках дробь можно сократить на (1 + х), так как в них 1 + х ≠ 0. Легко видеть, что односторонние пределы слева и справа в точке х = — 1 равны между собой и их можно вычислить: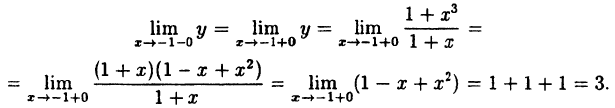
Таким образом, при x = -1 данная функция имеет устранимый разрыв.
Он будет устранен, если положить, что при x = -1 ⇒ у =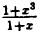 = 3.
= 3.
Определение:
Если в точке x₀ односторонние пределы слева и справа существуют, но не равны, точка x₀ называется точкой разрыва I рода.
Пример:
Исследовать на непрерывность функцию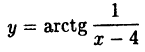 (рис. 90).
(рис. 90).
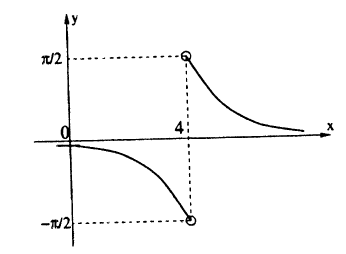
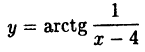
Решение: Вычислим односторонние пределы функции в точке ее разрыва х = 4.
Предел слева —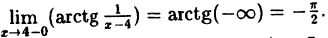 .
.
Предел справа — 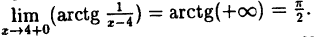 .
.
Пределы слева и справа существуют, но не равны, следовательно, точка x = 4 для данной функции — точка разрыва I рода (точка скачка).
Определение:
Точки разрыва, не являющиеся точками разрыва I рода, называются точками разрыва II рода.
В точках разрыва II рода не существует хотя бы один из односторонних пределов. Функция 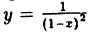 , представленная на рис. 89, не имеет ни левого, ни правого конечного предела в точке х = 1. Следовательно, для данной функции x = 1 является точкой разрыва II рода.
, представленная на рис. 89, не имеет ни левого, ни правого конечного предела в точке х = 1. Следовательно, для данной функции x = 1 является точкой разрыва II рода.
Действия над непрерывными функциями
Теорема:
Непрерывность суммы, произведения и частного непрерывных функций. Если функции ϕ(x) и ψ(x) непрерывны в точке Хо, то их сумма и произведение также непрерывны в точке x₀. Если, кроме того, знаменатель в рассматриваемой точке не равен нулю, то частное непрерывных функций есть функция непрерывная.
Докажем непрерывность произведения.
Дано: непрерывность функций в точке x₀: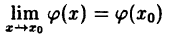 и
и 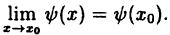
Доказать, что f(x) — ϕ(x) ∙ ψ(x) есть функция непрерывная в точке x₀, т. е. 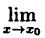 f(x) — f(x₀).
f(x) — f(x₀).
Доказательство: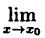 f(x) =
f(x) =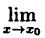 [ϕ(x) ∙ ψ(x)] =
[ϕ(x) ∙ ψ(x)] = 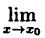 ϕ(x) ∙
ϕ(x) ∙ 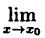 ψ(x) = ϕ(x₀) ∙ ψ(x₀) = f(x₀).
ψ(x) = ϕ(x₀) ∙ ψ(x₀) = f(x₀).
Можно строго доказать, что все основные элементарные функции непрерывны при всех значениях х, для которых они определены.
Например, степенная у = xⁿ, показательная у = 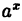 , тригонометрические у = sin х и у = cos х функции непрерывны на всей числовой оси (х ∈ R), логарифмическая функция
, тригонометрические у = sin х и у = cos х функции непрерывны на всей числовой оси (х ∈ R), логарифмическая функция 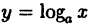 непрерывна при х > 0, а тригонометрическая у = tg x непрерывна в каждом из интервалов
непрерывна при х > 0, а тригонометрическая у = tg x непрерывна в каждом из интервалов 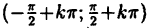 и терпит разрыв II рода в точках
и терпит разрыв II рода в точках 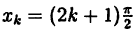 (k = 0; ±1; ±2;…).
(k = 0; ±1; ±2;…).
Теорема:
Непрерывность сложной функции. Если функция и = ϕ(x) непрерывна в точке x₀, а функция у = f(u) непрерывна в точке и₀ = ϕ(x₀), то сложная функция у = f [ϕ(x)] непрерывна в точке x₀.
Без доказательства.
В заключение этого раздела рассмотрим два предела, которые нам понадобятся в дальнейшем.
Пример:
Вычислить 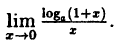
Решение:
Заметим, что при х → 0 числитель и знаменатель одновременно стремятся к нулю, т.е. имеет место неопределенность вида 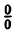 . Выполним преобразование
. Выполним преобразование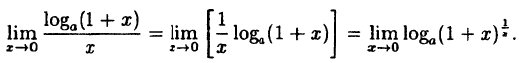
Так как данная логарифмическая функция непрерывна в окрестности точки х = 0, то можно перейти к пределу под знаком функции ( f(x)= f (
f(x)= f ( x)).
x)).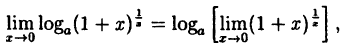
но 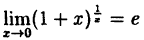 — второй замечательный предел.
— второй замечательный предел.
Следовательно,
(10.4) 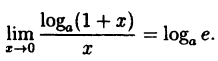
В частности, при а = е
(10.5) 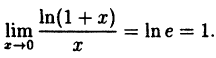
Таким образом, у = ln( 1 + х) и у = х — эквивалентные бесконечно малые функции при х → 0.
Пример:
Вычислить 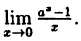
Решение:
Здесь мы имеем дело с неопределенностью вида 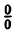 . Для нахождения предела сделаем замену переменной, положив
. Для нахождения предела сделаем замену переменной, положив 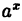 — 1 = t. Тогда
— 1 = t. Тогда 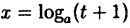 . При х → 0 также и t → 0.
. При х → 0 также и t → 0.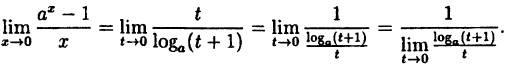
Так как на основании результата, полученного в предыдущем примере, 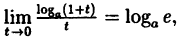 то
то
(10.6) 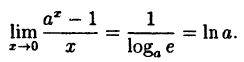
В частности, если а = е, имеем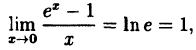
т.е. у = 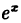 — 1 и y = x — эквивалентные бесконечно малые функции при х → 0.
— 1 и y = x — эквивалентные бесконечно малые функции при х → 0.
Свойства функций, непрерывных на сегменте
Определение:
Функция у = f(x) непрерывна на сегменте [а, b], если она непрерывна во всех внутренних точках Этого сегмента, а на концах сегмента (в точках a и b) непрерывна соответственно справа и слева.
Теорема:
Если функция у = f(x) непрерывна на сегменте [а, b], то она достигает на этом сегменте своего наибольшего и(или) наименьшего значения.
Простым доказательством этой теоремы, является геометрическая иллюстрация функции у = f(x) на рисунке 91. Непрерывная на сегменте [α, b] функция достигает наименьшего своего значения в точке х = x₁= а, а наибольшего значения в точке х₂.
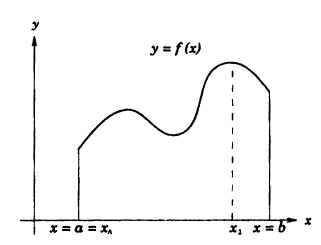
Следствие:
Если функция у = f(x) непрерывна на сегменте [a, b], то она ограничена на этом сегменте.
Действительно, если по теореме 10.3 функция достигает на сегменте наибольшего M и наименьшего т значений, то имеет место неравенство m ≤ f(x) ≤ M для всех значений функции на рассматриваемом сегменте. Т. е. |f(x)| ≤ M и, следовательно, функция у = f(x) ограничена на сегменте [а, b].
Теорема:
Теорема Больцано-Коши. Если функция у = f(x) непрерывна на сегменте [а, b] и на ее концах принимает значения разных знаков, то внутри этого сегмента найдется, по крайней мере, одна тонка С, в которой функция равна нулю.
Геометрический смысл теоремы заключается в следующем: если точки графика функции у = f(x), соответствующие концам сегмента [a, b], лежат по разные стороны от оси ОХ, то этот график хотя бы в одной точке сегмента пересекает ось OX. На данном рисунке 92 это три точки x₁, x₂, x₃.
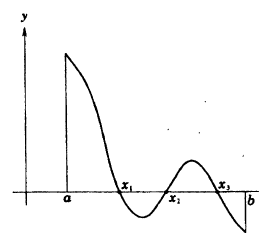
Теорема:
О промежуточных значениях функции. Если функция у = f(x) непрерывна на сегменте [α, b] и f(α) = A и f(b) = В, то для любого числа С, заключенного между A и B, найдется внутри этого сегмента такая точка с, что f(c) = С.
Из графика на рисунке 93 видно, что непрерывная функция, переходя от одного значения к другому, обязательно проходит через все промежуточные значения.
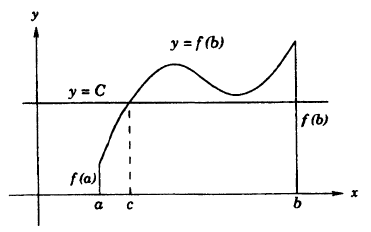
Теорема:
О непрерывности обратной функции.) Если функция у = f(x) непрерывна на сегменте [а, b] в возрастает (убывает) на этом сегменте, то обратная функция х = f⁻¹(y) на соответствующем сегменте оси OY существует и является также непрерывной возрастающей (убывающей) функцией.
Эту теорему мы принимаем без доказательства.
Решение на тему: Непрерывная функция
Пример:
Показать, что функция у = 4x² непрерывна в точке х = 2.
Решение:
Для этого необходимо показать, что в точке х = 2 выполняется все три условия непрерывности функции:
1) функция у = 4х² определена в точке х = 2 ⇒ f(2) = 16;
2) существует 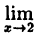 f(x) =
f(x) = 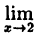 4x²= 16;
4x²= 16;
3) этот предел равен значению функции в точке х = 2
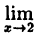 f(x) = f(2) = 16.
f(x) = f(2) = 16.
Пример:
Показать, что функция у = sin x непрерывна для любого значения аргумента х.
Решение:
Найдем приращение функции ∆y, используя формулы тригонометрических тождеств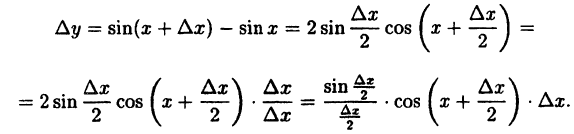
Так как 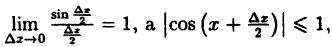 то при любом х имеем
то при любом х имеем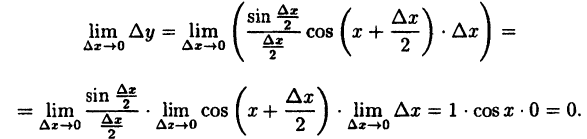
Следовательно, функция у = sin x непрерывна при -∞ < х < ∞.
Пример:
Исследовать на непрерывность функцию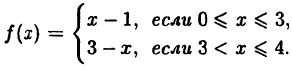
Решение:
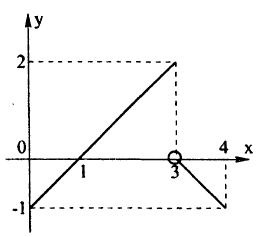
Эта функция (рис. 94) определена во всех точках сегмента [0,4] и ее значение при х = 3 ⇒ у = 2. Функция терпит разрыв, так как она не имеет предела при х → 3 :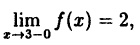
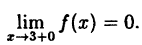
Следовательно, точка х = 3, точка разрыва первого рода. При этом в граничных точках исследуемого сегмента [0,4], функция f(x) непрерывна справа (х = 0) и непрерывна слева (х = 4).
Пример:
Исследовать на непрерывность функцию 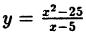
Решение:
В точке х = 5 функция не определена, т.к., выполнив подстановку, получаем неопределенность вида 0/0. Легко доказать, что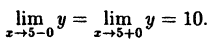
Следовательно, точка х = 5 точка устранимого разрыва.
Пример:
Исследовать на непрерывность функцию 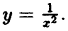
Решение:
В точке х = 0 функция (рис. 95) терпит разрыв, так как она не определена в этой точке. Пределы функции слева и справа от точки х = 0 равны ∞. Следовательно, точка х = 0 для данной функции является точкой разрыва второго
Пример:
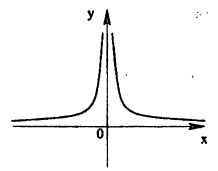
Исследовать на непрерывность функцию 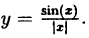
Решение:
В точке х = 0 функция терпит разрыв 1-го рода, так как односторонние пределы существуют в этой точке, но не равны:
предел слева 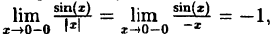
предел справа 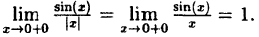
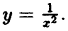
Пример:
Исследовать на непрерывность функцию 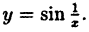 .
.
Решение:
Функция 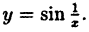 определена для всех значений х, кроме x = 0.B этой точке она имеет разрыв. Точка х = 0 есть точка разрыва II рода, так как при х → 0 как справа, так и слева, функция
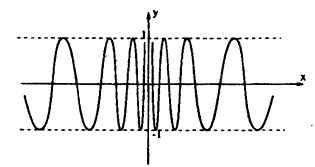
определена для всех значений х, кроме x = 0.B этой точке она имеет разрыв. Точка х = 0 есть точка разрыва II рода, так как при х → 0 как справа, так и слева, функция 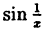 , колеблясь между -1 и 1, не приближается ни к какому числовому значению. График ее приведен на рис. 96.
, колеблясь между -1 и 1, не приближается ни к какому числовому значению. График ее приведен на рис. 96.
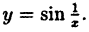
Пример:
Исследовать на непрерывность функцию 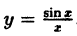
Решение:
Функция 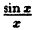 не определена в точке х = 0. Точка х = 0 является точкой разрыва I рода, так как при х → 0 существуют пределы справа и слева:
не определена в точке х = 0. Точка х = 0 является точкой разрыва I рода, так как при х → 0 существуют пределы справа и слева: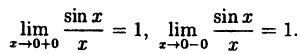
Если доопределить функцию 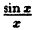 в точке х = 0, полагая f(0) = 1, то получим уже непрерывную функцию, определенную так:
в точке х = 0, полагая f(0) = 1, то получим уже непрерывную функцию, определенную так:
f(х) =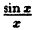 , если х ≠ 0; f(0) = 1.
, если х ≠ 0; f(0) = 1.
Доопределив функцию в точке х = 0, мы устранили разрыв.
Непрерывность функций




Смотрите также:
| Функции многих переменных. | Непрерывность композиции непрерывных функции. |
| Предел функции. | Теоремы о функциях, непрерывных на множествах. |
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

