Оглавление:
Многочлен от одной переменной — это сумма одночленов от одной переменной х (в которой приведены подобные слагаемые, то есть все одночлены-слагаемые имеют различную степень).
Тождественные преобразования многочленов
Основные законы алгебры: Читатель знаком с большим числом алгебраических формул: с формулой квадрата суммы и разности
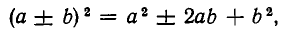
с формулой разложения разности квадратов на множители
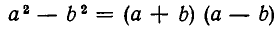
и т. д. Ему известны и многочисленные правила действий над алгебраическими выражениями: сложения многочленов, умножения одночленов и многочленов, правила действий с алгебраическими дробями и т. д.
Все многообразие формул алгебры основано на нескольких основных законах, относящихся к сложению, вычитанию, умножению и делению чисел. Эти основные законы таковы:
1) а + 0 = а. 2) а + (—а) = 0. 3) а+b=b + а (коммутативность сложения). 4) а + (b + с) = (а + b) + с (ассоциативность сложения). 5) аb = bа (коммутативность умножения). 6) а(bс) = (аb)с (ассоциативность умножения). 7) а(b + с) = аb + ас (дистрибутивность умножения относительно сложения). 8) 1 • а = а. 9) 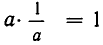 , где
, где 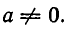
Покажем, например, как из этих законов выводится формула
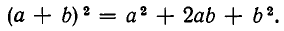
По закону дистрибутивности имеем:
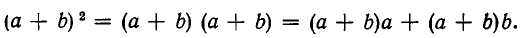
Используя коммутативность умножения, получаем:
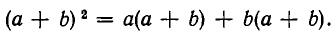
Вторично применяя дистрибутивность, а также коммутативность умножения и ассоциативность сложения, находим:
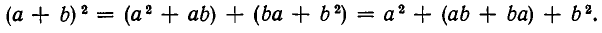
Поскольку
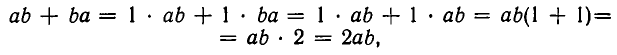
то и
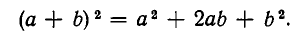
Если выводить аналогичным образом формулу
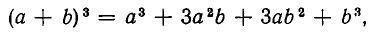
то придется использовать и ассоциативность умножения.
Роль законов 1) — 9) в алгебре аналогична роли аксиом в геометрии. Как в геометрии все теоремы выводятся из аксиом, так в алгебре все формулы выводятся из законов 1) —9).
Как и аксиомы геометрии, алгебраические законы 1)—9) не доказываются. Они являются обобщением многотысячелетнего опыта практической деятельности человечества. Прежде чем сформулировать закон а + b = b + а, надо было много раз подметить такие арифметические соотношения, как 5 + 3 = 3 + 5, 7+12 = 12 + 7 и т. д. Все остальные законы алгебры имеют то же происхождение — они являются буквенной записью многократно проверявшихся арифметических соотношений.
Целые рациональные выражения и функции
Мы уже говорили, что алгебраические законы 1)—9) составляют фундамент всего здания алгебры. Но каждый раз сводить решение того или иного алгебраического вопроса, вывод той или иной алгебраической формулы к непосредственному применению этих законов было бы крайне сложно. Точно так же, как в геометрии из аксиом выводят теоремы и потом на практике пользуются уже этими теоремами, в алгебре из законов 1)—9) выводят алгебраические формулы и правила, а потом пользуются этими формулами и правилами для решения более сложных задач.
В первую очередь надо вывести из алгебраических законов правила действий с одночленами и многочленами.
Введем сначала важные понятия рационального и целого рационального выражения.
Выражение, составленное из букв (например, а, b, с, . . . , х, у, z ) и чисел с помощью знаков арифметических действий (сложения, вычитания, умножения и деления), называется рациональным выражением относительно входящих в него букв.
Примерами рациональных выражений (или, как их называли в начальной алгебре, алгебраических дробей) могут служить:
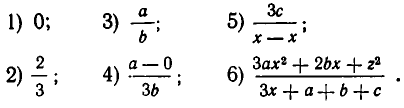
Если придавать буквам числовые значения, то рациональное выражение, как правило, будет принимать определенные числовые значения (исключение составляют случаи, когда при вычислениях пришлось бы делить на 0).
Поэтому, как правило, рациональное выражение является функцией от входящих в него букв.
Рациональное выражение называется целым относительно не которой буквы (например, х), если в нем нет операции деления на выражение, содержащее эту букву.
Например, выражения
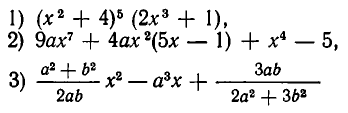
являются целыми относительно х.
Второе (и, конечно, первое!) выражение — целое относительно а, а третье — нет.
Целые рациональные выражения относительно буквы х являются, согласно сказанному выше, функциями от х.
Такие функции называют целыми рациональными функциями от х.
При сложении, вычитании и умножении целых рациональных выражений снова получаются выражения того же вида. Например, если
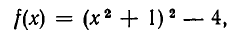
a
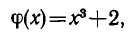
то
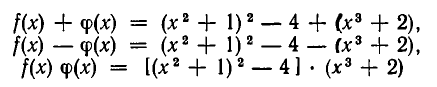
также целые рациональные выражения.
Два целых рациональных выражения относительно х называются тождественно равными, если они принимают одинаковые значения при всех значениях буквы х. В этом случае они задают одну и ту же функцию переменного x. Например, из формулы 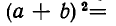
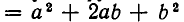 вытекает, что целые рациональные выражения
вытекает, что целые рациональные выражения 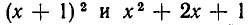 тождественно равны. Правила тождественных преобразований целых рациональных выражений знакомы читателю из начального курса алгебры. Мы укажем здесь более строгий и общий вывод некоторых из этих правил.
тождественно равны. Правила тождественных преобразований целых рациональных выражений знакомы читателю из начального курса алгебры. Мы укажем здесь более строгий и общий вывод некоторых из этих правил.
Степень с натуральным показателем и ее свойства
Напомним понятие степени с натуральным показателем. Пусть а — некоторое число, а n — натуральное число. Произведение n сомножителей, каждый из которых равен а, называют n-й степенью числа а и обозначают 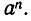 Число а называют основанием степени, а n — показателем степени. Например,
Число а называют основанием степени, а n — показателем степени. Например,
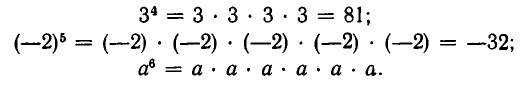
Хотя само число а нельзя взять сомножителем только один раз, естественно положить 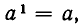 то есть считать, что первая степень числа равна этому числу. Из определения степени сразу вытекает, что для любого натурального п выполняются равенства
то есть считать, что первая степень числа равна этому числу. Из определения степени сразу вытекает, что для любого натурального п выполняются равенства 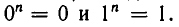
Операция возведения в степень с натуральным показателем обладает следующими свойствами: 1) Если а и b — любые числа и n — натуральное число, то

(дистрибутивность возведения в степень относительно умножения). Иными словами, чтобы возвести в степень произведение двух чисел, надо возвести в степень оба сомножителя и перемножить полученные результаты.
В самом деле, из определения степени следует, что
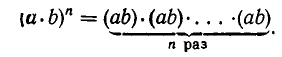
Используя ассоциативность и коммутативность умножения, переставим в правой части сомножители так, чтобы сначала шли все сомножители, равные а, а потом равные b. Мы получим:
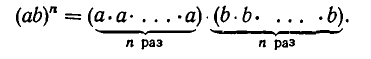
Но 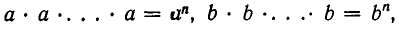 а потому
а потому

Соотношение (1) доказано.
2) Для любых чисел а и b, где 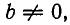 и любого натурального числа n выполняется равенство:
и любого натурального числа n выполняется равенство:

Иными словами, чтобы возвести в степень дробь, надо возвести в эту степень числитель и знаменатель дроби и разделить степень числителя на степень знаменателя. В самом деле, по правилу умножения дробей
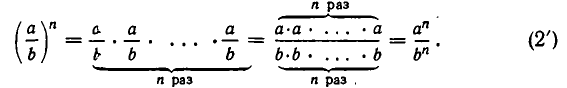
Из формулы (2) следует, в частности, что при 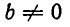
Ь ф О

3) Для любого числа а и любых натуральных чисел т и п выполняется равенство:

В самом деле, из определения степени с натуральным показателем и ассоциативности умножения следует, что
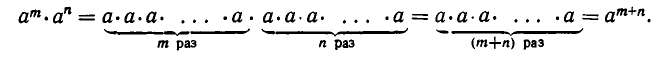
Формулу (4) читают так: при умножении степеней с одинаковы ми основаниями показатели степеней складываются.
4) Если а — любое число, отличное от нуля, а m и n — натуральные числа, причем m > n, то

Если же m < n, то

Иными словами, при делении степеней с одинаковыми основаниями показатели степеней вычитаются.
В самом деле, пусть m > n. Тогда имеем:
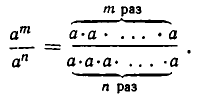
Сократим дробь на n множителей, равных а. Тогда в числителе останется m — n таких множителей, а знаменатель обратится в единицу. Поэтому мы получим, что
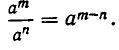
Разберите самостоятельно случай, когда m < n.
5) Для любого числа а и любых натуральных чисел т и п выполняется равенство:
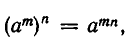
т. е. при возведении степени в степень показатели перемножаются.
В самом деле, из определения степени с натуральным показателем следует, что
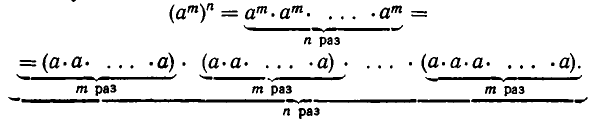
В правой части этого равенства имеем mn сомножителей, каждый из которых равен а, а потому все произведение равно 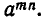 Итак,
Итак, 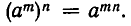
Если а — положительное число, то при любом натуральном n число 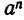 положительно. Если же а — отрицательное число, то
положительно. Если же а — отрицательное число, то 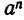 положительно при четном n и отрицательно при нечетном n.
положительно при четном n и отрицательно при нечетном n.
Правила 1), 2), 5) можно использовать для возведения в степень одночленов. Пусть, например, надо вычислить
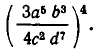
По правилам 2) и 1) имеем:
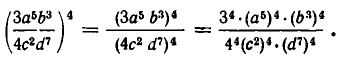
Применяя правило 5), получаем:
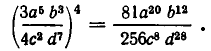
Рассмотрим еще пример:
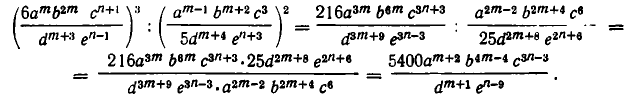
Многочлены
Пусть 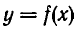 — целая рациональная функция. Как уже говорилось, ее выражение через х может иметь различный внешний вид. Например, выражения
— целая рациональная функция. Как уже говорилось, ее выражение через х может иметь различный внешний вид. Например, выражения
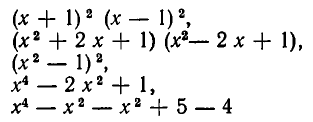
тождественно равны друг другу и потому задают одну и ту же функцию. Поэтому возникает задача — представить данную целую рациональную функцию в «стандартном», «каноническом» виде. Мы будем считать запись целой рациональной функции канонической, если она не содержит скобок и подобных членов, а слагаемые в ней расположены в порядке убывания показателей степеней х (для рассмотренного выше примера такой записью является 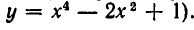
Приведение к канонической форме делается так. Раскрывают все скобки с помощью дистрибутивного закона а(b+ с) = аb + ас. После раскрытия скобок заменяют все произведения степеней переменного по правилам п. 3, приводят подобные члены и располагают члены в порядке убывания показателей степени. В результате получается выражение вида
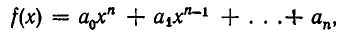
где 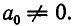 Такое выражение называют многочленом от х, а n — степенью этого многочлена. Числа
Такое выражение называют многочленом от х, а n — степенью этого многочлена. Числа  называют коэффициентами многочлена
называют коэффициентами многочлена 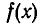 . В частности,
. В частности, 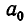 называют коэффициентом при старшем члене,
называют коэффициентом при старшем члене, 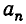 — свободным членом. Если
— свободным членом. Если 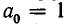 , многочлен называют приведенным. Например,
, многочлен называют приведенным. Например, 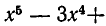
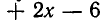 — приведенный многочлен пятой степени от х со свободным членом —6.
— приведенный многочлен пятой степени от х со свободным членом —6.
Числа 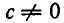 мы будем рассматривать как многочлены нулевой степени. Многочлен же, все коэффициенты которого равны нулю (нулевой многочлен), степени не имеет.
мы будем рассматривать как многочлены нулевой степени. Многочлен же, все коэффициенты которого равны нулю (нулевой многочлен), степени не имеет.
Приведение данного целого рационального выражения к каноническому виду можно выполнить различными путями. Например, в выражении
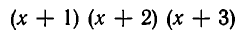
можно сначала перемножить (х+ 1) на (x + 2), а можно сначала перемножить (х+2) на (х+ 3). Поэтому возникает следующий вопрос: могут ли два различных многочлена тождественно равняться одному и тому же целому рациональному выражению?
Мы покажем ниже, что ответ на этот вопрос отрицателен: если два многочлена тождественно равны, то они имеют одинаковые степени, а коэффициенты при одинаковых степенях х в обоих многочленах совпадают. Поэтому, чтобы убедиться в тождественном равенстве двух целых рациональных выражений, надо привести их к каноническому виду (т. е. к виду многочленов) и проверить, что получившиеся многочлены совпадают.
Пример:
Доказать тождество
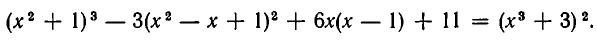
Имеем:
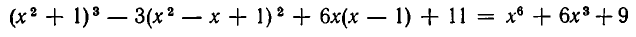
и
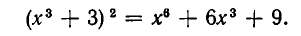
Так как получились одинаковые многочлены, то заданные целые рациональные выражения равны.
Умножение многочленов
Так как многочлены — это частный случай целых рациональных выражений, то над ними можно выполнять действия сложения, вычитания и умножения. При этом будут получаться целые рациональные выражения, но, вообще говоря, эти выражения не будут многочленами1. Например, складывая многочлены 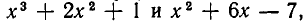 получим целое рациональное выражение
получим целое рациональное выражение 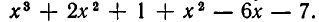 Однако после приведения подобных членов (и перегруппировки по убыванию степеней x:) мы уже получим многочлен
Однако после приведения подобных членов (и перегруппировки по убыванию степеней x:) мы уже получим многочлен 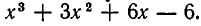 В дальнейшем под суммой, разностью, произведением двух многочленов мы будем понимать многочлен, получающийся после приведения соответствующего целого рационального выражения к каноническому виду. Например, произведением многочленов
В дальнейшем под суммой, разностью, произведением двух многочленов мы будем понимать многочлен, получающийся после приведения соответствующего целого рационального выражения к каноническому виду. Например, произведением многочленов
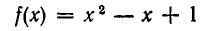
и
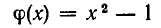
мы назовем многочлен
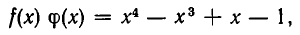
получающийся из целого рационального выражения
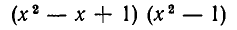
после раскрытия скобок и приведения подобных членов.
Действия над многочленами сводятся к действиям над их коэффициентами. Так, сложение многочленов сводится к сложению коэффициентов при одинаковых степенях х.
Рассмотрим, как выражаются через коэффициенты сомножителей коэффициенты произведения двух многочленов. Пусть даны многочлены:
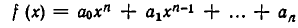
и
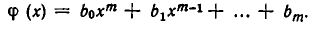
Перемножая их, получим целую рациональную функцию
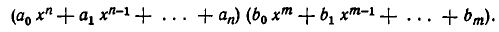
Раскроем скобки, воспользуемся формулой 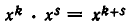 и приведем подобные члены. Получим многочлен:
и приведем подобные члены. Получим многочлен:
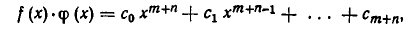
который и является произведением многочленов 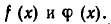
Старший член многочлена 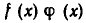 имеет степень m +n и является произведением старших членов многочленов
имеет степень m +n и является произведением старших членов многочленов 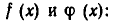
/ (х) и ф (х):
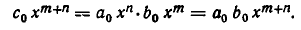
Поэтому 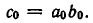
Точно так же свободный член в  является произведением свободных членов многочленов
является произведением свободных членов многочленов 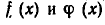
{ (х) и ф (х)
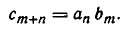
Выясним, какой вид имеют остальные коэффициенты многочлена 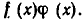 Член, содержащий
Член, содержащий 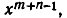 появляется дважды: при умножении
появляется дважды: при умножении 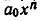 на
на 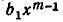 и при умножении
и при умножении 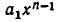 на
на 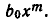 Поэтому коэффициент при этом члене равен
Поэтому коэффициент при этом члене равен 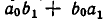 . Итак,
. Итак,
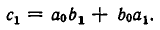
Точно так же доказывается формула:
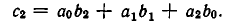
Легко заметить общий закон: сумма индексов в каждом слагаемом равна индексу искомого коэффициента:
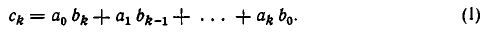
При этом если k > m или k > n, то некоторые члены в этом равенстве надо опустить — ведь в 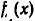 нет коэффициентов
нет коэффициентов 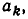 для которых k > n, а в
для которых k > n, а в 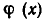 нет коэффициентов
нет коэффициентов 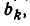 для которых k > m.
для которых k > m.
Например, по формуле (1) получаем, что
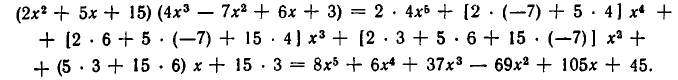
В дальнейшем нам понадобится следующее тождество:
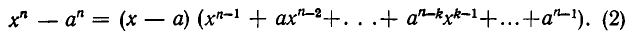
Чтобы доказать это тождество, раскроем скобки в правой части. Члены, содержащие 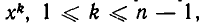 встретятся дважды: при умножении х на
встретятся дважды: при умножении х на 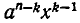 и при умножении (—а) на
и при умножении (—а) на 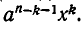
Сумма этих произведений равна нулю:
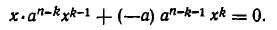
Поэтому остаются лишь члены 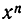 и
и 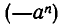 . Тем самым тождество (2) доказано.
. Тем самым тождество (2) доказано.
Точно так же доказывается тождество:
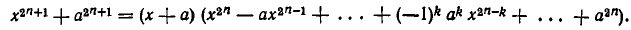
Числовые кольца и поля
Мы видели, что действия над многочленами сводятся к действиям над их коэффициентами. При этом для сложения, вычитания и умножения многочленов достаточно трех арифметических действий — деление чисел не понадобилось. Так как сумма, разность и произведение двух действительных чисел снова являются действительными числами, то при сложении, вычитании и умножении многочленов с действительными коэффициентами в результате получаются многочлены с действительными же коэффициентами.
Однако не всегда приходится иметь дело с многочленами, имеющими любые действительные коэффициенты. Возможны случаи, когда по самой сути дела коэффициенты должны иметь лишь целые или лишь рациональные значения. В зависимости от того, какие значения коэффициентов считаются допустимыми, меняются свойства многочленов. Например, если рассматривать многочлены с любыми действительными коэффициентами, то 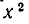 — 2 можно разложить на множители:
— 2 можно разложить на множители:
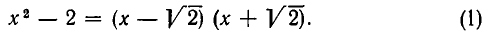
Если же ограничиться многочленами с целыми коэффициентами, то разложение (1) не имеет смысла и мы должны считать многочлен 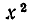 — 2 неразложимым на множители.
— 2 неразложимым на множители.
Отсюда видно, что теория многочленов существенно зависит от того, какие коэффициенты считаются допустимыми. Далеко не любую совокупность коэффициентов можно принять за допустимую. Например, рассмотрим все многочлены, коэффициенты которых — нечетные целые числа. Ясно, что сумма двух таких многочленов уже не будет многочленом того же типа: ведь сумма нечетных чисел — четное число.
Поставим вопрос: каковы «хорошие» множества коэффициентов? Когда сумма, разность, произведение многочленов с коэффициентами данного типа имеют коэффициенты того же типа? Для ответа на этот вопрос введем понятие числового кольца.
Определение. Непустое множество чисел R называется числовым кольцом, если вместе с любыми двумя числами а и b оно содержит их сумму, разность и произведение. Это выражают также короче, говоря, что числовое кольцо замкнуто относительно операций сложения, вычитания и умножения.
Примеры:
1) Множество целых чисел является числовым кольцом: сумма, разность и произведение целых чисел — целые числа. Множество же натуральных чисел числовым кольцом не является, так как разность натуральных чисел может быть отрицательной.
2) Множество всех рациональных чисел — числовое кольцо, так как сумма, разность и произведение рациональных чисел рациональны. 3) Образует числовое кольцо и множество всех действительных чисел. 4) Числа вида 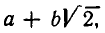 , где а и b — целые, образуют числовое кольцо. Это следует из соотношений:
, где а и b — целые, образуют числовое кольцо. Это следует из соотношений:
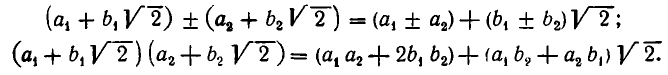
5) Множество нечетных чисел не является числовым кольцом, так как сумма нечетных чисел четна. Множество же четных чисел — числовое кольцо.
Если числовое кольцо R состоит не только из одного нуля и вместе с любыми двумя элементами а и b, где 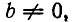 содержит и их частное
содержит и их частное 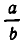 , то R называют числовым полем. Множества из примеров 2) и 3) — числовые поля. А множества целых чисел и всех четных чисел не являются числовыми полями. Например, частное
, то R называют числовым полем. Множества из примеров 2) и 3) — числовые поля. А множества целых чисел и всех четных чисел не являются числовыми полями. Например, частное 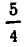 не является целым числом.
не является целым числом.
Кольцо многочленов над данным числовым полем
Пусть R — числовое поле. Рассмотрим множество всех многочленов, коэффициенты которых принадлежат числовому полю R, то есть многочленов вида
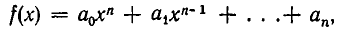
где 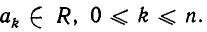 Это множество обозначают
Это множество обозначают 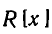 . Легко проверить, что сумма, разность и произведение двух многочленов из
. Легко проверить, что сумма, разность и произведение двух многочленов из 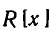 также принадлежит
также принадлежит 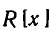 . По аналогии с числовыми кольцами множество многочленов
. По аналогии с числовыми кольцами множество многочленов 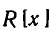 называют кольцом многочленов над числовым полем R.
называют кольцом многочленов над числовым полем R.
Ясно, что если 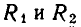 — Два числовых поля, причем
— Два числовых поля, причем 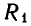 — подмножество
— подмножество 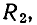 то всякий многочлен из кольца
то всякий многочлен из кольца 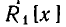 можно рассматривать и как многочлен из кольца
можно рассматривать и как многочлен из кольца 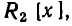 то есть
то есть 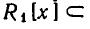
Бином Ньютона
При преобразовании целых рациональных выражений в многочлены час? о приходится разлагать выражения вида 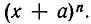 Выведем формулу для этого разложения. Случаи n = 2 и n = 3 известны из курса начальной алгебры:
Выведем формулу для этого разложения. Случаи n = 2 и n = 3 известны из курса начальной алгебры:
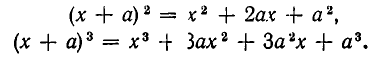
В разложение 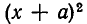 входят члены, содержащие
входят члены, содержащие 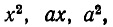 а в разложение
а в разложение 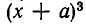 — члены, содержащие
— члены, содержащие 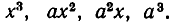
Естественно предположить, что в разложение 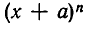 должны войти члены, содержащие
должны войти члены, содержащие

При этом старший член разложения должен равняться 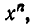 а свободный член равен
а свободный член равен 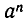 . Докажем это предположение с помощью индукции по
. Докажем это предположение с помощью индукции по 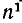 . Предположим, что уже доказана формула
. Предположим, что уже доказана формула
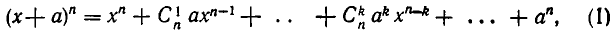
где через 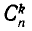 обозначен коэффициент при
обозначен коэффициент при 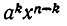 в разложении выражения
в разложении выражения 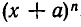 . Умножим обе части разложения (1) на (х + а):
. Умножим обе части разложения (1) на (х + а):
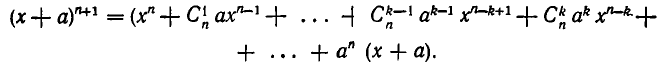
Посмотрим, какой коэффициент при 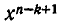 получится после раскрытия скобок. Ясно, что члены с
получится после раскрытия скобок. Ясно, что члены с 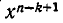 встретятся дважды: при умножении
встретятся дважды: при умножении 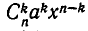 на х и при умножении
на х и при умножении 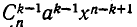 на а. Значит, коэффициент при
на а. Значит, коэффициент при 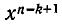 равен
равен 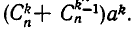 При этом коэффициент при
При этом коэффициент при 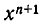 равен 1, а свободный член равен
равен 1, а свободный член равен 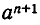 . Итак, мы доказали, что
. Итак, мы доказали, что

где

Итак, если разложение (1) справедливо для л, то оно справедливо и для n + 1. Так как оно имеет место при n = 1, то оно выполняется и при n = 2, а тогда и при n = 3 и т. д. Значит, оно верно для всех n.
Разложение (1) называют битном Ньютона. Коэффициенты 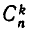 называются биномиальными коэффициентами. Мы получили для них соотношение (2).
называются биномиальными коэффициентами. Мы получили для них соотношение (2).
Так как первый и последний коэффициенты разложения (1) равны 1, то полагают по определению
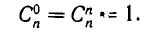
С помощью соотношения (2) можно вычислить все биномиальные коэффициенты 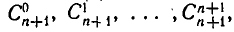 зная коэффициенты
зная коэффициенты 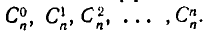
Именно
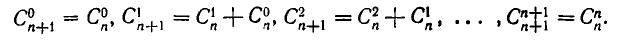
Заметим, что при вычислении 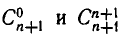 мы берем в формуле (2) лишь одно слагаемое.
мы берем в формуле (2) лишь одно слагаемое.
Найдя 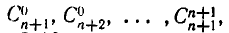 мы вычисляем
мы вычисляем 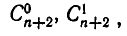

Такое вычисление удобно располагать в виде следующей таблицы:
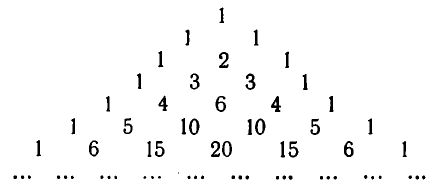
Здесь каждое число в следующей строке является суммой двух стоящих над ним чисел предыдущей строки (если с какой-нибудь стороны числа нет, соответствующее слагаемое полагают равным нулю). Этот числовой треугольник называют треугольником Пас каля. С помощью треугольника Паскаля можно вычислять биномиальные коэффициенты для любого n.
Явное выражение для любого биномиального коэффициента имеет следующий вид:

где 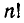 — произведение всех натуральных чисел от 1 до n (например,
— произведение всех натуральных чисел от 1 до n (например, 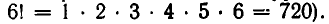 Принято считать, кроме того, что
Принято считать, кроме того, что 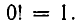 В главе IX равенство (3) будет выведено с помощью методов комбинаторики.
В главе IX равенство (3) будет выведено с помощью методов комбинаторики.
Деление многочленов. Корни многочленов
В отличие от операций сложения и умножения многочленов операция деления многочленов не всегда выполнима: если 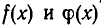 — два многочлена, то далеко не всегда найдется третий многочлен
— два многочлена, то далеко не всегда найдется третий многочлен 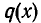 такой, что
такой, что 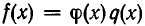 . В этом отношении множество многочленов больше напоминает множество целых чисел, чем множество рациональных чисел (иными слова ми кольцо многочленов не является полем). Но также, как и для целых чисел, для многочленов всегда определена операция деления с остатком. При этом будут рассматриваться многочлены, коэффициенты которых принадлежат некоторому числовому полю R (многочлены из кольца R [х ]). Читатель может при желании считать его полем всех действительных чисел или полем всех рациональных чисел.
. В этом отношении множество многочленов больше напоминает множество целых чисел, чем множество рациональных чисел (иными слова ми кольцо многочленов не является полем). Но также, как и для целых чисел, для многочленов всегда определена операция деления с остатком. При этом будут рассматриваться многочлены, коэффициенты которых принадлежат некоторому числовому полю R (многочлены из кольца R [х ]). Читатель может при желании считать его полем всех действительных чисел или полем всех рациональных чисел.
Определим для многочленов понятие деления с остатком. Пусть даны два многочлена
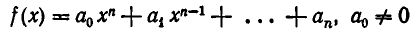
и
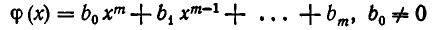
и пусть существуют многочлены 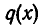 и
и 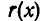 такие, что: 1) Имеет место тождество
такие, что: 1) Имеет место тождество
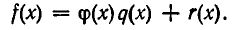
2) Степень многочлена r(х) меньше степени многочлена 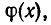 или r(х) = 0.
или r(х) = 0.
В этом случае многочлен 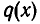 называют неполным частным при делении
называют неполным частным при делении 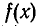 на
на 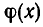 , а r(х) — остатком при этом делении. Если
, а r(х) — остатком при этом делении. Если 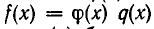 , то есть если r(х) = 0, то говорят, что
, то есть если r(х) = 0, то говорят, что 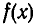 делится на
делится на 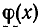 без остатка, а
без остатка, а 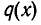 называют частным.
называют частным.
Например, если 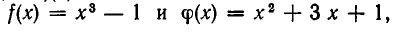 то из тождества
то из тождества
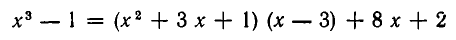
следует, что неполным частным является 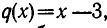 а остатком —
а остатком — 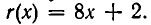 Многочлен
Многочлен 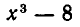 делится без остатка на
делится без остатка на 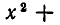
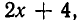 так как
так как
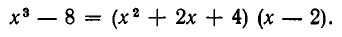
Выясним теперь: всегда ли возможно деление с остатком и однозначно ли оно определено? Иными словами, рассмотрим следующие вопросы:
Даны многочлены 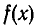 и
и 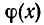 . Существуют ли такие многочлены
. Существуют ли такие многочлены 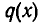 и
и 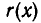 , что
, что 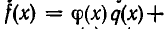
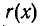 и степень
и степень 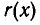 меньше степени
меньше степени 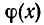 (или r(х) = 0)? Если эти многочлены существуют, то однозначно ли они определены?
(или r(х) = 0)? Если эти многочлены существуют, то однозначно ли они определены?
Вопросы такого типа возникают во многих областях математики. Их называют соответственно вопросами о существовании и единственности решения данной задачи.
Для рассматриваемой здесь задачи мы докажем существование решения, указав способ отыскания неполного частного и остатка по заданным многочленам 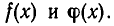 После этого будет доказано, что решение задачи единственно.
После этого будет доказано, что решение задачи единственно.
Рассмотрим сначала следующий пример. Пусть 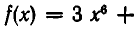
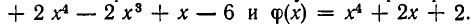 Заметим, что если умножить
Заметим, что если умножить 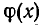 на
на 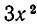 , то получится многочлен
, то получится многочлен 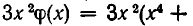
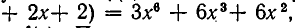 имеющий тот же старший член, что и
имеющий тот же старший член, что и 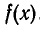 . Поэтому степень многочлена
. Поэтому степень многочлена
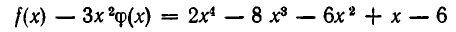
меньше степени многочлена 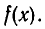
Если умножить 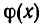 на 2, то получим многочлен
на 2, то получим многочлен 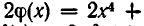
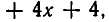 имеющий тот же старший член, что и
имеющий тот же старший член, что и 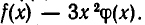 Многочлен
Многочлен 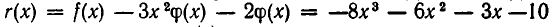 имеет меньшую степень, чем
имеет меньшую степень, чем 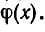
Таким образом, мы получили равенство:
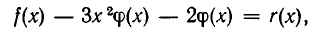
где r(х)—многочлен меньшей степени, чем 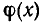 . Это равенство перепишем так:
. Это равенство перепишем так:
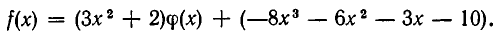
В этом случае
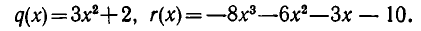
Рассмотрим теперь вопрос в общем виде.
Начнем с вопроса о существовании неполного частного и остатка, о возможности операции деления с остатком. Проще всего решается вопрос, если степень 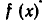 меньше степени
меньше степени 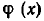 . В этом случае многочлены
. В этом случае многочлены 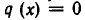 и
и 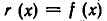 удовлетворяют всем поставленным условиям. Рассмотрим теперь случай, когда степень n многочлена
удовлетворяют всем поставленным условиям. Рассмотрим теперь случай, когда степень n многочлена 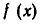 больше или равна степени m многочлена
больше или равна степени m многочлена 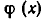 . В этом случае будем строить неполное частное
. В этом случае будем строить неполное частное 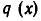 постепенно, вычисляя его члены один за другим. Заметим сначала, что при умножении многочлена
постепенно, вычисляя его члены один за другим. Заметим сначала, что при умножении многочлена 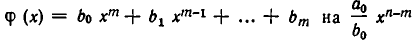 получим многочлен
получим многочлен 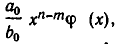 старший член которого равен
старший член которого равен 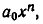 то есть старшему члену многочлена
то есть старшему члену многочлена 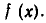 Отсюда ясно, что либо многочлен
Отсюда ясно, что либо многочлен
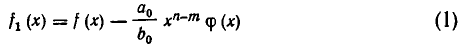
равен нулю, либо его степень меньше, чем степень многочлена 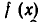 (при вычитании старшие члены взаимно уничтожаются). Если
(при вычитании старшие члены взаимно уничтожаются). Если 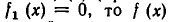 делится на
делится на 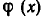 без остатка. Пусть
без остатка. Пусть 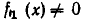 и пусть старший член многочлена
и пусть старший член многочлена 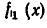 равен
равен 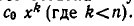 Тогда степень многочлена
Тогда степень многочлена
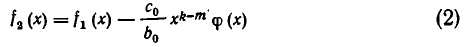
будет меньше степени многочлена 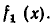 Так как степени многочленов являются целыми неотрицательными числами, то на каком-то шагу процесса мы получим многочлен
Так как степени многочленов являются целыми неотрицательными числами, то на каком-то шагу процесса мы получим многочлен 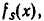 который либо равен нулю, либо имеет степень, меньшую степени
который либо равен нулю, либо имеет степень, меньшую степени 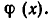 Тогда из равенств (1), (2) и т. д. получаем:
Тогда из равенств (1), (2) и т. д. получаем:
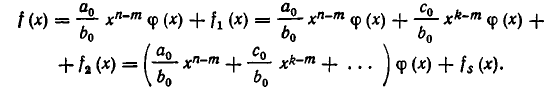
Положим:
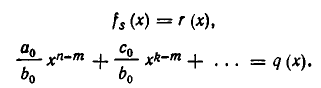
Мы получим, что
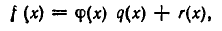
причем либо  либо степень многочлена
либо степень многочлена 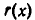 меньше степени многочлена
меньше степени многочлена 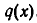 . Тем самым доказано, что операция деления с остатком на многочлен, не равный тождественно нулю, всегда определена.
. Тем самым доказано, что операция деления с остатком на многочлен, не равный тождественно нулю, всегда определена.
Докажем теперь, что эта операция определена однозначно. В самом деле, предположим, что
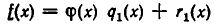
и
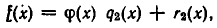
где степень многочленов 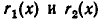 меньше степени
меньше степени 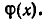 Тогда имеет место равенство
Тогда имеет место равенство
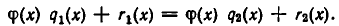
Из него следует, что
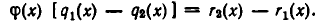
Если 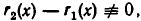 то степень правой части этого равенства не больше, чем степени многочленов
то степень правой части этого равенства не больше, чем степени многочленов 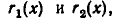 а потому меньше, чем степень многочлена
а потому меньше, чем степень многочлена 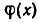 . Левая же часть равенства является произведением многочлена
. Левая же часть равенства является произведением многочлена 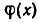 на многочлен
на многочлен 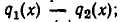 поэтому равенство может иметь место лишь в случае, когда
поэтому равенство может иметь место лишь в случае, когда 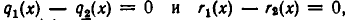 то есть когда
то есть когда 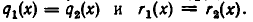 Тем самым однозначность операции деления с остатком доказана.
Тем самым однозначность операции деления с остатком доказана.
Деление многочленов обычно выполняют по схеме «деления уголком». Ниже приведен пример такого деления.
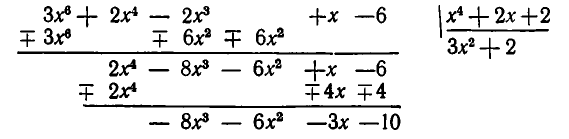
Здесь частное равно 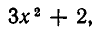 а остаток равен
а остаток равен 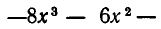
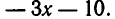
Отметим, что если 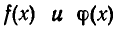 — приведенные многочлены с целыми коэффициентами, то и неполное частное
— приведенные многочлены с целыми коэффициентами, то и неполное частное 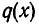 — многочлен того же вида. Это следует из того, что при отыскании частного нам не придется делить на
— многочлен того же вида. Это следует из того, что при отыскании частного нам не придется делить на 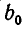 (оно равно 1).
(оно равно 1).
Теорема Безу. Схема Горнера
Пусть 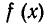 — многочлен n-й степени и b — некоторое число. Разделим многочлен
— многочлен n-й степени и b — некоторое число. Разделим многочлен 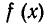 на двучлен (х — b). Так как степень этого двучлена равна единице, то остаток является некоторым числом r. Итак, мы получаем тождество
на двучлен (х — b). Так как степень этого двучлена равна единице, то остаток является некоторым числом r. Итак, мы получаем тождество
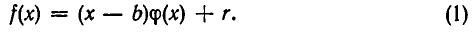
Чтобы вычислить значение r, подставим в обе части тождества (1) значение х = b. Мы получим, что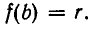 Итак, нами доказана следующая важная теорема.
Итак, нами доказана следующая важная теорема.
Теорема Безу:
Остаток от деления многочлена 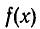 на двучлен х — b равен
на двучлен х — b равен 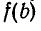 (то есть результату подстановки числа b в многочлен
(то есть результату подстановки числа b в многочлен 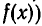
Примеры:
1) Остаток от деления многочлена
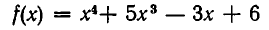
на х + 3 равен
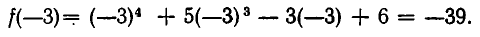
2) Многочлен 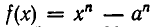 делится без остатка на х — а. В самом деле,
делится без остатка на х — а. В самом деле, 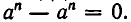 Многочлен делится без остатка на х + а. В самом деле,
Многочлен делится без остатка на х + а. В самом деле, 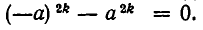
Деление многочлена
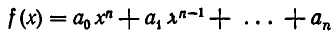
на двучлен х — b удобно выполнять по так называемой схеме Горнера. Обозначим неполное частное при делении 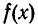 на х — b через
на х — b через 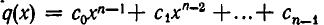 , а остаток — через
, а остаток — через 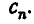 . Так как
. Так как 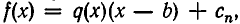 то имеем тождество
то имеем тождество
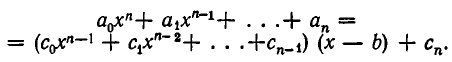
Раскроем в правой части этого равенства скобки и сравним коэффициенты при одинаковых степенях х слева и справа. Мы получим, что 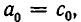 и при
и при 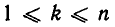 имеют место соотношения
имеют место соотношения 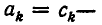
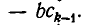 Отсюда следует, что
Отсюда следует, что 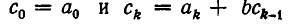 при
при 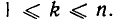
Вычисление коэффициентов многочлена 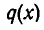 и остатка
и остатка 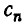 записывают в виде следующей таблицы:
записывают в виде следующей таблицы:
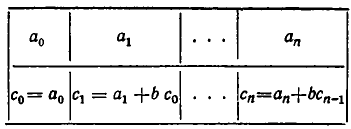
Она называется схемой Горнера. В первой строке этой таблицы за писаны коэффициенты многочлена 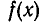 . При заполнении второй строки этой таблицы надо записать в первую клетку
. При заполнении второй строки этой таблицы надо записать в первую клетку 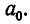 Если уже заполнено несколько клеток второй строки, то следующая пустая клетка заполняется так: берут стоящее над ней число первой строки и прибавляют к произведению числа b на предыдущий элемент второй строки.
Если уже заполнено несколько клеток второй строки, то следующая пустая клетка заполняется так: берут стоящее над ней число первой строки и прибавляют к произведению числа b на предыдущий элемент второй строки.
Так как по теореме Безу 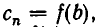 то схема Горнера позволяет находить значения многочлена
то схема Горнера позволяет находить значения многочлена 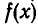 при х =b. Во многих случаях вычисление по схеме Горнера удобнее, чем непосредственная подстановка b в многочлен
при х =b. Во многих случаях вычисление по схеме Горнера удобнее, чем непосредственная подстановка b в многочлен 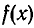 .
.
Пример:
Вычислим по схеме Горнера значение 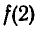 , где
, где
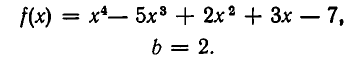

Значит, 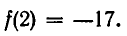
Корни многочлена
При различных значениях х многочлен

принимает различные значения. Нас будут интересовать те значения х , при которых многочлен 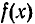 обращается в нуль. Эти значения называют корнями многочлена. Итак, число
обращается в нуль. Эти значения называют корнями многочлена. Итак, число 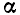 называется корнем многочлена
называется корнем многочлена 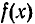 , если
, если 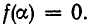 Таким образом, понятие корня многочлена (1) равносильно понятию корня уравнения
Таким образом, понятие корня многочлена (1) равносильно понятию корня уравнения
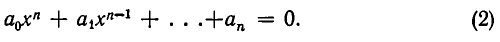
(Теория таких уравнений будет изложена в главе II.) Следует от метить, что вся теория многочленов (как, впрочем, и почти вся алгебра) развивалась в связи с решением уравнений.
В первую очередь установим связь между корнями многочлена и его линейными делителями, то есть делителями вида х — 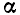 . Ясно, что если многочлен
. Ясно, что если многочлен 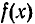 делится без остатка на х —
делится без остатка на х — 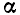 , то а является его корнем. В самом деле, пусть
, то а является его корнем. В самом деле, пусть 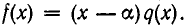 Тогда имеем
Тогда имеем
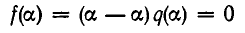
и, значит, 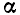 — корень многочлена
— корень многочлена 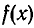 .
.
Справедливо и обратное утверждение: если число 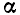 является корнем многочлена
является корнем многочлена 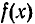 , то этот многочлен делится без остатка на х —
, то этот многочлен делится без остатка на х — 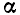 .
.
Для доказательства воспользуемся теоремой Везу. По этой теореме остаток от деления 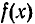 на x —
на x — 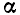 равен
равен 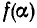 . Поэтому, если
. Поэтому, если 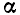 — корень многочлена
— корень многочлена 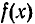 , то остаток r равен нулю:
, то остаток r равен нулю: 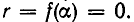
Итак, задача нахождения корней многочлена равносильна задаче отыскания его линейных делителей.
Покажем теперь, что если 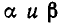 — различные корни многочлена
— различные корни многочлена 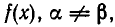 то
то 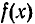 делится на
делится на 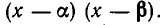 В самом деле, так как
В самом деле, так как 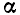 — корень для
— корень для 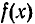 то
то 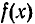 делится без остатка на х —
делится без остатка на х — 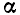 :
:
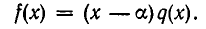
Подставим в обе части этого равенства 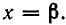 Так как
Так как 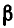 — корень многочлена
— корень многочлена 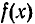 , то получаем
, то получаем 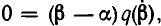 но
но 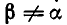 и потому
и потому 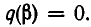 Таким образом,
Таким образом, 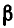 является корнем многочлена
является корнем многочлена 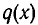 , а потому
, а потому 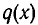 делится без остатка на
делится без остатка на 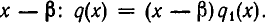 Таким образом,
Таким образом,
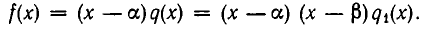
Это и означает, что 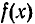 делится без остатка на
делится без остатка на 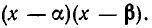
Точно так же доказывается, что если 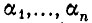 — попарно различные корни многочлена
— попарно различные корни многочлена 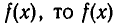 делится без остатка на выражение
делится без остатка на выражение 

Докажем теперь следующую теорему.
Теорема:
Если многочлен 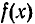 не является многочленом степени большей n и обращается в нуль при (n + 1) различных значениях х :
не является многочленом степени большей n и обращается в нуль при (n + 1) различных значениях х :  то этот многочлен является нулевым много членом.
то этот многочлен является нулевым много членом.
Доказательство:
Допустим, что многочлен 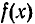 не является нулевым. Тогда по условию теоремы его степень не больше чем n. Так как числа
не является нулевым. Тогда по условию теоремы его степень не больше чем n. Так как числа  являются корнями многочлена
являются корнями многочлена 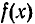 , то он делится без остатка на произведение
, то он делится без остатка на произведение 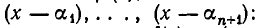

откуда видно, что степень многочлена 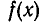 не меньше чем n + 1. Полученное противоречие показывает, что многочлен
не меньше чем n + 1. Полученное противоречие показывает, что многочлен 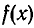 является нулевым многочленом.
является нулевым многочленом.
Из доказанной теоремы вытекает важное следствие. Возьмем два многочлена 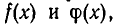 степень которых не превосходит n, и предположим, что они принимают одинаковые значения при (n+1) значении х. Покажем, что тогда многочлены
степень которых не превосходит n, и предположим, что они принимают одинаковые значения при (n+1) значении х. Покажем, что тогда многочлены 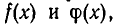 имеют одинаковые степени и коэффициенты.
имеют одинаковые степени и коэффициенты.
Для доказательства рассмотрим разность  данных многочленов. По условию многочлен
данных многочленов. По условию многочлен  обращается в нуль при (n + 1) значении х и не является многочленом степени, большей чем п. Поэтому в силу предыдущей теоремы все его коэффициенты равны нулю. А это и означает, что коэффициенты многочленов
обращается в нуль при (n + 1) значении х и не является многочленом степени, большей чем п. Поэтому в силу предыдущей теоремы все его коэффициенты равны нулю. А это и означает, что коэффициенты многочленов 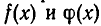 совпадают, а значит, совпадают и их степени.
совпадают, а значит, совпадают и их степени.
В частности, получаем следующее утверждение: если два много члена тождественно равны, то есть принимают одинаковые значения при всех значениях х, то они имеют одинаковые степени и коэффициенты при одинаковых степенях х. Иными словами, не может быть двух различных многочленов (в канонической форме!), принимающих одинаковые значения при всех х. Отсюда следует сформулированное ранее утверждение: целое рациональное выражение тождественно равно только одному многочлену. В самом деле, два многочлена, тождественно равные одному и тому же целому рациональному выражению, тождественно равны друг другу, а по этому их коэффициенты при одинаковых степенях х совпадают.
Интерполяционные формулы
Мы доказали, что многочлен степени п однозначно определяется своими значениями в (n + 1) точке. Иными словами, если взять любые (n+1) точку 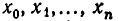
и любые значения  то существует не более одного многочлена
то существует не более одного многочлена 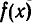 такого, что
такого, что 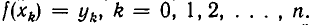 Естественно возникает вопрос, а существует ли хоть один такой многочлен? Покажем, что такой многочлен всегда существует.
Естественно возникает вопрос, а существует ли хоть один такой многочлен? Покажем, что такой многочлен всегда существует.
Именно, рассмотрим выражение
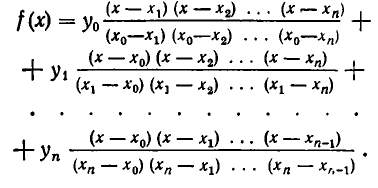
Здесь в числитель дроби с коэффициентом 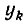 входят все множители
входят все множители 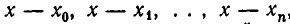 кроме
кроме 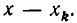 Знаменатель получается из числителя заменой х на
Знаменатель получается из числителя заменой х на 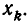
Так как каждый числитель в формуле (1) является произведением n линейных сомножителей, степень многочлена, тождествен но равного 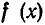 , не больше, чем n (она может оказаться меньше, чем n, если после раскрытия скобок и приведения подобных членов коэффициент при
, не больше, чем n (она может оказаться меньше, чем n, если после раскрытия скобок и приведения подобных членов коэффициент при 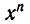 обратится в нуль).
обратится в нуль).
Покажем, что этот многочлен принимает нужные значения в точках 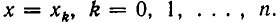 В самом деле, пусть
В самом деле, пусть 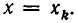 Так как множитель
Так как множитель 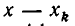 входит в числители всех слагаемых, кроме слагаемого с коэффициентом
входит в числители всех слагаемых, кроме слагаемого с коэффициентом 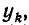 , то все эти слагаемые обратятся в нуль. В слагаемом же с коэффициентом
, то все эти слагаемые обратятся в нуль. В слагаемом же с коэффициентом 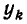 числитель дроби совпадет при
числитель дроби совпадет при 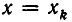 со знаменателем, и потому дробь равна 1, а само слагаемое равно
со знаменателем, и потому дробь равна 1, а само слагаемое равно 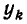 . Тем самым доказано, что
. Тем самым доказано, что 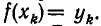
Формула (1) называется интерполяционной формулой Лагранжа. Существуют другие формы записи интерполяционной формулы. Однако надо иметь в виду, что любая запись интерполяционной формулы приводит к тому же многочлену, что и формула Лагранжа. Ведь мы знаем, что многочлен nй степени однозначно определяется своими значениями в точках 
Кратные корни
Если 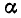 — корень многочлена
— корень многочлена 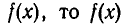 делится без остатка на
делится без остатка на 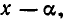 Может случиться, что
Может случиться, что 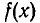 делится без остатка не только на
делится без остатка не только на 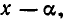 но и на
но и на 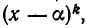 где k > 1. В этом случае говорят, что
где k > 1. В этом случае говорят, что 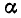 является кратным корнем много члена
является кратным корнем много члена 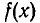 . При этом если
. При этом если 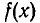 без остатка делится на
без остатка делится на 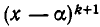 но уже не делится без остатка на
но уже не делится без остатка на 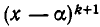 , то а называют корнем кратности k.
, то а называют корнем кратности k.
Рассмотрим, например, многочлен
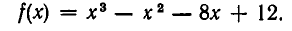
Мы имеем 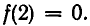 Значит, х = 2 является корнем этого много члена.
Значит, х = 2 является корнем этого много члена.
Деля 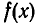 на х — 2, получим многочлен
на х — 2, получим многочлен 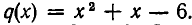
Снова подставим вместо х значение 2. Мы получим 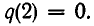 Значит, и
Значит, и 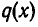 делится на х — 2 без остатка. Выполняя это деление, получим многочлен х + 3. Так как 2 не является корнем многочлена х + 3, то
делится на х — 2 без остатка. Выполняя это деление, получим многочлен х + 3. Так как 2 не является корнем многочлена х + 3, то 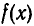 делится на
делится на 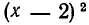 , но не делится на
, но не делится на 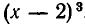 Значит, 2 — корень второй кратности многочлена
Значит, 2 — корень второй кратности многочлена 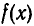 .
.
Многочлены второй степени
Применим полученные общие результаты к многочленам второй степени 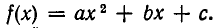 Корни этих многочленов выражаются формулой
Корни этих многочленов выражаются формулой
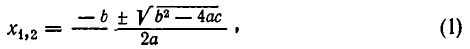
известной из начальной алгебры.
Обозначим 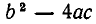 через D. Из формулы (1) видно, что если D > 0, то оба корня многочлена
через D. Из формулы (1) видно, что если D > 0, то оба корня многочлена 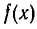 действительны и различны. Если D = 0, то эти корни совпадают (так как безразлично, будем мы прибавлять или вычитать нуль)
действительны и различны. Если D = 0, то эти корни совпадают (так как безразлично, будем мы прибавлять или вычитать нуль)
Наконец, если D<0, то многочлен f(х) не имеет действительных корней.
Рассмотрим случаи, когда многочлен f(x) имеет два действительных корня 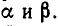 . Тогда по доказанному выше он делится на много член второй степени
. Тогда по доказанному выше он делится на много член второй степени 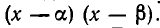 Частное от деления этих многочленов— некоторое число. Таким образом,
Частное от деления этих многочленов— некоторое число. Таким образом,
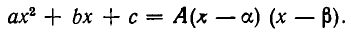
Значение А получим, сравнив коэффициенты при 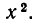 Находим А = а. Итак, мы доказали, что если многочлен второй степени
Находим А = а. Итак, мы доказали, что если многочлен второй степени 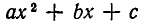 имеет действительные корни
имеет действительные корни 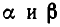 , то
, то
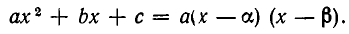
Разделим обе части этого равенства на а и выполним умножение в правой части равенства. Мы получим, что
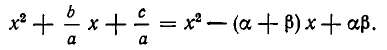
Сравнивая коэффициенты при одинаковых степенях х слева и справа, получаем:

Итак, мы доказали следующее утверждение: сумма корней квадратного трехчлена 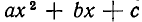 равна отношению коэффициентов при х и
равна отношению коэффициентов при х и 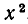 , взятому с обратным знаком, а их произведение равно отношению свободного члена к коэффициенту при
, взятому с обратным знаком, а их произведение равно отношению свободного члена к коэффициенту при 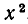 .
.
Формулы (2) называют формулами Виета. Позже мы увидим, что они справедливы и в случае, когда корни многочлена 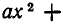
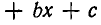 — комплексные числа.
— комплексные числа.
Многочлены с целыми коэффициентами
Мы установили не которые общие теоремы о корнях многочленов. Однако до сих пор мы можем искать лишь корни многочленов первой и второй степени — в начальной алгебре изучается, как решать линейные и квадратные уравнения. Позже мы научимся решать некоторые уравнения высших степеней и тем самым находить корни соответствующих многочленов. Но во многих случаях удается найти корни, не прибегая к теории уравнений высших степеней с произвольными коэффициентами или к методам вычислительной математики. Речь идет о случае, когда ищутся целые корни многочленов с целыми коэффициентами. При этом мы ограничимся случаем, когда многочлен f(х) приведен, то есть когда коэффициент при его старшем члене равен единице.
Докажем следующую теорему.
Теорема:
Пусть
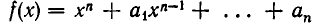
— приведенный многочлен п-й степени, все коэффициенты которого — целые числа. Тогда любой рациональный корень этого многочлена — целое число.
Доказательство:
Пусть 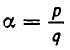 — корень многочлена f(х), причем
— корень многочлена f(х), причем 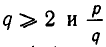 — несократимая дробь. Тогда имеет место равенство
— несократимая дробь. Тогда имеет место равенство 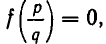 есть
есть
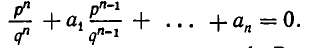
Умножим обе части этого равенства на 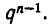 Все члены, кроме первого, окажутся целыми числами, а тогда и
Все члены, кроме первого, окажутся целыми числами, а тогда и 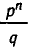 должно было бы быть целым числом. Но это не так: поскольку р и q не имеют общих делителей, то их не имеют и
должно было бы быть целым числом. Но это не так: поскольку р и q не имеют общих делителей, то их не имеют и 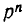 и q. Значит, многочлен f(x) не может иметь рациональных корней, не являющихся целыми числами.
и q. Значит, многочлен f(x) не может иметь рациональных корней, не являющихся целыми числами.
Перейдем к отысканию целых корней многочлена.
Имеет место следующая
Теорема:
Пусть
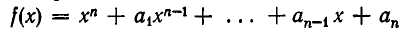
— приведенный многочлен с целыми коэффициентами. Любой целый корень а этого многочлена является делителем его свободного члена.
Доказательство:
Пусть 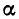 — целый корень многочлена f(x). Тогда имеет место равенство
— целый корень многочлена f(x). Тогда имеет место равенство
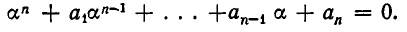
Его можно записать так:
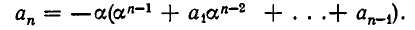
Так как 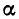 и
и 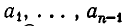 — целые числа, то выражение в скобках — целое число. Отсюда и следует, что
— целые числа, то выражение в скобках — целое число. Отсюда и следует, что 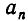 делится на
делится на 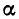 .
.
Из теоремы 3 вытекает следующий метод нахождения целых корней приведенного многочлена с целыми коэффициентами: надо выписать все делители свободного члена и по очереди подставить их в многочлен. Те делители, подстановка которых обратит многочлен в нуль, и являются его целыми корнями. Других целых корней этот многочлен не имеет. Для каждого найденного корня надо определить его кратность.
Подстановка делителей свободного члена может оказаться очень утомительным занятием. Чтобы уменьшить число проверяемых корней, полезно воспользоваться следующим обобщением теоремы 3.
Теорема:
Пусть 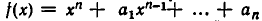 — приведенный многочлен с целыми коэффициентами и а — его целый корень. Тогда для любого целого k число f(к) делится на а — k.
— приведенный многочлен с целыми коэффициентами и а — его целый корень. Тогда для любого целого k число f(к) делится на а — k.
Для доказательства воспользуемся теоремой Безу. По этой теореме остаток от деления f(х) на (х — k) равен f(k). Поэтому f(х)= q(х)(х — k) + f(k). В силу замечания на стр. 40, q(х) также является приведенным многочленом с целыми коэффициентами. Подставим в обе части равенства х = 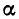 . Так как
. Так как 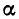 — корень многочлена f(x), то
— корень многочлена f(x), то 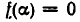 и мы получаем:
и мы получаем: 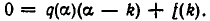 Таким образом,
Таким образом,

Так как 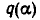 — целое число, то из равенства (1) следует, что f(k) делится на а — k.
— целое число, то из равенства (1) следует, что f(k) делится на а — k.
В силу доказанной теоремы отбор чисел, подлежащих проверке, надо проводить так. Сначала берут все делители свободного члена. Пусть это будут числа 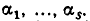 После этого вычисляют
После этого вычисляют 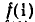 . Если
. Если 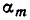 — корень многочлена f(x), то
— корень многочлена f(x), то 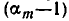 должно быть делителем
должно быть делителем 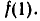 Поэтому из чисел
Поэтому из чисел 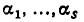 выбирают те, для которых (
выбирают те, для которых (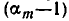 является делителем
является делителем 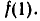 После этого вычисляют f(—1) и выбирают из оставшихся чисел то, для которых
После этого вычисляют f(—1) и выбирают из оставшихся чисел то, для которых 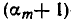 — делитель f(— 1). Если и после этого осталось слишком много «претендентов», то вычисляют f(2) и берут те из oставшихся чисел, для которых
— делитель f(— 1). Если и после этого осталось слишком много «претендентов», то вычисляют f(2) и берут те из oставшихся чисел, для которых 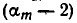 — делитель f(2) и т. д.
— делитель f(2) и т. д.
Пример:
Найти целые корни многочлена
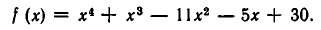
Делителями свободного члена являются числа
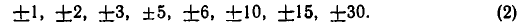
Мы имеем f (1) =16. Вычитая из чисел (2) единицу, получаем множество чисел 0, —2, 1, —3, 2, —4, 4, —6, 5, —7, 9, — 11 , 14, — 16, 29, —31. Из них лишь числа —2, 1, 2, —4, 4, — 16 являются делителями 16. Поэтому из делителей (2) остаются лишь — 1, 2, 3, —3, 5, — 15. Теперь находим f (— 1) =24; к числам — 1, 2, 3, —3, 5, — 15 прибавляем единицу и получаем 0, 3, 4, —2, 6, — 14. Из этих чисел лишь 3, 4, —2, 6 являются делителями числа 24. Поэтому остается проверить лишь делители свободного члена: 2, 3, —3, 5. Подстановка этих делителей в многочлен f (х) показывает, что его целыми корнями являются числа 2 и —3.
Из теоремы Безу вытекает, что многочлен f (х) делится на (х — 2) (х+ 3). Выполняя деление, получаем, что
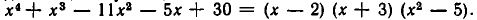
Отсюда видно, что оба корня не являются кратными: ни х = 2, ни х = — 3 не обращают в нуль ха — 5.
Краткие исторические сведения
Некоторые задачи, решаемые по сути дела алгебраическими методами, встречаются еще в вавилонских клинописных текстах (примерно 1700 г. до н. э.). В этих текстах изложены правила суммирования прогрессии, нахождения суммы квадратов, решения квадратного уравнения и т. д. Однако все эти правила лишь пояснялись на числовых примерах, но не формулировались в общем виде — не было буквенной символики.
В древней Греции начинается развитие алгебры как теоретической науки. Поскольку у греческих математиков не было общего понятия действительного числа, они развивали геометрическую алгебру. Например, вместо формулы 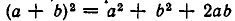 говорили, что площадь квадрата, по строенного на отрезке, равном сумме двух отрезков, равна сумме площадей квадратов, построенных на слагаемых отрезках и удвоенной площади прямоугольника, сторонами которого являются эти Отрезки. Выражения вида
говорили, что площадь квадрата, по строенного на отрезке, равном сумме двух отрезков, равна сумме площадей квадратов, построенных на слагаемых отрезках и удвоенной площади прямоугольника, сторонами которого являются эти Отрезки. Выражения вида 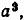
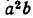 , аbс трактовались как объемы геометрических тел. Лишь к III веку н. э. у Диофанта Александрийского появляются зачатки буквенной символики.
, аbс трактовались как объемы геометрических тел. Лишь к III веку н. э. у Диофанта Александрийского появляются зачатки буквенной символики.
После крушения античной цивилизации центр математической мысли перемещается в арабские государства. Крупнейшим достижением арабов было создание алгебры как самостоятельной ветви математики (само название «алгебра» — арабского происхождения: от аль-джебр — восстановление; так назывался один из методов решения уравнений). Арабские математики установили формулы для разложения 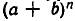 , для суммы
, для суммы 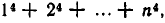 исследовали кубические уравнения и т. д.
исследовали кубические уравнения и т. д.
В странах, где в это время господствовала христианская церковь, математика почти не развивалась. В некоторых странах математические исследования были запрещены, они рассматривались как попытка возрождения язычества. Указ византийского императора Юстиниана запрещал заниматься математикой под страхом смертной казни. Лишь в отдельных трактатах по богословию и схоластической философии рассматривались некоторые математические вопросы.
Однако потребности практики, развитие промышленности, торговли и мореплавания привели к необходимости возродить науки, и в частности математику. Первоначально европейские ученые ограничивались изучением древнегреческой науки, но потом познакомились с достижениями арабских математиков, и в частности с алгеброй (многие европейские ученые получили образование в арабских университетах).
Как у арабов, так и у первых европейских алгебраистов, не было буквенной символики. Формулы излагались словесно, что затрудняло их чтение, преобразование и использование. Алгебраическая символика начинает развиваться с конца XV века. В это время у немецких алгебраистов появляются знаки + и — . Однако итальянские математики еще долгое время продолжали пользоваться знаками  — сокращениями латинских слов рlus и minus. Систематическое применение буквенных обозначений в алгебре начинается с работ французского алгебраиста Ф. Виета (1540— 1603). В его работах буквы используются лишь для обозначения положительных чисел, причем показатели степеней обозначаются словами. Вместо скобок Виета писал черту.
— сокращениями латинских слов рlus и minus. Систематическое применение буквенных обозначений в алгебре начинается с работ французского алгебраиста Ф. Виета (1540— 1603). В его работах буквы используются лишь для обозначения положительных чисел, причем показатели степеней обозначаются словами. Вместо скобок Виета писал черту.
Особые обозначения для степеней неизвестных впервые появляются у голландского ученого С. Стевина (1548— 1620) и его ученика француза Жирара (1595— 1633). Они вместо 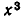 писали 3, а если в выражении содержались еще другие буквы, то писали 2 sес, 4ter (от латинских слов secundus — второй, tertius — третий). Жирар впервые ввел скобки.
писали 3, а если в выражении содержались еще другие буквы, то писали 2 sес, 4ter (от латинских слов secundus — второй, tertius — третий). Жирар впервые ввел скобки.
Символика Виета была усовершенствована английским математиком Т. Гэрриотом, который, однако, еще не применял обозначений для показателей степени, а выписывал все сомножители, входящие в одночлены. Современный вид алгебраических обозначений в основном принадлежит вели кому французскому математику и философу Р. Декарту (1596— 1650).
Приведем некоторые примеры обозначений, применявшихся разными учеными;
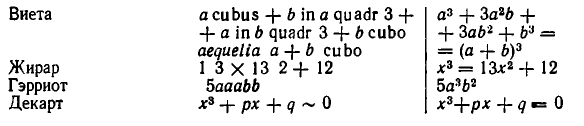
Основные свойства арифметических действий, лежащие в основе алгебраических преобразований, были установлены еще в древней Греции (в геометрической форме). Однако полная и последовательная система основ арифметики была построена лишь в XIX веке немецкими математиками Г. Грассманом и Р. Дедекиндом (общепринятая в настоящее время аксиоматика исходит от итальянского математика Д ж . Пеано). Такое построение оказалось необходимым после того, как были открыты величины (векторы, матрицы, кватернионы), правила действий над которыми отличались от правил действий над числами. Например, при изменении порядка сомножителей векторное произведение меняет знак. Д ля каждого типа величин надо было строить свою алгебру (векторная алгебра, матричная алгебра и т. д.). Это усилило интерес к изучению общих свойств алгебраических действий. Были построены теории колец и полей, структур и других алгебраических образований. Благодаря общности полученных в этих теориях результатов, они оказались приложимыми к величинам самых разных видов. В настоящее время изучение общих свойств алгебраических операций занимает важное место в алгебраической науке. Большой вклад в общую алгебру внесли советские математики О. Ю. Шмидт, А. Г. Курош, А. И. Мальцев и другие.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

