Оглавление:
Логарифм — это степень, в которую надо возвести основание, чтобы получить аргумент, т.е. функция от двух переменных.
Общие свойства логарифмов
- Свойство 1 Если два числа (при данной основе) имеют один и тот же логарифм, то эти числа равны.
- Свойство 2 Логарифм произведения положительных сомножителей равен сумме логарифмов этих сомножителей.
- Свойство 3 Логарифм доли положительных чисел равен разности логарифмов делимого и делителя.
- Свойство 4 Логарифм степени положительного числа равен показателю степени, умноженному на логарифм данного числа.
Два действия, обратные возвышению в степень
Возьмём равенство:
2³=2∙2∙2=8.
Это равенство выражает действие, называемое возвышением в степень. В этом действии даются основание степени (число 2) и показатель степени (число 3), а отыскивается самая степень (8). Посмотрим, какие действия обратны возвышению в степень. Таких действий можно указать следующие два:
1. Пусть требуется узнать, какое число надо возвысить в степень с показателем 3, чтобы получить число 12. Обозначив искомое число буквой х, мы можем написать уравнение x³=12. Действие, посредством которого находится основание х по данной степени и данному показателю её, называется извлечением корня; оно обозначается, как мы знаем, так: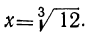
2. Положим, надо узнать, какой показатель должен быть у степени, в которую надо возвысить основание 4, чтобы получить 16. Обозначив искомый показатель буквой х, мы можем написать уравнение: 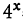 =16. Действие, посредством которого находится показатель степени по данной степени и данному основанию, называется нахождением логарифма данного числа (16) по данному основанию (4). В нашем примере х=2, так как 4²=16.
=16. Действие, посредством которого находится показатель степени по данной степени и данному основанию, называется нахождением логарифма данного числа (16) по данному основанию (4). В нашем примере х=2, так как 4²=16.
Итак, возвышение в степень имеет два обратных действия. Поставим вопрос: различны ли эти действия? Ведь и для умножения можно рассмотреть два обратных действия: первое—нахождение множимого по данным произведению и множителю, второе—нахождение множителя по данным произведению и множимому. Однако действия эти рассматриваются не как различные, а как одно и то же действие, называемое делением. Причина слияния этих двух обратных действий в одно заключается в переместительном свойстве умножения, по которому произведение не меняется от перемены мест множимого и множителя. В таком же положении находится и сложение (двух слагаемых); этому действию так же можно указать два обратных действия—нахождение неизвестного числа (первого слагаемого), к которому надо прибавить данное число (второе слагаемое), чтобы получить данную сумму; другое—нахождение неизвестного числа (второго слагаемого), которое надо прибавить к данному числу (к первому слагаемому), чтобы получить данную сумму. Однако эти два действия рассматриваются как одно, называемое вычитанием, вследствие того, что сложение обладает переместительным свойством, по которому сумма не зависит от порядка слагаемых. Если бы это свойство принадлежало также и возвышению в степень, то тогда и два указанных выше обратных действия составляли бы, в сущности, одно. Но возвышение в степень не обладает свойством переместительности, например 2³ не равно 3², 10² не равно 2¹ и т. д. Вследствие этого нахождение основания по данным показателю и степени (извлечение корня) существенно отличается от нахождения показателя по данным основанию и степени (нахождение логарифма).
Определение:
Логарифмом данного числа по данному основанию называется показатель степени, в которую надо возвысить это основание, чтобы получить данное число.
Если, например, основание будет 4, то:
Если возьмём за основание 10, то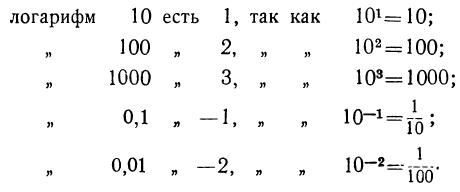
Вместо того чтобы писать: „логарифм числа 16 по основанию 4″, пишут сокращённо так: Iog₄ 16, помещая внизу знака log то число, которое служит основанием. Впрочем, если заранее известно, какое число взято за основание, то его принято не писать. Вместо знака log (сокращения слова „логарифм») пишут lg, если основанием служит число 10.
Прежде чем говорить о применениях логарифмов, мы предварительно рассмотрим некоторые свойства так называемой логарифмической функции.
Логарифмическая функция и её график
Если в равенстве y=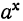 мы рассматриваем показатель х как независимое переменное, то тогда у будет функцией от х, которую мы назвали раньше показательной. Но если в этом равенстве за независимое переменное мы будем считать у, то тогда х будет некоторая функция от у, а именно: х есть логарифм числа у по основанию а, что можно записать так:
мы рассматриваем показатель х как независимое переменное, то тогда у будет функцией от х, которую мы назвали раньше показательной. Но если в этом равенстве за независимое переменное мы будем считать у, то тогда х будет некоторая функция от у, а именно: х есть логарифм числа у по основанию а, что можно записать так: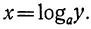
Обозначая по принятому независимое переменное буквой х, а функцию от этого переменного буквой у (т. е. заменяя х на у, и наоборот), мы ту же самую функцию можем выразить так: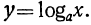
Такая функция называется логарифмической (она обратна показательной функции).
Построим графики следующих трёх логарифмических функций: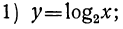
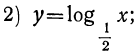
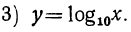
Для этого составим таблицы значений этих функций. Всего проще их можно составить из таблиц соответственных показательных функций: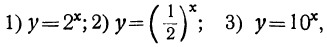
поменяв в этих таблицах значения абсциссы х на значения ординаты у, и наоборот. Сделав это, мы получим такие три таблицы:
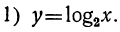
| x= | 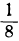 | 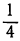 | 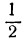 | 1 | 2 | 4 | 8 |
| y= | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
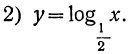
| x= | 8 | 4 | 2 | 1 | 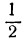 | 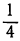 | 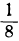 |
| y= | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
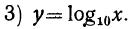
| x= | 0,1 | 0,17 | 0,32 | 0,56 | 1 | 1,78 | 3,16 | 5,62 | 10 |
| y= | -1 | 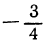 | 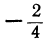 | 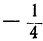 | 0 | 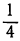 | 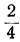 | 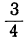 | 1 |
Нанеся все эти значения на чертёж и соединив точки кривыми линиями, получим (черт. 30) три графика взятых функций.
Имея график логарифмической функции, мы можем при помощи его найти приближённое значение логарифма данного числа. Возьмём, например, график функции 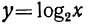 и найдём при его помощи
и найдём при его помощи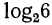 . Для этого возьмём на чертеже абсциссу, равную 6, и построим соответствующую ей ординату. Измерив эту ординату, найдём приблизительно 2,6; это и будет
. Для этого возьмём на чертеже абсциссу, равную 6, и построим соответствующую ей ординату. Измерив эту ординату, найдём приблизительно 2,6; это и будет 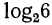 .
.
Основные свойства логарифмов
Возьмём логарифмическую функцию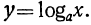
Согласно определению, имеем: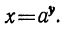
Выведем некоторые свойства логарифмов.
1. При положительном основании отрицательные числа не имеют логарифмов.
При рассмотрении показательной функции мы видели, что при α>0 функция 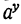 >0 при всяком у. Это значит, что каковы бы ни были (положительное) основание а и показатель (логарифм) у, функция
>0 при всяком у. Это значит, что каковы бы ни были (положительное) основание а и показатель (логарифм) у, функция 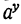 , т. е. х, всегда является положительным числом.
, т. е. х, всегда является положительным числом.

2. При всяком основании (не равном единице) логарифм единицы есть нуль.
Действительно, мы знаем, что при всяком а (не равном нулю)
a⁰=l.
3. При основании, большем единицы, логарифмы чисел, больших единицы, положительны, а логарифмы чисел, меньших единицы, отрицательны.
Относительно показательной функции 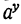 мы знаем, что при α > 1, если у > 0, то
мы знаем, что при α > 1, если у > 0, то 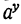 =x > 1, и если у < 0, то
=x > 1, и если у < 0, то 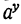 = x<1.
= x<1.
Но, согласно определению, у есть логарифм числа х. Значит, когда число х > 1, то логарифм его y > 0, т. е. положителен. Когда же число х< 1, то логарифм его y < 0, т. е. отрицателен.
Если a < 1, то у < 0 для значений х > 1, и у > 0, если х < 1.
4. Логарифм самого основания равен единице.
В самом деле:
а¹=а, отсюда: logₐa = l.
5. При основании, большем единицы, большему числу соответствует больший логарифм.
Мы видели, что при a> 1 функция 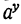 возрастает вместе с возрастанием у. Если обозначим два различных значения у через y₁, у₂, соответствующие значения
возрастает вместе с возрастанием у. Если обозначим два различных значения у через y₁, у₂, соответствующие значения 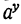 через x₁, х₂, то будем иметь:
через x₁, х₂, то будем иметь: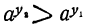 >, если y₂>y₁,
>, если y₂>y₁,
или
x₂> x₁, если y₂> y₁.
Но y₁ и y₂ являются соответственно логарифмами чисел x₁ и х₂.
Значит:
x₂> x₁ , если logₐx₂ > logₐx₁.
Все указанные свойства логарифмов можно иллюстрировать, рассматривая график логарифмической функции. Так, первое свойство означает, что график функции у=logₐx лежит весь вправо от оси у-ов. Второе свойство говорит о том, что график функции y= logₐx проходит через точку (1,0). Третье свойство означает, что если a > 1, то при x > 1 ординаты кривой положительны, а при x < 4 -отрицательны и т. д.
Практическое значение логарифмических таблиц
Различные числа можно выражать как степени одного и того же числа, например, как степени числа 10. Такие числа, как 10; 100; 1000;… или 0,1; 0,01; 0,001 и т. п., выражаются как степени 10 очень просто: 10=10¹; 100 = 10²; 1000= 10³;. ..; 0,1 =10⁻¹; 0,01 = 10⁻² ; 0,001 = 10⁻³ и т. п. Другие числа выразить степенью числа 10 труднее. Так, если требуется найти показатель степени, в которую нужно возвысить 10, чтобы получить число 5, то мы можем только сказать, что искомый показатель больше 0, но меньше 1, так как 10⁰=1, что меньше 5, а 10¹=10, что больше 5; значит, показателем степени, в которую надо возвысить 10 для получения 5, должно быть некоторое положительное число, меньшее 1. Мы можем даже сказать, что это число больше 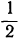 , но меньше
, но меньше 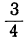 , так как
, так как 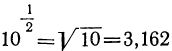 , что меньше 5, а
, что меньше 5, а 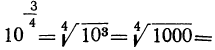
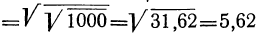 , что больше 5. Есть отделы математики, в которых указываются способы, как можно для всякого данного числа N найти такой показатель х, при котором степень 10 или в точности равняется N, или отличается от этого числа как угодно мало. Пользуясь этими способами, составлены так называемые логарифмические таблицы, в которых помещены различные числа и около каждого из этих чисел указан показатель степени (логарифм), в которую надо возвысить 10, чтобы получить это число. Разъясним, для какой цели могут служить такие таблицы.
, что больше 5. Есть отделы математики, в которых указываются способы, как можно для всякого данного числа N найти такой показатель х, при котором степень 10 или в точности равняется N, или отличается от этого числа как угодно мало. Пользуясь этими способами, составлены так называемые логарифмические таблицы, в которых помещены различные числа и около каждого из этих чисел указан показатель степени (логарифм), в которую надо возвысить 10, чтобы получить это число. Разъясним, для какой цели могут служить такие таблицы.
Пусть требуется вычислить число х по формуле: 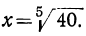
Извлекать корень пятой степени мы не умеем. В подобных случаях могут помочь логарифмические таблицы. Находим в этих таблицах число 40 и около него соответствующий логарифм. Пусть это будет 1,6… Это значит, что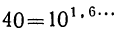
и, следовательно,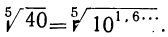
Так как при извлечении корня из степени показатель подкоренного числа (какой бы он ни был) делится на показатель корня, то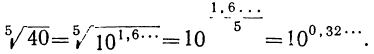
Теперь в тех же таблицах, в столбце логарифмов, находим 0,32 и около него соответствующее число; пусть это будет, положим, 2,09… Это и будет приближённое значение 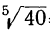 .
.
Мы вскоре увидим, что логарифмические таблицы во многих случаях позволяют производить такие действия над числами, которые без таблиц были крайне затруднительны (как в примере, только что указанном) или на выполнение которых потребовалось бы очень много времени.
Теперь нам предстоит ознакомиться, во-первых, с тем, как при совершении какого-либо действия над данными числами можно найти логарифм искомого числа при помощи логарифмов данных чисел (взятых из таблиц) и, во-вторых, как, найдя такой логарифм, отыскать по нему в таблицах искомое число.
Логарифм произведения, частного, степени и корня
а) Пусть требуется произвести умножение:
378 ‧ 45,2.
Попробуем выполнить это действие посредством логарифмов. Найдём в таблицах логарифмы чисел 378 и 45,2. Пусть они будут: 2,5775 и 1,6551 (по основанию 10). Это значит, что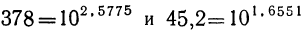
и, следовательно, 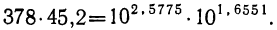
Так как при умножении степеней одного и того же числа показатели этих степеней складываются (какие бы ни были эти показатели), то: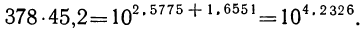
Значит, логарифм произведения 378 ‧ 45,2 есть число 4,2326, получившееся от сложения логарифмов данных сомножителей (по этому логарифму в таблицах найдём и само произведение).
Положим вообще, что N₁ и N₂ будут два числа, произведение которых требуется вычислить. Пусть мы нашли в таблицах логарифмы этих чисел: x₁ и х₂ . Основанием логарифмов может быть число 10, но может быть и какое-нибудь другое положительное число, которое мы обозначим через а. Тогда мы будем иметь равенства: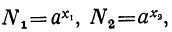 , следовательно,
, следовательно, 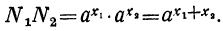 .
.
Отсюда видно, что log( N₁N₂)= x₁+ х₂. Но x₁ — это logN₁, а x₂ — это logN₂; значит:
log( N₁N₂)= logN₁ + logN₂
Логарифм произведения (по какому угодно основанию) равен сумме логарифмов сомножителей (взятых по тому же основанию).
Заключение это остаётся верным и тогда, когда сомножителей будет более двух, так как при умножении степеней одного и того же числа показатели степеней складываются и при любом числе сомножителей.
б) Положим, надо произвести деление:
5637 : 26,3.
Найдём в таблицах логарифмы этих чисел (например, по основанию 10). Пусть log5637 = 3,751 и log 26,3=1,42. Тогда: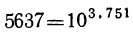 и
и 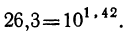
Следовательно,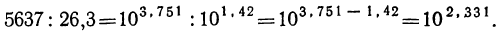
Отсюда видно, что логарифм частного 5637 : 26,3 есть число 2,331, получившееся от вычитания логарифма делителя из логарифма делимого. Вообще, если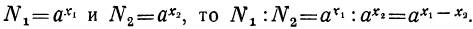
Следовательно, 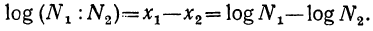
Логарифм частного равен разности логарифмов делимого и делителя.
Так как всякая дробь есть частное от деления числителя на знаменатель, то:
Логарифм дроби равен разности логарифмов числителя и знаменателя.
Например: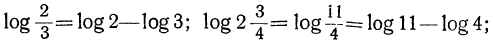
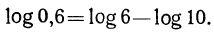
в) Если 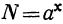 , тo
, тo 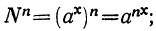
следовательно,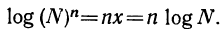
Логарифм степени равен показателю этой степени, умноженному на логарифм числа, возвышаемого в степень.
Например, log(15,3)²=2 log 15,3; log3⁻²=-2 log 3.
Так как 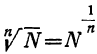 , то, применяя правило о логарифме степени, получим:
, то, применяя правило о логарифме степени, получим: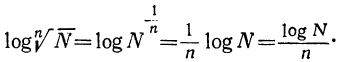
Логарифм корня равен логарифму подкоренного числа, делённому на показатель корня.
Логарифмирование алгебраического выражения
Логарифмировать алгебраическое выражение—значит выразить логарифм его посредством логарифмов отдельных чисел, составляющих это выражение. Выводы позволяют это сделать в применении к произведению, частному, степени и дроби. Например: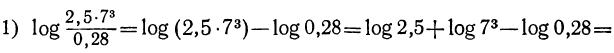
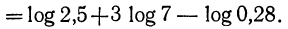
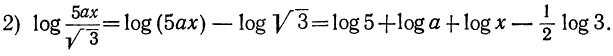
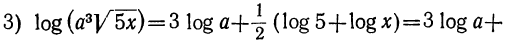
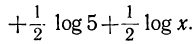
Замечания:
а) Если в выражении, которое требуется вычислить, встречается сумма или разность чисел, то их надо находить без помощи таблиц, обыкновенным сложением или вычитанием. Например:
log (35+7,24)⁵=5 log (35+7,24) = 5 log 42,24.
б) Умея логарифмировать выражения, мы можем, обратно, по данному результату логарифмирования найти то выражение, от которого получился этот результат; так, если
log х = log α+ log b — 3 log с,
то легко сообразить, что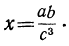
Эту операцию называют потенцированием.
в) Прежде чем перейти к рассмотрению устройства логарифмических таблиц, мы укажем некоторые свойства десятичных логарифмов, т. е. таких, в которых за основание принято число 10.
Свойства десятичных логарифмов
Свойства десятичных логарифмов: а) Так как 10¹=10; 10² = 100; 10³=1000; 10⁴ = 10000 и т. д., то Ig10=1; Ig 100=2; Ig 1000 =3; Ig10000= 4 и т. д.
Логарифм целого числа, изображаемого единицей с последующими нулями, есть целое положительное число, содержащее столько единиц, сколько нулей в изображении числа.
Таким образом, Ig 100000=5, Ig1 000000=6 и т. д.
б) Так как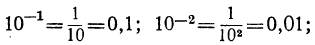
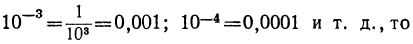
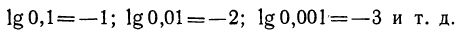
Логарифм десятичной дроби, изображаемой единицей с предшествующими нулями, есть целое отрицательное число, содержащее столько отрицательных единиц, сколько нулей в изображении дроби, считая в том числе и 0 целых.
Таким образом, lg 0,00001 =-5, lg 0,000001 = -6 и т. д.
в) Возьмём целое число, не изображаемое единицей с нулями, например 35, или целое число с дробью, например 10,7. Логарифм такого числа не может быть целым числом, так как, возвысив 10 в степень с целым показателем (положительным или отрицательным), мы получим единицу с нулями (следующими за единицей или ей предшествующими). Предположим теперь, что логарифм такого числа есть какая-нибудь дробь 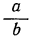 . Тогда мы имели бы равенства:
. Тогда мы имели бы равенства:
для числа 35: 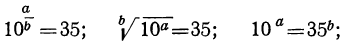
для числа 10,7: 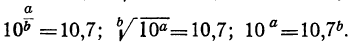
Но эти равенства невозможны, так как 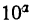 есть единица с нулями, тогда как степени
есть единица с нулями, тогда как степени 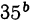 и
и 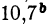 ни при каком показателе b не могут дать единицы с нулями. Логарифм числа, не являющегося степенью десяти, есть число иррациональное, он (т. е. логарифм) не может быть выражен точно каким бы то ни было рациональным числом. Обыкновенно иррациональные логарифмы выражают приближённо в виде десятичной дроби с несколькими десятичными знаками. Целая часть этой дроби называется характеристикой, а дробная часть — мантиссой логарифма. Если, например, логарифм есть 1,5441, то характеристика его равна 1, а мантисса есть 0,5441.
ни при каком показателе b не могут дать единицы с нулями. Логарифм числа, не являющегося степенью десяти, есть число иррациональное, он (т. е. логарифм) не может быть выражен точно каким бы то ни было рациональным числом. Обыкновенно иррациональные логарифмы выражают приближённо в виде десятичной дроби с несколькими десятичными знаками. Целая часть этой дроби называется характеристикой, а дробная часть — мантиссой логарифма. Если, например, логарифм есть 1,5441, то характеристика его равна 1, а мантисса есть 0,5441.
г) Возьмём какое-нибудь целое или смешанное число, например 623 или 623,57. Логарифм такого числа состоит из характеристики и мантиссы. Оказывается, что десятичные логарифмы обладают тем удобством, что характеристику их мы всегда можем найти по одному виду данного числа. Для этого сосчитаем, сколько цифр в данном целом числе или в целой части смешанного числа. В наших примерах этих цифр три. Поэтому каждое из чисел 623 и 623,57 больше 100, но меньше 1000; значит, и логарифм каждого из них больше Ig100, т. е. двух, но меньше Ig1000, т. е. трёх (вспомним, что большее число имеет и больший логарифм). Следовательно, lg623=2, …и lg623,57=2, … (точки заменяют собой неизвестные мантиссы).
Подобно этому найдём: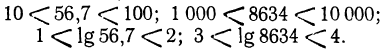
Следовательно: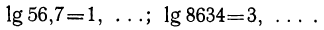
Пусть вообще в данном целом числе N или в его целой части содержится m цифр. Так как самое малое целое число, содержащее m цифр, есть 1 с m — 1 нулями, то можем написать неравенство: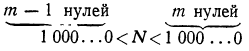
и, следовательно,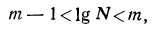
а потому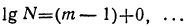
Значит, характеристика IgN равна m — 1.
Мы видим, таким образом, что:
Характеристика логарифма целого или смешанного числа содержит столько положительных единиц, сколько цифр в целой части числа без одной.
Заметив это, мы можем прямо писать: lg7,205 = 0, Ig83=1, lg720,4=2, … и т. п.
д) Возьмём несколько десятичных дробей, меньших 1 (т. е. имеющих 0 целых): 0,35; 0,07; 0,0056; 0,0008 и т. п.
| Очевидно, что 0,1 <0,35 <1; 0,01 <0,07 <0,1; 0,001 <0,0056 <0,01; 0,0001 <0,0008 <0,001. | Следовательно: — 1< lg 0,35 < 0; — 2 < lg 0,07 <—1; — 3 < lg 0,0056 < — 2; — 4 < lg 0,0008 <— 3. |
Таким образом, каждый из этих логарифмов заключён между двумя целыми отрицательными числами, различающимися на одну единицу, поэтому каждый из них равен меньшему из этих отрицательных чисел, увеличенному на некоторое положительное число, меньшее единицы. Например, lg 0,0056=-3+0, …. Предположим, что второе слагаемое будет 0,7482. Тогда
lg 0,0056= — 3+0,7482= -2,2518.
Такие суммы, как — 3+0,7482, состоящие из целого отрицательного числа и положительной десятичной дроби, условились при логарифмических вычислениях писать сокращённо так: 3,7482, т. е. ставить знак минус над характеристикой с целью показать, что он относится только к характеристике, а не к мантиссе, которая остаётся положительной. Таким образом, из приведённой выше таблички видно, что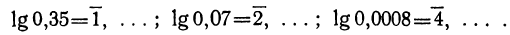
Пусть вообще 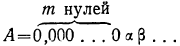 есть десятичная дробь, у которой перед первой значащей цифрой а стоит m нулей, считая в том числе и 0 целых. Тогда очевидно, что
есть десятичная дробь, у которой перед первой значащей цифрой а стоит m нулей, считая в том числе и 0 целых. Тогда очевидно, что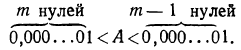
Следовательно: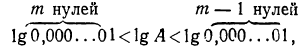
т. е.
— m < Ig А < — (m— 1).
Так как из двух чисел: — m и —( m — 1) меньшее есть — m , то
lg А= —m + 0, …
и поэтому характеристика lg А равна — m (при положительной мантиссе).
Характеристика логарифма десятичной дроби, меньшей 1, содержит в себе столько отрицательных единиц сколько нулей в данной десятичной дроби перед первой значащей цифрой, считая и 0 целых; мантисса же такого логарифма положительна.
е) Умножим какое-нибудь число N (целое или дробное—всё равно) на 10, на 100, на 1000,…, вообще на единицу с нулями. Посмотрим, как от этого изменится lg N. Так как логарифм произведения равен сумме логарифмов сомножителей, то:
lg(N‧10) = lgN+ lg10=lgN +1;
lg (N‧100) = lgN+ lgl100= lgN +2;
lg (N‧1000) = lgN+Ig1000= lgN +3 и т. д.
Когда к lgN мы прибавляем какое-нибудь целое число, то это число увеличивает лишь характеристику, а не мантиссу. Так, если lgN = =2,7804, то 2,7804+2=3,7804; 2,7804+2=4,7804 и т. п.; или если lgN =3,5649, то 3,5649 + 1=2,5649; 3,5649+2=1,5649 и т. п. Поэтому:
От умножения числа на 10, 100, 1000, …, вообще на единицу с нулями, мантисса логарифма не изменяется, а характеристика увеличивается на столько единиц, сколько нулей во множителе.
Подобно этому, приняв во внимание, что логарифм частного равен логарифму делимого без логарифма делителя, мы получим: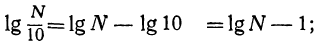
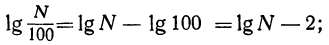
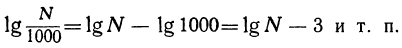
Если условимся при вычитании целого числа из логарифма вычитать это целое число всегда из характеристики, а мантиссу оставлять без изменения, то можно сказать, что
от деления числа на единицу с нулями мантисса логарифма не изменяется, а характеристика уменьшается на столько единиц, сколько нулей в делителе.
Следствия, а) Мантисса логарифма десятичного числа не изменяется от перенесения в числе запятой, потому что перенесение запятой равносильно умножению или делению числа на 10, 100, 1000 и т. д. Таким образом, логарифмы чисел: 0,00423; 0,0423; 4,23; 423 отличаются только характеристиками, но не мантиссами (при условии, что все мантиссы положительны).
б) Мантиссы логарифмов чисел, имеющих одну и ту же значащую часть, одинаковы; так, логарифмы чисел: 23; 230; 2300; 23000 отличаются только характеристиками.
Замечание. Из указанных свойств десятичных логарифмов видно, что характеристику логарифма любого данного числа мы можем находить без помощи таблиц (в этом заключается большое удобство десятичных логарифмов); вследствие этого в логарифмических таблицах помещаются только одни мантиссы; кроме того, так как нахождение логарифмов дробей сводится к нахождению логарифмов целых чисел (логарифм дроби равняется логарифму числителя без логарифма знаменателя), то в таблицах помещаются мантиссы логарифмов только целых чисел.
Устройство и употребление таблиц
До появления компьютеров и калькуляторов люди считали логарифмы с помощью логарифмических таблиц. Эти таблицы по-прежнему могут использовать для быстрого вычисления логарифмов или умножения больших чисел.
Система логарифмов
Системой логарифмов называется совокупность логарифмов, вычисленных для ряда последовательных целых чисел по одному и тому же основанию. Употребительны две системы: система обыкновенных, или десятичных, логарифмов, в которых за основание взято число 10, и система так называемых натуральных логарифмов, в которых за основание (по причинам, которые уясняются в высшей математике) взято иррациональное число 2,7182818. . . Для вычислений употребляются десятичные логарифмы вследствие тех удобств.
Натуральные логарифмы называются также неперовыми, по имени изобретателя логарифмов шотландского математика Непера (1550— 1617), а десятичные логарифмы — бригговыми, по имени профессора Бригга (современника и друга Непера), впервые составившего таблицы этих логарифмов.
Преобразование отрицательного логарифма
Мы видели, что логарифмы чисел, меньших 1, отрицательны. Значит, они могут быть представлены при помощи отрицательных десятичных дробей. Такие логарифмы всегда можно преобразовать так, что у них мантисса будет положительная, а характеристика останется отрицательной. Для этого достаточно прибавить к мантиссе положительную единицу, а к характеристике — отрицательную (отчего, конечно, величина логарифма не изменится). Если, например, мы имеем логарифм— 2,0873, то можно его преобразовать так:
-2,0873=- 2-1+1-0,0873= -(2 + 1) + (1 -0,0873) = -3+0,9127,
или сокращённо:
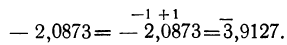
Обратно, всякий логарифм с отрицательной характеристикой и положительной мантиссой можно представить при помощи отрицательной десятичной дроби. Для этого достаточно к положительной мантиссе прибавить отрицательную единицу, а к отрицательной характеристике— положительную1); так, можно написать: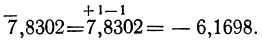
Описание четырёхзначных таблиц и пользование ими
Для решения большинства практических задач вполне достаточны четырёхзначные таблицы, обращение с которыми весьма просто. Небольшая часть их (для объяснения расположения) напечатана на следующей странице. В них содержатся мантиссы логарифмов всех целых чисел от 1 до 9999 включительно, вычисленные с четырьмя десятичными знаками, причём последний из этих знаков увеличен на 1 во всех тех случаях, когда 5-й десятичный знак должен был бы оказаться 5 или более 5; следовательно, четырёхзначные таблицы дают приближённые мантиссы с точностью до 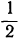 десятитысячной доли (с недостатком или с избытком).
десятитысячной доли (с недостатком или с избытком).
и
| N | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 123 | 456 | 789 |
| 50 | 6990 | 6998 | 7007 | 7016 | 7024 | 7033 | 7033 | 7050 | 7059 | 7067 | 123 | 345 | 678 |
| 51 | 7076 | 7084 | 7093 | 7101 | 7110 | 7118 | 7126 | 7135 | 7143 | 7152 | 123 | 345 | 678 |
| 52 | 7160 | 7168 | 7177 | 7185 | 7193 | 7202 | 7210 | 7218 | 7226 | 7235 | 122 | 345 | 677 |
| 53 | 7243 | 7251 | 7259 | 7267 | 7275 | 7284 | 7292 | 7300 | 7308 | 7316 | 122 | 345 | 677 |
| 54 | 7324 | 7332 | 7340 | 7348 | 7356 | 7364 | 7372 | 7380 | 7388 | 7396 | 122 | 345 | 667 |
| 55 | — | — | — | — | — | — | — | — | — | — | — | — | — |
Так как характеристику логарифма целого числа или десятичной дроби мы можем на основании свойств десятичных логарифмов проставить непосредственно, то в таблицах помещены только мантиссы; при этом надо помнить, что положение запятой в десятичном числе, а также число нулей, стоящих в конце числа, не имеет влияния на величину мантиссы. Поэтому при нахождении мантиссы по данному числу мы отбрасываем в этом числе запятую, а также и нули на конце его, если таковые есть, и находим мантиссу логарифма целого числа, образовавшегося после этого. При этом могут представиться следующие случаи:
1) Целое число состоит из трёх цифр. Например, пусть надо найти мантиссу логарифма числа 536. Первые две цифры этого числа, т. е. 53, находим в таблицах в первом слева вертикальном столбце (см. таблицу, напечатанную на этой странице). Найдя число 53, продвигаемся от него по горизонтальной строке вправо до пересечения этой строки с вертикальным столбцом, проходящим через ту из цифр О, 1, 2, 3,…, 9, поставленных наверху (и внизу) таблицы, которая представляет собой третью цифру данного числа, т. е. в нашем примере цифру 6. В пересечении получим мантиссу 7292 (т. е. 0,7292), принадлежащую логарифму числа 536. Подобно этому, для логарифма числа 508 найдём мантиссу 0,7059, для логарифма числа 500 найдём 0,6990 и т. п.
2) Целое число состоит из двух или из одной цифры. Тогда мысленно приписываем к этому числу один или два нуля и находим мантиссу для логарифма образовавшегося таким образом трёхзначного числа. Например, к числу 51 приписываем один нуль, отчего получаем 510, и находим мантиссу 7076; к числу 5 приписываем два нуля и находим мантиссу 6990 и т. д.
3) Целое число выражается четырьмя цифрами. Например, надо найти мантиссу lg 5436. Тогда сначала находим в таблицах, как было сейчас указано, мантиссу для логарифма числа, изображённого первыми тремя цифрами данного числа, т. е. для 543 (эта мантисса будет 0,7348); затем продвигаемся от найденной мантиссы по горизонтальной строке направо (в правую часть таблицы, расположенную за жирной вертикальной чертой) до пересечения с вертикальным столбцом, проходящим через ту из цифр; 1, 2, 3,…, 9, стоящих наверху (и внизу) этой части таблицы, которая представляет собой четвёртую цифру данного числа, т. е. в нашем примере цифру 6. В пересечении находим поправку (число 5), которую надо приложить в уме к мантиссе 7348, чтобы получить мантиссу логарифма числа 5436; мы получим, таким образом, мантиссу 0,7353.
4) Целое число выражается пятью или более цифрами. Тогда отбрасываем все цифры, кроме первых четырёх, и берём приближённое значение в виде четырёхзначного числа, причём последнюю цифру этого числа увеличиваем на 1 в том случае, когда отбрасываемая пятая цифра числа есть 5 или больше 5. Так, вместо 57842 мы берём 5784, вместо 30257 берём 3026, вместо 583263 берём 5833 и т. п. Для логарифма этого округлённого четырёхзначного числа находим мантиссу так, как было сейчас объяснено.
Руководствуясь этими указаниями, найдём для примера логарифмы следующих чисел:
36,5; 804,7; 0,26; 0,00345; 7,2634; 3456,86.
Прежде всего, не обращаясь пока к таблицам, проставим одни характеристики, оставляя место для мантисс, которые выпишем после:
lg 36,5=1, … ; lg 0,00345=3, .. . ;
lg 804,7=2, … ; lg 7,2634 =0, . . . ;
lg 0,26=1, … ; lg 3456,86=3, … .
Далее по таблицам выставляем прямо мантиссы:
lg 36,5=1,5623; lg 0,00345=3,5378;
lg 804,7 = 2,9056; lg 7,2634 = 0,8611;
lg 0,26=1,4150; lg 3456,86=3,5387.
Интерполирование
В некоторых четырёхзначных таблицах поправки на четвёртую цифру данного числа не помещены. Имея дело с такими таблицами, приходится поправки эти находить при помощи простого вычисления, которые можно выполнять на основании следующего положения: если числа превосходят 100, а разности между ними меньше 1, то без чувствительной погрешности можно принять, что
разности между логарифмами пропорциональны разности между соответствующими числами.
Рассматривая график логарифмической функции y=logt0x, мы
замечаем, что даже для чисел небольших (например, для чисел от 3 до 10) график очень мало отличается от прямой линии. Если бы этот график продолжить направо для чисел от 10 до 100 (т. е. на 90 единиц длины вдоль оси х-ов), то ординаты возросли бы только от 1 до 2, так как lg 10=1 a lg 100=2; при дальнейшем его продолжении для чисел от 100 до 1000 (т. е. на 900 единиц длины) ординаты увеличились бы снова только на 1 единицу. Значит, для чисел, больших 100, без чувствительной ошибки можно принять, что график функции y= Iog10X совпадает с прямой. Но допустить это — значит
принять, что для таких чисел приращения ординат пропорциональны приращениям абсцисс, т. е., другими словами, что разности между логарифмами пропорциональны разности между числами.
Пусть, например, надо найти мантиссу логарифма числа 5367. Мантисса эта, конечно, та же самая, что и для логарифма числа 536,7. Находим в таблицах для логарифма числа 536 мантиссу 7292. Сравнивая эту мантиссу с соседней вправо мантиссой 7300, соответствующей числу 537, мы замечаем, что если число 536 увеличится на 1, то мантисса увеличится на 8 десятитысячных (8 есть так называемая табличная разность между двумя соседними мантиссами); если же число 536 увеличится на 0,7, то мантисса увеличится не на 8 десятитысячных, а на некоторое меньшее число: х десятитысячных, которое согласно допущенной пропорциональности должно удовлетворять пропорции х :8=0,7:1, откуда x=8∙0,7=5,6, что по округлении составляет 6 десятитысячных. Значит, мантисса для логарифма числа 536,7 (и, следовательно, для числа 5367) будет: 7292+6=7298, т. е. 0,7298.
Заметим, что нахождение по двум рядом стоящим в таблицах числам промежуточного числа называется интерполированием. Интерполирование, описанное здесь, называется пропорциональным, так как оно основано на допущении, что изменение логарифма пропорционально изменению числа. Оно называется также линейным, так как предполагает, что графически изменение логарифмической функции изображается прямой линией.
Таблицы антилогарифмов
Для нахождения числа по данному логарифму могут служить те же таблицы, по которым отыскиваются мантиссы логарифмов данных чисел, но удобнее пользоваться другими таблицами, в которых помещены так называемые антилогарифмы, т. е. числа, соответствующие данным мантиссам. Небольшая часть их помещена на странице 121 (для объяснения).
Пусть дана четырёхзначная мантисса 2863 (на характеристику не обращаем внимания) и требуется найти соответствующее целое число. Тогда, имея таблицы антилогарифмов, надо пользоваться ими совершенно так же, как было раньше объяснено для нахождения мантисс по данному числу, а именно: первые две цифры мантиссы мы находим в первом слева столбце (точка, стоящая перед цифрами, заменяет собой запятую, отделяющую целое число логарифма от мантиссы). Затем подвигаемся от этих цифр по горизонтальной строке вправо до пересечения с вертикальным столбцом, идущим от третьей цифры мантиссы, которую надо искать в верхней строке (или в нижней). В пересечении находим четырёхзначное число 1932, соответствующее мантиссе 286. Затем от этого числа продвигаемся дальше по горизонтальной строке направо, до пересечения с вертикальным столбцом, идущим от четвёртой цифры мантиссы. Эту цифру надо найти наверху (или внизу) среди поставленных там цифр 1, 2, 3, … , 9. В пересечении мы находим поправку 1, которую надо приложить (в уме) к найденному раньше числу 1932, чтобы получить число, соответствующее мантиссе 2863.
Антилогарифмы
| m | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 123 | 456 | 789 |
| .25 | 1778 | 1782 | 1786 | 1791 | 1795 | 1799 | 1803 | 1807 | 1811 | 1116 | 011 | 222 | 334 |
| .26 | 1820 | 1824 | 1828 | 1832 | 1837 | 1841 | 1845 | 1849 | 1854 | 1854 | 011 | 223 | 334 |
| .27 | 1862 | 1866 | 1871 | 1875 | 1879 | 1884 | 1888 | 1892 | 1897 | 1901 | 011 | 223 | 334 |
| .28 | 1905 | 1910 | 1914 | 1919 | 1923 | 1928 | 1932 | 1936 | 1941 | 1945 | 011 | 223 | 344 |
| .29 | 1950 | 1954 | 1959 | 1963 | 1968 | 1972 | 1977 | 1982 | 1986 | 1991 | 011 | 223 | 344 |
| .30 | — | — | — | — | — | — | — | — | — | — | — | — | — |
Таким образом, число это будет 1933. После этого, обращая внимание на характеристику, надо в числе 1933 поставить запятую на надлежащем месте.
Приведем несколько примеров:
Если lg x=3,2863, то x= 1933;
„ lg x =1,2863, „ x = 19,33;
„ lg x =0,2863, „ x = 1,933;
„ lg x =2,2863, „ x =0,0193;
„ lg x =O,2287, „ x =1,693;
„ lg x = 1,7635, „ x =0,5801;
„ lg x =3,5029, „ x =3184;
„ lg x =2,0436, „ x =0,01106 и т. п.
Если в мантиссе указано 5 или более цифр, то берём только первые 4 цифры, отбрасывая остальные (и увеличивая четвёртую цифру на 1, если пятая цифра есть 5 или более). Например, вместо мантиссы 35478 берём 3548, вместо 47562 берём 4756.
Замечание об интерполировании: Поправку на четвёртую и следующие цифры мантиссы можно находить и посредством интерполирования. Так, если мантисса будет 84357, то, найдя число 6966, соответствующее мантиссе 843, мы можем рассуждать далее так: если мантисса увеличится (на 1 тысячную), т. е. сделается 844, то число, как видно из таблиц, увеличится на 16 единиц; если же мантисса увеличится не на 1 (тысячную), а на 0,57 (тысячных), то число увеличится на x единиц, причём х должно удовлетворять пропорции:
х : 16=0,57 : 1, откуда x = 16∙0,57=9,12.
Значит, искомое число будет 6966+9,12= 6975,12, или (ограничиваясь только четырьмя цифрами) 6975.
Действия над логарифмами с отрицательными характеристиками
Сложение и вычитание логарифмов не представляют никаких затруднений, как это видно из следующих примеров: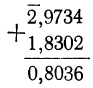
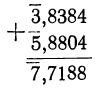
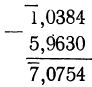
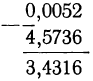
Не представляет никаких затруднений также и умножение логарифма на положительное число, например: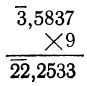
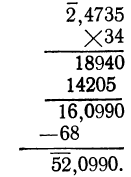
В последнем примере отдельно умножена положительная мантисса на 34, затем отрицательная характеристика на 34.
Если логарифм с отрицательной характеристикой и положительной мантиссой умножается на отрицательное число, то поступают двояко: или предварительно данный логарифм обращают в отрицательный, или же умножают отдельно мантиссу и характеристику и результаты соединяют вместе, например:
3,5632 • (-4) = -2,4368 • (-4) = 9,7472;
3,5632 • (-4) = +12-2,2528=9,7472.
При делении могут представиться два случая: во-первых, отрицательная характеристика делится на делитель; во-вторых, отрицательная характеристика не делится на делитель. В первом случае отдельно делят характеристику и мантиссу:
10,3784 : 5 = 2,0757.
Во втором случае прибавляют к характеристике столько отрицательных единиц, чтобы образовавшееся число делилось на делитель, к мантиссе прибавляют столько же положительных единиц:
3,7608 :8 = (-8+5,7608) : 8=1,7201.
Это преобразование надо совершать в уме, так что действие располагается так:
3,7608: 8 = 1,7201, или 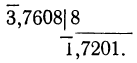
Замена вычитаемых логарифмов слагаемыми
При вычислении какого-нибудь сложного выражения с помощью логарифмов приходится некоторые логарифмы складывать, другие вычитать; в таком случае при обыкновенном способе совершения действий находят отдельно суммы слагаемых логарифмов, потом сумму вычитаемых и из первой суммы вычитают вторую. Например, если имеем:
lgx = 2,7305 — 2,0740+3,5464 — 8,3589,
то обыкновенно выполнение действий расположится так: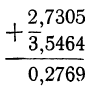
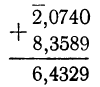
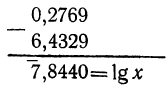
Есть, однако, возможность заменить вычитание сложением. Так: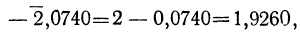
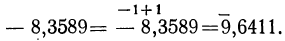
Теперь можно расположить вычисление так: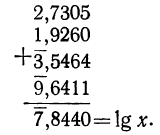
Примеры вычислений с помощью логарифмов
Пример:
Вычислить выражение: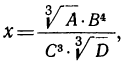
если А=0,8216, В=0,04826, С=0,005127 и D=7,246.
Логарифмируем данное выражение: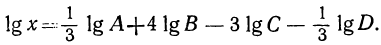
Теперь для избежания излишней потери времени и для уменьшения возможности ошибок прежде всего расположим все вычисления, не исполняя пока их и не обращаясь, следовательно, к таблицам:
После этого берём таблицы и проставляем логарифмы на оставленных свободных местах:
Пример:
Вычислить: 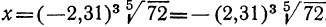 .
.
Так как отрицательные числа не имеют логарифмов, то предварительно находим 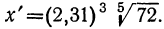
После вычисления окажется: x’=28,99, следовательно, x =-28,99.
Пример:
Вычислить: 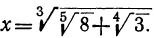
Сплошного логарифмирования здесь применить нельзя, так как под знаком корня стоит сумма. В подобных случаях вычисляют формулу по частям. Сначала находим 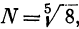 , потом
, потом 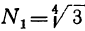 ; далее простым сложением определяем N + N₁ и, наконец, вычисляем
; далее простым сложением определяем N + N₁ и, наконец, вычисляем 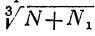 ; окажется:
; окажется:
N =1,516; N₁ = 1,316; N + N₁ = 2,832;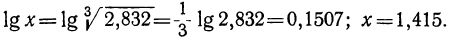
Употребление пятизначных таблиц
Для более точных вычислений употребляются пятизначные таблицы логарифмов. В этих таблицах логарифмы чисел вычислены с точностью до 0,00001 (вернее, с точностью до 0,000005). Наиболее употребительными являются таблицы, составленные Е. Пржевальским. Дадим краткие указания к пользованию ими.
1. Первая страница таблиц содержит мантиссы логарифмов чисел до 100. Но этой страницей можно не пользоваться, а искать мантиссу среди мантисс логарифмов трёхзначных чисел. Так, чтобы найти мантиссу логарифмов чисел 67; 6,7; 0,0067 и т. д., пишут соответствующую характеристику и ищут мантиссу логарифма числа 670.
2. Пусть число имеет три значащие цифры. (Напомним, что нуль, стоящий между значащими цифрами, принимается тоже за значащую цифру.) Ищут это число на соответствующей странице в левом крайнем столбце (он обозначен буквой N). В столбце, стоящем рядом, под значком 0 находят соответствующую мантиссу.
3. Пусть число имеет четыре значащие цифры. Ищут в столбце N число, составленное первыми тремя цифрами данного.
Пример:
Найти lg 84,37. Характеристика равна 1.
Ищем в столбце N число 843. Идём от этого числа вправо. В столбце под цифрой 7 находим соответствующую мантиссу 92619. Итак, lg 84,37 = 1,92619.
4. Число содержит более четырёх значащих цифр. Берём число, составленное первыми четырьмя цифрами, и ищем его мантиссу. Дальше поступаем так же, как и в четырёхзначных таблицах, т. е. или составляем пропорцию, или пользуемся табличками, помещёнными в крайнем правом столбце под знаком P. P. (partes proportionates).
Пример:
Ig 187,367.
Ищем число 187 и в столбце 3 находим мантиссу 27254. Находим разность между следующей мантиссой и найденной (табличную разность). Она равна 23. В крайнем правом столбце под числом 23 для цифры 6 находим 13,8 стотысячных долей, для 7 находим 16,1. Вычисления располагаем так
Итак, lg 187,367 =2,27269.
Показательные и логарифмические уравнения
Примеры уравнений:
Показательными уравнениями называются такие уравнения, в которых неизвестное входит в показатель степени, а логарифмическими—такие, в которых неизвестное находится под знаком логарифма. Такие уравнения могут быть разрешаемы элементарными приёмами только в частных случаях, причём приходится основываться на свойствах логарифмов и на том положении, что если числа равны, то равны и их логарифмы и, обратно, если логарифмы равны, то равны и соответствующие им числа.
Пример:
Решить уравнение: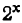 = 1024.
= 1024.
Логарифмируем обе части уравнения: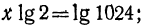
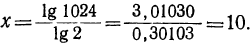
Пример:
Решить уравнение: 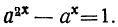
Положив 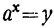 , получим квадратное уравнение: у² — у—1=0,
, получим квадратное уравнение: у² — у—1=0,
откуда: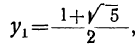 и
и 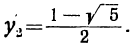
Следовательно,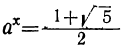 и
и 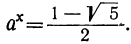
Так как 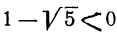 ,-τo последнее уравнение не имеет решений
,-τo последнее уравнение не имеет решений
(если а — положительное число), а первое дает: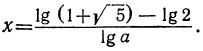
Пример:
Решить уравнение: lg(α+ x)+ lg(b+x)=lg (c+x). Уравнение можно написать так:
lg[(α+ x ) (b+x )]=lg (c+x ).
Из равенства логарифмов заключаем о равенстве чисел при равных основаниях:
(α+ x) (b+x ) = c+x,
это есть квадратное уравнение, которое легко решается.
Формула сложных процентов
Задача:
В какую сумму обратится в течение t лет вклад а рублей, если он ежегодно приносит р сложных процентов?
Говорят, что на вклад начисляются сложные проценты, если принимаются во внимание так называемые „проценты на проценты», т. е. если причитающиеся на вклад процентные деньги присоединяются в конце каждого года к вкладу для наращения их процентами в следующие годы.
Каждый рубль вклада, отданного по р процентов, в течение одного года принесёт дохода 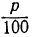 рубля, и, следовательно, каждый рубль вклада через 1 год обратится в
рубля, и, следовательно, каждый рубль вклада через 1 год обратится в 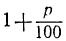 рубля (например, если вклад сделан по 5%, то каждый рубль его через год обратится в
рубля (например, если вклад сделан по 5%, то каждый рубль его через год обратится в 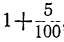 , т. e. в 1,05 рубля). Обозначив для краткости дробь
, т. e. в 1,05 рубля). Обозначив для краткости дробь 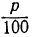 одной буквой, например r, можем сказать, что каждый рубль вклада через год обратится в 1+r рублей, следовательно, а рублей обратятся через 1 год в α(1+r) рублей. Ещё через год, т. е. через 2 года от начала роста, каждый рубль из этих a(1+r) рублей обратится снова в l+r рублей; значит, весь вклад обратится в α(1+r)² рублей. Таким же образом найдём, что через 3 года вклад будет α (1+r)³, через 4 года будет a(1+r)⁴,…, вообще через t лет, если t — целое число, он обратится в
одной буквой, например r, можем сказать, что каждый рубль вклада через год обратится в 1+r рублей, следовательно, а рублей обратятся через 1 год в α(1+r) рублей. Ещё через год, т. е. через 2 года от начала роста, каждый рубль из этих a(1+r) рублей обратится снова в l+r рублей; значит, весь вклад обратится в α(1+r)² рублей. Таким же образом найдём, что через 3 года вклад будет α (1+r)³, через 4 года будет a(1+r)⁴,…, вообще через t лет, если t — целое число, он обратится в 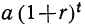 рублей. Таким образом, обозначив через А сумму денег, в которую обратится вклад через t лет, будем иметь следующую формулу сложных процентов:
рублей. Таким образом, обозначив через А сумму денег, в которую обратится вклад через t лет, будем иметь следующую формулу сложных процентов: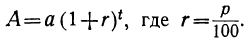
Из этой формулы легко найти любое из четырёх чисел: А, а, r (или р) и t, если остальные три заданы.
Пример:
Пусть a=2300 руб., p=4, t=20 лет; тогда: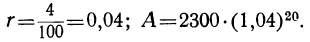
lgA=lg2300+20 lg 1,04=3,3617+20-0,0170=3,3617+0,3400= =3,7017.
А=5031 рубль.
| p | 1+r | lg(1+r) |
| 3 | 1,03 | 0,0128372 |
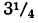 | 1,0325 | 0,0138901 |
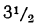 | 1,035 | 0,0149403 |
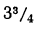 | 1,0375 | 0,0159881 |
| 4 | 1,04 | 0,0170333 |
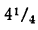 | 1,0425 | 0,0180761 |
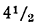 | 1,045 | 0,0191163 |
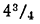 | 1,0475 | 0,0201540 |
| 5 | 1,05 | 0,0211893 |
Замечания:
1) В этом примере нам пришлось lg 1,04 умножить на 20. Так как число 0,0170 есть приближённое значение Ig 1,04 с точностью до 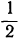 десятитысячной доли, то произведение этого числа на 20 будет точно только до
десятитысячной доли, то произведение этого числа на 20 будет точно только до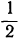 ‧20, т. е. до 10 десятитысячных, или до одной тысячной. Поэтому в сумме 3,7017 мы не можем ручаться не только за цифру десятитысячных, но и за цифру тысячных. Чтобы в подобных случаях можно было получить большую точность, лучше для числа 1-+r брать логарифмы не четырёхзначные, а с большим числом цифр, например семизначные. Для этой цели мы приводим здесь небольшую табличку, в которой выписаны семизначные логарифмы для некоторых значений р.
‧20, т. е. до 10 десятитысячных, или до одной тысячной. Поэтому в сумме 3,7017 мы не можем ручаться не только за цифру десятитысячных, но и за цифру тысячных. Чтобы в подобных случаях можно было получить большую точность, лучше для числа 1-+r брать логарифмы не четырёхзначные, а с большим числом цифр, например семизначные. Для этой цели мы приводим здесь небольшую табличку, в которой выписаны семизначные логарифмы для некоторых значений р.
2) Формулой сложных процентов приходится пользоваться не только в финансовых вопросах, но иногда и при решении задач, взя
тых из естественных процессов, например при вычислении численности населения какой-нибудь страны, прироста числа деревьев в лесу и т. п.
Дополнительный материал по логарифмам в математике

Смотрите также:
Решение задач по математическому анализу
| Существование корня. Степень с рациональным показателем. | Измерение отрезков. |
| Степень с любым вещественным показателем. | Переменная величина. |
Что такое логарифм в математике
Пользуясь равенством, например 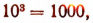 мы можем сказать, что число 3 есть тот показатель степени, в который надо возвысить 10, чтобы получить 1000.
мы можем сказать, что число 3 есть тот показатель степени, в который надо возвысить 10, чтобы получить 1000.
Из равенства 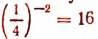 следует, что число — 2 есть показатель степени, в который надо возвысить число
следует, что число — 2 есть показатель степени, в который надо возвысить число 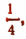 чтобы получить 16.
чтобы получить 16.
5°= 1. Значит, нуль есть тот показатель степени, в который надо возвысить число 5, чтобы получить единицу.
Подобных примеров можно привести сколько угодно.
Обобщая изложенное, можно сказать так: если  , то число q есть тот показатель степени, в которую надо возвысить основание а, чтобы получить число N.
, то число q есть тот показатель степени, в которую надо возвысить основание а, чтобы получить число N.
Вот этот показатель степени q и принято называть логарифмом числа N при основании а (или по основанию а).
Определение:
Логарифмом числа N при основании а называется показатель степени q, в которую надо возвысить основание а, чтобы получить число N.
Логарифм числа N при основании а обозначается символом
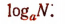

Символ называется знаком логарифма при основании а.
называется знаком логарифма при основании а.
Символ 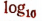 есть знак логарифма при основании 10.
есть знак логарифма при основании 10.
Выражение же 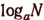 есть логарифм числа N при основании а. Выражение
есть логарифм числа N при основании а. Выражение 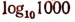 есть логарифм 1000 при основании 10.
есть логарифм 1000 при основании 10.
По определению логарифма из равенства
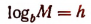
следует, что  или
или 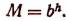
Например, если
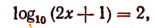
то 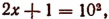 или х = 49,5.
или х = 49,5.
Убедитесь в справедливости равенств:

Отыщем логарифмы в некоторых простых случаях.
1. Сразу трудно узнать значение 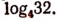 Поэтому напишем:
Поэтому напишем:
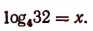
Отсюда 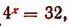 или
или 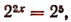 или х = 2,5. Следовательно,
или х = 2,5. Следовательно, 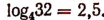
2. 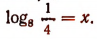
Отсюда 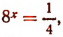 или
или 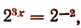 или
или  . Следовательно,
. Следовательно,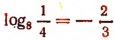 .
.
Изучать логарифмы при отрицательном основании или при основании, равном нулю или единице, не имеет смысла. Поэтому мы всегда будем брать за основания логарифмов числа положительные, отличные от единицы, т. е. в выражениях вида
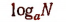
мы всегда будем предполагать, что а>0 и 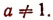
Для практических целей употребляются логарифмы при основании 10, которые называются десятичными.
Например:
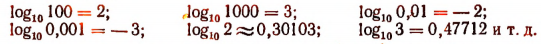
Последние два логарифма взяты из напечатанных таблиц десятичных логарифмов.
Для теоретических целей употребляются логарифмы при основании е, которые называются натуральными логарифмами.
Например:


Эти логарифмы взяты из напечатанных таблиц натуральных логарифмов.
Приближенные значения логарифмов вычисляются удобно и сравнительно легко с помощью методов, излагаемых в высшей математике. Еще проще и быстрее эти вычисления можно сделать на современных электронных машинах.
Не касаясь этих способов,, мы покажем принципиальную возможность вычисления логарифмов с помощью только элементарных средств.
Идею элементарного способа вычисления логарифмов мы изложим на примере.
Пусть требуется найти приближенное значение 
Обозначим, искомый логарифм буквой х, т е. положим, что

Отсюда 
Так как 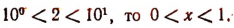
Положим, что 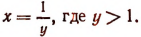
Тогда 
Так как 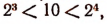 значит,
значит, 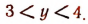
Положим, что 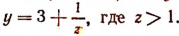
Теперь
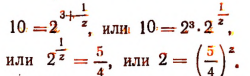
Так как 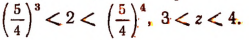
Положим, что 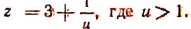
Теперь
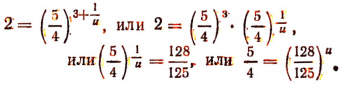
Так как 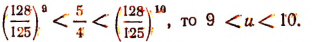
Остановившись на этом и пользуясь тем, что
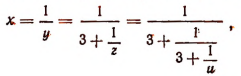
найдем, что х, т. е. 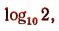 заключается между числами
заключается между числами
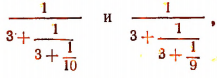
т. е. между числами 0,3009 и 0,3017. По более точным вычислениям
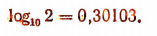
О десятичных логарифмах положительных чисел
Десятичные логарифмы положительных чисел, отличных от 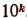 , где k — рациональное число, являются иррациональными числами.
, где k — рациональное число, являются иррациональными числами.
Докажем, например, что  не является ни целым, ни дробным числом, т. е. не является рациональным числом.
не является ни целым, ни дробным числом, т. е. не является рациональным числом.
Доказательство:
Легко видеть, что

Отсюда следует, что никакая целая степень числа 10 не может оказаться равной числу 2. Следовательно,  не может равняться никакому целому числу. Теперь допустим, что
не может равняться никакому целому числу. Теперь допустим, что
 где р и q — целые положительные числа. Тогда
где р и q — целые положительные числа. Тогда

Но равенство 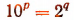 невозможно. Число
невозможно. Число 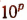 изображается единицей с р нулями. Последняя же цифра в изображении числа
изображается единицей с р нулями. Последняя же цифра в изображении числа 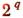 отлична от нуля.
отлична от нуля.
Существование единственного действительного числа, равного  , вытекает из того, что уравнение
, вытекает из того, что уравнение 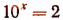 имеет единственный действительный корень (см. стр. 456, 457). Теперь из всего изложенного следует, что
имеет единственный действительный корень (см. стр. 456, 457). Теперь из всего изложенного следует, что  есть число иррациональное.
есть число иррациональное.
Иррациональными числами будут также, например, 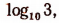
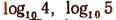 и им подобные.
и им подобные.
Приближенно 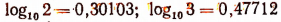 и т. д.
и т. д.
Существуют логарифмы, являющиеся рациональными числами.
Например,
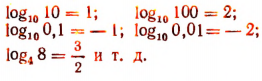
Общие свойства логарифмов
Общие свойства логарифмов
(а > 0 и 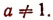 )
)
1. Очевидно, что 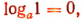 т. е. логарифм единицы равен нулю.
т. е. логарифм единицы равен нулю.
2. Очевидно, что
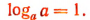
т. е. логарифм основания логарифмов равен единице.
3. Пусть 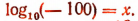 Тогда должно быть:
Тогда должно быть:
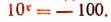
Но последнее равенство невозможно ни при каком значении буквы х, так как всегда

Следовательно, логарифмы отрицательных чисел не являются действительными числами.
4. Рассматривая равенства
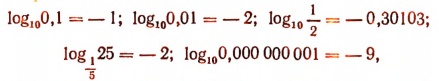
легко заметить, что существуют числа, логарифмы которых выражаются отрицательными числами.
Теорема. Если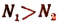 и а> 1, то
и а> 1, то
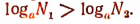
Доказательство:
Пусть 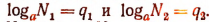
Тогда 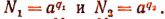
Но так как  то
то
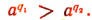
Отсюда при а>1 следует, что 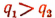 , т. е. что
, т. е. что
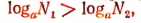
что и требовалось доказать.
Основные теоремы
Прежде чем формулировать и доказывать основные теоремы о логарифмах, рассмотрим несколько частных примеров.
1. Проверить, справедливо ли равенство
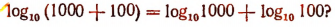
В этом равенстве левая часть представляет собой логарифм числа 1100 при основании 10. Так как 1000 < 1100 < 10000, то 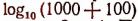 будет представлять собой число,4 заключенное между 3 и 4. Правая же часть равна сумме чисел 3 и 2, т. е. равна 5.
будет представлять собой число,4 заключенное между 3 и 4. Правая же часть равна сумме чисел 3 и 2, т. е. равна 5.
Следовательно, логарифм суммы не равен сумме логарифмов слагаемых, т. е.
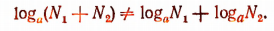
2. Убедитесь в том, что
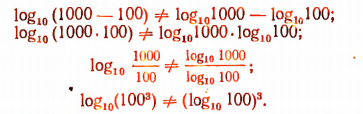
3. Убедитесь в справедливости следующих равенств:
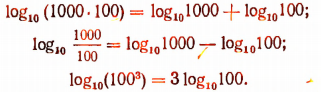
Теперь перейдем к формулировке и доказательству основных теорем.
Теорема:
Логарифм произведения равен сумме логарифмов сомножителей, т. е.
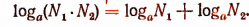
Доказательство:
Пусть
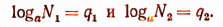
Тогда
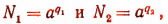
или
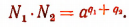
Здесь 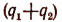 есть показатель степени, в который возводится а для получения числа, равного произведению
есть показатель степени, в который возводится а для получения числа, равного произведению 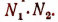 Следовательно,
Следовательно,
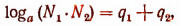
т. е.
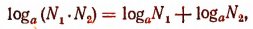
что и требовалось доказать.
Теорема:
Логарифм частного (дроби) равен разности логарифмов делимого и делителя, т. е.
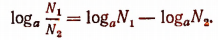
Доказательство:

Тогда
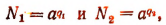
или
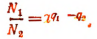
Отсюда 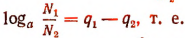
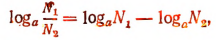
что и требовалось доказать.
Теорема:
Логарифм степени равен показатели степени, умноженному на логарифм основания этой степени, т. е.
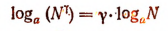
(здесь 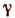 — любое число, не обязательно натуральное).
— любое число, не обязательно натуральное).
Пусть

Возведя обе части этого равенства в степень 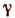 , получим:
, получим:

Отсюда
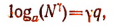
т. е.

что и требовалось доказать.
Следствие:
Логарифм корня равен логарифму подкоренного числа, деленному на показатель корня.
Действительно,
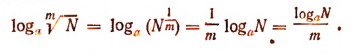
Логарифмирование произведения, частного, степени и корня
На основании теорем, доказанных в предыдущем параграфе, можно выразить логарифм любого одночленного выражения через логарифмы составляющих его чисел. Например, пусть
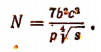
Тогда
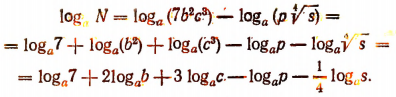
Другой пример. Пусть
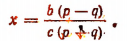
Тогда
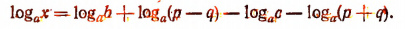
Практическое значение логарифмов
Пусть мы имеем таблицу, например; десятичных логарифмов. Пусть мы научились находить с помощью такой таблицы десятичные логарифмы любых положительных чисел и пусть мы научились находить также неизвестное число по известному его десятичному логарифму. Тогда с помощью такой таблицы можно производить многие сложные вычисления однообразно и при том с большой легкостью.
Поясним это на примере.
Пусть требуется вычислить значение выражения
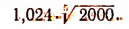
Обозначим значение этого выражения буквой х. Тогда получим:

или
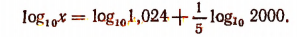
С помощью таблицы найдем, что
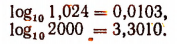
Значит,
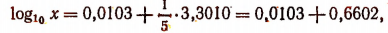
т. е.
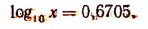
С помощью таблиц найдем, что
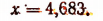
Свойства десятичных логарифмов
1. Десятичный логарифм числа, изображенного единицей с последующими нулями, равен стольким единицам, сколько нулей в изображении числа.
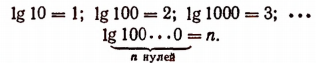
2. Логарифм правильной десятичной дроби, изображенной единицей с предшествующими нулями, равен стольким отрицательным единицам, сколько нулей предшествует единице, считая и нуль целых.
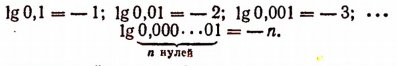
3. Десятичный логарифм всякого числа, не являющегося рациональной степенью числа 10, представляет собой число иррациональное.
Например, число 2 не является рациональной степенью числа 10. Поэтому lg2 есть число иррациональное.
4. Логарифм целого числа, изображенного п цифрами, заключается между числами (n—1) и n.
Например,
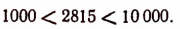
Значит,
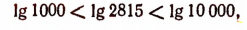
т. е.

Логарифм десятичной дроби, целая часть которой содержит n цифр, заключается также между (n—1) и n.
Например,
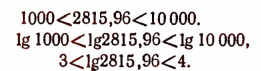
Легко убедиться, что

5. Логарифм правильной десятичной дроби, содержащей до первой значащей цифры n нулей, считая и нуль целых, заключается между числами —n и —(n—1).
Например,
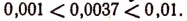
Значит,
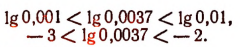
Легко убедиться, что

и т. д.
Характеристика и мантисса десятичного логарифма
Мы видели, например, что
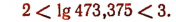
Следовательно,
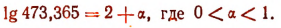
Число 2 называют характеристикой логарифма, а  — мантиссой.
— мантиссой.
При пользовании таблицей логарифмов за  принимается соответствующая правильная десятичная дробь, изображающая значение
принимается соответствующая правильная десятичная дробь, изображающая значение  с той или иной степенью точности.
с той или иной степенью точности.
Определение:
Целая часть логарифма называется характеристикой, а дробная часть—мантиссой.
Например, lg 300 = 2,47712. Здесь число 2 есть характеристика логарифма, а 0,47712 — его мантисса.
Характеристика логарифма числа, большего единицы, содержит столько единиц, сколько цифр в целой части числа без одной.
Например,
характеристика lg 7568,24 равна 3;
характеристика lg 2,568 равна нулю.
Мы видели, например, что

Следовательно,
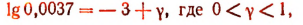
либо

Из этих двух форм изображения логарифма принято пользоваться формой:
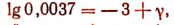
т. е. такой, при которой та часть логарифма, которая называется мантиссой, положительна.
При этих условиях можно высказать следующее: Характеристика логарифма правильной десятичной дроби содержит столько отрицательных единиц, сколько нулей предшествует первой значащей цифре, считая в том числе и нуль целых. (Мантисса при этом положительна.)
Например,
lg 0,0037 = — 3 + 0,5682.
Здесь —3 — характеристика, а 0,5682 — мантисса.
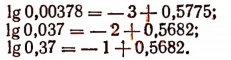
Приведенные здесь мантиссы взяты из таблицы логарифмов. Такую сумму, состоящую из целого отрицательного числа и положительной правильной дроби, условились записывать так:
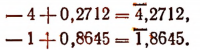
В дальнейшем будем записывать логарифмы правильных десятичных дробей в следующей искусственной форме:
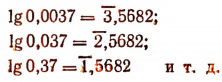
Действия над логарифмами, записанными в искусственной форме
Сложение.
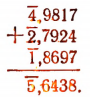
Вычитание.

Умножение на целое положительное число.
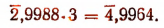
Пояснение. 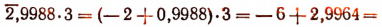
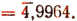
Деление на целое положительное число.
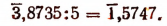
(Мы здесь прибавили —2 к отрицательной характеристике и +2 к мантиссе.)
Пояснение. 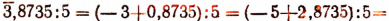
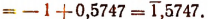
Умножение чисел, изображенных в искусственной форме:
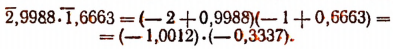
Далее умножаем по обычным правилам.
Деление чисел, изображенных в искусственной форме:
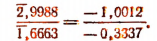
Далее делим по обычным правилам.
Покажем еще, как преобразовать отрицательное число к искусственной форме:
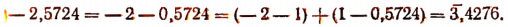
Правило. Чтобы преобразовать отрицательное наело в искусственную форму, надо к целой, части числа прибавить отрицательную единицу и поставить над результатом знак (—) сверху; одновременно с этим вычесть следующие после запятой цифры из 9, а последнюю цифру — из 10. Например,
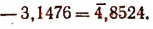
Неизменяемость мантиссы от умножения числа на целую степень десяти
Пусть
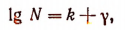
где k — характеристика, a 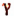 — мантисса.
— мантисса.
Пусть n — натуральное число. Тогда
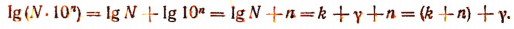
При умножении числа N на 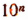 характеристика логарифма увеличивается на n единиц, а мантисса остается без изменения.
характеристика логарифма увеличивается на n единиц, а мантисса остается без изменения.
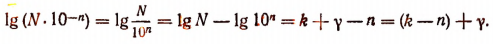
При делении числа на 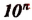 характеристика логарифма уменьшается на n единиц, а мантисса остается неизменной.
характеристика логарифма уменьшается на n единиц, а мантисса остается неизменной.
Примеры:

Таким образом, мантисса не зависит от положения запятой, а зависит лишь от цифр, изображающих число, и от их расположения. Например, мантиссы логарифмов чисел 372; 37,2; 3,72; 0,372; 3720 будут одинаковыми. Также будут одинаковыми между собой и мантиссы логарифмов чисел 327; 3,27; 0,327.
Характеристика логарифма зависит только от числа цифр в целой части числа и нисколько не зависит от самих цифр, изображающих это число.
Например, логарифмы чисел 356; 783,4; 101,75 имеют одну и ту же характеристику, равную 2.
Таблица четырехзначных десятичных логарифмов Брадиса
В таблицах Брадиса даются приближенные значения мантисс логарифмов целых чисел от 1 до 9999 с четырьмя десятичными знаками, но по этим же таблицам можно находить мантиссы логарифмов и десятичных дробей, так как мантисса логарифма не зависит от положения запятой. Для определения характеристики логарифма никакой таблицы не требуется, она определяется по правилам, изложенным в предыдущем параграфе.
Пусть требуется найти lg502. Характеристика этого логарифма равна 2.
Чтобы найти мантиссу, воспользуемся приведенной ниже частью таблицы логарифмов.
Берем из первого столбца, помеченного сверху и снизу буквой N, число, образованное первыми двумя цифрами числа 502, т. е. берем число 50; затем продвигаемся от числа 50 по горизонтали до пересечения с вертикальным столбцом, помеченным сверху и снизу третьей значащей цифрой числа 502, т. е. цифрой 2. В пересечении прочитываем мантиссу 7007, что означает 0,7007.
Следовательно,
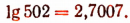
Из ранее изложенного следует, что
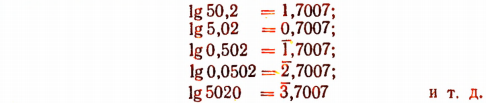
Мантисса логарифмов
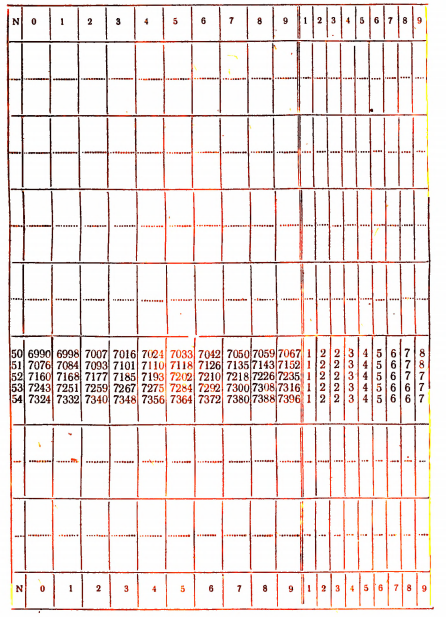
Мантисса логарифма двузначного числа или трехзначного числа, оканчивающегося нулем, а также и мантисса четырехзначного числа, оканчивающегося двумя нулями, берется из столбца, помеченного сверху и снизу числом нуль. Например, мантисса логарифма числа 53, или 530, или 5300 будет 0,7243.
Чтобы найти мантиссу lg 5, достаточно взять мантиссу
lg 50.
Мантисса lg 3 будет та же, что и мантисса lg30. Мантисса lg0,006 будет та же, что и мантисса lg60. Теперь изложим правило нахождения мантисс логарифмов многозначных чисел.
Чтобы найти мантиссу логарифма четырехзначного числа, например 52,48, достаточно найти мантиссу
lg 5248.
Для нахождения этой мантиссы надо поступать так.
Сначала надо найти мантиссу логарифма трехзначного числа 524, т. е. числа, изображенного первыми тремя цифрами данного числа.. Этой мантиссой окажется число 0,7193. После этого надо от этой мантиссы передвинуться вправо по горизонтальной строке до вертикального столбца, расположенного за двойной вертикальной чертой и помеченного сверху и снизу цифрой 8, т. е. последней цифрой данного четырехзначного числа. На пересечении с этой вертикалью находим число 7 (т. е. 7 десятитысячных). Эту поправку на четвертую значащую цифру прибавляем к найденной раньше мантиссе 0,7193 и получаем, что
lg 5248 = 3,7200.
Таким же способом находится мантисса логарифма и всякого другого четырехзначного числа.
Зная, что lg 5248 = 3,7200, можем записать:
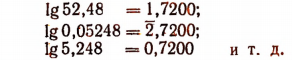
За мантиссу логарифма пятизначного числа или числа с большим количеством цифр принимают мантиссу четырехзначного числа, полученного после округления данного многозначного числа.
Например,

Антилогарифмы

Таблица четырехзначных антилогарифмов
С помощью таблицы антилогарифмов можно находить неизвестное чисто но данному его логарифму. Это неизвестное число и называют антилогарифмом. Пусть, например,

Чтобы найти неизвестное число х, воспользуемся приведенной частью таблицы антилогарифмов.
Не обращая внимание на характеристику, берем число, изображенное первыми двумя цифрами мантиссы, т. е. число 94. Это число находим в столбце, помеченном сверху и снизу буквой т (мантисса), и продвигаемся по этой горизонтали до пересечения со столбцом, помеченным сверху и снизу третьей цифрой мантиссы 8; на этом пересечении находим число 8872. Далее ищем поправку на 4-ю цифру мантиссы (эта цифра в данном случае равна 8).
Для этого по той же горизонтали продвигаемся вправо до вертикального столбца, расположенного за двойной вертикальной чертой и помеченного сверху и снизу цифрой 8, т. е. последней цифрой данной мантиссы; на пересечении находим поправку 16. Эту поправку прибавляем к найденному уже числу 8872 и получаем
8888.
Поскольку характеристика данного логарифма была равна 3, то х=8888.

Существуют таблицы логарифмов, в которых мантиссы даны с более высокой степенью точности, например пятизначные таблицы Пржевальского.
Примеры вычислений с помощью таблиц логарифмов
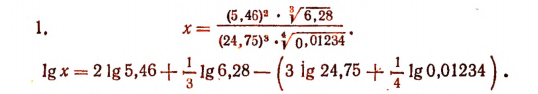
Вычисление Ig х

Нахождение значения х
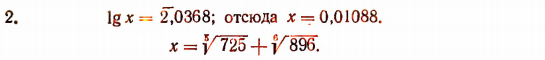
Сумму логарифмировать нельзя. Поэтому вычислим отдельно

Следовательно,
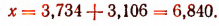
Переход от натуральных логарифмов к десятичным и обратный переход
Натуральный логарифм числа N, т. е.  принято обозначать ради краткости
принято обозначать ради краткости 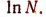
Пусть InN = q. Тогда 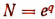 , или
, или 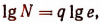 или, наконец,
или, наконец, 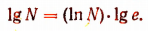
Но
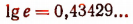
Поэтому, чтобы получить десятичный логарифм какого-нибудь числа, достаточно его натуральный логарифм умножить на число 0,43429…
Число 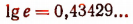 называется модулем перехода от натуральных логарифмов к десятичным. Из равенства
называется модулем перехода от натуральных логарифмов к десятичным. Из равенства
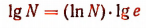
следует, что
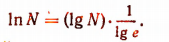
Но
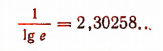
Поэтому, чтобы получить натуральный логарифм какого-нибудь числа, достаточно его десятичный логарифм умножить на число 2,30258.
Число 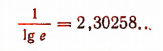 называется модулем перехода от десятичных логарифмов к натуральным.
называется модулем перехода от десятичных логарифмов к натуральным.
Некоторые употребительные формулы
1. Легко убедиться, что
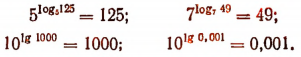
Обобщая это, заметим, что по определению логарифма
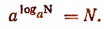
Справедливость этой формулы поясним еще и так:
Пусть 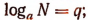 тогда
тогда  Подставляя в последнее равенство вместо числа q равное ему выражение
Подставляя в последнее равенство вместо числа q равное ему выражение 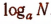 , получим
, получим 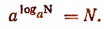
Итак, если имеется степень, показателем которой является логарифм числа N при основании таком же, как и основание этой степени, то вся степень равна N.
Примеры:
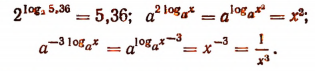
2. Справедлива и следующая формула:
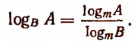
Доказательство:
Пусть 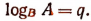 Тогда
Тогда  или
или 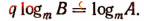 Отсюда
Отсюда
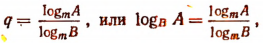
что и требовалось доказать.
Значит, любой логарифм можно представить в виде отношения двух логарифмов, взятых по одному и тому же произвольному основанию.
Примеры:
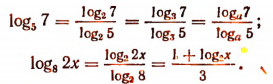
Положив в формуле
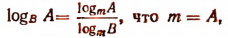
получим, что
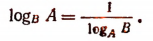
3. Выведем еще одну формулу
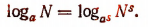
Доказательство:
Пусть 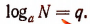 Тогда
Тогда 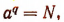 или
или 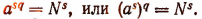
Здесь q есть показатель степени, в которую надо возвысить выражение 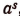 , чтобы получить число
, чтобы получить число 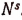 . Следовательно, q есть логарифм числа
. Следовательно, q есть логарифм числа 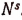 при основании
при основании 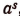 , т. е.
, т. е.
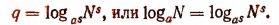
Итак, если возвысить число, стоящее под знаком логарифма, и одновременно основание логарифма в какую-либо степень, то величина логарифма не изменится.
Примеры.
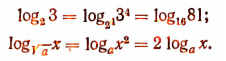
Потенцирование
Из основных теорем, доказанных в § 3, следует:
1. Сумма логарифмов равна логарифму произведения:
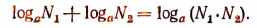
2. Разность логарифмов равна логарифму дроби:
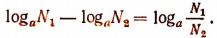
3. Произведение числа на логарифм равно логарифму степени:
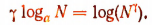
Потенцированием называется действие, с помощью которого отыскивается число по данному его логарифму.
Пример:
Пусть 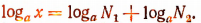
Тогда 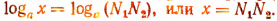
Пример:
Пусть 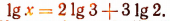
Тогда 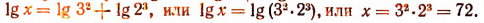
Пример:
Пусть
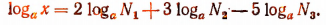
Тогда
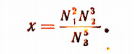
Пример:
Пусть

Тогда
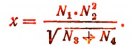
Логарифмические уравнения
Уравнение, в котором неизвестное содержится под знаком логарифма, называется логарифмическим.
Покажем на примерах, как решаются логарифмические уравнения.
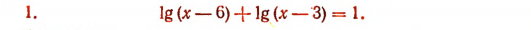
Решение:
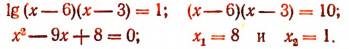
Корень, равный 1, должен быть отброшен, так как его подстановка в данное уравнение приводит к логарифму отрицательного числа, между тем как нами определены логарифмы лишь положительных чисел.
Уже из этого примера видно, что при решении логарифмических уравнений полученные корни нуждаются, вообще говоря, в проверке.
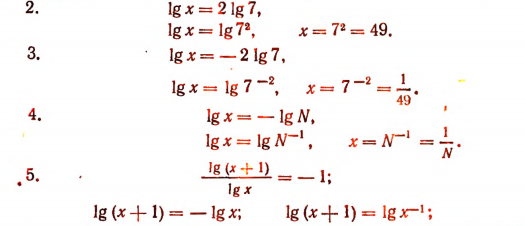
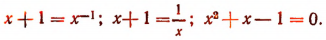 Отсюда
Отсюда 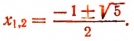
Окончательно 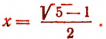 Второй корень должен быть отброшен, так как логарифм отрицательного числа не является действительным числом.
Второй корень должен быть отброшен, так как логарифм отрицательного числа не является действительным числом.
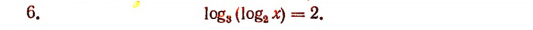
Под знаком логарифма при основании 3 стоит число 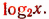 По определению логарифма это число должно равняться З2, т. е. 9. Значит,
По определению логарифма это число должно равняться З2, т. е. 9. Значит,
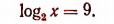
Отсюда
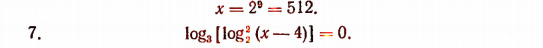
Здесь под знаком логарифма при основании 3 стоит число 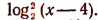 По определению логарифма это число должно равняться 3°, т. е. единице. Поэтому
По определению логарифма это число должно равняться 3°, т. е. единице. Поэтому
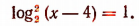
Отсюда
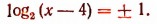
Из уравнения 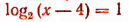 находим, что х — 4 = 2, т. е. х = 6.
находим, что х — 4 = 2, т. е. х = 6.
Из уравнения 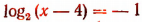 находим, что
находим, что 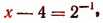 или
или 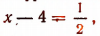 т. е.
т. е. 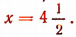
Оба полученных корня удовлетворяют данному уравнению.
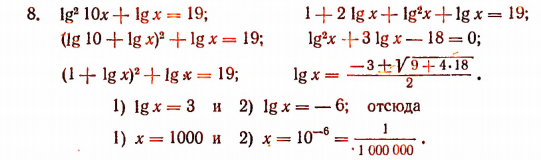
Оба полученных корня удовлетворяют данному уравнению.
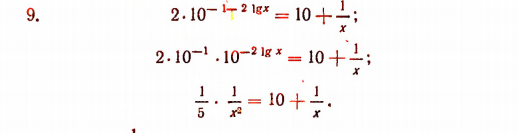
Положим, что 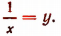
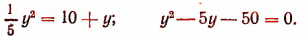
Отсюда
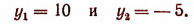
Следовательно,
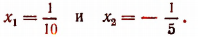
Окончательно, х = 0,1.
Второй корень должен быть отброшен.
10. Доказать тождество
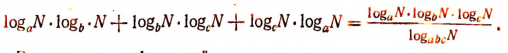
Воспользуемся формулой
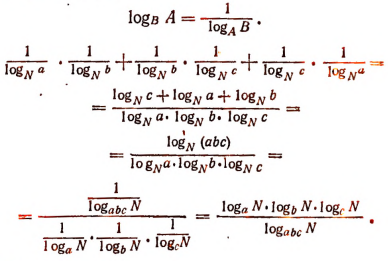
11. Решить систему:
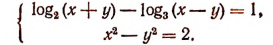
В силу первого уравнения 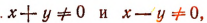 так как log 0 не существует.
так как log 0 не существует.
Поэтому второе уравнение можно записать в виде:
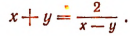
Подставив в первое уравнение вместо х + у выражение 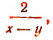 получим:
получим:
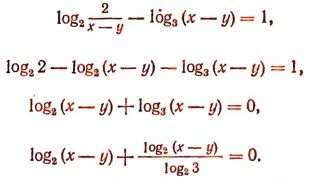
Это уравнение удовлетворяется лишь тогда, когда
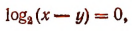
т.е. когда
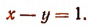
Присоединяя это уравнение к уравнению 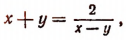 получим систему:
получим систему:
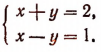
Решив эту систему, получим:
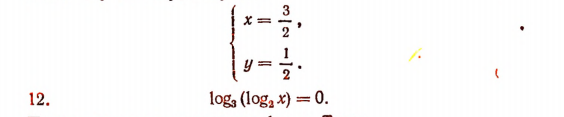
Примем за новое неизвестное 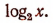 Тогда
Тогда
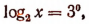
или
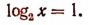
Отсюда
х = 2.
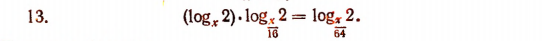
Применим формулу
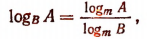
приняв m = 2.
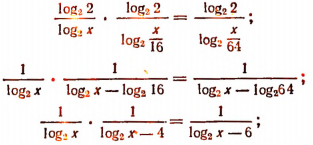
Приняв за новую неизвестную 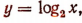 получим:
получим:

Приняв 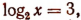 получим х=8.
получим х=8.
Приняв 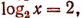 получим х =4.
получим х =4.
Оба полученных корня удовлетворяют данному уравнению.
14. Решить неравенство

Решение:
Обозначив lg х буквой у, сведем дело к решению неравенства
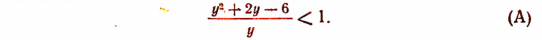
Преобразуем это, неравенство в другое, ему равносильное:
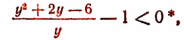
или
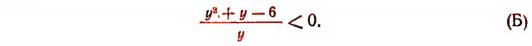
Последнее неравенство удовлетворяется в том случае, когда
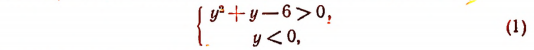
а также и тогда, когда
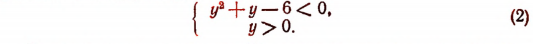
Решив систему неравенств (1), получим, что она удовлетворяется лишь при всех значениях у, меньших, чем —3.
Решив систему неравенств (2), получим, что она удовлетворяется лишь при всех значениях у, заключенных между числами 0 и 2.
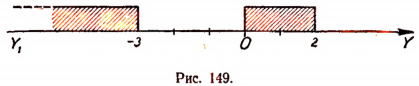
Итак, неравенство (Б), а следовательно, и неравенство (А) удовлетворяются как при всех значениях у, меньших, чем число — 3, так и при всех значениях у, заключенных между 0 и 2, т. е. у< — 3 и 0<у<2.
На рисунке 149 представлено решение неравенства (А) в наглядной форме.
Теперь перейдем к нахождению значений х, учитывая, что у означает log х. Из неравенств
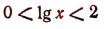
следует, что
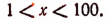
Из неравенства
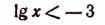
следует, что
х< 0,001.
Итак, первоначальное неравенство удовлетворяется как при всех значениях х, заключенных между 1 и 100, так и при всех значениях х, заключенных между 0 и 0,001.
При значениях х, меньших или равных нулю, данное неравенство не удовлетворяется, так как при этих значениях х выражение lg x не равняется никакому действительному числу.
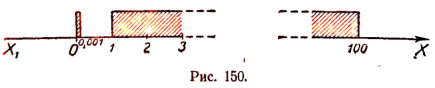
На рисунке 150 представлено решение первоначального неравенства в наглядной форме.
Графики логарифмических функций
Выражение lg x есть функция аргумента х, определенная нами лишь для положительных значений х. Составим таблицу значений этой функции для нескольких значений х.
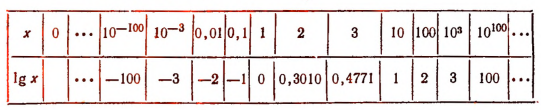
На рисунке 151 изображен график функции 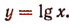
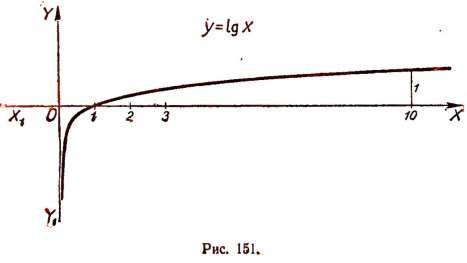
Если  то
то 
Если 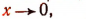 то
то 
Составим таблицу значений функции 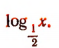

На рисунке 152 изображен график функции

График функции 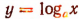 при а>1 сходен с графиком на рисунке 151, а при а < 1 сходен с графиком на рисунке 152.
при а>1 сходен с графиком на рисунке 151, а при а < 1 сходен с графиком на рисунке 152.
Логарифмы были изобретены в начале XVII века. Их открытие было связано в первую очередь с быстрым развитием астрономии. Для обработки астрономических наблюдений требовалось производить большие по объему и сложности вычисления. Появление логарифмов облегчило эту работу.
Некоторые замечания:
В настоящее время необычайно большие по объему и сложности вычисления производятся сказочно быстро на математических вычислительных и счетнорешающих электронных машинах.
Широко распространенным среди инженеров, техников и многих других работников счетным прибором является логарифмическая линейка. Однако ею можно пользоваться лишь для таких вычислений, в которых не требуется высокая степень точности.
Логарифмическая линейка дает приближенные результаты с точностью лишь до трех цифр.
Научиться пользоваться логарифмической линейкой можно, например, по краткому руководству К. А. Семендяева «Счетная линейка».
Примеры зависимостей, выражающихся с помощью логарифмических функций.
Первый пример.
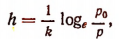
где 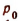 — атмосферное давление на уровне моря;
— атмосферное давление на уровне моря;
k — некоторая известная постоянная; 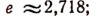
h —высота над уровнем моря;
р — атмосферное давление на высоте h над уровнем моря.
Здесь р есть независимая переменная, или аргумент, а h есть зависимая переменная, или функция.
По этой формуле можно определять высоту h над уровнем моря по данному атмосферному давлению р на этой высоте. Эту формулу можно получить, решив относительно h уравнение
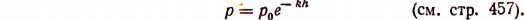
Второй пример. 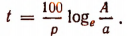
Буква а обозначает первоначальный вклад;
Р — число годовых процентов;
А — сумма, образовавшаяся при органическом росте вклада через t лет.
Здесь А можно рассматривать как независимую переменную, а t как зависимую. По этой формуле можно определять t по данному значению А .
Эту формулу можно получить, решив относительно t уравнение
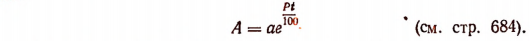
Логарифмическая функция, например у = log х, относится к классу так называемых элементарных функций. К классу элементарных функций относятся и следующие функции:
1. Целая рациональная функция
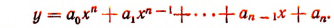
2. Дробная рациональная функция.
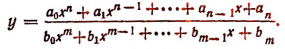
3. Иррациональная функция, например,
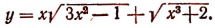
4. Показательная функция

5. Степенная функция
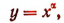
где а —любое действительное число.
Во всех этих функциях аргумент обозначен буквой х. В следующих двух главах мы ознакомимся еще с двумя другими типами элементарных функций,называемых тригонометрическими и обратными тригонометрическими.
Более сложные функции, не принадлежащие к числу элементарных, изучаются в курсе высшей математики.
Логарифм — основные понятия и определения
Логарифмы по произвольному основанию. Определение и свойства логарифмов
В соотношении
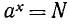
может быть поставлена задача отыскания любого из трех чисел a, N, х по двум другим, заданным. Если даны а и х, то N находят действием возведения в степень. Если даны N и х, то а находят извлечением корня степени х (или возведением в степень 1/х). Теперь рассмотрим случай, когда по заданным а и N требуется найти х.
Пусть число N положительно: 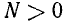 , число а положительно и не равно единице:
, число а положительно и не равно единице: 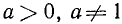 .
.
Определение. Логарифмом числа N по основанию а называется показатель степени, в которую нужно возвести а, чтобы получить число N; логарифм обозначается через 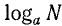 :
:
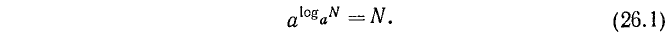
Таким образом, в равенстве (26.1) показатель степени х находят как логарифм N по основанию а. Записи
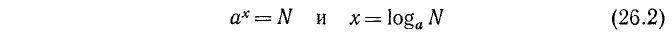
имеют одинаковый смысл. Равенство (26.1) иногда называют основным тождеством теории логарифмов; в действительности оно выражает определение понятия логарифма. По данному определению основание логарифма а всегда положительно и отлично от единицы, логарифмируемое число N положительно.
Отрицательные числа и нуль логарифмов не имеют. Можно доказать, что всякое число 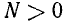 при данном основании а
при данном основании а 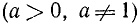 имеет вполне определенный логарифм. Поэтому равенство
имеет вполне определенный логарифм. Поэтому равенство 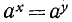 влечет за собой
влечет за собой 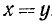 . Заметим, что здесь существенно условие
. Заметим, что здесь существенно условие 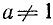 , в противном случае вывод
, в противном случае вывод 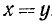 был бы не обоснован, так как равенство
был бы не обоснован, так как равенство 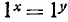 верно при любых значениях х и у.
верно при любых значениях х и у.
Пример:
Найти 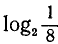 .
.
Решение:
Для получения числа 1/8 следует возвести основание 2 в степень —3: 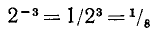 . Поэтому
. Поэтому 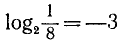 .
.
Можно проводить записи при решении таких примеров в следующей форме:
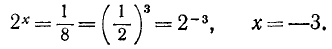
Пример:
Найти 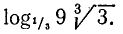 .
.
Решение:
Имеем
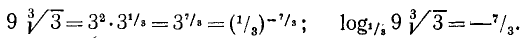
В примерах 1 и 2 мы легко находили искомый логарифм, представляя логарифмируемое число как степень основания с рациональным показателем. В общем случае, например для 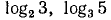 и т.д., этого сделать не удастся, так как логарифм имеет иррациональное значение. Обратим внимание на один связанный с этим утверждением вопрос. В п. 12 мы дали понятие о возможности определения любой действительной степени данного положительного числа. Это было необходимо для введения логарифмов, которые, вообще говоря, могут быть иррациональными числами.
и т.д., этого сделать не удастся, так как логарифм имеет иррациональное значение. Обратим внимание на один связанный с этим утверждением вопрос. В п. 12 мы дали понятие о возможности определения любой действительной степени данного положительного числа. Это было необходимо для введения логарифмов, которые, вообще говоря, могут быть иррациональными числами.
Рассмотрим некоторые свойства логарифмов.
Свойство:
Если число и основание равны, то логарифм равен единице, и, обратно, если логарифм равен единице, то число и основание равны.
Доказательство:
Пусть N = a. По определению логарифма имеем 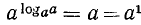 , откуда
, откуда
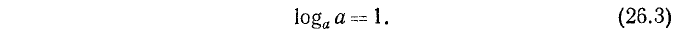
Обратно, пусть 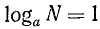 . Тогда по определению
. Тогда по определению 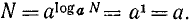
Свойство:
Логарифм единицы по любому основанию равен нулю.
Доказательство:
По определению логарифма 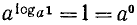 (нулевая степень любого положительного основания равна единице, см. (10.1)). Отсюда
(нулевая степень любого положительного основания равна единице, см. (10.1)). Отсюда
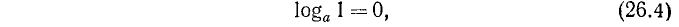
что и требовалось доказать.
Верно и обратное утверждение: если 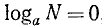 , то N = 1. Действительно, имеем
, то N = 1. Действительно, имеем 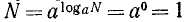 .
.
Прежде чем сформулировать следующее свойство логарифмов, условимся говорить, что два числа а и b лежат по одну сторону от третьего числа с, если они оба либо больше с, либо меньше с. Если одно из этих чисел больше с, а другое меньше с, то будем говорить, что они лежат по разные стороны от с.
Свойство:
Если число и основание лежат по одну сторону от единицы, то логарифм положителен; если число и основание лежат по разные стороны от единицы, то логарифм отрицателен.
Доказательство:
Доказательство свойства 3 основано на том, что степень 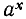 больше единицы, если основание больше единицы и показатель положителен или основание меньше единицы и показатель отрицателен. Степень меньше единицы, если основание больше единицы и показатель отрицателен или основание меньше единицы и показатель положителен.
больше единицы, если основание больше единицы и показатель положителен или основание меньше единицы и показатель отрицателен. Степень меньше единицы, если основание больше единицы и показатель отрицателен или основание меньше единицы и показатель положителен.
Требуется рассмотреть четыре случая:
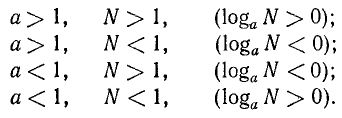
Ограничимся разбором первого из них, остальные читатель рассмотрит самостоятельно.
Пусть 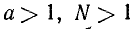 ; тогда в равенстве
; тогда в равенстве 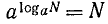 показатель степени не может быть ни отрицательным, ни равным нулю, следовательно, он положителен, т. е.
показатель степени не может быть ни отрицательным, ни равным нулю, следовательно, он положителен, т. е. 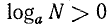 , что и требовалось доказать.
, что и требовалось доказать.
Пример:
Выяснить, какие из указанных ниже логарифмов положительны, какие отрицательны: а) 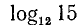 б)
б) 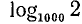 ; в)
; в) 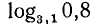 ; г)
; г) 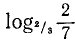 ; д)
; д) 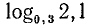 .
.
Решение:
а) 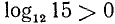 , так как число 15 и основание 12 расположены по одну сторону от единицы;
, так как число 15 и основание 12 расположены по одну сторону от единицы;
б) 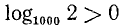 , так как 1000 и 2 расположены по одну сторону от единицы; при этом несущественно, что основание больше логарифмируемого числа;
, так как 1000 и 2 расположены по одну сторону от единицы; при этом несущественно, что основание больше логарифмируемого числа;
в) 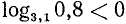 , так как 3,1 и 0,8 лежат по разные стороны от единицы;
, так как 3,1 и 0,8 лежат по разные стороны от единицы;
г) 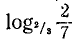 ; так как 2/3 и 2/7 расположены по одну сторону от единицы
; так как 2/3 и 2/7 расположены по одну сторону от единицы
д) 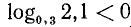 ; так как 0,3 и 2,1 расположены по одну сторону от единицы
; так как 0,3 и 2,1 расположены по одну сторону от единицы
Следующие свойства 4—6 часто называют правилами логарифмирования: они позволяют, зная логарифмы некоторых чисел, найти логарифмы их произведения, частного, степени каждого из них.
Свойство:
Правило логарифмирования произведения. Логарифм произведения нескольких положительных чисел по данному основанию равен сумме логарифмов этих чисел по тому же основанию.
Доказательство:
Пусть даны положительные числа 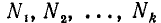 . Для логарифма их произведения напишем определяющее логарифм равенство (26.1):
. Для логарифма их произведения напишем определяющее логарифм равенство (26.1):
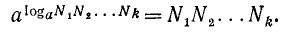
Отсюда найдем
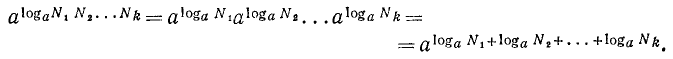
Сравнив показатели степени первого и последнего выражений, получим требуемое равенство:
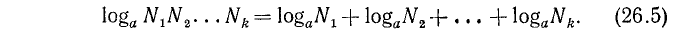
Заметим, что условие  существенно; логарифм произведения двух отрицательных чисел
существенно; логарифм произведения двух отрицательных чисел 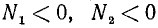 имеет смысл, но в этом случае получим
имеет смысл, но в этом случае получим
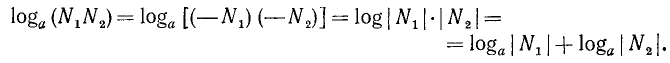
В общем случае, если произведение нескольких сомножителей положительно, то его логарифм равен сумме логарифмов модулей этих сомножителей.
Свойство:
Правило логарифмирования частного. Логарифм частного положительных чисел равен разности логарифмов делимого и делителя, взятых по тому же основанию.
Доказательство:
Последовательно находим
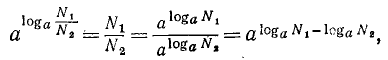
откуда
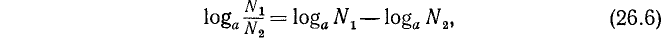
что и требовалось доказать.
Свойство:
Правило логарифмирования степени. Логарифм степени какого-либо положительного кисла равен логарифму этого числа, умноженному на показатель степени.
Доказательство:
Запишем снова основное тождество (26.1) для числа 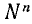 :
:
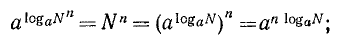
отсюда
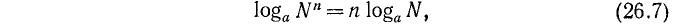
что и требовалось доказать.
Следствие:
Логарифм корня из положительного числа равен логарифму подкоренного числа, деленному на показатель корня:
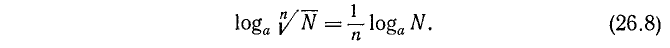
Доказать справедливость этого следствия можно, представив 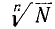 как
как 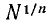 и воспользовавшись свойством 6.
и воспользовавшись свойством 6.
Пример:
Прологарифмировать по основанию а:
а) 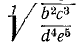 (предполагается, что все величины b, с, d, е положительны);
(предполагается, что все величины b, с, d, е положительны);
б) 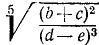 (предполагается, что
(предполагается, что 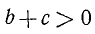 и
и 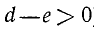 .
.
Решение:
а) Удобно перейти в данном выражении к дробным степеням:
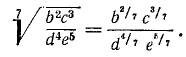
На основании равенств (26.5)—(26.7) теперь можно записать:
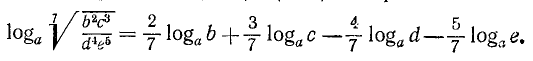
б) Имеем
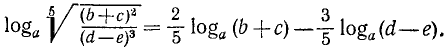
Мы замечаем, что над логарифмами чисел производятся действия более простые, чем над самими числами: при умножении чисел их логарифмы складываются, при делении —вычитаются и т. д.
Именно поэтому логарифмы получили применение в вычислительной практике (см. п. 29).
Действие, обратное логарифмированию, называется потенцированием, а именно: потенцированием называется действие, с помощью которого по данному логарифму числа находится само это число. По существу потенцирование не является каким-либо особым действием: оно сводится к возведению основания в степень (равную логарифму числа). Термин «потенцирование» можно считать синонимом термина «возведенение в степень».
При потенцировании надо пользоваться правилами, обратными по отношению к правилам логарифмирования: сумму логарифмов заменить логарифмом произведения, разность логарифмов — логарифмом частного и т. д. В частности, если перед знаком логарифма находится какой-либо множитель, то его при потенцировании нужно переносить в показатель степени под знак логарифма.
Пример:
Найти N, если известно, что
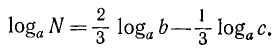
Решение:
В связи столько что высказанным правилом потенцирования множители 2/3 и 1/3, стоящие перед знаками логарифмов в правой части данного равенства, перенесем в показатели степени под знаками этих логарифмов; получим
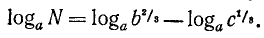
Теперь разность логарифмов заменим логарифмом частного:
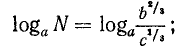
отсюда
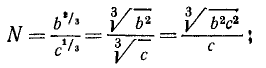
для получения последней дроби в этой цепочке равенств мы предыдущую дробь освободили от иррациональности в знаменателе (п. 25).
Свойство:
Если основание больше единицы, то большее число имеет больший логарифм (а меньшее — меньший)-, если основание меньше единицы, то большее число имеет меньший логарифм (а меньшее — больший).
Это свойство формулируют также и как правило логарифмирования неравенств, обе части которых положительны:
При логарифмировании неравенств по основанию, большему единицы, знак неравенства сохраняется, а при логарифмировании по основанию, меньшему единицы, знак неравенства меняется на противоположный (см. также п. 80).
Доказательство основано на свойствах 5 и 3. Рассмотрим случай, когда 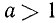 . Если
. Если 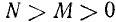 , то
, то 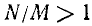
и, логарифмируя, получим
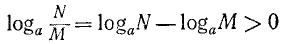
(а и N/M лежат по одну сторону от единицы). Отсюда
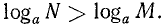
Случай 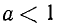 , в котором из
, в котором из 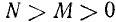 следует
следует 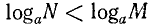 , читатель разберет самостоятельно.
, читатель разберет самостоятельно.
Логарифмы по различным основаниям. Модуль перехода
Здесь мы установим некоторые свойства, относящиеся к логарифмам по различным основаниям. Для удобства продолжим нумерацию свойств п. 26.
Свойство:
При вождении основания в некоторую (ненулевую) степень логарифм делится на этот показатель степени:
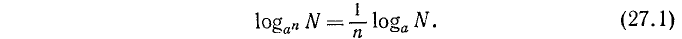
Доказательство:
Пользуясь оснозным тождеством (26.1), находим последовательно
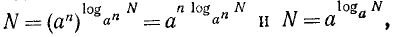
откуда
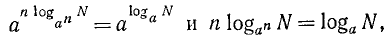
т.е. 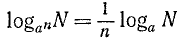 , что и требовалось получить.
, что и требовалось получить.
Следствие:
При возведении основания и числа в одну и ту же (ненулевую) степень логарифм не изменяется.
Доказательство:
Последовательно применяя свойства 8 и 6, находим
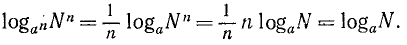
Пример:
Выразить через логарифм по основанию 3:
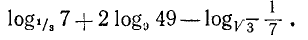
Решение:
Имеем l
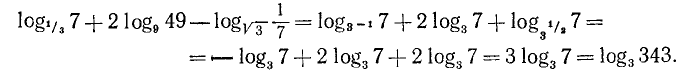
Пример:
Вычислить 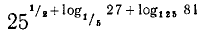 .
.
Решение:
Перепишем данное выражение, сведя основания логарифмов к 5:
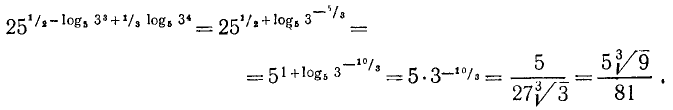
Свойство:
Если а, N положительны и оба не равны единице, то
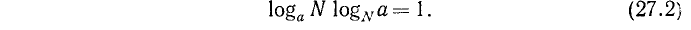
Доказательство:
Напишем основное тождество
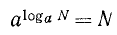
и прологарифмируем обе его части по основанию N (это возможно, так как 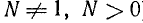 ), применив свойства 4 и 1:
), применив свойства 4 и 1:
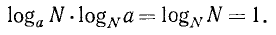
Свойство 9 доказано.
Следующее важнейшее свойство дает общее правило перехода от логарифмов с основанием а к логарифмам с другим основанием b:
Свойство:
Имеет место следующее равенство:
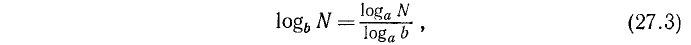
которое также в силу свойства 9 пишут в виде
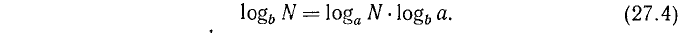
Коэффициент 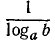 в формуле (27.3) называют модулем перехода от логарифмов по основанию а к логарифмам по основанию b.
в формуле (27.3) называют модулем перехода от логарифмов по основанию а к логарифмам по основанию b.
Доказательство:
Напишем снова основное тождество
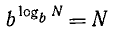
и прологарифмируем обе его части по основанию а:
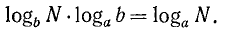
Отсюда прямо вытекает требуемое равенство (27.3).
Пример:
Упростить выражение 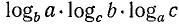 .
.
Решение:
В силу (27.4) и (27.2) имеем
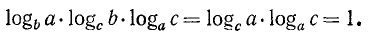
Десятичные логарифмы
Характеристика и мантисса десятичного логарифма
Десятичным логарифмом числа называется его логарифм по основанию 10. Кроме общего обозначения 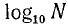 для десятичных логарифмов обычно применяют сокращенное обозначение lg N.
для десятичных логарифмов обычно применяют сокращенное обозначение lg N.
Десятичные логарифмы широко применяются в приближенных вычислениях; в связи с этим имеются подробные и весьма точные таблицы десятичных логарифмов. Читателю известны четырехзначные таблицы В. М. Брадиса, применяемые при изучении логарифмов в школьном курсе математики. Об использовании таблиц функций вообще говорится специально в п. 220.
Для пользования таблицами десятичных логарифмов и для их применения к приближенным вычислениям нам потребуются некоторые свойства и понятия, относящиеся к десятичным логарифмам.
Рассмотрим все числа вида 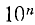 , где n — целое число:
, где n — целое число:
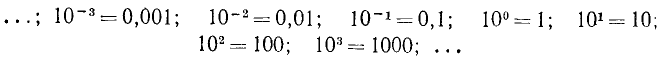
Будем говорить, что эти числа представляются единицей с нулями (с последующими нулями, если n > 0, и с предшествующими нулями, если n < 0). Из определения логарифма видно, что эти числа имеют целые десятичные логарифмы: 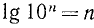 . Удобно сформулировать следующее правило:
. Удобно сформулировать следующее правило:
Десятичный логарифм числа, представляемого единицей с нулями, равен числу нулей в этом числе, если оно есть единица с последующими нулями, и числу нулей с противоположным знаком, если оно есть единица с предшествующими нулями.
Например:
lg 0,0001= —4, Ig 0,01= — 2, lg 1000 = 3, lg 1000000 = 6.
Десятичный логарифм любого числа, не равного целой степени десяти, является числом дробным (вообще говори, иррациональным).
Напомним, что всякое число (рациональное или иррациональное) однозначно разлагается на сумму своей целой части и дробней части (см. пп. 4, 6). При этом целой частью данного числа называется наибольшее целое число, не превосходящее данного; дробная часть любого числа заключена между нулем и единицей:
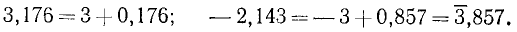
Введем теперь следующее.
Определение:
Для любого положительного числа целая часть десятичного логарифма называется характеристикой, а дробная часть — мантиссой этого логарифма.
Характеристику логарифма любого положительного числа можно найти точно, и делается это с помощью простого правила. Действительно, пусть дано число N > 0; тогда можно указать такие две степени числа 10 с последовательными целыми показателями n и n + 1, между которыми находится данное число N:

Прологарифмируем эти неравенства по основанию 10:
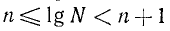
в соответствии со свойством 5 логарифмов (п. 26). Отсюда следует, что целая часть, т. е. характеристика lg N, равна n: lg N = n, … Многоточием обозначены неизвестные десятичные знаки мантиссы, т.е. дробной части lg N. При этом в случае n < 0 применяется искусственная форма записи lg N (п. 4).
Для формулировки соответствующего правила рассмотрим два случая: N > 1 и N < 1.
Пусть N > 1 (десятичный логарифм lg N в этом случае положителен). Обозначим через k число цифр в записи целой части N. Ясно, что в этом случае
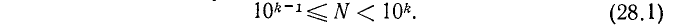
Например, для N = 378,6 (трехзначная целая часть)
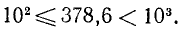
Логарифмируя неравенства (28.1), получаем
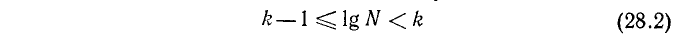
и видим, что характеристика lg N равна k — 1 (например, характеристика логарифма 378,6 равна 2).
Итак, характеристика десятичного логарифма числа, больишго единицы, на единицу меньше количества цифр его целой части. Например:
lg 3,524 — 0, …; lg 47,01 — 1; …, Ig 936,3 — 2, …
Пусть теперь положительное число N меньше единицы: 0 < N < 1. Тогда lg N по свойству 4 из п. 26 будет отрицательным числом: числа N и 10 в рассматриваемом случае лежат по разные стороны от единицы.
Запись числа N начинается в этом случае с нуля целых; за этим нулем может следовать еще несколько нулей перед первой отличной от нуля цифрой числа. Если число нулей перед первой ненулевой цифрой (включая и нуль целых) равно l, то
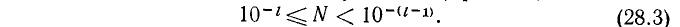
Например:

Неравенства (28.3) показывают, что
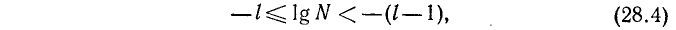
т.е. характеристика логарифма lg N равна —l.
Итак, характеристика десятичного логарифма положительного числа, меньшего единицы, равна взятому со знаком минус числу нулей в данном числе, предшествующих первой значащей цифре, включая и нуль целых.
Например:
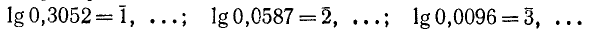
Мы выяснили, что характеристика десятичного логарифма числа определяется непосредственно по виду самого числа, если оно целое или представлено в виде десятичной дроби. Для определения характеристики, таким образом, не нужны никакие вычисления (и таблицы). Что же касается мантиссы, то она, как правило, берется из таблиц (например, из таблиц Брадиса). При этом следует пользоваться одним замечательным свойством мантиссы: если в логарифмируемом числе перенести запятую на любое количество знаков влево или вправо, то мантисса десятичного логарифма от этого не изменится (изменится только характеристика логарифма). В самом деле, перенести в числе запятую — это значит умножить его на некоторую целую (положительную или отрицательную) степень числа 10. Например, при переносе запятой на 2 знака вправо число умножится на 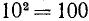 , а при переносе запятой на 2 знака влево оно умножится на
, а при переносе запятой на 2 знака влево оно умножится на 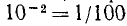 . Пусть
. Пусть
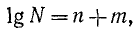
где n — характеристика, а m — мантисса этого логарифма. После переноса запятой в числе N на k знаков получится число 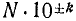 (верхний знак относится к случаю переноса запятой вправо, а нижний — к случаю переноса запятой влево). На основании правил логарифмирования (п. 25) имеем
(верхний знак относится к случаю переноса запятой вправо, а нижний — к случаю переноса запятой влево). На основании правил логарифмирования (п. 25) имеем
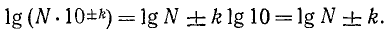
Но k — целое число, так что прибавление ± k к lg N может отразиться лишь на его характеристике:

Из рассмотренного можно заключить, что если числа записаны с помощью одних и тех же и одинаково расположенных цифр и отличаются одно от другого только местоположением в них запятой, то десятичные логарифмы таких чисел имеют одну и ту же мантиссу (но, конечно, разные характеристики!). Таковы, например, числа 42,59, 4,259, 0,4259, 0,04259 и т. д.
В качестве примера найдем без таблиц разность lg 28,76 — lg 0,002876 .
Логарифмы, из которых составлена данная разность, отличаются лишь характеристиками, а мантиссы у них одинаковы и при вычитании взаимно уничтожаются. Поэтому искомая разность логарифмов равна разности их характеристик: lg 28,76 — lg 0,002876 = 1 — ( — 3) = 1 + 3 = 4. . Этот пример можно решить и так:
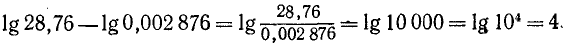
Применение десятичных логарифмов к вычислениям
Как уже было указано выше, над логарифмами чисел производятся более простые действия, чем над самими числами: умножение заменяется сложением, деление —вычитанием, возведение в степень — умножением на показатель степени и т. д. В сочетании с наличием удобных таблиц десятичных логарифмов это позволяет широко использовать десятичные логарифмы для упрощения вычислений.
Пример:
Вычислить с помощью таблиц: а) 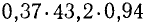 ; б)
; б) 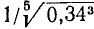 .
.
Решение:
а) Обозначим искомое число через х. С помощью правила логарифмирования произведения (26.5) найдем
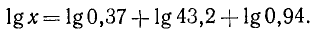
Логарифмы в правой части равенства найдем по таблицам, запишем в столбец и сложим:
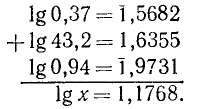
Дадим пояснение к тому, как получена характеристика: в конце действия сложения мантисс получаются две целых и одна десятая. Ясно, что одну десятую мы оставляем мантиссе — так определяется ее первая цифра, а две единицы отдаем характеристике: 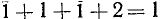 . Теперь по найденному lg x из таблиц получаем х = 15,03. Характеристика lg x оказалась равной 1, а она, как известно, на единицу меньше числа цифр в целой части логарифмируемого числа. Поэтому в числе 1503, взятом из таблиц, мы и отделили два знака целой части.
. Теперь по найденному lg x из таблиц получаем х = 15,03. Характеристика lg x оказалась равной 1, а она, как известно, на единицу меньше числа цифр в целой части логарифмируемого числа. Поэтому в числе 1503, взятом из таблиц, мы и отделили два знака целой части.
б) Используя правила логарифмирования степени и корня (п. 26), найдем
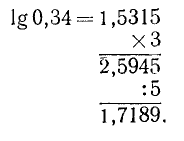
Мы получили 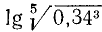 . Характеристика
. Характеристика 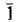 найдена так: в промежуточном результате характеристика
найдена так: в промежуточном результате характеристика 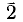 получилась от сложения
получилась от сложения 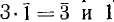 (которая «набежала» от умножения первой цифры 5 мантиссы на 3); далее, число
(которая «набежала» от умножения первой цифры 5 мантиссы на 3); далее, число 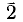 на 5 не делится без остатка; поэтому к
на 5 не делится без остатка; поэтому к 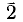 мы прибавили
мы прибавили 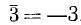 , а чтобы не изменить логарифма, тут же прибавили 3 к мантиссе.
, а чтобы не изменить логарифма, тут же прибавили 3 к мантиссе.
Далее,
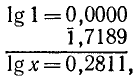
откуда x = 1,911.
Пользуясь десятичными логарифмами, можно также находить логарифмы чисел по произвольному основанию. Рассматривая свойства логарифмов, мы ввели в п. 26 понятие модуля перехода. Именно, модулем перехода от логарифмов по основанию а к логарифмам но основанию b названо число 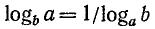 , являющееся множителем пропорциональности между логарифмами с основаниями а и Ь:
, являющееся множителем пропорциональности между логарифмами с основаниями а и Ь:
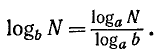
Если теперь положить здесь а = 10, то логарифм числа N по основанию b выразится через десятичные логарифмы чисел N и b:
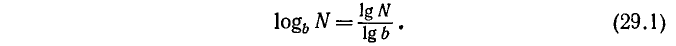
Итак, мы получили следующее правило: для вычисления недесятичного логарифма по таблице десятичных логарифмов нужно десятичный логарифм данного числа разделить на десятичный логарифм данного основания.
Число 1 / lg a является модулем перехода от логарифмов по основанию а к логарифмам по основанию 10 (к десятичным логарифмам).
Пример:
Найти a) 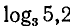 ; б)
; б) 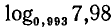 .
.
Решение:
а) В соответствии с формулой (29.1) запишем:
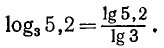
Найдем lg 5,2 и lg 3 из таблиц Брадиса и получим
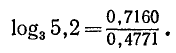
Разделить у этой дроби числитель на знаменатель (чтобы получить ответ в виде десятичной дроби) можно «вручную», а можно опять-таки с помощью таблиц. Обозначим для этого
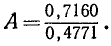
Далее найдем
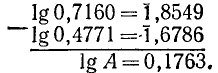
Отсюда 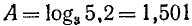 .
.
б) Имеем
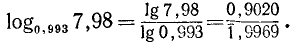
Представим знаменатель этой дроби в естественной форме:
1,9969 = — 1 + 0,9969 = —0,0031,
и, таким образом, найдем
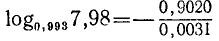
(отрицательность логарифма объясняется тем, что число 7,98 и основание 0,993 лежат по разные стороны от единицы (свойство 4 п.26)). Чтобы выполнить деление с помощью таблиц логарифмов, положим
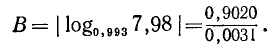
Отсюда
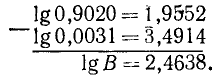
Найдем теперь, что В = 290,9 и, следовательно.
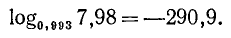
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

