Оглавление:
Пример:
Найти положительный корень уравнения 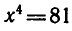
( По определению арифметического корня имеем- 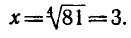
Пример:
Решить уравнение 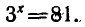
Запишем данное уравнение так: 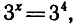 откуда х = 4. В задаче 1 неизвестным является основание степени, а в задаче 2 — показатель степени; Способ решения задачи 2 состоял в том, что левую и правую части уравнения удалось представить в виде степени с одним тем же основанием 3. Но уже, например, уравнение
откуда х = 4. В задаче 1 неизвестным является основание степени, а в задаче 2 — показатель степени; Способ решения задачи 2 состоял в том, что левую и правую части уравнения удалось представить в виде степени с одним тем же основанием 3. Но уже, например, уравнение 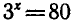 таким способом решить не удается. Однако вы знаете, что это уравнение имеет корень. Чтобы уметь решать такие уравнения, вводите понятие логарифма числа.
таким способом решить не удается. Однако вы знаете, что это уравнение имеет корень. Чтобы уметь решать такие уравнения, вводите понятие логарифма числа.
Уравнение 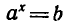 , где а > 0 , а
, где а > 0 , а 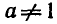 , имеет единственный корень. Этот корень называют ло-1
, имеет единственный корень. Этот корень называют ло-1
гарифмом числа b по основанию а и обозначают 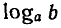 . Например
. Например
корнем уравнения 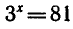 является число 4, т. е.
является число 4, т. е. 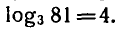
Лаплас Пьер Симон (1749— 1827)— французский математик, физик и астроном, адъюнкт Французской Академии Наук. После Великой Французской революции принимал активное участие в реорганизации системы образования. Важнейшие направления его исследований — математика, небесная механика и математическая физика. Один из создателей теории вероятностей.
Итак, логарифмом положительного числа b по основанию а, где
а > 0, 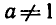 , называется показатель степени, и которую надо возвести число а, чтобы получить b .
, называется показатель степени, и которую надо возвести число а, чтобы получить b .
Например, 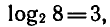 так как
так как 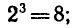
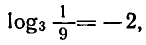
так как 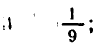
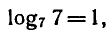 так как
так как 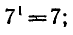
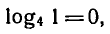
так как 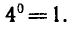
Определение логарифма можно кратко записать так:
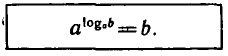
Это равенство справедливо при b > 0, а > 0, 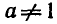 . Его обычно
. Его обычно
называют основным логарифмическим тождеством.
Например, 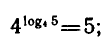
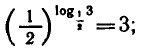
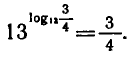
С помощью основного логарифмического тождества можио
показать, например, что 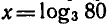 является корнем уравнения
является корнем уравнения 
В самом деле, 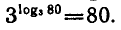
Действие нахождения логарифма числа называют логарифмированием.
Пример:
Вычислить 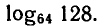
Обозначим 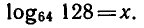 По определению логарифма
По определению логарифма 
Так как 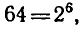
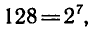 то
то 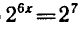 ,
,
откуда 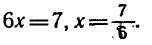
Ответ. 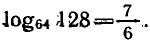
Пример:
Вычислить 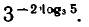
Используя свойства степени и основное логарифмическое равенство, находим:
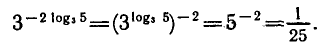
Пример:
Решить уравнение 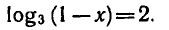
Но определению логарифма 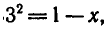 откуда х = — 8.
откуда х = — 8.
Пример:
При каких значениях х существует 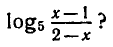
Так как основание логарифма 5 > 0 и 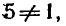 то данный логарифм
то данный логарифм
существует тогда и только тогда, когда 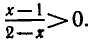
Получено неравенство, находим 1 < х < 2.
Свойства логарифмов
При выполнении преобразований выражений, содержащих логарифмы, при вычислениях и при решении уравнений часто используются различные свойства логарифмов. Рассмотрим основные из них.
Пусть а>0, 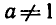 , b > 0, с > 0, r —любое действительное число. Тогда справедливы формулы:
, b > 0, с > 0, r —любое действительное число. Тогда справедливы формулы:
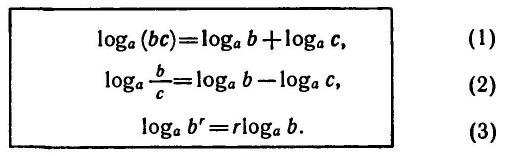
По основному логарифмическому тождеству

1) Перемножая равенства (4) и (5), получаем:
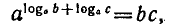
откуда по определению логарифма 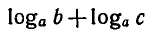
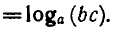
Формула (1) доказана.
2) Разделив равенства (4) и (5), получим:
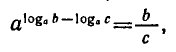
откуда по определению логарифма следует формула (2).
3) Возводя основное логарифмическое тождество 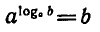
в степень с показателем r, получаем:
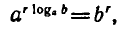
откуда по определению логарифма следует формула (3). •
Приведем примеры применения формул (1) — (3):
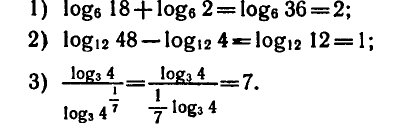
Пример:
Вычислить 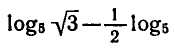
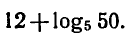
Применяя формулы (1) — (3), находим:
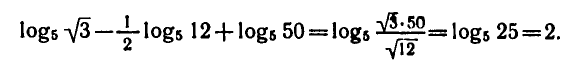
Десятичные и натуральные логарифмы
Для логарифмов чисел составлены специальные таблицы
(таблицы логарифмов). Логарифмы вычисляют также с помощью
микрокалькулятора. И в том и в другом случае находятся только
десятичные или натуральные логарифмы.
Десятичным логарифмом числа называют логарифм этого числа по основанию 10 и пишут lg b вместо 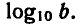
Натуральным логарифмом числа называют логарифм этого числа по основанию e, где е — иррациональное число, приближенно равное 2,7. При этом пишут ln e вместо 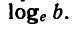
Иррациональное число е играет важную роль в математике
и ее приложениях. Число е можно представить как сумму:
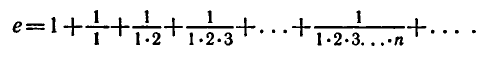
Вычисление числа е на микрокалькуляторе проводится по
программе:
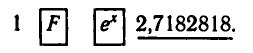
Вычисления на микрокалькуляторе lg b и ln b проводятся
соответственно по программам:
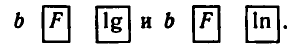
Например, вычисляя lg 13, получаем:
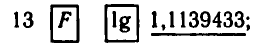
вычисляя ln 13, получаем:
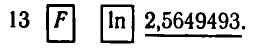
Оказывается, что достаточно знать значения только десятичных или только натуральных логарифмов чисел, чтобы находить
логарифмы чисел по любому основанию. Для этого используется
формула перехода от логарифма по одному основанию к
логарифму по другому основанию:

где b > 0, а > 0 , 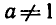 , с > 0 ,
, с > 0 , 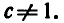
Докажем справедливость формулы (1).
Запишем основное логарифмическое тождество 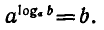
Возьмем от обеих его частей логарифмы по основанию с:
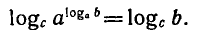
Используя свойство логарифма степени, получаем:
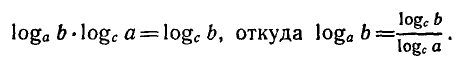
Из формулы (1) при с = 10 и с = е получаются формулы
перехода к десятичным и натуральным логарифмам:
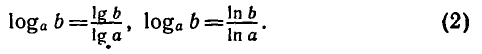
Пример:
С помощью микрокалькулятора МК-54 вычислить 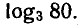
1) С помощью десятичных логарифмов:

2) С помощью натуральных логарифмов:
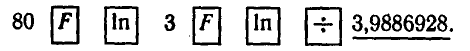
Ответ. 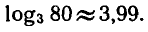 ▲
▲
Формула перехода от одного основания логарифма к другому
иногда используется при решении уравнений.
Пример:
Решить уравнение 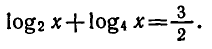
По формуле перехода
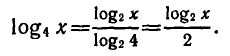
Поэтому уравнение принимает вид 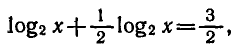 откуда
откуда 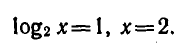 ▲
▲
Пример:
Двухпроцентный вклад в Сбербанк, равный
а рублям, через п лет становится равным 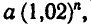 а
а
трехпроцентный вклад становится равным 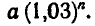
Через сколько лет каждый из вкладов удвоится?
1) Для первого вклада 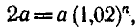 откуда
откуда 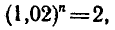
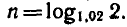
2. Вычисления проведем на МК-54:
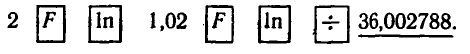
2) Для второго вклада 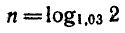 и программа вычислений
и программа вычислений
такова:

Ответ. По первому вкладу приближенно через 36 лет, а
по второму — через 23,5 года.
Логарифмическая функция и ее график
В математике и ее приложениях часто встречается
логарифмическая функция
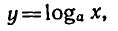
где а — заданное число, а > 0, 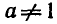 .
.
Логарифмическая функция обладает следующими свойствами:
1) Область определения логарифмической функции — множество всех положительных чисел.
Это следует из определения логарифма, так как выражение 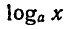 ; имеет смысл только при x > 0.
; имеет смысл только при x > 0.
2) Множество значений логарифмической функции — множество R всех действительных чисел.
Это следует из того, что для любого действительного числа
b есть такое положительное число х, что 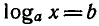 , т. е. уравнение
, т. е. уравнение 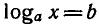 имеет корень. Такой корень существует и равен
имеет корень. Такой корень существует и равен 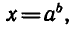 так как
так как 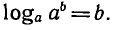
3) Логарифмическая функция 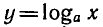 является возрастающей на промежутке x > 0, если а > 1 , и убывающей, если
является возрастающей на промежутке x > 0, если а > 1 , и убывающей, если
0 < а < 1 .
Пусть а > 1. Докажем, что если 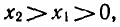 то
то  т. е.
т. е. 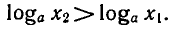
Пользуясь основным логарифмическим
тождеством, условие 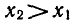 можно записать так:
можно записать так:  Из этого неравенства по свойству степени с основанием a > 1 следует, что
Из этого неравенства по свойству степени с основанием a > 1 следует, что 
Пусть 0 < a < 1 . Докажем, что если 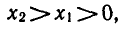 то
то 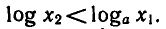 Записав условие
Записав условие  в виде
в виде 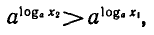 получим
получим 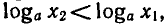 так как 0 < а < 1 .
так как 0 < а < 1 .
4) Если а > 1, то функция 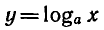 принимает положительные значения при х >1, отрицательные — при 0 < x < ;1. Если 0 < а < 1 , то функция
принимает положительные значения при х >1, отрицательные — при 0 < x < ;1. Если 0 < а < 1 , то функция 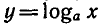 принимает положительные значения при 0 < x < 1, отрицательные — при х > 1.
принимает положительные значения при 0 < x < 1, отрицательные — при х > 1.
Это следует из того, что функция 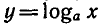 принимает
принимает
значение, равное нулю, при x = 1 и является возрастающей на промежутке x > 0, если а > 1, и убывающей, если 0 < а < 1 .
Из рассмотренных свойств логарифмической функции 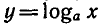 следует, что ее график расположен правее оси Оу и имеет вид, указанный на рисунке 7, если а > 1, и на рисунке 8, если 0 < a < 1 .
следует, что ее график расположен правее оси Оу и имеет вид, указанный на рисунке 7, если а > 1, и на рисунке 8, если 0 < a < 1 .
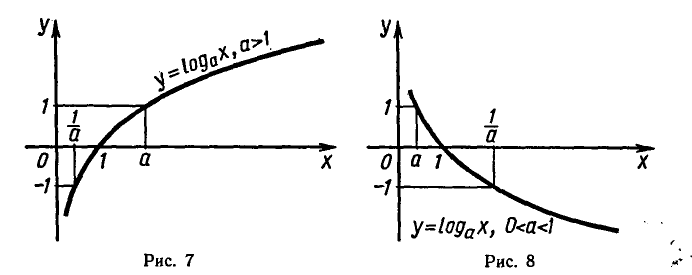
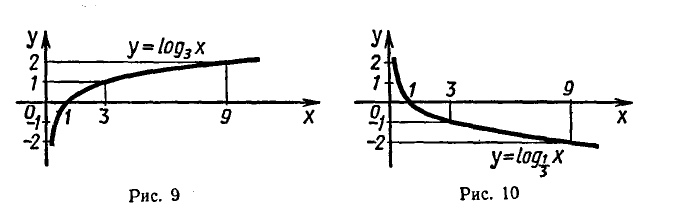
На рисунке 9 изображен график функции 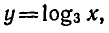 а на рисунке 10 — график функции
а на рисунке 10 — график функции 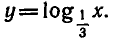
Отметим, что график любой логарифмической функции 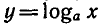 проходит через точку ( 1 ; 0). При решении уравнений часто используется следующая теорема:
проходит через точку ( 1 ; 0). При решении уравнений часто используется следующая теорема:
Теорема:
Если 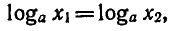 где a > 0,
где a > 0, 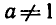 ,
,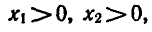 то
то 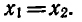
Предположим, что 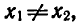 например
например 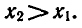 Если a > 1, то из неравенства
Если a > 1, то из неравенства  следует, что
следует, что  если
если
0 < а < 1 , то из неравенства  следует, что
следует, что 
В обоих случаях получилось противоречие с условием 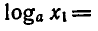
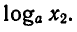 Следовательно,
Следовательно, 
Пример:
Решить уравнение 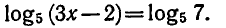
Используя доказанную теорему, получаем Зх — 2 = 7, откуда Зх = 9,
х = 3.
Пример:
Решить неравенство 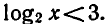
Пользуясь тем, что 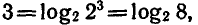 запишем данное неравенство так:
запишем данное неравенство так: 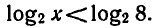 Так как функция
Так как функция 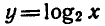 определена при x > 0 и возрастает, то неравенство
определена при x > 0 и возрастает, то неравенство 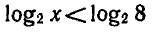 выполняется при х > 0 и x < 8.
выполняется при х > 0 и x < 8.
Ответ. 0 < х < 8 .
Пример:
Решить неравенство 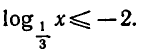
Запишем данное неравенство так: 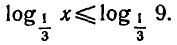
Функция 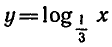 определена при
определена при 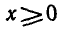 и убывает, поэтому неравенство выполняется при х > 0 и
и убывает, поэтому неравенство выполняется при х > 0 и 
Ответ. 
Обратная функция
Известно, что зависимость скорости v от времени t движения
тела, брошенного вверх с начальной скоростью 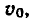 выражается
выражается
формулой 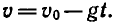
Из этой формулы можно найти обратную зависимость — времени от скорости: 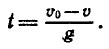 Функцию
Функцию 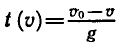 называют обратной к функции
называют обратной к функции 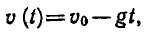 а функцию v (t) — обратной к функции t (v ). Отметим, что в этом примере каждому значению t соответствует единственное значение v и, наоборот, каждому значению v соответствует единственное значение t.
а функцию v (t) — обратной к функции t (v ). Отметим, что в этом примере каждому значению t соответствует единственное значение v и, наоборот, каждому значению v соответствует единственное значение t.
Рассмотрим теперь показательную и логарифмическую
функции. Обозначим символом f(х) показательную функцию,
a g (х) — логарифмическую функцию:
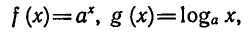
где а — заданное число, а > 0, 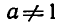 .
.
Решим уравнение 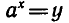 относительно х. По определению
относительно х. По определению
логарифма 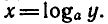 Поменяв в этом равенстве местами х и у,
Поменяв в этом равенстве местами х и у,
получим логарифмическую функцию 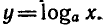 Функцию
Функцию 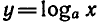 называют обратной к функции
называют обратной к функции 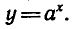 Если из равенства
Если из равенства 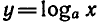 найти х, то получим
найти х, то получим 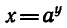 , а поменяв местами х и у — показательную функцию
, а поменяв местами х и у — показательную функцию 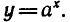 Функцию
Функцию 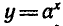 называют обратной к функции
называют обратной к функции 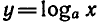 . Поэтому функции f (х) и g (х) называют взаимно обратными.
. Поэтому функции f (х) и g (х) называют взаимно обратными.
Вообще если функция y = f(x) задана формулой, то для
нахождения обратной функции нужно решить уравнение
f (x) = у относительно х и затем поменять местами х и у.
Если уравнение f(x)= y имеет более чем один корень, то
функции, обратной к y = f (x), не существует.
Например, функция 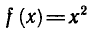 не имеет обратной, так как
не имеет обратной, так как
уравнение 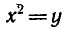 имеет два корня
имеет два корня 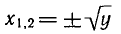 для любого
для любого
у > 0.
Если функцию 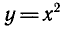 рассматривать только на промежутке
рассматривать только на промежутке 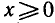 , то она будет иметь обратную
, то она будет иметь обратную 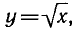 так как уравнение
так как уравнение 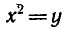 при
при 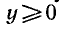 имеет только один неотрицательный корень.
имеет только один неотрицательный корень.
Пример:
Найти функцию, обратную к функции 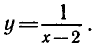
Решая это уравнение относительно х, получаем 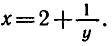
Заменив х на у и у на х, находим 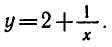
В этой задаче область определения функции 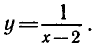 есть
есть
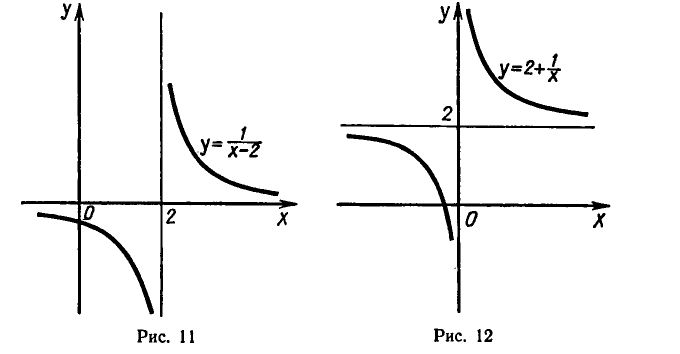
множество действительных чисел, не равных 2, а множество ее значений — все действительные числа, не равные 0. График этой
функции изображен на рисунке 11.
Для обратной функции 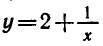 область определения —
область определения —
множество действительных чисел, не равных 0, а множество значений — все действительные числа, не равные 2. График обратной функции изображен на рисунке 12.
Вообще область определения обратной функции совпадает
с множеством значений исходной функции, а множество
значений обратной функции совпадает с областью определения
исходной функции.
Можно показать, что если функция имеет обратную, то
график обратной функции симметричен графику данной
функции относительно прямой у = х.
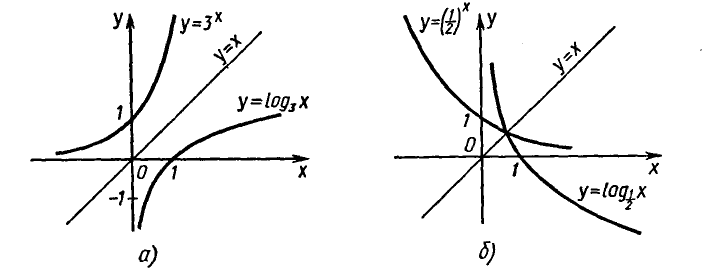
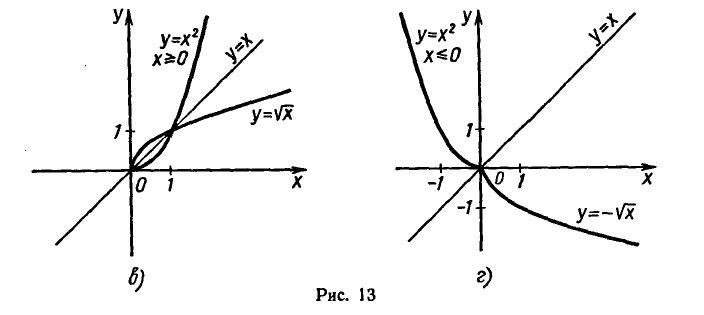
Примеры графиков взаимно обратных функций показаны на
рисунке 13.
Логарифмические уравнения
Пример:
Решить уравнение
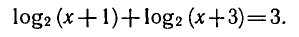
( 1 )
Предположим, что х — такое число, при котором равенство ( 1 ) является верным, т. е. х — корень уравнения ( 1 ).
Тогда по свойству логарифма верно равенство
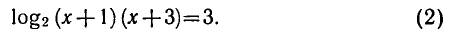
Из этого равенства по определению логарифма получаем:
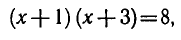
откуда 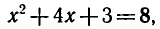 т. е.
т. е. 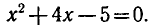
Последнее равенство верно, если 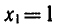 или
или 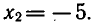
Итак, предположив, что число х — корень уравнения (1),
мы показали, что х может быть равным или 1, или —5.
Проверим, являются ли эти числа корнями уравнения (1).
Подставляя в левую часть данного уравнения х = 1 , получаем
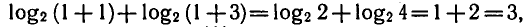
т. е. х = 1 — корень уравнения ( 1 ).
При х = — 5 числа х + 1 и х + З отрицательны, и поэтому
левая часть уравнения ( 1 ) не имеет смысла, т. е. х = — 5 не
является корнем этого уравнения.
Ответ. х = 1 .
Заметим, что х = — 5 является корнем уравнения (2), так
как
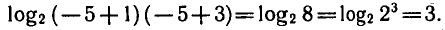
Получилось, что число х = 1 является корнем обоих уравнений
( 1 ) и (2), а число х = — 5 не является корнем уравнения (1 ), но является корнем уравнения (2). Таким образом, при переходе от уравнения (1) к уравнению (2 ) корень х = 1 сохранился и появился посторонний корень х = —5. В этом случае уравнение (2) называют следствием уравнения (1 ).
Если все корни первого уравнения являются корнями второго уравнения, то второе уравнение называется следствием первого уравнения.
Отметим, что в уравнении, которое является следствием
данного, не всегда появляются посторонние корни; важно лишь
то, чтобы корни исходного уравнения не терялись.
В большинстве случаев, как и в задаче 1, уравнения решаются постепенным переходом к более простым уравнениям,
которые являются следствием исходного уравнения. В таких
случаях после нахождения корней необходима их проверка.
Пример:
Решить уравнение
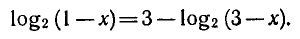
Перенесем логарифм из правой части в левую;
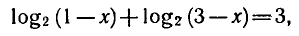
откуда
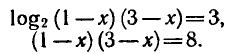
Решая это уравнение, получаем 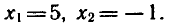
Число  не является корнем исходного уравнения, так
не является корнем исходного уравнения, так
как при x = 5 левая и правая части уравнения теряю т смысл.
Проверка показывает, что число х = — 1 является корнем
исходного уравнения.
Ответ. х = — 1. ▲
Пример:
Решить уравнение
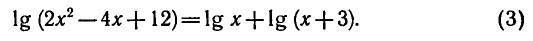
По свойству логарифмов
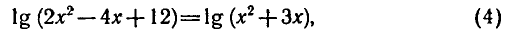
откуда
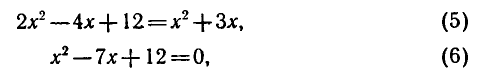
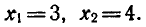 Проверка показывает, что оба значения x
Проверка показывает, что оба значения x
являются корнями исходного уравнения.
Ответ. 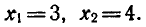 ▲
▲
Проверкой можно убедиться в том, что числа 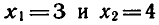 являются корнями не только уравнений (6) и (3), но и уравнений
являются корнями не только уравнений (6) и (3), но и уравнений
(4) и (5). Все эти уравнения других корней не имеют. Такие
уравнения называют равносильными.
Уравнения, имеющие одно и то же множество корней,
называют равносильными.
В частности, два уравнения, не имеющие корней, являются
равносильными.
Отметим, что любое из двух равносильных уравнений является следствием другого.
Большинство уравнений, с которыми вы встречались в курсе
алгебры, решались с помощью перехода от данного уравнения
к равносильному. Так решались уравнения первой степени с
одним неизвестным, квадратные уравнения, показательные
уравнения.
Напомним, что уравнение заменяется ему равносильным при
следующих преобразованиях:
любой член уравнения можно переносить из одной части
в другую, изменив его знак на противоположный;
обе части уравнения можно умножить или разделить на
одно и то же число, не равное нулю.
Однако не при любом преобразовании уравнение заменяется
на равносильное. Например, при возведении обеих частей
уравнения 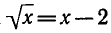 в квадрат получается уравнение
в квадрат получается уравнение 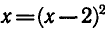 , которое является следствием первого, но не равносильным ему. Поэтому после решения второго уравнения необходимо проверить, являются ли его корни корнями исходного уравнения.
, которое является следствием первого, но не равносильным ему. Поэтому после решения второго уравнения необходимо проверить, являются ли его корни корнями исходного уравнения.
Пример:
Решить уравнение
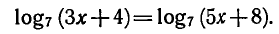
Приравнивая выражения, стоящие под знаком логарифма,
получаем:
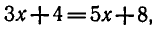
откуда х = — 2. Выполняя проверку, убеждаемся, что при х = — 2
левая и правая части исходного уравнения не имеют смысла.
Ответ. Корней нет.
Здесь посторонний корень появился потому, что при переходе
от равенства логарифмов к равенству чисел не было учтено
требование, чтобы эти числа были положительными.
Рассмотренные примеры логарифмических уравнений
показывают, что при их решении с использованием свойств логарифмов получаются уравнения, которые являются следствиями исходного. Поэтому необходима проверка, которая позволяет
обнаружить посторонние корни. ▲
Пример:
Решить уравнение
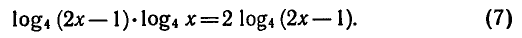
Преобразуем данное уравнение:
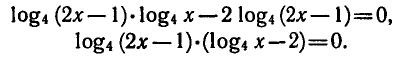
Приравнивая каждый из множителей левой части уравнения
к нулю, получаем:
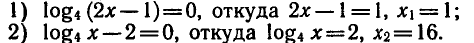
Проверка показывает, что оба значения х являются корнями
исходного уравнения.
Ответ. 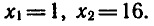
Отметим, что если обе части уравнения (7) разделить на
выражение 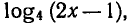 то будет потерян корень х = 1.
то будет потерян корень х = 1.
Вообще при делении обеих частей уравнения на выражение, содержащее неизвестное, может произойти потеря корней.
Поэтому уравнение, обе части которого содержат общий
множитель, решают переносом всех членов в одну часть и
разложением на множители.
При решении уравнений главное не потерять корни, а наличие посторонних корней можно установить проверкой. Поэтому важно следить за тем, чтобы при преобразовании уравнения каждое следующее уравнение было следствием предыдущего.
Пример:
Решить систему уравнений
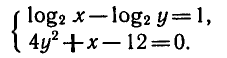
Из первого уравнения выразим х через 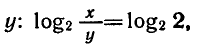
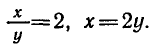 Подставив х = 2у во второе уравнение системы,
Подставив х = 2у во второе уравнение системы,
получим 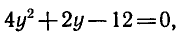 откуда
откуда 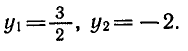
Найдем значения х : 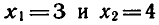 Проверкой убеждаемся,
Проверкой убеждаемся,
что 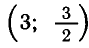 — решение системы, а ( — 4; —2) — постороннее
— решение системы, а ( — 4; —2) — постороннее
решение.
Ответ. 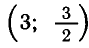
Логарифмические неравенства
При изучении логарифмической функции рассматривались
неравенства вида 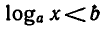 и
и 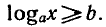
Приведем примеры решения более сложных логарифмических неравенств. Обычный способ решения таких неравенств заключается в переходе от них к более простому неравенству или системе неравенств, имеющей то же самое множество решений.
Пример:
Решить неравенство

Правая часть данного неравенства имеет смысл при всех значениях x, а левая часть — при x + 1 > 0, т. е. при х > — 1.
Промежуток х > — 1 называют областью определения неравенства (1). Так как логарифмическая функция с основанием
10 возрастающая, то неравенство ( 1 ) при условии x + 1 > 0
выполняется, если 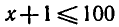 (так как 2 = lg 100). Таким
(так как 2 = lg 100). Таким
образом, неравенство ( 1 ) равносильно системе неравенств
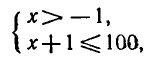
т. е. неравенство ( 1 ) и система (2) имеют одно и то же множество решений. Решая систему (2), находим 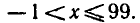
Пример:
Решить неравенство
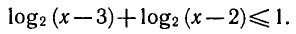
Логарифмическая функция определена при положительных значениях аргумента, поэтому левая часть неравенства имеет смысл при х — 3 > 0 и х — 2 > 0.
Следовательно, областью определения этого неравенства является промежуток х > 3 . По свойствам логарифма неравенство (3)
при х > 3 равносильно неравенству
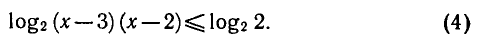
Логарифмическая функция с основанием 2 возрастающая. Поэтому при х > 3 неравенство (4) выполняется, если 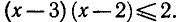
Таким образом, исходное неравенство (3) равносильно системе неравенств
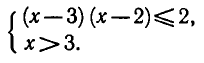
Решая первое неравенство этой системы, получаем 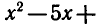
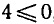 откуда
откуда 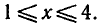
Совмещая этот отрезок с промежутком х > 3 , получаем 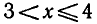 (рис. 14).
(рис. 14).
Пример:
Решить неравенство
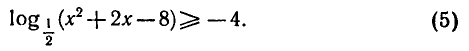
Область определения неравенства находится из условия
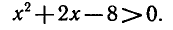
Неравенство (5) можно записать в следующем виде:
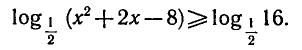
Так как логарифмическая функция с основанием 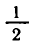 является
является
убывающей, то для всех х из области определения неравенства
получаем:
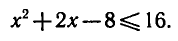
Таким образом, исходное неравенство (5) равносильно системе неравенств
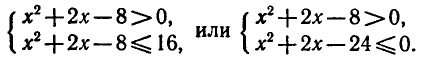

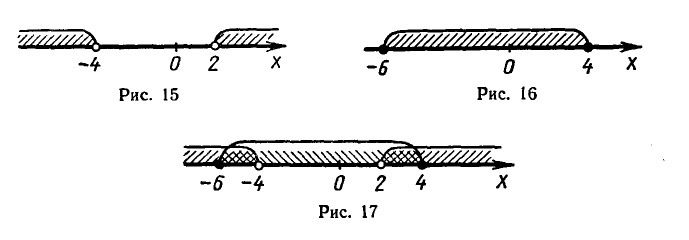
Решая первое квадратное неравенство, получаем х < — 4, х > 2 (рис. 15). Решая второе квадратное неравенство, получаем  (рис. 16). Следовательно, оба неравенства систе
(рис. 16). Следовательно, оба неравенства систе
мы выполняются одновременно при 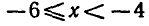 и при
и при 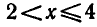 . (рис. 17).
. (рис. 17).
Ответ. 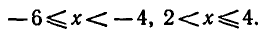
Определение:
Логарифмом числа а по основанию b называется показатель степени, в которую надо возвести а, чтобы получить число b.
В качестве основания мы будем всегда брать положительное число а, отличное от 1.
В записи b = 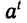 число а является основанием степени, t — показателем, b — степенью. Число t — это показатель степени, в которую надо возвести основание а, чтобы получить число b. Следовательно, t — это логарифм числа b по основанию а:
число а является основанием степени, t — показателем, b — степенью. Число t — это показатель степени, в которую надо возвести основание а, чтобы получить число b. Следовательно, t — это логарифм числа b по основанию а:
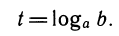
Можно сказать, что формулы 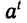 = b и t =
= b и t = 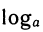 равносильны, выражают одну и ту же связь между числами a, t и b (при а>0, а ≠ 1, b>0). Число t — произвольно, никаких ограничений на показатель степени не накладывается.
равносильны, выражают одну и ту же связь между числами a, t и b (при а>0, а ≠ 1, b>0). Число t — произвольно, никаких ограничений на показатель степени не накладывается.
Подставляя в равенство 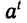 = b запись числа t в виде логарифма, получаем равенство, называемое основным логарифмическим тождеством:
= b запись числа t в виде логарифма, получаем равенство, называемое основным логарифмическим тождеством:
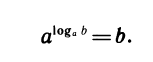
Представляя в равенстве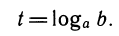 выражение b в виде степени, получим еще одно тождество:
выражение b в виде степени, получим еще одно тождество:
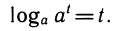
Свойства логарифмов
Теорема:
Верны следующие тождества, выражающие свойства логарифмов:
1)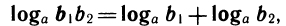 , т. е. логарифм произведения равен сумме логарифмов множителей;
, т. е. логарифм произведения равен сумме логарифмов множителей;
2) 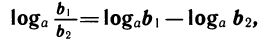 т. е. логарифм дроби равен разности логарифмов числителя и знаменателя;
т. е. логарифм дроби равен разности логарифмов числителя и знаменателя;
3) 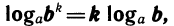 т. е. логарифм степени равен показателю степени, умноженному на логарифм основания.
т. е. логарифм степени равен показателю степени, умноженному на логарифм основания.
Доказательство:
Свойства логарифмов выводятся из свойств степеней с помощью основного логарифмического тождества, выражающего определение логарифма. Выведем для примера первое свойство.
Обозначим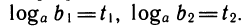 По основному логарифмическому тождеству имеем:
По основному логарифмическому тождеству имеем:
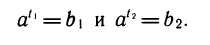
Перемножим эти равенства: 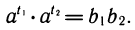 По свойству степеней
По свойству степеней
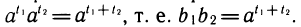
По определению логарифма t1+ t2 = 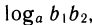 т. е.
т. е. 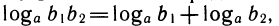 что и требовалось доказать. Свойства 2 и 3 выведите самостоятельно.
что и требовалось доказать. Свойства 2 и 3 выведите самостоятельно.
Свойства степеней и логарифмов тесно связаны между собой. Они фактически выражают одно и то же, только один раз мы обращаем внимание на поведение самих степеней, а другой — на поведение показателей:
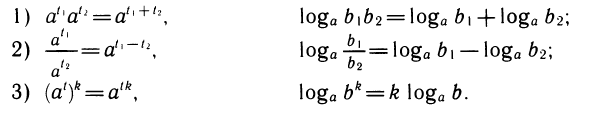
С помощью свойств логарифмов можно логарифмировать выражения, составленные с помощью операций умножения, деления и возведения в степень.
Примеры.
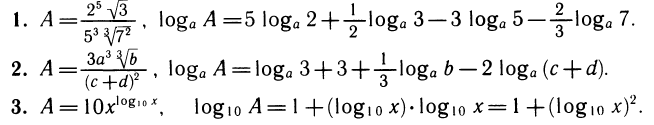
Иногда приходится искать выражение по его логарифму. Такую операцию называют потенцированием.
Примеры:
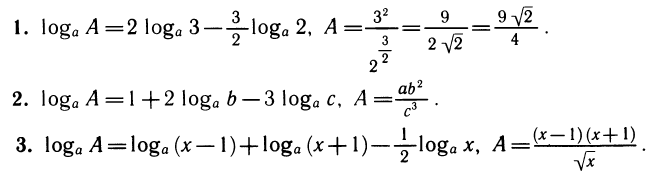
Замечание. Запись 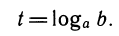 имеет смысл лишь при b> 0. Поэтому в тождествах, отражающих свойства логарифмов, все выражения, стоящие под знаком логарифма, будем считать положительными. При логарифмировании буквенных выражений надо их раскладывать на множители так, чтобы все множители были положительны. Например, пусть необходимо прологарифмировать выражение А=х(х — 1). Сделать это можно лишь тогда, когда А >0, т. е. когда либо х<0, либо х> 1. Если х> 1, то оба множителя х и х— 1 положительны и мы можем записать:
имеет смысл лишь при b> 0. Поэтому в тождествах, отражающих свойства логарифмов, все выражения, стоящие под знаком логарифма, будем считать положительными. При логарифмировании буквенных выражений надо их раскладывать на множители так, чтобы все множители были положительны. Например, пусть необходимо прологарифмировать выражение А=х(х — 1). Сделать это можно лишь тогда, когда А >0, т. е. когда либо х<0, либо х> 1. Если х> 1, то оба множителя х и х— 1 положительны и мы можем записать:
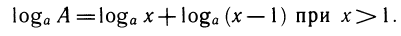
Если же х<0, то оба множителя отрицательны и А нужно разложить на множители так: А =( — x)(1 — x), откуда
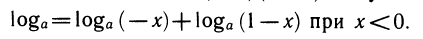
Аналогично 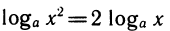 при
при 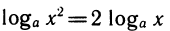 ( —x) при x<0. С помощью модуля это можно записать короче:
( —x) при x<0. С помощью модуля это можно записать короче:
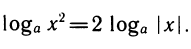
Модуль перехода
В вычислениях в качестве основания а часто берется число а=10. В то же время зачастую необходимы вычисления степеней и логарифмов с разными основаниями. Возникает вопрос: как связать между собой степени и логарифмы с разными основаниями?
Пусть дана степень b = 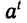 . Мы хотим перейти к новому основанию с, т. е. записать число
. Мы хотим перейти к новому основанию с, т. е. записать число 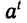 в виде сх при некотором х. Записав равенство
в виде сх при некотором х. Записав равенство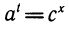 и прологарифмировав его по основанию а, получим
и прологарифмировав его по основанию а, получим 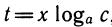 , откуда
, откуда 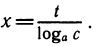 Так как
Так как 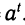 = b,
= b, 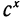 = b, то можно с помощью логарифмов записать:
= b, то можно с помощью логарифмов записать: 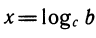 ,
, 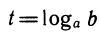 , откуда
, откуда
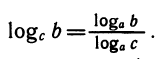
Выведенную формулу называют формулой перехода от одного основания логарифма к другому.
Таким образом, мы видим, что при изменении основания значения логарифмов изменяются пропорционально. Коэффициент пропорциональности 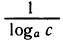 называют модулем перехода.
называют модулем перехода.
Отметим простые следствия выведенной формулы:
1) 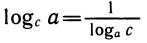 (положим в формуле перехода b = а)
(положим в формуле перехода b = а)
2) 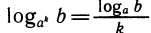 (положим в формуле перехода с = аk)
(положим в формуле перехода с = аk)
3) 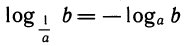 (положим в предыдущей формуле k=-l).
(положим в предыдущей формуле k=-l).
С помощью логарифмов все степени можно привести к одному основанию. Если в качестве основания берется число a =10, то соответствующие логарифмы обозначаются знаком lg и называются десятичными. Можно записать:
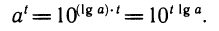
Если в качестве основания берется число е, то соответствующие логарифмы обозначаются знаком ln и называются натуральными:
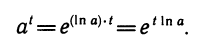
Значения модулей перехода от десятичных логарифмов к натуральным и наоборот таковы:
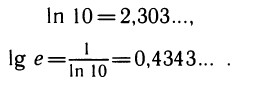
Исследование логарифмической функции
Определение:
Логарифмической функцией называется функция вида 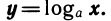
Напомним, что в качестве основания логарифмов выбирается число а> 0, отличное от 1.
Основные свойства логарифмической функции (схема X).
- 1) Область определения: множество всех положительных чисел, т. е. промежуток (0; + ∞).
- 2) Монотонность: если а>1, то логарифмическая функция строго возрастает; если 0<а<1, то она строго убывает.
- 3) Область значений: множество всех вещественных чисел R.
Так как определение логарифмов основано на понятии степени,
то при доказательстве свойств логарифмической функции используют свойства показательной функции.
Свойство 1 в доказательстве не нуждается: оно опирается на определение логарифма числа х, по которому необходимо, чтобы число х было положительным.
Докажем свойство 2. Для этого сначала рассмотрим случай а>1. Возьмем два положительных числа х1 и x2, такие, что x1 <x2, и докажем, что 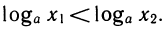 Обозначив первое из этих чисел через t1, второе — через t2, по определению логарифма получим
Обозначив первое из этих чисел через t1, второе — через t2, по определению логарифма получим 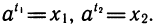
Если бы выполнялось неравенство t1 ≥ t2, то по свойству монотонности показательной функции выполнялось бы неравенство т. е. 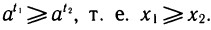 Это противоречит условию.
Это противоречит условию.
Следовательно, t1<t2, что и требовалось доказать. Случай 0<а<1 рассматривается аналогично.
Свойство 3 утверждает, что всякое вещественное число t может быть логарифмом некоторого числа х. Так как степень 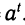 определена при любом t, то, взяв х =
определена при любом t, то, взяв х =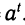 , получим
, получим 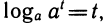 что и требовалось доказать.
что и требовалось доказать.
Графики логарифмических функций при различных основаниях показаны на рисунке 108.
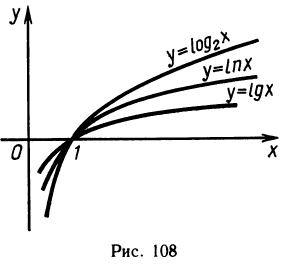
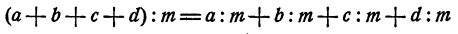
Графики функций 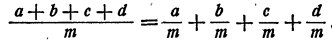 симметричны друг другу относительно прямой у = х. Действительно, если точка Р {с; d) лежит на графике функции у = ах, то d = ac. Но тогда
симметричны друг другу относительно прямой у = х. Действительно, если точка Р {с; d) лежит на графике функции у = ах, то d = ac. Но тогда 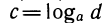 и точка Q {d; с) лежит на графике функции
и точка Q {d; с) лежит на графике функции 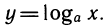
Так как точки Р (с; d) и Q (d; с) симметричны относительно прямой у = х (рис. 109), то симметричны и графики показательной и логарифмической функций.
Вместо логарифмических функций с произвольным основанием удобно рассматривать функции вида у = с ln х. Так как 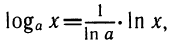 то указанные функции исчерпывают все логарифмические функции.
то указанные функции исчерпывают все логарифмические функции.
Функция у = ln х растет с ростом х, однако медленнее, чем любая степенная функция вида 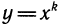 (k>0), в частности медленнее, чем
(k>0), в частности медленнее, чем 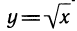 (схема IX).
(схема IX).
Производная логарифмической функции
Рассмотрим две функции у = 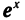 и у = ln х. Мы знаем, что их графики симметричны относительно прямой у = х. Это поможет нам найти производную логарифмической функции, зная производную экспоненты. Возьмем точку Р (с; d) на графике экспоненты (т. е. d = ec) и симметричную точку Q (d; с) на графике логарифмической функции (т. е. c = lnd). Касательные к графикам в этих точках тоже будут симметричны (рис. 109). Угловой коэффициент k1 касательной к графику экспоненты равен значению производной функции у = ех при х = с, т. е. k1=ec, так как
и у = ln х. Мы знаем, что их графики симметричны относительно прямой у = х. Это поможет нам найти производную логарифмической функции, зная производную экспоненты. Возьмем точку Р (с; d) на графике экспоненты (т. е. d = ec) и симметричную точку Q (d; с) на графике логарифмической функции (т. е. c = lnd). Касательные к графикам в этих точках тоже будут симметричны (рис. 109). Угловой коэффициент k1 касательной к графику экспоненты равен значению производной функции у = ех при х = с, т. е. k1=ec, так как 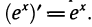
Пусть a1 и а2 — углы, образованные проведенными касательными с осью абсцисс. Из рисунка 109 ясно, что 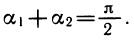
Так как
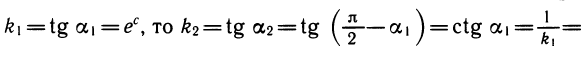
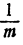
Таким образом, производная функции у = ln х в точке x = d равна 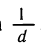
Можно написать:
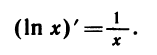
Мы видим, что производная логарифмической функции y = ln х равна степенной функции 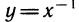 . Интересно заметить, что функция
. Интересно заметить, что функция 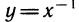 не получается как производная какой-либо другой степенной функции вида у = схк. Действительно, хотя
не получается как производная какой-либо другой степенной функции вида у = схк. Действительно, хотя 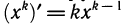 при любом к, но получить значение к— 1, равное —1, можно лишь при k = 0, а (x°)’ = 0.
при любом к, но получить значение к— 1, равное —1, можно лишь при k = 0, а (x°)’ = 0.
Так как 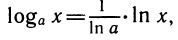 то
то
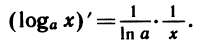
По формулам производной показательной функции 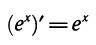 и
и
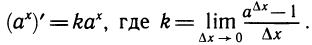
Известно, что ,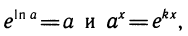 где k= ln а. Поэтому
где k= ln а. Поэтому 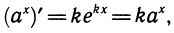 т. е.
т. е.
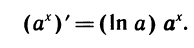
Примеры:
Зная производные экспоненты и логарифма, можно получить приближенные формулы для их вычисления.
Пусть 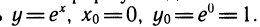
Разность 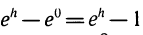 —это приращение у на отрезке [0; h]. Вычислив dy при хо = 0, получим dy = y’ (0) dx. Так как у’ = ех, то у'(0)= 1. Заменив ∆у на dy и подставив dx = h, получим приближенную формулу
—это приращение у на отрезке [0; h]. Вычислив dy при хо = 0, получим dy = y’ (0) dx. Так как у’ = ех, то у'(0)= 1. Заменив ∆у на dy и подставив dx = h, получим приближенную формулу
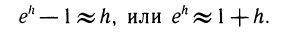
Более точная формула для вычисления экспоненты такова:
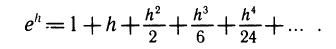
Пусть теперь у =lnх. Выберем дго=1, xо = ln l =0. Положим dx = h и вычислим ln (l+h). Найдем dy при xo=1. Так как
(In то y’ (jc0)= 1 и dy= 1 •dx = h.
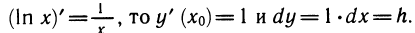
Заменяя ∆y= ln (1+h) — ln l = ln (l+h), получаем приближенную формулу
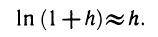
Более точная формула для вычисления логарифма такова:
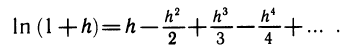
Вычисление логарифмов
Более 300 лет логарифмы использовались для облегчения вычислений. Их основное достоинство — способность сводить умножение к сложению по формуле 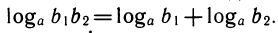
Были составлены обширные таблицы логарифмов чисел, с помощью которых можно легко переходить от чисел к их логарифмам и обратно.
Все таблицы логарифмов до 1950 г. являлись перепечаткой или сокращением таблиц Бриггса. Генри Бриггс (1561 —1630) с очень большой точностью (16 знаков после запятой) извлек подряд 57 квадратных корней из 10 и получил значения 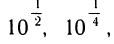
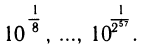
Комбинируя эти значения, он получил густую сетку чисел с известными десятичными логарифмами: 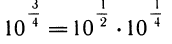 и т. п. После этого десятичный логарифм любого числа х из промежутка [1; 10] с хорошей точностью находится округлением до ближайшего известного.
и т. п. После этого десятичный логарифм любого числа х из промежутка [1; 10] с хорошей точностью находится округлением до ближайшего известного.
Это огромная работа, и за 300 лет не нашлось никого, кто повторил бы ее. Любопытно, что немного раньше Бриггса таблицу натуральных логарифмов составил Джон Непер (1550—1617).
С появлением ЭВМ ситуация переменилась. Умножение по-прежнему выполняется дольше, чем сложение, но логарифмирование требует еще больше времени. Поиск числа в таблице очень дорогая операция для ЭВМ. Поэтому теперь значение логарифмов как инструмента вычисления резко упало, а с распространением калькуляторов оно сходит на нет. С другой стороны, сами по себе логарифмические зависимости легко обрабатываются и используются при вычислениях на ЭВМ. Например, формула xk = exp(k ln x) служит основным средством возведения в степень (кроме k= l, 2, 3) на всех ЭВМ и на калькуляторах.
На современных ЭВМ (и на калькуляторах) значения In х и 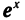 вычисляют, пользуясь заранее найденными приближенными формулами. По этим формулам вычисление логарифмов становится довольно простым. Пользователю ЭВМ никогда не приходится думать о вычислении логарифмов: на всех ЭВМ для этого имеются стандартные программы.
вычисляют, пользуясь заранее найденными приближенными формулами. По этим формулам вычисление логарифмов становится довольно простым. Пользователю ЭВМ никогда не приходится думать о вычислении логарифмов: на всех ЭВМ для этого имеются стандартные программы.
Прикладные примеры
Во вводной беседе мы уже говорили о том, что многие процессы описываются с помощью показательных функций. Почему так происходит, это мы обсудим в следующей главе, а сейчас приведем примеры зависимостей, в которых встречаются экспоненты и логарифмы.
- Радиоактивный распад. Изменение массы радиоактивного вещества происходит по формуле
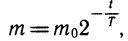 , где m0 — масса вещества в начальный момент t = 0, m — масса вещества в момент времени t, Т — некоторая константа, смысл которой мы сейчас выясним.
, где m0 — масса вещества в начальный момент t = 0, m — масса вещества в момент времени t, Т — некоторая константа, смысл которой мы сейчас выясним.
Вычислим значение m при t — Т. Так,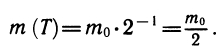
Это означает, что через время Т после начального момента масса радиоактивного вещества уменьшается вдвое. Поэтому число Т называют периодом полураспада. Период полураспада радия равен 1600 лет, урана-238 — 4,5 млрд. лет, цезия-137 —31 год, иода-131 —8 суток.
Закон радиоактивного распада часто записывают в стандартном виде 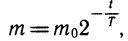 . Связь константы т с периодом полураспада нетрудно найти:
. Связь константы т с периодом полураспада нетрудно найти:
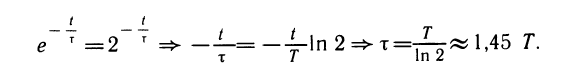
2. Рост народонаселения. Изменение количества людей в стране на небольшом отрезке времени с хорошей точностью описывается формулой 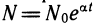 , где Nо — число людей при t= 0, N — число людей в момент времени t, а — некоторая константа.
, где Nо — число людей при t= 0, N — число людей в момент времени t, а — некоторая константа.
Барометрическая формула. Давление воздуха убывает с высотой (при постоянной температуре) по закону 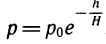 где ро — давление на уровне моря (А = 0), р — давление на высоте h, H — некоторая константа, зависящая от температуры. Для температуры 20 °С величина Н ≈ 7,7 км.
где ро — давление на уровне моря (А = 0), р — давление на высоте h, H — некоторая константа, зависящая от температуры. Для температуры 20 °С величина Н ≈ 7,7 км.
4. Формула Циолковского. Эта формула, связывающая скорость ракеты у с ее массой m, такова: 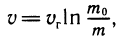 , где vr — скорость вылетающих газов, mо — стартовая масса ракеты. Скорость истечения газа при сгорании топлива vr невелика (в настоящее время она меньше или равна 2 км/с). Логарифм растет очень медленно, и, для того чтобы достичь космической скорости, необходимо сделать большим отношение
, где vr — скорость вылетающих газов, mо — стартовая масса ракеты. Скорость истечения газа при сгорании топлива vr невелика (в настоящее время она меньше или равна 2 км/с). Логарифм растет очень медленно, и, для того чтобы достичь космической скорости, необходимо сделать большим отношение 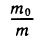 , т. е. почти всю стартовую массу отдать под топливо.
, т. е. почти всю стартовую массу отдать под топливо.
5. Коэффициент звукоизоляции стен измеряется по формуле 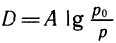 где po — давление звука до поглощения, р — давление звука, прошедшего через стену, А — некоторая константа, которая в расчетах принимается равной 20 дБ. Если коэффициент звукоизоляции D равен, например, 20 дБ, то это означает, что
где po — давление звука до поглощения, р — давление звука, прошедшего через стену, А — некоторая константа, которая в расчетах принимается равной 20 дБ. Если коэффициент звукоизоляции D равен, например, 20 дБ, то это означает, что 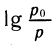 =1 и po = 10 p, т. е. стена снижает давление звука в 10 раз (такую звукоизоляцию имеет деревянная дверь).
=1 и po = 10 p, т. е. стена снижает давление звука в 10 раз (такую звукоизоляцию имеет деревянная дверь).
Дополнение к логарифмической функции


Смотрите также:
| Тригонометрические функции. Радианная мера угла | Некоторые простые неявные функции |
| Показательная функция | Примеры и определения |
Логарифмическая функция
Определение логарифма: Логарифмом числа N по данному основанию а называется такой показатель степени, в который надо возвести основание а, чтобы получить число N; запись 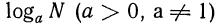
Примеры:

Таким образом, 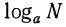 это другое название для показателя степени.
это другое название для показателя степени.
Примеры:
1. Проверить справедливость следующих равенств:
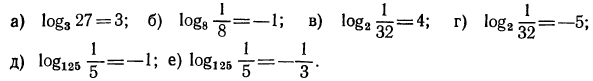
Решение:
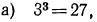 следовательно,
следовательно, 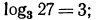 равенства
равенства
б), г), е) верны; 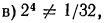 следовательно,
следовательно, 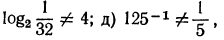 следовательно,
следовательно, 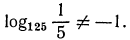
2.Следующие равенства переписать в виде логарифмических равенств: 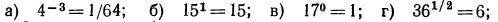
Решение:
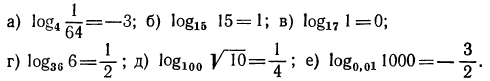
Указать, какие из нижеследующих уравнений имеют решение. Запишите это решение с помощью логарифма: 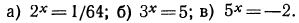
Решение:
а) Уравнение 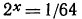 можно переписать в вид
можно переписать в вид 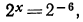 откуда х = —6, или
откуда х = —6, или 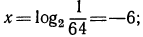
б) Уравнение 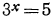 также имеет решение
также имеет решение 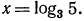 Так как
Так как 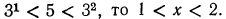
в) Уравнение 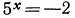 не имеет решения (показательная функция не может принимать отрицательных значений). Таким образом, выражение
не имеет решения (показательная функция не может принимать отрицательных значений). Таким образом, выражение 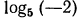 не имеет смысла.
не имеет смысла.
Десятичные логарифмы
Если основанием логарифмов служит число 10, то такие логарифмы называются десятичными. Десятичный логарифм числа N принято обозначать 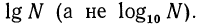
Примеры:
Найти десятичные логарифмы следующих чисел: 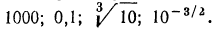
Решение:
Так как 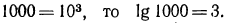 Аналогично:
Аналогично: 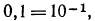 поэтому
поэтому 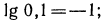 наконец,
наконец, 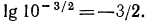
2.Решить следующие уравнения:
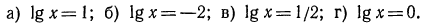
Решение:
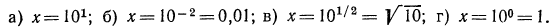
Функция 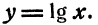
Функция 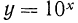 является монотонно возрастающей, поэтому у нее есть обратная функция. Для того чтобы найти эту обратную функцию, поменяем в равенстве
является монотонно возрастающей, поэтому у нее есть обратная функция. Для того чтобы найти эту обратную функцию, поменяем в равенстве 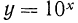 переменные х и у местами. Получим
переменные х и у местами. Получим 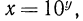 откуда
откуда 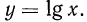 Этой формулой задается функция, обратная показательной функции
Этой формулой задается функция, обратная показательной функции 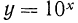 Как отмечалось выше (см. стр. 118), графики взаимно обратных функций симметричны относительно прямой у = х—биссектрисы первого и третьего координатных углов (рис. 88). Отметим основные свойства функции
Как отмечалось выше (см. стр. 118), графики взаимно обратных функций симметричны относительно прямой у = х—биссектрисы первого и третьего координатных углов (рис. 88). Отметим основные свойства функции 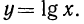
1.Областью определения функции является множество всех положительных чисел.
2.Областью значений функции является множество всех действительных чисел.
Справедливость этих двух свойств вытекает из того факта, что функции 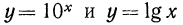 являются взаимно обратными и, следовательно, область определения и множество значений у них меняются местами.
являются взаимно обратными и, следовательно, область определения и множество значений у них меняются местами.
3.Функция 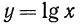 является монотонно возрастающей (большему числу соответствует больший логарифм).
является монотонно возрастающей (большему числу соответствует больший логарифм).
4.При 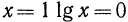 (график пересекает ось абсцисс в точке (1; 0)); если
(график пересекает ось абсцисс в точке (1; 0)); если 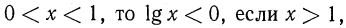 то
то 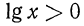 (рис. 88).
(рис. 88).
Примеры:
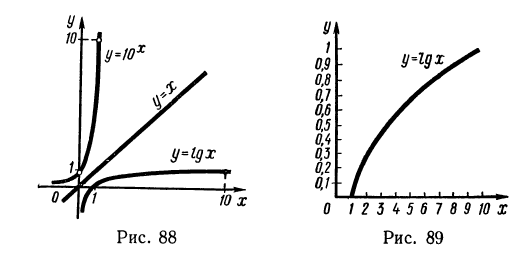
1. На рис. 89 изображен график функции 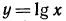 в случае, когда масштаб по оси Оу в 10 раз крупнее масштаба по оси Ох. Воспользовавшись этим графиком:
в случае, когда масштаб по оси Оу в 10 раз крупнее масштаба по оси Ох. Воспользовавшись этим графиком:
а) найти 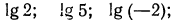 б) найти х, если
б) найти х, если 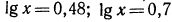
Решение:
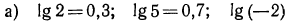 не существует, так как
не существует, так как 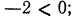
б) если 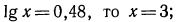
Если 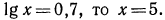
2.Сравнить значения выражений: 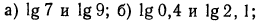
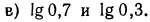
Решение:
а) Функция 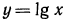 возрастающая, значит,
возрастающая, значит, 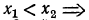
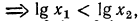 так как
так как 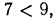 то, следовательно,
то, следовательно, 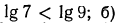 б) так как
б) так как 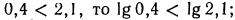 в) так как
в) так как 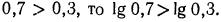
3.Решить уравнения и неравенства:
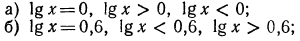
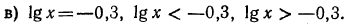
Решение:
Воспользовавшись изображенным на рис. 89 графиком функции 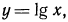 получим следующие результаты:
получим следующие результаты:
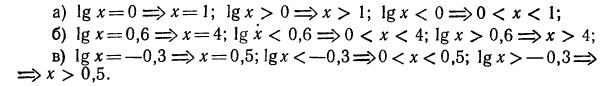
4.Найти область определения функции:
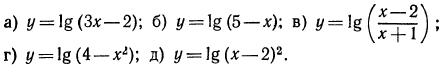
Решение:
При решении этих примеров надо помнить о том, что область определения функции 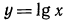 есть множество положительных чисел.
есть множество положительных чисел.
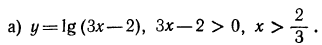 Таким образом областью определения служит множество
Таким образом областью определения служит множество 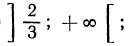
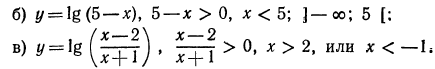
Область определения —объединение двух множеств
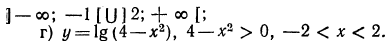
Область определения —множество 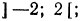
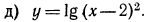 Выражение, стоящее под знаком логарифма, положительно при всех значениях х, кроме х = 2 (при котором оно обращается в ноль), а поэтому область определения этой функции есть множество
Выражение, стоящее под знаком логарифма, положительно при всех значениях х, кроме х = 2 (при котором оно обращается в ноль), а поэтому область определения этой функции есть множество 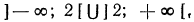
5.Решить уравнения:
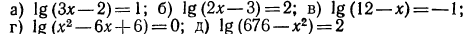
Решение:
а) Так как 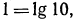 то уравнение
то уравнение 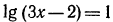 можно переписать в виде
можно переписать в виде 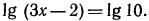 Далее из свойства монотонности функции
Далее из свойства монотонности функции 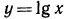 вытекает, что эта функция каждое значение принимает только один раз. Следовательно,
вытекает, что эта функция каждое значение принимает только один раз. Следовательно, 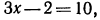 откуда х = 4.
откуда х = 4.
Аналогично решаются и остальные уравнения;
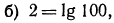 т.е. данное уравнение может быть записано в виде
т.е. данное уравнение может быть записано в виде 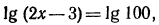 откуда
откуда 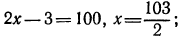
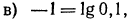 поэтому
поэтому 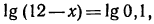 откуда
откуда 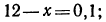
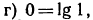 поэтому
поэтому 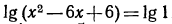 откуда
откуда 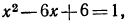 или
или 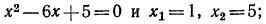
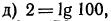 поэтому
поэтому 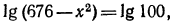 откуда
откуда 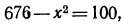 или
или 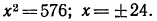
Логарифмирование и потенцирование
Применение логарифмов позволяет во многих случаях значительно упростить вычисления. Чтобы убедиться в этом, прежде всего выясним, как находятся логарифмы произведения, частного, степени и корня.
Теорема:
Логарифм произведения любых двух положительных чисел равен сумме логарифмов множителей, т. е.
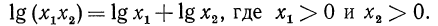
Доказательство:
Пусть 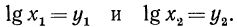 Тогда по определению логарифма
Тогда по определению логарифма 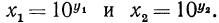 Перемножив эти равенства почленно, получим
Перемножив эти равенства почленно, получим
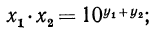
значит,
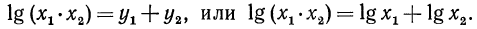
Предлагаем читателю самому доказать, что установленное свойство справедливо для любого числа положительных множителей.
Теорема:
Логарифм степени с положительным основанием равен произведению показателя степени и логарифма ее основания, т. е.
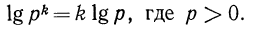
Доказательство:
Пусть 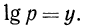 Тогда по определению логарифма
Тогда по определению логарифма 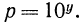 Возведем обе части этого равенства в степень
Возведем обе части этого равенства в степень 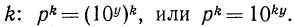 Следовательно,
Следовательно, 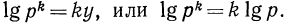
Покажем, что знания этих теорем достаточно для нахождения логарифмов дроби и корня. Действительно, пусть дано выражение 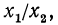 где
где 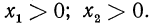 Это выражение можно переписать в виде
Это выражение можно переписать в виде 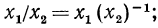 тогда
тогда
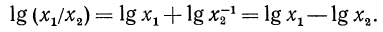
Пусть теперь дано выражение 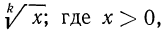 тогда
тогда 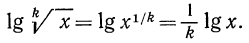 Таким образом, если некоторое выражение составлено из положительных чисел с помощью операций умножения, деления, возведения в степень и извлечения корня, то его логарифм можно выразить через логарифмы входящих в него чисел. Такое преобразование называется логарифмированием. Действие, обратное логарифмированию, называется потенцированием.
Таким образом, если некоторое выражение составлено из положительных чисел с помощью операций умножения, деления, возведения в степень и извлечения корня, то его логарифм можно выразить через логарифмы входящих в него чисел. Такое преобразование называется логарифмированием. Действие, обратное логарифмированию, называется потенцированием.
Примеры:
1. Найти приближенные значения следующих логарифмов: 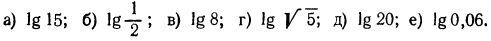
Решение:
Прежде всего, воспользовавшись графиком функции 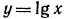 (см. рис. 89), выпишем приближенные значения следующих логарифмов:
(см. рис. 89), выпишем приближенные значения следующих логарифмов:
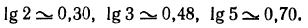
Теперь имеем:
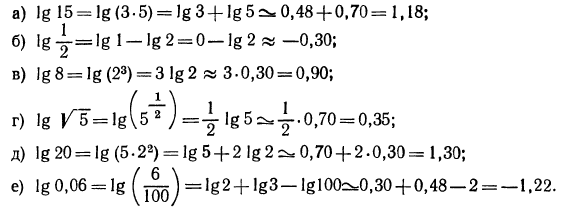
2.Прологарифмировать следующие выражения (буквами обозначены положительные числа):
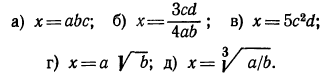
Решение:
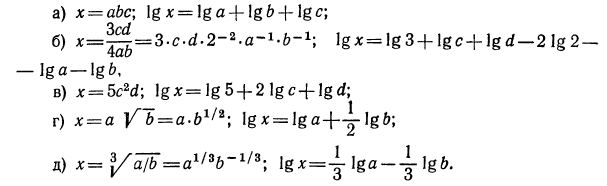
3.Решить уравнения:
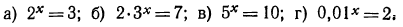
Решение:
а) Прологарифмировав обе части данного равенства, получим 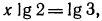 откуда
откуда 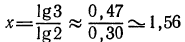 (значения
(значения 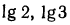 найдены графически с помощью рис. 89);
найдены графически с помощью рис. 89);
б) в результате логарифмирования имеем равенство 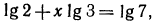 откуда
откуда 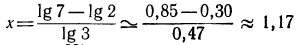 (значение
(значение 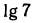 найдено с помощью рис. 89);
найдено с помощью рис. 89);
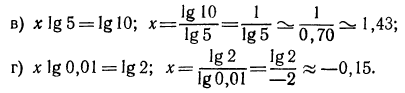
4.Найти x, если: 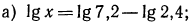
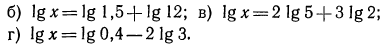
Решение:
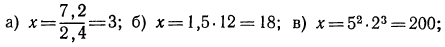
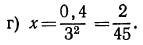
5.Решить уравнения:
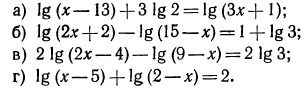
Решение:
а) Потенцируя обе части равенства, получаем уравнение
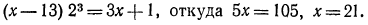
Сделаем проверку. Подставив в уравнение найденное решение х = 21, получим:
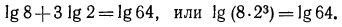
Таким образом, корень данного уравнения x=21;
б) прежде чем потенцировать, заметим, что 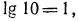 и перепишем уравнение в виде
и перепишем уравнение в виде
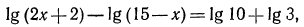
откуда
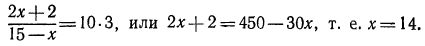
Сделаем проверку: 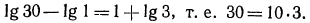 Итак, х= 14 —корень уравнения; в) потенцируя, получаем
Итак, х= 14 —корень уравнения; в) потенцируя, получаем
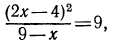
откуда
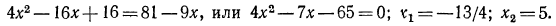
Сделаем проверку. Корень  является посторонним, так как при этом значении x выражение 2х—4 будет отрицательным, а, как мы знаем, область определения логарифмической функции есть множество положительных чисел.
является посторонним, так как при этом значении x выражение 2х—4 будет отрицательным, а, как мы знаем, область определения логарифмической функции есть множество положительных чисел.
Корень x = 5, как легко видеть, удовлетворяет уравнению (Проверьте сами!);
г) уравнение 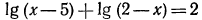 не имеет корней, так как искомое значение х должно удовлетворять системе неравенств
не имеет корней, так как искомое значение х должно удовлетворять системе неравенств
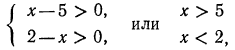
а эта система противоречива и решения не имеет.
Стандартный вид числа. Характеристика и мантисса
Любое положительное число х можно записать в так называемом стандартном виде: 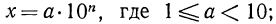
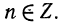 Число n называется порядком числа х.
Число n называется порядком числа х.
Примеры:
Записать следующие числа в стандартном виде и указать их порядок: а) 273; б) 51,83; в) 0,8912; г) 400012; д) 0,00051; е) 1,002.
Решение:
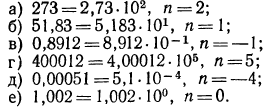
Легко видеть, что если  то порядок числа неотрицателен,
то порядок числа неотрицателен,  причем трехзначное число, например 273, имеет порядок 2; а число, содержащее две цифры в целой части, например 51,83, имеет порядок n= 1; наконец, число, содержащее одну цифру в целой части, имеет порядок n= 0. Можно сделать следующий вывод: если число
причем трехзначное число, например 273, имеет порядок 2; а число, содержащее две цифры в целой части, например 51,83, имеет порядок n= 1; наконец, число, содержащее одну цифру в целой части, имеет порядок n= 0. Можно сделать следующий вывод: если число  содержит в целой части m цифр, то его порядок будет
содержит в целой части m цифр, то его порядок будет 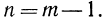
Если же число 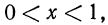 то его порядок отрицателен,
то его порядок отрицателен, 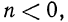 причем
причем 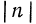 равен числу нулей в x: до первой значащей цифры, включая ноль целых. Так, если x: = 0,8912, то n = —1; если х = 0,00051, то n = —4.
равен числу нулей в x: до первой значащей цифры, включая ноль целых. Так, если x: = 0,8912, то n = —1; если х = 0,00051, то n = —4.
Пример:
Не переходя к стандартному виду записи, найти порядок чисел: а) х = 373,25; б) x: = 0,00085.
Решение:
а) Число 373,25 больше единицы и содержит в целой части три цифры. Следовательно, его порядок n= 2;
б) число 0,00085 меньше единицы и содержит четыре нуля до первой значащей цифры. Следовательно, n =—4.
Пусть х=375,8. Запишем это число в стандартном виде и найдем его логарифм:
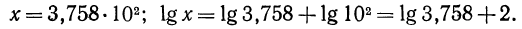
Так как 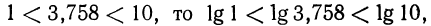 т. е.
т. е. 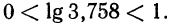 Таким образом,
Таким образом, 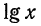 представлен в виде суммы целого числа 2 и положительного числа, меньшего единицы
представлен в виде суммы целого числа 2 и положительного числа, меньшего единицы 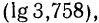 т. е. в виде суммы его целой и дробной частей. Целая часть логарифма числа х равна порядку этого числа, а дробная часть равна
т. е. в виде суммы его целой и дробной частей. Целая часть логарифма числа х равна порядку этого числа, а дробная часть равна 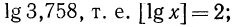
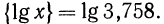
Целая часть логарифма числа называется его характеристикой, а дробная часть — мантиссой.
Теорема:
Характеристика логарифма числа 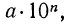 где
где 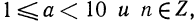 равна порядку этого числа, т. е. n, а мантисса равна
равна порядку этого числа, т. е. n, а мантисса равна 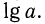
Доказательство:
Пусть 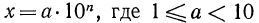 и
и 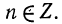 Тогда
Тогда 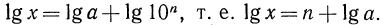 Так как
Так как 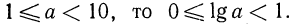 Следовательно,
Следовательно, 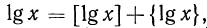 причем
причем 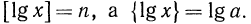
Следствие:
Логарифмы чисел, отличающихся друг от друга только порядком, имеют одну и ту же мантиссу.
Доказательство:
Пусть 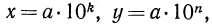 где
где 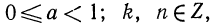 тогда
тогда 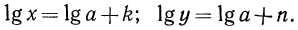
Таким образом,
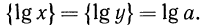
Например, пусть 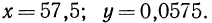 Запишем эти числа в стандартном виде и найдем их логарифмы:
Запишем эти числа в стандартном виде и найдем их логарифмы: 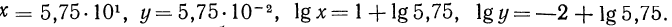
Таким образом, доказанное следствие можно сформулировать иначе: мантисса логарифма числа не зависит от положения запятой в числе.
Примеры:
1. Найти характеристику логарифма числа а) 302;б) 87,5; в) 0,015.
Решение:
Как было доказано Выше, характеристика логарифма числа равна его порядку, а поэтому 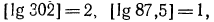
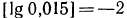
2.Зная, что 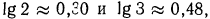 найти:
найти: 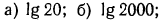
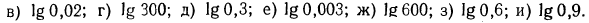
Решение:
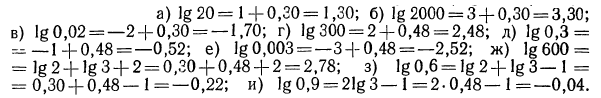
Вычисления с помощью таблиц логарифмов
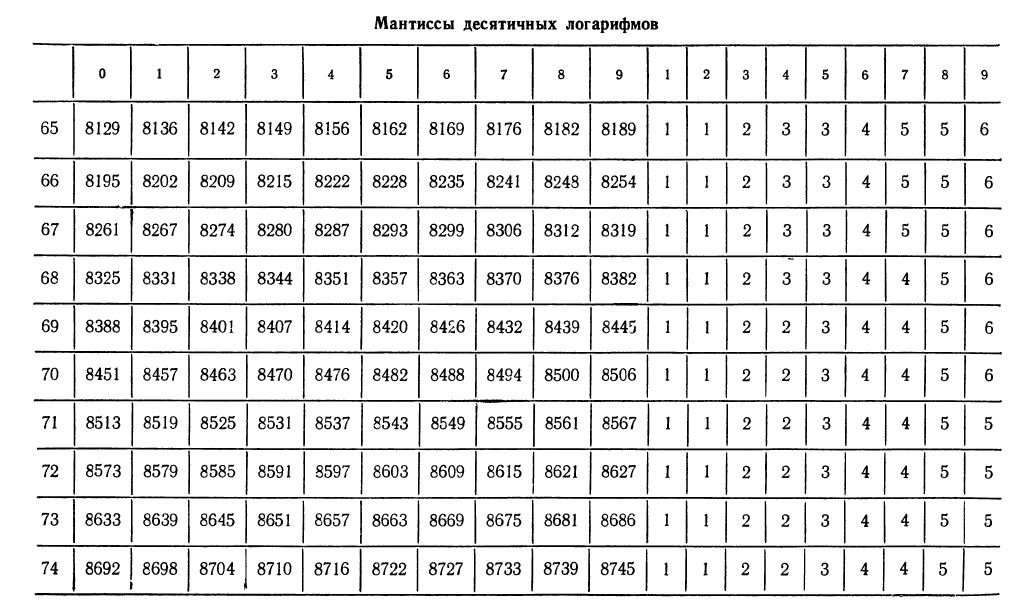
Как известно, характеристика логарифма числа легко находится устно (она равна порядку числа). Значения мантисс приведены в таблице «Четырехзначных математических таблиц» В. М. Брадиса. Приведем часть этой таблицы и укажем как ею пользоваться.
Примеры:
1. Найти логарифмы следующих чисел: 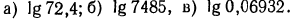
Решение:
а) Характеристика  равна 1, так как
равна 1, так как 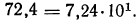 Мантиссу найдем на пересечении строки с меткой «72» и столбца с меткой «4». Получаем число 8597. Значит, мантисса равна (приблизительно) 0,8597. Отсюда:
Мантиссу найдем на пересечении строки с меткой «72» и столбца с меткой «4». Получаем число 8597. Значит, мантисса равна (приблизительно) 0,8597. Отсюда:
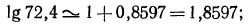
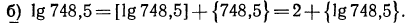
Для отыскания мантиссы мы, прочитав число 8739 на пересечении строки с меткой «74» и столбца с меткой «8», прибавим к этому числу поправку на четвертую цифру. Эта поправка расположена в правой части таблицы на пересечении той же строки и столбца поправок с меткой «5». Поправка равна 3, следовательно, мантисса равна 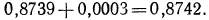 Таким образом,
Таким образом,
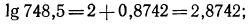
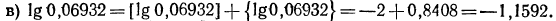 Для решения обратной задачи —нахождения числа по его логарифму пользуются таблицей, с которой мы уже знакомы (см. стр. 198)4
Для решения обратной задачи —нахождения числа по его логарифму пользуются таблицей, с которой мы уже знакомы (см. стр. 198)4
2.Найти x:, если: 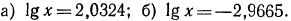
Решение:
а) По таблице значений функции 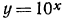 найдем число 1,077, соответствующее мантиссе
найдем число 1,077, соответствующее мантиссе 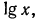 равной 0,0324. Так как характеристика логарифма равна 2, то
равной 0,0324. Так как характеристика логарифма равна 2, то
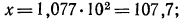
б) представим данный логарифм в виде суммы характеристики и мантиссы:
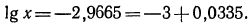
Мантиссу 0,0335 имеет любое число вида 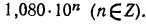 Характеристика равна —3, поэтому
Характеристика равна —3, поэтому
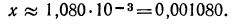
В заключение приведем пример вычисления с помощью таблиц логарифмов.
3.Вычислить значение х, если 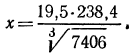
Решение:
Логарифмируя, имеем:
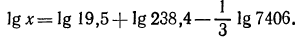
По таблице логарифмов найдем:
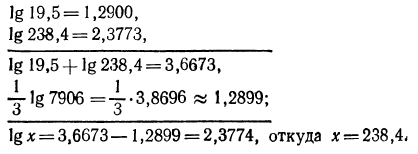
Решение:
а) Характеристика  равна 1, так как
равна 1, так как 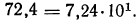 Мантиссу найдем на пересечении строки с меткой «72» и столбца с меткой «4». Получаем число 8597. Значит, мантисса равна (приблизительно) 0,8597. Отсюда:
Мантиссу найдем на пересечении строки с меткой «72» и столбца с меткой «4». Получаем число 8597. Значит, мантисса равна (приблизительно) 0,8597. Отсюда:
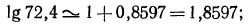
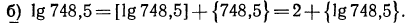
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

