Оглавление:
Мы рассматриваем системы линейных алгебраических уравнений вида
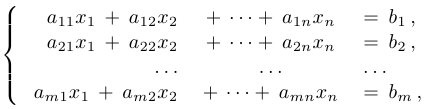
где 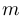 ,
, 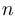 — натуральные числа (
— натуральные числа (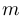 — количество уравнений,
— количество уравнений, 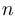 — количество неизвестных),
— количество неизвестных), 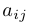 — коэффициенты при неизвестных, которые предполагаются заранее заданными;
— коэффициенты при неизвестных, которые предполагаются заранее заданными; 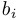 — также априори заданные постоянные, называемые свободными членами.
— также априори заданные постоянные, называемые свободными членами.
Матрицей системы называется следующая матрица (прямоугольная таблица чисел), составленная из коэффициентов системы
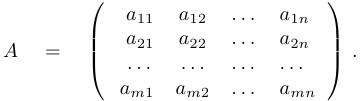
Расширенной матрицей системы называется матрица системы, к которой справа приписан столбец свободных членов. Обычно его отделяют от матрицы системы вертикальной чертой:

Решением системы называется такой набор постоянных 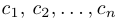 , что при подстановке вместо переменных
, что при подстановке вместо переменных 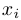 значений
значений 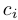 каждое из равенств системы обратится в тождество.
каждое из равенств системы обратится в тождество.
Системы линейных уравнений классифицируются по числу решений следующим образом:
- совместная система — система линейных уравнений, имеющая хотя бы одно решение;
- несовместная (противоречивая) система — система, не имеющая ни одного решения;
- определенная система — система, имеющая единственное решение;
- неопределенная система — система, имеющая более одного решения.
Существуют два основных способа решения линейных систем: метод Гаусса и, если 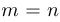 (то есть если матрица системы квадратная), метод (или правило) Крамера.
(то есть если матрица системы квадратная), метод (или правило) Крамера.
Метод Гаусса.
Для решения системы не обязательно «таскать за собой» полную запись системы — достаточно работать с расширенной матрицей. При этом с ней можно производить операции, которые называются элементарными преобразованиями. К таковым относятся следующие действия со строками расширенной матрицы:
- перемена мест строк;
- умножение одной из строк на число, отличное от нуля;
- прибавление к одной из строк линейной комбинации нескольких других.
Отметим, что лучше не производить операции со столбцами расширенной матрицы, ибо без этих преобразований всегда можно обойтись, хотя они иногда и упрощают вид системы. Неудобство, связанное с ними, состоит в том, что при этом приходится «вести протокол», чтобы затем правильно интерпретировать ответ. Например, перемена мест столбцов означает соответствующее изменение нумерации переменных и после получения ответа ее надо восстановить.
Если в процессе преобразований появляется нулевая строчка, то мы ее вычеркиваем, уменьшая количество строк на единицу.
При элементарных преобразованиях может получиться матрица, у которой есть строчка, все элементы которой слева от черты равны нулю, а справа стоит ненулевое число. В этом случае мы отмечаем, что система несовместна (противоречива), то есть не имеет решения. То же самое происходит, если совпадают две строчки за исключением свободных членов, которые различны. Например, несовместной является следующая система:

Желательной целью цепочки элементарных преобразований является приведение расширенной матрицы к такому виду, что на месте основной матрицы системы стоит единичная матрица, то есть единичная матрица стоит слева от черты в расширенной матрице. В этом случае процедура закончена и система является определенной, то есть имеет одно решение (один набор значений переменных). Этот набор переменных указан столбцом свободных членов.
Пример 1.
Рассмотрим систему
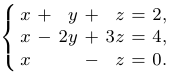
Выпишем расширенную матрицу системы и сделаем пару элементарных преобразований:

Из первой и второй строк мы вычли третью. После этого все элементы второй строки разделим на 2 и полученную строку сложим с первой, записав сумму на место первой строки:

В получившейся матрице все элементы первой строки сократим на 4, элементы второй строки умножим на —1 и затем поменяем первую и третью строки местами, чтобы получилась треугольная матрица, то есть матрица, у которой все элементы ниже главной диагонали равны 0:

Наконец, мы приводим матрицу к диагональному виду и выписываем ответ:
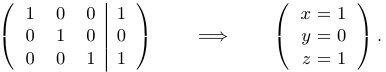
Таким образом, мы нашли некоторое решение. Это означает, что система совместна.
Найденное решение оказалось единственным. Это означает, что система определённа.
Если к единичной матрице не удается привести левую часть, но в то же время система не является противоречивой, то в этом случае система является совместной, но неопределенной, то есть имеет бесконечное множество решений. В этом случае одной или нескольким переменным можно придать произвольные значения, которые обычно не фиксируются, условно обозначаются буквами, например  , и называются параметрами. Остальные переменные однозначно выражаются через эти параметры.
, и называются параметрами. Остальные переменные однозначно выражаются через эти параметры.
Пример 2.
Рассмотрим систему
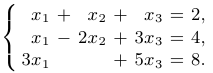
Выпишем расширенную матрицу системы и сделаем естественные преобразования:
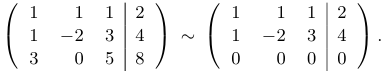
Из третьей строки мы вычли вторую и удвоенную первую. После этого вычеркнем нулевую строку и из второй строки вычтем первую. Затем выделим единичную матрицу коэффициентов перед 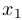 и
и 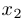 :
:
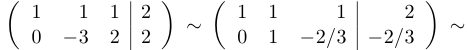
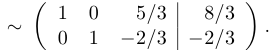
Отсюда следует, что 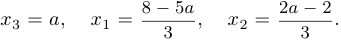 .
.
Таким образом, система имеет решение, то есть она совместна. Найденное решение оказалось не единственным. Это означает, что система является неопределенной. Если ставится задача найти какое-нибудь решение, то мы можем положить а равным, например, 1, и тогда 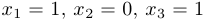 .
.
Правило Крамера.
Этот метод используется для решения систем в случае, когда число уравнений совпадает с числом неизвестных, то есть 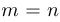 :
:
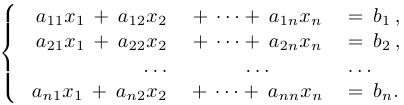
Обозначим через  определитель матрицы системы
определитель матрицы системы
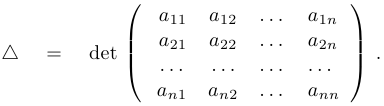
Предполагается, что определитель системы не равен нулю (в противном случае система является либо неопределенной, либо несовместной). Обозначим через 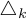 определитель системы, которая получается из основной путем замены
определитель системы, которая получается из основной путем замены 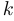 -ro столбца на столбец свободных членов:
-ro столбца на столбец свободных членов:
Формулы Крамера: 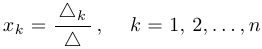 .
.
Теорема Крамера. Рассматривается линейная система, в которой число уравнений совпадает с числом неизвестных.
Если определитель матрицы системы равен нулю, то система является либо несовместной, либо неопределенной.
Если определитель матрицы системы не равен нулю, то система является совместной и определенной, причем решения системы находятся по формулам Крамера.
Обратная матрица.
Квадратная матрица 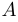 называется особой, если ее определитель равен нулю. В противном случае матрица называется не особой. Заметим (без доказательства), что определитель произведения двух квадратных матриц одной размерности равен произведению определителей этих матриц, то есть
называется особой, если ее определитель равен нулю. В противном случае матрица называется не особой. Заметим (без доказательства), что определитель произведения двух квадратных матриц одной размерности равен произведению определителей этих матриц, то есть 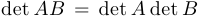 . Отсюда следует, что матрица
. Отсюда следует, что матрица 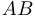 является не особой тогда и только тогда, когда каждая их матриц-множителей является не особой.
является не особой тогда и только тогда, когда каждая их матриц-множителей является не особой.
Пусть 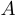 — квадратная матрица (
— квадратная матрица ( ). Квадратная матрица
). Квадратная матрица 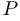 той же размерности называется матрицей, обратной к
той же размерности называется матрицей, обратной к 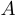 , если
, если 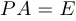 , где
, где 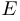 — единичная матрица той же размерности. Если обратная матрица существует, то она обозначается через
— единичная матрица той же размерности. Если обратная матрица существует, то она обозначается через 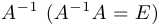 .
.
Теорема об обратной матрице. Квадратная матрица 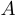 имеет обратную тогда и только тогда, когда она не особая, то есть
имеет обратную тогда и только тогда, когда она не особая, то есть 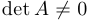 . При этом:
. При этом:
1) 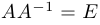 , то есть матрица
, то есть матрица 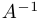 коммутирует с матрицей
коммутирует с матрицей 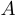 ;
;
2) обратная матрица (если она существует) единственна:
3) если 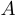 и
и 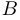 — не особые матрицы, то существует обратная к их произведению, причем
— не особые матрицы, то существует обратная к их произведению, причем 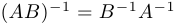 ;
;
4) 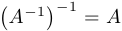 .
.
Метод Гаусса нахождения обратной матрицы.
Существует несколько способов нахождения обратной матрицы. Покажем, как это делается методом Гаусса.
Для произвольной квадратной матрицы 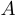 построим спаренную прямоугольную матрицу (
построим спаренную прямоугольную матрицу (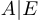 ). Задача состоит в том, чтобы допустимыми элементарными преобразованиями «перевести» матрицу
). Задача состоит в том, чтобы допустимыми элементарными преобразованиями «перевести» матрицу 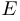 в левую часть, то есть к виду (
в левую часть, то есть к виду (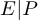 ). Матрица
). Матрица 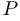 и окажется обратной к матрице
и окажется обратной к матрице 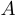 .
.
Пример 3.
Найти матрицу, обратную к матрице 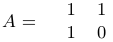 .
.
Решение:
Выпишем спаренную матрицу, вычтем из первой строки вторую, а затем поменяем строки местами:

Таким образом, обратная матрица найдена: 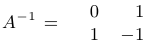 . Произведем проверку:
. Произведем проверку: 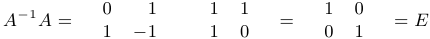 .
.
Пример 4.
Найти матрицу, обратную к матрице 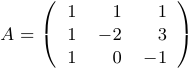 .
.
Решение:
Выпишем спаренную матрицу и сделаем пару элементарных преобразований:
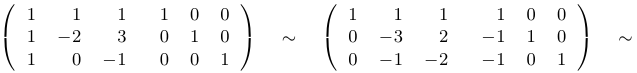
Из второй и третьей строк мы вычли первую. После этого у всех элементов третьей строки поменяем знак и трижды прибавим ко второй строке. Далее разделим вторую строку на 8, а затем вычтем вторую строку из первой и дважды из третьей)
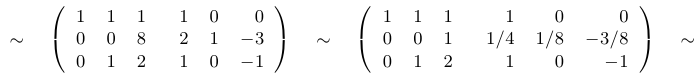

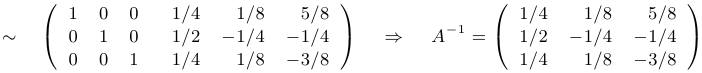
Таким образом, обратная матрица найдена. Произведем проверку:
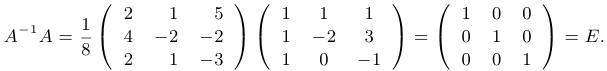
Матричная запись решения линейной системы.
Рассмотрим линейную систему, в которой число уравнений совпадает с числом неизвестных, то есть систему вида
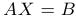 , где
, где 
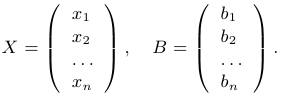
Если 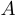 — не особая матрица, то существует обратная к ней. Умножив обе части равенства на
— не особая матрица, то существует обратная к ней. Умножив обе части равенства на 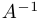 , получим, что
, получим, что
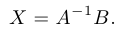
Это и есть решение системы.
На этой странице найдёте другие готовые курсовые работы во высшей математике:
Много готовых курсовых работ по высшей математике
Можете посмотреть другие готовые курсовые работы по высшей математике:

