Оглавление:
При построении графиков функций, задаваемых явными формулами, то есть в виде 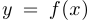 , рекомендуется прежде всего потратить время на то, чтобы сначала упростить выражение, определяющее функцию. Затем выделить цепочку элементарных операций с графиками, позволяющую упростить построение: сдвиг вдоль одной из осей, растяжение или сжатие, взятие модуля и так далее.
, рекомендуется прежде всего потратить время на то, чтобы сначала упростить выражение, определяющее функцию. Затем выделить цепочку элементарных операций с графиками, позволяющую упростить построение: сдвиг вдоль одной из осей, растяжение или сжатие, взятие модуля и так далее.
К таким элементарным операциям относятся:
1) сдвиг вдоль вертикальной оси  (вверх при
(вверх при 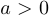 , вниз при
, вниз при 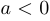 );
);
2) сдвиг вдоль оси абсцисс 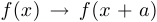 (влево при
(влево при 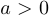 , вправо при
, вправо при 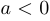 );
);
3) сжатие вдоль оси ординат 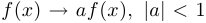 , растяжение при
, растяжение при 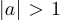 (при
(при 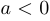 — дополнительно меняется направление оси ординат);
— дополнительно меняется направление оси ординат);
4) сжатие вдоль оси абсцисс 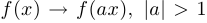 , растяжение при
, растяжение при 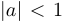 (при
(при 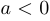 — дополнительно меняется направление оси абсцисс).
— дополнительно меняется направление оси абсцисс).
Упр. 1. Ниже изображены графики двух функций: 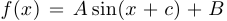 и
и 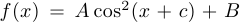 . Определите в обоих случаях значения параметров
. Определите в обоих случаях значения параметров 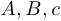 .
.
Упр. 2. Постройте график функции: 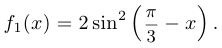
План полного исследования функции.
При исследовании функции следует постараться ответить на следующие вопросы.
1°. ОДЗ функции (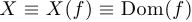 ).
).
2°. Множество значений (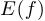 ). Заметим, что весьма часто множество
). Заметим, что весьма часто множество 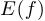 определяется в последнюю очередь, то есть после того, как указаны экстремумы функции и ее асимптоты.
определяется в последнюю очередь, то есть после того, как указаны экстремумы функции и ее асимптоты.
3°. Является ли функция четной (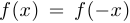 ) или нечетной (
) или нечетной (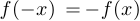 ), или не обладает симметрией (свойством четности-нечетности)?
), или не обладает симметрией (свойством четности-нечетности)?
4°. Является ли функция периодической? Если да, то каков ее период?
5°. Найти нули функции, то есть корни уравнения 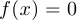 .
.
6°. Найти производную 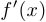 .
.
7°. Найти стационарные (критические) точки функции 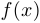 , то есть нули ее производной (
, то есть нули ее производной (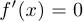 ).
).
8°. Определить участки монотонности, то есть участки возрастания и убывания функции. Для этого на вещественной прямой отмечаются критические точки и точки разрыва производной, после чего выясняются знаки производной на полученных интервалах.
9°. Указать экстремумы, то есть максимумы и минимумы.
10°. Найти асимптоты функции:
a) вертикальные асимптоты. Они появляются, если функция стремится к бесконечности при приближении к точке разрыва или к точке, являющейся границей области определения;
b) горизонтальные асимптоты. Определяются поведением функции при 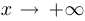 и
и 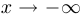 ; появляются, если при этом функция стремится к постоянной;
; появляются, если при этом функция стремится к постоянной;
c) наклонные асимптоты, то есть асимптоты вида 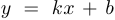 . Необходимым условием наличия наклонной асимптоты является существование предела
. Необходимым условием наличия наклонной асимптоты является существование предела 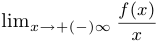 . Этот предел и является коэффициентом
. Этот предел и является коэффициентом 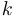 . Параметр
. Параметр 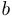 определяется соотношением
определяется соотношением 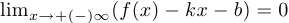 . Таким образом,
. Таким образом,
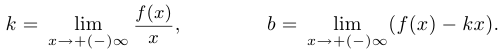
11°. Вычислить вторую производную.
12°. Найти точки перегиба и участки выпуклости и вогнутости.
Замечание. Разумеется, не обязательно выдерживать указанную программу полностью, тем более что во многих ситуациях построение упрощается после удачного и аккуратного преобразования формулы, определяющей исследуемую функцию, к виду, позволяющему использовать уже известные свойства элементарных функций.
Пример 1.
Построить график функции 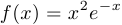 .
.
Решение.
1°. 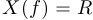 .
.
2°. 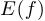 определится позже. Заметим, что, во всяком случае,
определится позже. Заметим, что, во всяком случае, 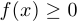 .
.
3°. График функции не обладает симметрией (функция не обладает свойством четности или свойством нечетности).
4°. Функция не является периодической. Действительно, в противном случае значение  , которое функция принимает в точке 0, должно было бы повторяться.
, которое функция принимает в точке 0, должно было бы повторяться.
5°. 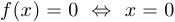 .
.
6°. 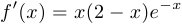 .
.
7°. 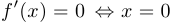 или
или 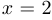 .
.
8°. 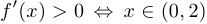 .
.
9°. 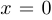 является минимумом, а
является минимумом, а 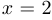 — максимумом. Находим значения:
— максимумом. Находим значения: 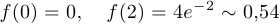 .
.
10°. 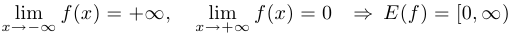 .
.
Асимптота только одна (горизонтальная): при 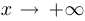 график приближается к прямой
график приближается к прямой 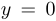 .
.
Характер поведения функции понятен, однако для уточнения формы графика полезно более точно найти участки выпуклости и вогнутости.
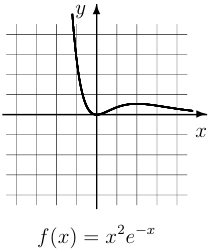
Зачастую это отнимает много времени, поскольку вторая производная не всегда имеет «хороший вид». Но в данном случае найти ее несложно.
11°. 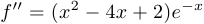 .
.
12°. 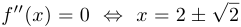 .
.
Следовательно, на участках 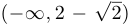 и
и 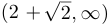 функция выпукла. На участке
функция выпукла. На участке 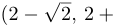
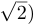 — вогнута.
— вогнута.
Подсчитав значения дополнительно в нескольких точках, рисуем график.
Графики тригонометрических функций.
План исследования тригонометрических функций не отличается от обычного, стоит лишь заметить, что тригонометрические функции, как правило, являются периодическими. Кроме обычной четности-нечетности зачастую тригонометрические функции обладают дополнительными свойствами:
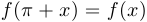 , — в этом случае мы будем говорить, что
, — в этом случае мы будем говорить, что 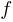
 -четна, — или
-четна, — или 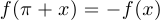 —
—  -нечетна.
-нечетна.
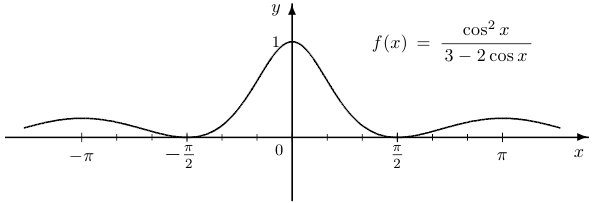
Пример 2.
Построить график функции 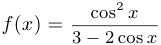 .
.
Решение. 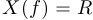 .
. 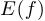 определится позже. Функция четна, поскольку
определится позже. Функция четна, поскольку 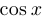 — четная функция. Функция периодическая с периодом
— четная функция. Функция периодическая с периодом 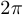 . Если определить
. Если определить 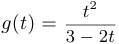 , то
, то 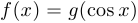 .
.
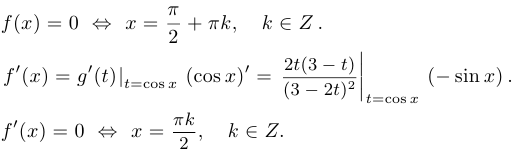
Заметим теперь, что график достаточно построить на промежутке 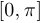 . В силу четности функции его можно отразить симметрично относительно оси ординат на интервал
. В силу четности функции его можно отразить симметрично относительно оси ординат на интервал 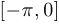 , а затем по периодичности продолжить на всю прямую. Таким образом, для построения схемы графика достаточно определить значения в точках
, а затем по периодичности продолжить на всю прямую. Таким образом, для построения схемы графика достаточно определить значения в точках 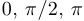 . Имеем:
. Имеем:
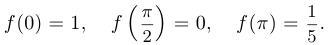
Наконец выясняем, что 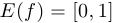 . Характер поведения функции таким образом ясен. Подсчитав значения дополнительно в нескольких точках, можно уточнить форму графика.
. Характер поведения функции таким образом ясен. Подсчитав значения дополнительно в нескольких точках, можно уточнить форму графика.
Асимптот у графика нет. Выпуклость определите самостоятельно.
Выше мы уже говорили об асимптотах. Вернемся к этой теме еще раз.
Вертикальные асимптоты.
Прямая 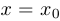 называется вертикальной асимптотой графика функции
называется вертикальной асимптотой графика функции 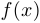 , если существует последовательность
, если существует последовательность 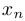 , стремящаяся к
, стремящаяся к 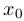 такая, что
такая, что 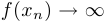 .
.
Если 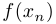 стремится к бесконечности при приближении
стремится к бесконечности при приближении 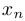 к
к 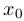 только с одной стороны, то асимптота называется односторонней.
только с одной стороны, то асимптота называется односторонней.
Асимптота называется нечетной или простой, если 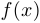 стремится к бесконечности некоторого знака при приближении
стремится к бесконечности некоторого знака при приближении 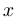 к
к 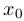 с одной стороны и меняет знак, стремясь к бесконечности, при приближении
с одной стороны и меняет знак, стремясь к бесконечности, при приближении 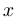 к
к 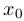 с другой стороны.
с другой стороны.
Асимптота называется четной, если 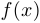 стремится к бесконечности некоторого знака при приближении
стремится к бесконечности некоторого знака при приближении 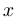 к
к 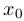 с каждой стороны.
с каждой стороны.
Пример 3.
Прямая 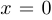 является для функции
является для функции 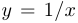 простой асимптотой, а для функции
простой асимптотой, а для функции 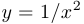 четной.
четной.
Пример 4.
Ниже изображены графики трех функций. Везде прямая  является асимптотой, причем в третьем случае она является односторонней (правосторонней) асимптотой.
является асимптотой, причем в третьем случае она является односторонней (правосторонней) асимптотой.
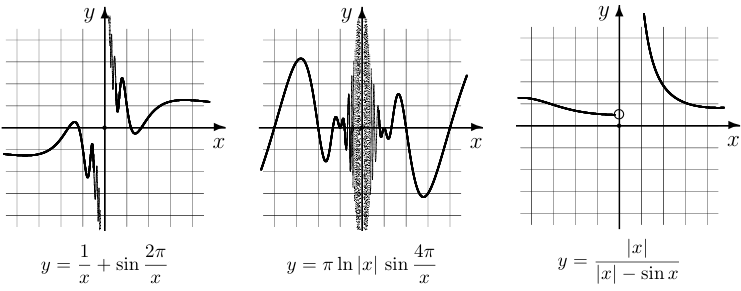
Пример 5.
Найти асимптоты графика функции 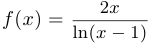 .
.
Решение, 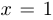 — вертикальная (правосторонняя) асимптота,
— вертикальная (правосторонняя) асимптота, 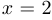 — двусторонняя вертикальная асимптота. Наклонных (в частности, горизонтальных) асимптот нет.
— двусторонняя вертикальная асимптота. Наклонных (в частности, горизонтальных) асимптот нет.
Асимптотические кривые.
Кривая 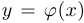 называется правой асимптотой графика функции
называется правой асимптотой графика функции 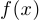 , если
, если 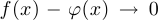 при
при 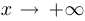 . Аналогично определяется левая асимптота. Если кривая
. Аналогично определяется левая асимптота. Если кривая 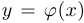 является правой или левой асимптотой (или одновременно и левой и правой), то она называется просто асимптотой или асимптотической кривой. Заметим, что если
является правой или левой асимптотой (или одновременно и левой и правой), то она называется просто асимптотой или асимптотической кривой. Заметим, что если 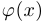 является асимптотой для
является асимптотой для 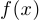 , то и наоборот,
, то и наоборот, 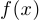 является асимптотой для
является асимптотой для 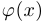 . Таким образом,
. Таким образом, 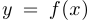 и
и 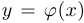 — взаимно асимптотические кривые.
— взаимно асимптотические кривые.
Наклонные и горизонтальные асимптоты.
Чаще всего в качестве асимптотических кривых рассматривают прямые 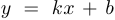 . При этом, если
. При этом, если 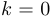 , то асимптоты называют горизонтальными. В общем случае их называют наклонными. В дальнейшем мы тоже, как правило, будем этим ограничиваться.
, то асимптоты называют горизонтальными. В общем случае их называют наклонными. В дальнейшем мы тоже, как правило, будем этим ограничиваться.
Необходимым условием того, что прямая 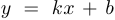 есть правая наклонная асимптота графика
есть правая наклонная асимптота графика 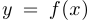 , является равенство
, является равенство
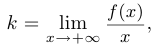
которое подразумевает, естественно, что указанный предел существует. Достаточным условием является существование и второго предела:
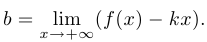
Пример 6.
Ниже изображены графики трех функций. У первой из них асимптотой является парабола 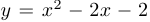 и другой асимптотой (вертикальной) прямая
и другой асимптотой (вертикальной) прямая 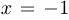 . У второй есть правая асимптота (наклонная):
. У второй есть правая асимптота (наклонная): 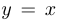 . У третьей две разные наклонные асимптоты:
. У третьей две разные наклонные асимптоты: 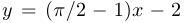 (правая) и
(правая) и 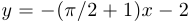 (левая).
(левая).
Построение графиков дробно-рациональных функций. Напомним, что дробно-рациональной функцией называется функция вида 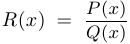 , где
, где 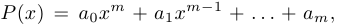
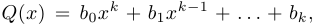
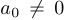 ,
, 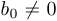 . Мы при этом предполагаем, что дробь
. Мы при этом предполагаем, что дробь 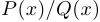 несократима, то есть числитель и знаменатель не имеют общих корней.
несократима, то есть числитель и знаменатель не имеют общих корней.
При построении графиков таких функций мы рекомендуем следующий алгоритм.
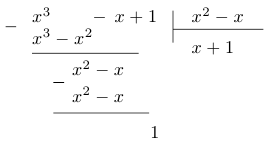
Шаг 1. Если степень числителя больше или равна степени знаменателя, то следует привести дробь к стандартному виду, выделив целую часть и правильную дробь. Это можно сделать, разделив многочлен на многочлен «уголком».
Например, 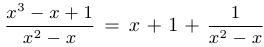 . Целая часть этого разложения и является асимптотической кривой
. Целая часть этого разложения и является асимптотической кривой 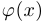 . В нашем примере это прямая
. В нашем примере это прямая 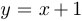 , которая будет наклонной асимптотой.
, которая будет наклонной асимптотой.
Шаг 2. Обозначим числитель получившейся правильной дроби через 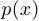 , а саму правильную дробь через
, а саму правильную дробь через 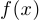 . Пусть
. Пусть 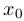 — некоторый корень знаменателя кратности
— некоторый корень знаменателя кратности  . Тогда
. Тогда 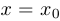 является асимптотой той же четности, что и число
является асимптотой той же четности, что и число 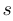 .
.
Обозначим через 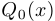 многочлен, стоящий в знаменателе, но без множителя
многочлен, стоящий в знаменателе, но без множителя 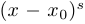 и найдем число
и найдем число 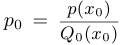 . Тогда вблизи изоклины будет справедливо соотношение
. Тогда вблизи изоклины будет справедливо соотношение 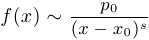 при
при 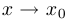 .
.
Шаг 3. Находим корни функции 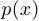 и на асимптотической кривой отмечаем точки, абсциссы которых совпадают с этими корнями. Используя то, что график функции
и на асимптотической кривой отмечаем точки, абсциссы которых совпадают с этими корнями. Используя то, что график функции 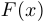 пересекает асимптотическую кривую
пересекает асимптотическую кривую 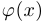 только в этих точках, строим эскиз графика.
только в этих точках, строим эскиз графика.
Упр. 3. На рисунке изображены графики трех дробно-рациональных функций, представленных в стандартном виде. Пунктиром выделены асимптотические кривые и вертикальные асимптоты. Укажите тип этих асимптот и точки пересечения графика с асимптотической кривой.
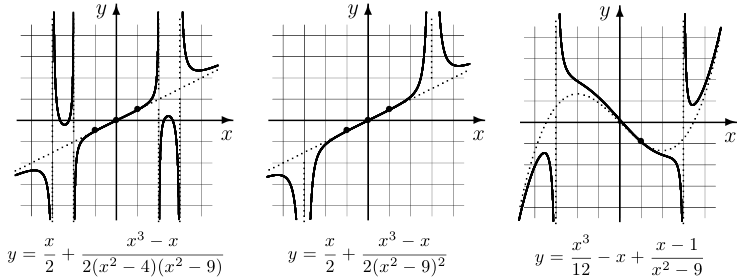
Разумеется, находить наклонные асимптоты можно и другим путем — используя пределы для нахождения постоянных  и
и  .
.
Пример 7.
Найти асимптоты графика функции 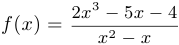 .
.
Решение. Вертикальные асимптоты определяются уравнениями 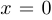 и
и 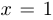 (нули знаменателя), поскольку при этих значениях числитель не равен нулю.
(нули знаменателя), поскольку при этих значениях числитель не равен нулю.
Чтобы найти наклонные асимптоты, следует рассмотреть предел отношения
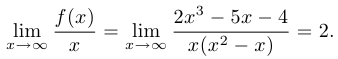
После этого рассматриваем предел разности
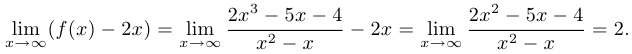
Таким образом, наклонные асимптоты — прямые, задающиеся уравнением 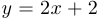 .
.
Иррациональные особенности.
В этом коротком параграфе мы должны договориться об областях определения.
Функция 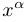 определена при всех
определена при всех 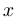 (кроме нуля при
(кроме нуля при 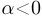 ), если
), если 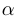 — целое или рациональная дробь вида
— целое или рациональная дробь вида 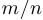 , где
, где 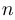 — нечетное, а
— нечетное, а 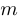 — четное целое число. В последнем случае принято записывать
— четное целое число. В последнем случае принято записывать во избежание неприятностей, связанных с равенством
во избежание неприятностей, связанных с равенством 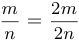 .
.
В остальных случаях функция 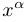 определена при
определена при 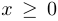 , если
, если 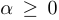 , и при
, и при 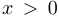 , если
, если 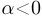 .
.
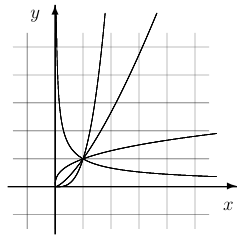
Упр. 4. Справа изображены графики функций 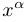 при
при
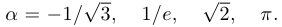
Сопоставьте каждому графику свое 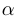 .
.
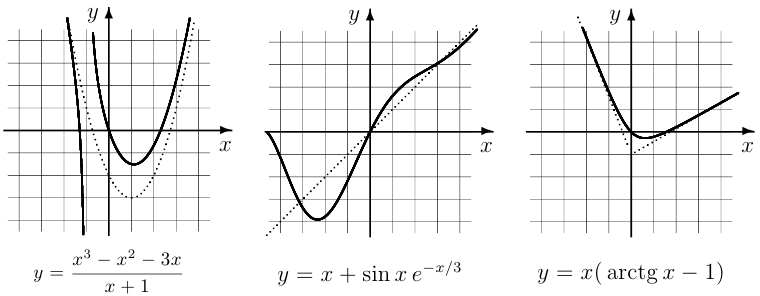
Приведем еще три примера графиков функций, содержащих иррациональности. Во всех случаях функция имеет вид 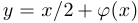 . Функция
. Функция 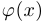 указана под графиком.
указана под графиком.
План полного исследования функции:

На этой странице найдёте другие готовые курсовые работы во высшей математике:
Много готовых курсовых работ по высшей математике
Можете посмотреть другие готовые курсовые работы по высшей математике:

