Криволинейные интегралы в математике с примерами решения и образцами выполнения

При изучении темы «Криволинейные интегралы» вы познакомитесь с понятиями криволинейных интегралов первого рода (по длине дуги) и второго рода (по координатам) от функций двух и трех переменных и научитесь вычислять их вдоль различных плоских и пространственных кривых, заданных параметрически, в декартовых и в полярных координатах, приводя криволинейные интегралы к определенным.

Криволинейные интегралы первого рода

Постановка задачи. Вычислить криволинейный интеграл

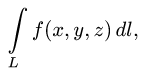
где L — часть гладкой кривой, заданной параметрически

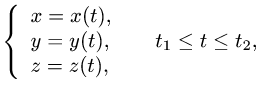
и dl — дифференциал длины дуги.

План решения. Криволинейный интеграл первого рода по кривой L определяется формулой

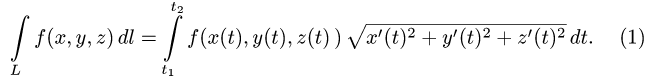
Подчеркнем, что криволинейный интеграл первого рода не зависит
от направления обхода кривой и всегда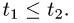

1.Вычисляем 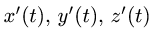и

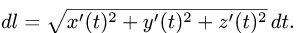
2.Вычисляем криволинейный интеграл по формуле (1) и записываем ответ.

Замечание:

Если граничные точки кривой L 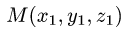и
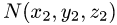заданы в декартовых координатах, то 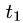и 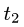определяем, решая системы уравнений

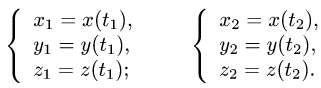
Замечание:

Если кривая задана как линия пересечения двух
поверхностей:

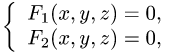
то ее необходимо параметризовать.

Замечание:

Если плоская кривая задана уравнением у = у(х)
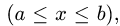то дифференциал длины дуги равен 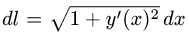и формула (1) имеет вид

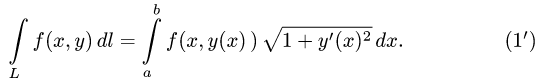
Если плоская кривая задана в полярных координатах 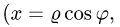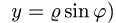уравнением 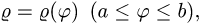то дифференциал длины дуги равен

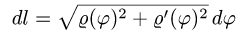
и формула (1) имеет вид

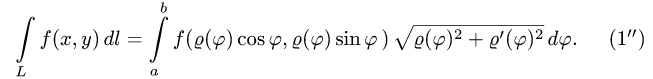
Пример:

Вычислить криволинейный интеграл

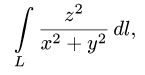
где L — первый виток винтовой линии

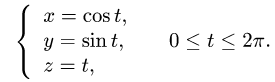
Решение:

1.Вычисляем: x'(t) = — sin t, y'(t) = cos t, z'(t) = 1, 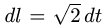и

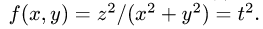
2.Подставляем эти результаты в формулу (1) и вычисляем определенный интеграл:

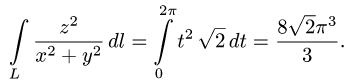
Ответ.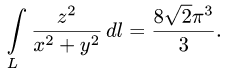

Пример:

Вычислить криволинейный интеграл

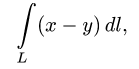
где L — отрезок прямой от точки А(0, 0) до точки В(4, 3).

Решение:

1.В данном случае уравнение прямой есть 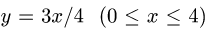и, следовательно, 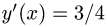и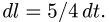

2.Подставляем эти результаты в формулу (1) и вычисляем определенный интеграл:

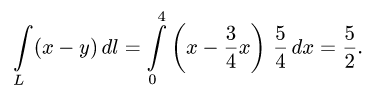
Ответ.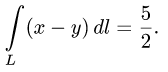

Пример:

Вычислить криволинейный интеграл

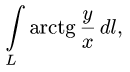
где L — часть спирали Архимеда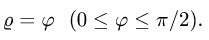

Решение:

1.Вычисляем: 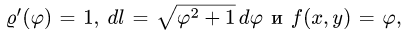так как 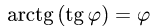при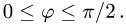

2.Подставляем эти результаты в формулу (1″) и вычисляем определенный интеграл:

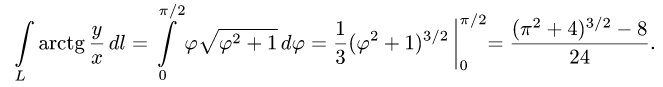
Ответ.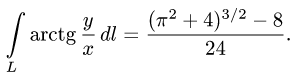

Криволинейные интегралы второго рода

Постановка задачи. Вычислить криволинейный интеграл

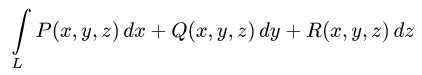
где L — часть гладкой кривой, заданной параметрически

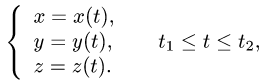
План решения. Криволинейный интеграл второго рода по кривой L определяется формулой

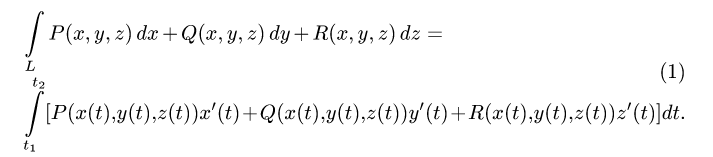
1.Вычисляем x'(t), y'(t) и z'(t).

2.Вычисляем криволинейный интеграл по формуле (1) и записываем ответ.

Замечание:

Если граничные точки кривой L 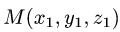и
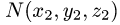заданы в декартовых координатах, то 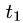и 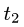определяем, решая системы уравнений

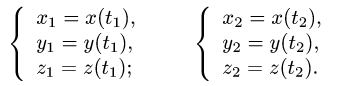
Замечание:

Если кривая задана как линия пересечения двух
поверхностей:

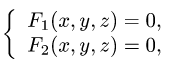
то ее необходимо параметризовать.

Пример:

Вычислить криволинейный интеграл

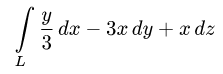
по части кривой L, заданной параметрически

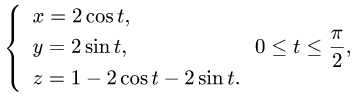
Решение:

1.Вычисляем: x'(t) = — 2sin t, y'(t) = 2cos t и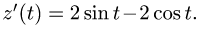

2.Вычисляем криволинейный интеграл по формуле (1):

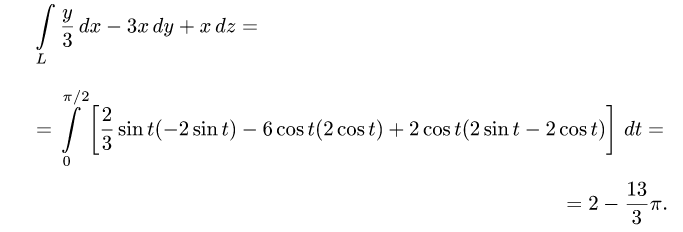
Ответ.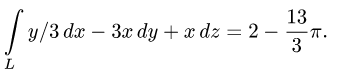

Пример:

Вычислить криволинейный интеграл

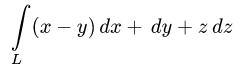
от точки М(2,0, 4) до точки N(—2,0,4) 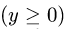по кривой L, образованной пересечением параболоида 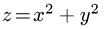и плоскости z = 4,

Решение:

В сечении получается окружность

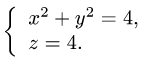
Поэтому параметрические уравнения кривой L имеют вид

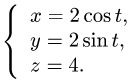
1.Вычисляем: х'(t) = -2sin t, у'(t) = 2cos t и z'(t) = 0.

Определяем из условий

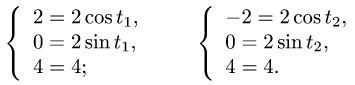
Учитывая, что 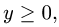получаем 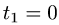и

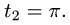
2.Вычисляем криволинейный интеграл по формуле (1):

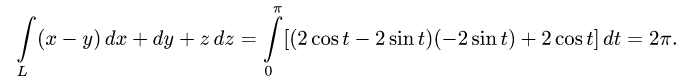
Ответ.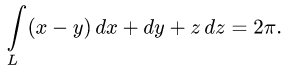

Дополнение к криволинейному интегралу

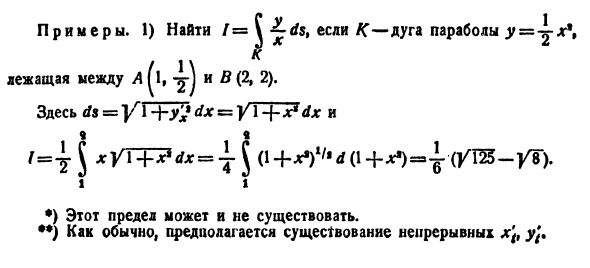
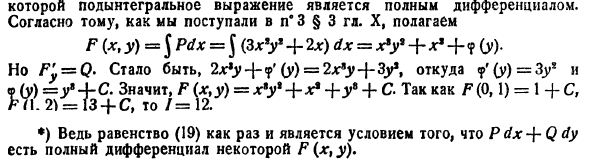
Смотрите также:

Предмет высшая математика

Двойной интеграл	Дальнейшие сведения из теории рядов
Тройной интеграл	Координаты на плоскости

Решение криволинейных интегралов

Кривая АВ, заданная параметрическими уравнениями

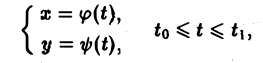
называется гладкой, если функции φ(t) и ψ(t) имеют на отрезке [tо, t1] непрерывные производные φ'(t) и ψ'(t), причем

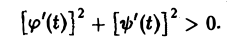
Если в конечном числе точек отрезка [tо, t1] эти производные не существуют или одновременно обращаются в нуль, то кривая называется кусочно-гладкой.

Пусть АВ — плоская кривая, гладкая или кусочно-гладкая. Пусть f(M) — функция, заданная на кривой АВ или в некоторой области D, содержащей эту кривую. Рассмотрим разбиение кривой АВ на части точками

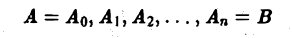
(рис. 1).

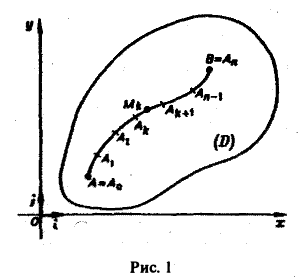
Выберем на каждой из дуг AkAk+1 произвольную точку Мk и составим сумму

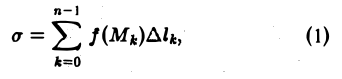
где ∆lk — длина дуги AkAk+1 и назовем ее интегральной суммой для функции f(M) по длине дуги кривой. Пусть ∆l — наибольшая из длин частичных дуг, т.е.

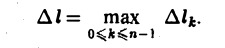
Определение:

Если при ∆l —► 0 интегральная сумма (1) имеет конечный предел, не зависящий ни от способа разбиения кривой АВ на части, ни от выбора точек на каждой из дуг разбиения, то этот предел называется криволинейным интегралом 1 -го рода от функции f(M) по кривой АВ (интеграл по длине дуги кривой) и обозначается символом

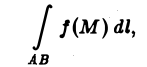
или

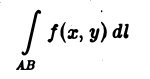
(точка М(х, у) лежит на кривой АВ).
В этом случае функция f(M) называется интегрируемой вдоль кривой АВ, кривая АВ называется контуром интегрирования, А — начальной, В — конечной точками интегрирования. Таким образом, по определению,
(2)

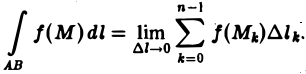
Пример:

Пусть вдоль некоторой гладкой кривой L распределена масса с переменной линейной плотностью f(M). Найти массу т кривой L.

Разобьем кривую L на п произвольных частей MkMk+1 (k = 0,1,… , n —1) и вычислим приближенно массу каждой части, предполагая, что на каждой из частей MkMk+1 плотность постоянна и равна плотности в какой-нибудь из ее точек, например, в крайней левой точке f(Mk). Тогда сумма

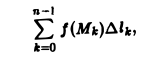
где ∆lk — длина k-ой части, будет приближенным значением массы т. Ясно, что погрешность будет тем меньше, чем мельче разбиение кривой L. В пределе при ∆l → 0 (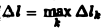) получим точное значение массы всей кривой L, т.е.

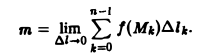
Но предел справа есть криволинейный интеграл 1-го рода. Значит,

Существование криволинейного интеграла 1-го рода

Примем на кривой АВ за параметр длину дуги I, отсчитываемую от начальной точки А (рис. 2). Тогда кривую АВ можно описать уравнениями
(3)

где L — длина кривой АВ.

Уравнения (3) называются натуральными уравнениями кривой АВ. При переходе к натуральным уравнениям функция f(x, у), заданная на кривой АВ, сведется к функции переменной l: f(x(l), y(l). Обозначив через lk (k = 0, 1,…, п — 1) значение параметра l, отвечающее точке Мk, перепишем интегральную сумму (1) в виде

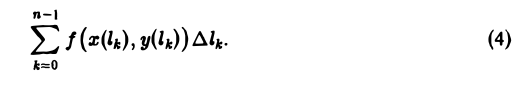
Это — интегральная сумма, отвечающая определенному интегралу

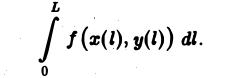
Поскольку интегральные суммы (1) и (4) равны между собой, то равны и отвечающие им интегралы. Таким образом,
(5)

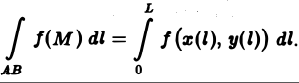
Теорема:

Если функция f(M) непрерывна вдоль гладкой кривой АВ, то существует криволинейный интеграл

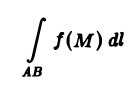
(поскольку при этих условиях существует определенный интеграл, стоящий в равенстве (5) справа ).

Свойства криволинейных интегралов 1-го рода

1, Из вида интегральной суммы (1) следует, что

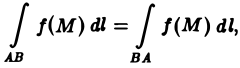
т.е. величина криволинейного интеграла 1-го рода не зависит от направления интегрирования.

2. Линейность. Если для каждой из функций f(M) и д(М) существует криволинейный интеграл по кривой АВ, то для функции af(M) + βg{М), где а и β — любые постоянные, также существует криволинейный интеграл по кривой АВ, причем

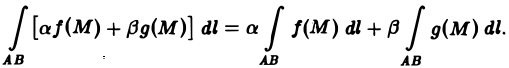
3. Аддитивность. Если кривая АВ состоит из двух кусков АС и С В и для функции f(М) существует криволинейный интеграл по AВ, то существуют интегралы

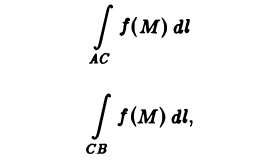
причем

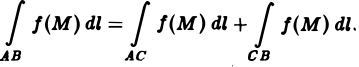
4. Если f(M) ≥ 0 на кривой AB, то

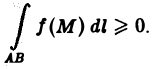
5. Если функция f(M) интегрируема на кривой АВ, то функция |f(М)| также интегрируема на АВ, и при этом

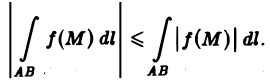
6. Формула среднего значения. Если функция f(M) непрерывна вдоль кривой АВ, то на этой кривой найдется точка Мс такая, что

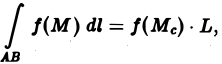
где L — длина кривой AB.

Вычисление криволинейного интеграла 1-го рода

Пусть кривая АВ задана параметрическими уравнениями

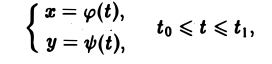
причем точке А соответствует значение t = t0, а точке В — значение t = t1. Будем предполагать, что функции φ(t) и ψ(t) непрерывны на [to, t1] вместе со своими производными φ'(t) и ψ'(t) и выполнено неравенство

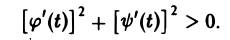
Тогда дифференциал дуги кривой вычисляется по формуле

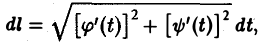
и

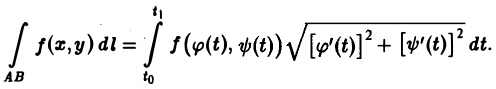
В частности, если кривая АВ задана явным уравнением

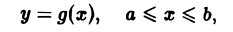
причем функция g(х) непрерывно дифференцируема на [а, b] и точке А соответствует значение х = а, а точке В — значение х = b, то, принимая х за параметр, получаем

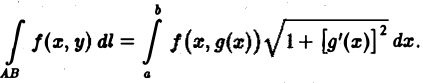
Криволинейные интегралы 1-го рода для пространственных кривых

Определение криволинейного интеграла 1-го рода, сформулированное выше для плоской кривой, дословно переносится на случай, когда функция f(M) задана вдоль некоторой пространственной кривой АВ.

Пусть кривая АВ задана параметрическими уравнениями

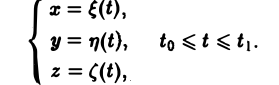
Тогда криволинейный интеграл 1-го рода от функции f, взятый вдоль этой кривой, можно свести к определенному интегралу при помоши следующей формулы:

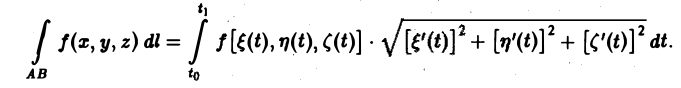
Пример:

Вычислить криволинейный интеграл

где L — контур треугольника с вершинами в точках O(0,0), A(1,0), B(0, I) (рис. 3).

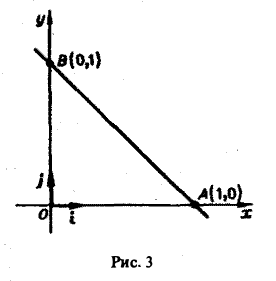
По свойству аддитивности имеем

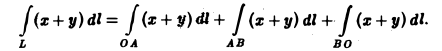
Вычислим каждый из интегралов в отдельности. Так как на отрезке OA имеем: 0 ≤ x ≤ 1, у = 0 и dl = dx, то

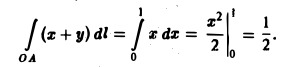
На отрезке АВ имеем х + у = 1, откуда у = 1 — х, т.е.

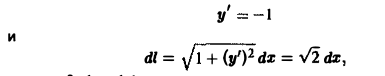
причем 0 ≤ х ≤ 1, тогда

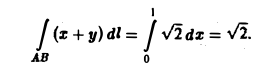
Наконец,

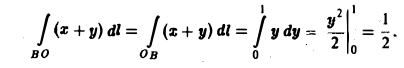
Следовательно,

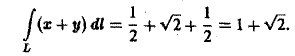
Замечание:

При вычислении интегралов

мы воспользовались свойством 1, согласно которому

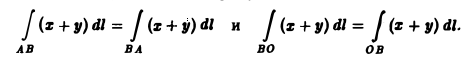
Криволинейные интегралы 2-го рода

Пусть АВ — гладкая или кусочно-гладкая ориентированная кривая на плоскости хОу и пусть

F(M) = Р(М) i + Q(M) j

— вектор-функция, определенная в некоторой области D, содержащей кривую АВ. Разобьем кривую АВ на части точками

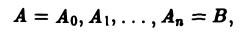
координаты которых обозначим соответственно через

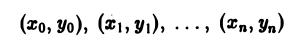
(рис. 4).

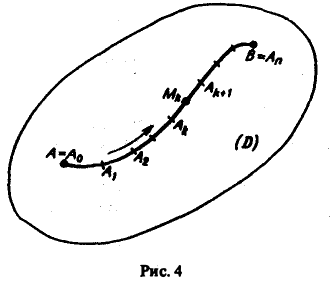
На каждой из элементарных дуг АkАk+1, возьмем произвольно точку Мk(ξk, ηk) и составим сумму

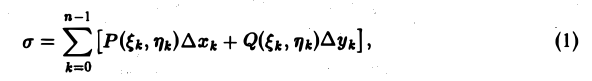
где

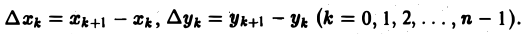
Пусть ∆l — длина наибольшей из дуг АkАk+1.

Определение:

Если при ∆l → 0 сумма (1) имеет конечный предел, не зависящий ни от способа разбиения кривой АВ. ни от выбора точек (ξk, ηk) на элементарных дугах, то этот предел называется криволинейным интегралом 2-го рода от вектор-функции F(M) по кривой АВ и обозначается символом

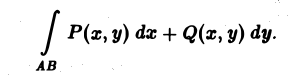
Так что по определению (2)

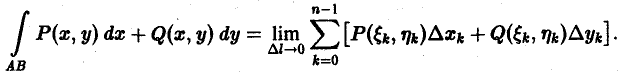
Теорема:

Если в некоторой области D, содержащей кривую АВ, функции Р(х,у) и Q(х, у) непрерывны, то криволинейный интеграл 2-го рода

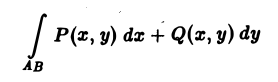
существует.
Пусть

r(М) = xi + yj

— радиус-вектор точки М(х, у). Тогда

dr = i dx + j dy,

и подынтегральное выражение

Р(х, у) dx + Q(x, у) dy

в формуле (2) можно представить в виде скалярного произведения векторов F(Af) и dr. Так что интеграл 2-го рода от вектор-функции

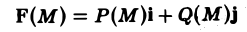
по кривой АВ можно записать коротко так:

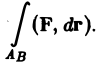
Вычисление криволинейного интеграла 2-го рода

Пусть кривая АВ задана параметрическими уравнениями,

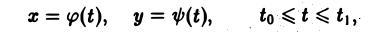
где функции φ(t) и ψ(t) непрерывны вместе с производными φ'(t), ψ'(t) на отрезке [to, t1] причем изменению параметра t от to до t1 соответствует движение точки М(х, у) по кривой АВ от точки А к точке В.

Если в некоторой области D, содержащей кривую АВ, функции Р(х, у) и Q(x, у) непрерывны, то криволинейный интеграл 2-го рода

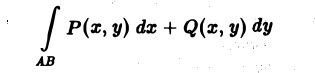
сводится к следующему определенному интегралу:
(3)

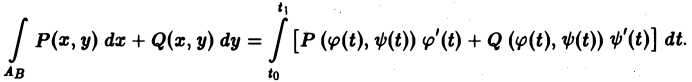
Таким образом, вычисление криволинейного интеграла 2-го рода также может быть сведено к вычислению определенного интеграла.

Пример:

Вычислить интеграл

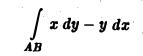
1) вдоль прямолинейного отрезка, соединяющего точки A(0,0) и В{1, 1);

2) вдоль параболы у = х , соединяющей те же точки (рис.5).

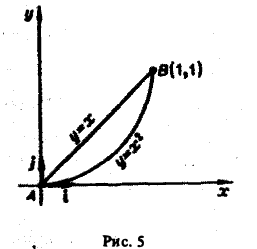
1) Уравнение линии АВ: у = х (х — параметр, 0 ≤ х ≤ 1), откуда dy = dx. Так что

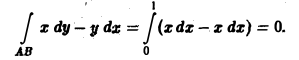
2) Уравнение линии AB:

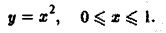
Отсюда

dy = 2х dx,

поэтому

x dy = 2x² dx

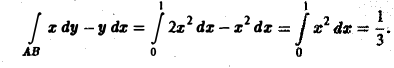
Рассмотренный пример помазывает, что величина криволинейного интеграла 2-го рода, вообще говоря, зависит от формы пути интегрирования.

Свойства криволинейного интеграла 2-го рода

1. Линейность. Если существуют криволинейные интегралы

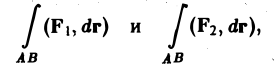
то при любых действительных а и β существует и интеграл

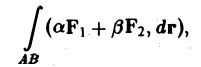
причем

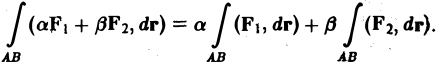
2. Аддитивность. Если кривая АВ разбита на части АС и С В и криволинейный интеграл

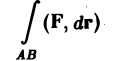
существует, то существуют интегралы

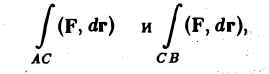
причем

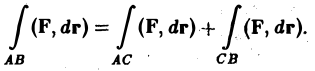
Криволинейный интеграл второго рода (в отличие от криволинейного интеграла 1-го рода) зависит от того, в каком направлении (от A к В или от В к А) проходится кривая АВ, и меняет знак при изменении направления движения по кривой, т. е.

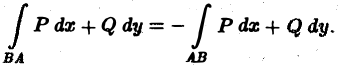
Замечание:

Последнее свойство cotrmrrayer физической интерпретации криволинейного интеграла 2-го рода как работы силового паля F вдоль некоторого путь: при изменении направления движения по кривой работа силового поля вдоль этой кривой меняет знак на противоположный.

Связь между криволинейными интегралами 1-го и 2-го рода

Рассмотрим криволинейный интеграл 2-го рода

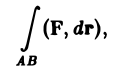
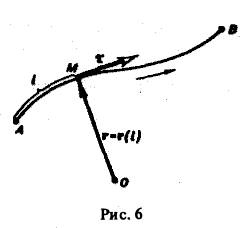
где ориентированная кривая АВ (А — начальная точка, В — конечная точка) задана векторным уравнением

r = r(l)

(здесь l — длина кривой, отсчитываемая в том направлении, в котором ориентирована кривая АВ) (рис. 6).

Тогдa

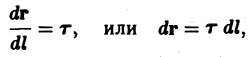
где т = т(l) — единичный вектор касательной к кривой АВ в точке М(l). Тогда

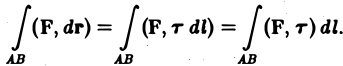
Заметим, что последний интеграл в этой формуле — криволинейный интеграл 1-го рода. При изменении ориентации кривой АВ единичный вектор касательной т заменяется на противоположный вектор (—т), что влечет изменение знака его подынтегрального выражения и, значит, знака самого интеграла.

Формула Грина

Выведем формулу Грина, связывающую криволинейный интеграл

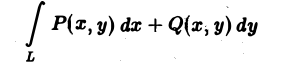
по границе L некоторой плоской области D с двойным интегралом по этой области.

Теорема:

Если в замкнутой области D, ограниченной кусочно-гладким контуром L, функции Р(х, у) и Q{x, у) непрерывны и имеют непрерывные частные производные 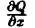и 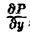то справедливо равенство (формула Грина):

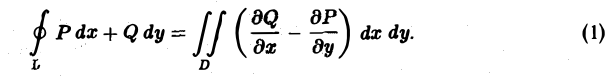
Здесь символ означает интегрирование по границе L области D, причем граница L проходится так, что область D остается слева (рис. 7).

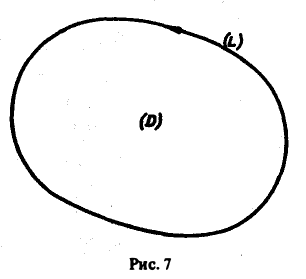
Граница L плоской области D может состоять из одной или нескольких простых замкнутых кривых (компонент). В первом случае она называется односвязной, а во втором — многосвязной. Если граница L состоит из конечного числа кусочно-гладких замкнутых кривых Li, то кривые L, называются связными компонентами границы. На рис. 8 изображена трехсвязная область.

Односвязная область D (область «без дырок») обладает тем свойством, что любая лежащая в ней замкнутая кривая может быть стянута в точку Р ∈ D, оставаясь в процессе стягивания в области D.
Доказательство теоремы проведем для односвязной области.

В силу свойства линейности достаточно доказать, что

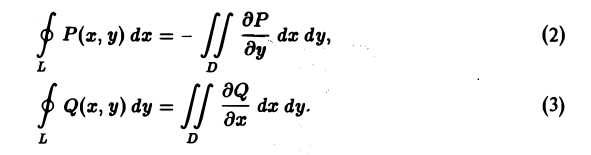
Докажем первую из этих формул.

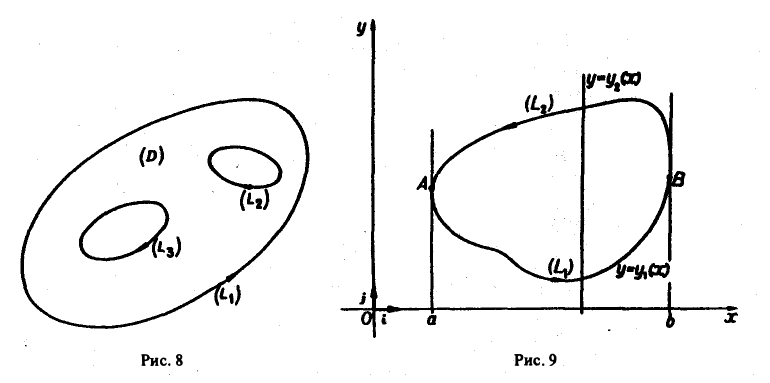
Предположим сначала, что кривая L пересекается каждой прямой, параллельной оси Оу, не более чем в двух точках или по целому отрезку (рис. 9). Если каждая такая прямая пересекает кривую L не более чем в двух точках, то кривую L можно разбить на две части L1 и L2 (верхнюю и нижнюю), каждая из которых проектируется взаимно однозначно на некоторый отрезок [а, b] оси Ох. В силу аддитивности криволинейного интеграла имеем

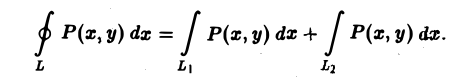
На каждой из кривых L1 и L2 возьмем в качестве параметра абсциссу х и запишем уравнения этих кривых соответственно в виде

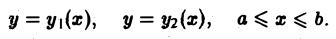
Тогда

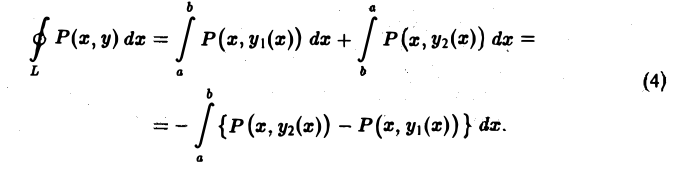
По предположению производная 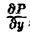непрерывна в D, и значит, в силу известной формулы интегрального исчисления, приращение функции можно записать через интеграл от производной этой функции:

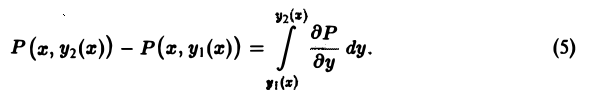
Из формул (4) и (5) получаем

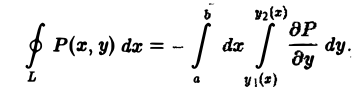
Повторный интеграл в правой части последнего соотношения равен двойному интегралу от функции 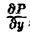по области D, так что окончательно имеем

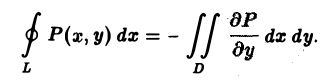
Формула (2) доказана.

Соотношение (3) доказывается аналогично. Складывая почленно соотношения (2) и (3), получаем формулу Грина (1).

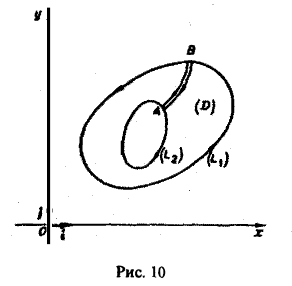
Отметим, что формула Грина имеет место и для более сложных контуров L, и для неодносвязных областей D. Рассмотрим, например, случай двухсвязной области (рис. 10). Сделаем разрез АВ этой области, превращающий ее в односвязную. Тогда

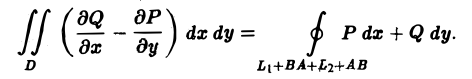
Отсюда, учитывая, что

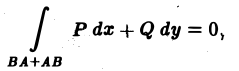
получим

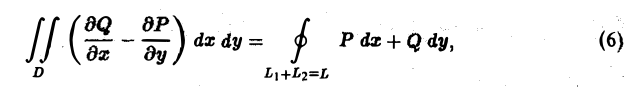
где интегрирование по кривой L1 ведется в направлении против движения часовой стрелки, а по кривой L2 — в направлении движения часовой стрелки. Отметим, что при этом кривые L1 и L2 проходятся так, что область D остается слева. Такое направление обхода контура принимается за положительное.

Площадь плоской области

Возьмем

Р(х, y) = -y и Q(x,y) = x.

Тогда

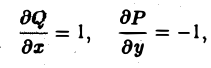
и по формуле Грина (1) получаем

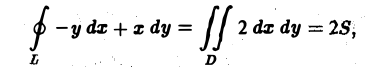
где S — площадь области D.

Отсюда получаем формулу для вычисления площади S плоской области D с помощью криволинейного интеграла по границе L этой области: (7)

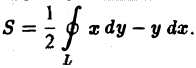
Пример:

Вычислить площадь области, ограниченной эллипсом L:

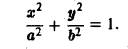
Запишем уравнение эллипса в параметрической форме

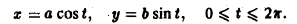
Искомая площадь находится no формуле (7), где криволинейный интеграл берется по эллипсу при обходе контура в положительном направлении, что соответствует изменен ию параметра t от 0 до 2 π. Так как

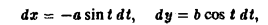
то отсюда получаем, что

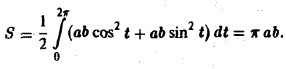
Замечание:

Пусть в пространстве задана ориентированная кусочно-гладкая кривая АВ и пусть, кроме того, в некоторой области Ω, содержащей кривую А В, задана вектор-функция

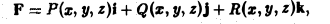
где Р, Q, R — непрерывные в Ω функции. Аналогично плоскому случаю криволинейный интеграл от вектор-функции F по ориентированной кривой АВ определим выражением

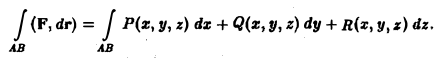
Это — криволинейный интеграл 2-го рода в пространстве.

Приложения криволинейных интегралов

Масса кривой

В примере 1 из § 1 было показано, что масса кривой L вычисляется с помощью интеграла 1-го рода

где f(M) — переменная линейная плотность на кривой L. (Мы предполагаем, что f(М) — непрерывная функция на АВ.)

Площадь цилиндрической поверхности

Пусть в плоскости хОу задана некоторая спрямляемая (т. е. имеющая длину) кривая АВ и на этой кривой определена непрерывная функция f(М) ≥ 0. Тогда совокупность точек (х, y, f(x, у)), или (М, f(M)), составит некоторую кривую, лежащую на цилиндрической поверхности, для которой кривая АВ является направляющей, а ее образующая параллельна оси Oz. Требуется определить площадь цилиндрической поверхности ABDC, ограниченной снизу кривой АВ, сверху — кривой z = f(M), где М ∈ АВ, и вертикальными прямыми АС и BD (рис. 11).

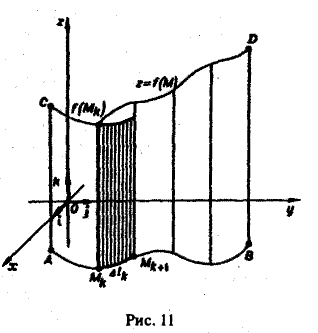
Для решения этой задачи поступим так:

1) разобьем кривую АВ на п частей точками

так, как показано на рис. 11;

2) из каждой точки Мk проведем перпендикуляр к плоскости хОу высотой f(Mk) (при этом цилиндрическая поверхность ABDC разобьется на n полосок);

3) каждую полоску заменим прямоугольником с основанием ∆lk, где ∆lk — длина дуги МkМk+1, и высотой, равной значению функции f{M) в какой-нибудь точке этой дуги, например, в точке Мk.

Тогда площадь k-ой полоски будет приближенно равна f(Mk) ∆lk, а площадь всей поверхности ABDC

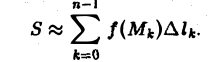
Это приближенное равенство будет тем точнее, чем мельче будут частичные дуги МkМk+1, на которые разбита кривая АВ. Пусть ∆l — наибольшая из длин ∆lk частичных дуг MkMk+1. Тогда при ∆l —> 0 в пределе получим точное значение искомой площади

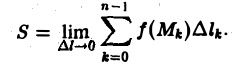
Предел справа по определению есть криволинейный интеграл первого рода от функции f(М) по кривой АВ. Итак, (2)

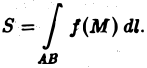
Пример:

Вычислить площадь части боковой поверхности цилиндра

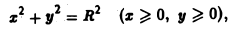
срезанного сверху поверхностью

ху = 2Rz.

Сведем задачу к вычислению криволинейного интеграла 1-го рода от функции

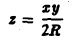
вдоль дуги окружности, расположенной в первой четверти. Будем иметь

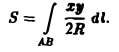
Параметрические уравнения линии АВ —

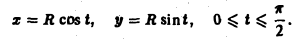
Тогда

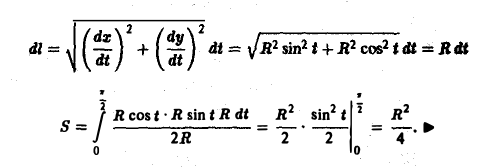
Площадь плоской фигуры

Ранее мы установили, что площадь S плоской фигуры D, ограниченной линией L, вычисляется по формуле

Правая часть есть криволинейный интеграл 2-го рода.

Работа силы:

Пусть в некоторой плоской области D, содержащей кривую АВ, задана сила

F(M) = P(M)i + Q(M)J, (4)

где функции Р(М) и Q(M), а следовательно, и F(M) предполагаются непрерывными функциями точки М. Требуется найти работу силы F, если под действием этой силы материальная точка М, имеющая единичную массу, переместилась из точки А в точку В по кривой АВ.

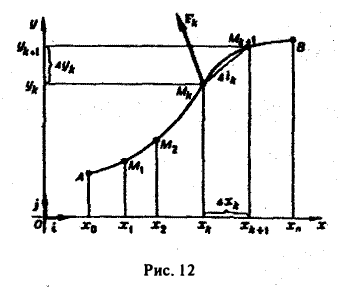
Для решения этой задачи разделим кривую АВ на п частей точками

(рис. 12), заменим каждую дугу хордой MkMk+1 и, предполагая для простоты, что на участке кривой (а значит, и на хорде MkMk+1) сила Fk имеет постоянное значение, например, равное ее значению в точке Мk,

получим приближенное выражение работы силы на участке пути :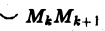

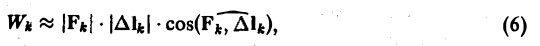
где |Fk| — длина вектора Fk, |∆lk| — длина вектора ∆lk

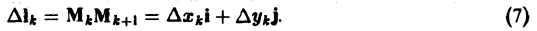
Из формулы (4) с учетом (5) получим

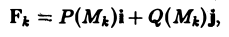
ИЛИ

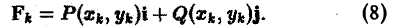
Так как правая часть формулы (6) есть скалярное произведение векторов Fk и ∆lk, то, учитывая (7) и (8), будем иметь

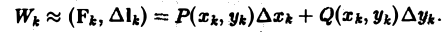
Суммируя по всем значениям k(k = 0,1,2,…, п — 1), получим величину

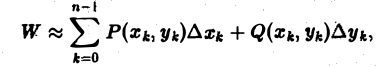
приближенно выражающую работу силы F(M) на всем пути от А до В.

Предел этой суммы при ∆хk → 0 и ∆уk → 0 принимают за точное значение работы. Но с другой стороны, предел этой суммы есть криволинейный интеграл 2-го рода от вектор-функции F(M) по кривой АВ. Итак, работа силы вычисляется по формуле
(9)

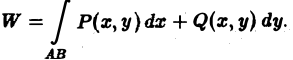
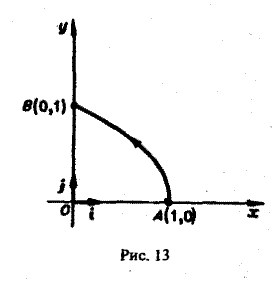
Пример:

Найти работу силы

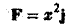
при перемещении единичной массы по параболе

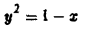
от точки A(1,0) до точки В(0,1) (рис. 13). 4 Применим формулу (9), положив в ней

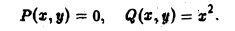
Так как

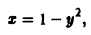
то искомую работу можно вычислить так:

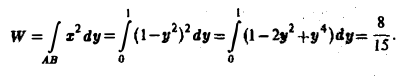
Обобщение на случай пространственной кривой(рис. 14),

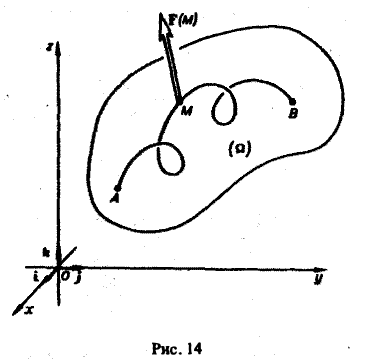
Если в некоторой пространственной области Ω, содержащей пространственную кривую АВ, задана сила

F(M) = Р(М)i + Q(M)j + R(M)k,

где Р(М), Q(M) и R(M) — непрерывные функции в области Ω, то работа, совершаемая силой F(М) по перемещению материальной точки М с единичной массой из точки А в точку В по пространственной кривой АВ, равна

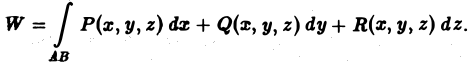
Решение заданий и задач по предметам:

• Математика
• Высшая математика
• Математический анализ
• Линейная алгебра

Дополнительные лекции по высшей математике:

1. Тождественные преобразования алгебраических выражений
2. Функции и графики
3. Преобразования графиков функций
4. Квадратная функция и её графики
5. Алгебраические неравенства
6. Неравенства
7. Неравенства с переменными
8. Прогрессии в математике
9. Арифметическая прогрессия
10. Геометрическая прогрессия
11. Показатели в математике
12. Логарифмы в математике
13. Исследование уравнений
14. Уравнения высших степеней
15. Уравнения высших степеней с одним неизвестным
16. Комплексные числа
17. Непрерывная дробь (цепная дробь)
18. Алгебраические уравнения
19. Неопределенные уравнения
20. Соединения
21. Бином Ньютона
22. Число е
23. Непрерывные дроби
24. Функция
25. Исследование функций
26. Предел
27. Интеграл
28. Двойной интеграл
29. Тройной интеграл
30. Интегрирование
31. Неопределённый интеграл
32. Определенный интеграл
33. Поверхностные интегралы
34. Несобственные интегралы
35. Кратные интегралы
36. Интегралы, зависящие от параметра
37. Квадратный трехчлен
38. Производная
39. Применение производной к исследованию функций
40. Приложения производной
41. Дифференциал функции
42. Дифференцирование в математике
43. Формулы и правила дифференцирования
44. Дифференциальное исчисление
45. Дифференциальные уравнения
46. Дифференциальные уравнения первого порядка
47. Дифференциальные уравнения высших порядков
48. Дифференциальные уравнения в частных производных
49. Тригонометрические функции
50. Тригонометрические уравнения и неравенства
51. Показательная функция
52. Показательные уравнения
53. Обобщенная степень
54. Взаимно обратные функции
55. Логарифмическая функция
56. Уравнения и неравенства
57. Положительные и отрицательные числа
58. Алгебраические выражения
59. Иррациональные алгебраические выражения
60. Преобразование алгебраических выражений
61. Преобразование дробных алгебраических выражений
62. Разложение многочленов на множители
63. Многочлены от одного переменного
64. Алгебраические дроби
65. Пропорции
66. Уравнения
67. Системы уравнений
68. Системы уравнений высших степеней
69. Системы алгебраических уравнений
70. Системы линейных уравнений
71. Системы дифференциальных уравнений
72. Арифметический квадратный корень
73. Квадратные и кубические корни
74. Извлечение квадратного корня
75. Рациональные числа
76. Иррациональные числа
77. Арифметический корень
78. Квадратные уравнения
79. Иррациональные уравнения
80. Последовательность
81. Ряды сходящиеся и расходящиеся
82. Тригонометрические функции произвольного угла
83. Тригонометрические формулы
84. Обратные тригонометрические функции
85. Теорема Безу
86. Математическая индукция
87. Показатель степени
88. Показательные функции и логарифмы
89. Множество
90. Множество действительных чисел
91. Числовые множества
92. Преобразование рациональных выражений
93. Преобразование иррациональных выражений
94. Геометрия
95. Действительные числа
96. Степени и корни
97. Степень с рациональным показателем
98. Тригонометрические функции угла
99. Тригонометрические функции числового аргумента
100. Тригонометрические выражения и их преобразования
101. Преобразование тригонометрических выражений
102. Комбинаторика
103. Вычислительная математика
104. Прямая линия на плоскости и ее уравнения
105. Прямая и плоскость
106. Линии и уравнения
107. Прямая линия
108. Уравнения прямой и плоскости в пространстве
109. Кривые второго порядка
110. Кривые и поверхности второго порядка
111. Числовые ряды
112. Степенные ряды
113. Ряды Фурье
114. Преобразование Фурье
115. Функциональные ряды
116. Функции многих переменных
117. Метод координат
118. Гармонический анализ
119. Вещественные числа
120. Предел последовательности
121. Аналитическая геометрия
122. Аналитическая геометрия на плоскости
123. Аналитическая геометрия в пространстве
124. Функции одной переменной
125. Высшая алгебра
126. Векторная алгебра
127. Векторный анализ
128. Векторы
129. Скалярное произведение векторов
130. Векторное произведение векторов
131. Смешанное произведение векторов
132. Операции над векторами
133. Непрерывность функций
134. Предел и непрерывность функций нескольких переменных
135. Предел и непрерывность функции одной переменной
136. Производные и дифференциалы функции одной переменной
137. Частные производные и дифференцируемость функций нескольких переменных
138. Дифференциальное исчисление функции одной переменной
139. Матрицы
140. Линейные и евклидовы пространства
141. Линейные отображения
142. Дифференциальные теоремы о среднем
143. Теория устойчивости дифференциальных уравнений
144. Функции комплексного переменного
145. Преобразование Лапласа
146. Теории поля
147. Операционное исчисление
148. Системы координат
149. Рациональная функция
150. Интегральное исчисление
151. Интегральное исчисление функций одной переменной
152. Дифференциальное исчисление функций нескольких переменных
153. Отношение в математике
154. Математическая логика
155. Графы в математике
156. Линейные пространства
157. Первообразная и неопределенный интеграл
158. Линейная функция
159. Выпуклые множества точек
160. Система координат