Оглавление:
Задание: Нахождение определённых интегралов методом непосредственного интегрирования.
Цель: формирование умения находить определённые интегралы методом непосредственного интегрирования и как интегралы от некоторых сложных функций.
Задание для самостоятельной внеаудиторной работы:
26.1. Выучите определение определенного интеграла. Разберите, в чём заключается техника непосредственного интегрирования в определённом интеграле. Ответьте на контрольные вопросы:
- Что называют определенным интегралом
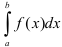 ?
? - Какими свойствами обладает определенный интеграл?
- Запишите формулу Ньютона-Лейбница.
- Какова техника нахождения определённого интеграла при помощи формулы Ньютона-Лейбница?
- Какова глобальные отличия определенного интеграла от неопределенного?
26.2. Найдите определённые интегралы методом непосредственного интегрирования и как интегралы от «некоторых сложных» функций:
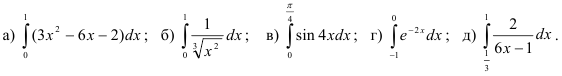

Вам известно, что одним из создателей интегрального исчисления был Готфрид Вильгельм Лейбниц.
Много гениальных открытий принадлежит Лейбницу. И действительно это была неординарная личность! Современников Лейбница поражали его фантастическая эрудиция, почти сверхъестественная память и удивительная работоспособность.
А как же любовь? Лейбницу посчастливилось и здесь. Он полюбил одну из лучших германских женщин — первую королеву Пруссии.

Лейбниц стал её учителем, когда юной принцессе было 12 лет. В 16 лег принцессу выдали замуж за тщеславного, недалёкого, любившего блеск и роскошь брандербургского принца Фридриха.
Серьёзная, вдумчивая, мечтательная принцесса не могла выносить пустой и бессмыссленной придворной жизни. Её отдушиной стала переписка с дорогим и любимым учителем. Эта переписка прекращалась лишь на время свиданий. В письмах теперь уже королевы при всей её сдержанности, нравственной чистоте и сознании долга перед мужем, никогда не ценившем и не понимавшем её, прорывалось сильное чувство.
Выполнив задание 26.2 и заменив получившиеся ответы буквами из таблицы, Вы узнаете, как звали королеву, рано ушедшую из жизни, которую искренне и беззаветно любил Готфрид Вильгельм Лейбниц.
Имя королевы:

Карта ответов:

26.3. Найдите определённые интегралы:
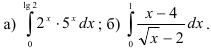
Методические указания по выполнению работы:
Определенным интегралом от функции 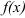 на отрезке
на отрезке 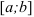 называют предел интегральных сумм
называют предел интегральных сумм 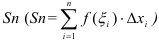 при
при 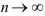 и
и 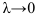 (
(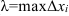 , где
, где 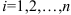 ), который не зависит ни от способа разбиения отрезка
), который не зависит ни от способа разбиения отрезка 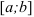 на части, ни от выбора точек
на части, ни от выбора точек 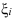 :
: 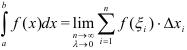 .
.
Числа 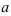 и
и 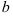 называются соответственно нижней и верхней границами интегрирования,
называются соответственно нижней и верхней границами интегрирования, 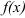 — подынтегральной функцией,
— подынтегральной функцией, 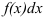 — подынтегральным выражением,
— подынтегральным выражением,  — переменной интегрирования, отрезок
— переменной интегрирования, отрезок 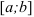 — областью (отрезком) интегрирования.
— областью (отрезком) интегрирования.
При нахождении определённых интегралов используют следующие методы:
1. Непосредственное интегрирование — метод, основанный на использовании свойств определённого интеграла и формулы Ньютона-Лейбница.
Основные свойства определенного интеграла:
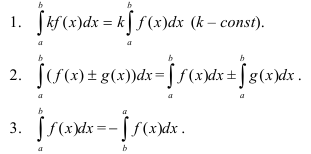
Формула Ньютона-Лейбница: 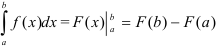 .
.
Для нахождения определённых интегралов методам непосредственного интегрирования можно использовать следующий алгоритм:
- Найдите неопределённый интеграл от заданной функции (если возникают сложности, перечитайте методические указания к выполнению задания 22).
- Выпишите получившуюся первообразную функции, в которую вместо слагаемого
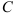 запишите вертикальную черту с верхними и нижними границами интегрирования.
запишите вертикальную черту с верхними и нижними границами интегрирования. - По формуле Ньютона-Лейбница в первообразную вместо переменной подставьте сначала верхнюю границу, затем запишите знак «минус», затем подставьте нижнюю границу интегрирования.
Советуем рассмотреть реализацию данного метода на примере:
Пример 1.
Вычислите 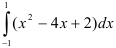 .
.
Решение:
1. Найдем неопределенный интеграл от заданной функции: 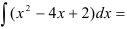
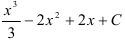 .
.
2. Для нахождения определённого интеграла вместо константы 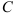 введём границы интегрирования:
введём границы интегрирования:
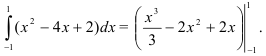
3. В полученную первообразную подставим сначала верхнюю, потом нижнюю границы интегрирования: 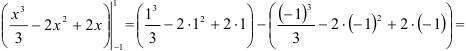
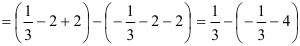 . Раскроем скобки:
. Раскроем скобки: 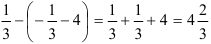 .
.
Ответ: 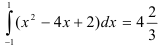 .
.
2. Интегрирование некоторых сложных функций — метод, основанный на использовании техники интегрирования некоторых сложных функций и формулы Ньютона-Лейбница.
Для нахождения определённых интегралов от некоторых сложных функций можно использовать следующий алгоритм:
- Найдите неопределённый интеграл от заданной функции, используя формулу
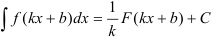 (если возникают сложности, перечитайте методические указания к выполнению задания 20).
(если возникают сложности, перечитайте методические указания к выполнению задания 20). - Для получившейся первообразной вместо слагаемого
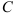 запишите вертикальную черту с верхними и нижними границами интегрирования.
запишите вертикальную черту с верхними и нижними границами интегрирования. - По формуле Ньютона-Лейбница в первообразную вместо переменной подставьте сначала верхнюю границу, затем знак «минус», затем нижнюю границу интегрирования.
Советуем рассмотреть реализацию данного метода на примере:
Пример 2.
Вычислите 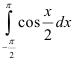 .
.
Решение:
1.Сначала найдем неопределенный интеграл от заданной функции как интеграл от некоторой сложной функции, введя границы интегрирования: 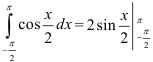 .
.
2. Подставим сначала верхнюю, потом нижнюю границы интегрирования: 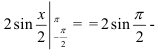
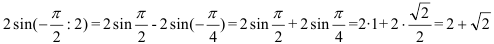 .
.
Ответ: 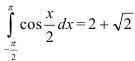 .
.
На этой странице вы сможете посмотреть все остальные темы готовых контрольных работ по высшей математике:
Готовые контрольные работы по высшей математике
Обратите внимание на похожие контрольные работы возможно они вам будут полезны:

