Оглавление:
Задание: Действия над комплексными числами в алгебраической форме. Решение квадратных уравнений.
Целы формирование умения выполнять операции над комплексными числами в алгебраической форме, решать квадратные уравнения с отрицательным дискриминантом.
Задание для самостоятельной внеаудиторной работы:
51.1. Повторите, что называют мнимой единицей. Какой вид имеет алгебраическая форма комплексного числа? Какова геометрическая интерпретация комплексных чисел? Разберите, как выполнить сложение, вычитание, умножение и деление комплексных чисел в алгебраической форме. Какова техника решения квадратных уравнений с отрицательным дискриминантом?
51.2. Закончите высказывания:
а)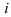 
— мнимая единица — число, …. = ….
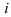б) Алгебраическая форма комплексного числа имеет вид: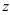 
= …, где … — действительная часть, … -мнимая часть комплексного числа.
в) Множество комплексных чисел обозначают ….
г) Сопряжённым данному комплексному числу называют число, ….
д) Операции над комплексными числами в алгебраической форме аналогичны операциям с ….
При делении комплексных чисел в алгебраической форме необходимо домножить числитель и знаменатель дроби на число, … знаменателю.
е) Комплексное число 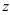= … можно изобразить в виде … или ….
ж) При решении квадратного уравнения с отрицательным дискриминантом получают два … корня.
51.3. Выполните действия над комплексными числами в алгебраической форме, заполнив цифрами пустые ячейки:
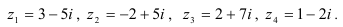
Откуда берут своё начало комплексные числа? В XVI веке в связи с изучением кубических уравнений оказалось необходимым извлекать квадратные корни из отрицательных чисел. В формуле для решения кубических уравнений вида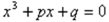 
корни находят по формуле:
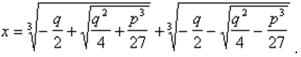
Она безотказно действует в случае, когда уравнение имеет один корень, а если оно имеет три действительных корня (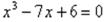
), то под знаком квадратного корня оказывается отрицательное число. Получалось, что путь к этим корням ведет через невозможную операцию извлечения квадратного корня из отрицательного числа.
Тогда итальянский алгебраист Джероламо Кардано в 1545 г. предложил ввести числа новой природы. Кардано называл такие величины “чисто отрицательными» и даже “софистически отрицательными”, считал их бесполезными и старался не употреблять. В самом деле, с помощью таких чисел нельзя выразить ни результат измерения какой-нибудь величины, ни изменение какой-нибудь величины.
Но уже в 1572 году вышла книга итальянского алгебраиста Р. Бомбелли, в которой были установлены первые правила арифметических операций над такими числами, вплоть до извлечения из них кубических корней. Название “мнимые числа» ввел в 1637 году французский математик и философ Рене Декарт. Осталось ввести обозначение мнимых чисел. Именно тогда был придуман символ 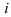. Учёные полагают, что 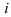— первая буква латинского 
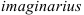— воображаемый, мнимый.
Выполнив задание 51.3, впишите цифры из заштрихованных ячеек в соответствующие ячейки таблицы. Вы узнаете, в каком году впервые для обозначения мнимой единицы был использован символ .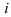
Год введения символа:
51.4. Решите квадратное уравнение:
51.5. Изобразите комплексные числа в виде точек на комплексной плоскости и, используя таблицу «Операции над векторами», найдите расстояние между ними:
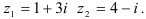
51.6. Вычислите: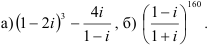 
Методические указания по выполнению работы:
Мнимой единицей 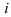будем называть такое число, квадрат которого равен — 1.
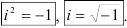
Числа вида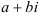 
, где 
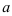и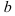 
— действительные числа (
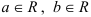), a 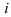— мнимая единица, называются комплексными числами.
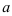— деиствительная часть комплексного числа;
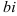— мнимая часть комплексного числа ( 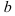— коэффициент при мнимой части).
Запись комплексного числа в виде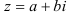 
называется алгебраической формой комплексного числа.
Множество комплексных чисел принято обозначать буквой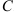 
.
В алгебраической форме над комплексными числами удобно выполнять операции: сложение, вычитание, умножение и деление.
Сложение, вычитание и умножение комплексных чисел производят по правилам соответствующих действий над многочленами.
Пример 1.
Для комплексных чисел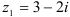 
и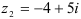 
найдите: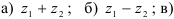 
.
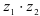Решение:
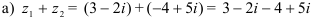
Действительную часть комплексного числа будем складывать с действительной частью, мнимую — с мнимой: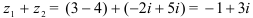 
.
При сложении двух комплексных чисел в алгебраической форме получили комплексное число также в алгебраической форме.
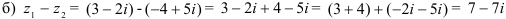— комплексное число в алгебраической форме.
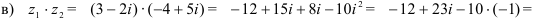
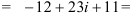
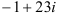— комплексное число в алгебраической форме.
Ответ: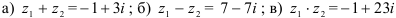 
.
Для того чтобы ввести операцию деления для комплексных чисел, заданных в алгебраической форме, используем понятие сопряженных чисел.
Два комплексных числа называются сопряженными, если они отличаются друг от друга только знаками перед мнимой частью.
Например, числа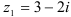 
и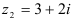 
— сопряженные, 
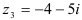и 
— также сопряженные.
Чтобы выполнить деление комплексных чисел в алгебраической форме, необходимо домножить числитель и знаменатель дроби на число, сопряженное знаменателю.
Пример 2.
Для комплексных чисел 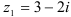и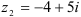 
найдите 
.
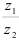Решение.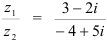 
. Домножим числитель и знаменатель дроби на число 
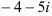, сопряженное знаменателю: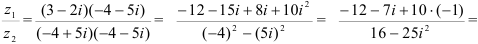 
— комплексное число в алгебраической форме.
Ответ: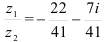 
.
На множестве комплексных чисел возможно решение квадратных уравнений с отрицательным дискриминантом.
Пример 3.
Решите уравнение: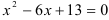 
.
Решение:
Найдем дискриминант: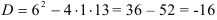 
.
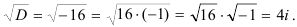
Тогда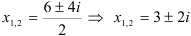 
.
Ответ: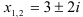 
.
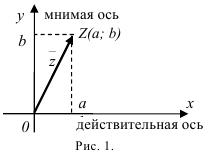
Геометрически комплексное число 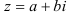можно представлять как
- точку на комплексной плоскости с координатами
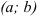; - вектор
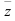на комплексной плоскости с началом в начале координат и концом в точке 
.
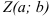Действительную часть 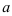комплексного числа будем откладывать на оси 
, коэффициент при мнимой части 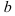— на оси 
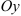(рис. 1). Ось называется действительной осью, а ось 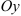— мнимой осью комплексной плоскости.
Плоскость, точкам которой сопоставлены комплексные числа, называется комплексной плоскостью.
На этой странице вы сможете посмотреть все остальные темы готовых контрольных работ по высшей математике:
Готовые контрольные работы по высшей математике
Обратите внимание на похожие контрольные работы возможно они вам будут полезны:
