Оглавление:
Задание: Действия над комплексными числами в тригонометрической форме.
Цель: формирование умения выполнять операции над комплексными числами в тригонометрической форме.
Задание для самостоятельной внеаудиторной работы:
1. Выучите, какой вид имеет тригонометрическая форма комплексного числа. Разберите, как выполнить умножение, деление, возведение в степень и извлечение корня из комплексных чисел в тригонометрической форме.
52.2. Закончите высказывания:
а)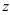 
= … — тригонометрическая форма комплексного числа, где 
— …, 
— ….
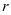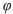б) заполните таблицу по технике действий над комплексными числами в тригонометрич. форме:
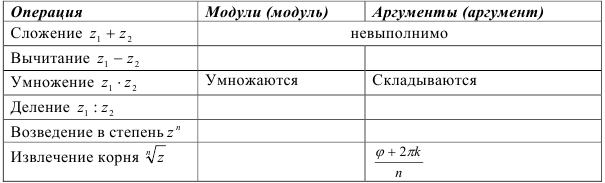
в) Корень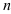 
-й степени из числа 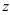имеет ровно … значений.
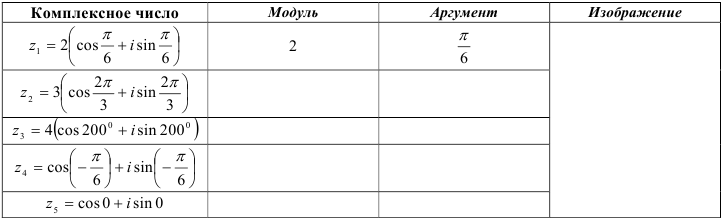
52.3. Заполните таблицу и постройте на одном чертеже векторы, соответствующие заданным комплексным числам:
52.4. Заданы числа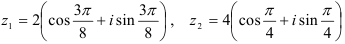 
. Выполните указанные действия над комплексными числами в тригонометрической форме:
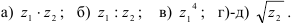
Вам известно, что символ для обозначения мнимой единицы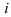 
был введён в … году (задание 51.3). Автором этого знака является гений, один из величайших математиков всех времен и народов. Его творчество, едва умещающееся в 760 книгах и научных статьях, охватило все разделы математики того времени. Кроме того, значительная часть его жизни была отдана России.
Выполнив задание 52.4 и заменив получившиеся ответы буквами из таблицы. Вы узнаете фамилию этого великого математика.
Фамилия математика, предложившего символ :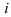
Карта ответов:
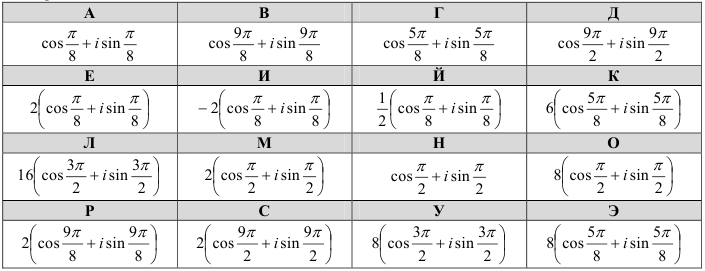
52.5. Вычислите: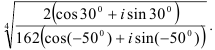 
Методические указания по выполнению работы:
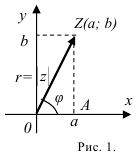
Модулем (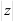 
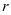или ) комплексного числа 
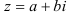называется длина соответствующего ему вектора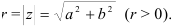 
Аргументом комплексного числа 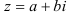называется угол 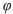, который образует вектор 
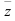с положительным направлением оси 
.
Тригонометрическая форма комплексного числа имеет вид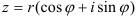 
.
Пример 1.
Изобразите на комплексной плоскости числа:
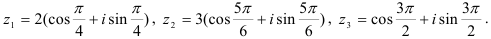
Решение:
Все числа заданы в тригонометрической форме. Выделим в записи каждого числа модуль и аргумент:
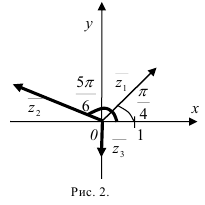
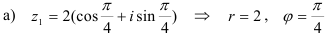. Отложим от положительного направления оси угол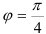 
, и на полученном луче отметим вектор длиной 2 ед. с центром в начале координат (рис. 43.2).
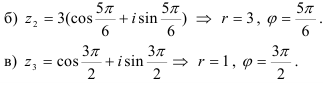
Действия над комплексными числами в тригонометрической форме:
Пусть заданы два комплексных числа в тригонометрической форме: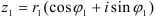 
и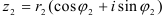 
.
1. Умножение: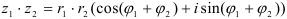 
(1) — при умножении комплексных чисел в тригонометрической форме их модули перемножаются, а аргументы складываются.
2. Деление: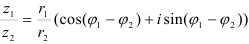 
(2) — при делении комплексных чисел в тригонометрической форме их модули делятся, а аргументы вычитаются.
3. Возведение в степень: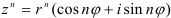 
(3) — при возведении в степень комплексного числа в тригонометрической форме модуль числа нужно возвести в 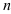-ю степень, а аргумент умножить на .
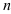4. Извлечение корня 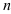-й степени: корень 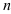-й степени из числа 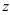имеет ровно 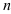значений, которые находятся по формуле: 
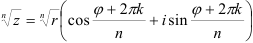(4). Для их нахождения необходимо
менять значения параметра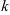 
, начиная с 
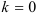(первый корень 
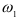), затем 
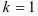(второй корень 
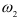) и т.д. до 
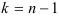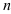(-й корень 
).
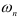Рассмотри, как выполняются операции над комплексными числами в тригонометрической форме на конкретных примерах.
Пример 2.
Для комплексных чисел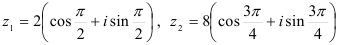 
найдите:
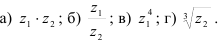
Решение:
а) Согласно формуле (1) получим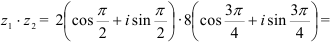 
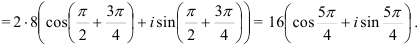
б) Используя формулу (2), находим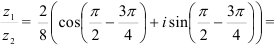 
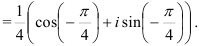
в) Применяя формулу (3), находим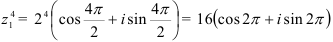 
.
г) Для извлечения кубического корня из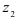 
воспользуемся формулой (4): 
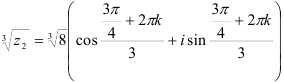, где параметр 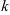будет принимать значения 0, 1 и 2 (поскольку число корней 3-й степени из числа имеет ровно 3 значения).
При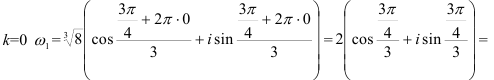 
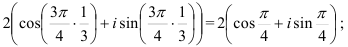
При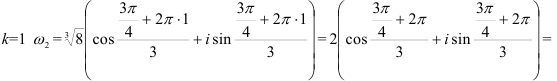 
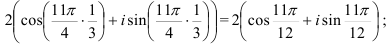
При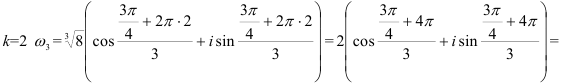 
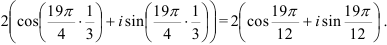
Ответ: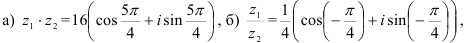 
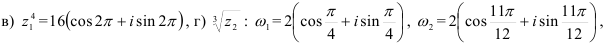
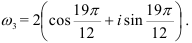
На этой странице вы сможете посмотреть все остальные темы готовых контрольных работ по высшей математике:
Готовые контрольные работы по высшей математике
Обратите внимание на похожие контрольные работы возможно они вам будут полезны:
