Классификация точек разрыва функции
а) Устранимый, разрыв.
Если функция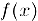 
определена в некотором интервале, содержащем точку 
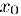, кроме, возможно, самой этой точки и существует конечный предел 
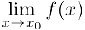(неравный 
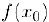). если функция определена в точке 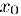), то по определению 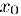— точка устранимого разрыва данной функции.
Из определения непрерывности следует, что, если в этом случае доопределить или переопределить в точке 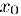функцию ее предельным значением, то она становится непрерывной в этой точке.
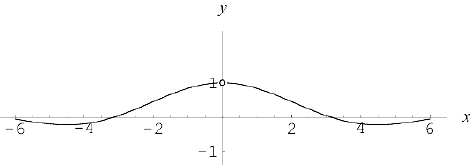
В качестве примера рассмотрим функцию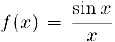 
. Она неопределена в нуле, но, как известно (§1, путает 3)
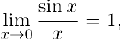
следовательно, данная функция имеет устранимый разрыв в точке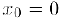 
.
b) Разрыв первого рода.
Пусть функция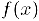 
определена в некотором интервале, содержащем точку 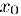, кроме, возможно, самой этой точки и существуют конечные односторонние, неравные друг другу пределы 
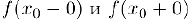. Тогда будем говорить, ото :гр, — точка разрыва первого рода.
Разность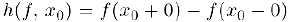 
называется скачком функции 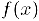в точке .
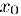Примером разрыва первого рода может служить точка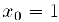 
для функции
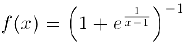
Действительно, здесь
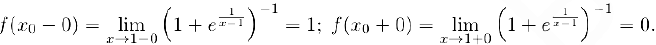
Скачок функции в точке разрыва равен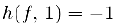 
.
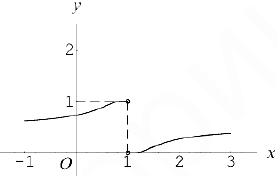
c) Разрыв второго рода.
Предположим, что функция 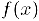определена в некотором интервале, содержащем точку 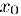, кроме, может быть, самой этой точки и по крайней мере один из односторонних пределов в точке 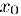не существует или равен бесконечности. В этом случае по определению х<) — точка разрыва второго рода.
Рассмотрим два примера такого сложного разрыва.
1) Для функции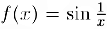 
предел 
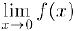не существует. Действительно, на бесконечно малой последовательности 
мы имеем:
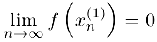
Аналогично вдоль другой бесконечно малой последовательности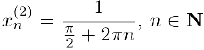 
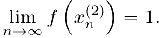
Отсюда, ввиду единственности предела функции (§4. пункт 2, свойство 3)) и следует, что предел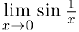 
не существует и. таким образом, 
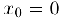— точка разрыва второго рода данной функции.
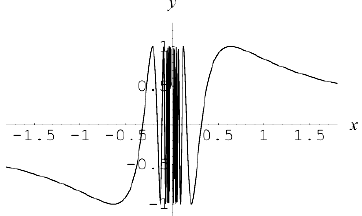
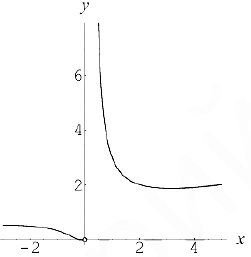
2) Исследуем на непрерывность функцию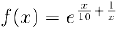 
в точке 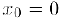. Дня этого вычисли в этой точке односторонние пределы:
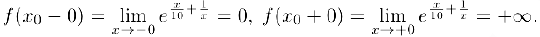
Следовательно, в точке 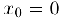функция испытывает разрыв второго рода.
Эта лекция взята со страницы онлайн помощи по математическому анализу:
Математический анализ онлайн помощь
Возможно эти страницы вам будут полезны:
