Оглавление:
Квадратный корень легко извлекается с помощью калькулятора. Для этого достаточно набрать на нём исходное число и нажать клавишу корня √ .
Если калькулятора под рукой нет, то квадратный корень извлекают пользуясь алгоритмом извлечения квадратного корня.
Определение действия извлечения корня
Корнем n-й степени из числа а называется число х, n-я степень которого равна а. Например, число 2 есть корень пятой степени из 32, ибо 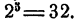 Корень второй степени иначе называется квадратным корнем, корень третьей степени — кубическим корнем.
Корень второй степени иначе называется квадратным корнем, корень третьей степени — кубическим корнем.
Действие, посредством которого по данному числу а и показателю n находится корень n-й степени из а, называется извлечением корня. Показатель n называется показателем корня. Извлечение корня есть
действие, обратное действию возведения в степень. Корень n-й степени из числа а обозначается следующим образом:
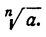
В случае квадратного корня показатель не указывается, так что квадратный корень из числа а обозначается 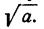
Из определения корня следует, что 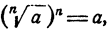 в частности
в частности
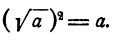
Арифметическое значение квадратного корня
Допустим, что нам дано положительное число а такое, что для него существует квадратный корень, например а = 4. Мы видим, что не одно, а целых два числа удовлетворяют определению квадратного корня из 4, именно числа 2 и —2. Действительно, 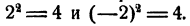 Таким же образом обстоит дело и для всякого другого положительного числа а: если х удовлетворяет условию
Таким же образом обстоит дело и для всякого другого положительного числа а: если х удовлетворяет условию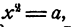 то и число —х удовлетворяет этому условию, именно
то и число —х удовлетворяет этому условию, именно 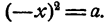 Поэтому каждое из двух противоположных чисел х и —х с одинаковым основанием может быть названо квадратным корнем из числа а. Из этих двух чисел одно положительно, другое отрицательно. Однако положительное значение квадратного корня из положительного числа может существовать только одно.
Поэтому каждое из двух противоположных чисел х и —х с одинаковым основанием может быть названо квадратным корнем из числа а. Из этих двух чисел одно положительно, другое отрицательно. Однако положительное значение квадратного корня из положительного числа может существовать только одно.
Действительно, допустим, что
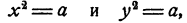
причем х и у оба положительны. Тогда
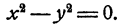
Разлагая на множители левую часть, мы придем к равенству
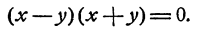
Произведение двух чисел х—у и х + у равно нулю. Следовательно, равен нулю один из сомножителей. Однако х + у есть положительное число, как сумма двух положительных чисел.
Следовательно,
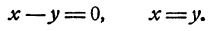
Положительное значение квадратного корня из положительного числа называется арифметическим значением квадратного корня.
Условимся знаком 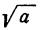 обозначать именно арифметическое значение квадратного корня. Это условие вносит определенность при пользовании знаком корня. Так, согласно этому условию,
обозначать именно арифметическое значение квадратного корня. Это условие вносит определенность при пользовании знаком корня. Так, согласно этому условию, 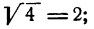
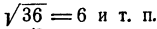
Однако приняв это условие, о нем необходимо помнить, чтобы не делать ошибок при пользовании знаком квадратного корня.
Так, 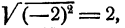 а не —2, что, казалось бы, более естественно. Равенство
а не —2, что, казалось бы, более естественно. Равенство 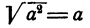 есть верное равенство только при
есть верное равенство только при 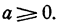
При 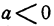 мы должны считать
мы должны считать 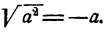 В то же время равенство
В то же время равенство 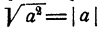 будет верно всегда.
будет верно всегда.
Постановка вопроса о приближенном вычислении корня
Извлечение квадратного корня из данного числа выполнимо далеко не всегда, если ограничиться рассмотрением рациональных чисел. Так, извлечение квадратного корня из отрицательного числа есть действие невыполнимое, ибо квадрат любого рационального числа не может быть отрицательным.
Более того, далеко не из каждого рационального положительного числа можно извлечь рациональный квадратный корень. Действительно, рассмотрим таблицу квадратов целых чисел:

Мы видим, что квадраты целых чисел очень быстро возрастают, так что промежутки между квадратами соседних целых чисел тоже довольно быстро растут. Целые числа, находящиеся внутри таких промежутков, не являются квадратами целых чисел. Докажем, что они не являются и квадратами дробных чисел.
Для этого достаточно установить, что квадрат дробного числа не может быть числом целым.
Действительно, каждое дробное число а может быть представлено в виде несократимой дроби 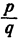 т. е. в виде частного от деления двух целых чисел р и q, не имеющих общих простых множителей, причем q > 1.
т. е. в виде частного от деления двух целых чисел р и q, не имеющих общих простых множителей, причем q > 1.
Если 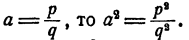 Очевидно, что
Очевидно, что 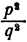 тоже есть
тоже есть
несократимая дробь, ибо 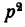 содержит только те простые множители, которые входят в
содержит только те простые множители, которые входят в 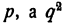 — только те простые множители, которые входят в q а р и q общих множителей не имеют. Таким образом,
— только те простые множители, которые входят в q а р и q общих множителей не имеют. Таким образом, 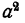 не может быть целым числом.
не может быть целым числом.
Итак, числа 2, 3, 5, 6, 7, 8, 10, 11, 12… не являются ни квадратами целых чисел, ни квадратами чисел дробных. Следовательно, извлечение квадратного корня из этих чисел есть действие невыполнимое, если оставаться в области рациональных чисел.
Рассмотрим теперь более подробную таблицу квадратов, придавая числу а значения через 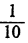 Ограничимся при этом рассмотрением промежутка от а = 1 до а = 2:
Ограничимся при этом рассмотрением промежутка от а = 1 до а = 2:
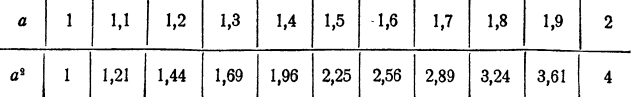
Промежуток между двумя соседними квадратами в этой таблице в среднем в 10 раз меньше, чем промежуток между соседними квадратами 1 и 4 в предшествующей таблице.
Рассмотрим теперь таблицу квадратов, придавая числу а значения через 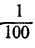 , ограничившись промежутком от а = 1,4 до а =1,5:
, ограничившись промежутком от а = 1,4 до а =1,5:

По сравнению с предыдущей таблицей, промежутки между соседними квадратами еще уменьшились, в среднем в 10 раз.
Таким образом, если брать значения а все более «густо», т. е. делая промежутки между соседними значениями для а все меньше и меньше, то и промежутки между соседними значениями 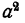 будут становиться все меньше и меньше. Поэтому, если взять промежутки
будут становиться все меньше и меньше. Поэтому, если взять промежутки
между соседними значениями для а достаточно малыми, мы можем приблизиться посредством значений 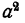 к любому положительному числу b с любой степенью точности.
к любому положительному числу b с любой степенью точности.
Проследим, например, за приближениями к числу 2 посредством квадратов на протяжении составленных таблиц. Из первой таблицы мы находим, что наиболее близкие к числу 2 квадраты имеют числа 1 и 2; 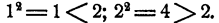 Во второй таблице числами, дающими наиболее близкие к числу 2 квадраты, являются 1,4 и 1,5, причем
Во второй таблице числами, дающими наиболее близкие к числу 2 квадраты, являются 1,4 и 1,5, причем 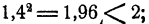
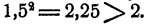 Третья таблица дает еще лучшие приближения:
Третья таблица дает еще лучшие приближения:
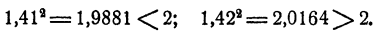
Если мы пожелаем еще улучшить приближения, мы можем рассмотреть квадраты чисел между 1,41 и 1,42, взяв их через 0,001. Это рассмотрение нам даст
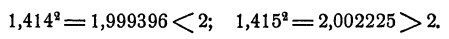
Таким образом, среди рациональных чисел не существует числа, квадрат которого равен 2, но существуют числа, квадраты которых сколь угодно близко подходят к 2.
То же самое можно сказать о любом другом положительном числе, для которого точное извлечение корня в области рациональных чисел невозможно. Поэтому имеет смысл ставить вопрос о приближенном
вычислении квадратного корня с некоторой наперед заданной точностью. Так, числа 1 и 2 являются приближенными значениями для 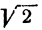 с точностью до 1; числа 1,4 и 1,5 являются приближенными значениями для
с точностью до 1; числа 1,4 и 1,5 являются приближенными значениями для 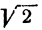 с точностью до 0,1; 1,41 и 1,42 — приближенные значения
с точностью до 0,1; 1,41 и 1,42 — приближенные значения 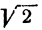 с точностью до 0,01; 1,414 и 1,415 — приближенные значения
с точностью до 0,01; 1,414 и 1,415 — приближенные значения 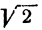 с точностью до 0,001 и т. д.
с точностью до 0,001 и т. д.
Дадим теперь строгое определение приближенных значений квадратного корня из данного положительного числа.
Приближенным значением с недостатком для квадратного корня из данного положительного числа bс точностью до а называется такое положительное число а, что 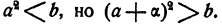
В свою очередь, число а + а называется приближенным значением с избытком для 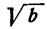 с точностью до а.
с точностью до а.
Для практических целей в качестве меры точности а принимаются числа 0,1, 0,01, 0,001 и т. д. В этих случаях за приближенное значение корня принимаются десятичные дроби с соответствующим числом цифр после запятой.
Приближенные значения корня можно находить посредством испытаний, постепенно увеличивая точность до той, которая требуется в задаче. Рассмотрим еще один пример.
Пример:
Вычислить 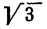 с точностью до 0,01.
с точностью до 0,01.
Решение:
Приближения с точностью до 0,1. мы находим из приведенной выше таблицы. Приближение с недостатком есть 1,7 ибо 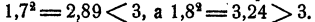 Для вычисления приближения с точностью до 0,01 испытываем
Для вычисления приближения с точностью до 0,01 испытываем 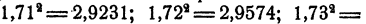
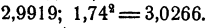 Таким образом, с точностью до 0,01 (с
Таким образом, с точностью до 0,01 (с
недостатком)
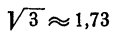
Способом испытаний мы можем приближенно вычислять корень из любого положительного числа с любой степенью точности. Однако этот способ требует хотя и простых, но утомительных вычислений. В следующих параграфах мы познакомимся с более удобными способами вычисления квадратного корня.
Отметим, что ставить вопрос о приближенном вычислении квадратного корня из отрицательного числа бессмысленно, так как приближаться к данному отрицательному числу посредством квадратов рациональных чисел невозможно.
Извлечение квадратного корня при помощи графика
Выведенные в предшествующих параграфах свойства и особенности действия извлечения квадратного корня становятся особенно наглядными, если перейти от рассмотрения таблицы квадратов к графику зависимости 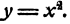 Этот график нами уже рассматривался в § 17 гл. II
Этот график нами уже рассматривался в § 17 гл. II
Приводим снова этот график (рис. 26). Он имеет вид кривой линии, состоящей из двух бесконечных ветвей, симметричных относительно оси ординат. Эти ветви сходятся в начале координат, плавно переходя одна в другую. Как уже было сказано, эта кривая называется параболой.
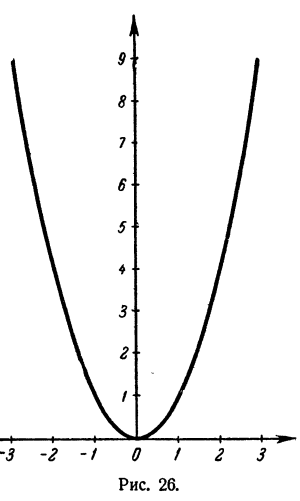
Задача извлечения
квадратного корня заключается в
определении числа х из зависимости 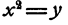
при данном у. Для решения этой задачи при помощи
графика нужно на параболе
найти точки, имеющие данную ординату у, и определить абсциссы этих точек.
Очевидно, что при у < 0 таких точек нет, ибо весь график расположен выше оси абсцисс, касаясь ее лишь в начале координат. При у = 0 такая точка единственна, это начало координат. Абсцисса ее равна тоже нулю. При у > 0 таких точек оказывается две, расположенных симметрично относительно оси ординат. Это соответствует тому, что квадратный корень из положительного числа имеет два значения, имеющие одинаковую абсолютную величину, но отличающиеся знаками. Выбор арифметического значения квадратного корня соответствует тому, что из двух ветвей параболы мы рассматриваем только одну, именно правую ветвь. На этой ветви точка с заданной ординатой оказывается уже единственной. Измерив абсциссу этой точки, мы получим приближенное значение 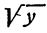 с той точностью, которую допускает график.
с той точностью, которую допускает график.
Таким образом, из графика зависимости 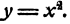 мы видим, что корень из отрицательного числа не существует и что корень из любого положительного числа существует и имеет два значения.
мы видим, что корень из отрицательного числа не существует и что корень из любого положительного числа существует и имеет два значения.
Увеличивая масштаб, мы можем построить график с любой заданной степенью точности. Следовательно, и само извлечение корня из данного положительного числа можно осуществить с любой точностью.
График зависимости 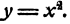 может служить для фактического вычисления квадратных корней с небольшой точностью.
может служить для фактического вычисления квадратных корней с небольшой точностью.
С этой целью следует тщательно построить график на
миллиметровой бумаге, приняв за единицу масштаба 10 см и придавая переменной х значения от 0 до 1 через каждые 0,1 (рис. 27). Тогда непосредственно по графику находятся квадратные корни чисел, заключенных между 0 и 1.
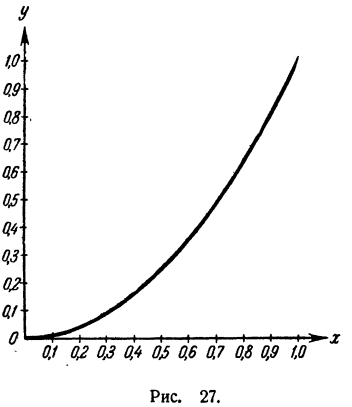
При помощи этого графика можно также находить значения корня из любого положительного числа b. Для этого нужно найти какое либо число а, удовлетворяющее условию 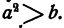 Затем, найдя частное
Затем, найдя частное 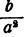 , которое будет меньше единицы, извлечь из него корень при помощи графика и умножить этот корень на а. Результат даст
, которое будет меньше единицы, извлечь из него корень при помощи графика и умножить этот корень на а. Результат даст 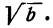 Действительно,
Действительно,
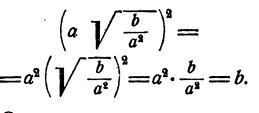
Следовательно,
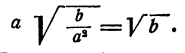
Если подобрать а так, 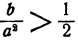 то точность при применении этого способа достигает 1 — 2% величины искомого корня.
то точность при применении этого способа достигает 1 — 2% величины искомого корня.
Пусть, например, требуется найти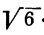 Возьмем
Возьмем 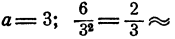
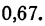 По графику,
По графику, 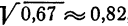 и следовательно,
и следовательно, 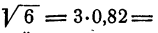
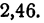 Ручаться за точность второго знака после запятой здесь нельзя,
Ручаться за точность второго знака после запятой здесь нельзя,
возможна ошибка на 0,02 — 0,03 в ту или другую сторону. В действительности с точностью до 0,001 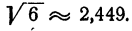
Извлечение квадратного корня из числа, заключенного между 1 и 100, с точностью до 0,1
Приступим к объяснению одной удобной арифметической схемы для приближенного извлечения квадратного корня с заданной точностью.
Допустим, что нам уже известно, что число 7,236 есть
приближенное значение квадратного корня из числа A= 52,365, взятое с недостатком, с точностью до 0,001. Тогда числа 7; 7,2; 7,23 и 7,236 представляют собой приближенные значения 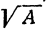 с недостатком, и каждое последующее из этих приближений является более точным, чем предыдущее. Мы можем считать, что каждое последующее получается из предыдущего прибавлением некоторой поправки. Именно, 7,2 = 7 + 0,2; 7,23 = 7,2 + 0,03; 7,236 = 7,23 + 0,006.
с недостатком, и каждое последующее из этих приближений является более точным, чем предыдущее. Мы можем считать, что каждое последующее получается из предыдущего прибавлением некоторой поправки. Именно, 7,2 = 7 + 0,2; 7,23 = 7,2 + 0,03; 7,236 = 7,23 + 0,006.
Мы сможем вычислять квадратные корни с любой степенью точности, если нам удастся указать способ вычисления поправки к уже известному приближению с недостатком так, чтобы после прибавления этой поправки получалось бы снова приближение с недостатком, но значительно более точное.
Для вывода удобного способа вычисления таких поправок рассмотрим задачу в общем виде.
Пусть а есть приближенное значение с недостатком для
квадратного корня из положительного числа A, и пусть b есть поправка, которую нужно добавить к числу а, чтобы получить более точное приближение к корню, тоже с недостатком. Предположим, что эта поправка мала по сравнению с самим числом а.
Примем сначала, что a + b есть точное значение 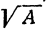 . Тогда имеет место равенство
. Тогда имеет место равенство 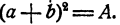 Раскрывая скобки, получим
Раскрывая скобки, получим
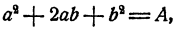
откуда
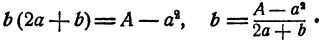
Вспомним теперь, что поправку b мы ищем только приближенно. Ввиду сделанного предположения, что искомая поправка мала по сравнению с числом а мы можем отбросить в знаменателе слагаемое b, и тогда получим для b приближенное равенство
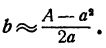
В знаменателе мы отбросили положительное слагаемое, тем самым мы уменьшили знаменатель, а всю дробь увеличили. Следовательно, число 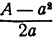 больше истинной поправки. Поэтому если мы хотим получить значение корня снова с недостатком, то мы должны взять в качестве поправки число, несколько меньшее, чем
больше истинной поправки. Поэтому если мы хотим получить значение корня снова с недостатком, то мы должны взять в качестве поправки число, несколько меньшее, чем 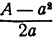 , например округлить это частное, приняв во внимание только первую значащую цифру.
, например округлить это частное, приняв во внимание только первую значащую цифру.
Для того чтобы проверить, что вычисленная таким способом поправка дает после прибавления к а снова приближение с недостатком, надо проверить, что разность 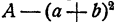 положительна. Эту разность удобно представить в виде
положительна. Эту разность удобно представить в виде 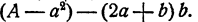
Действительно, число  уже вычислялось при вычислении поправки, а вычисление произведения
уже вычислялось при вычислении поправки, а вычисление произведения 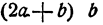 выполняется без труда. Если исследуемая разность все же окажется отрицательной, то это обозначает, что вычисленная поправка велика и ее следует еще уменьшить.
выполняется без труда. Если исследуемая разность все же окажется отрицательной, то это обозначает, что вычисленная поправка велика и ее следует еще уменьшить.
Рассмотрим пример на применение этих соображений. Пример. Вычислить 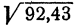 с точностью до 0,1.
с точностью до 0,1.
Решение. В качестве первого приближения возьмем а = 9. В качестве поправки следует взять число, немного меньшее, чем
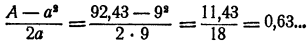
Берем поправку b = 0,6. Эта поправка дает значение с недостатком, ибо
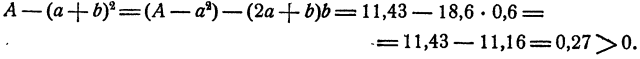
Таким образом, число a + b = 9,6 есть приближение к 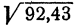 с недостатком. Число 9,7 является приближением с избытком, ибо поправка
с недостатком. Число 9,7 является приближением с избытком, ибо поправка 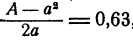 , в силу сказанного выше, уже больше
, в силу сказанного выше, уже больше
истинной, а поправка 0,7 и подавно. Итак, с точностью до 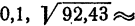
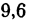 (с недостатком).
(с недостатком).
Все вычисления очень удобно производить по следующей схеме:
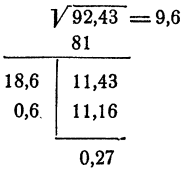
Порядок действий следующий:
1) пишем данное число под знаком корня;
2) определяем целую часть корня 9, возводим ее в квадрат и вычитаем из подкоренного выражения;
3) слева от полученной разности проводим вертикальную черту и слева от нее запишем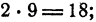 4) приближенно делим разность 11,43 на 18 с точностью до 0,1 с недостатком. Получаем 0,6;
4) приближенно делим разность 11,43 на 18 с точностью до 0,1 с недостатком. Получаем 0,6;
5) к числу 18 добавляем 0,6 и сумму умножаем на 0,6. Произведение записываем под ранее вычисленной разностью 11,43 и вычитаем из нее. Так как последняя разность 0,27 оказалась положительной, то вычисление заканчивается. Число 0,6 присоединяется к числу 9 в качестве поправки. Напоминаем, что последняя разность 0,27 есть разность чисел 92,43 и 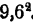
Пример:
Вычислить 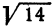 с точностью до 0,1.
с точностью до 0,1.
Решение:
Решаем этот пример, пользуясь той же схемой:
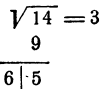
При делении числа 15 на 6 мы получим, после округления, 0,8. Однако такая поправка слишком велика, так как 6,8 • 0,8 = 5,44 > 5. Примем в качестве поправки 0,7.
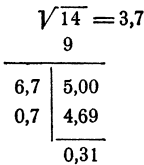
Поправка 0,7 оказалась подходящей.
Последняя разность 0,31 есть 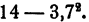 К числу 5 мы приписали нули после запятой, чтобы было удобнее производить вычитание.
К числу 5 мы приписали нули после запятой, чтобы было удобнее производить вычитание.
Пример:
Вычислить 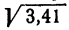 с точностью до 0,l. Решение.
с точностью до 0,l. Решение.
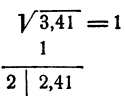
При делении числа 2,41 на 2 получается с точностью до 0,1 число 1,2, которое явно велико в качестве поправки. Такой плохой результат получается потому, что здесь поправка совсем немала по сравнению с первым приближением, и поэтому приближенное равенство 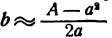 оказывается очень грубым.
оказывается очень грубым.
Даже 0,9 велико в качестве поправки, ибо 2,9 • 0,9 = 2,61 >2,41. Берем 0,8.
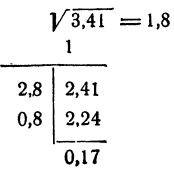
Извлечение квадратного корня из числа, заключенного между 1 и 100, с точностью до 0,01
Пример:
Извлечь квадратный корень из числа 92,4317 с
точностью до 0,01.
Решение:
Сначала извлекаем корень с точностью до 0,1,
пользуясь уже рассмотренным способом:
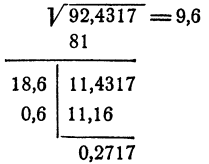
Легко сообразить, что следует делать дальше. Примем а = 9,6 за исходное приближение и ищем для него поправку по прежнему правилу. Вычислять снова разность 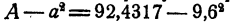 нам не нужно, ибо эта разность уже вычислена, ©на равна последней разности 0,2717. Мы должны поделить эту разность на 2-9,6 = 19,2 с точностью до 0,01. Получившуюся поправку b = 0,01 добавить к 2а =19,2, полученное число 2а -}-&= 19,21 умножить на 6 = 0,01 и сравнить с разностью 0,2717. Все эти действия удобно провести по прежней схеме. Полная запись будет выглядеть так:
нам не нужно, ибо эта разность уже вычислена, ©на равна последней разности 0,2717. Мы должны поделить эту разность на 2-9,6 = 19,2 с точностью до 0,01. Получившуюся поправку b = 0,01 добавить к 2а =19,2, полученное число 2а -}-&= 19,21 умножить на 6 = 0,01 и сравнить с разностью 0,2717. Все эти действия удобно провести по прежней схеме. Полная запись будет выглядеть так:
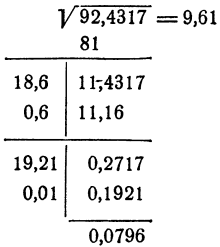
Последняя разность 0,0796 есть 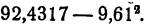
Заметим, что мы могли бы не записывать в третьей строчке две последние цифры, так как их роль сказывается только в пятой строчке. Далее, для упрощения записи можно было бы не писать запятых и
нулей перед значащими цифрами, имея при этом в виду, что тогда при делении 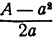 последнюю цифру делимого нужно отбрасывать, выполняя деление с точностью до целого.
последнюю цифру делимого нужно отбрасывать, выполняя деление с точностью до целого.
Принимая все это во внимание, запись можно провести так:
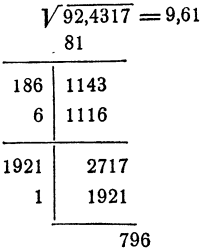
Продолжая вычисления, мы можем извлечь корень с точностью до 0,001; 0,0001 и т. д.
Извлечение квадратного корня из любого данного числа с любым заданным числом десятичных знаков
Способ извлечения квадратного корня, изложенный в § 5 и 6, применялся там только к числам, заключенным между 1 и 100, т. е. к числам с однозначной или двузначной целой частью. Однако этот способ легко распространяется на любые положительные числа, целые или заданные десятичной дробью. Это следует из того, что при умножении подкоренного числа на 100 корень увеличивается в 10 раз, а при делении подкоренного числа на 100 корень уменьшается в 10 раз.
Действительно, если 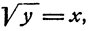 то
то 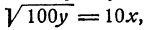
так как 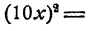
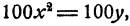 а
а
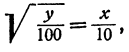
ибо
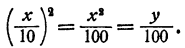
Умножение или деление на 100 равносильно перенесению запятой на два разряда вправо или влево. Умножение или деление на 10 равносильно перенесению запятой на один разряд. Повторное умножение или деление на 100 равносильно перенесению запятой на четное число урядов. Очевидно, что за счет такого перенесения запятой в подкоренном числе можно добиться того, чтобы целая часть нового подкоренного числа оказалась однозначным или двузначным числом.
К этому числу можно применить указанный прием для извлечения квадратного корня. Чтобы получить корень из исходного числа, нужно в полученном корне перенести запятую в обратном направлении на вдвое меньшее число разрядов.
Например, чтобы извлечь корень 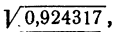 мы сначала перенесем запятую на два разряда вправо.
мы сначала перенесем запятую на два разряда вправо. 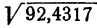 мы вычислили; он равен 9,61 (с точностью до 0,01). Следовательно,
мы вычислили; он равен 9,61 (с точностью до 0,01). Следовательно, 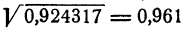 (с точностью до 0,001).
(с точностью до 0,001).
Сформулируем теперь общее правило для извлечения корня из данного числа с данным числом десятичных знаков, обобщив в этом правиле все высказанные выше соображения.
Правило. Чтобы извлечь квадратный корень из данного положительного целого или записанного в виде десятичной дроби числа с, данной точностью, нужно:
Целая часть, вычисляемая в п. 5 правила, может оказаться больше 9 только на первом шагу вычислений, т. е. при вычислении второй цифры.
- Записать это число под знаком квадратного корня и разбить его цифры на «грани» по две цифры в каждой, начиная от запятой, вправо и влево. Если требуется вычислить корень с точностью до 1, то грани, расположенные направо от запятой, можно отбросить. Если требуется вычислить корень с точностью до 0,1, следует справа от запятой сохранить одну грань, при вычислении с точностью до 0,01 оставить две грани и т. д. Если при этом окажется, что цифр для заполнения нужного числа граней не хватает, приписать надлежащее количество нулей.
- Извлечь корень из старшей грани с точностью до 1, с недостатком (или точно, если это возможно). Полученное число принять за первую цифру искомого корня.
- Из старшей грани вычесть квадрат первой цифры и к полученной разности приписать вторую грань. Слева от полуденного результата провести вертикальную черту.
- Слева от черты записать удвоенную первую цифру.
- Найти целую часть частного от деления числа десятков первой разности на число, записанное слева. Если полученное число окажется больше 10, заменить числом 9.
- Полученное однозначное число подвергнуть следующему испытанию: приписать его в качестве цифры к числу, записанному слева, получившееся число умножить на испытуемое однозначное число и сравнить произведение с разностью, записанной справа от черты. Если это произведение больше указанной разности, уменьшить испытуемое число на одну единицу и вновь подвергнуть испытанию.
- Если после испытания произведение окажется меньше указанной разности, подписать его под ней и вычесть. Испытанное однозначное число принять за вторую цифру корня.
- К вновь полученной разности приписать следующую грань и определить третью цифру тем же приемом, каким била определена вторая цифра.
- Продолжать аналогичные вычисления до тех пор, пока не будет достигнута требуемая точность.
- Запятую в результате нужно поставить после того, как будут исчерпаны грани, предшествующие запятой в подкоренном числе.
Отрицательный результат испытания в п. 6 правила довольно часто имеет место на первом шагу вычислений, когда поправка еще не очень мала, по
сравнению с первым приближением. На дальнейших шагах вычислений отрицательный результат испытания получается крайне редко.
Если подкоренное число имеет 0 целых и вслед затем следует нуль, корень имеет тоже 0 целых и затем столько нулей, сколько граней из нулей следует за запятой в подкоренном числе. Первая значащая цифра корня есть целая часть корня из первой значащей грани подкоренного числа.
Применение графиков для приближенного решения уравнений и систем двух уравнений с двумя неизвестными
Мы уже не раз пользовались графиками для приближенных вычислений. Графический способ решения задач является очень полезным для приложений вследствие большой простоты и наглядности. Конечно, им следует пользоваться только в тех случаях, когда не требуется очень большой точности результата. Достоинством графического
способа является также его большая общность. В частности, с помощью графиков можно решать приближенно даже довольно сложные уравнения и системы уравнений. Не вдаваясь в общую теорию построения графиков и их применений* ограничимся рассмотрением двух примеров.
Пример:
Решить приближенно уравнение
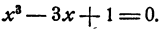
Решение:
Построим сначала график зависимости
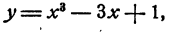
а затем найдем на этом графике точки, для которых у = 0. Абсциссы этих точек и дадут решения уравнения. Прежде всего вычислим таблицу значений:

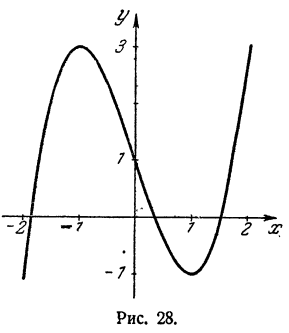
По этой таблице строим график (рис. 28), соединяя точки возможно более плавной линией. Из этого графика мы видим, что интересующих нас точек имеется три. Их абсциссы приближенно равны —1,8; 0,3 и 1,5. Следовательно, уравнение
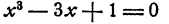
имеет три решения
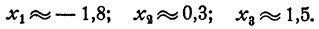
Чтобы найти более точные значения для корней уравнения, нужно построить с большей точностью и в большем масштабе участки графика, примыкающие к интересующим нас точкам.
Пример:
Решить приближенно систему уравнений
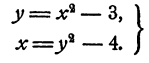
Для решения задачи строим на одном чертеже графики зависимостей 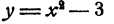 и
и 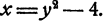 Нас интересуют точки, координаты которых связаны обеими зависимостями, т.е. точки, принадлежащие обоим графикам. Такими точками, являются точки пересечения графиков. Вычислим таблицы значений.
Нас интересуют точки, координаты которых связаны обеими зависимостями, т.е. точки, принадлежащие обоим графикам. Такими точками, являются точки пересечения графиков. Вычислим таблицы значений.
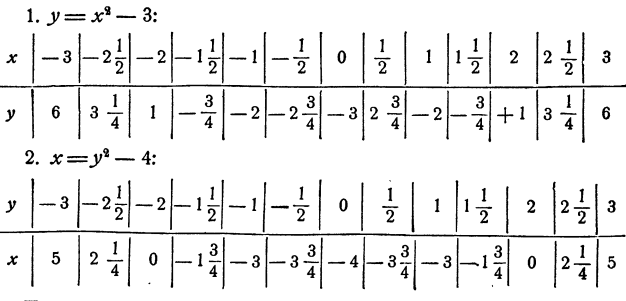
При вычислении второй таблицы мы придавали конкретные значения величине у и вычисляли соответствующие значения для х. Здесь это удобно, так как уравнение, определяющее зависимость, решено относительно х.
Графики по этим таблицам изображены на рис. 29. Мы видим, что графики пересекаются в четырех точках. Следовательно, система имеет четыре решения.
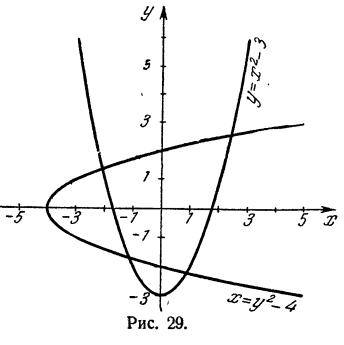
Приближенные решения системы даются следующими значениями для х и у:
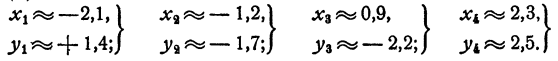
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

