Оглавление:
Задача:
В треугольнике ABC (рис. 75):
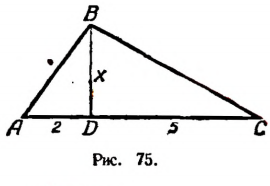
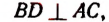
AD = 2 см, DC = 5 см,
АВ + ВС = 9 см.
Найти BD.
Решение:
Пусть длина отрезка BD равна х см. Тогда
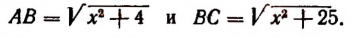
По условию
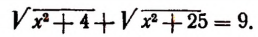
Получилось уравнение, в котором неизвестное входит в подкоренное выражение. Такое уравнение называется иррациональным. Решение этого уравнения приведено на странице 310.
Определение:
Уравнение, в котором неизвестное входит в какое-либо выражение, стоящее под знаком корня, называется иррациональным.
Во многих случаях иррациональное уравнение, как это ниже показано на примерах, может быть преобразовано в рациональное, являющееся его следствием. Но прежде чем показать это на примерах, мы изложим предварительные сведения, необходимые для понимания процесса решения иррациональных уравнений.
1. Всякий корень четной степени из положительного числа, входящий в иррациональное уравнение, мы будем считать, как и раньше, арифметическим. Поясним это. Если А > 0 и в иррациональное уравнение входит 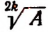 , то всегда будем считать, что
, то всегда будем считать, что
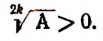
Принимая во внимание сказанное выше, мы должны считать, что, например, уравнение
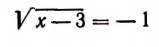
не имеет корней. Действительно,
при 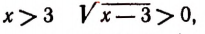
при 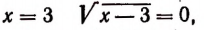
при 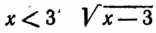 — мнимое число.
— мнимое число.
Таким образом, 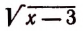 никогда не может равняться числу — 1, а это и значит, что уравнение
никогда не может равняться числу — 1, а это и значит, что уравнение
Vjnз = -1
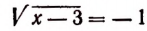
корней не имеет.
Было бы ошибкой считать число 4 корнем уравнения 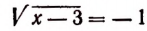 , так как
, так как 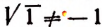 . Аналогично можно убедиться, что ни одно из следующих уравнений
. Аналогично можно убедиться, что ни одно из следующих уравнений 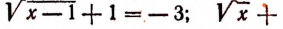
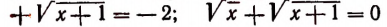 также не имеет корней.
также не имеет корней.
Теорема:
Если обе части уравнения А=В возвысить в квадрат, то полученное уравнение 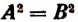 будет иметь своими корнями все корни данного уравнения А = В и корни уравнения А = — В, (Уравнение А = —В будем называть сопряженным уравнению А = В.) Но прежде чем доказывать эту теорему, поясним ее содержание на примере. Рассмотрим уравнение х + 1 = 5 и уравнение, ему сопряженное, т. е. х + 1 = —5. У первого уравнения имеется единственный корень 4, а у второго —6. Возведя левую и правую части уравнения х + 1 = 5 в квадрат, получим, что
будет иметь своими корнями все корни данного уравнения А = В и корни уравнения А = — В, (Уравнение А = —В будем называть сопряженным уравнению А = В.) Но прежде чем доказывать эту теорему, поясним ее содержание на примере. Рассмотрим уравнение х + 1 = 5 и уравнение, ему сопряженное, т. е. х + 1 = —5. У первого уравнения имеется единственный корень 4, а у второго —6. Возведя левую и правую части уравнения х + 1 = 5 в квадрат, получим, что 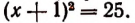
Решив это уравнение, убедимся, что его корнями будут числа 4 и — 6, т. е. только корни данного уравнения х + 1 = 5 и сопряженного ему уравнения х + 1 = —5 .
Как раз в этом и заключается смысл сформулированной выше теоремы.
Доказательство:
Уравнение 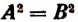 равносильно уравнению
равносильно уравнению 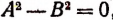 , или уравнению
, или уравнению 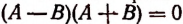 . Но. это последнее уравнение удовлетворяется как при А = В, так и при А = — В и никогда больше. Теорема доказана.
. Но. это последнее уравнение удовлетворяется как при А = В, так и при А = — В и никогда больше. Теорема доказана.
Следствие:
Из доказанной теоремы вытекает, что при переходе от уравнения А = В к уравнению 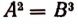 потери корней не произойдет, но могут появиться посторонние корни, а именно корни уравнения
потери корней не произойдет, но могут появиться посторонние корни, а именно корни уравнения
А = —В.
Если окажется, что уравнение А = — В не имеет корней, то не появляется и посторонних корней.
Иррациональные уравнения, содержащие только один радикал
Возьмем уравнение
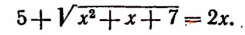
Уединив корень, получим:
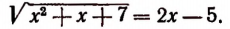
Возведем обе части этого уравнения в квадрат. В результате получим рациональное уравнение
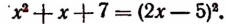
Решив последнее уравнение, получим, что
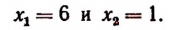
Теперь необходимо проверить, являются ли числа 6 и 1 корня-ми данного уравнения. Проверка показывает, что число 6 является корнем уравнения 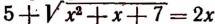 , а число 1 его корнем не является. Мы возводили в квадрат левую и правую части уравнения
, а число 1 его корнем не является. Мы возводили в квадрат левую и правую части уравнения 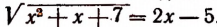 . Значит, число 1 есть корень сопряженного уравнения, т. е. уравнения
. Значит, число 1 есть корень сопряженного уравнения, т. е. уравнения
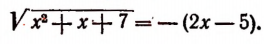
Итак, иррациональное уравнение
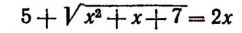
имеет лишь один корень, равный числу 6.
Возьмем еще одно уравнение, содержащее только один радикал, а именно:
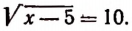
Здесь корень уже уединен. Поэтому, возведя обе части уравнения в квадрат, получим:
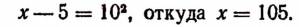
Проверка показывает, что число 105 является корнем данного уравнения. Здесь мы не получили постороннего корня, потому что сопряженное уравнение, т. е. уравнение 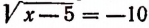 , корней не имеет.
, корней не имеет.
Примеры:
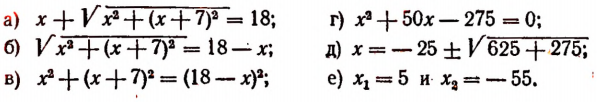
Проверка показывает, что оба числа 5 и —55 являются корнями уравнения
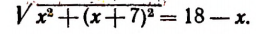
Значит, сопряженное уравнение, т. е. уравнение
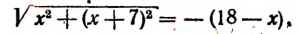
корней не имеет.
Уравнения, содержащие два квадратных радикала
Пример:
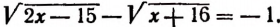
Уединим один из корней:
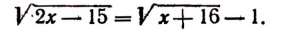
Возведем в квадрат левую и правую части последнего уравнения:
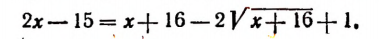
Уединим один оставшийся корень:
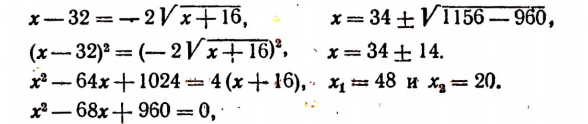
Проверкой устанавливаем, что данное уравнение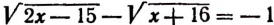 имеет только один корень, равный числу 20.
имеет только один корень, равный числу 20.
Пример:
В качестве второго примера решим уравнение
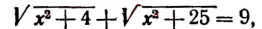
составленное по условиям задачи, поставленной в начале настоящей главы.
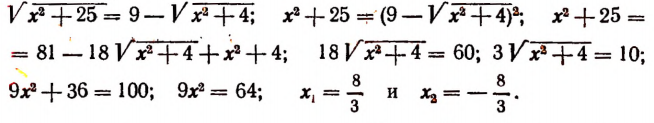
Легко убедиться, что оба числа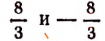 являются корнями уравнения
являются корнями уравнения 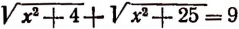 . Но мы знаем, что не всякий корень уравнения, составленного по условиям задачи, обязательно должен являться и решением самой задачи. В данном случае решением задачи будет только положительный корень
. Но мы знаем, что не всякий корень уравнения, составленного по условиям задачи, обязательно должен являться и решением самой задачи. В данном случае решением задачи будет только положительный корень 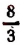 . Значит, искомая высота BD треугольника ABC будет равна
. Значит, искомая высота BD треугольника ABC будет равна 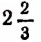 см.
см.
Пример:
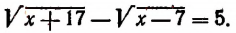
Уединим один из корней: 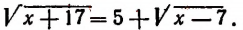
Возведем в квадрат левую и правую части этого уравнения:
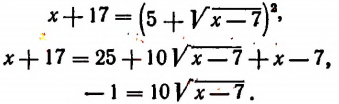
Последнее уравнение корней не имеет, ибо его левая часть есть отрицательное число, а правая часть ни при каком значении х не может быть числом отрицательным. Значит, и первоначальное уравнение корней не имеет.
Искусственные приемы решения иррациональных уравнений
Пример:
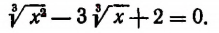
Примем 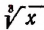 новое неизвестное и положим, что
новое неизвестное и положим, что 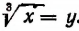 Тогда
Тогда 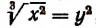 и данное уравнение примет вид: ^-3(/ + 2 = 0.
и данное уравнение примет вид: ^-3(/ + 2 = 0.
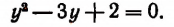
Отсюда 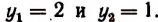
Приняв 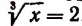 , получим, что
, получим, что 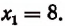
Приняв затем 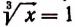 . получим, что
. получим, что 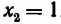 . Оба числа 8 и 1 являются корнями данного уравнения.
. Оба числа 8 и 1 являются корнями данного уравнения.
Пример:
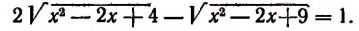
Положим, что 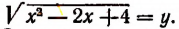 Тогда
Тогда 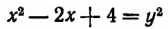 и
и 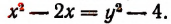 Относительно нового неизвестного у данное уравнение примет вид:
Относительно нового неизвестного у данное уравнение примет вид:
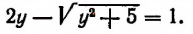
Освободившись от корня, получим:
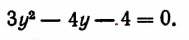
Отсюда 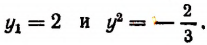
Значение  следует отбросить, так как буквой у мы
следует отбросить, так как буквой у мы
обозначили 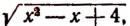 который отрицательных значений принимать не может.
который отрицательных значений принимать не может.
Взяв у = 2 и подставив это значение неизвестного у в уравнение 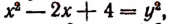 получим
получим 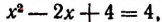 или
или 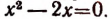 Откуда
Откуда 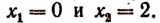
Числа 0 и 2 являются корнями первоначального уравнения. Других действительных корней данное уравнение не имеет.
Пример:
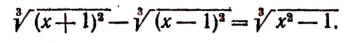
Подстановкой убеждаемся, что 1 не есть корень данного уравнения. Поэтому, разделив обе части уравнения на 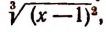 получим уравнение
получим уравнение
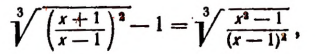
равносильное данному.
После сокращения последнее уравнение принимает вид:
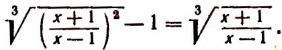
Обозначив 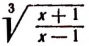 через у, получим:
через у, получим:
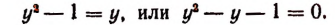
Отсюда
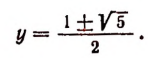
Следовательно,
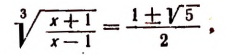
или
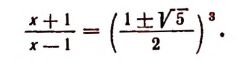
Составим производную пропорцию, воспользовавшись тем, что сумма членов первого отношения так относится к их разности, как сумма членов второго отношения к их разности. Получим, что
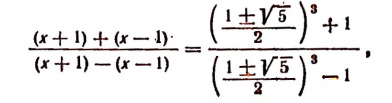
т.е.
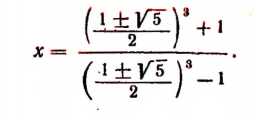
Способ решения иррационального уравнения с помощью системы рациональных уравнений
Решение всякого иррационального уравнения можно свести к решению соответствующей системы рациональных уравнений. Общий метод, позволяющий это сделать, покажем на примерах.
1. Решить уравнение
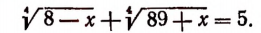
Полагая
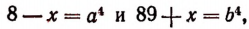
получим систему:
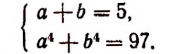
Пользуясь тем, что
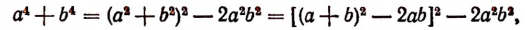
и тем, что 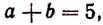 получим уравнение
получим уравнение
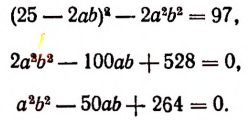
Отсюда 1) аb = 6 и 2) аb = 44.
Теперь остается решить две системы:
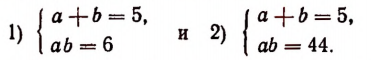
Первая система дает а = 2, b = 3 и а = 3, b = 2.
Вторая система действительных решений не имеет.
Пользуясь, например, уравнением 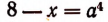 и полученными значениями неизвестного а, найдем действительные корни данного иррационального уравнения:
и полученными значениями неизвестного а, найдем действительные корни данного иррационального уравнения:
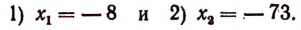
2. Решить уравнение:
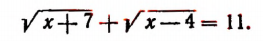
Полагая
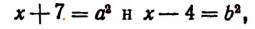
получим систему:
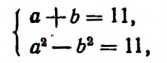
или равносильную ей систему:
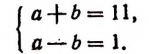
Отсюда а = 6.
Из уравнения 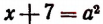 находим, что х = 29.
находим, что х = 29.
3. Решить уравнение:
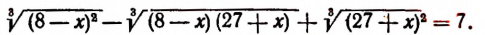
Полагая
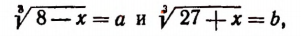
получим;
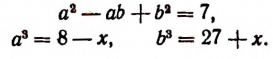
Из последних двух равенств будем иметь:
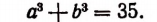
Решая систему:
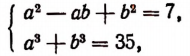
илн равносильную ей систему:
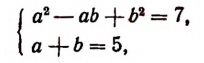
получим:
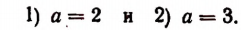
Пользуясь уравнением 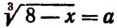 и найденными значениями неизвестного а, найдем корни первоначального уравнения:
и найденными значениями неизвестного а, найдем корни первоначального уравнения:
Дополнение к иррациональным уравнениям и примеры с решением
Уравнения, в которых переменная находится под знаком корня, называются иррациональными. Решение иррациональных уравнений сводится к переходу от иррационального уравнения к рациональному путем возведения обеих частей уравнения в степень, равную показателю степени корня. Если показатель степени четный, то необходимо либо предварительно выписывать ограничения: подкоренное выражение должно быть неотрицательным, выражение, равное арифметическому корню, также должно быть неотрицательным, т. к. в четную степень без приобретения посторонних корней можно возводить только неотрицательные выражения, либо делать проверку полученных решений.



Этот материал взят со страницы решения задач по математике:
Возможно вам будут полезны эти страницы:
| Биквадратные уравнение задачи с решением |
| Уравнения с модулем задачи с решением |
| Показательные и логарифмические уравнения задачи с решением |
| Тригонометрические уравнения задачи с решением |
Уравнения, содержащие знак модуля
1.Методы решения иррациональных уравнений, как правило, основаны на возможности замены (с помощью некоторых преобразований) иррационального уравнения рациональным уравнением, которое либо равносильно исходному иррациональному уравнению, либо является его следствием. Чаще всего обе части уравнения возводят в одну и ту же степень. При этом получается уравнение, являющееся следствием исходного.
При решении иррациональных уравнений необходимо учитывать следующее:
1) если показатель радикала — четное число, то подкоренное выражение должно быть неотрицательным; при этом значение радикала также является неотрицательным;
2) если показатель радикала — нечетное число, то подкоренное выражение может быть любым действительным числом; в этом случае знак радикала совпадает со знаком подкоренного выражения.
Рассмотрим уравнение вида
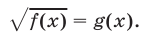
Если 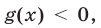 то уравнение (1) не имеет корней, так как левая часть уравнения (1) не может принимать отрицательные значения ни при каких значениях
то уравнение (1) не имеет корней, так как левая часть уравнения (1) не может принимать отрицательные значения ни при каких значениях 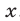 .
.
Если же 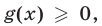 то при возведении обеих частей уравнения (1) в квадрат получим равносильное уравнение. Таким образом, уравнение (1) равносильно системе
то при возведении обеих частей уравнения (1) в квадрат получим равносильное уравнение. Таким образом, уравнение (1) равносильно системе
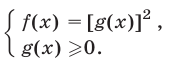

Замечание:
При решении уравнения (1) нет необходимости предварительно находить ОДЗ левой части (1), решая неравенство 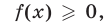 которое может оказаться довольно сложным. Достаточно найти корни уравнения (2) и, не прибегая к непосредственной подстановке этих корней в уравнение (1), выяснить, какие из найденных корней удовлетворяют неравенству (3). Эти корни, и только они, являются корнями уравнения (1).
которое может оказаться довольно сложным. Достаточно найти корни уравнения (2) и, не прибегая к непосредственной подстановке этих корней в уравнение (1), выяснить, какие из найденных корней удовлетворяют неравенству (3). Эти корни, и только они, являются корнями уравнения (1).
2.Из определения модуля (абсолютной величины) числа следует, что
1)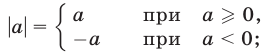
2) 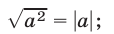
3) если 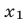 и
и 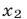 — произвольные точки числовой оси, то расстояние между ними равно
— произвольные точки числовой оси, то расстояние между ними равно 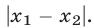
Пример:
Решить уравнение
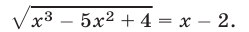
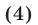
Решение:
Уравнение (4) равносильно системе
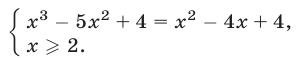
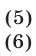
Уравнение (5), равносильное каждому из уравнений 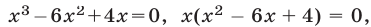 имеет корни
имеет корни 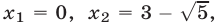
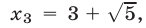 из которых лишь корень
из которых лишь корень 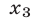 удовлетворяет условию (6).
удовлетворяет условию (6).
Ответ. 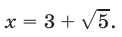
Пример:
Решить уравнение
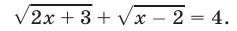
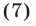
Решение:
Возведя обе части уравнения (7) в квадрат, получим уравнение
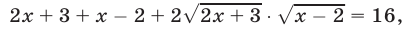
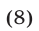
равносильное (7), так как обе части уравнения (7) неотрицательны. Уравнение (8) равносильно уравнению
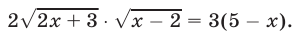
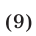
Возведя в квадрат обе части уравнения (9), получим уравнение
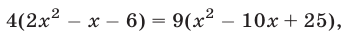
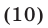
равносильное уравнению
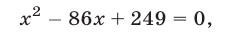
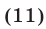
которое имеет корни 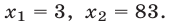
Заметим, что уравнение (11) является следствием уравнения (7), так как 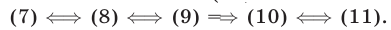 Число
Число 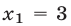 — корень уравнения (7), а число
— корень уравнения (7), а число 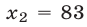 — посторонний корень для уравнения (7): при
— посторонний корень для уравнения (7): при 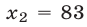 левая часть уравнения (7) больше четырех.
левая часть уравнения (7) больше четырех.
Ответ. 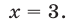
В рассмотренном примере можно было сначала перенести один из радикалов в правую часть уравнения (метод уединения радикала), а затем возвести обе части полученного уравнения в квадрат.
Воспользуемся этим приемом при решении следующего примера.
Пример:
Решить уравнение
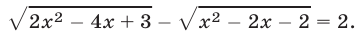
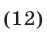
Решение:
Применив метод уединения радикала, получим уравнение
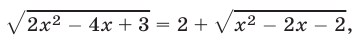
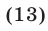
равносильное уравнению (12).
Заметим, что нет необходимости находить ОДЗ уравнения (13), но следует обратить внимание на подкоренные выражения. Если ввести новое неизвестное (выполнить замену переменной), полагая 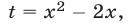 , то уравнение (13) примет вид
, то уравнение (13) примет вид
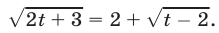
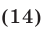
При 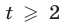 (в ОДЗ уравнения (14)) это уравнение равносильно каждому из уравнений
(в ОДЗ уравнения (14)) это уравнение равносильно каждому из уравнений
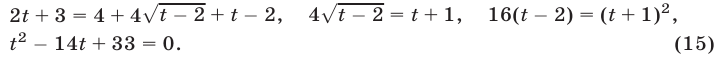
Корни 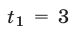 и
и 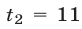 уравнения (15) удовлетворяют условию
уравнения (15) удовлетворяют условию 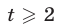 и поэтому являются корнями уравнения (14).
и поэтому являются корнями уравнения (14).
Если 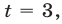 то
то 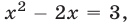 откуда
откуда 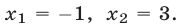 Если
Если 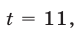 то
то 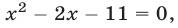 откуда
откуда 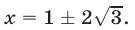
Ответ. 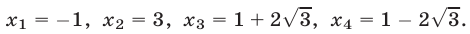
В примерах 1-3 был использован метод возведения обеих частей уравнения в квадрат. В отдельных случаях применяются другие приемы, которые могут оказаться более эффективными.
Пример:
Решить уравнение
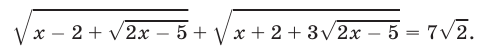
Решение:
Положим 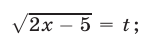 тогда
тогда 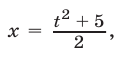 и уравнение (16) примет вид
и уравнение (16) примет вид
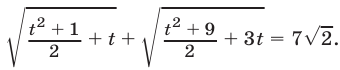
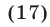
Уравнение (17) равносильно каждому из уравнений
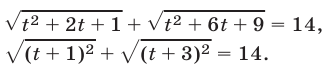
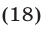
Используя тождество 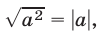 запишем уравнение (18) в виде
запишем уравнение (18) в виде
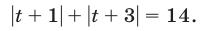
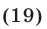
Так как 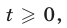 то уравнение (18) и равносильное ему уравнение (19) можно записать в виде
то уравнение (18) и равносильное ему уравнение (19) можно записать в виде 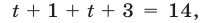 откуда
откуда 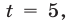 т. е.
т. е.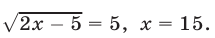
Ответ. 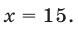
Пример:
Решить уравнение
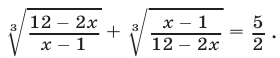
Решение:
Полагая 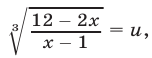 преобразуем уравнение к виду
преобразуем уравнение к виду
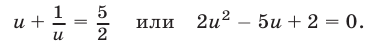
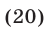
Уравнение (20) имеет корни 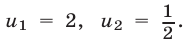 Если
Если 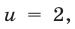 то
то 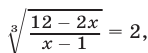 откуда
откуда 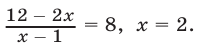 Если
Если 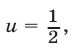 то
то 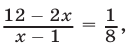 откуда
откуда 
Оба найденных корня являются корнями исходного уравнения, так как в процессе решения было использовано (наряду с заменой неизвестного) только преобразование вида 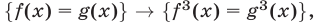 при котором получается равносильное уравнение.
при котором получается равносильное уравнение.
Ответ. 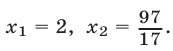
Пример:
Решить уравнение
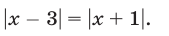
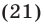
Решение:
Так как 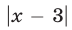 и
и 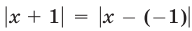 — это расстояния от искомой точки
— это расстояния от искомой точки 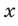 до точек
до точек 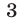 и
и 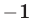 соответственно, то из равенства (21) следует, что искомая точка
соответственно, то из равенства (21) следует, что искомая точка 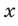 находится на одинаковом расстоянии от точек
находится на одинаковом расстоянии от точек 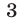 и
и 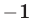 . Таким образом, точка
. Таким образом, точка 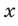 — середина отрезка
— середина отрезка 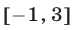 и поэтому
и поэтому 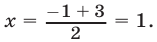
Ответ. 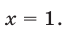
Пример:
Решить уравнение
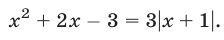
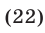
Решение:
Полагая 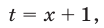 получаем уравнение
получаем уравнение
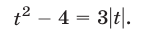
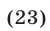
Если 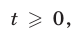 то (23) имеет вид
то (23) имеет вид 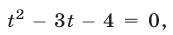 откуда находим
откуда находим 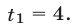
Поскольку при замене 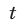 на
на 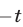 уравнение (23) не меняется, число
уравнение (23) не меняется, число 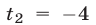 также является корнем уравнения (23), а корни уравнения (2) — числа
также является корнем уравнения (23), а корни уравнения (2) — числа  и
и 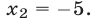
Ответ. 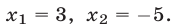
Пример:
Решить уравнение
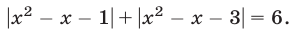
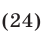
Решение:
Положим 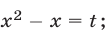 тогда уравнение (24) примет вид
тогда уравнение (24) примет вид
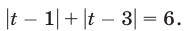
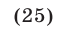
Решить уравнение (25) — значит найти все такие точки числовой оси 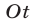 (рис. 8.1), для которых сумма расстояний от каждой из них до точек 1 и 3 равна 6. Заметим, что искомые точки лежат вне отрезка [1,3], так как сумма расстояний от любой точки отрезка до его концов равна 2.
(рис. 8.1), для которых сумма расстояний от каждой из них до точек 1 и 3 равна 6. Заметим, что искомые точки лежат вне отрезка [1,3], так как сумма расстояний от любой точки отрезка до его концов равна 2.

Пусть 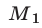 — искомая точка, лежащая правее точки 3;
— искомая точка, лежащая правее точки 3; 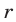 -расстоя-ние от точки
-расстоя-ние от точки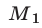 до точки 3,
до точки 3, 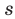 — сумма расстояний от точки
— сумма расстояний от точки 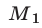 до точек 3 и 1. Тогда
до точек 3 и 1. Тогда 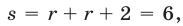 откуда
откуда 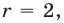 а точке
а точке 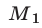 соответствует число
соответствует число 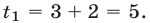 Аналогично, корнем уравнения (25) является точка
Аналогично, корнем уравнения (25) является точка 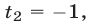 находящаяся на расстоянии 2 от точки 1.
находящаяся на расстоянии 2 от точки 1.
Таким образом, задача сводится к решению уравнений 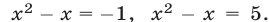 Первое из них не имеет действительных корней, а второе имеет два корня.
Первое из них не имеет действительных корней, а второе имеет два корня.
Ответ. 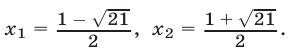
Пример:
Решить уравнение
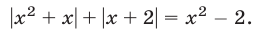
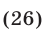
Решение:
Функция 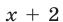 меняет знак при
меняет знак при 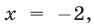 а функция
а функция 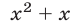 — при
— при  и
и 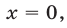 причем
причем 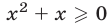 при
при 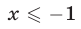 и
и 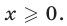 Поэтому
Поэтому
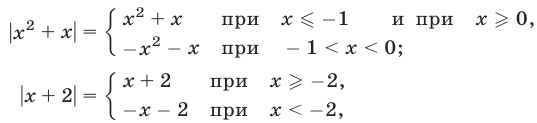
а уравнение (26), записанное без знака модуля на промежутках 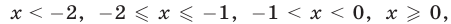 равносильно совокупности следующих систем:
равносильно совокупности следующих систем:
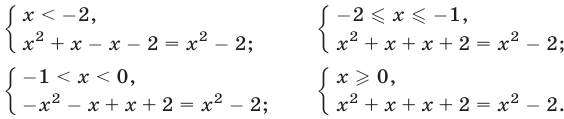
Первой из этих систем удовлетворяют все значения 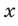 из промежутка
из промежутка 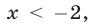 второй системе — значение
второй системе — значение  остальные две системы не имеют решений.
остальные две системы не имеют решений.
Ответ. 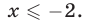
Решение иррациональных уравнений



Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

