Иррациональные числа в математике и их свойства с примерами решения и образцами выполнения

Оглавление:

На первый взгляд может показаться, что никаких других чисел, кроме рациональных, и быть не может. В действительности же это не так. Мы увидим, что, кроме рациональных чисел, существуют и другие.

Станем исходить из того, что нам известны лишь рациональные числа и никакие другие. Тогда действие возведения в квадрат иад этими числами окажется выполнимым всегда.

Например:

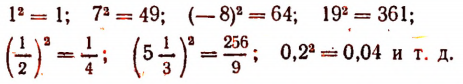
Между тем действие извлечения квадратного корня выполнимо уже далеко не всегда.

Например, действие извлечения квадратного корня из двух окажется невыполнимым, так как во множестве рациональных чисел нет такого числа, квадрат которого был бы равен двум (см. стр. 244).

Таким образом, чтобы сделать возможным выполнение действия извлечения арифметического квадратного корня, во всех случаях снова требуется прибегнуть к дальнейшему расширению нашего понятия о числе.

Здесь мы снова видим, что для выполнения прямого действия (возведения в квадрат) не требовалось расширять рациональную числовую область, а для безотказного выполнения обратного действия (извлечения квадратного корня) такое расширение уже становится необходимым.

К расширению области рациональных чисел нас приводит и рассмотрение вопроса об отношении несоизмеримых отрезков (см. стр. 247).

Действительно, оставаясь в области рациональных чисел, мы не можем выразить точно отношение несоизмеримых отрезков, а следовательно, и длину отрезка, несоизмеримого с единицей длины (см. стр. 248).

Таким образом, к расширению рациональной числовой области приводят нас потребности не только алгебры, но и геометрии.

Существование на числовой оси точек, не являющихся рациональными

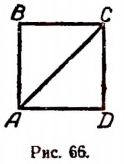
Было доказано, что диагональ и сторона квадрата несоизмеримы (см. стр. 246). Отсюда вытекает следующее: если длину стороны квадрата принять за единицу, то не будет существовать никакого рационального числа, которое выражало бы точно длину диагонали.

Пусть ABCD (рис. 66) есть квадрат, сторона которого принята за единицу длины.

Отложим на числовой оси Иррациональные числа (рис. 67) отрезки ОМ и равные диагонали АС. Тогда точки М и не будут рациональными («черными») точками числовой оси, а следовательно, будут точками, которые мы назвали образно «красными».

Но так как отрезков, несоизмеримых с единицей; длины, существует бесконечное множество то и точек на числовой оси, не являющихся рациональными, также существует бесконечное множество.

Выше мы назвали образно все рациональные точки числовой оси «черными», а все остальные «красными». Отсюда следует, что «черные» и «красные» точки заполняют собой всю числовую ось сплошь. Иначе говоря, на числовой оси, кроме рациональных («черных») и нерациональных («красных») точек, никаких других точек нет.

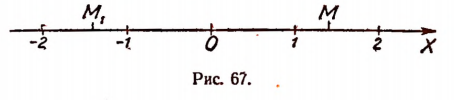
В § 5, гл. XVII было доказано, что между двумя любыми различными рациональными («черными») точками существует бесконечное множество других рациональных («черных») точек. В связи с этим примем к сведению без доказательства следующее: на любом сколь угодно малом отрезке числовой, оси, где бы он ни был расположен, имеется бесконечное множество рациональных („черных») и бесконечное множество „красных» точек.

При этом оказывается, что бесконечное множество нерациональных (т. е. «красных») точек числовой оси существенно «богаче» множества ее рациональных (т. е. «черных») точек. Это же самое в точных терминах можно сформулировать так: множество нерациональных (т. е. «красных») точек числовой оси имеет мощность (см. §6 этой же главы) более высокую, чем мощность множества рациональных (т. е. «черных») точек.

Выражаясь образно, можно сказать, что числовая ось настолько сильно насыщена «красными» (т. е. нерациональными) точками, что вся она, по нашей условной терминологии, представлялась бы нам как бы сплошь красной.

Понятие об иррациональном числе

1. Мы убедились в том, что одних рациональных чисел недостаточно для потребностей алгебры и геометрии.

Мы видели, что нет такого рационального числа, которое равнялось бы точно 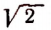Иррациональные числа . (Аналогично можно было бы убедиться, что нет таких рациональных чисел, которые равнялись бы точно, например, 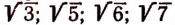и многим другим квадратным корням.) Мы знаем еще и то, что существуют отрезки, точное отношение которых не выражается никаким рациональным числом (см. стр. 247). Мы также знаем, что на числовой оси существуют такие точки, точные расстояния которых от начальной точки числовой оси не выражаются никакими рациональными числами (см. стр. 254). Значит, для изображения этих величин необходимы какие-то новые числа.

Как же составить представление об этих новых числах.

Во-первых, заметим, что такими новыми числами никак не могут быть ни конечные десятичные дроби, ни бесконечные периодические десятичные дроби, так как те и другие являются числами рациональными (см. стр. 251).

Во-вторых, заметим, что никакая бесконечная непериодическая дробь не может изображать собой рациональное число, так как всякое рациональное число (как известно из арифметики), будучи изображенным в форме бесконечной дроби, дает дробь обязательно периодическую.

Чтобы составить себе представление об этих новых числах, рассмотрим еще раз вопрос об измерении отрезка, несоизмеримого с единицей длины, и вопрос о квадратном корне из двух.

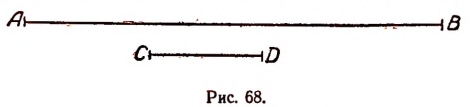
Пусть отрезки АВ и CD (рис. 68)

Первый шаг. Примем отрезок CD за единицу измерения и станем откладывать его последовательно на отрезке АВ. Пусть отрезок CD отложился 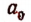Иррациональные числа раз и получился остаток MB, меньший CD. (На рис. 69 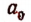= 5.) Эту операцию назовем первым шагом.

Второй шаг. Разделим отрезок CD на десять равных частей и будем откладывать 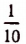Иррациональные числа часть CD на остатке MB. Пусть 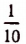часть CD отложилась на MB 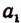раз (на рис. 70 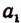= 6).

Тогда обязательно получится второй остаток 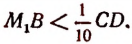Иррациональные числа

Третий шаг. На втором остатке откладываем 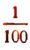Иррациональные числа часть CD. Получим целое число 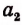и третий остаток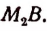

Этот процесс мы продолжаем дальше, делая четвертый, пятый и дальнейшие шаги.

В силу несоизмеримости отрезков АВ и CD этот процесс теоретически никогда не кончится и длина АВ выразится бесконечной десятичной дробью. Эта бесконечная десятичная дробь не будет периодической, так как в таком случае отрезки АВ и CD оказались бы соизмеримыми, тогда как по условию они несоизмеримы.

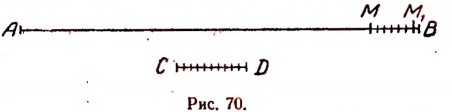
Вот эта бесконечная непериодическая десятичная дробь и будет примером нового числа, не являющегося рациональным и называемого иррациональным. Этим числом и будет выражаться длина отрезка АВ.

Определение:

Иррациональным числом называется бесконечная непериодическая десятичная (положительная или отрицательная) дробь.

Например, бесконечная непериодическая дробь

8,121121112…

есть вполне определенное иррациональное число.

Ниже будет показано, что математическое выражение, например 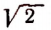Иррациональные числа есть также определенное иррациональное число.

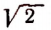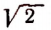Мы уже умеем находить приближенные значения Иррациональные числа с любой сколь угодно высокой степенью точности, т. е. мы можем находить сколько угодно десятичных знаков, идущих после запятой в десятичной дроби, которая изображает приближенное значение Иррациональные числа .

При этом нам ясно, что процесс извлечения 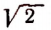Иррациональные числа никогда не может закончиться. Если бы этот процесс мог закончиться, то 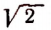был бы равен некоторой дроби 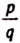, что невозможно.

Нам также ясно, что в результате бесконечного процесса извлечения не может получиться периодическая бесконечная дробь. Если бы получилась периодическая бесконечная дробь, то это означало бы опять, что 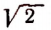Иррациональные числа равен некоторой дроби 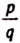, что невозможно. (Ведь периодическая бесконечная дробь есть число рациональное.)

Бесконечный ряд чисел

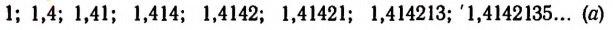
представляет собой приближенные значения 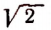Иррациональные числа с недостатком, с точностью до и т. д.

Бесконечный же ряд чисел

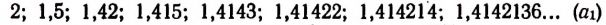
представляет собой приближенные значения 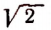Иррациональные числа с избытком, с точностью до 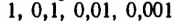и т. д.

Квадратами чисел ряда (а) будут

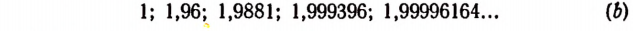
Квадратами чисел ряда (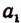 Иррациональные числа ) будут

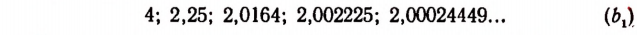
Числа, записанные в рядах (b) и 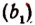Иррациональные числа , становятся тем ближе к числу 2, чем больше десятичных знаков мы берем.

Ряд (а) обладает той особенностью, что раз полученный десятичный знак навсегда сохраняется при продолжении процесса.

Это, естественно, приводит к мысли принять за 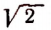Иррациональные числа бесконечную десятичную дробь

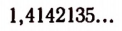
Но эта бесконечная дробь не может оказаться периодической, как это уже было доказано выше.

Итак, квадратный корень из двух изображается бесконечной непериодической десятичной дробью. Следовательно, 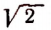Иррациональные числа есть число иррациональное.

Написать бесконечную непериодическую десятичную дробь, разумеется, нельзя. Мы, однако, считаем ее определенной, если имеется то или иное правило, позволяющее написать любой его десятичный знак, как бы далеко ни стоял этот знак в последовательности десятичных знаков.

Например, тысячный знак в бесконечной десятичной дроби

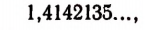
изображающей иррациональное число 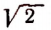Иррациональные числа имеет вполне определенную величину, несмотря на то, что его едва ли кто знает. Впрочем, при помощи современных электронных цифровых вычислительных машин найти этот тысячный знак можно довольно быстро.

Аналогично тому, как мы доказали, что 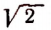Иррациональные числа есть число иррациональное, можно доказать, что числа 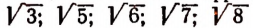и т. д. также являются иррациональными.

Чтобы показать существование других иррациональных чисел, введем понятие арифметического корня n-й степени.

Определение:

Арифметическим корнем n-й степени из положительного числа а называется такое новое положительное число, п-я степень которого равна а.

Корень n-й степени из а обозначается символом

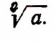
Число а называется подкоренным выражением; число n называется показателем корня; символ 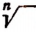Иррациональные числа называется знаком корня n-й степени, а выражение 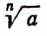называется корнем n -й степепи.

Примеры:

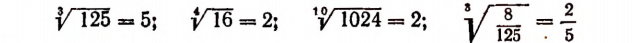
и т. д.

Корни 3-й степени называют кубическими корнями. Например, 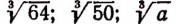Иррациональные числа суть кубические корни.

Примем к сведению без доказательства, что, например,

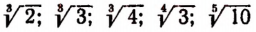
и им подобные представляют собой числа иррациональные.

Но ошибочно было бы думать, что иррациональные числа порождаются только корнями. Наоборот, существует много других источников, порождающих иррациональные числа. Например, мы видели, что длина всякого отрезка, несоизмеримого с единицей длины, есть число иррациональное, независимо от того, может или не может эта длина выражаться точно с помощью одного или нескольких корней.

Доказано, что отношение длины окружности к своему диаметру есть число иррациональное. Доказано, кроме того, что это иррациональное число не может быть точно представлено с помощью одного или нескольких корней.

Отношение длины окружности к своему диаметру принято обозначать греческой буквой 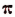Иррациональные числа («пи»).

Иррациональность числа 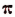Иррациональные числа впервые была доказана немецким математиком Ламбертом в 1766 году.

Число 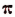Иррациональные числа изображается бесконечной непериодической дробью

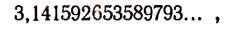
первые 15 десятичных знаков которой здесь выписаны.

Число 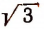Иррациональные числа изображается бесконечной непериодической дробью

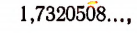
первые 7 десятичных знаков которой здесь выписаны.

Мы уже знаем, что любая бесконечная непериодическая десятичная дробь представляет собой число иррациональное.

Теперь может возникнуть вопрос о том, как же понимать смысл самой бесконечной непериодической десятичной дроби.

Возьмем какую-нибудь бесконечную непериодическую десятичную дробь, например 4,25 225 2225… Составим две последовательности чисел.

Первая последовательность: 4,2; 4,25; 4,252; 4,2522; 4,25225…

Вторая последовательность: 4,3; 4,26; 4,253; 4,2523, 4,25226…

Доказано (доказательства мы здесь не приводим), что этими двумя бесконечными последовательностями определяется единственное число, которое больше каждого числа первой последовательности и меньше каждого числа второй последовательности. Это единственное число мы и понимаем под символом

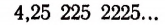
Таким образом, конкретное представление об иррациональном числе

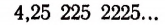
мы можем себе составить путем рассмотрения указанных выше двух бесконечных последовательностей. Эти две бесконечные последовательности дают возможность находить приближенные значения определяемого ими иррационального числа с любой точностью— с недостатком и с избытком. Например, число 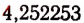Иррациональные числа есть приближенное значение с недостатком с точностью до 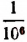. Число же 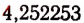есть приближенное значение с избытком с точностью до .

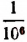Мы уже убедились в том, что всякая бесконечная десятичная непериодическая дробь является числом иррациональным. Однако существуют и другие бесконечные процессы, определяющие собой то или иное иррациональное число. Например, бесконечный процесс

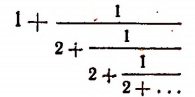
определяет собой иррациональные числа 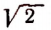, так что

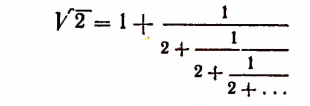
Пояснения к формуле

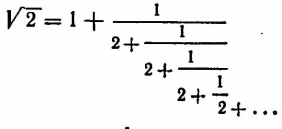
Выражение

представляет собой некоторый, идущий по определенному закону, бесконечный процесс. Если допустить, что этот бесконечный процесс определяет собой некоторое число то получим

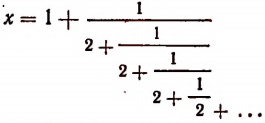
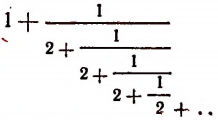
Перепишем эту формулу в следующем виде:

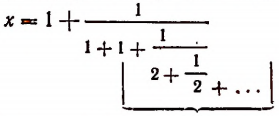
Выражение в предыдущей формуле, отмеченное одной фигурной скобкой, представляет тот же самый бесконечный процесс, которым (как мы допустили) определяется число х. Поэтому получим, что

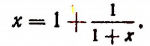
Из этого уравнения следует, что

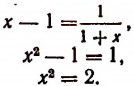
Но так как х — число положительное, то

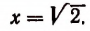
Итак, доказано следующее. Если допустить, что бесконечным процессом

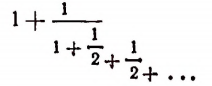
определяется некоторое число, то этим числом будет как раз иррациональное число 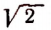Иррациональные числа .

Примем к сведению без доказательства, что, беря все большее и большее число звеньев этого бесконечного процесса, мы можем получать рациональные приближения иррационального числа 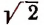Иррациональные числа все с большей и большей точностью.

Например, значение выражения

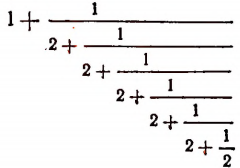
равно 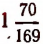Иррациональные числа . Отсюда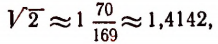

что как раз и представляет приближенное значение 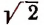Иррациональные числа с недостатком с точностью до 0,0001.

Сравнение иррациональных чисел

Два иррациональных числа называются равными, если их изображения с помощью бесконечных непериодических десятичных дробей одинаковы (тождественны).

Из двух положительных иррациональных чисел больше то, у которого целая часть больше. Если же целые части равны, то большим будет то, у которого больше первый десятичный знак после запятой. Если же и первые десятичные знаки одинаковы, то большим будет то, у которого больше второй десятичный знак и т. д.

Например, сравним следующие иррациональные числа:

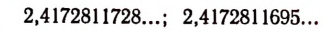
Здесь одинаковы целые части; первые семь десятичных знаков во втором числе такие же, как и в первом. Восьмой десятичный знак первого числа больше восьмого десятичного знака второго числа. Поэтому первое иррациональное число больше второго. Выписав достаточное число десятичных знаков бесконечных непериодических десятичных дробей изображающих иррациональные числа 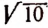и 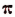, убедитесь, что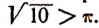

Сложение и умножение иррациональных чисел

Поясним, что такое сумма двух иррациональных чисел. Пусть иррациональное число а изображается следующей бесконечной непериодической десятичной дробью

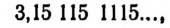
а иррациональное число b — дробью

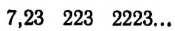
Тогда сумма а + b изобразится дробью

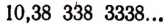
Эта дробь бесконечная, непериодическая, десятичная; значит, она изображает собой определенное иррациональное число.

Напишем последовательности чисел, изображающих приближенные значения числа а:

с недостатком: 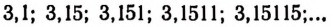Иррациональные числа
с избытком: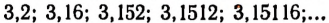

Сделаем то же самое и для числа b:

Составим еще две следующие последовательности:

В последовательности (I) идут суммы соответствующих приближенных значений чисел a и b с недостатком, ав(II)с избытком.

Под суммой а + b подразумевается такое число, которое больше каждого члена бесконечной последовательности (I) и меньше каждого члена бесконечной последовательности (II).

Таким числом как раз будет дробь

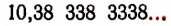
Определение:

Суммой двух положительных иррациональных чисел называется число, которое больше суммы любых их приближенных значений с недостатком, но меньше суммы любых их приближенных значений с избытком. Такое число, как это доказано в строгой теории иррациональных чисел, всегда существует и притом только одно.

Сумма двух иррациональных чисел, вообще говоря, будет числом иррациональным, но может оказаться и рациональным.

Например, числа 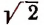Иррациональные числа и 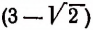оба иррациональные, между тем как их сумма

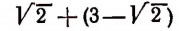
есть рациональное число 3.

Определение:

Произведением двух положительных иррациональных чисел называется число, которое больше произведений любых их приближенных значений с недостатком, но меньше произведений любых их приближенных значений с избытком.

Такое число также всегда существует и притом только одно.

Произведение двух иррациональных чисел, вообще говоря, будет числом иррациональным, но может оказаться и рациональным.

Например, произведение иррациональных чисел 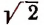Иррациональные числа и 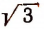будет иррациональным числом, равным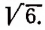

Произведение же иррациональных чисел 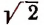Иррациональные числа и 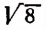будет равно 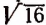, т. е. рациональному числу 4.

По аналогии с приведенными рассуждениями читатель сможет сам составить определения сложения и умножения двух чисел для того случая, когда одно из них рациональное, а другое иррациональное.

Подобно этому определяется вычитание и деление иррациональных чисел.

Понятие действительного числа

Определение:

Все рациональные и иррациональные числа, как положительные, так и отрицательные, называются действительными, или вещественными, числами.

Примем к сведению без доказательства, что особенности нуля и единицы (см. стр. 41), а также переместительный и сочетательный законы сложения и переместительный сочетательный и распределительный законы умножения (см. стр. 32 и 39) остаются в силе для всех действительных чисел (рациональных и иррациональных).

Примеры для закрепления терминологии

Число 2 есть действительное, рациональное, целое, натуральное.
Число (— 2) есть действительное, рациональное, целое, отрицательное.
Число 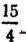есть действительное, рациональное, дробное, положительное.
Число 2,333… есть действительное, рациональное, дробное, положительное (2,333… = ).
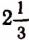Число 2,1333… есть действительное, рациональное, дробное, положительное (2,1333… = ).
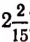Число 2, 12 112 11112… есть действительное, иррациональное, положительное.
Число 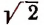есть действительное, иррациональное, положительное.
Число (— 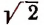) есть действительное, иррациональное, отрицательное.

Слово «рациональный» происходит от латинского слова «rationalis», что означает — «разумный», «обоснованный».

Слово «иррациональный» происходит также от латинского слова «irratlonalis», что означает — «неразумный», «необоснованный».

Можно было бы подумать, что числа, несоизмеримые с единицей, были названы «иррациональными» потому, что их действительно считали не поддающимися логическому пониманию. На самом деле это не так. Еще у древнегреческого математика Евклида встречаются такие определения, из которых видно, что он отнюдь не считал «иррациональные числа» «неразумными», «нелогичными».

Термин «иррациональное число» возник вследствие чисто формального перевода на латинский язык греческого слова «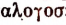 Иррациональные числа » . Употребляя это слово, греческие математики вовсе не хотели назвать новые числа «нелогичными», а хотели подчеркнуть лишь то, что каждое из них нельзя выразить отношениями двух целых чисел.

Строгая теория иррациональных чисел была построена впервые лишь во второй половине XIX века немецким математиком Дедекиндом. Со строгой теорией иррациональных чисел можно ознакомиться, например, по книге А. Н. Колмогорова и П. С. Александрова «Введение в теорию функций действительного переменного».

Примечание:

Примем к сведению без доказательства, что правила и формулы, выведенные для рациональных чисел, остаются в силе и для всех действительных чисел. Например, правила умножения и деления степеней, формулы умножения, свойства пропорций, свойство ряда равных отношений и т. д.

Некоторые понятия и предложения элементарной теории множеств

О бесконечных множествах

В математике постоянно приходится иметь дело с бесконечными множествами.

Приведем несколько примеров таких множеств:

1) множество всех натуральных чисел;
2) множество всех четных чисел;
3) множество всех простых чисел;
4) множество всех, рациональных чисел;
5) множество всех иррациональных чисел;
6) множество всех действительных чисел;
7) множество всех различных прямоугольных треугольников с гипотенузой, равной единице;
8) множество всех различных квадратных уравнений с действительными числовыми коэффициентами.

Введем понятие о взаимно однозначном соответствии.

Мы уже знаем, что каждому действительному числу соответствует определенная точка числовой оси и, наоборот, каждой точке числовой оси соответствует определенное действительное число. Имея это в виду, говорят, что между множеством действительных чисел и множеством точек числовой оси имеет место взаимно однозначное соответствие.

Приведем другой пример взаимно однозначного соответствия.

Между множеством всех целых положительных чисел и множеством целых отрицательных чисел можно установить взаимно однозначное соответствие. Например, каждому целому положительному числу можно поставить в соответствие число, ему противоположное.

Определение:

Если между элементами двух множеств можно установить взаимно однозначное соответствие, то такие два множества называются эквивалентными.

Пример:

Множество точек числовой оси и множество действительных чисел эквивалентны. Каждой точке числовой оси соответствует одно и только одно определенное действительное число и, наоборот, каждому действительному числу соответствует одна и только одна определенная точка числовой оси.

Пример:

Множество точек отрезка АВ (рис. 71) и множество точек отрезка Иррациональные числа — эквивалентны.

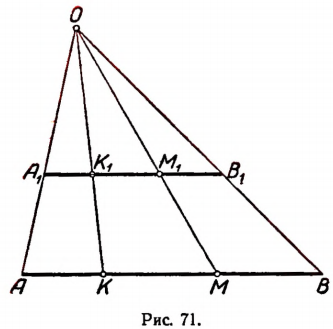
Каждой точке М отрезка А В можно поставить в соответствие одну и только одну точку Иррациональные числа отрезка лежащую на луче ОМ. Наоборот, каждой точке 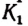отрезка 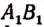можно поставить в соответствие одну и только одну точку К отрезка АВ, лежащую на луче ОК.

Пример:

Множество всех целых положительных чисел

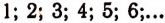
эквивалентно множеству всех положительных четных чисел

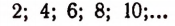
В самом деле, мы можем поставить в соответствие каждому целому числу число, вдвое большее его. Наоборот, каждому четному числу мы можем поставить в соответствие число, вдвое меньшее его.

Взаимно однозначное соответствие между рассмотренными множествами (пример 3) мы можем записать в виде следующей таблицы:

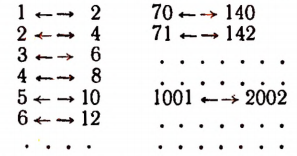
Относительно двух эквивалентных бесконечных множеств говорят также, что они имеют одинаковую мощность. Другими словами, два бесконечных множества имеют одинаковую мощность, если эти множества эквивалентны.

Счетные множества и множества мощности континуума

Множество, эквивалентное множеству всех целых положительных чисел, называется счетным множеством. Например, множество всех положительных четных чисел есть счетное множество. Множество всех положительных нечетных чисел также будет счетным, так как оно тоже эквивалентно множеству всех целых положительных чисел.

Так как всякое множество эквивалентно самому себе, то и множество целых положительных чисел также является счетным множеством.

Множество, эквивалентное множеству всех действительных чисел, называется множеством мощности континуума.

Множество точек числовой оси эквивалентно множеству действительных чисел. Поэтому множество точек числовой оси также имеет мощность континуума.

Приведем еще примеры множеств, имеющих мощность континуума.

Пример:

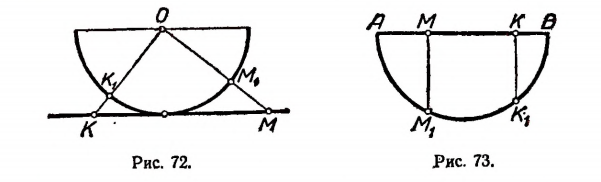
Множество точек полуокружности имеет мощность континуума. В самом деле, легко убедиться в том, что множество точек полуокружности эквивалентно множеству точек числовой оси. Каждой точке Иррациональные числа полуокружности (рис. 72) можно поставить в соответствие одну и только одну точку М числовой оси, лежащую на луче 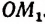. Наоборот, каждой точке К числовой оси можно поставить в соответствие одну и только одну точку 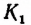Иррациональные числа полуокружности, лежащую на луче ОК.

Пример:

Множество точек любого отрезка прямой имеет мощность континуума.

Доказательство:

Множество точек отрезка прямой эквивалентно множеству точек полуокружности, построенной на этом отрезке как на диаметре.

В самом деле, каждой точке М отрезка АВ (рис. 73) можно поставить в соответствие одну и только одну определенную точку Иррациональные числа полуокружности, лежащую на перпендикуляре к прямой АВ, восставленном из точки М. Далее, каждой точке 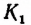полуокружности можем поставить в соответствие одну и только одну точку К отрезка АВ, лежащую на перпендикуляре, опущенном из точки 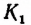Иррациональные числа на прямую АВ.

Но ранее было доказано, что множество точек полуокружности имеет мощность континуума. Следовательно, и мощность множества точек любого отрезка прямой также ийеет мощность континуума, что и требовалось доказать.

Так как всякое множество эквивалентно самому себе, то множество действительных чисел также имеет мощность континуума.

Примем к сведению без доказательства следующее.

Множество рациональных чисел эквивалентно множеству натуральных чисел, т. е. есть счетное множество.
Множество же одних иррациональных чисел не является счетным, а имеет такую же мощность, как и множество всех действительных чисел, т. е. мощность континуума.
Из множества, имеющего мощность континуума, можно выделить сколько угодно бесконечных счетных множеств и прн этом оставшиеся элементы составят бесконечное множество опять же мощности континуума.
Мощность счетного множества н мощность континуума — это различные мощности.
Мощность счетного множества есть наименьшая мощность нз всех возможных мощностей бесконечных множеств.
Мощность континуума есть более высокая мощность, чем мощность счетного множества.

С теорией множеств можно ознакомиться, например, по книге А. Н. Колмогорова и С. Ф. Фомина «Элементы теории функций и функционального анализа».

Дополнение к иррациональным числам

Смотрите также:

Действительные переменные	Действительные числа
Касание n-го порядка	Соотношения величины между действительными числами

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике: