Оглавление:
Рациональные и иррациональные алгебраические выражения: Назовем алгебраическим всякое выражение, получающееся из чисел и некоторых букв с помощью арифметических операций и возведения в степень с рациональным показателем. Мы не включили в число операций извлечение корня, так как оно сводится к возведению в степень (с показателем 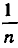 ).
).
Примерами алгебраических выражений являются:
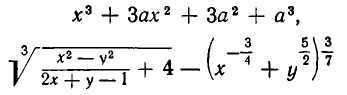
и т. д. Ясно, что многочлены — частный случай алгебраических выражений.
Говорят, что алгебраическое выражение рационально относительно некоторой буквы а, если никакая содержащая эту букву часть этого выражения не возводится в степень с нецелым показателем. В противном случае говорят, что выражение иррационально относительно буквы а. Например, выражение
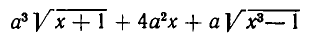
рационально относительно буквы а и иррационально относительно буквы х
Одночленные иррациональные выражения
Иррациональное выражение называется одночленным, если оно получается из чисел и букв с помощью операций умножения и возведения в степень с рациональным показателем. Примерами одночленных иррациональных выражений являются:
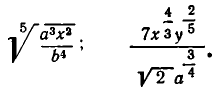
Иррациональное же выражение 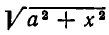
не является одночленным.
Некоторые одночленные иррациональные выражения можно упростить. Для этого надо:
а) Раскрыть все скобки, используя формулы
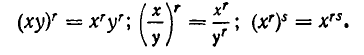
б) Объединить степени с одинаковыми основаниями, используя формулу 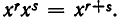
в) Сократить дроби в показателях отдельных букв.
В результате получается выражение вида
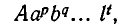
где А —некоторое число (быть может, иррациональное), а 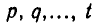 — несократимые дроби.
— несократимые дроби.
Здесь уже отсутствуют скобки и каждая буква входит лишь один раз. Такой вид одночленного иррационального выражения мы будем называть каноническим.
Пример:
Привести к каноническому виду иррациональное выражение
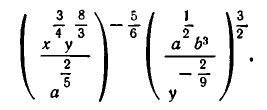
По формулам (1), (2), (3), это выражение равно:
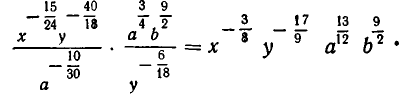
Сокращение показателей и приведение корней к общему показателю
Так как 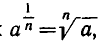 то из каждого свойства степеней с рациональными показателями вытекает соответствующее свойство корней.
то из каждого свойства степеней с рациональными показателями вытекает соответствующее свойство корней.
Равенство 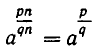 (см. формулу (3), п. 2) переписывается так: при а > О имеем
(см. формулу (3), п. 2) переписывается так: при а > О имеем

Таким образом, если подкоренное выражение является степенью положительного числа, причем показатель степени имеет общий делитель с показателем корня, то можно сократить эти показатели на общий делитель. Например, 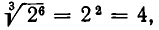
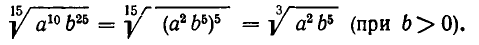
Из равенства (1) вытекает, что любые два корня с натуральными показателями можно привести к общему показателю.
Именно пусть даны корни 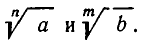 Тогда по формуле (1) имеем
Тогда по формуле (1) имеем 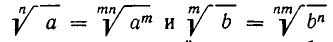 (разумеется, в качестве общего показателя корней можно выбрать не mn, а наименьшее общее кратное чисел m и n).
(разумеется, в качестве общего показателя корней можно выбрать не mn, а наименьшее общее кратное чисел m и n).
Отметим, что формула (1) справедлива лишь при условии а > 0. В случае, когда а < 0, эта формула, вообще говоря, неверна. Например, рассмотрим 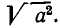 Если а > 0, то по формуле (1) получаем
Если а > 0, то по формуле (1) получаем 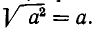 Пусть теперь а < 0 . Тогда — а > 0 и
Пусть теперь а < 0 . Тогда — а > 0 и 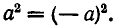 Поэтому при а < 0 имеем:
Поэтому при а < 0 имеем:
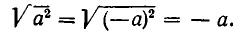
Например,
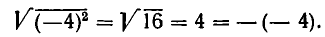
Наконец, если а — 0, то 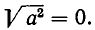 . Полученные значения для
. Полученные значения для 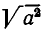 можно выразить одной формулой
можно выразить одной формулой
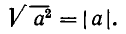
В самом деле, как 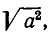 так и |а | равны а при
так и |а | равны а при 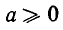 (—а) при а < 0.
(—а) при а < 0.
Вообще, если общий делитель п, на который сокращают показатели корня и подкоренного выражения, четен и рассматриваются любые значения а, формулу (1) следует переписать так:

Пример:
Вычислить
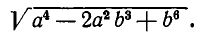
По формуле (2) получаем:
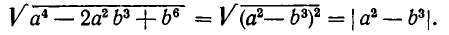
Значит, если 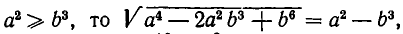 а если
а если 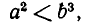 то этот корень равен
то этот корень равен 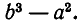
Извлечение корня из произведения и степени
Положим в формуле (1), п. 2, 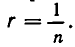 Мы получим, что при х > 0, у > 0:
Мы получим, что при х > 0, у > 0:

Точно так же из формулы (2), п. 2, выводится, что при х > 0, у > 0:

Полученные свойства корней формулируются следующим образом:
а) Корень n-й степени из произведения двух положительных чисел равен произведению корней п-й степени из отдельных сомножителей.
б) Корень n-й степени из отношения двух положительных чисел равен отношению корней n-й степени из этих чисел
Например, 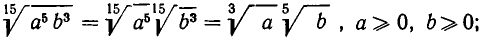
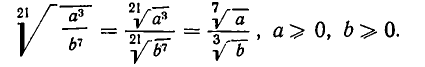
Пользуясь свойствами (1) и (2), можно записать произведение нескольких корней с помощью одного знака корня. Если перемножаемые корни имеют один и тот же показатель, то для получения произведения надо перемножить их подкоренные выражения и извлечь из полученного произведения корень той же степени. Например,
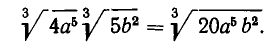
Если же перемножаемые корни имеют различные показатели, то и с надо предварительно привести к общему показателю (см. стр. 103). Например,
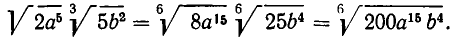
Совершенно так же выполняется деление корней. Например,
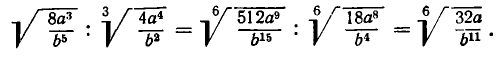
Вынесение алгебраических выражений из-под корня и внесение их под корень
Из формулы (1), п. 7, вытекает, что при а > 0 и b > 0:
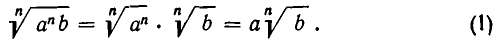
Итак, если часть подкоренного выражения для корня n-й степе ни является n-й степенью некоторого положительного алгебраического выражения, то это выражение можно вынести из-под корня.
Следует иметь в виду, что формула (1) справедлива лишь при условии а >0, b > 0. Если же это условие не выполняется, а n = 2k — четное число, то вместо формулы (1) надо писать:
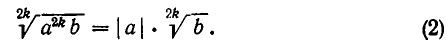
Возведение корня в степень
Эта операция основана на формуле (6 ). Из нее следует, что 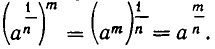 Это равенство можно записать так:
Это равенство можно записать так:
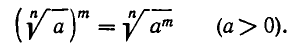
Таким образом, чтобы возвести корень с положительным под коренным выражением в некоторую степень, надо возвести в эту степень подкоренное выражение. Например,
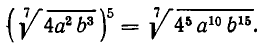
Извлечение корня из корня
Эта операция также основана на формуле (6 ). Из нее следует, что 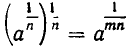 , и потому
, и потому
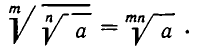
Таким образом, при извлечении корня из корня показатели корней перемножаются, а подкоренное выражение остается неизменным. Например,
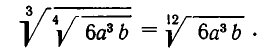
Подобные корни
Два корня называются подобными, если их можно преобразовать к такому виду, чтобы они отличались лишь рациональным множителем (при этом предполагается, что переменные, от которых зависит подкоренное выражение, положительны). Например, корни
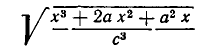
и
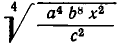
подобны, так как при а > 0 , b > 0 , с > 0 , x> 0 имеем:
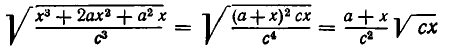
и
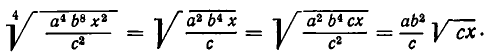
Второй корень получается из первого умножением на рациональный множитель.
Корни из одночленов подобны тогда и только тогда, когда в их канонической форме иррациональные множители одинаковы. Поэтому, чтобы убедиться в подобии двух корней из одночленов, надо привести их к канонической форме.
Сложение и вычитание корней
Вообще говоря, сумму не скольких корней не удается записать с помощью лишь одного знака корня. Однако, если среди рассматриваемых корней есть подобные, их можно сгруппировать вместе и вынести за скобки общий множитель.
Пример:
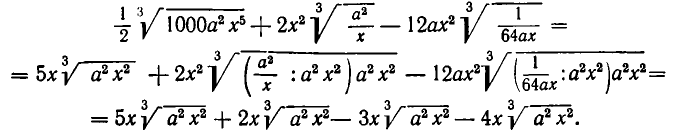
Уничтожение иррациональности в знаменателе или в числи теле алгебраической дроби
Часто бывает нужно найти численное значение иррационального выражения при заданных значениях входящих в него букв. При этом бывает неудобно делить на иррациональные числа. В таких случаях стараются преобразовать за данное иррациональное выражение так, чтобы его знаменатель не содержал корней.
Посмотрим сначала, как выполняется это преобразование в случае, когда знаменатель дроби — корень из одночлена. Пусть дано иррациональное выражение 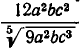 . Если мы хотим освободиться от иррациональности в знаменателе этой дроби, то надо помножить и числитель, и знаменатель на такой множитель, чтобы в знаменателе извлекся корень. Ясно, что для этого надо умножить подкоренное выражение в знаменателе дроби на
. Если мы хотим освободиться от иррациональности в знаменателе этой дроби, то надо помножить и числитель, и знаменатель на такой множитель, чтобы в знаменателе извлекся корень. Ясно, что для этого надо умножить подкоренное выражение в знаменателе дроби на 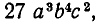 тогда оно станет равно
тогда оно станет равно 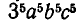 и корень извлечется. Вспоминая правило умножения корней, видим, что числитель и знаменатель надо умножить на
и корень извлечется. Вспоминая правило умножения корней, видим, что числитель и знаменатель надо умножить на 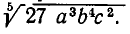 Тогда мы получим, что
Тогда мы получим, что
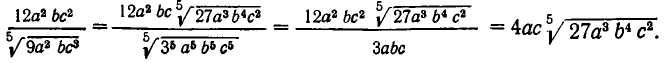
Вообще, если дано выражение вида 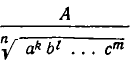 , причем все показатели
, причем все показатели  меньше n, то надо умножить числитель и знаменатель дроби на один и тот же множитель
меньше n, то надо умножить числитель и знаменатель дроби на один и тот же множитель
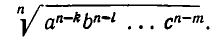
Тогда при а >0, b > 0 , …, с > 0 получим:
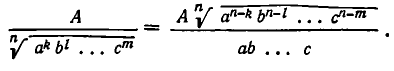
Этот ответ остается справедливым при нечетном n для любых а, b, …, с. Если же n четно, то в общем случае в знаменателе надо писать 
Теперь рассмотрим случай, когда знаменатель алгебраической дроби имеет вид 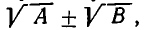 где A и В — положительные рациональные выражения. В этом случае надо умножить и числитель, и знаменатель на выражение
где A и В — положительные рациональные выражения. В этом случае надо умножить и числитель, и знаменатель на выражение 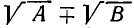 (оно получается из знаменателя изменением знака при
(оно получается из знаменателя изменением знака при 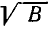 ). Так как (а +b) (а—b) =
). Так как (а +b) (а—b) = 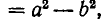 то при А > 0 и В > 0
то при А > 0 и В > 0
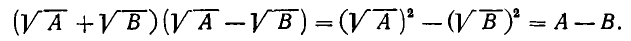
Поскольку (А — В) — рациональное выражение, мы избавляемся от иррациональности в знаменателе дроби. (Точно так же избавляются от иррациональности в знаменателе, если он имеет вид 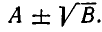 ) Например,
) Например,
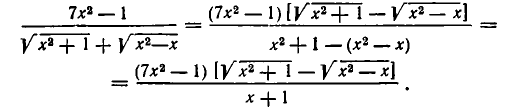
Аналогично действуют в случае, когда знаменатель дроби имеет вид 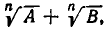 , где А и В — рациональные выражения. Уничтожение иррациональности в знаменателе основывается здесь на формуле
, где А и В — рациональные выражения. Уничтожение иррациональности в знаменателе основывается здесь на формуле
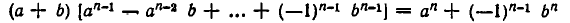
(см. стр. 32). Именно, положим 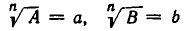 и умножим числитель и знаменатель на одно и то же выражение
и умножим числитель и знаменатель на одно и то же выражение
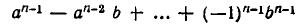
(где надо заменить а на 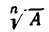 и b на
и b на 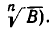 Тогда знаменатель примет вид:
Тогда знаменатель примет вид:
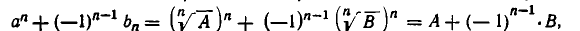
то есть станет рациональным выражением. Случай, когда знаменатель равен 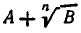 , разбирается точно так же. Здесь надо положить
, разбирается точно так же. Здесь надо положить 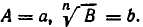
Если знаменатель имеет вид 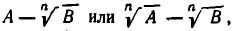 то надо положить
то надо положить 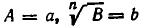 (соответственно
(соответственно 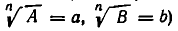 и воспользоваться формулой
и воспользоваться формулой
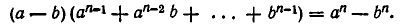
Если знаменатель имеет вид 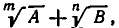 то корни
то корни 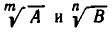 надо сначала привести к общему показателю. Например,
надо сначала привести к общему показателю. Например,
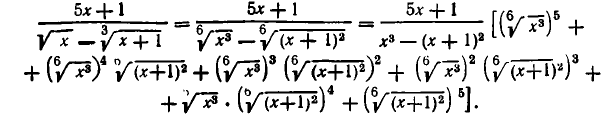
Случай, когда знаменатель является суммой трех или большего числа корней, сложнее. Однако можно показать, что какой бы сложный вид ни имел знаменатель, всегда можно освободиться от иррациональности в знаменателе. Общие методы таких преобразований изучаются в высшей алгебре.
В некоторых задачах, наоборот, бывает целесообразно уничтожить иррациональность в числителе алгебраической дроби, т. е. преобразовать дробь к такому виду, чтобы ее числитель содержал лишь рациональные выражения. Читателю должно быть ясно, что эта цель достигается теми же способами, как уже в разобранных выше примерах.
Преобразование выражений вид 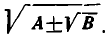
Пусть задано алгебраическое выражение 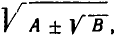 где А > 0, В > 0,
где А > 0, В > 0, 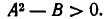 Мы покажем сейчас, что его можно представить в следующем виде суммы двух корней:
Мы покажем сейчас, что его можно представить в следующем виде суммы двух корней:
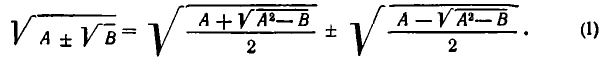
Для доказательства покажем сначала, что квадраты выражений в обеих частях равенства (1) совпадают. В самом деле,
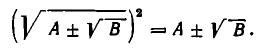
С другой стороны,
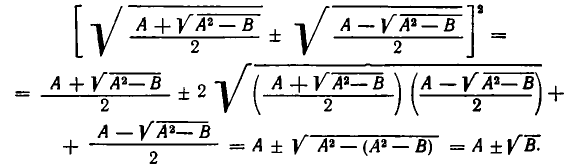
Осталось показать, что обе части равенства (1) положительны. Для левой части это очевидно, так как мы рассматриваем лишь арифметические значения корней. Д ля правой это справедливо, поскольку при А >0, В > 0 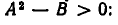
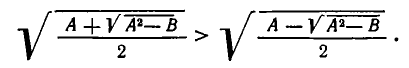
Формула (1) позволяет упростить выражение 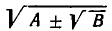 в случае, когда разность
в случае, когда разность 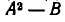 есть полный квадрат. Например, имеем:
есть полный квадрат. Например, имеем:
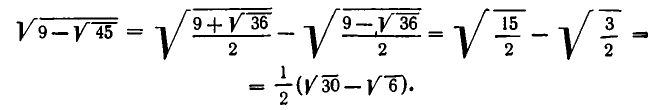
Иррациональные уравнения и неравенства
Определение:
Иррациональным уравнением называется уравнение вида R(х)=0, где R(х) — иррациональное выражение от х. К такому виду приводятся уравнения 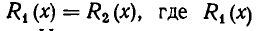 и
и 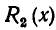 — иррациональные выражения от х. Например,
— иррациональные выражения от х. Например,
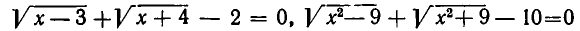
являются иррациональными уравнениями, а
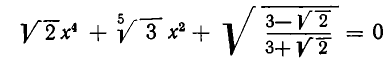
— рациональное алгебраическое уравнение (так как х не находится под знаком корня).
В иррациональных уравнениях все радикалы понимаются в смысле арифметического значения. Поэтому, если показатель корня — четное число, то подкоренное выражение и значение корня должны быть неотрицательными. Отсюда ясно, например, что иррациональное уравнение 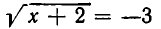 не имеет решений — его левая часть неотрицательна при всех допустимых значениях х.
не имеет решений — его левая часть неотрицательна при всех допустимых значениях х.
Сведение иррациональных уравнений к рациональным
Для решения иррациональных уравнений стараются свести их к рациональным уравнениям. С этой целью обе части уравнения после соответствующих преобразований возводят в одну и ту же степень. Чтобы показать, что при этом не происходит потери корней, докажем следующую теорему.
Теорема:
Если число а — корень уравнения 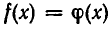 , то это число удовлетворяет и уравнению
, то это число удовлетворяет и уравнению
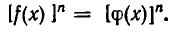
Доказательство:
По условию имеет место равенство 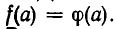 Возведем обе части этого равенства в n-ю степень. Равенство от этого не нарушится, и мы получим,» что
Возведем обе части этого равенства в n-ю степень. Равенство от этого не нарушится, и мы получим,» что 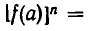
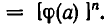 Это показывает, что а — корень уравнения
Это показывает, что а — корень уравнения
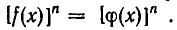
Итак, при возведении обеих частей уравнения в одну и ту же степень мы получаем уравнение, являющееся следствием исходного. Однако это уравнение при четных п неравносильно исходному. Ведь если из равенства 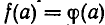 вытекает
вытекает 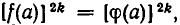 то обратное неверно. Именно из
то обратное неверно. Именно из 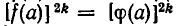 следует лишь, что
следует лишь, что 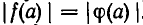 Если при этом
Если при этом 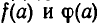 имеют одинаковые знаки, то
имеют одинаковые знаки, то 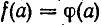 . Если же они имеют различные знаки, то
. Если же они имеют различные знаки, то 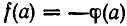 . Таким образом, корень уравнения
. Таким образом, корень уравнения 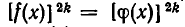 может удовлетворять не только уравнению
может удовлетворять не только уравнению 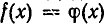 , но и уравнению
, но и уравнению 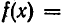
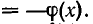 Во втором случае он является посторонним для уравнения
Во втором случае он является посторонним для уравнения 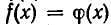 . Если же показатель n нечетен, n=2k+1, то из
. Если же показатель n нечетен, n=2k+1, то из 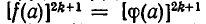 следует, что
следует, что 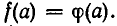 Поэтому уравнения
Поэтому уравнения 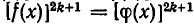 и
и 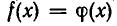 равносильны.
равносильны.
Итак, если при решении уравнения нам пришлось возводить обе его части в степень с четным показателем, то могли получиться посторонние корни. Чтобы выяснить, какие из корней уравнения 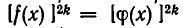 удовлетворяют исходному уравнению
удовлетворяют исходному уравнению 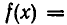
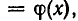 надо подставить их в исходное уравнение и посмотреть, удовлетворяют они уравнению или нет.
надо подставить их в исходное уравнение и посмотреть, удовлетворяют они уравнению или нет.
Примеры:
1) Решить уравнение
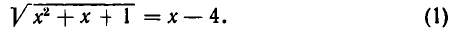
Возводя обе части уравнения в квадрат, получим уравнение:
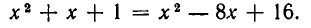
Его корнем является 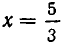 . Но
. Но 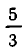 не удовлетворяет уравнению (1)— после подстановки
не удовлетворяет уравнению (1)— после подстановки 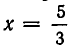 получается неверное равенство. Следовательно, уравнение (1) решений не имеет.
получается неверное равенство. Следовательно, уравнение (1) решений не имеет.
2) Решить уравнение
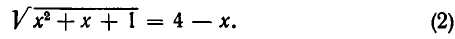
Здесь после возведения в квадрат получаем уравнение:
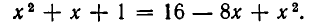
Его корнем является 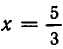 . Проверка показывает, что
. Проверка показывает, что 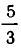 удовлетворяет уравнению (2).
удовлетворяет уравнению (2).
3) Решить уравнение
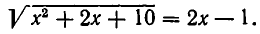
Возводя обе части уравнения в квадрат, получаем квадратное уравнение 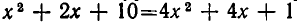 . Его корнями являются
. Его корнями являются 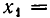
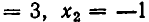 . Проверка показывает, что только корень x = 3 удовлетворяет заданному уравнению. Корень же x = —1 удовлетворяет уравнению
. Проверка показывает, что только корень x = 3 удовлетворяет заданному уравнению. Корень же x = —1 удовлетворяет уравнению
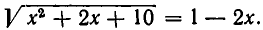
Уединение радикала
Мы видели, что при решении иррациональных уравнений приходится возводить обе части уравнения в одну и ту же степень. При этом, разумеется, желательно, чтобы хоть одна из частей уравнения имела вид 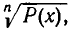 где Р(х) — рациональное выражение. В этом случае после возведения обеих частей уравнения в n-ю степень мы получим в соответствующей части уравнения рациональное выражение. Поэтому при решении иррациональных уравнений обычно поступают так.
где Р(х) — рациональное выражение. В этом случае после возведения обеих частей уравнения в n-ю степень мы получим в соответствующей части уравнения рациональное выражение. Поэтому при решении иррациональных уравнений обычно поступают так.
Выбирают один из радикалов, входящих в уравнение, оставляют его в одной стороне уравнения, а все остальные члены переносят в другую сторону. После этого возводят обе части получившегося уравнения в степень, показатель которой равен показателю уединенного радикала. Повторяя этот процесс, освобождаются от всех радикалов, входящих в уравнение, и получают рациональное уравнение. При этом, если при решении приходилось хоть раз возводить обе части равенства в степень с четным показателем, полученные корни необходимо проверить. Проверка осуществляется путем подстановки корней в исходное уравнение.
Рассмотрим некоторые примеры.
1) Решить уравнение
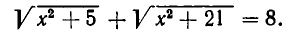
Перенесем 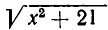 в правую часть уравнения и возведем обе части получившегося равенства в квадрат. Мы получим:
в правую часть уравнения и возведем обе части получившегося равенства в квадрат. Мы получим:
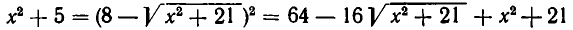
или
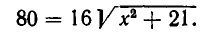
Отсюда находим 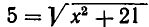 . Снова возведем обе части уравнения в квадрат:
. Снова возведем обе части уравнения в квадрат: 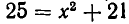 . Корнями этого уравнения являются
. Корнями этого уравнения являются 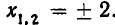
Проверим полученные корни. Подставляя корень 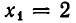 заданное уравнение, получаем
заданное уравнение, получаем 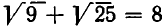 или 8 = 8. Значит, этот корень удовлетворяет заданному уравнению. Корень
или 8 = 8. Значит, этот корень удовлетворяет заданному уравнению. Корень 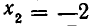 также удовлетворяет этому уравнению.
также удовлетворяет этому уравнению.
2) Решить уравнение
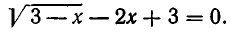
Уединим радикал 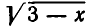 и возведем обе части уравнения в квадрат. Получим
и возведем обе части уравнения в квадрат. Получим
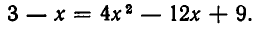
Корнями этого уравнения являются 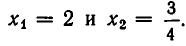 Однако из этих корней заданному уравнению удовлетворяет лишь
Однако из этих корней заданному уравнению удовлетворяет лишь 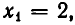
корень же 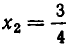 является посторонним. Он удовлетворяет уравнению
является посторонним. Он удовлетворяет уравнению
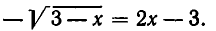
Введение нового неизвестного
Иногда при решении иррациональных уравнений оказывается полезным введение нового неизвестного. Рассмотрим уравнение
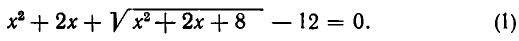
Если попробовать уединить радикал, то после возведения в квадрат получится уравнение четвертой степени. Поэтому мы будем решать это уравнение иначе. Положим 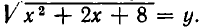 Так как
Так как 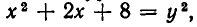 то уравнение (1) можно переписать так:
то уравнение (1) можно переписать так:
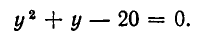
Решая это квадратное уравнение, находим корни 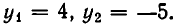 Таким образом, решение уравнения (1) свелось к решению уравнения
Таким образом, решение уравнения (1) свелось к решению уравнения
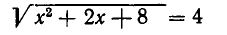
(уравнение 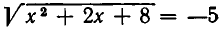 не имеет решений, так как ради кал понимается в смысле арифметического значения, а потому не может равняться отрицательному числу).
не имеет решений, так как ради кал понимается в смысле арифметического значения, а потому не может равняться отрицательному числу).
Из уравнения (2) находим, что 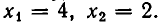 Проверка показывает, что оба корня уравнению (1) удовлетворяют.
Проверка показывает, что оба корня уравнению (1) удовлетворяют.
Особые случаи решения иррациональных уравнений
В разобранных выше примерах после освобождения от иррациональности получались уравнения, имевшие один или несколько корней. В этом случае удается обнаружить посторонние корни путем подстановки их в первоначальное уравнение. В некоторых примерах, однако, после освобождения от иррациональности получается равенство, тождественно выполняющееся на всей числовой оси или на некотором бесконечном числовом множестве. В этом случае проверка корней путем подстановки становится уже невозможной, поскольку найденное множество корней бесконечно. Для таких уравнений в ходе решения выясняют дополнительные условия на возможные корни, имеющие форму неравенств, и отбирают лишь корни, удовлетворяющие этим условиям.
Рассмотрим некоторые примеры.
Пусть дано иррациональное уравнение:
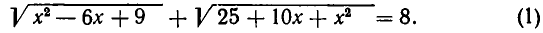
Решим его путем освобождения от иррациональности. Для этого уединим первый радикал и возведем обе части равенства в квадрат. Мы получим, что
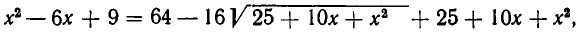
то есть
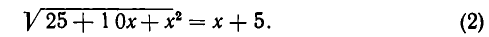
Вновь возводя в квадрат, получаем:
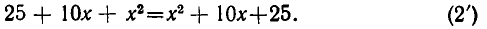
Это равенство тождественно выполняется для всех значений х. Однако, подставляя в уравнение (1), например, х = 4, получаем неверное соотношение: 1 + 9 = 8. Таким образом, первоначальному уравнению удовлетворяют не все значения х. Как мы уже говорили, отобрать корни уравнения (1) методом подстановки невозможно, поскольку множество корней уравнения (2′) бесконечно.
Выясним, откуда появились посторонние корни. Дело в том, что мы рассматриваем здесь лишь арифметические значения радикалов. Из-за этого на х налагаются дополнительные ограничения, имеющие вид неравенств. А при возведении обеих частей уравнения в квадрат эти ограничения были сняты. Таким образом, чтобы найти, при каких же значениях х удовлетворяется первоначальное уравнение, нам надо отобрать числа, удовлетворяющие соответствующим неравенствам.
В первую очередь должны выполняться неравенства 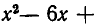
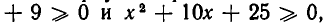 поскольку подкоренные выражения должны быть неотрицательными. Эти неравенства выполняются для всех значений х:
поскольку подкоренные выражения должны быть неотрицательными. Эти неравенства выполняются для всех значений х:
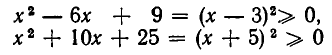
и не дают нужных нам ограничений на х.
Далее, так как 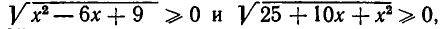 то
то 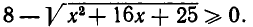
Это неравенство выполняется лишь в области, где 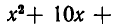
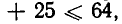 то есть
то есть  Решением этого квадратного неравенства является отрезок—
Решением этого квадратного неравенства является отрезок— 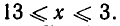 Дальнейшие ограничения на х получаем из равенства (2). Так как левая часть этого равенства заведомо неотрицательна, то должно выполняться условие
Дальнейшие ограничения на х получаем из равенства (2). Так как левая часть этого равенства заведомо неотрицательна, то должно выполняться условие 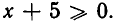
Итак, мы нашли два дополнительных условия на х:

Решением системы неравенств (3) является отрезок  Поскольку, кроме неравенств (3), никаких ограничений на х не накладывается, а уравнение, полученное после освобождения от иррациональностей, выполняется тождественно на всей числовой оси, решением уравнения (1) является отрезок
Поскольку, кроме неравенств (3), никаких ограничений на х не накладывается, а уравнение, полученное после освобождения от иррациональностей, выполняется тождественно на всей числовой оси, решением уравнения (1) является отрезок 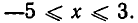 Иными словами, равенство (1) справедливо для любой точки этого отрезка.
Иными словами, равенство (1) справедливо для любой точки этого отрезка.
Уравнение (1) можно решить иначе. Для этого заметим, что
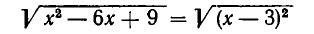
и
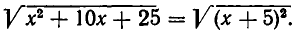
Так как 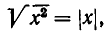 то уравнение (1) переписывается так:
то уравнение (1) переписывается так:
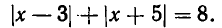
Точки —5 и 3 разбивают числовую ось на участки 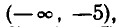
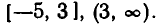 На каждом из этих участков знаки (х—3) и (х + 5) постоянны. Принимая во внимание эти знаки, получаем, что уравнение можно записать так:
На каждом из этих участков знаки (х—3) и (х + 5) постоянны. Принимая во внимание эти знаки, получаем, что уравнение можно записать так:
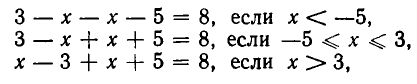
или
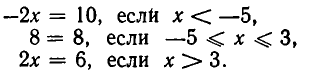
Отсюда снова видно, что равенство (1) тождественно выполняется на отрезке 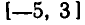 и не выполняется ни в одной точке, лежащей вне этого отрезка.
и не выполняется ни в одной точке, лежащей вне этого отрезка.
Точно так же решается иррациональное уравнение
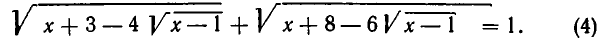
Здесь мы имеем условие на х вида 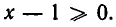 Представим уравнение так:
Представим уравнение так:
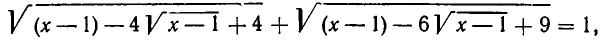
или
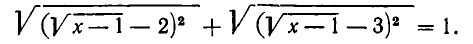
Отсюда получим:
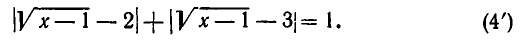
Возможны три случая:
1) 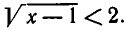 В этой области уравнение
В этой области уравнение 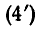 равносильно уравнению
равносильно уравнению
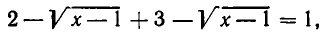
то есть 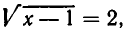 а по условию
а по условию 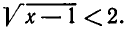
2) 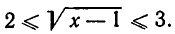 Здесь уравнение (4) равносильно уравнению
Здесь уравнение (4) равносильно уравнению
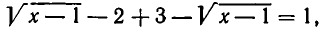
или 1 = 1. Это значит, что любое значение х, удовлетворяющее неравенству 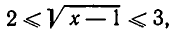 удовлетворяет и уравнению
удовлетворяет и уравнению 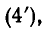 а значит, и исходному уравнению.
а значит, и исходному уравнению.
з ) 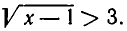 В этом случае уравнение (4′) принимает вид:
В этом случае уравнение (4′) принимает вид:
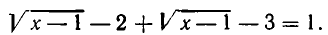
Отсюда 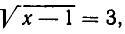 а по условию
а по условию 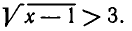
Итак, чтобы найти решение уравнения (4), нам осталось решить иррациональное неравенство
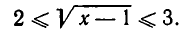
Возводя все члены этого неравенства в квадрат, получаем, что  то есть
то есть 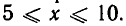 Значит, решением уравнения (4) является отрезок [5, 10].
Значит, решением уравнения (4) является отрезок [5, 10].
Иррациональные неравенства
Рассмотрим теперь иррациональные неравенства, то есть неравенства, содержащие неизвестное под знаком корня. Решение таких неравенств осложняется рядом обстоятельств. Во-первых, для иррациональных неравенств, как и для иррациональных уравнений, рассматриваются лишь арифметические значения корня. Иными словами, если показатель корня — четное число, то подкоренное выражение должно быть неотрицательным, равно как и значение корня. Кроме этого, неравенство  , вообще говоря, неравносильно неравенству
, вообще говоря, неравносильно неравенству 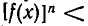
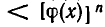 . Ведь только для положительных а и b из а <b заведомо вытекает
. Ведь только для положительных а и b из а <b заведомо вытекает  , а из
, а из  следует а < b.
следует а < b.
Пример:
Решить иррациональное неравенство
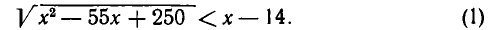
Сначала найдем область его определения. Ясно, что подкоренное выражение должно быть неотрицательно:
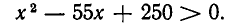
Решая это неравенство, получаем множество А, состоящее из двух лучей 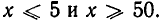 Кроме того, корень принимает лишь неотрицательные значения, а потому и правая часть неравенства (1) должна быть неотрицательной:
Кроме того, корень принимает лишь неотрицательные значения, а потому и правая часть неравенства (1) должна быть неотрицательной: 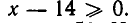 Пересекая множество А с лучом
Пересекая множество А с лучом 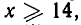 получаем луч
получаем луч  Итак, мы доказали, что неравенство (1) задано в области
Итак, мы доказали, что неравенство (1) задано в области  В этой области обе части неравенства (1) принимают положительные значения и потому неравенство (1) равносильно неравенству
В этой области обе части неравенства (1) принимают положительные значения и потому неравенство (1) равносильно неравенству
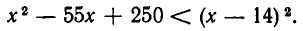
Наша задача свелась к решению системы неравенств:
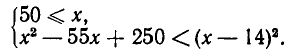
Из второго неравенства получаем x > 2. Значит, решением служит пересечение луча  с лучом x > 2, то есть луч
с лучом x > 2, то есть луч 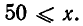
Пример:
Решить иррациональное неравенство
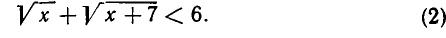
Это неравенство задано в области, определяемой ограничениями 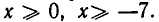 Их можно заменить одним неравенством
Их можно заменить одним неравенством 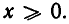 В области
В области 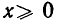 обе части неравенства (2) положительны, и потому оно равносильно неравенству
обе части неравенства (2) положительны, и потому оно равносильно неравенству 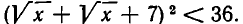 Итак, мы заменили неравенство (2) равносильной ему системой неравенств:
Итак, мы заменили неравенство (2) равносильной ему системой неравенств:
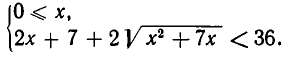
Она решается так же, как в примере 1. В результате получаем систему неравенств, равносильную неравенству (2)
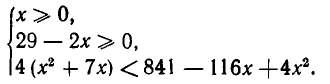
Решая эту систему, находим, что 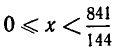 .
.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

